Gibbs Paradox and the Concepts of Information, Symmetry, Similarity and Their Relationship
Definition of Information
- Information () is the amount of the data after data compression.
- The first law of information theory: the total amount of data L (the sum of entropy and information, ) of an isolated system remains unchanged.
- The second law of information theory: Information (I) of an isolated system decreases to a minimum at equilibrium.
- The third law of information theory: For a solid structure of perfect symmetry (e.g., a perfect crystal), the information I is zero and the (information theory) entropy (called by me as static entropy for solid state) S is at the maximum.
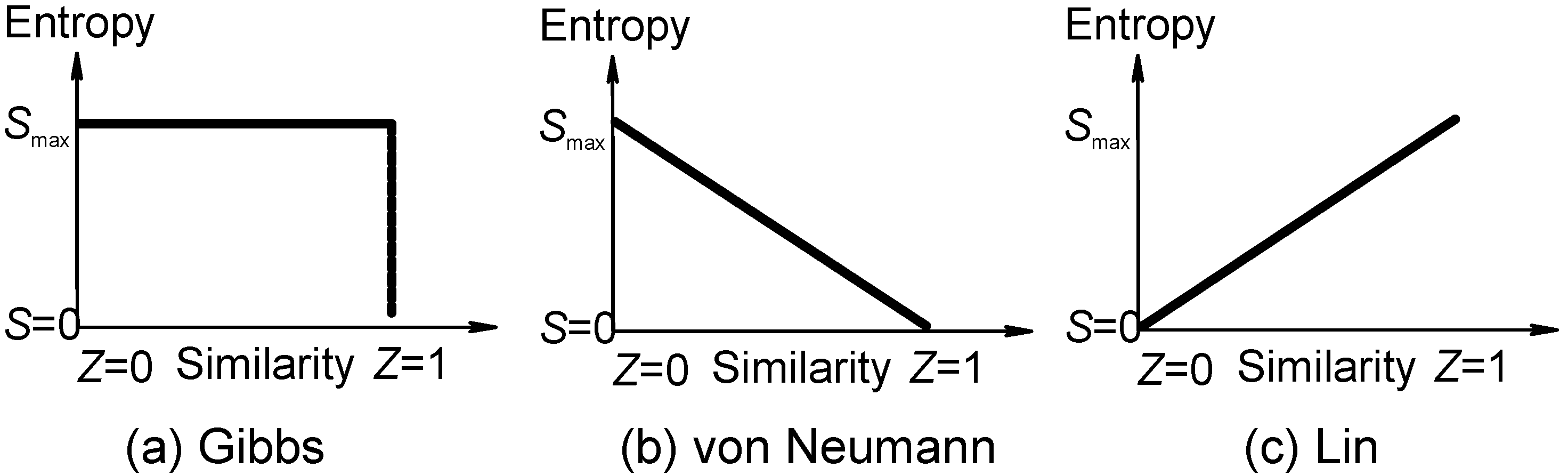
Gibbs Paradox
Acknowledgements
References
- Lin, S.-K. Correlation of entropy with similarity and symmetry. J. Chem. Inf. Comp. Sci. 1996, 36, 367–376. [Google Scholar] [CrossRef]
- Lin, S.-K. Molecular Diversity Assessment: Logarithmic Relations of Information and Species Diversity and Logarithmic Relations of Entropy and Indistinguishability After Rejection of Gibbs Paradox of Entropy of Mixing. Molecules 1996, 1, 57–67. [Google Scholar] [CrossRef]
- Lin, S.-K. Gibbs paradox of entropy of mixing: Experimental facts, its rejection, and the theoretical consequences. J. Theoret. Chem. 1996, 1, 135–150. [Google Scholar] [CrossRef]
- Lin, S.-K. Understanding structural stability and process spontaneity based on the rejection of the Gibbs paradox of entropy of mixing. Theochem–J. Mol. Struc. 1997, 398, 145–153. [Google Scholar] [CrossRef]
- Lin, S.-K. The Nature of the Chemical Process. 1. Symmetry Evolution – Revised Information Theory, Similarity Principle and Ugly Symmetry. Int. J. Mol. Sci. 2001, 2, 10–39. [Google Scholar] [CrossRef]
- Rosen, J. The Symmetry Principle. Entropy 2005, 7, 308–313. [Google Scholar] [CrossRef]
- Jaynes, E.T. The Gibbs paradox. In Maximum Entropy and Bayesian Methods; Smith, C. R., Erickson, G.J., Neudorfer, P. O. Eds., Eds.; Kluwer Academic: Dordrecht, 1992; pp. 1–22. [Google Scholar]
- Urusov, V.S. Gibbs paradox and symmetrization of a multicomponent system. Dokl. Phys. Chem. 2007, 417(Part 2), 337–341. [Google Scholar] [CrossRef]
- Estrada, E.; Avnir, D. Continuous Symmetry Numbers and Entropy. J. Am. Chem. Soc. 2003, 125, 4368–4375. [Google Scholar] [CrossRef] [PubMed]
- Allahverdyan, A.E.; Nieuwenhuizen, T.M. Explanation of the Gibbs paradox within the framework of quantum thermodynamics. Phys. Rev. E 2006, 73. Art. No. 066119. [Google Scholar] [CrossRef]
- von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, 1955; Ch. 5. [Google Scholar]
- Crusats, J.; Veintemillas-Verdaguer, S.; Ribo, J.M. Homochirality as a Consequence of Thermodynamic Equilibrium? Chem. Eur. J. 2006, 12, 7776–7781. [Google Scholar] [CrossRef] [PubMed]
- Mauksch, M.; Tsogoeva, S.B.; Wei, S.; Martynova, I. M. Demonstration of spontaneous chiral symmetry breaking in asymmetric Mannich and Aldol reactions. Chirality 2007, 19, 816–825. [Google Scholar] [CrossRef] [PubMed]
- Bywater, R.P.; Conde-Frieboes, K. Did Life Begin on the Beach? Astrobiology 2005, 5, 568–574. [Google Scholar] [CrossRef] [PubMed]
- Petitjean, M. Chirality and Symmetry Measures: A Transdisciplinary Review. Entropy 2003, 5, 271–312. [Google Scholar] [CrossRef]
- Marijuán, P.C. Information and Life: Towards a Biological Understanding of Informational Phenomena. TripleC 2004, 2, 6–19. [Google Scholar]
- Jakulin, A. Symmetry and information theory. Symmetry Cult. Sci. 2005, 16, 7–26. [Google Scholar]
- Xiao, X.; Shao, S.; Ding, Y.; Chen, X. Digital Coding for Amino Acid Based on Cellular Automata. IEEE International Conference on Systems, Man and Cybernetics 2004, Volume 5, 4593–4598. [Google Scholar]
- Digilov, R.M. Solid-liquid interfacial tension in metals: correlation with the melting point. Physica B: Cond. Matt. 2004, 352, 53–60. [Google Scholar] [CrossRef]
© 2008 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Lin, S.-K. Gibbs Paradox and the Concepts of Information, Symmetry, Similarity and Their Relationship. Entropy 2008, 10, 1-5. https://doi.org/10.3390/entropy-e10010001
Lin S-K. Gibbs Paradox and the Concepts of Information, Symmetry, Similarity and Their Relationship. Entropy. 2008; 10(1):1-5. https://doi.org/10.3390/entropy-e10010001
Chicago/Turabian StyleLin, Shu-Kun. 2008. "Gibbs Paradox and the Concepts of Information, Symmetry, Similarity and Their Relationship" Entropy 10, no. 1: 1-5. https://doi.org/10.3390/entropy-e10010001
APA StyleLin, S.-K. (2008). Gibbs Paradox and the Concepts of Information, Symmetry, Similarity and Their Relationship. Entropy, 10(1), 1-5. https://doi.org/10.3390/entropy-e10010001



