Abstract
The prediction of the entropy generation rate in laminar shear layers is treated as steady, even in the presence of high levels of free stream turbulence. Here we highlight the deficiencies of this approach by quantifying the magnitude of entropy generation rate fluctuations in the laminar boundary layer subjected to free stream turbulence. We find fluctuation levels in excess of 100% in the near wall region, thereby indicating the need to account for the unsteadiness in laminar boundary layers subjected to free stream turbulence.
Introduction
Entropy generation rates in the laminar boundary layer are modelled as steady even in the presence of high levels of free stream turbulence. The most common approach to laminar boundary layer entropy generation prediction is to implement the correlation of Truckenbrodt [1,2] in approximate solutions and to solve the laminar boundary layer equations numerically in computational codes. Neither method considers the effects of free stream turbulence and hence makes the assumption that the volumetric entropy generation rate is steady. A large number of investigations have shown that the presence of free stream turbulence results in higher levels of time averaged wall shear stress and elevated levels of “turbulence intensity” within the laminar boundary layer [3,4,5,6,7]. However, none to date have considered the effect of this unsteadiness upon the instantaneous volumetric entropy generation rate, and hence the time averaged value.
This paper aims to elucidate, through experimentation, the magnitude of such fluctuations in laminar boundary layers subjected to free stream turbulence. Based upon hot wire measurements, the upper and lower bounds of the entropy generation rate per unit volume about the mean are quantified. Such work identifies the real challenges for computational codes to successfully predict entropy generation rates in the laminar boundary layer and indeed to fully understand the inefficiencies of engineering fluid flow systems. From the results it is clear that the instantaneous volumetric entropy generation rates in the laminar region are heavily time dependent and unsteady, and hence attempts at predicting the time averaged quantity accurately is made difficult. This paper gives us new insights into the mechanisms of entropy production within a laminar boundary layer. The importance of such work is evident as the entropy generation rate represents the inefficiencies of fluid systems and any increased understanding of thermodynamic inefficiency by way of the entropy function is key to both accurate predictions and hence more efficient designs in many engineered systems.
Experimental Facility and Data Reduction
The wind tunnel utilized in the present experiments is of the non-return type with continuous airflow supplied by a centrifugal fan. Within the settling chamber honeycomb and wire gauze grids reduce the flow disturbances generated by the fan. A background turbulence intensity level is present within the tunnel and found to be approximately 0.2%. The test section dimensions are 1m in length, with a width and height of 0.3m. Figure 1 shows a schematic of the working section. The test vehicle for the current investigation is a flat plate manufactured from 10 mm thick aluminium, approximately 1 m long by 0.295 m wide. The leading edge is semi-cylindrical and one mm in radius. The flow over the flat plate was qualified as two-dimensional over all measurement planes. The design of the trailing edge flap was shown to anchor the stagnation streamline on the upper test surface, thus allowing for a well defined zero-pressure gradient flow to be established. Changing either the turbulence grid or the position of the plate varies the turbulence intensities at the leading edge. Further details on the design, manufacture and characterization of the turbulence grids and the flat plate can be found in Walsh et al. (2005). Mean and fluctuating velocities were measured using an A.A. Lab Systems AN-1005 constant temperature anemometer operated at an overheat temperature of 250 °C. The measurements were recorded over 10 second periods at a sampling frequency of 10 kHz. Positioning of the hot wire relative to the wall was achieved by forming an electronic circuit between the hot-wire probe and the wall. Mean and fluctuating streamwise velocity components were measured using a Dantec 55P11 single normal probe. The hot-wire probe holder was connected to a Digiplan Pk 3 stepper motor drive which traversed in 10 µm increments and was controlled by a PC to obtain full boundary layer traverses.
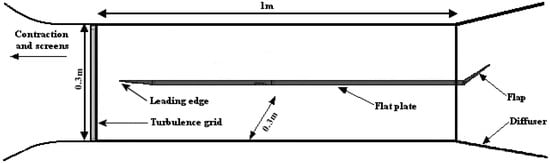
Figure 1.
Diagram of experimental set-up (not to scale).
The dissipation function [8] can be used to determine the volumetric entropy generation rate for two-dimensional, laminar, incompressible adiabatic flows:
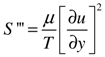 In the near wall region, where the velocity profile is linear, the instantaneous entropy generation rate per unit volume can easily be calculated from a single point hot wire measurement using:
In the near wall region, where the velocity profile is linear, the instantaneous entropy generation rate per unit volume can easily be calculated from a single point hot wire measurement using:
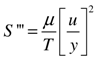 Outside of the linear region it is difficult to estimate the entropy per unit volume from a single point measurement as the velocity gradient ceases to be linear. To determine the upper and lower bounds of the entropy generation rate per unit volume about the mean the minimum and maximum velocity recorded during each of the ten second time traces was extracted for each measurement station. Based upon these measurements we can construct velocity profiles representing the upper and lower bounds on the deviation from the mean. From the resultant velocity gradients we can implement equation 1 to calculate the upper and lower bounds of the generation rates per unit volume at each location across the boundary layer thickness. This analysis was done for two full boundary layer traverses at inlet turbulence levels of 1.3% and 6% with Reθ, Reynolds number based upon momentum thickness, values of 391 and 83 respectively. The corresponding free stream velocities were 17 and 3.5 meters per second respectively. The flow was laminar, as confirmed by the first turbulent spots being detected downstream of the measurement location using a single hot film sensor attached to the wall.
Outside of the linear region it is difficult to estimate the entropy per unit volume from a single point measurement as the velocity gradient ceases to be linear. To determine the upper and lower bounds of the entropy generation rate per unit volume about the mean the minimum and maximum velocity recorded during each of the ten second time traces was extracted for each measurement station. Based upon these measurements we can construct velocity profiles representing the upper and lower bounds on the deviation from the mean. From the resultant velocity gradients we can implement equation 1 to calculate the upper and lower bounds of the generation rates per unit volume at each location across the boundary layer thickness. This analysis was done for two full boundary layer traverses at inlet turbulence levels of 1.3% and 6% with Reθ, Reynolds number based upon momentum thickness, values of 391 and 83 respectively. The corresponding free stream velocities were 17 and 3.5 meters per second respectively. The flow was laminar, as confirmed by the first turbulent spots being detected downstream of the measurement location using a single hot film sensor attached to the wall.
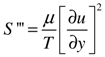
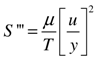
Results and Discussion
Figure 2 shows a plot of the measured instantaneous velocity in the near wall region with a free stream turbulence level of 6%. The velocity trace, although in the laminar region, is seen to contain large levels of fluctuations. Also shown on this figure is the resultant volumetric entropy generation rate obtained through equation 2, which is normalised upon the maximum volumetric entropy generation rate within the one second time frame. Clearly the result is variations in the volumetric entropy generation rate with time, which cannot be accounted for in steady computational codes. Indeed the extent of the fluctuations is surprising. This is the first time such unsteadiness in the dissipation of energy by way of the entropy function has been shown in a laminar boundary layer and demonstrates the potential difficulty of predicting laminar boundary layers subjected to free stream turbulence in a time dependent sense. Failure to predict this entropy generation rate will lead to inaccurate predictions in irreversibilities in flow systems.
Taking the instantaneous maximum and minimum velocity measurement recorded in each time trace, the upper and lower bounds on the velocity profile are plotted in Figure 3(a) and Figure 4(b) for the free stream turbulence levels of 1.3% and 6% respectively. Also plotted in these figures are the resultant upper and lower bounds of the entropy generation rates per unit volume. The Pohlhausen velocity profile is included in these figures and shows good agreement with the low turbulence level case of 1.3%, while the 6% turbulence level case shows significant deviation in the near wall region as previously noted by a number of authors [3-30] for similar levels of free stream turbulence. The normalised entropy generation rate per unit volume was calculated by curved fitting using a third order polynomial and setting the velocity to zero at the wall. The anticipated trend becomes clear where the entropy generation rate per unit volume obtained from the instantaneous maximum velocities exceeds that of the mean. The peak level of unsteadiness at any distance from the wall may be found from calculating the difference between the instantaneous maximum and minimum values. The unsteadiness in both the velocity and entropy generation rates per unit volume is seen to be significantly greater for the higher turbulence level case of Figure 4.
To determine the upper and lower bounds on the entropy generation rate per unit area with time the entropy generation rate per unit volume of Figure 3(b) and Figure 4(b) may be integrated over the boundary layer thickness. This results in a calculated variation in the entropy generation rate per unit volume of 25% for the 1.3% free stream turbulence intensity case and up to 60% for the high turbulence level case above the mean entropy generation rate per unit area calculated from the mean velocity profile. It is however, unlikely that such variations of the entropy generation rate per unit area will be seen with time as it would require the instantaneous maximum and minimum velocity profiles to exist across the entire boundary layer at one instant in time. It is hypothesised that while a significant proportion of the boundary layer may consist of region of high velocity above the mean, an instantaneous profile would consist of regions both above and below the mean velocity profile. Figure 3 and Figure 4 simply represent the upper and lower bounds in the unsteadiness of the entropy generation rates within a laminar boundary layer subjected to free stream turbulence.
Hence, free stream turbulence causes increased levels of unsteadiness and higher shear rates in a laminar boundary layer, which in turn generates higher levels of both instantaneous and time averaged entropy generation rates per unit volume. This insight into entropy generation rates within a laminar boundary layer is important, because to understanding the origins of thermodynamics losses in fluid flows, such fluctuations must be understood and integrated into predictive computational codes.
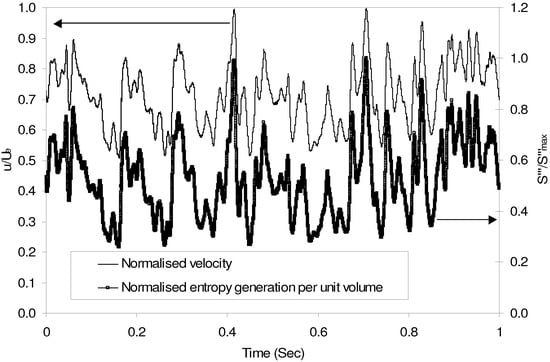
Figure 2.
Illustration of the potential variation in the velocity and entropy generation rate per unit volume with time in the near wall region for a laminar boundary layer subjected to 6% free stream turbulence.
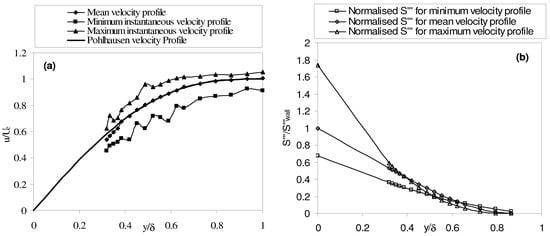
Figure 3.
(a) Maximum variation in velocity profiles and (b) entropy generation rates per unit volume across a laminar boundary layer subjected to free stream turbulence of 1.3%; Reθ = 391.
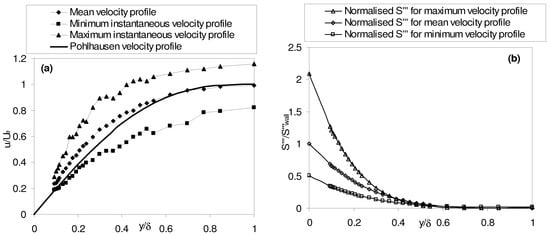
Figure 4.
(a) Maximum variation in velocity profiles and (b) entropy generation rates per unit volume across a laminar boundary layer subjected to free stream turbulence of 6%; Reθ = 83.
Conclusion
We have demonstrated the unsteadiness of the entropy generation rate per unit volume in the near wall region for laminar boundary layers subjected to free stream turbulence. Furthermore it has been shown that a significant unsteadiness in the entropy generation rate is found across the majority of the boundary layer profile. This region is usually treated as steady in existing predictive codes. This is the first time that such fluctuations have been quantified, and demonstrates the great challenges to computational codes to predict this quantity accurately even in a times averaged sense. The importance of this work stems from the need to increase basic understanding of the effect of free stream turbulence on the thermodynamic irreversibility in laminar boundary layer, which is a common problem in many real engineering applications such as turbine aerodynamic design.
Nomenclature
| Reθ=ρUeθ/μ | Reynolds number based on momentum thickness | |
| S´´´ | Entropy generation rate per unit volume | Wm-3K |
| T | Absolute temperature | K |
| u | Instanteous streamwise velocity | m s-1 |
| Ue | Boundary layer edge velocity (0.99 U∞) | m s-1 |
| x | Stream-wise coordinate, distance from leading edge | m |
| y | Cross-stream coordinate, distance from wall | m |
Greek
| δ | Boundary layer thickness | m |
| μ | Dynamic viscosity | N s m-2 |
| θ | Momentum thickness | m |
| ρ | Density | Kg m-3 |
Subscripts
| ()max | Maximum value |
| ()wall | Conditions at the wall for mean profiles |
References
- Denton, J.D. Loss Mechanisms in Turbomachines. J. of Turbomach. 1993, vol. 115, 621–656. [Google Scholar] [CrossRef]
- Truckenbrodt, E. A method of quadrature for the calculation of laminar and turbulent boundary layers in Plane and Rotational Symmetric Flow. Ingenieur-Archiv 1952, Vol. 20. translated as NACA TM 1379. [Google Scholar]
- Roach, P.E.; Brierley, D.H. The influence of a turbulent free stream on zero pressure gradient transitional boundary layer development. Part 1: Test cases T3A and T3B. In Numerical Simulation of Unsteady Flows and Transition to Turbulence; Cambridge University Press, 1990. [Google Scholar]
- Sharma, O.P.; Wells, R.A.; Schlinker, R.H.; Bailey, D.A. Boundary layer development on turbine airfoil suction surfaces. J. Eng. Power 1982, 104, 699–706. [Google Scholar]
- Fransson, J.H.M.; Matsubara, M.; Alfredsson, P.H. Transition induced by free stream turbulence. J. Fluid Mech. 2005, 527, 1–25. [Google Scholar] [CrossRef]
- Matsubara, M.; Alfredsson, P.H. Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 2001, 430, 149–168. [Google Scholar] [CrossRef]
- Mayle, R.E.; Schulz, A. The path to predicting bypass transition. J. Turbomach 1997, 119, 405–411. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 7th ed.Mc-Graw Hill: New York, 1979. [Google Scholar]
2006 by MDPI. (http://www.mdpi.org) Reproduction for noncommercial purposes permitted.