Abstract
In the present work the approach - density matrix deformation - earlier developed by the author to study a quantum theory of the Early Universe (Planck’s scales) is applied to study a quantum theory of black holes. On this basis the author investigates the information paradox problem, entropy of the black hole remainders after evaporation, and consistency with the holographic principle. The possibility for application of the proposed approach to the calculation of quantum entropy of a black hole is considered.
MSC 2000 codes:
1 Introduction. Deformed Density Matrix in QMFL
Quantum entropy of a black hole is commonly considered as a formula for the communal entropy representing a series, where the major term is coincident with Bekenstein-Hawking entropy in a semiclassical approximation, whereas other terms are its quantum corrections. This paper presents the development of a new approach to a quantum theory close to the singularity (Early Universe), whose side product is the application to a quantum theory of black holes the calculations of entropy including. The principal method of this paper is deformation of a quantum-mechanical density matrix in the Early Universe. And a quantum mechanics of the Early Universe is considered as Quantum Mechanics with Fundamental Length (QMFL), the associated deformed density matrix being referred to as a density pro-matrix. The deformation is understood as an extension of a particular theory by inclusion of one or several additional parameters in such a way that the initial theory appears in the limiting transition. In Section 1 the formalism of the density pro-matrix in QMFL is described in detail. In Section 2 the entropy density matrix on the unit minimum area is introduced for different observers. Then it is used in a detailed study of the information problem of the Universe, and in particular, for the information paradox problem. This problem is reduced to comparison of the initial and final densities of entropy for one and the same observer. It’s shown that according to the natural standpoint, there is no information loss at the closed Universe. Based on the proposed approach, in Section 3 the quantity of the entropy for Planck’s remainders of black holes is analyzed in case when the latter are incompletely evaporated, in an effort to give an answer for the recent J.Bekenstein’s question. Besides, consideration is given to the coordination between the obtained results and the holographic principle. The last Section is devoted to the possibility for application of the proposed approach to calculation of the black hole entropy.
Besides, in Section 1 the principal features of QMFL construction using the deformed density matrix are briefly outlined [1,2,3,4,5,6,7]. It is suggested that in quantum gravitation, similar to a quantum theory of the Early Universe, the introduction of the fundamental length lmin is a must, as follows from the generalized uncertainty relations [8,9,10,11,12] and not only [13]. Then, as noted earlier(e.g., see [2]), the fundamental length may be included into quantum mechanics by the use of the density matrix deformation. Recall the main features of the associated construction. We begin with the Generalized Uncertainty Relations (GUR) [8]:
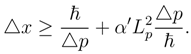 Here Lp is the Planck’s length:
Here Lp is the Planck’s length: 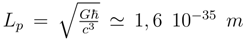 and α′ > 0 is a constant. In [9] it was shown that this constant may be chosen equal to 1. However, here we will use α′ as an arbitrary constant without giving it any definite value. Equation (1) is identified as the Generalized Uncertainty Relations in Quantum Mechanics.
and α′ > 0 is a constant. In [9] it was shown that this constant may be chosen equal to 1. However, here we will use α′ as an arbitrary constant without giving it any definite value. Equation (1) is identified as the Generalized Uncertainty Relations in Quantum Mechanics.
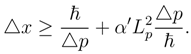
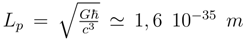 and α′ > 0 is a constant. In [9] it was shown that this constant may be chosen equal to 1. However, here we will use α′ as an arbitrary constant without giving it any definite value. Equation (1) is identified as the Generalized Uncertainty Relations in Quantum Mechanics.
and α′ > 0 is a constant. In [9] it was shown that this constant may be chosen equal to 1. However, here we will use α′ as an arbitrary constant without giving it any definite value. Equation (1) is identified as the Generalized Uncertainty Relations in Quantum Mechanics.The inequality (1) is quadratic in △p:
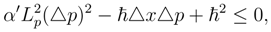 from whence the fundamental length is
from whence the fundamental length is
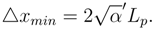 Since in what follows we proceed only from the existence of fundamental length, it should be noted that this fact was established apart from GUR as well. For instance, from an ideal experiment associated with Gravitational Field and Quantum Mechanics a lower bound on minimal length was obtained in [14], [15] and improved in [16] without using GUR to an estimate of the form ∼ Lp. As reviewed previously in [13], the fundamental length appears quite naturally at Planck scale, being related to the quantum-gravitational effects.Let us consider equation (3) in some detail. Squaring both its sides, we obtain
Since in what follows we proceed only from the existence of fundamental length, it should be noted that this fact was established apart from GUR as well. For instance, from an ideal experiment associated with Gravitational Field and Quantum Mechanics a lower bound on minimal length was obtained in [14], [15] and improved in [16] without using GUR to an estimate of the form ∼ Lp. As reviewed previously in [13], the fundamental length appears quite naturally at Planck scale, being related to the quantum-gravitational effects.Let us consider equation (3) in some detail. Squaring both its sides, we obtain
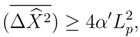 Or in terms of density matrix
Or in terms of density matrix
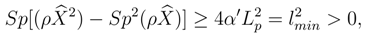 Where
Where 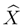 is the coordinate operator. Expression (5) gives the measuring rule used in well-known quantum mechanics QM. As distinct from QM, however, in the are considered here the right-hand side of (5) can not be brought arbitrary close to zero as it is limited by
is the coordinate operator. Expression (5) gives the measuring rule used in well-known quantum mechanics QM. As distinct from QM, however, in the are considered here the right-hand side of (5) can not be brought arbitrary close to zero as it is limited by 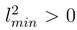 , where because of GUR lmin ∼ Lp.
, where because of GUR lmin ∼ Lp.
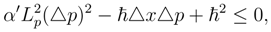
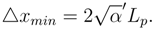
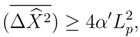
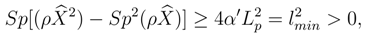
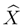 is the coordinate operator. Expression (5) gives the measuring rule used in well-known quantum mechanics QM. As distinct from QM, however, in the are considered here the right-hand side of (5) can not be brought arbitrary close to zero as it is limited by
is the coordinate operator. Expression (5) gives the measuring rule used in well-known quantum mechanics QM. As distinct from QM, however, in the are considered here the right-hand side of (5) can not be brought arbitrary close to zero as it is limited by 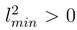 , where because of GUR lmin ∼ Lp.
, where because of GUR lmin ∼ Lp.As demonstrated in [1],[2],[5], [7],QMFL may be considered as deformation of QM, the density matrix being the principal object of this deformation and the deformation parameter being dependent on the measuring scale. This means that in QMFL ρ = ρ(x), where x is the scale, and for 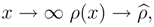 where
where 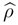 is the density matrix in QM. Since from [2],[5], [7] it follows that at Planck’s scale Sp[ρ] < 1, then for such scales ρ = ρ(x), where x is the scale, is not a density matrix as it is generally defined in QM. On Planck’s scale ρ(x) is referred to as ”density pro-matrix”. As follows from the above, the density matrix
is the density matrix in QM. Since from [2],[5], [7] it follows that at Planck’s scale Sp[ρ] < 1, then for such scales ρ = ρ(x), where x is the scale, is not a density matrix as it is generally defined in QM. On Planck’s scale ρ(x) is referred to as ”density pro-matrix”. As follows from the above, the density matrix 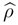 appears in the limit [1],[2]:
appears in the limit [1],[2]:
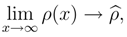 when QMFL turns to QM. Thus, on Planck’s scale the density matrix is inadequate to obtain all information about the mean values of operators. A ”deformed” density matrix (or pro-matrix) ρ(x) with Sp[ρ] < 1 has to be introduced because a missing part of information 1−Sp[ρ] is encoded in the quantity
when QMFL turns to QM. Thus, on Planck’s scale the density matrix is inadequate to obtain all information about the mean values of operators. A ”deformed” density matrix (or pro-matrix) ρ(x) with Sp[ρ] < 1 has to be introduced because a missing part of information 1−Sp[ρ] is encoded in the quantity 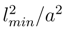 , whose specific weight decreases as the scale a expressed in units of lmin is going up. In the notation system used for
, whose specific weight decreases as the scale a expressed in units of lmin is going up. In the notation system used for 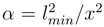 , where x is the scale for the fundamental deformation parameter.
, where x is the scale for the fundamental deformation parameter.
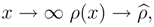 where
where 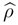 is the density matrix in QM. Since from [2],[5], [7] it follows that at Planck’s scale Sp[ρ] < 1, then for such scales ρ = ρ(x), where x is the scale, is not a density matrix as it is generally defined in QM. On Planck’s scale ρ(x) is referred to as ”density pro-matrix”. As follows from the above, the density matrix
is the density matrix in QM. Since from [2],[5], [7] it follows that at Planck’s scale Sp[ρ] < 1, then for such scales ρ = ρ(x), where x is the scale, is not a density matrix as it is generally defined in QM. On Planck’s scale ρ(x) is referred to as ”density pro-matrix”. As follows from the above, the density matrix 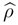 appears in the limit [1],[2]:
appears in the limit [1],[2]:
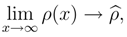
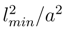 , whose specific weight decreases as the scale a expressed in units of lmin is going up. In the notation system used for
, whose specific weight decreases as the scale a expressed in units of lmin is going up. In the notation system used for 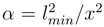 , where x is the scale for the fundamental deformation parameter.
, where x is the scale for the fundamental deformation parameter.Definition 1. (Quantum Mechanics with Fundamental Length)
Any system in QMFL is described by a density pro-matrix of the form 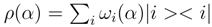 , where
, where
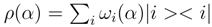 , where
, where
- 0 < α ≤ 1/4.
- The vectors |i > form a full orthonormal system.
- ωi(α) ≥ 0, and for all i the finite limit
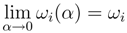 exists.
exists. - Sp[ρ(α)] = ∑i ωi(α) < 1, ∑i ωi = 1.
- For every operator B and any α there is a mean operator B depending on α:
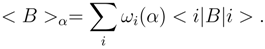
Finally, in order that our definition 1 be in agreement with the result of ([1], Section 2), the following condition must be fulfilled:
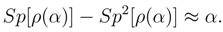 Hence we can find the value for Sp[ρ(α)] satisfying the condition of definition 1:
Hence we can find the value for Sp[ρ(α)] satisfying the condition of definition 1:
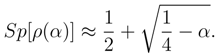 As regards Definition 1., some explanatory remarks are needed. Of course, any theory may be associated with a number of deformations. In case under consideration the deformation is ”minimal” as only the probabilities are deformed rather than the state vectors. This is essential for the external form of the density pro-matrix, and also for points 2 and 3 in Definition 1.. This suggests point 5 of the Definition: deformation of the average values of the operators. And point 4 follows directly from point 3,(6) and remark before this limiting transition. Finally, limitation on the parameter
As regards Definition 1., some explanatory remarks are needed. Of course, any theory may be associated with a number of deformations. In case under consideration the deformation is ”minimal” as only the probabilities are deformed rather than the state vectors. This is essential for the external form of the density pro-matrix, and also for points 2 and 3 in Definition 1.. This suggests point 5 of the Definition: deformation of the average values of the operators. And point 4 follows directly from point 3,(6) and remark before this limiting transition. Finally, limitation on the parameter 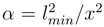 is inferred from the relation
is inferred from the relation
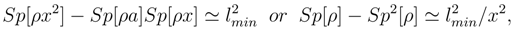 that follows from (5) with the use of the R-procedure [1],[2].
that follows from (5) with the use of the R-procedure [1],[2].
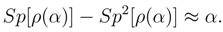
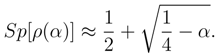
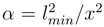 is inferred from the relation
is inferred from the relation
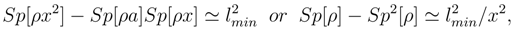
According to point 5, < 1 >α = Sp[ρ(α)]. Therefore for any scalar quantity f we have < f >α = f Sp[ρ(α)]. In particular, the mean value < [xµ, pν ] >α is equal to
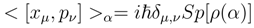 We denote the limit
We denote the limit 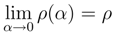 as the density matrix. Evidently, in the limit α → 0 we return to QM.
as the density matrix. Evidently, in the limit α → 0 we return to QM.
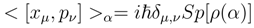
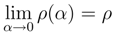 as the density matrix. Evidently, in the limit α → 0 we return to QM.
as the density matrix. Evidently, in the limit α → 0 we return to QM.It should be noted that:
- The above limit covers both Quantum and Classical Mechanics. Indeed, since
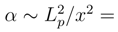 Għ/c3x2, we obtain:
Għ/c3x2, we obtain:
- (ħ ≠ 0, x → ∞) ⇒ (α → 0) for QM;
- (ħ → 0, x → ∞) ⇒ (α → 0) for Classical Mechanics;
- As a matter of fact, the deformation parameter α should assume the value 0 < α ≤ 1. As seen from (8), however, Sp[ρ(α)] is well defined only for 0 < α ≤ 1/4. That is if x = ilmin and i ≥ 2, then there is no any problem. At the point of x = lmin there is a singularity related to the complex values following from Sp[ρ(α)] , i.e. to the impossibility of obtaining a diagonalized density pro-matrix at this point over the field of real numbers. For this reason definition 1 has no sense at the point x = lmin.
- We consider possible solutions for (7). For instance, one of the solutions of (7), at least to the first order in α, iswhere all αi > 0 are independent of α and their sum is equal to 1. In this way Sp[ρ∗(α)] = exp(−α). We can easily verify that
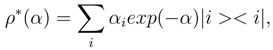 Note that in the momentum representation
Note that in the momentum representation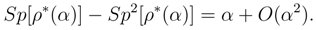
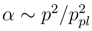 , where ppl is the Planck momentum. When present in the matrix elements, exp(−α) can damp the contribution of great momenta in a perturbation theory.
, where ppl is the Planck momentum. When present in the matrix elements, exp(−α) can damp the contribution of great momenta in a perturbation theory.
2 Entropy Density Matrix and Information Loss Problem
In [2] the authors were too careful, when introducing for density pro-matrix ρ(α) the value Sα generalizing the ordinary statistical entropy:
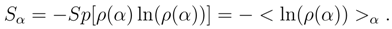 In [1],[2] it was noted that Sα means of the entropy density on a unit minimum area depending on the scale. In fact a more general concept accepts the form of the entropy density matrix [4],[5],[7]:
In [1],[2] it was noted that Sα means of the entropy density on a unit minimum area depending on the scale. In fact a more general concept accepts the form of the entropy density matrix [4],[5],[7]:
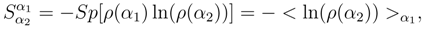 where 0 < α1, α2 ≤ 1/4.
where 0 < α1, α2 ≤ 1/4.
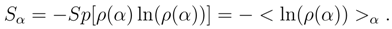
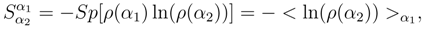
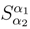 has a clear physical meaning: the entropy density is computed on the scale associated with the deformation parameter α2 by the observer who is at a scale corresponding to the deformation parameter α1. Note that with this approach the diagonal element Sα = ,of the described matrix
has a clear physical meaning: the entropy density is computed on the scale associated with the deformation parameter α2 by the observer who is at a scale corresponding to the deformation parameter α1. Note that with this approach the diagonal element Sα = ,of the described matrix 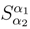 is the density of entropy measured by the observer who is at the same scale as the measured object associated with the deformation parameter α. In [2] Section 6 such a construction was used implicitly in derivation of the semiclassical Bekenstein-Hawking formula for the Black Hole entropy:
is the density of entropy measured by the observer who is at the same scale as the measured object associated with the deformation parameter α. In [2] Section 6 such a construction was used implicitly in derivation of the semiclassical Bekenstein-Hawking formula for the Black Hole entropy:
- a)
- For the initial (approximately pure) state
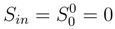
- b)
- Using the exponential ansatz(9),we obtain:
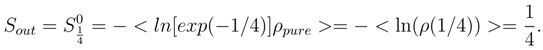
So increase in the entropy density for an external observer at the large-scale limit is 1/4. Note that increase of the entropy density (information loss) for the observer that is crossing the horizon of the black hole’s events and moving with the information flow to singularity will be smaller:
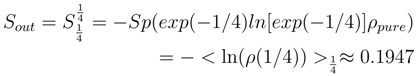 It is clear that this fact may be interpreted as follows: for the observer moving together with information its loss can occur only at the transition to smaller scales, i.e. to greater deformation parameter α.
It is clear that this fact may be interpreted as follows: for the observer moving together with information its loss can occur only at the transition to smaller scales, i.e. to greater deformation parameter α.
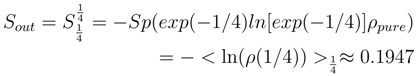
Now we consider the general Information Problem. Note that with the classical Quantum Mechanics (QM) the entropy density matrix 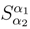 (10) is reduced only to one element
(10) is reduced only to one element 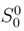 and so we can not test anything. Moreover, in previous works relating the quantum mechanics of black holes and information paradox [19],[35,36] the initial and final states when a particle hits the hole are treated proceeding from different theories(QM and QMFL respectively):
and so we can not test anything. Moreover, in previous works relating the quantum mechanics of black holes and information paradox [19],[35,36] the initial and final states when a particle hits the hole are treated proceeding from different theories(QM and QMFL respectively):
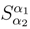 (10) is reduced only to one element
(10) is reduced only to one element 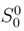 and so we can not test anything. Moreover, in previous works relating the quantum mechanics of black holes and information paradox [19],[35,36] the initial and final states when a particle hits the hole are treated proceeding from different theories(QM and QMFL respectively):
and so we can not test anything. Moreover, in previous works relating the quantum mechanics of black holes and information paradox [19],[35,36] the initial and final states when a particle hits the hole are treated proceeding from different theories(QM and QMFL respectively):
(Large-scale limit, QM, density matrix) → (Black Hole, singularity, QMFL, density pro-matrix),
Of course in this case any conservation of information is impossible as these theories are based on different concepts of entropy. Simply saying, it is incorrect to compare the entropy interpretations of two different theories (QM and QMFL, where this notion is originally differently understood. So the chain above must be symmetrized by accompaniment of the arrow on the left ,so in an ordinary situation we have a chain:
(Early Universe, origin singularity, QMFL, density pro-matrix) → (Large-scale limit, QM, density matrix)→ (Black Hole, singularity, QMFL, density pro-matrix),
So it’s more correct to compare entropy close to the initial and final (Black hole) singularities. In other words, it is necessary to take into account not only the state, where information disappears, but also that whence it appears. The question arises, whether the information is lost in this case for every separate observer. For the event under consideration this question sounds as follows: are the entropy densities S(in) and S(out) equal for every separate observer? It will be shown that in all conceivable cases they are equal.
- 1)
- For the observer in the large-scale limit (producing measurements in the semiclassical approximation) α1 = 0S(in) =
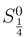 (Origin singularity)S(out) =
(Origin singularity)S(out) =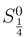 (Singularity in Black Hole)So S(in) = S(out) =
(Singularity in Black Hole)So S(in) = S(out) =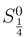 . Consequently, the initial and final densities of entropy are equal and there is no any information loss.
. Consequently, the initial and final densities of entropy are equal and there is no any information loss. - 2)
- For the observer moving together with the information flow in the general situation we have the chain:where S(large − scale) =
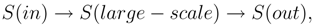
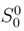 = S. Here S is the ordinary entropy at quantum mechanics(QM), but S(in) = S(out) =
= S. Here S is the ordinary entropy at quantum mechanics(QM), but S(in) = S(out) = 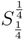 ,value considered in QMFL. So in this case the initial and final densities of entropy are equal without any loss of information.
,value considered in QMFL. So in this case the initial and final densities of entropy are equal without any loss of information. - 3)
- This case is a special case of 2), when we do not come out of the early Universe considering the processes with the participation of black mini-holes only. In this case the originally specified chain becomes shorter by one Section:and member S(large − scale) =(Early Universe, origin singularity, QMFL, density pro-matrix)→ (Black Mini-Hole, singularity, QMFL, density pro-matrix),
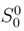 = S disappears at the corresponding chain of the entropy density associated with the large-scale consideration:
It is, however, obvious that in case S(in) = S(out) =
= S disappears at the corresponding chain of the entropy density associated with the large-scale consideration:
It is, however, obvious that in case S(in) = S(out) =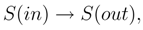
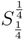 the density of entropy is preserved. Actually this event was mentioned in [2],where from the basic principles it has been found that black mini-holes do not radiate, just in agreement with the results of other authors [21,22,23,24]. As a result, it’s possible to write briefly
where α - any value in the interval 0 < α ≤ 1/4.
the density of entropy is preserved. Actually this event was mentioned in [2],where from the basic principles it has been found that black mini-holes do not radiate, just in agreement with the results of other authors [21,22,23,24]. As a result, it’s possible to write briefly
where α - any value in the interval 0 < α ≤ 1/4.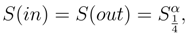
It should be noted that in terms of deformation the Liouville’s equation (Section 4 [2]) takes the form:
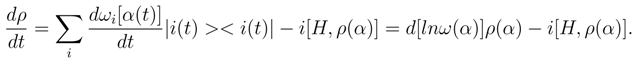 The main result of this Section is a necessity to account for the member d[lnω(α)]ρ(α),deforming the right-side expression of α ≈ 1/4.
The main result of this Section is a necessity to account for the member d[lnω(α)]ρ(α),deforming the right-side expression of α ≈ 1/4.
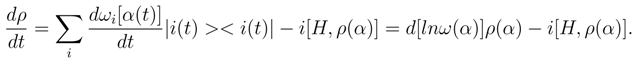
3 Entropy Bounds, Entropy Density and Holographic Principle
In the last few years Quantum Mechanics of black holes has been studied under the assumption that GUR are valid [21],[22],[24]. As a result of this approach, it is indicated that the evaporation process of a black hole gives a stable remnant with a mass on the order of the Planck’s Mp. However, J.Bekenstein in [25] has credited such an approach as problematic, since then the objects with dimensions on the order of the Planck length ∼ 10−33cm should have very great entropy thus making problems in regard to the entropy bounds of the black hole remnants [26].
In connection with this remark of J.Bekenstein [25] the following points should be emphasized:
- An approach proposed in [34],[4] and in the present paper gives a deeper insight into the cause of high entropy for Planck’s black hole remnants, namely: high entropy density that by this approach at Planck scales takes place for every fixed observer including that on a customary scale, i.e. on α ≈ 0. In [4] using the exponential ansatz (Section 3) it has been demonstrated how this density can increase in the vicinity of the singularities withup to
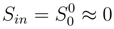 when the initial state measured by the observer is pure.
when the initial state measured by the observer is pure.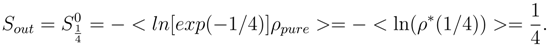 As demonstrated in [34],[4], increase in the entropy density will be realized also for the observer moving together with the information flow:
As demonstrated in [34],[4], increase in the entropy density will be realized also for the observer moving together with the information flow: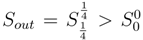 , though to a lesser extent than in the first case. Obviously, provided the existing solutions for (7) are different from the exponential ansatz, the entropy density for them
, though to a lesser extent than in the first case. Obviously, provided the existing solutions for (7) are different from the exponential ansatz, the entropy density for them 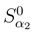 will be increasing as compared to
will be increasing as compared to 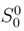 with a tendency of α2 to 1/4.
with a tendency of α2 to 1/4. - In works of J.Bekenstein, [26] in particular, a ”universal entropy bound” has been used [27]:where M is the total gravitational mass of the matter and R is the radius of the smallest sphere that barely fits around a system. This bound is, however, valid for a weakly gravitating matter system only. In case of black hole remnants under study it is impossible to assume that on Planck scales we are concerned with a weakly gravitating matter system, as in this case the transition to the Planck’s energies is realized where quantum-gravitational effects are appreciable, and within the proposed paradigm parameter α ≈ 0 is changed by the parameter α > 0 or equally QM is changed by QMFL.
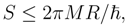
- This necessitates mentioning of the recent findings of R.Bousso [28],[29], who has derived the Bekenstein’s ”universal entropy bound” for a weakly gravitating matter system, and among other things in flat space, from the covariant entropy bound [30] associated with the holographic principle of Hooft-Susskind [31],[32],[33].
Also it should be noted that the approach proposed in [4],[2] and in the present paper is consistent with the holographic principle [31,32,33]. Specifically, with the use of this approach one is enabled to obtain the entropy bounds for nonblack hole objects of L.Susskind [32]. Of course, in ([2], Section 6) and ([4], Section 4) it has been demonstrated, how a well-known semiclassical Bekenstein- Hawking formula for black hole entropy may be obtained using the proposed paradigm. Then we can resort to reasoning from [32]: ”using gedanken experiment, take a neutral non-rotating spherical object containing entropy S which fits entirely inside a spherical surface of the area A, and it to collapse to black hole”. Whence
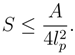 Note also that the entropy density matrix
Note also that the entropy density matrix 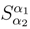 by its definition [34],[4] falls into 2D objects, being associated with
by its definition [34],[4] falls into 2D objects, being associated with 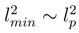 [2] and hence implicitly pointing to the holographic principle.
[2] and hence implicitly pointing to the holographic principle.
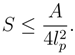
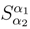 by its definition [34],[4] falls into 2D objects, being associated with
by its definition [34],[4] falls into 2D objects, being associated with 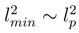 [2] and hence implicitly pointing to the holographic principle.
[2] and hence implicitly pointing to the holographic principle.Qualitative analysis performed in this work reveals that the Information Loss Problem in black holes with the canonical problem statement [19],[35], [36] suggests in principle positive solution within the scope of the proposed method - high-energy density matrix deformation. Actually, this problem necessitates further (now quantitative) analysis. Besides, it is interesting to find direct relations between the described methods and the holographic principle. Of particular importance seems a conjecture following from [29]: is it possible to derive GUR for high energies (of strong gravitational field) with the use of the covariant entropy bound [30] in much the same manner as R.Bousso [29] has developed the Heisenberg uncertainty principle for the flat space?
4 Quantum corrections to black hole entropy. Heuristic approach
This paper presents certain results pertinent to the application of the above methods in a Quantum Theory of Black Holes. Further investigations are still required in this respect, specifically for the complete derivation of a semiclassical Bekenstein-Hawking formula for the Black Hole entropy, since in Section 2 the treatment has been based on the demonstrated result: a respective number of the degrees of freedom is equal to A, where A is the surface area of a black hole measured in Planck’s units of area 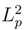 (e.g.[37],[38]). Also it is essential to derive this result from the basic principles given in this paper.
(e.g.[37],[38]). Also it is essential to derive this result from the basic principles given in this paper.
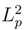 (e.g.[37],[38]). Also it is essential to derive this result from the basic principles given in this paper.
(e.g.[37],[38]). Also it is essential to derive this result from the basic principles given in this paper.As indicated in papers [6],[7], the calculation procedure in the described theory may be reduced to a series expansion in terms of α parameter and to finding of the factors for the ever growing powers of this parameter, that may be considered in some cases as the calculation of quantum corrections. Specifically, this approach to calculation of the quantum correction factors may be used in the formalism for density pro-matrix (Definition 1 of Section 1). In this case, the value 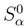 point b), in Section 2 may be written in the form of a series
point b), in Section 2 may be written in the form of a series
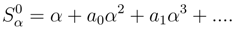 As a result, a measurement procedure using the exponential ansatz may be understood as the calculation of factors a0,a1,... or the definition of additional members in the exponent ”destroying” a0,a1,... [4]. It is easy to check that close to the singularity α = 1/4 the exponential ansatz gives a0 = −3/2, being coincident with the logarithmic correction factor for the black hole entropy [39]. However, by the proposed approach - density matrix deformation at Planck’s scales - the quantum entropy receives a wider and more productive interpretation due to the notion of entropy density matrix introduced in [4],[5],[7],[34] and Section 3. Indeed, the value
As a result, a measurement procedure using the exponential ansatz may be understood as the calculation of factors a0,a1,... or the definition of additional members in the exponent ”destroying” a0,a1,... [4]. It is easy to check that close to the singularity α = 1/4 the exponential ansatz gives a0 = −3/2, being coincident with the logarithmic correction factor for the black hole entropy [39]. However, by the proposed approach - density matrix deformation at Planck’s scales - the quantum entropy receives a wider and more productive interpretation due to the notion of entropy density matrix introduced in [4],[5],[7],[34] and Section 3. Indeed, the value 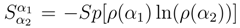 may be considered as a series of two variables α1 and α2. Fixing one of them, e.g. α1, it is possible to expand the series in terms of α2 parameter and to obtain the quantum corrections to the main result as more and more higher-order terms of this series. In the process, (13) is a partial case of the approach to α1 = 0 and α2 close to 1/4.
may be considered as a series of two variables α1 and α2. Fixing one of them, e.g. α1, it is possible to expand the series in terms of α2 parameter and to obtain the quantum corrections to the main result as more and more higher-order terms of this series. In the process, (13) is a partial case of the approach to α1 = 0 and α2 close to 1/4.
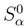 point b), in Section 2 may be written in the form of a series
point b), in Section 2 may be written in the form of a series
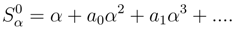
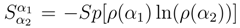 may be considered as a series of two variables α1 and α2. Fixing one of them, e.g. α1, it is possible to expand the series in terms of α2 parameter and to obtain the quantum corrections to the main result as more and more higher-order terms of this series. In the process, (13) is a partial case of the approach to α1 = 0 and α2 close to 1/4.
may be considered as a series of two variables α1 and α2. Fixing one of them, e.g. α1, it is possible to expand the series in terms of α2 parameter and to obtain the quantum corrections to the main result as more and more higher-order terms of this series. In the process, (13) is a partial case of the approach to α1 = 0 and α2 close to 1/4.5 Conclusion
Thus, in this paper it is demonstrated that the developed approach to study a quantum theory of the Early Universe - density matrix deformation at Planck’s scales - leads to a new method of studying the black hole entropy its quantum aspects including. Despite the fact that quite a number of problems require further investigation, the proposed approach seems a worthy contribution: first, it allows for the direct calculations of entropy and, second, the method enables its determination proceeding from the basic principles with the use of the density matrix. Actually, we deal with a substantial modification of the conventional density matrix known from the quantum mechanics - deformation at Planck’s scales or minimum length scales. Moreover, within this approach it is possible to arrive at a very simple derivation and physical interpretation for the Bekenstein-Hawking formula of black hole entropy in a semi-classical approximation. Note that the proposed approach enables one to study the information problem of the Universe proceeding from the basic principles and two types of the existing quantum mechanics only: QM that describes nature at the well known scales and QMFL at Planck’s scales. The author is of the opinion that further development of this approach will allow to research the information problem in greater detail. Besides, it is related to other methods, specifically to the holographic principle, as the entropy density matrix studied in this work is related to the two-dimensional objects.
To conclude, it should be noted that an important problem of the extremal black holes was beyond the scope of this paper. In the last decade this problem has, however, attracted much attention in connection with a string theory and quantum gravitation(e.g., [40,41,42,43]). Specifically, the Bekenstein-Hawking formula has been proved for this case by different methods. The author is hopeful that the approaches proposed in this paper may be developed further to include this very important problem as well.
References
- Shalyt-Margolin, A.E.; Suarez, J.G. Quantum Mechanics of the Early Universe and its Limiting Transition.
- Shalyt-Margolin, A.E.; Suarez, J.G. Quantum Mechanics at Planck’s scale and Density Matrix. Intern.Journ.of Mod.Phys. 2003, D.12, 1265. [Google Scholar]
- Shalyt-Margolin, A.E.; Ya, A. Tregubovich,Deformed Density Matrix and Generalized Uncertainty Relation in Thermodynamics. Mod. Phys. Lett. 2004, A19, 71. [Google Scholar]
- Shalyt-Margolin, A.E. Non-Unitary and Unitary Transitions in Generalized Quantum Mechanics, New Small Parameter and Information Problem Solving. Mod. Phys. Lett. 2004, A19, 391. [Google Scholar]
- Shalyt-Margolin, A.E. Pure States, Mixed States and Hawking Problem in Generalized Quantum Mechanics. Mod. Phys. Lett. 2004, A19, 2037. [Google Scholar] [CrossRef]
- Shalyt-Margolin, A.E. The Universe as a Nonuniform Lattice in Finite-Volume Hypercube.I.Fundamental Definitions and Particular Features. Intern.Journ.of Mod.Phys. 2004, D.13, 853. [Google Scholar]
- Shalyt-Margolin, A.E. The Density Matrix Deformation in Physics of the Early Universe and Some of its Implications. In Quantum Cosmology Research Trends. Horizons in World Physics; Volume 246, pp. 49–91. Nova Science Publishers, Inc.: Hauppauge, NY, 2005. [Google Scholar]
- Veneziano, G. A stringly nature needs just two constant. Europhys.Lett. 1986, 2, 199. [Google Scholar] Amati, D.; Ciafaloni, M.; Veneziano, G. Can spacetime be probed below the string size? Phys.Lett. 1989, B216, 41. [Google Scholar] Witten, E. Reflections on the Fate of Spacetime. Phys.Today 1996, 49, 24. [Google Scholar]
- Adler, R.J.; Santiago, D.I. On Gravity and the Uncertainty Principle. Mod.Phys.Lett. 1999, A14, 1371. [Google Scholar]
- Ahluwalia, D.V. Wave-Particle duality at the Planck scale: Freezing of neutrino oscillations. Phys.Lett. 2000, A275, 31. [Google Scholar] Interface of Gravitational and Quantum Realms. Mod.Phys.Lett. 2002, A17, 1135. Maggiore, M. A Generalized Uncertainty Principle in Quantum Gravity. Phys.Lett. 1993, B304, 65. [Google Scholar]
- Maggiore, M. Quantum Groups,Gravity and Generalized Uncertainty Principle. Phys.Rev. 1994, D49, 5182. [Google Scholar] Capozziello, S.; Lambiase, G.; Scarpetta, G. The Generalized Uncertainty Principle from Quantum Geometry. Int.J.Theor.Phys. 2000, 39, 15. [Google Scholar]
- Maggiore, M. The algebraic structure of the generalized uncertainty principle. Phys.Lett. 1993, B319, 83. [Google Scholar]
- Garay, L. Quantum Gravity and Minimum Length. Int.J.Mod.Phys.A. 1995, 10, 145. [Google Scholar]
- Ng, Y.J.; van Dam, H. Measuring the Foaminess of Space-Time with Gravity-Wave Interferometers. Found.Phys. 2000, 30, 795. [Google Scholar]
- Ng, Y.J.; van Dam, H. On Wigner’s clock and the detectability space-time foam with gravitational-wave interferometers. Phys.Lett. 2000, B477, 429. [Google Scholar]
- Baez, J.C.; Olson, S.J. Uncertainty in Measurment of Distance. Class.Quant.Grav. 2002, 19, L121. [Google Scholar]
- Guth, A.H. Inflation and EternaL Inflation. Phys.Rept. 2000, 333, 555. [Google Scholar]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert Space Representation of the Minimal Length Uncertainty Relation. Phys.Rev. 1995, D52, 1108. [Google Scholar]
- Hawking, S. Phys.Rev. 1976, D14, 2460.
- Heisenberg, W. Zeitsch.fur Phys 1927, 43, 172.
- Adler, R.; Chen, P.; Santiago, D. Gen.Rel.Grav. 2001, 33, 2101.
- Chen, P.; Adler, R. Nucl.Phys.Proc.Suppl. 2003, 124, 103.
- Helfer, A.D. Rept.Prog.Phys. 2003, 66, 943.
- Custodio, P.S.; Horvath, J.E. Class.Quant.Grav. 2003, 20, L197.
- Bekenstein, J.D. Black holes and information theory. Contemp.Phys. 2003, 45, 31. [Google Scholar]
- Bekenstein, J.D. Entropy bounds and black hole remnants. Phys.Rev. 1994, D49, 1912. [Google Scholar]
- Bekenstein, J.D. A universal upper bound on the entropy to energy ratio for bounded systems. Phys.Rev. 1981, D23, 287. [Google Scholar] [CrossRef]
- Bousso, R. Light-sheets and Bekenstein’s bound. Phys.Rev.Lett. 2003, 90, 1213. [Google Scholar]
- Bousso, R. Flat space physics from holography. JHEP 2004, 0405, 050. [Google Scholar]
- Bousso, R. A Covariant Entropy Conjecture. JHEP 1999, 9907, 004. [Google Scholar]
- Hooft, G.’t. Dimension reduction in quantum gravity. The Holographic Principle. (Opening Lecture).
- Susskind, L. The world as a hologram. Journ.Math.Phys. 1995, 36, 6377. [Google Scholar]
- Bousso, R. The holographic principle. Rev.Mod.Phys. 2002, 74, 825. [Google Scholar]
- Shalyt-Margolin, A.E. Deformed density matrix, Density of entropy and Information problem.
- Strominger, A. preprint. hep-th/9501071.
- Giddings, S. preprint. hep-th/9508151.
- Khriplovich, I.B.; Korkin, R.V. How Is the Maximum Entropy of a Quantized Surface Related to Its Area?
- Khriplovich, I.B. Quantization and entropy of black holes. Khriplovich, I.B. Entropy and Area of Black Holes in Loop Quantum Gravity. Phys.Lett. 2002, B537, 125. [Google Scholar]
- Majumdar, P. Black hole entropy: classical and quantum aspects. In Expanded version of lectures given at the YATI Conference on Black Hole Astrophysics, Kolkata, India, April 2001. Das, S.; Majumdar, P.; Bhaduri, R.K. Class.Quant.Grav. 2002, 19, 2355. Vagenas, E.C. Phys.Lett. 2002, B533, 302.
- Majumdar, J. Black Holes in String Theory. Black Holes and D-branes. Nucl.Phys.Proc.Suppl. 1998, 61A. Nucl.Phys.Proc.Suppl. 1998, 62, 428.
- Maldacena, J.; Strominger, A. Statistical Entropy for Four-Dimensional Extremal Black Holes. Phys.Rev.Lett. 1996, 77, 428. [Google Scholar]
- Johnson, C.V.; Khuri, R.R.; Myers, R.C. Entropy of 4D Extremal Black Holes. Phys.Lett. 1996, B378, 78. [Google Scholar]
- Horowitz, G.T. Quantum States of Black Holes. gr-qc/9704072.
©2006 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.