Abstract
Recently we used the maximum entropy principle for finding the price density in a multi agent insurance market. The result is similar to what the Buhlmann had obtained by maximizing the utility function. Here we begin with the price density that is derived by applying the maximum entropy principle to a conservative economic system (exchange market), then reverse the Buhlmann calculation to find the utility function and the risk aversion of agents with respect to this density.
PACS codes:
89.65.Gh, 05.20.-y.
1 Introduction
Utility function is one of the most important and useful concepts in the economics which show the tendency of an economic agent for acquiring more benefit. It is borrowed from the concept of potential energy in physics for modeling the economic equilibrium in similar fashion to mechanical equilibrium [1]. There is no direct way for finding the utility function of an agent with respect to it’s financial condition, namely its wealth. The utility function of an agent may be computed empirically from analysis of its trading data that demonstrates its tolerance with respect to the market risks.
Recently the insurance market, which is one of the important branches of economy, have attracted the attention of physicists [2, 3, 4, 5, 6, 7, 8]. Some concepts of the statistical mechanics, specially the maximum entropy principle is used for pricing the insurance [5, 6, 7, 8]. The well known results on economic premium calculation [10, 11] are retrieved.
In the next section we follow the work of Darooneh [7] which use the approach of Jaynes to the maximum entropy principle [9] and obtain the price density based on the maximum entropy principle then in the last section we apply it to multi agents model of insurance market [10, 7]. Finally the utility function will be derived. The main assumption here is the correspondence between the concept of the equilibrium in physics (statistical) and economics (mechanical). It is proved that economic equilibrium can be viewed as an asymptotic approximation to physical equilibrium and some difficulties with mechanical picture of the equilibrium may be improved by considering the statistical description of it [12, 13, 14, 15, 16, 7]. Simulations and empirical data also confirm this matter [17, 18, 19, 20].
The power of statistical mechanics enables us to extend and apply this method for calculation of utility function in other cases such as finite markets and take into the account the effects of other constraint in the market.
2 The Maximum Entropy Method in Economics
The consistency of the classical mechanics persuaded the economist in the end of nineteenth century, to use the mechanical concepts for modeling the evolution of prices in the financial market. The competition between the supply and demand forces let the price changes in the time. The utility function characterize the excess demand in analogy to the potential energy in the mechanical systems. The maximum of the utility function shows the equilibrium condition in the market. The prices become stationary in this case [21] . Up to now there isn’t any evidence for the economical equilibrium in the financial markets and prices exhibit out of equilibrium behavior [22, 23].
The physical (statistical) approach to the economic equilibrium recently has been suggested by some economists and physicists [5, 6, 7, 8, 12, 13, 14, 17, 18, 19, 20]. The prices are obtained by averaging process over the market situation [5, 7]. This fact lead us to probabilistic picture for price evolution. In the following the same method is used for insurance market and the utility function of the agents are derived as its consequence.
The risky events affect the financial market. As a consequence of the risks the randomness in the market will be increased with time. The state of the market with maximum randomness is called equilibrium. In the equilibrium state we lose much information about the status of economic agents in the market, in this respect the adoption of a strategy for trading becomes more cumbersome. The important task of a trader, and also an economist, is the prediction of the market state. This is carried out by calculation of the distribution function for falling of the market into a possible equilibrium microstate. The maximum entropy principle appears as the best way when we make inference about an unknown distribution based only on few restriction conditions. The Shannon-Jaynes entropy may be written as [9],
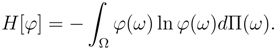 Where ω is an element of the risk’s probability space Ω. The measure of the integral demonstrates the weight for occurrence of a random event (risk).
Where ω is an element of the risk’s probability space Ω. The measure of the integral demonstrates the weight for occurrence of a random event (risk).
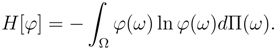
The distribution function ϕ(ω) is a normalized function.
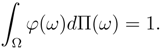 It is assumed that the average of the market’s wealth in the equilibrium state should be constant.
It is assumed that the average of the market’s wealth in the equilibrium state should be constant.
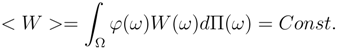 This is a legal assumption in conservative economy (exchange market) because money is only exchanged between different agents and it doesn’t alter the market’s wealth totally [14, 17, 20]. The eqs. 2 and 3 should be satisfied simultaneously when we attempt to maximize the entropy 1.
This is a legal assumption in conservative economy (exchange market) because money is only exchanged between different agents and it doesn’t alter the market’s wealth totally [14, 17, 20]. The eqs. 2 and 3 should be satisfied simultaneously when we attempt to maximize the entropy 1.
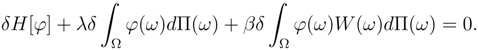 The canonical distribution is the well known solution to above equation [24].
The canonical distribution is the well known solution to above equation [24].
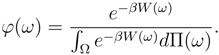 The above result is confirmed analytically [12, 13, 14], by simulation [17, 20] and empirical data [18].
The above result is confirmed analytically [12, 13, 14], by simulation [17, 20] and empirical data [18].
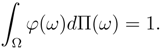
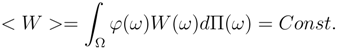
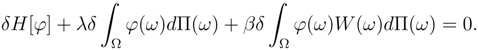
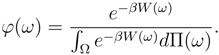
The Parameter β can be calculated in the same way as previous works of the author [4, 6], But by comparison between insurance market and the similar cases in thermal physics, it is understood that the parameter β is related to average wealth of the market [24, 25].
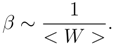 In the case of insurance market the wealth of a typical agent; insurer or insurant (policy holders), is given by,
In the case of insurance market the wealth of a typical agent; insurer or insurant (policy holders), is given by,
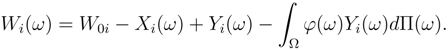 The index i indicates the different agents.
The index i indicates the different agents.
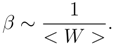
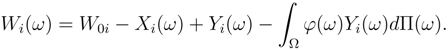
Each agent will incur a loss Xi(ω) if ω is happening. Hence an insurant has insured himself for the price of 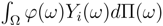 and receives Yi(ω) upon occurrence of this event.
and receives Yi(ω) upon occurrence of this event.
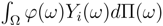 and receives Yi(ω) upon occurrence of this event.
and receives Yi(ω) upon occurrence of this event.As we mentioned before the money is only exchanged between agents and doesn’t alter the total money in the market. It is what is called the clear condition.
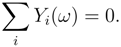 The market’s wealth is sum of the individual wealth of the agents.
The market’s wealth is sum of the individual wealth of the agents.
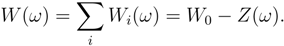 It is also true for initial wealth W0 and aggregate risk Z(ω),
It is also true for initial wealth W0 and aggregate risk Z(ω),
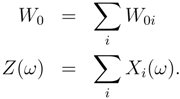 With the aid of eq. 9 we can rewrite eq. 6 to retrieve the Bühlmann result on economic premium calculation [10, 11].
With the aid of eq. 9 we can rewrite eq. 6 to retrieve the Bühlmann result on economic premium calculation [10, 11].
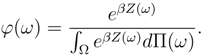 In the next section we try to obtain the utility function from the results that have been fund in this section.
In the next section we try to obtain the utility function from the results that have been fund in this section.
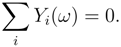
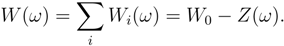
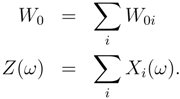
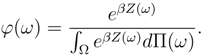
3 Utility Function
The utility function demonstrates the specific profit that an agent intends to make in a competitive market. The utility function should depend on financial status of an economic agent which is frequently described by its wealth, ui(Wi). The index i runs over different agents. It is assumed that the utility function has positive first derivative, 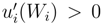 , to guarantee that the agent desires the profit and negative second derivative,
, to guarantee that the agent desires the profit and negative second derivative, 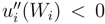 , to restrict it’s avarice (rational agent should be risk averse). The risk aversion parameter,
, to restrict it’s avarice (rational agent should be risk averse). The risk aversion parameter, 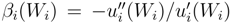 , is also involved in the utility function to scale the agent’s desire in the market with respect to it’s wealth. The market arrives at the equilibrium state upon the agents satisfaction from their trade. In this respect given the equilibrium prices, each agent maximizes utility by choosing his level of Yi(ω) in each contingency.
, is also involved in the utility function to scale the agent’s desire in the market with respect to it’s wealth. The market arrives at the equilibrium state upon the agents satisfaction from their trade. In this respect given the equilibrium prices, each agent maximizes utility by choosing his level of Yi(ω) in each contingency.
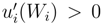 , to guarantee that the agent desires the profit and negative second derivative,
, to guarantee that the agent desires the profit and negative second derivative, 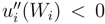 , to restrict it’s avarice (rational agent should be risk averse). The risk aversion parameter,
, to restrict it’s avarice (rational agent should be risk averse). The risk aversion parameter, 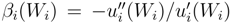 , is also involved in the utility function to scale the agent’s desire in the market with respect to it’s wealth. The market arrives at the equilibrium state upon the agents satisfaction from their trade. In this respect given the equilibrium prices, each agent maximizes utility by choosing his level of Yi(ω) in each contingency.
, is also involved in the utility function to scale the agent’s desire in the market with respect to it’s wealth. The market arrives at the equilibrium state upon the agents satisfaction from their trade. In this respect given the equilibrium prices, each agent maximizes utility by choosing his level of Yi(ω) in each contingency.Because of the risks in the market which induce the randomness, the equilibrium condition may be expressed in an average form.
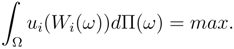 The only function that can be changed upon our request is Yi(ω) hence maximizing of the utility function means,
The only function that can be changed upon our request is Yi(ω) hence maximizing of the utility function means,
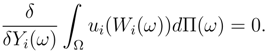 It is not so hard to derive the following result by using variational technique.
It is not so hard to derive the following result by using variational technique.
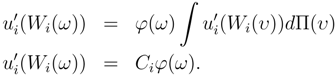 Where the derivatives is taken with respect to function’s argument. The Ci is a constant value for the i−th agent.
Where the derivatives is taken with respect to function’s argument. The Ci is a constant value for the i−th agent.
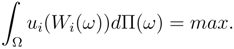
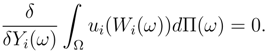
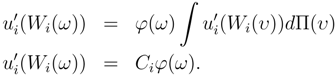
We have the freedom to rescale the risk exchange function Yi(ω), up to a constant number since the agent’s wealth remains unaltered.
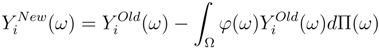 The risk function is also revised to absorb the risk exchange function.
The risk function is also revised to absorb the risk exchange function.
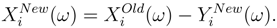 When a loss event happens in the market all of the agents are affected by it. The agent’s risk function depends on ω through the aggregated loss, ζ = Z(ω) hence it is suitable and very often necessary to deal with ζ instead of ω, [11].
When a loss event happens in the market all of the agents are affected by it. The agent’s risk function depends on ω through the aggregated loss, ζ = Z(ω) hence it is suitable and very often necessary to deal with ζ instead of ω, [11].
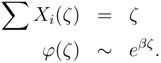 Taking the logarithmic derivative of eq. 14 we obtain,
Taking the logarithmic derivative of eq. 14 we obtain,
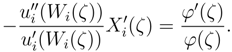 From the definition of the risk aversion parameter we have,
From the definition of the risk aversion parameter we have,
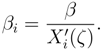 If the risk function for an agent is specified then the utility function is given by the following relation.
If the risk function for an agent is specified then the utility function is given by the following relation.
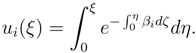 In the above equation we standardize the utility function by assuming ui(0) = 0 and
In the above equation we standardize the utility function by assuming ui(0) = 0 and 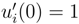 , the amount of wealth may be rescaled regarding with this assumption. The parameter ξ is used for the rescaled wealth. For constant risk aversion parameter the exponential form for utility function is obtained.
, the amount of wealth may be rescaled regarding with this assumption. The parameter ξ is used for the rescaled wealth. For constant risk aversion parameter the exponential form for utility function is obtained.
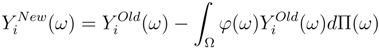
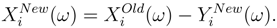
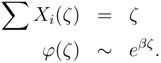
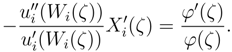
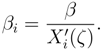
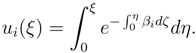
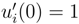 , the amount of wealth may be rescaled regarding with this assumption. The parameter ξ is used for the rescaled wealth. For constant risk aversion parameter the exponential form for utility function is obtained.
, the amount of wealth may be rescaled regarding with this assumption. The parameter ξ is used for the rescaled wealth. For constant risk aversion parameter the exponential form for utility function is obtained.4 Conclusion
The maximum entropy concept is extended to the insurance market. Money in this market plays the role of energy for thermal systems. Optimization of the market’s entropy in accompany with the clearing condition leads us to the canonical price distribution which is used for calculation of the premium. We show how an agent may derive a risk aversion parameter that maximize his utility in an insurance contract. It is necessary for him to know about his probable loss events.
References
- Burda, Z.; Jurkiewicz, J.; Nowak, M. A. Is Econophysics a Solid Science? Acta Physica Polonica 2003, B 34, 87. [Google Scholar] [PubMed]
- Acharyya, M.; Acharyya, A. B. Modelling and Computer Simulation of an Insurance Policy: A Search for Maximum Profit. Int. J. of Mod. Phys. C 2003, 14(8), 1041–1046. [Google Scholar] [CrossRef]
- Fouladvand, M. E.; Darooneh, A. H. Int. J. of Mod. Phys. C 2005, 16(3), 377–387.
- Darooneh, A. H. Non Life Insurance Pricing: Statistical Mechanics Viewpoint. Int. J. of Mod. Phys. C 2005, 16(1), 167–176. [Google Scholar] [CrossRef]
- Darooneh, H. Physical Premium Principle: A New Way for Insurance Pricing. Entropy 2005, 7[1], 97–107. [Google Scholar] [CrossRef]
- Darooneh, H. Premium Calculation Based on Physical Principles. Iranian Quarterly J. of Insurance 2005, 19(4), 72–82, In persian. [Google Scholar]
- Darooneh, H. Non Life Insurance Pricing: Multi Agent Model. Eur. Phys. J. B 2004, 42, 119–122. [Google Scholar] [CrossRef]
- Darooneh, H. Non Life Insurance Pricing: Agent- Environment Model, Will be published in Proc. of 10th IASBS Conf. in Condensed Matter, IASBS (Zanjan), 27-31 (2004). In persian.
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phy. Rev. 1957, 106, 620. [Google Scholar] Jaynes, E.T. Where Do We Stand on Maximum Entropy? In Papers on Probability, Statistics and Statistical Physics; Rosenkrantz, R. D., Ed.; Klower Acad. Pub.: Dordrecht, 1989. [Google Scholar]
- Buhlmann, H. An Economic Premium Principle. ASTIN Bulletin 1980, 11, 52. [Google Scholar]
- Buhlmann, H. General Economic Premium Principle. ASTIN Bulletin 1984, 14, 13. [Google Scholar]
- Foley, D. K. A Statistical Equilibrium Theory of Markets. J. Economic Theory 1994, 62(2), 321. [Google Scholar] [CrossRef]
- Foley, D. K. Statistical Equilibrium in a Simple Labor Market. Metroeconomica 1996, 47(2), 125. [Google Scholar] [CrossRef]
- Smith, E.; Foley, D. K. SFI Working papers. 2002. [Google Scholar]
- Sergeev, V. Limit of Rationality. Fasis, Moscow, 1999; V. Sergeev, SFI Working papers. [Google Scholar]
- Milakovic’, M. LEM Working Papers. 2003. [Google Scholar]
- Drăgulescu, A.; Yakovenko, V. M. Statistical Mechanics of Money. Eur. Phys. J. B 2000, 17, 723. [Google Scholar]
- Drăgulescu, A.; Yakovenko, V. M. Evidence for the Exponential Distribution of Incomes in the USA. Eur. Phys. J. B 2001, 20, 585. [Google Scholar]
- Drăgulescu, A.; Yakovenko, V. M. Exponential and Power Law Probability Distribution of Wealth and Incomes in the United Kingdom and United States. Physica A 2001, 299, 213. [Google Scholar]
- Chatterjee, A.; Chakarbarti, B. K.; Manna, S. S. Money in Gas-Like Market: Gibbs and Pareto Laws. Physica Scripta 2003, T90, 36. [Google Scholar] —, Econophysics of the Wealth Distribution; Chatterjee, A.; Yarlagadda, S.; Chakarbarti, B. K. New Economic Windows Series; Springer Verlag: Milano, 2005. [Google Scholar]
- Debreu, G. Theory of Value; Yal Univ. Press: New Haven, 1987. [Google Scholar]
- McCauley, J. L. Thermodynamic analogies in economics and finance. Physica A 2003, 329, 199–212. [Google Scholar] [CrossRef]
- McCauley, J. L.; Kuffner, C. M. Economic System Dynamics. Discrete Dynamics in Nature and Society 2004, 1, 213–220. [Google Scholar]
- Pathria, R. K. Statistical Mechanics; Pergamon Press: Oxford, 1972. [Google Scholar]
- Prentis, J. J.; Andrus, A. E.; Stasevich, T. J. Crossover from the Exact Factor to the Boltzman Factor. Am. J. of Phys. 1999, 67(6), 508–515. [Google Scholar] [CrossRef]
© 2006 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.