Abstract
The entropy generation rate in a laminar flow through a channel filled with saturated porous media is investigated. The upper surface of the channel is adiabatic and the lower wall is assumed to have a constant heat flux. The Brinkman model is employed. Velocity and temperature profiles are obtained for large Darcy number (Da) and used to obtain the entropy generation number and the irreversibility ratio. Generally, our result shows that heat transfer irreversibility dominates over fluid friction irreversibility (i.e. 0 ≤ φ < 1), and viscous dissipation has no effect on the entropy generation rate at the centerline of the channel.
Introduction
Studies related to laminar flow in a channel filled with saturated porous media have increased significantly during recent years. This type of geometry and flow configuration are commonly observed in field of electronics cooling system, solid matrix heat exchanger, geothermal system, nuclear waste disposal, microelectronic heat transfer equipment, coal and grain storage, petroleum industries, and catalytic converters. Meanwhile, the improvement in thermal systems as well as energy utilization during the convection in any fluid is one of the fundamental problems of the engineering processes, since improved thermal systems will provide better material processing, energy conservation and environmental effects, (Makinde, [12]).
Another potential application of convection processes in porous media is found in thermoacoustic prime movers and heat pumps ( Rott [15], Swift [20]), where the fluid-gap within stacks of a ther- moacoustic engine/refrigerator are treated as porous media. Thermoacoustic engines are devices which make use of the thermoacoustic phenomena and function as heat pumps or prime movers. They can provide cooling or heating using enviromentally benign gases (such as oxygen or nitrogen) as the work- ing fluid. Despite recent developments in thermoacoustic engines (see Swift [20]), there are many areas requiring further investigation in order to better predict their performance and guide future designs for thermoacoustic engines. Any thermoacoustic device (system) can be divided into four basic compo- nents (resonant tube, speaker, heat exchangers, and regenerator or stacks);among them the stack serves as the heart of the thermoacoustic device. In engine and heat pump, stacks are finely subdivided into many parallel channels or pores. Starting from the single plate, stacks are available in different sizes and shapes. Multi-plate arrays, honeycombs, spiral roles, and pin arrays’ are some example of stacks commonly used in thermoacoustics engines and refrigerators. (see Swift [20]). To improve the thermal contact and heat transfer area, a porous medium ( a fine wire mesh made of a material with moderate to good thermal conductivity) of moderate permeability may be embedded inside the fluid gap between two consecutive stacks. Most of the existing theories (of thermoacoustics engines/prime movers) consider a non-porous medium and very few of them use a single pore (of circular or square cross-section) to model thermoacoustic systems. In thermoacoustic devices, stacks are repeated along the transverse direction of fluid motion. The fluid gap between two consecutive stacks is usually kept constant. Two consecutive stacks plates and the fluid gap may be approximated as a unit-channel and inside the resonant chamber the stack (or regenerator) consists of many unit-channels. The fluid dynamics of all unit-channel must be similar (neglecting resonant chamber wall effects). Therefore, this present research can be applicable to one unit-channel.
One of the methods used for predicting the performance of the engineering processes is the second law analysis. The second law of thermodynamics is applied to investigate the irreversibilities in terms of the entropy generation rate. Since the entropy generation is the measure of the destruction of the available work of the system, the determination of the active sites motivating the entropy generation is also impor- tant in upgrading the system performances. This method was introduced by Bejan[2,3,4] and followed by many other investigators e.g. Arpaci[1], Sahin[14],Sahin[16],Narusawa[13], Erbay et al.[6],Mahmud and Fraser[9], Sahin[16], Salah et al.[18]. In this present paper, special attention has been given to the effect of porous medium permeability on the entropy generation and irreversibility ratio.
Mathematical Formulation
For the steady-state hydrodynamically developed situation we have unidirectional flow in the -direction between impermeable boundaries at = 0 and = a, as illustrated in Fig.1. The channel is composed of a fixed lower heated wall with constant heat flux while the upper wall is fixed and adiabatic. Other physical properties of the fluid like viscosity and density are taken as constant.
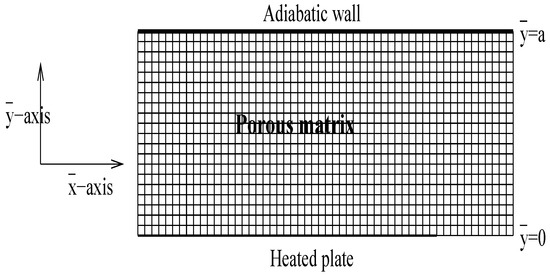
Figure 1.
Geometry of the problem
The Brinkman momentum equation is
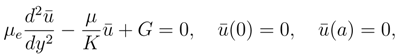 where µe is an effective viscosity, µ is the fluid velocity, K is the permeability, and G is the applied pressure gradient.
where µe is an effective viscosity, µ is the fluid velocity, K is the permeability, and G is the applied pressure gradient.
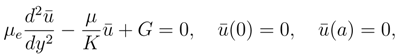
We define dimensionless variables
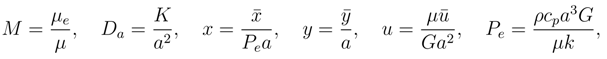 where M is the viscosity ratio, Da the Darcy number, pe the Peclet number, k the thermal conductivity and ρ the fluid density.
where M is the viscosity ratio, Da the Darcy number, pe the Peclet number, k the thermal conductivity and ρ the fluid density.
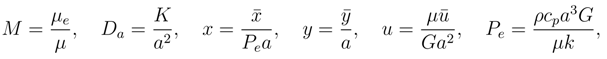
The dimensionless form of Eq. (1) is
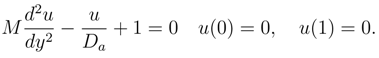
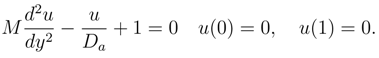
Using algebraic package (MAPLE), the solution of the equation (3) is given as
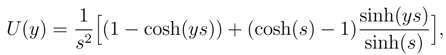 where
where
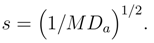
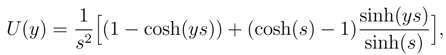
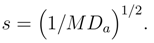
It will be noted that, M and Da appear only in the combination of M times Da, hence, without loss of generality, we take M = 1 in our analysis.
Using algebraic package (taylor()) in MAPLE the Taylor expansion of Eq.(4) (for large Da) yeilds
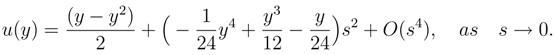
The steady-state thermal energy equation for the problem is given as
 with the following inlet and boundary conditions:
with the following inlet and boundary conditions:
Inlet condition
 Constant heat flux at the lower wall
Constant heat flux at the lower wall
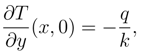 Adiabatic wall
Adiabatic wall
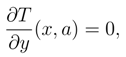 where T is the absolute temperature and T0 is the temperature at the inlet. The dimensionless energy equation is given as
where T is the absolute temperature and T0 is the temperature at the inlet. The dimensionless energy equation is given as
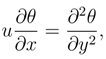 with
with
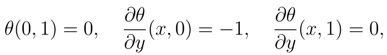 where the dimensionless temperature θ = k(T − T0)/qa.
where the dimensionless temperature θ = k(T − T0)/qa.
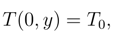
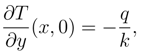
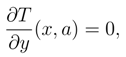
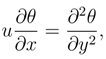
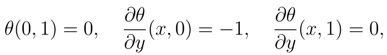
The problem is now to solve Eq. (11) subject to the conditions Eq.(12). We employed the analytical method of separation of variables. Let
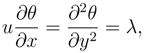 then
then
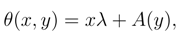 where
where
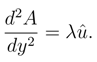 The above equation is solved completely and the integration constants were obtained from conditions (12). We obtain
The above equation is solved completely and the integration constants were obtained from conditions (12). We obtain
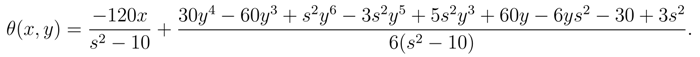
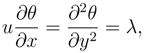
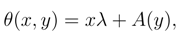
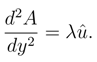
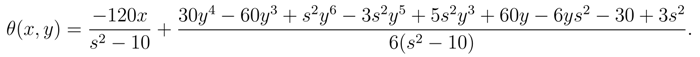
Entropy Generation Rate
According to Mahmud and Fraser[10], the entropy generation rate is define as
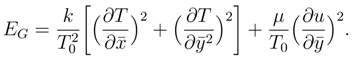
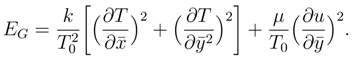
The dimensionless entropy generation number may be defined by the following relationship:
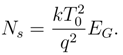
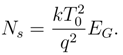
In terms of the dimensionless velocity and temperature, the entropy generation number becomes
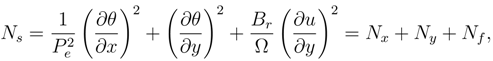 where the dimensionless parameters Br = G2a3/qµ is the Brinkman number, Ω = qa/kT0 the di- mensionless temperature difference. Nx and Ny are the entropy generation by heat transfer due to both axial and transverse heat conduction respectively and Nf is the entropy generation due to fluid friction.
where the dimensionless parameters Br = G2a3/qµ is the Brinkman number, Ω = qa/kT0 the di- mensionless temperature difference. Nx and Ny are the entropy generation by heat transfer due to both axial and transverse heat conduction respectively and Nf is the entropy generation due to fluid friction.
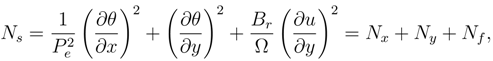
In convective problem, both fluid friction and heat transfer contribute to the rate of entropy gener- ation. In order to have an idea whether fluid friction or heat transfer entropy generation dominates, a criterion known as the irreversibility ratio defined by φ is utilised, where
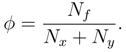
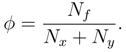
For 0 ≤ φ < 1 implies that heat transfer irreversibility dominates and fluid friction dominates when φ > 1. The case where both the heat transfer and fluid friction have the same contribution for entropy generation is characterised by φ = 1
Results and Discussions
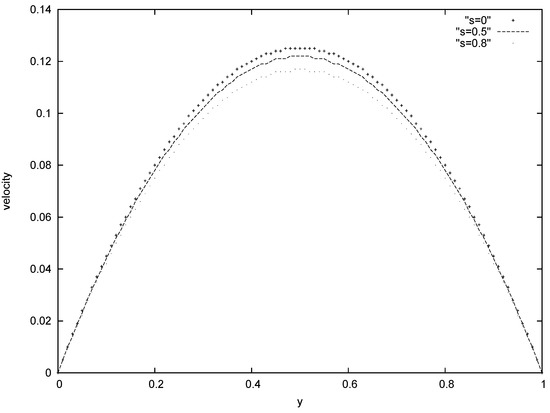
Figure 2.
Velocity profiles for different values of s
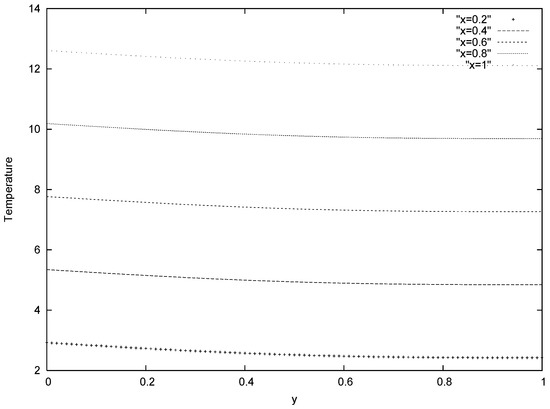
Figure 3.
Temperature profiles for different values of x with s = 0.3
Figure 4.
Temperature profiles for different values of x with s = 0.4
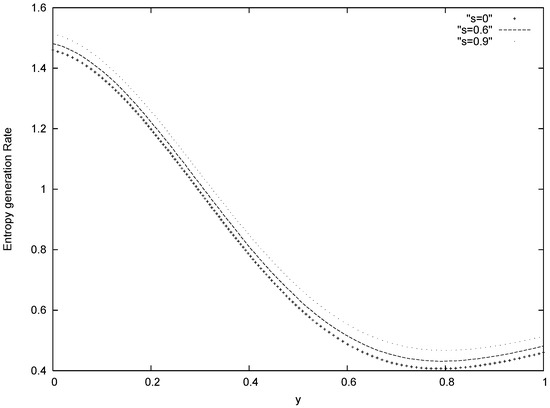
Figure 5.
Entropy generation number for different values of s ( Pe = 20 and BrΩ−1 = 0.4)
Fig.2 shows a parabolic velocity profile across the channel with maximum velocity along the cen- terline of the channel. The case of s = 0 (s = 1/) coincides with the well known plane Poiseuille flow. It is observed that fluid velocity decreases as porous media permeability decreases (s increases). Fig.3 shows the temperature profiles across the channel for different axial distance. We observed that the fluid temperature increases downstream i.e. axially and decreases transversely across the channel. In Fig.(4) we observed that the fluid temperature decreases in the transverse direction and increases with a decrease in porous media permeability.
The spartial distribution of the entropy generation number for different values of s is plotted in Fig 5. It is interesting to note that entropy generation rate decreases in transverse direction and increases with a decrease in porous media permeability. Such result is expected because high restrictive medium would lead to more disorderliness in the fluid particle. Fig 6 shows the spartial distribution of the entropy generation number for different group parameters. For all values of the group parameters, the entropy generation rate decreases in the transverse direction from the lower wall towards the channel centerline and gradually increases towards the upper wall. This clearly implies that viscous dissipation has no ef- fect on the entropy generation rate at the centerline of a channel filled with porous media.
Graph of Irreversibility ration for different values of Br For a specific case of s = 0.5, and Pe = 20, irreversibility ratio is plotted in Fig7. as a function of transverse distance (y) for different group param-eters (Br/Ω). The group parameter is an important dimensionless number for irriversibility analysis. It determines the relative importance of viscous effects to temperature gradient entropy generation. Irre- versibility ratio profile is asymmetric about the centerline of the channel due to the asymmetric tem- perature distribution. For all group parameters, each wall acts as a strong concetrator of irriversibility because of the high near-wall gradients of velocity and temperature. Maximum irreversibility ration occurs near the adiabatic wall fo all group parameters. Fluid friction irreversibility is zero at channel centerline(y = 0.5) due to zero velocity gradient (∂u/∂y). Also irreversibility ratio (φ) is independent of the group parameter at y=0.5. Therefore, the magnitude of irreversibility ratio is same at centerline of the channel for all group parameters. Minimum irreversibility ratio occur very near where the temperature gradient is zero. Generally, it is observed that an increase in group parameter strengthens the effect of fluid friction irreversibility, but heat transfer irreversibility dominates over fluid friction irreversibility (i.e. 0 ≤ φ < 1).
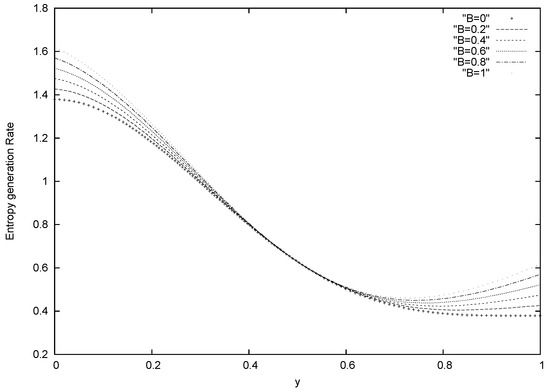
Figure 6.
Entropy generation number for different values of B = BrΩ−1 ( Pe = 20 and s = 0.5)
Conclusion
This paper presents the application of the second law of thermodynamics to the flow in a channel filled with saturated porous media. The velocity and temperture profiles are obtained and use to compute the entropy generation number and the irreversibility ratio for large Darcy number (Da) and group param- eter (BrΩ−1). Generally, our result shows that heat transfer irreversibility dominates over fluid friction irreversibility and viscous dissipation has no effect on the entropy generation rate at the centerline of the channel.
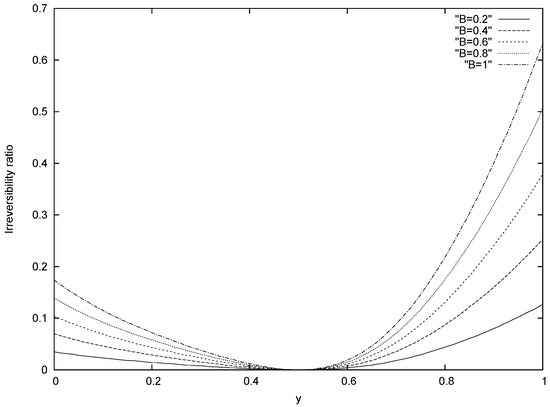
Figure 7.
Irreversibility ratio for different values of BrΩ−1 ( s = 0.5 and Pe = 20.)
Acknowledgement
The support received from African Institute for Mathematical Sciences (AIMS) in Cape Town and the Department of Applied Mathematics, University of Limpopo, South Africa are highly appreciated.
Nomenclature
| a | channel width |
| Br | Brinkman number |
| cp | specific heat at constant pressure |
| Da | Darcy number |
| G | applied pressure gradient |
| k | fluid thermal conductivity |
| K | Permeability |
| M | µe/µ |
| Pe | Peclet number |
| q | fluid flux rate |
| s | (M Da)−1/2) |
| T0 | wall temperature |
| T | absolute temperature |
| U | dimensionless fluid velocity |
| u | dimensionless fluid velocity as s → 0 |
fluid velocity | |
| x | dimensionless axial coordinate |
| y | dimensionless transverse coordinate |
axial coordinate | |
transverse coordinate | |
| Greek symbols | |
| µ | fluid viscosity |
| µe | effective viscosity in the Brinkman term |
| θ | dimensionless temperature |
| Ω | dimensionless temperature difference qa/kT0 |
| ρ | fluid density |
References
- Arpaci, V. S. Radiative entropy production - lost heat into entropy. Int. J. Heat Mass Transfer 1993, 36, 4193–4197. [Google Scholar]
- Bejan, A. Second law analysis in heat transfer. Energy - The Int. J. 1980, 5, 721–732. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Through Heat and Fluid Flow. John Wiley & Sons. Inc.: Canada, 1994; Chapter 5; p. 98. [Google Scholar]
- Bejan, A. Entropy Generation Minimization, CRC Press Flow. In CRC Press Flow; John Wiley & Sons. Inc.: Canada, 1996; Chapter 5; p. 98. [Google Scholar]
- Bejan, A. Entropy Generation Minimization. CRC Press: USA, 1996. [Google Scholar]
- Erbay, L.B.; Altaç, Z.; Sülü, B. Entropy Generation in a Square Enclosure Heated From a Vertical Lateral Wall. In Proceedings of the 15th International Symposium on Efficiency, Costs, Optimization, Simulation and Environmental Aspects of Energy Systems; 2002; 3, pp. 1609–1616. [Google Scholar]
- Krane, R. J. A. Second law analysis of the optimum design and operation of thermal energy storage systems. Int. J. Heat Mass Transfer 1987, 30, 43–57. [Google Scholar] [CrossRef]
- Latife, B. E.; Mehmet, S. E.; Birsen, S.; Yalcum, M. M. Entropy generation during fl flow between two parallel plates with moving bottom plate. Entropy 2003, 5, 506–518. [Google Scholar]
- Mahmud, S.; Fraser, R. A. Thermodynamic analysis of flow and heat transfer inside channel with two parallel plates. Exergy, an International Journal 2002, 2, 140–146. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R. A. The second law analysis in fundamental convective heat transfer problems. Int. J. of Thermal Sciences 2002, 42(2), 177–186. [Google Scholar] [CrossRef]
- Nag, P.K.; Kumar, N. Second law optimization of convective heat transfer through a duct with constant heat flux. Int. J. Energy Research 1989, 13(5), 537–543. [Google Scholar]
- Makinde, O. D. Exothermic explosions in a slab: A case study of series summation technique. Int. Comm. Heat and Mass Transfer 2004, 31(8), 1227–1231. [Google Scholar] [CrossRef]
- Narusawa, U. The second law analysis of mixed convection in rectangular ducts. Heat and Mass Transfer 2001, 37, 197–203. [Google Scholar] [CrossRef]
- Nield, D. A.; Kuznetsov, A. V.; Ming, X. Thermally developing forced convection in a porous medium: parallel plate channel with walls at uniform temperature, with axial conduction and viscous dissipation effects. Int. J. Heat and Mass Transfer 2003, 46, 643–651. [Google Scholar] [CrossRef]
- Rott, N. Themoacoustics. Adv. Appl. Mech. 1980, 20, 135–175. [Google Scholar]
- Sahin, A.Z. Irreversibilities in various duct geometries with constant wall heat flux and laminar flow. Energy, The International J. 1998, 23(6), 465–473. [Google Scholar] [CrossRef]
- Sahin, A.Z. Entropy generation in turbulent liquid flow through a smooth duct subjected to constant wall temperature. Int. J. Heat and Mass Transfer 2000, 43, 1469–1478. [Google Scholar] [CrossRef]
- Sahin, A.Z. Entropy generation and pumping power in a turbulent fluid flow through a smooth pipe subjected to constant heat flux. Exergy, an International Journal 2002, 2, 314–321. [Google Scholar] [CrossRef]
- Salah, S.; Soraya, A. Second law analysis of laminar falling liquid fi along an inclined heated plate. Int. Comm. Heat Mass Transfer 2004, 31(No. 6), 879–886. [Google Scholar]
- Swift, G. W. Themoacoustics: A unifying perspective for some engines and refrigerators. ASA Publication: New York, 2002. [Google Scholar]
- Syeda, H. T.; Shohel, M. Entropy generation in a verical concentric channel with temperature dependent viscosity. Int. Comm. Heat Mass Transfer 2002, 29(No. 7), 907–918. [Google Scholar]
© 2005 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.