On the Linear Combination of Exponential and Gamma Random Variables
Abstract
:1 Introduction
- In automatic control, one often encounters the problem of maximizing the expected sum of n variables, chosen from a sequence of N sequentially arriving i.i.d. scalar random variables, X1, X2, . . . , XN. The objective is to devise a decision rule so as to maximize , where ki ∈ {1, 2, . . . , N} is the index of the ith random variable selected. At time k, the random variable Xk is observed, and the decision to select the value or not must be taken online. This problem is known as the sequential screening problem and many decision problems can be formulated in this way (Pronzato [1]).
- The theory of congruence equations (see, for example, Cerruti [2]) has applications in computer science. There is a wide literature about congruence equations and the last twenty years has seen interesting formulas and functions derived: among these, expressions giving the number of solutions of linear congruences. Counting such solutions has relations with statistical problems like the distribution of the values taken by particular sums.
- In neurocomputing, linear combinations are used for combining multiple probabilistic classifiers on different feature sets. In order to achieve the improved classification performance, a generalized finite mixture model is proposed as a linear combination scheme and implemented based on radial basis function networks. In the linear combination scheme, soft competition on different feature sets is adopted as an automatic feature rank mechanism so that different feature sets can be always simultaneously used in an optimal way to determine linear combination weights (Chen and Chi [3]).
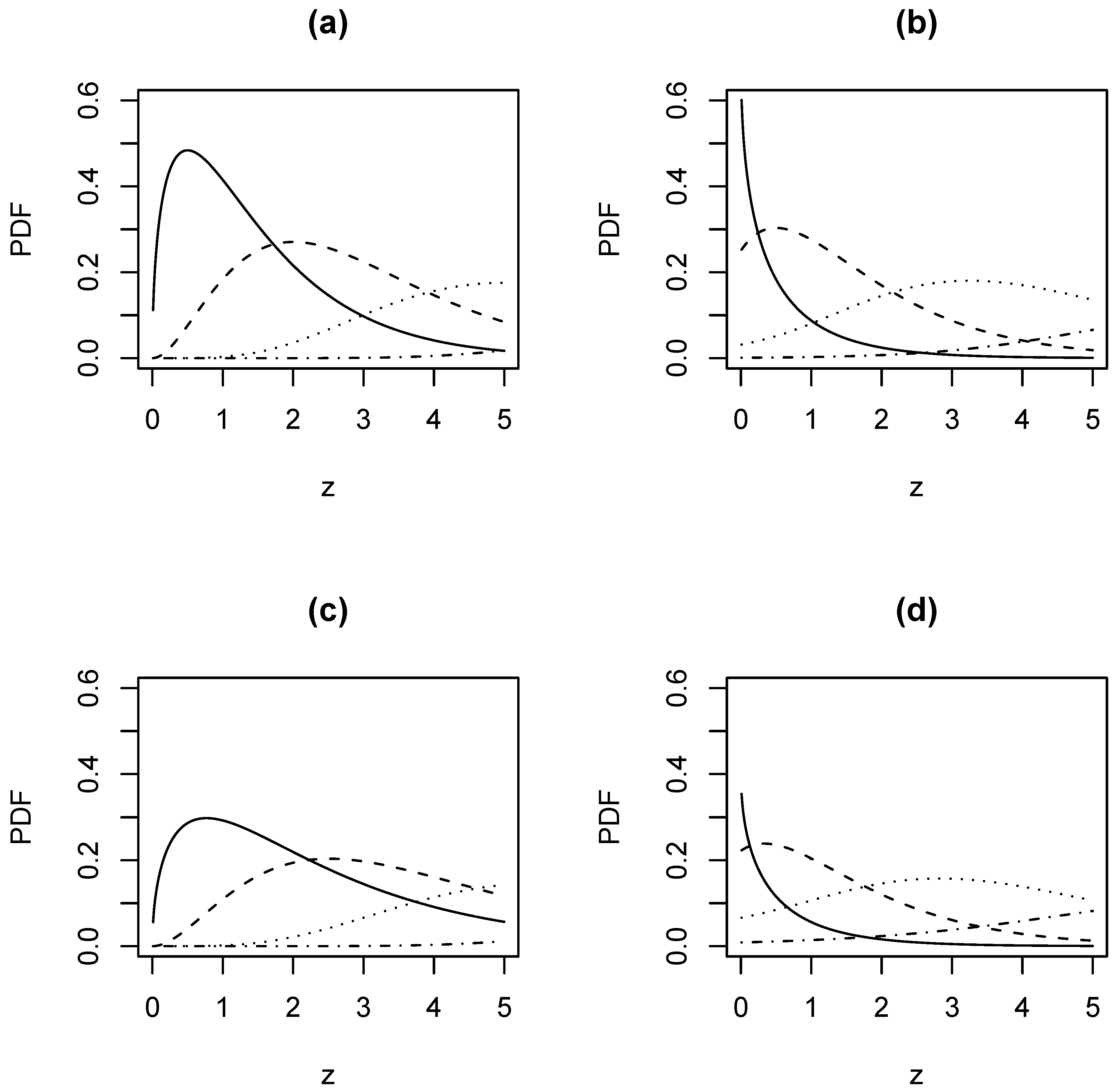
2 PDF and CDF

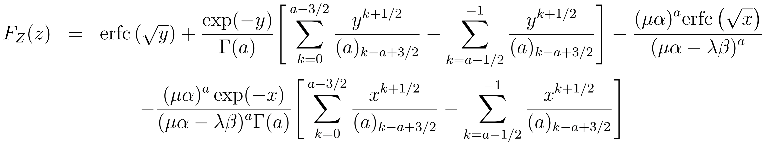
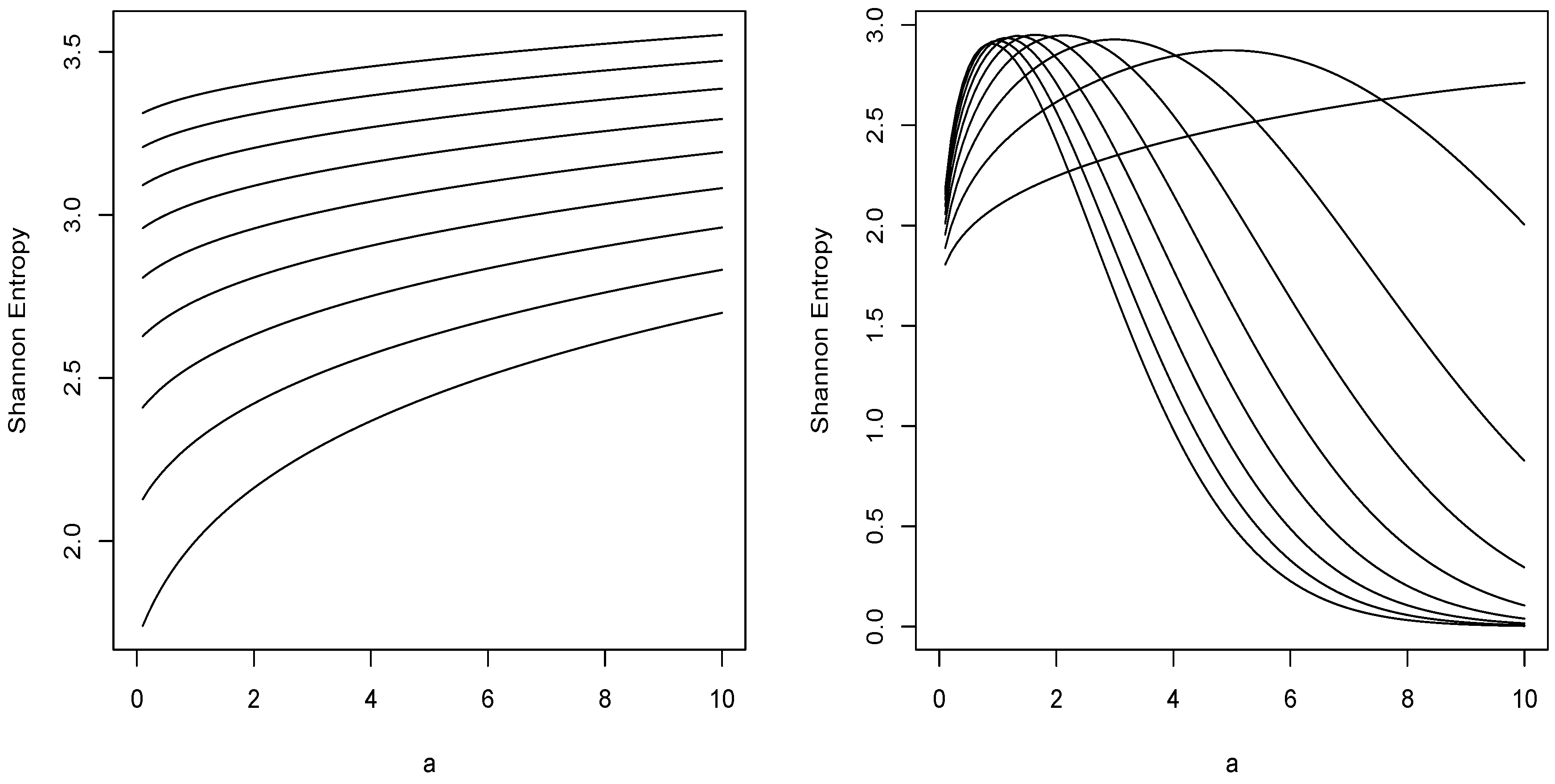
3 Entropy
cc<-lambda*((mu*alpha)**a)/(alpha*gamma(a)*(mu*alpha-lambda*beta)**a)
ff<-function (x)
{tt<-gamma(a)*pgamma(x*(mu*alpha-lambda*beta)/(alpha*beta),shape=a)
tt<-exp(-lambda*x/alpha)*tt*log(tt)
return(tt)}
ent<-1+lambda*beta*a/(alpha*mu)-log(cc)
ent<-ent-cc*integrate(ff,lower=0,upper=Inf)$value
4 Percentiles
#this program gives percentiles when beta > 0 ff:=(1/GAMMA(a))*((mu*alpha)/(mu*alpha-lambda*beta))**a*exp(-lambda*z/alpha): ff:=ff*(GAMMA(a)-GAMMA(a,z*(mu*alpha-lambda*beta)/(alpha*beta))): ff:=1-GAMMA(a,mu*z/beta)/GAMMA(a)-ff: p1:=fsolve(ff=0.01,z=0..1000): p2:=fsolve(ff=0.05,z=0..1000): p3:=fsolve(ff=0.1,z=0..1000): p4:=fsolve(ff=0.90,z=0..1000): p5:=fsolve(ff=0.95,z=0..1000): p6:=fsolve(ff=0.99,z=0..1000): print(p1,p2,p3,p4,p5,p6); #this program gives percentiles when beta < 0 ff1:=(1/GAMMA(a))*((mu*alpha)/(mu*alpha-lambda*beta))**a: ff1:=ff1*exp(-lambda*z/alpha): ff1:=ff1*GAMMA(a,z*(mu*alpha-lambda*beta)/(alpha*beta)): ff1:=GAMMA(a,mu*z/beta)/GAMMA(a)-ff1: ff2:=1-((mu*alpha)/(mu*alpha-lambda*beta))**a*exp(-lambda*z/alpha): bd:=1-((mu*alpha)/(mu*alpha-lambda*beta))**a: if (bd>0.01) then p1:=fsolve(ff1=0.01,z=-1000..0): end if: if (bd<=0.01) then p1:=fsolve(ff2=0.01,z=0..1000): end if: if (bd>0.05) then p2:=fsolve(ff1=0.05,z=-1000..0): end if: if (bd<=0.05) then p2:=fsolve(ff2=0.05,z=0..1000): end if: if (bd>0.1) then p3:=fsolve(ff1=0.1,z=-1000..0): end if: if (bd<=0.1) then p3:=fsolve(ff2=0.1,z=0..1000): end if: if (bd>0.9) then p4:=fsolve(ff1=0.9,z=-1000..0): end if: if (bd<=0.9) then p4:=fsolve(ff2=0.9,z=0..1000): end if: if (bd>0.95) then p5:=fsolve(ff1=0.95,z=-1000..0): end if: if (bd<=0.95) then p5:=fsolve(ff2=0.95,z=0..1000): end if: if (bd>0.99) then p6:=fsolve(ff1=0.99,z=-1000..0): end if: if (bd<=0.99) then p6:=fsolve(ff2=0.99,z=0..1000): end if: print(p1,p2,p3,p4,p5,p6);We hope these programs will be of use to the practitioners of the linear combination (see Section 1).
Acknowledgments
References
- Pronzato, L. Optimal and asymptotically optimal decision rules for sequential screening and resource allocation. Transactions on Automatic Control 2001, 46, 687–697. [Google Scholar] [CrossRef]
- Cerruti, U. Counting the number of solutions of congruences. In Application of Fibonacci Numbers; Bergum, G. E., et al., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993; vol 5, pp. 85–101. [Google Scholar]
- Chen, K.; Chi, H. A method of combining multiple probabilistic classifiers through soft competition on different feature sets. Neurocomputing 1988, 20, 227–252. [Google Scholar] [CrossRef]
- Boswell, S. B.; Taylor, M. S. A central limit theorem for fuzzy random variables. Fuzzy Sets and Systems 1987, 24, 331–344. [Google Scholar] [CrossRef]
- Williamson, R. C. The law of large numbers for fuzzy variables under a general triangular norm extension principle. Fuzzy Sets and Systems 1991, 41, 55–81. [Google Scholar] [CrossRef]
- Inoue, H. Randomly weighted sums for exchangeable fuzzy random variables. Fuzzy Sets and Systems 1995, 69, 347–354. [Google Scholar] [CrossRef]
- Jang, L. -C.; Kwon, J. -S. A uniform strong law of large numbers for partial sum processes of fuzzy random variables indexed by sets. Fuzzy Sets and Systems 1998, 99, 97–103. [Google Scholar] [CrossRef]
- Feng, Y. Sums of independent fuzzy random variables. Fuzzy Sets and Systems 2001, 123, 2011. 11–18. [Google Scholar] [CrossRef]
- Feng, Y. Note on: “Sums of independent fuzzy random variables” [Fuzzy Sets and Systems 2001, 123, 11–18]. Fuzzy Sets and Systems 2004, 143, 479–485. [Google Scholar]
- Fisher, R. A. The fiducial argument in statistical inference. Annals of Eugenics 1935, 6, 391–398. [Google Scholar] [CrossRef]
- Chapman, D. G. Some two-sample tests. Annals of Mathematical Statistics 1950, 21, 601–606. [Google Scholar] [CrossRef]
- Christopeit, N.; Helmes, K. A convergence theorem for random linear combinations of independent normal random variables. Annals of Statistics, 1979, 7, 795–800. [Google Scholar] [CrossRef]
- Davies, R. B. Algorithm AS 155: The distribution of a linear combination of chi-squared random variables. Applied Statistics 1980, 29, 323–333. [Google Scholar] [CrossRef]
- Farebrother, R. W. Algorithm AS 204: The distribution of a positive linear combination of chi-squared random variables. Applied Statistics 1984, 33, 332–339. [Google Scholar] [CrossRef]
- Ali, M. M. Distribution of linear combinations of exponential variates. Communications in Statistics—Theory and Methods 1982, 11, 1453–1463. [Google Scholar] [CrossRef]
- Moschopoulos, P. G. The distribution of the sum of independent gamma random variables. Annals of the Institute of Statistical Mathematics 1985, 37, 541–544. [Google Scholar] [CrossRef]
- Provost, S. B. On sums of independent gamma random variables. Statistics 1989, 20, 583–591. [Google Scholar] [CrossRef]
- Dobson, A. J.; Kulasmaa, K.; Scherer, J. Confidence intervals for weighted sums of Poisson parameters. Statistics in Medicine 1991, 10, 457–462. [Google Scholar] [CrossRef] [PubMed]
- Pham-Gia, T.; Turkkan, N. Bayesian analysis of the difference of two proportions. Communications in Statistics—Theory and Methods 1993, 22, 1755–1771. [Google Scholar] [CrossRef]
- Pham, T. G.; Turkkan, N. Reliability of a standby system with beta-distributed component lives. IEEE Transactions on Reliability 1994, 43, 71–75. [Google Scholar] [CrossRef]
- Kamgar-Parsi, B.; Kamgar-Parsi, B.; Brosh, M. Distribution and moments of weighted sum of uniform random variables with applications in reducing Monte Carlo simulations. Journal of Statistical Computation and Simulation 1995, 52, 399–414. [Google Scholar] [CrossRef]
- Albert, J. Sums of uniformly distributed variables: a combinatorial approach. College Mathematical Journal 2002, 33, 201–206. [Google Scholar] [CrossRef]
- Hitezenko, P. A note on a distribution of weighted sums of iid Rayleigh random variables. Sankhyā, A 1998, 60, 171–175. [Google Scholar]
- Hu, C. -Y.; Lin, G. D. An inequality for the weighted sums of pairwise i.i.d. generalized Rayleigh random variables. Journal of Statistical Planning and Inference 2001, 92, 1–5. [Google Scholar] [CrossRef]
- Witkovský, V. Computing the distribution of a linear combination of inverted gamma variables. Kybernetika 2001, 37, 79–90. [Google Scholar]
- Prudnikov, A. P.; Brychkov, Y. A.; Marichev, O. I. Integrals and Series (volumes 1, 2 and 3); Gordon and Breach Science Publishers: Amsterdam, 1986. [Google Scholar]
- Gradshteyn, I. S.; Ryzhik, I. M. Table of Integrals, Series, and Products, (sixth edition); Academic Press: San Diego, 2000. [Google Scholar]
- Shannon, C. E. A mathematical theory of communication. Bell System Technical Journal 1948, 27, 379–432. [Google Scholar] [CrossRef]
- Ihaka, R.; Gentleman, R. R: A language for data analysis and graphics. Journal of Computational and Graphical Statistics 1996, 5, 299–314. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, 1961; Vol. I, pp. 547–561. [Google Scholar]
© 2005 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Nadarajah, S.; Kotz, S. On the Linear Combination of Exponential and Gamma Random Variables. Entropy 2005, 7, 161-171. https://doi.org/10.3390/e7020161
Nadarajah S, Kotz S. On the Linear Combination of Exponential and Gamma Random Variables. Entropy. 2005; 7(2):161-171. https://doi.org/10.3390/e7020161
Chicago/Turabian StyleNadarajah, Saralees, and Samuel Kotz. 2005. "On the Linear Combination of Exponential and Gamma Random Variables" Entropy 7, no. 2: 161-171. https://doi.org/10.3390/e7020161
APA StyleNadarajah, S., & Kotz, S. (2005). On the Linear Combination of Exponential and Gamma Random Variables. Entropy, 7(2), 161-171. https://doi.org/10.3390/e7020161


