On the Entropy Production Due to Explosion in Seawater
Abstract
:Introduction
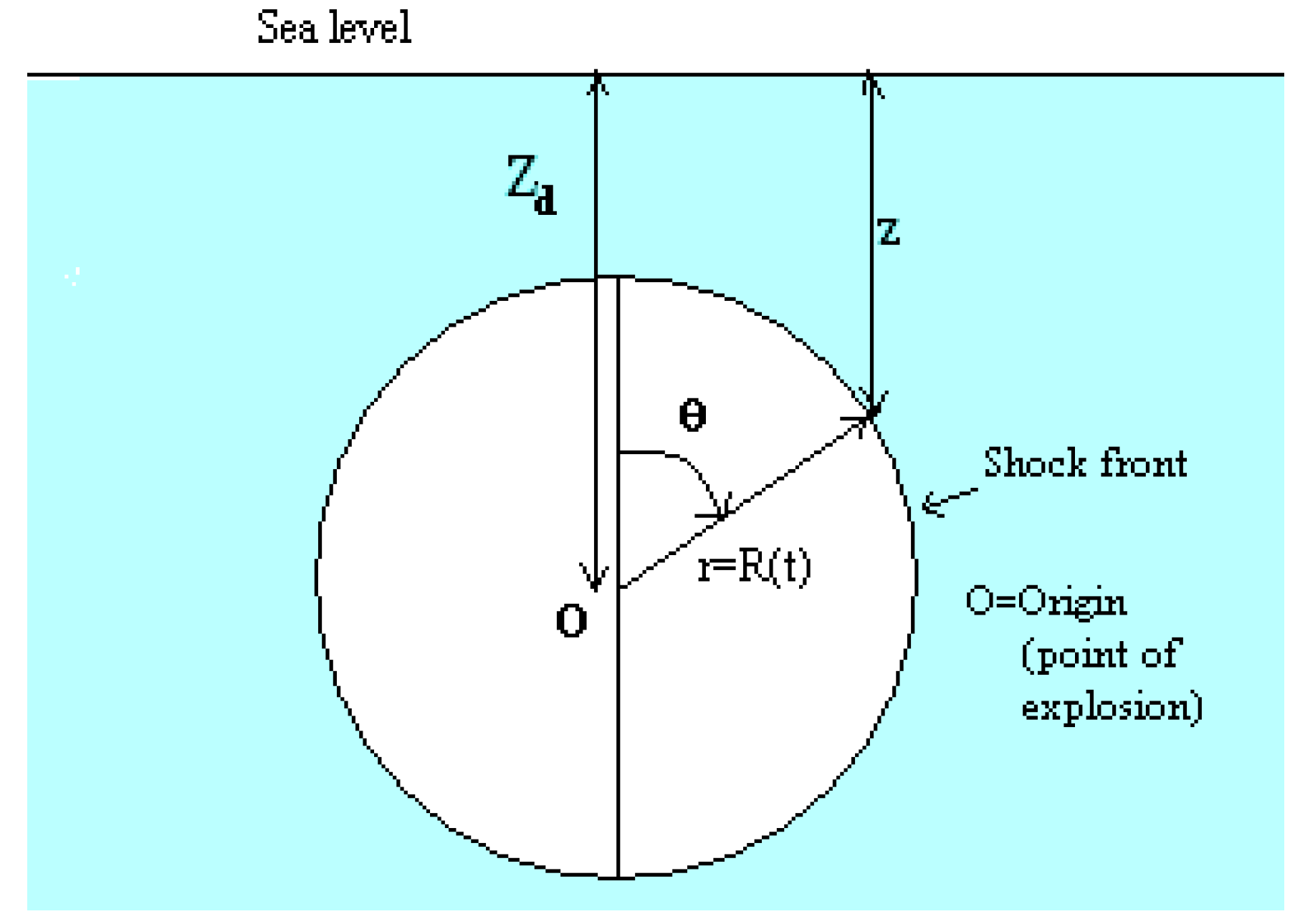
Basic formulation
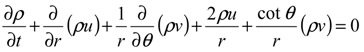


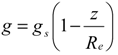

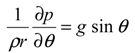

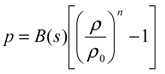

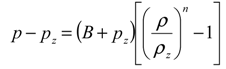
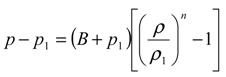
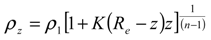
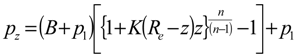
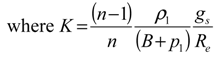
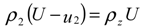
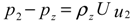
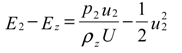

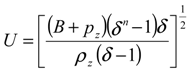
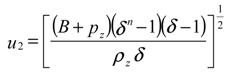

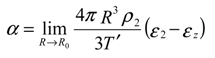
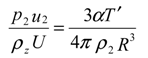



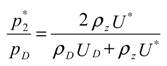
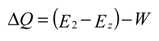
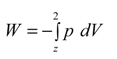
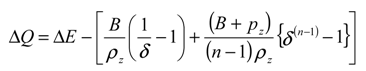
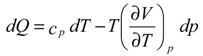
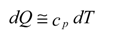
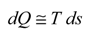

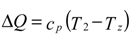
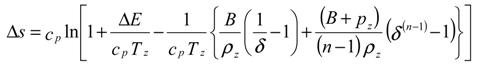
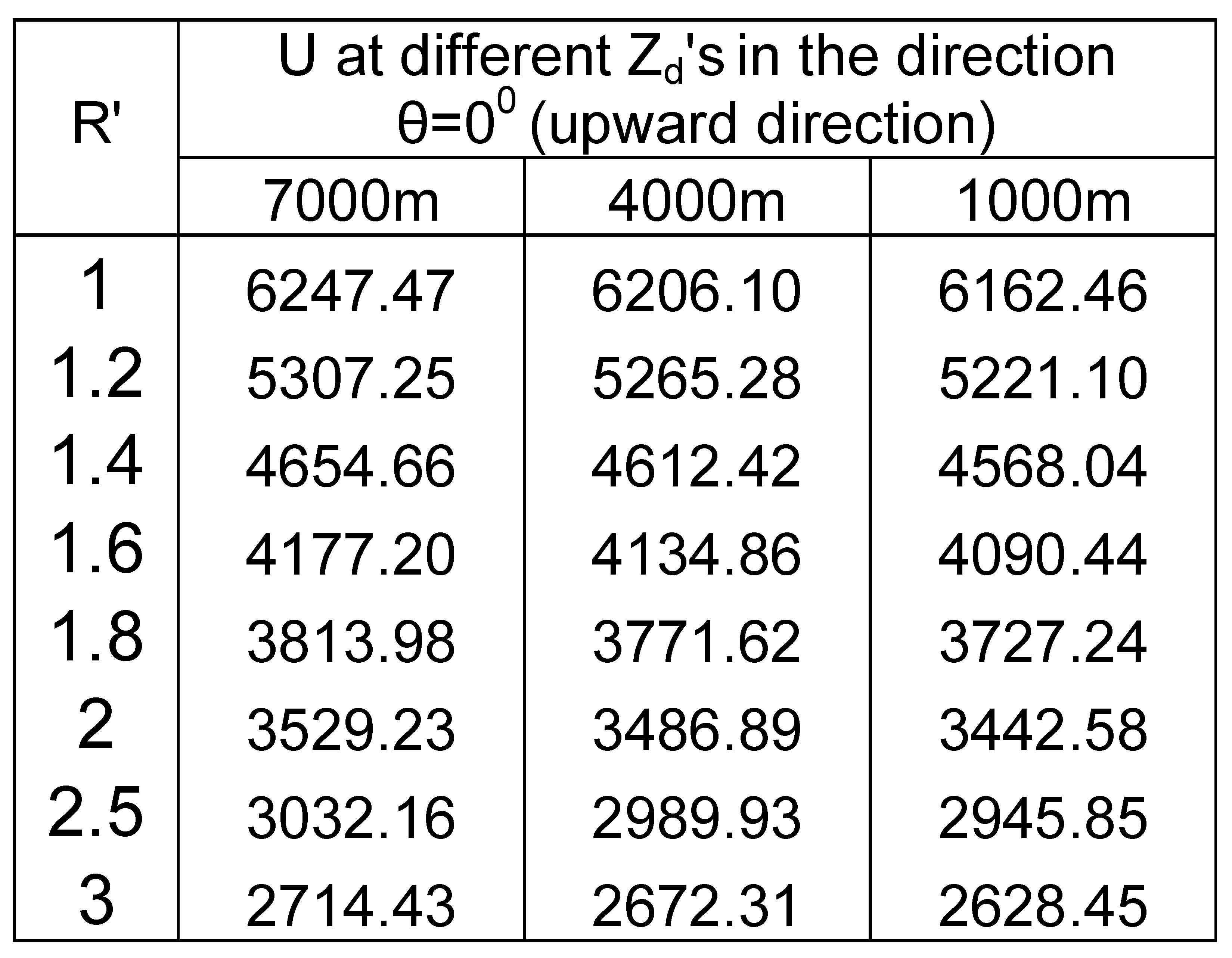
Results
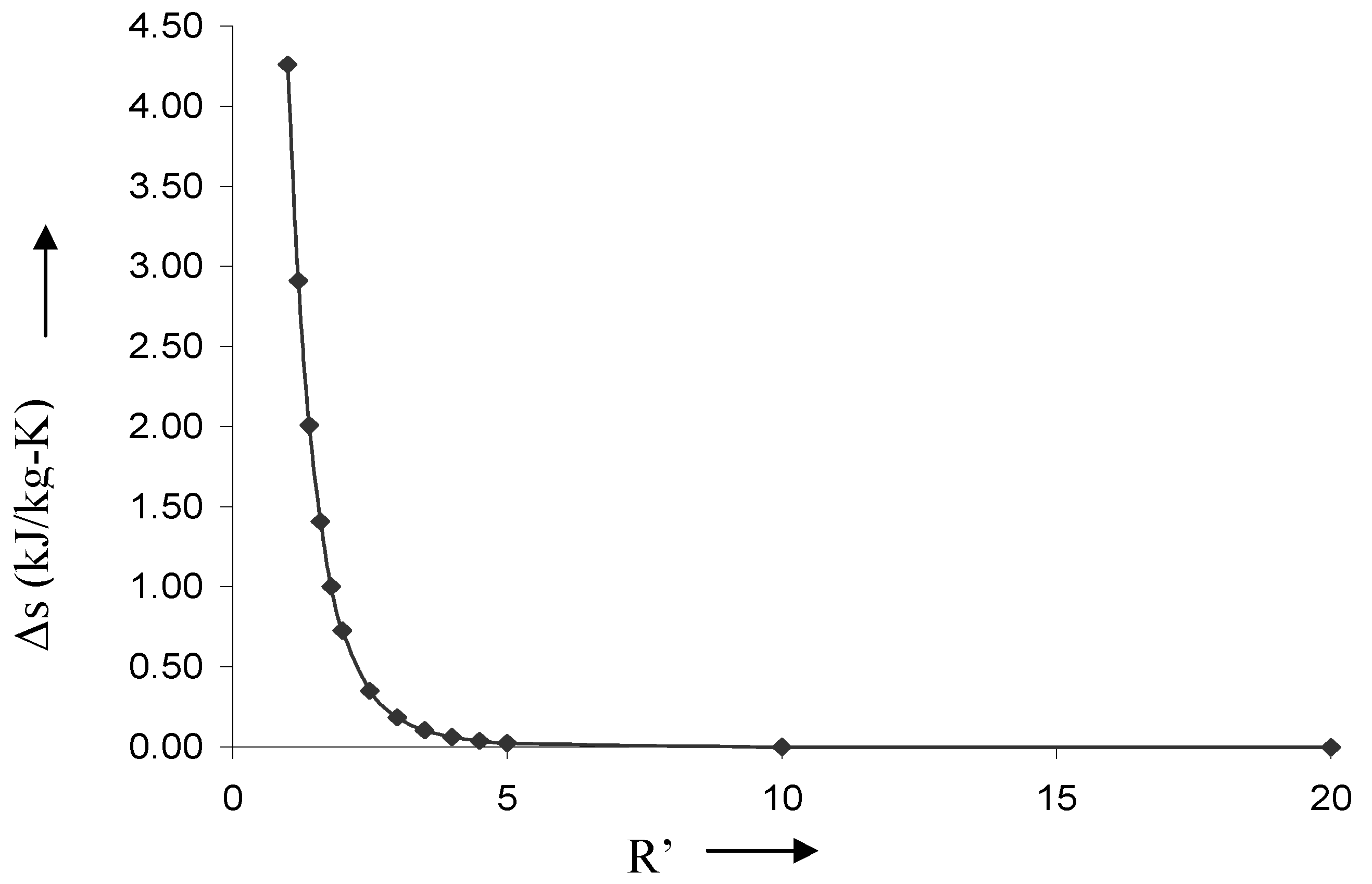
Analysis of results
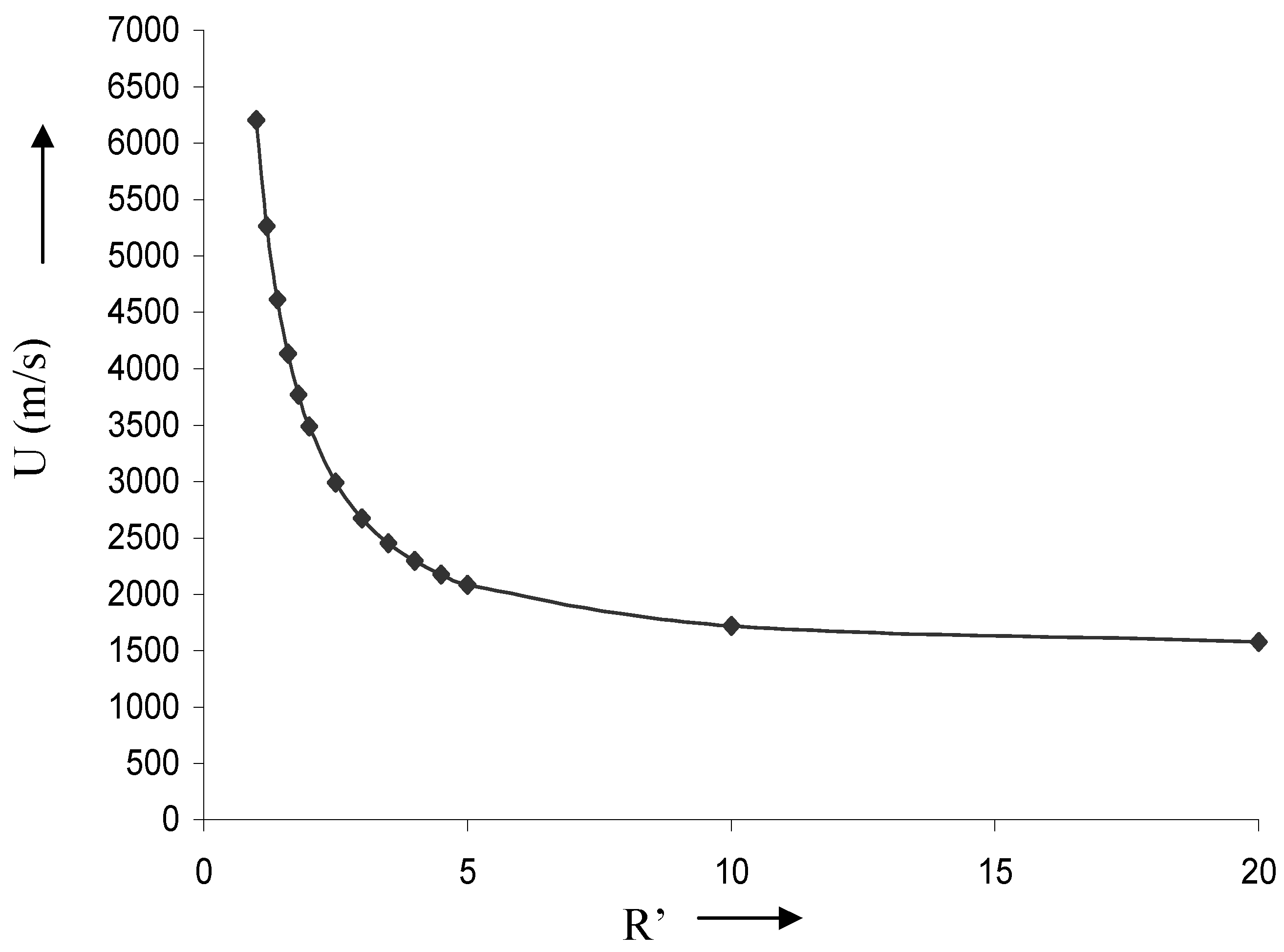
Characteristics curves for blast waves:
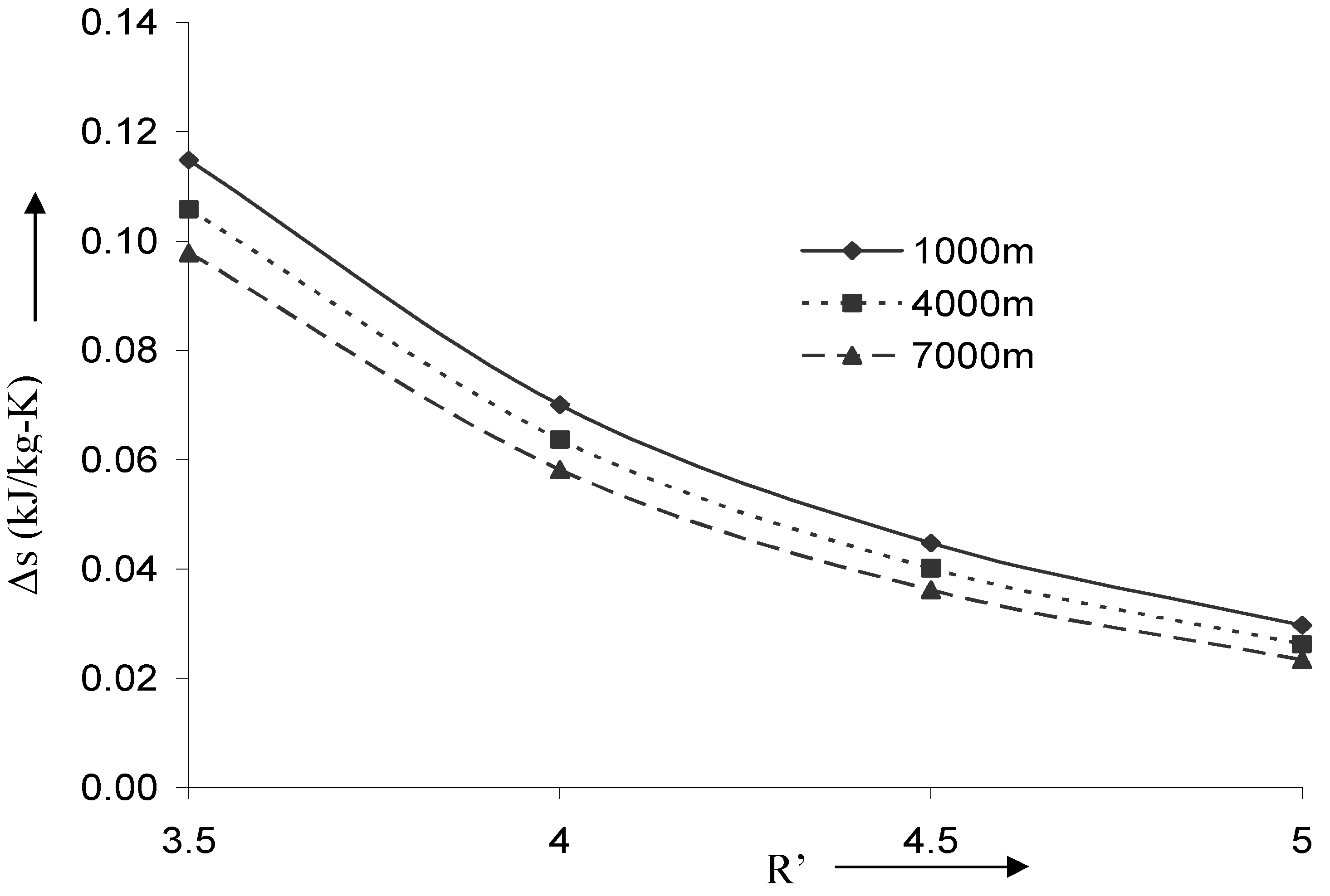
Effect of depth of explosion:
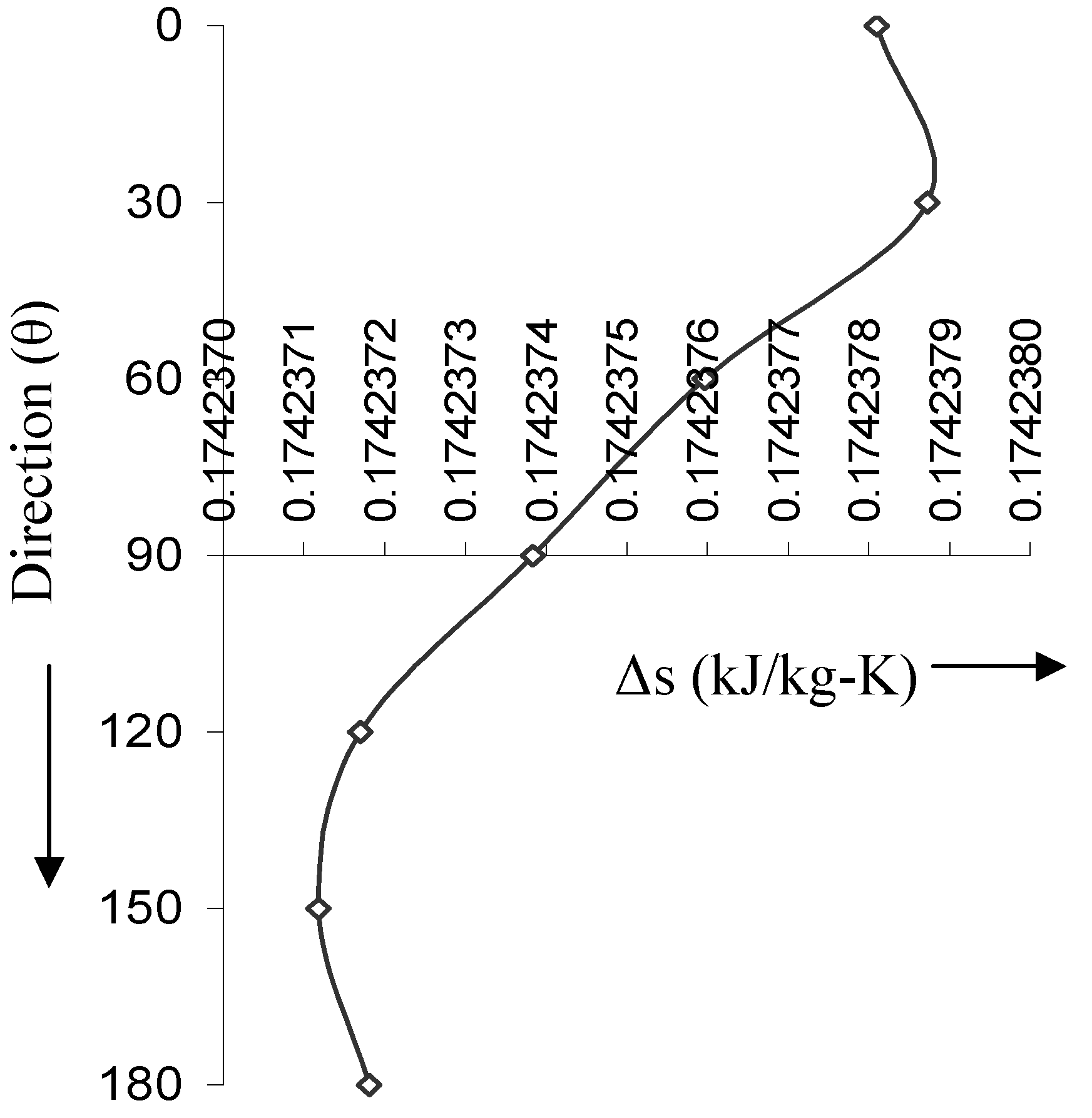
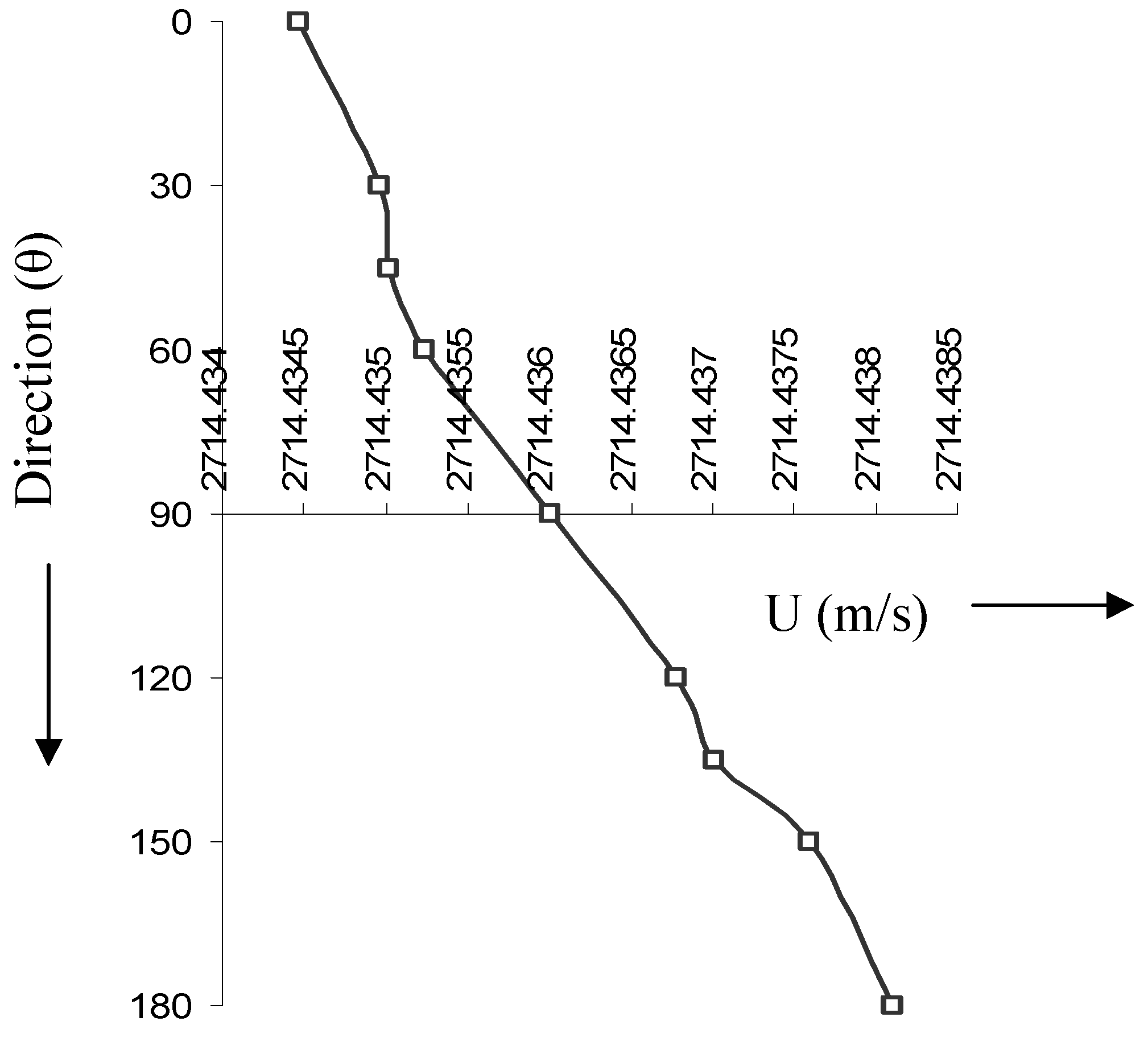
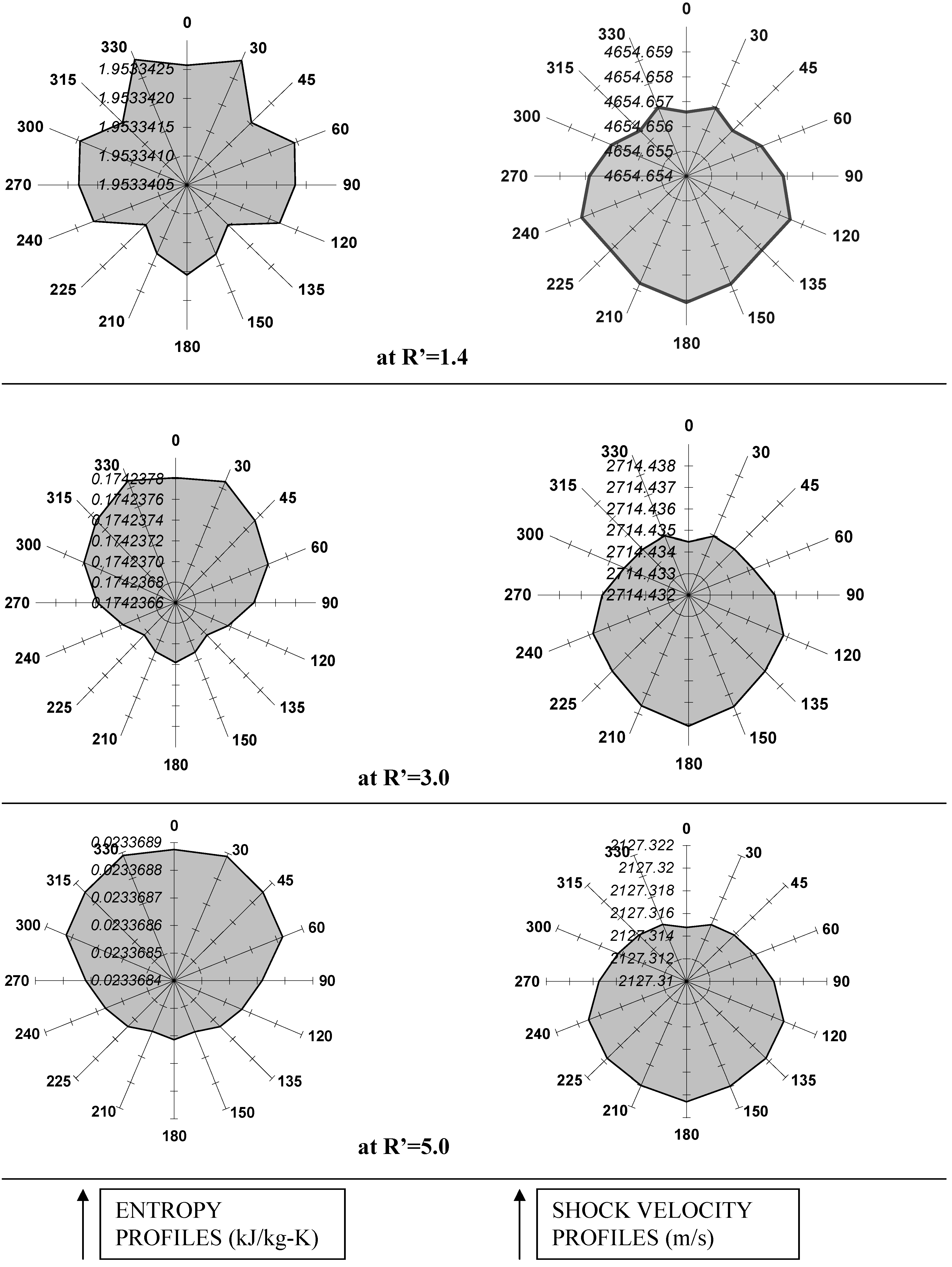
Directional dependence of entropy production:
Conclusion
Data used:
| 1. Re = 6371230 m | 2. gs = 9.81 m/s2 | |
| 3. B(s) = 2.94 kb [4,11] | 4. n = 7.25 [4,11] | |
| 5. p1 = 1 b | 6. ρ1 = 1027 kg/m3 [23] | |
| 7. Tz (average temperature in deep sea) = 276 K [ 23] | ||
| 8. cp = 4.186 kJ/kg-K | ||
| 9. Detonation data for the explosive RDX/TNT (60:40), [18]:- | ||
| • R0 = 0.0375 m | • Mass of the charge = 0.365 kg | |
| • ρD = 1680 kg/m3 | • UD = 7800 m/s | |
| • pD = 255.528 kb | • T’ = 2252.11 kJ | |
Nomenclature
| R0 = radius of spherical charge (m) | |
| Z d = depth of explosion (m) | Superscripts |
| p = pressure of fluid (seawater) | * = at the explosive boundary |
| g = defined in equation (4) | |
| gs= acceleration due to gravity at the surface of earth (m/s2) | Subscripts |
| Re= radius of earth (m) | z = unshocked state at a depth z |
| r = radial distance from the point of explosion | 0 = state at zero pressure |
| z = depth of any point from the water surface (m) | 1 = state at the water surface |
| u = radial component of fluid velocity (m/s) | 2 = state just behind the shock front |
| v = transverse component of fluid velocity (m/s) | D = detonation |
| U = shock velocity (m/s) | |
| R = shock radius (m) | |
| R’ = nondimensional shock radius (=R/R0) | |
| n = a constant for water | Greek letters |
| B(s)= slowly varying function of entropy, normally considered as constant (kb) | ρ =density of fluid (seawater) |
| θ = angle measured from vertical direction | |
| T’ =energy released during explosion (J) | δ = compression ratio (ρ2/ρz) |
| UD= detonation velocity (m/s) | ε = total energy /unit mass (sum of internal and kinetic energies for unit mass = E+½ u2) |
| cp =specific heat of water (kJ/kg-K) | |
| T = absolute temperature (K) | |
| E = internal energy/unit mass (J/kg) | α =constant defined in equation (22) |
| V = specific volume (m3/kg) | |
| W = work, defined in equation (29) | |
| s = specific entropy (entropy /unit mass)(kJ/kg-K) | |
| ∆Q = heat flow / unit mass (J/kg) |
References
- Berger, S.A.; Holt, M. Implosive phase of spherical explosion in sea water. Phy. Fluids 1962, 5(no.4), 426–431. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Sachdev, P.L.; Prasad, P. Spherical piston problem in water. J. Fluid Mech. 1969, 39, 587–600. [Google Scholar] [CrossRef]
- Bhutani, O.P. Propagation and attenuation of a cylindrical blast wave in magnetogasdynamics. J. Math. Anal. Applic. 1966, 13, 565–576. [Google Scholar] [CrossRef]
- Brand, R.S. Development in mechanics; Ostrach, S., Scanlin, R.H., Eds.; 1965; vol.2, part1; p. 507. [Google Scholar]
- Buchanan, J.S.; James, H.J. Measurement of high intensity stress pulses. British J. Appl. Phys. 1959, 10, 290–295. [Google Scholar] [CrossRef]
- Cole, R.H. Under water explosions; Dover, 1948; p. 40. [Google Scholar]
- Courant, R.; Friedrichs, K.O. Supersonic flow and shock waves; Interscience, 1948; p. 132. [Google Scholar]
- Dincer, I.; Cengel, Y.A. Energy, Entropy and Exergy concepts and their role in thermal engineering. Entropy 2001, 3, 116–149. [Google Scholar] [CrossRef]
- Hartree, D.R. Numerical analysisOxford university press: London, 1962, 2 nd ed. [Google Scholar]
- Henderson, L.F. On the thermodynamic stability of steady state adiabatic systems. J. Fluid Mech. 1988, 189, 509–529. [Google Scholar] [CrossRef]
- Hunter, C. On the collapse of an empty cavity in water. J. Fluid Mech. 1960, 8, 241–263. [Google Scholar] [CrossRef]
- Kirwood, J.G.; Bethe, H.A. Basic propagation theory. OSRD 588, 1942. [Google Scholar]
- Kirwood, J.G.; Brinkley, S.R., Jr. Theory of the propagation of shock waves from explosive sources in air and water. OSRD 4814, 1945. [Google Scholar]
- Penny, W.G.; Dasgupta, H.K. Underwater explosion research. ONRB report RC-333. 1942. [Google Scholar]
- Prigogine, I. Introduction to thermodynamics of irreversible processInterscience Pub., 1955, 2nd ed.; p. 81. [Google Scholar]
- Ranga Rav, M.P.; Ramana, B.V. Self similar flow with increasing energy, forth piston driven flow of water. Int. J. Engng. Sci. 1973, 11, 1317–1327. [Google Scholar] [CrossRef]
- Resnick, R.; Halliday, D.; Walker, J. Fundamentals of Physics; Willey eastern: New Delhi, 2004; p. 301. [Google Scholar]
- Singh, V.P. Modification of energy hypothesis for the case of explosive charge. Ind. J. Pure Appl. Math. 1976, 7(no.2), 147–150. [Google Scholar]
- Singh, V.P. Spherical shock wave in water. Ind. J. Phys. 1972, 46, 547–555. [Google Scholar]
- Singh, V.P. On underwater explosions- A comparative study. Def. Sci. J. 1982, 32, 327–332. [Google Scholar] [CrossRef]
- Singh, V.P.; Bola, M.S. A note on explosive shock in homogeneous water. Ind. J. Pure Appl. Math. 1976, 7(no. 12), 1405–1410. [Google Scholar]
- Singh, V.P.; Madan, A.K.; Suneja, S.R.; Lal, C. Propagation of spherical shock wave in water. Proc. Ind. Acad. Sci.,(Engg. Sci.) 1980, 3, 169–175. [Google Scholar]
- The times atlas of the oceans. Van nostrand reinhold co.: New York, 1983.
- Thomas, T.Y. On the propagation and decay of spherical blast waves. J. Math. Mech. 1957, 6, 607–620. [Google Scholar] [CrossRef] [Green Version]
- Vishvakarma, J.P.; Nagar, K.S.; Mishra, R.B. On the propagation of shock wave produced by explosion of a spherical charge in deep sea. Def. Sci. J. 1988, 38(no.1), 69–76. [Google Scholar] [CrossRef]
- Zemansky, M.W.; Dittman, R.H. Heat and thermodynamics; Mc Graw Hill.: NewYork, 1997; pp. 52–53, 267, 215. [Google Scholar]
2005 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Yadav, R.P.; Agarwal, P.K.; Sharma, A. On the Entropy Production Due to Explosion in Seawater. Entropy 2005, 7, 134-147. https://doi.org/10.3390/e7020134
Yadav RP, Agarwal PK, Sharma A. On the Entropy Production Due to Explosion in Seawater. Entropy. 2005; 7(2):134-147. https://doi.org/10.3390/e7020134
Chicago/Turabian StyleYadav, R. P., P. K. Agarwal, and Atul Sharma. 2005. "On the Entropy Production Due to Explosion in Seawater" Entropy 7, no. 2: 134-147. https://doi.org/10.3390/e7020134
APA StyleYadav, R. P., Agarwal, P. K., & Sharma, A. (2005). On the Entropy Production Due to Explosion in Seawater. Entropy, 7(2), 134-147. https://doi.org/10.3390/e7020134