Abstract
Characterizing the topology and random walk of a random network is difficult because the connections in the network are uncertain. We propose a class of the generalized weighted Koch network by replacing the triangles in the traditional Koch network with a graph according to probability and assign weight to the network. Then, we determine the range of several indicators that can characterize the topological properties of generalized weighted Koch networks by examining the two models under extreme conditions, and , including average degree, degree distribution, clustering coefficient, diameter, and average weighted shortest path. In addition, we give a lower bound on the average trapping time (ATT) in the trapping problem of generalized weighted Koch networks and also reveal the linear, super-linear, and sub-linear relationships between ATT and the number of nodes in the network.
1. Introduction
Complex networks are acknowledged as an invaluable system for describing nature and society [1,2]; many endeavors have been devoted to exploring the structure and properties of complex networks for characterizing and simulating the properties of some real-world systems in our life. Among all of these properties, the scale-free nature, diameter, and clustering coefficient have attracted considerable attention [3,4,5]. In addition, the weight of the network has important research significance in air transportation [6], biological neural networks [7] and so on. Therefore, it is necessary to explore the influence of weight on the topological properties and dynamic process of the network, so we also determine the bound of the average weighted shortest path of network designed in this paper.
To better understand the properties of random networks in complex networks, extensive technical methods were developed for establishing a variety of theoretical models of random networks. For example, the well-known ER-model was proposed by Erdos and Renyi [8] to try to explain a low clustering coefficient and low variation in the node degrees; its degree distribution was verified to be Poisson distribution. Watts and Strogatz put forward a small-world WS-model [9], which can rationally reflect the statistical properties of the network that are neither completely regular nor entirely random and explain small-world phenomena in various real-world networks by exploring the diameter and clustering coefficient. The BA model was built by Barabasi et al. [10] using two rules, growth and preferential attachment; the degree distribution of the latter two networks obeys a power–law distribution. In this paper, we introduce a class of generalized weighted Koch networks with probability p. The ranges of their topological parameters are given by characterizing the topological characteristics of the deterministic network models under the two extreme states.
Random walk as a fundamental tool to describe the dynamic process of networks, such as page search in the world wide web [11], signal propagation [12] and energy transport [13]. The trapping problem is defined as a kind of random walk that takes place in networks in the presence of a fixed trap, absorbing all particles that visit it [14,15]. A basic quantity relevant to the trapping problem is called the mean first-passage time (MFPT). The MFPT from a node i to the trap is the expected time taken by a walker starting from i to reach the trap for the first time. The average trapping time (ATT) is the average of MFPTs over all starting nodes other than the trap. The ATT for a given trap is used as a indicator of the trapping efficiency to evaluate the process of trapping; it has a core position in many disciplines, including computer, biology, engineering and so on [16,17,18].
The organization of this paper is as follows. In Section 2, we introduce a method about constructs the generalized weighted Koch networks, according to probability p. In Section 3, we characterize several parameters that reveal the topological properties and dynamic processes of our network, including average degree, degree distribution, clustering coefficient, diameter, average weighted shortest path, and average trapping time. In the last section, we draw the conclusion with a concise narrative.
2. The Generalized Weighted Koch Network
The generalized weighted Koch network presented in this paper is controlled by three parameters , where r is the weight factor and t is the time step, and s and t are positive integers. We mainly explore the influence of the parameter s and the weight r related to the topology on the topological properties and dynamic characteristics of the network.
Let and be a cycle with s nodes and a fully connected graph with s nodes, respectively. We introduce a probability , then can be created in the following way: for , the network starts with a graph of s nodes, and its edge with unit weight corresponds to . When , is a cycle of s nodes, and when , is a complete graph of s nodes. For , is obtained by adding a node group for each node in every existing graph of , where each node group can be a cycle with probability p or a complete graph with complementary probability ; this rule is shown in Figure 1. We repeat this growth process until the network becomes what we need.
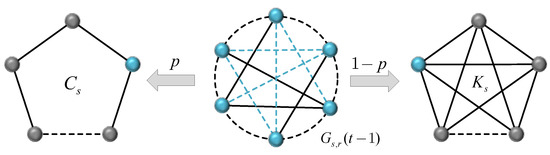
Figure 1.
Iterative rule of the generalized weighted Koch network.
Additionally, for the generalized weighted Koch network we proposed, if and are satisfied, we can obtain the classic Koch network mentioned in the literature [19]; when , we can obtain the expanded Koch networks referred to in Ref. [20]. For , the network is simplified to the weighted Koch network in Ref. [21]. The above network models are all special cases of the generalized weighted Koch networks constructed in this paper.
That is to say, can be obtained from by the recursive method, where one can connect each node of existing cluster in with a graph of s nodes according to probability . We denote the two networks corresponding to the extreme conditions and as and , respectively. Figure 2 and Figure 3 show the growing process of the two determined networks at . Some topological properties and ATT of have been described in the literature [22,23], so we mainly focus on the topological properties and ATT of , then estimate the range of parameters of random network by studying the characteristics of two deterministic networks and .
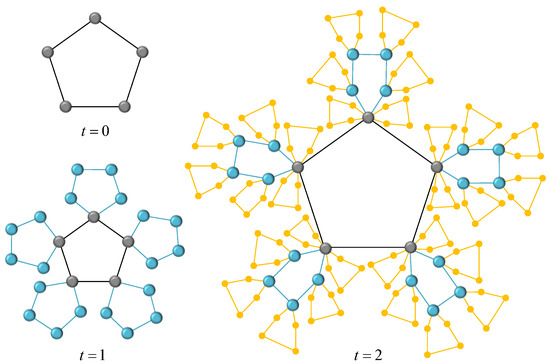
Figure 2.
The network at first three time steps when and .
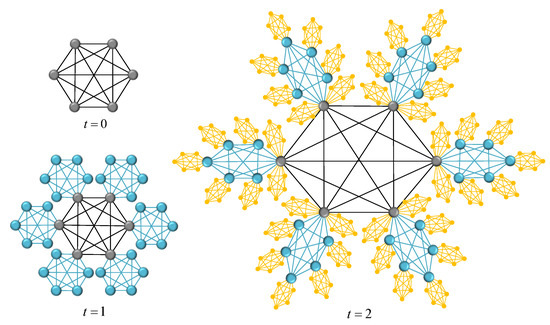
Figure 3.
The network at first three time steps when and .
Let and be the number of nodes and edges of network , and let and be the number of new nodes and new edges created at time step t, that is and . Additionally, or in Figure 1 is regarded as a cluster , the total number of new generated clusters in the at time step t is recorded as , and combining and the initial value , we have . Based on the construction method, we obtain
The number of nodes and edges of networks and are denoted by and , . The difference between and is that the cluster selected by the probability p is not the same, the number of nodes of all is s, but the number of their edges is different. So, we have , and they can be calculated as
For the number of new edges created at time step t in the network , we obtain . According to the iterative construction of , we calculate the total number of edges in the network as follows,
Similarly, we examine the number of new edges created at time step t in , it is equal to , thus, the total number of edges in is equal to
Therefore, we can obtain the range of the number of edges of the generalized weighted Koch network , which satisfies .
Referring to Ref. [22], the average degree of is for . On the other hand, the solution of average degree of is
where is approximately s for a large t, which shows that the two networks and are sparse networks according to the standard proposed in the literature [24] because the condition is clearly established. Therefore, we obtain that the range of average degree of the generalized weighted Koch network satisfies .
3. Topological Properties and ATT
Next, we discuss some relevant topological characteristics of our network, including degree distribution, clustering coefficient, diameter and average weighted shortest path, and give the lower bound of the ATT for our networks.
3.1. Degree Distribution
The degree distribution is a physical quantity that describes the overall characteristics of the network. It is defined as the probability that a randomly selected node in the graph has exactly k associated edges. Cumulative degree distribution is defined as the probability that the degree of a node is greater than or equal to k, that is, . Many networks are regarded as scale-free when their cumulative degree distribution approximately follows a power–law distribution and the power exponent lies between 2 and 3 [25].
Theorem 1.
The cumulative degree distribution of the network obeys a power law distribution
and is a scale-free network if, and only if, .
Proof.

Let be the degree of node i in network at time step t. When node i joins the network at time step , there is only one connected to it, so we have . We can find that the degree of node i depends on the number of cluster , including it. Let be the number of cluster including node i at time step t. We can establish the following relation , considering the initial condition , so . Further, there is a relationship between and ,
We know that the degree of node i satisfies , which shows that the degree spectrum of is discrete. Table 1 lists the degree spectrum of the two networks and , and represents the number of nodes with degree .

Table 1.
The degree spectrum of and .
Analyzing the degree spectrum of , we can obtain its cumulative degree distribution,
we can solve for from Equation (7) and substitute into Equation (8), then
when t is large enough, the cumulative degree distribution follows a power law with exponent if, and only if, , considering that the range of the parameter s is , so the network is a scale-free network when . On the other hand, the cumulative degree distribution of can be found in [22]. It is expressed as , which shows that the network also satisfies the properties of the scale-free network when . Therefore, we can judge that the generalized weighted Koch network has a remarkable scale-free property when . When , the degree distribution of obeys a power-law distribution and the exponent is . □
3.2. Clustering Coefficient
The overall clustering coefficient of a network is used to quantity the ability of the network to agglomerate, while the local clustering coefficient can measure the agglomeration near each node in the network. The local clustering coefficient corresponding to node i is defined as the ratio between the number of existing edges connecting its neighbors and the number of all possible edges between them, that is, [26]. The overall clustering coefficient of the network is denoted as ; it is defined as the average of over all nodes in the network.
Theorem 2.
For the network , the solution of the overall clustering coefficient of the whole network satisfies
Proof.

According to the structure of the network , it can be judged that the nodes with the same degree have the same local clustering coefficient. Therefore, Table 2 shows the local clustering coefficient and the corresponding number of nodes. represents the number of nodes with degree , and is the local clustering coefficient of each node with degree . Therefore, the overall clustering coefficient of is

Table 2.
The local clustering coefficient of node in network .
In the limit of , we have , which indicates that the network is high clustered. We can control the clustering coefficient by adjusting parameter s. For network , when , the clustering coefficient is approximately in the large limit of t; otherwise, the clustering coefficient of in other cases is always equal to zero. Therefore, the generalized weighted Koch networks transition from low clustered to high clustered, as the probability p keeps increasing in the interval . □
3.3. Diameter
The diameter of a network is used to measure information transmission delays and find vital nodes in the network. It is defined as the largest distance between any pair of nodes. Let and denote the diameters of and , respectively.
Theorem 3.
The diameter of the network is equal to
The diameter of the network is
Proof.
By the topological structure of , we find that a node on the cycle can only reach another node through a path on the cycle, so we discuss the diameter of the network according to the parity of the number of nodes.
Case 1. When s is even, we assume that the two nodes with the farthest distance in the network are and . In network , is the farthest node to among the new neighbors of , and is the farthest node to among the new neighbors of . New neighbors refer to those nodes generated at time step t among all neighbors. Then, the diameter of refers to the distance between nodes and ; we can obtain the following equation,
with the help of , we can obtain
Case 2. When s is odd, the diameter of the network at two consecutive time steps and t satisfies the following relationship:
where it is obvious that the diameter of the smallest network is , so the expression of diameter can be obtained according to the above recursive formula,
Considering the construction algorithm of , the diameters of and at two consecutive time steps have the following rule:
the initial condition is , then for any , we have
Theorem 3 shows that the propagation efficiency of is more efficient than that of . Among all generalized weighted Koch networks, the network has the largest diameter and the network has the smallest diameter. Thus, we can determine that the diameter of the generalized weighted Koch network satisfies . □
3.4. Average Weighted Shortest Path
In this subsection, we take the weight into account to examine the shortest path between two nodes in our networks. The average weighted shortest path is defined as , where , denotes the weighted shortest path connecting node i and j in network [27,28]. We only determine the lower bound of for our network by calculating the average weighted shortest path of .
Theorem 4.
For the networks , when , its average weighted shortest path is
when , then
the values are in Appendix A. They are constants that depend on the parameter s and the weight r, and do not depend on the time step t.
Proof.
The recursive construction of the network allows us to calculate the . The network can be divided into branches, which we label as for , the center branch is a copy of , and , , ⋯, have the same structure as , but their edge weights are scaled by a factor of r. We denote the connected nodes as , which connect the copy and other copies , . Therefore, the total of the shortest distances satisfies the following relation,
where is the sum over all shortest paths whose nodes are not in the same copy of , that is to say, the paths in must all go though at least one of the s connected nodes , , ⋯, . The first term on Equation (22) is the sum of weighted shortest path linking node i and j in every , . Considering the scaling of the edges, we have
Next, the analytical expression for is not difficult to find. We denote as the sum of all shortest paths with nodes in and ; there are two different situations that need to be discussed. Let denote the sum of the distances of the nodes in to the nodes in for . Moreover, represents the sum of nodes in different , which must pass through , but their end node is not in . Thus, we have
It can be seen from the above formula that we need to calculate and to obtain . We define a variable
which represents the sum of the distances from all nodes in to node ; specifically, we can obtain the following result for ,
Considering the self-similar structure at time step t, we know that the quantity evolves recursively as
We obtained the recursive relation of , and combined with the initial condition given by Equation (26), we can calculate the expression of ,
Then, we calculate the two variables and through the variable , and the following two cases are discussed.
Case 1. This situation shows that one of and must be equal to 1 because only copy and other copies have a common node. Let and have a common node , where . For two nodes , and , we have
Case 2. and have no common node, so it must cross two nodes and in copy from node i to j.
where is used, and refers to other nodes on except node . Substituting Equations (29) and (30) into Equation (24), we have
Considering Equations (2) and (28), then substituting them into Equation (31), we obtain the following.
If , then
If , we have
According to Equation (22) and the initial condition , the result of can be obtained by the recursive formula. If , we have
When , we obtain
Further, according to the equation , substituting Equations (34) and (35) into it, we can obtain the average weighted shortest path for ,
For , we can obtain
where are constants that do not depend on the time step t, they are only related to s and r. Appendix A contains the detailed values of . Therefore, we can determine that the lower bound of the average weighted shortest path of network is equal to . □
3.5. ATT on Random Walk with Weight
Next, we derive analytically the average trapping time on random walk with weight and show how it scales with the network order and parameters r and s. The strength of a node integrates the information concerning its connectivity and the weights of its edges. Let be the strength of node i. The walker starting from a given node i moves to its neighbor node j with probability at each step, and the transition probability from node i to j is
where is the neighbors of node i. For the convenience of description, let us denote all nodes in by , and represent other nodes generated at time step t. Let be the MFPT from node i to the trap. denotes the ATT, which is defined as the mean of starting from all sources of nodes over the whole network to the trap node. It is the core issue considered in this subsection. By definition, is given by
and further, we denote the sum of MFPTs for all nodes to absorption at the trap located the one of the nodes of as , that is
Theorem 5.
Let be a weight factor. When , the average trapping time of the network is
when , then
where is in Appendix B. The relationship between the average trapping time and the network order can be expressed as
Proof.
For a certain time step , the nodes generated at time step are called new nodes, and the nodes added to the network before time step are called old nodes. Then, we let X be the MFPT starting from node i to any of its old neighbors, and let Y be the MFPT from any of new neighbors of node i to one of its old neighbors; thus, we can establish the following relations among X and Y,
We obtain that the result is . Upon the evolution of the weighted network from time step t to time step , the trapping time for an arbitrary node i increases by a factor of , that is
Next, we consider the MFPT of all nodes in light of the classification of new nodes and old nodes, which is written as the following formula:
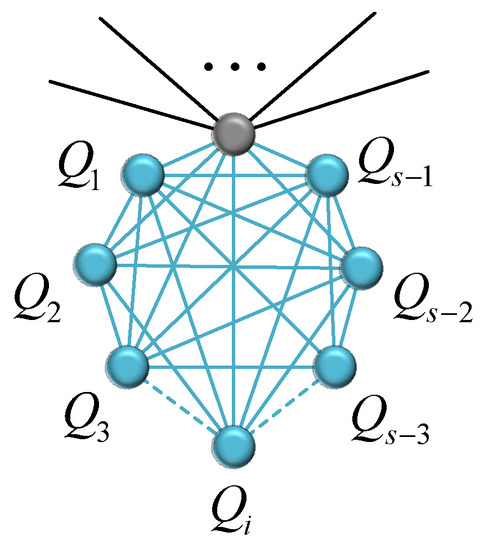
where is the sum of MFPTs for all new nodes. Equation (46) shows that the focus of our calculation is . According to the construction of network , as shown in Figure 4, for the new complete graph involving a node v, the first passage times for its nodes , , ⋯, and , and that of its old node v follow the relations,

Figure 4.
The positional relationship between node v and its neighbors.
According to the above equations, we obtain
summing Equation (48) over all the old pre-existing at the time step t. Let be the set of all nodes of the . It contains all old nodes in network ,
Similarly, it is not difficult to write as
Considering , substituting into Equation (51), we can compute Equation (51) to yield
substituting Equation (52) into Equation (46) and taking the initial value into consideration. When , we have
If , we obtain
Substituting Equations (53) and (54) into Equation (40), if , we obtain
where are constants independent of t, so for . Additionally, if , we can obtain
where are parameters that have nothing to do with t, as they are only related to parameters r and s. The detailed values of are given in Appendix B. Next, we show how to express in terms of network order . We can obtain from , so we have
for . The above results show that grows linearly with the network order when , while grows sub-linearly and super-linearly with if and , respectively. We find that the weight r can modify not only the prefactor of , but also the scaling of . This means that the lower bound of the ATT with the weight of the generalized weighted Koch network is . □
4. Conclusions
In this paper, we construct a class of random networks according to probability p and normal Koch networks, and give the necessary and sufficient conditions for such networks to be scale free. For two deterministic network models and corresponding to two extreme conditions and , we give exact solutions for topological parameters, including the clustering coefficient, diameter, average weighted shortest path and average trapping time. In view of this, we determine the range of topological parameters of random network . Furthermore, we reveal the effect of weights on ATT, that is, ATT grows linearly with the network order when the weight ; otherwise, ATT grows superlinearly and sub-linearly with the network order when and . These topological features and dynamic characteristics allow us to better understand some fundamental properties of complex networks.
Author Contributions
Conceptualization, B.Y. and J.S.; writing—original draft preparation, J.S. and M.Z.; writing—review and editing, J.S. and B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Plan under Grant No. 2019YFA0706401 and the National Natural Science Foundation of China under Grants No. 61872166 and No. 61662066. The Technological Innovation Guidance Program of Gansu Province: Soft Science Special Project (21CX1ZA285). The Northwest China Financial Research Center Project of Lanzhou University of Finance and Economics (JYYZ201905).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Values of A1–A6
In Appendix A, we give the analytical values of involved in Theorem 4.
Appendix B. The Values of B1–B6
In Appendix B, we give the values of involved in Theorem 5.
References
- Al-Tarawneh, A.; Al-Saraireh, J. Efficient detection of hacker community based on twitter data using complex networks and machine learning algorithm. J. Intell. Fuzzy Syst. 2021, 40, 12321–12337. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, Y.; Guo, Y.; Xie, Y. Evolutionary dynamics of cooperation with the celebrity effect in complex networks. Chaos 2021, 31, 013130. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhang, H.; Zeng, C.; Xue, Y. Scale-free and small-world properties of a multiple-hub network with fractal structure. Phys. A Stat. Mech. Its Appl. 2020, 558, 125001. [Google Scholar] [CrossRef]
- Pi, X.; Tang, L.; Chen, X. A directed weighted scale-free network model with an adaptive evolution mechanism. Phys. A Stat. Mech. Its Appl. 2021, 572, 125897. [Google Scholar] [CrossRef]
- Rak, R.; Rak, E. The Fractional Preferential Attachment Scale-Free Network Model. Entropy 2020, 22, 509. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wang, J.; Huang, G.Q. Efficiency and robustness of weighted air transport networks. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 14–26. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, J.; Liu, J. Neural Network With Multiple Connection Weights. Pattern Recognit. 2020, 107, 107481. [Google Scholar] [CrossRef]
- Erdos, P.; Renyi, A. On Random Graphs I. Publ. Math. 1959, 4, 3286–3291. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 5439, 509–512. [Google Scholar] [CrossRef] [Green Version]
- Hwang, S.; Lee, D.S.; Kahng, B. First passage time for random walks in heterogeneous networks. Phys. Rev. Lett. 2012, 109, 088701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, X.H.; Zhao, S.Y.; Chen, X.Y. Community Detection Algorithm Based on Random Walk of Signal Propagation with Bias. Comput. Sci. 2019, 46, 45–55. [Google Scholar] [CrossRef]
- Defrenne, Y.; Zhdankin, V.; Ramanna, S.; Ramaswamy, S.; Ramarao, B.V. The dual phase moisture conductivity of fibrous materials using random walk techniques in X-ray microcomputed tomographic structures. Chem. Eng. Sci. 2018, 195, 565–577. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Julaiti, A.; Hou, B.Y.; Zhang, H.J.; Chen, G.R. Mean first-passage time for random walks on undirected networks. Eur. Phys. J. B—Condens. Matter 2011, 84, 691–697. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Zhang, Z.Z. Random walks in weighted networks with a perfect trap: An application of laplacian spectra. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 87, 062140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chelali, M.; Kurtz, C.; Puissant, A.; Vincent, N. From pixels to random walk based segments for image time series deep classification. In Proceedings of the International Conference on Pattern Recognition and Artificial Intelligence, Zhongshan, China, 19–23 October 2020. [Google Scholar]
- Baum, D.; Weaver, J.C.; Zlotnikov, I.; Knötel, D.; Tomholt, L.; Dean, M.N. High-throughput segmentation of tiled biological structures using random walk distance transforms. Integr. Comp. Biol. 2019, 59, 1700–1712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, K.; Gui, H.; Luo, Z.; Li, D. Matching for navigation map building for automated guided robot based on laser navigation without a reflector. Ind. Robot 2019, 46, 17–30. [Google Scholar] [CrossRef]
- Xie, P.C.; Lin, Y.; Zhang, Z.Z. Spectrum of walk matrix for Koch network and its application. J. Chem. Phys. 2015, 142, 175. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Z.; Gao, S.Y.; Xie, W.L. Impact of degree heterogeneity on the behavior of trapping in Koch networks. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, M.F.; Chen, D.D.; Dong, Y.J.; Liu, J. Scaling of average receiving time and average weighted shortest path on weighted Koch networks. Phys. A Stat. Mech. Its Appl. 2012, 391, 6165–6173. [Google Scholar] [CrossRef]
- Hou, B.Y.; Zhang, H.J.; Liu, L. Expanded Koch networks: Structure and trapping time of random walks. Eur. Phys. J. B 2013, 64, 156. [Google Scholar] [CrossRef]
- Ye, D.D.; Dai, M.F.; Sun, Y.Q.; Shao, S.; Xie, Q. Average receiving scaling of the weighted polygon Koch networks with the weight-dependent walk. Phys. A Stat. Mech. Its Appl. 2016, 458, 1–8. [Google Scholar] [CrossRef]
- Del Genio, C.I.; Gross, T.; Bassler, K.E. All scale-free network are sparse. Phys. Rev. Lett. 2011, 107, 178701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barabasi, A.L. Scale-free network. Sci. Am. 2003, 288, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, M. Mean clustering coefficient-on clustering measures for small-world networks. New J. Phys. 2008, 10, 083042. [Google Scholar] [CrossRef]
- Carletti, T.; Righi, S. Weighted Fractal Networks. Phys. A Stat. Mech. Its Appl. 2009, 389, 2134–2142. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Dai, M.F.; Xi, L.F. Scaling of average weighted shortest path and average receiving time on weighted hierarchical networks. Phys. A Stat. Mech. Its Appl. 2014, 407, 110–118. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).