The Potential of a Thick Present through Undefined Causality and Non-Locality
Abstract
1. Introduction
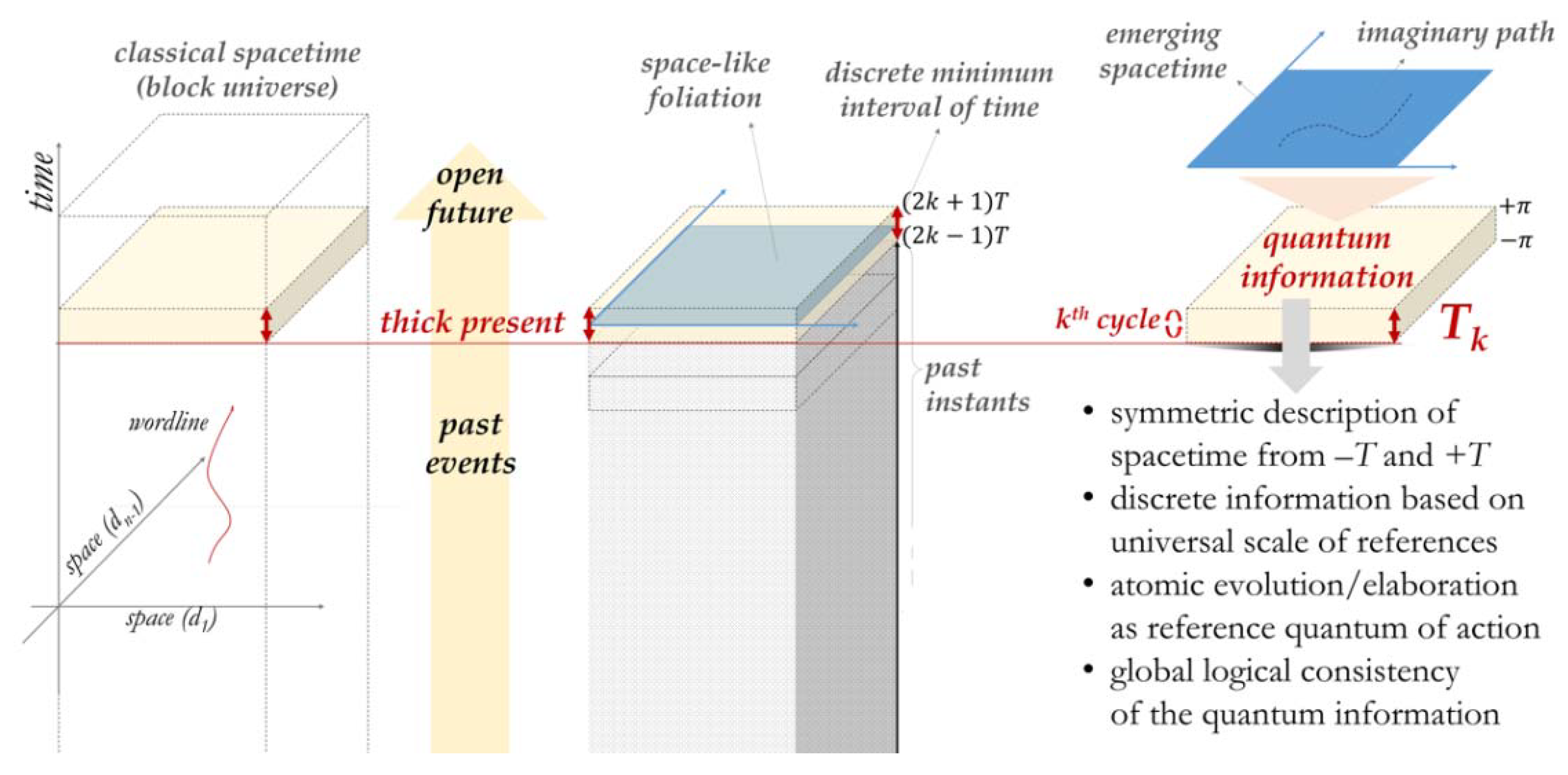
2. Existence in a Thick Present
2.1. Understandings on the Nature of Time
2.2. Identifying a Quantum of Evolution
2.3. Conclusion on Presentism and Open Challenges
3. Undefined Orders in Imaginary Times
3.1. Causality and Logical Consistency
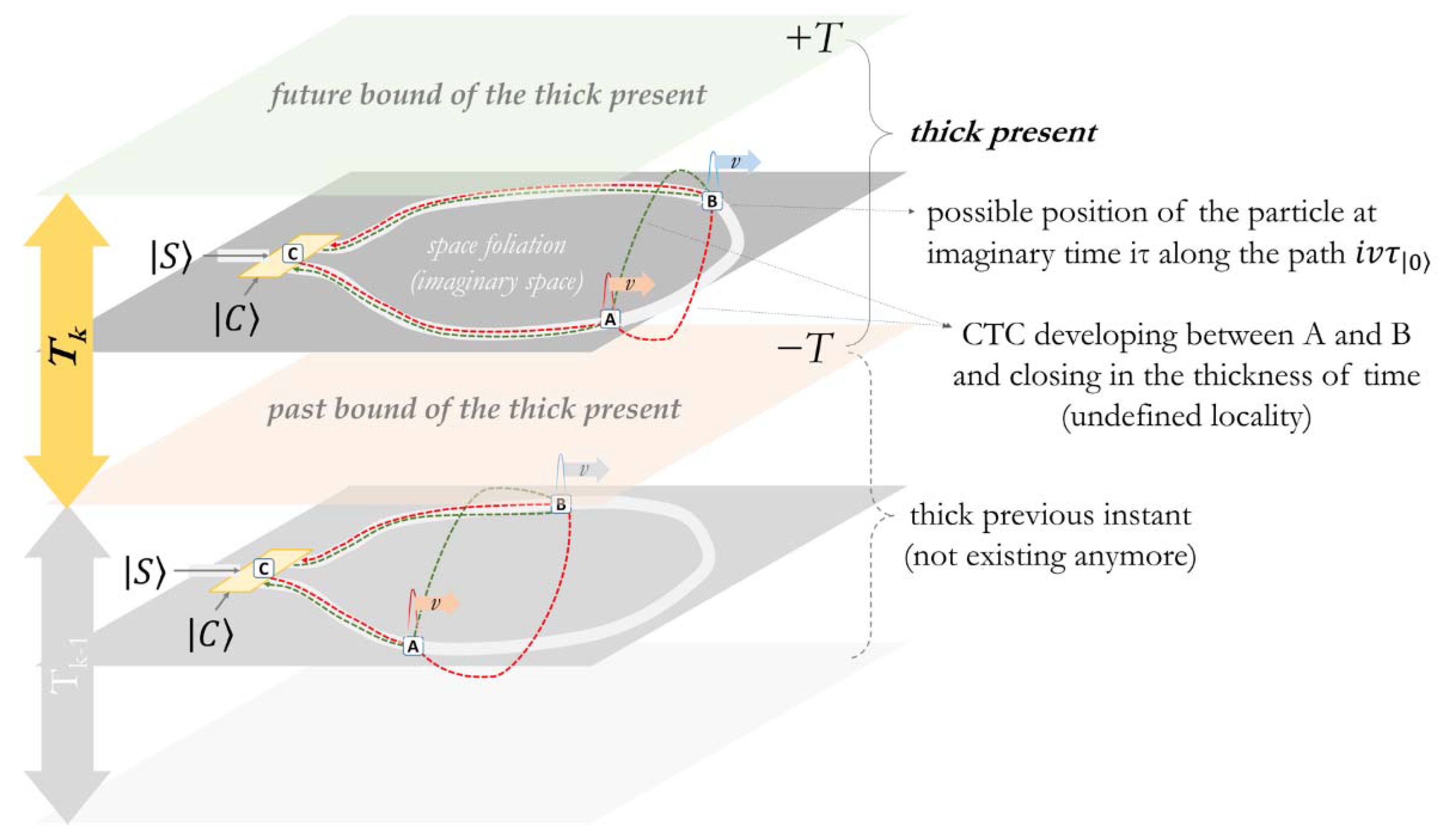
3.2. Imaginary Closed Paths
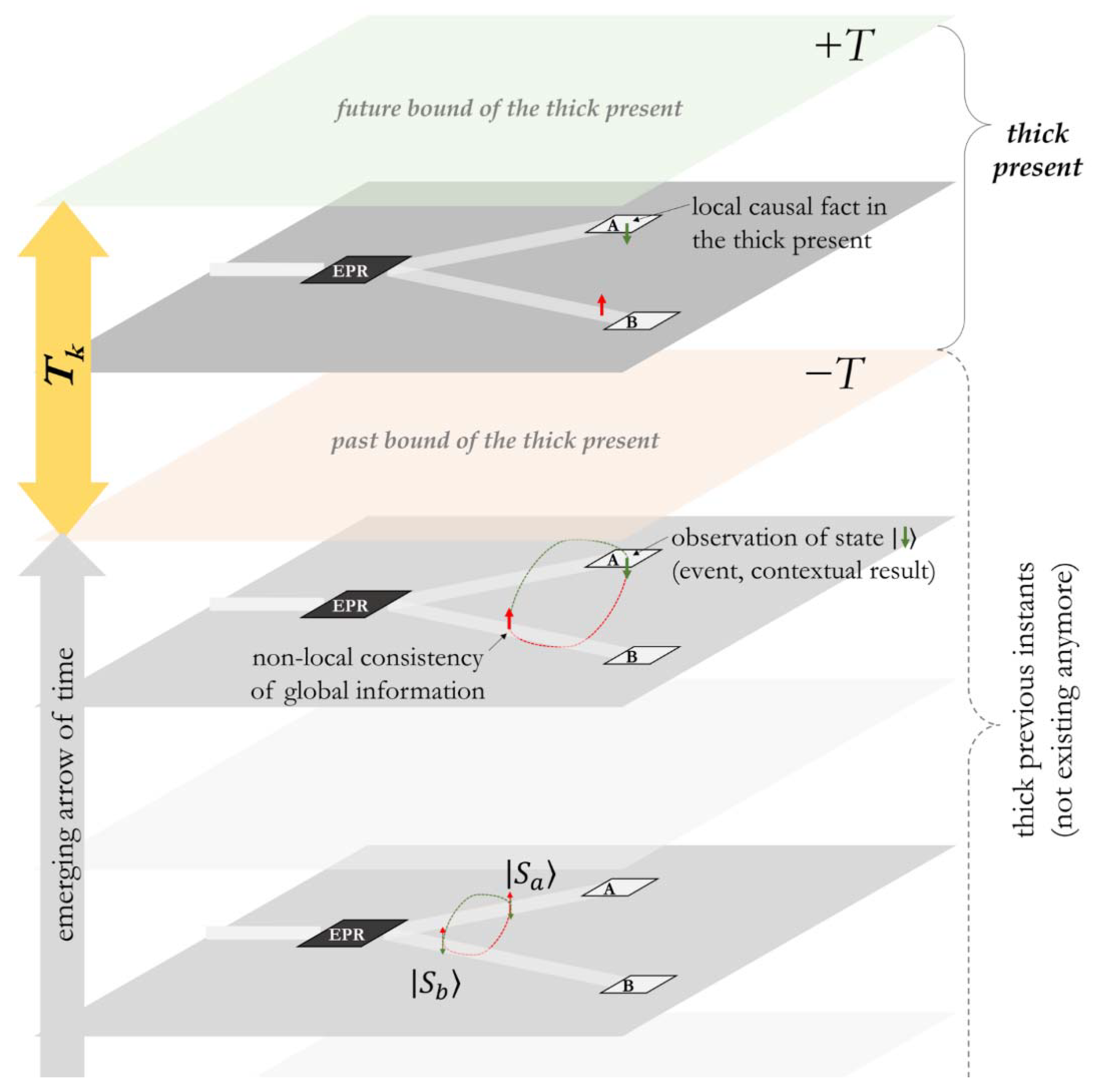
4. CTC, Entanglement, and Non-Locality
4.1. The Potential Hidden in a Choice
4.2. Chasing Non-Local Information
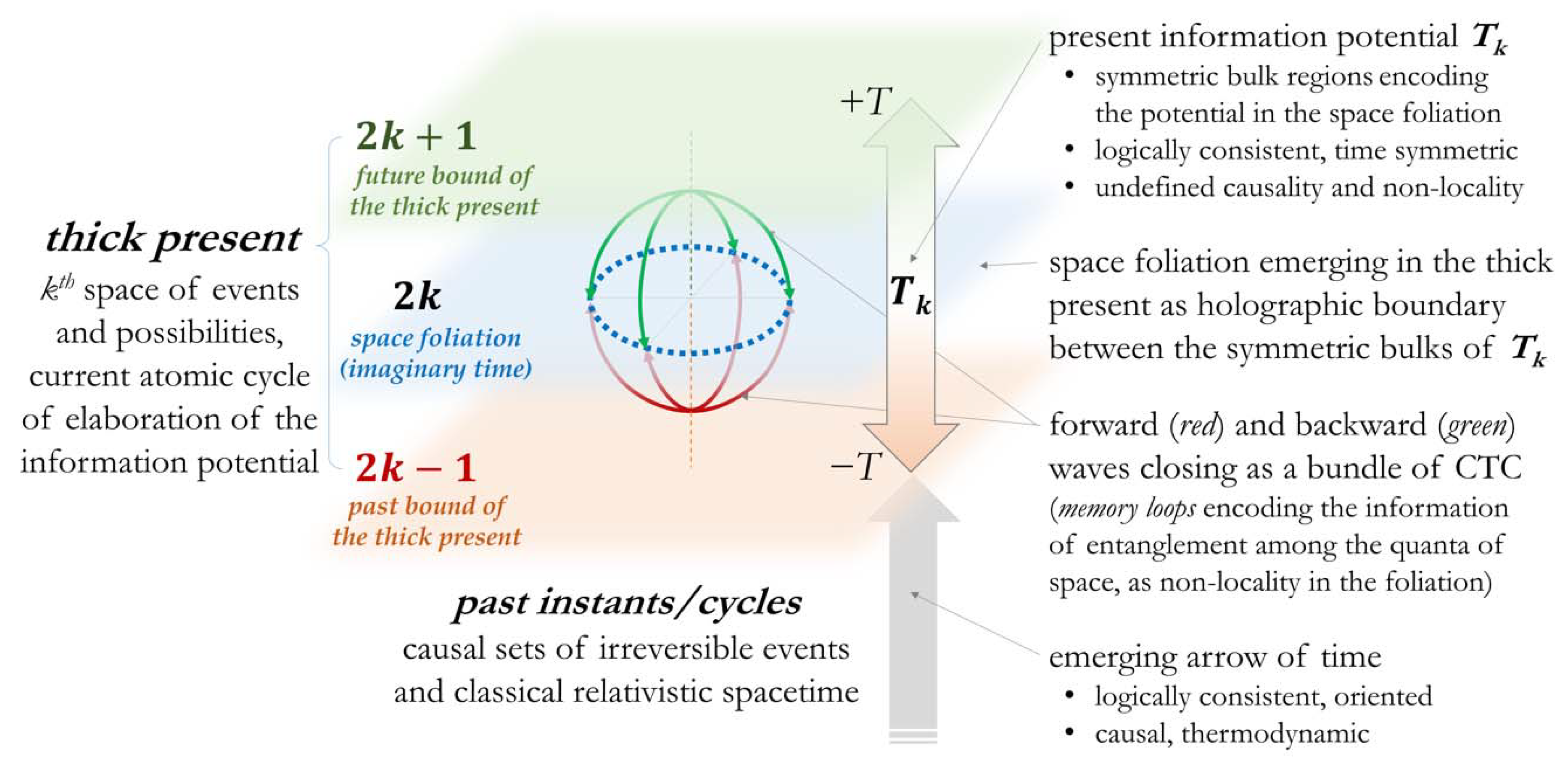
5. Towards a Holographic Perspective
6. Synthesis and Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| C-NOT | Controlled-NOT quantum gate. It operates on a quantum register consisting of 2 qubits C and S (Controller C and Target S) and flips the qubit S if and only if . Used to create entangled pairs (EPR particles) |
| CTC | Closed Time-like Curves. Closed paths in spacetime. No events occur on their path, and time has no causal or thermodynamic orientation along them. They represent an information potential in the superposition of the outcomes of an open choice (e.g., direction of travel along the curve). When developing between −T and +T in the thick present, they cross the imaginary time axis in distant quanta of space that result connected (non-locality, entanglement in space). When developing in the imaginary space foliation they represent indefinite orders of traversed quanta of space (undefined causality, entanglement in time). They are considered in the paper as “memory loops”. |
| EPR | Einstein–Podolsky–Rosen. Reference to the 1935 famous contribution on the incompleteness of QM. Intended in the paper as the EPR paradox, a synonym of entanglement and entangled particles (EPR pairs) |
| ER | Einstein–Rosen bridge. Quantum wormhole connecting far regions of spacetime. Intended in the paper as entanglement between distant quanta in the imaginary space foliation (non-local information potential) |
| GR | General Relativity (theory of) |
| ICT | Information and Communication Technologies |
| ict | Imaginary coherent time. Described as the imaginary time of motion (it) at the speed of light (c) between distant quanta of space. It is proposed in the paper as an imaginary axis of spatial distance and, in the absence of additional information potential, it defines a flat space foliation emerging in the present |
| OPT | Operational Probabilistic Theories. Description of QM from first principles based on Information Theory |
| PI | Path Integral formulation of QM |
| QG | Quantum Gravity |
| QIS | Quantum Information Science |
| QM | Quantum Mechanics |
| Tk | Quantum potential existing in the thick present (at the current evolution cycle, after 2kT instants from the origin of the universe). Time symmetric description from (2k – 1)T and (2k + 1)T of the entanglement in space (non-local potential in the imaginary space foliation emerging at 2kT along ict) and of the entanglement in time (undefined causality and indefinite time orders) |
| TSVF | Two State Vector Formalism. Time-symmetric description of QM |
| UCO | Undefined Causal Orders. Entanglement in time (order) |
References
- Buonomano, D.; Rovelli, C. Bridging the neuroscience and physics of time. arXiv 2021, arXiv:2110.01976. [Google Scholar]
- Conway, J.; Kochen, S. The free will theorem. Found. Phys. 2006, 36, 1441–1473. [Google Scholar] [CrossRef]
- Dyson, F. Thought experiments in Honor of John Archibald Wheeler. In Science and Ultimate Reality; Cambridge University Press: Cambridge, UK, 2004; p. 89. [Google Scholar]
- Smolin, L. The dynamics of difference. Found. Phys. 2018, 48, 121–134. [Google Scholar] [CrossRef]
- Boekholt, T.C.N.; Zwart, S.F.P.; Valtonen, M. Gargantuan Chaotic Gravitational Three-Body Systems and Their Irreversibility to the Planck Length. Mon. Not. R. Astron. Soc. 2020, 493, 3932–3937. [Google Scholar] [CrossRef]
- Watanabe, S. Symmetry of physical laws. Part III. Prediction and retrodiction. Rev. Mod. Phys. 1955, 27, 179–186. [Google Scholar] [CrossRef]
- Scarani, V.; Buscemi, F. Fluctuation theorems from Bayesian retrodiction. Phys. Rev. E 2021, 103, 052111. [Google Scholar]
- Scarani, V.; Buscemi, F.; Aw, C.C. Fluctuation theorems with retrodiction rather than reverse processes. AVS Quantum Sci. 2021, 3, 045601. [Google Scholar] [CrossRef]
- Baumeler, Ä. Causal Loops: Logically Consistent Correlations, Time Travel, and Computation. Ph.D. Thesis, Università della Svizzera Italiana, Lugano, Switzerland, 2017. [Google Scholar]
- Cohen, E.; Cortes, M.; Elitzur, A.C.; Smolin, L. Realism and causality I: Pilot wave and retrocausal models as possible facilitators. Phys. Rev. D 2020, 102, 124027. [Google Scholar] [CrossRef]
- Cohen, E.; Cortes, M.; Elitzur, A.C.; Smolin, L. Realism and causality II: Retrocausality in energetic causal sets. Phys. Rev. D 2020, 102, 124028. [Google Scholar] [CrossRef]
- Tallant, J.; Ingram, D. The rotten core of presentism. Synthese 2021, 199, 3969–3991. [Google Scholar] [CrossRef]
- Mariani, C.; Torrengo, G. The indeterminate present and the open future. Synthese 2021, 199, 3923–3944. [Google Scholar] [CrossRef]
- Gisin, N. Classical and intuitionistic mathematical languages shape our understanding of time in physics. Nat. Phys. 2020, 16, 114–116. [Google Scholar] [CrossRef]
- Smolin, L.; Verde, C. The quantum mechanics of the present. arXiv 2021, arXiv:2104.09945v1. [Google Scholar]
- Schlatter, A. On the principle of synchronization. Entropy 2018, 20, 741. [Google Scholar] [CrossRef] [PubMed]
- Schlatter, A. On the reality of quantum collapse and the emergence of space-time. Entropy 2019, 21, 323. [Google Scholar] [CrossRef] [PubMed]
- Schlatter, A. On the foundation of space and time by quantum-events. Found. Phys. 2022, 52, 7. [Google Scholar] [CrossRef]
- Fletcher, S.C. Light clocks and the clock hypothesis. Found. Phys. 2013, 43, 1369–1383. [Google Scholar] [CrossRef]
- Margolus, N. Finite-state classical mechanics. In International Conference on Reversible Computation; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Jaroszkiewicz, G. Quantized Detector Networks: The Theory of Observation; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Hardy, L. Foliable operational structures for general probabilistic theories. In Deep Beauty Understanding the Quantum World through Mathematical Innovation; Cambridge University Press: Cambridge, UK, 2011; pp. 409–442. [Google Scholar] [CrossRef]
- D’Ariano, G.M. Physics as quantum information processing. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2011. [Google Scholar]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Informational derivation of quantum theory. Phys. Rev. A 2011, 84, 012311. [Google Scholar] [CrossRef]
- Hardy, L. Time symmetry in operational theories. arXiv 2021, arXiv:2104.00071v1. [Google Scholar]
- Oreshkov, O.; Cerf, N. Operational formulation of time reversal in quantum theory. Nat. Phys. 2015, 11, 853–858. [Google Scholar] [CrossRef]
- Di Biagio, A.; Donà, P.; Rovelli, C. The arrow of time in operational formulations of quantum theory. Quantum 2021, 5, 520. [Google Scholar] [CrossRef]
- Christian, J. Passage of time in a Planck scale rooted local inertial structure. Int. J. Mod. Phys. D 2004, 13, 1037–1071. [Google Scholar] [CrossRef]
- Rovelli, C. The layers that build up the notion of time. arXiv 2021, arXiv:2105.00540. [Google Scholar]
- Zych, M.; Costa, F.; Pikovski, I.; Brukner, C. Bell’s theorem for temporal order. Nat. Commun. 2019, 10, 3772. [Google Scholar] [CrossRef] [PubMed]
- Rubino, G.; Rozema, L.A.; Massa, F.; Araújo, M.; Zych, M.; Brukner, Č.; Walther, P. Experimental entanglement of temporal orders. In Quantum Information and Measurement; Optical Society of America: Washington, DC, USA, 2019; p. S3B-3. [Google Scholar]
- Rubino, G.; Rozema, L.A.; Felix, A.; Araújo, M.; Zeuner, J.M.; Procopio, L.M.; Brukner, Č.; Walther, P. Experimental verification of an indefinite causal order. Sci. Adv. 2017, 3, e1602589. [Google Scholar] [CrossRef] [PubMed]
- Procopio, L.M.; Moqanaki, A.; Araújo, M.; Costa, F.; Calafell, A.; Dowd, E.G.; Hamel, D.R.; Rozema, L.A.; Brukner, Č.; Walther, P. Experimental superposition of orders of quantum gates. Nat. Commun. 2015, 6, 7913. [Google Scholar] [CrossRef] [PubMed]
- Chiribella, G.; Liu, Z. Quantum operations with indefinite time direction. arXiv 2021, arXiv:2012.03859. [Google Scholar]
- Hawking, S. The Universe in a Nutshell; Bantam Spectra: New York, NY, USA, 2001. [Google Scholar]
- Diaz, N.L.; Matera, J.M.; Rossignoli, R. Spacetime quantum actions. Phys. Rev. D 2021, 103, 065011. [Google Scholar] [CrossRef]
- Koch, B.; Muñoz, E. Path integral of the relativistic point particle in Minkowski space. Phys. Rev. D 2021, 103, 105025. [Google Scholar] [CrossRef]
- Gödel, K. An example of a new type of cosmological solutions of Einstein’s field equations of gravitation. Rev. Mod. Phys. 1949, 21, 447–450. [Google Scholar] [CrossRef]
- Lewis, D. The paradoxes of time travel. Am. Philos. Q. 1976, 13, 145–152. [Google Scholar]
- Nikolic, H. Causal paradoxes: A conflict between relativity and the arrow of time. Found. Phys. Lett. 2006, 19, 259–267. [Google Scholar] [CrossRef][Green Version]
- Rovelli, C. Can we travel to the past? Irreversible physics along closed timelike curves. arXiv 2019, arXiv:1912.04702v2. [Google Scholar]
- Paganini, C.F. No events on closed causal curves. Found. Phys. 2022, 52, 26. [Google Scholar] [CrossRef]
- Barrett, J.; Lorenz, R.; Oreshkov, O. Cyclic quantum causal models. Nat. Commun. 2021, 12, 885. [Google Scholar] [CrossRef] [PubMed]
- Baumeler, A.; Gilani, A.S.; Rashid, J. Unlimited non-causal correlations and their relation to non-locality. arXiv 2021, arXiv:2104.06234v1. [Google Scholar]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E. The problem of hidden variables in quantum mechanics. In The Logico-Algebraic Approach to Quantum Mechanics; Springer: Dordrecht, The Netherlands, 1975; pp. 293–328. [Google Scholar]
- Chiribella, G. Indefinite causal order enables perfect quantum communication with zero capacity channels. New J. Phys. 2021, 23, 033039. [Google Scholar] [CrossRef]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capurso, A. The Potential of a Thick Present through Undefined Causality and Non-Locality. Entropy 2022, 24, 410. https://doi.org/10.3390/e24030410
Capurso A. The Potential of a Thick Present through Undefined Causality and Non-Locality. Entropy. 2022; 24(3):410. https://doi.org/10.3390/e24030410
Chicago/Turabian StyleCapurso, Alessandro. 2022. "The Potential of a Thick Present through Undefined Causality and Non-Locality" Entropy 24, no. 3: 410. https://doi.org/10.3390/e24030410
APA StyleCapurso, A. (2022). The Potential of a Thick Present through Undefined Causality and Non-Locality. Entropy, 24(3), 410. https://doi.org/10.3390/e24030410





