Abstract
A scheme is proposed to generate maximally entangled states of two -type atoms trapped in separate overdamped optical cavities using quantum-jump-based feedback. This proposal can stabilize not only the singlet state, but also the other three triplet states by alternating the detuning parameter and relative phase of the classical fields. Meanwhile it is convenient to manipulate atoms, and much more robust against spontaneous emission of atoms. The parameters related to the potential experiment are analyzed comprehensively and it is confirmed that the quantum feedback technology is a significant tool for entanglement production with a high fidelity.
1. Introduction
It is well known that quantum dissipation is a notorious obstacle for various quantum information processing tasks, such as quantum algorithms [1,2], generation of entanglement [3,4], and quantum communication [5,6,7,8,9], which results from the inevitable interaction between the quantum system and the surrounding environment. However, by virtue of the quantum dissipation, more and more triumphs of quantum computation and quantum information have come, such as dissipative preparations of quantum entanglement [10,11,12,13,14,15,16,17], autonomous quantum error correction [18,19,20,21,22,23,24,25], directional quantum state transfer [26,27,28], and so on. These efforts reveal the spectacular promise of quantum dissipation. In particular, Plenio et al. [10] proposed a scheme to generate entangled states with a model consisting of an atom coupled to two distinct leaky, white-noise-field driven optical cavities, and proved the requisite of noise can play a constructive role in certain tasks. Tacchino et al. [16] showed that a bipartite quantum system can be optically pumped into a maximally entangled steady state by exploiting purely incoherent resources, with the largest concurrence reaching the limiting value of 0.5 if one of the two Bell states is coupled to a bath at a negative effective temperature.
On the other hand, the realization of a purely steady entangled state cannot be ensured by the dissipation alone. Therefore, various manners are combined with the disspation to improve the purity of target state such as purification and feedback control [29,30,31,32,33,34,35]. For instance, based on continuous monitoring of quantum jumps, Wang et al. [29] and Mancini [30] showed that the Markovian feedback scheme is able to increase the steady-state entanglement for two two-level atoms coupled to a single Bosonic mode that is driven and heavily damped. Additionally, Carvalho et al. [31] presented a strategy that is insensitive to detection inefficiencies and robust against errors in the control Hamiltonian. Its model consists of a pair of two-level atoms equally, and resonantly, coupled to a single cavity mode in the limit of where cavity decay rate is very large. In [32], they also investigated the effects of different control Hamiltonians and detection processes on entanglement production and showed that the quantum-jump-based feedback can protect highly entangled states against decoherence. Nevertheless, in the above schemes, only the singlet state can be prepared as the restriction on the symmetry of the system and the fidelity of the entangled state is significantly reduced by atomic spontaneous emission. Furthermore it is inconvenient to achieve the local feedback control on a single atom since all atoms are trapped into a cavity.
In this work, we present a flexible scheme to generate different Bell states by suitable regulation of relevant parameters, where two -type atoms are respectively trapped in an array of coupled cavities. The photon hopping rate G between two cavity provides an additional controllable parameter to realize different Bell states. The atomic spontaneous emission is drastically suppressed by the adiabatic elimination of the excited states. And we will execute a local feedback control to improve the fidelity of the target state as the leakage of photon from the local cavity modes is detected. Ultimately, the system can be stabilized into the target state and needs no requirement of precise control on the time of evolution. We also make a systemic analysis of the relevant parameters in the current experiment and confirm that the quantum-jump-based feedback is reliably useful in stabilization of all kinds of Bell entangled states with high fidelities.
2. Effective Master Equation of the Coupled-Cavity Array System
In Figure 1, the system consists of a pair of identical atoms with a -type configuration trapped in a coupled-cavity array and simultaneously driven by classical fields. The transition is coupled to a single-mode cavity with a coupling constant g and detuning , and the transition is driven by a classical field with Rabi frequency and detuning . Additionally, the microwave field is applied to drive the transition with Rabi frequency . The photon can hop between adjacent cavities with coupling strength G. The atoms are assumed to spontaneously radiate from the excited state to the ground states and with an equal decay rate and the decay rate of each cavity mode is . In a rotating frame, the Hamiltonian of the system reads ().
where a () and b () denote the annihilation (creation) operators of the local cavities, respectively. In the regime of the large detuning , we can adiabatically eliminate the excited states and then the Hamiltonian is simplified as
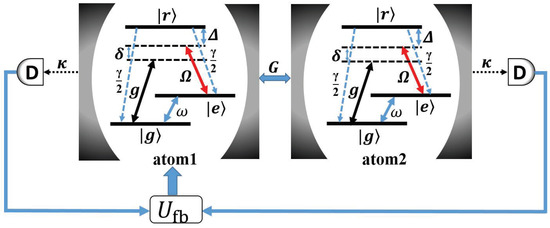
Figure 1.
Schematic view of the atom-cavity system. The transition is driven by a classical field with a time-independent Rabi frequency ; the transition is coupled to the cavity with coupling constant g; and are corresponding detuning parameters. is the decay rate of each cavity mode. The transition is additionally driven by a microwave field with a Rabi frequency and the hopping rate between neighbouring cavities is G.
The Stark-shift terms of ground states and can be canceled via introducing other ancillary levels, thence the reduced Hamiltonian could be reexpressed as
In order to achieve a further simplification of the system, we introduce two normal boson models and , which are not coupled to each other but interact with atoms, due to the contributions of the cavity fields. Then we have and and substitute the relations into Equation (3). The corresponding Hamiltonian is
We further utilize the formula to reformulate the Hamiltonian H in a rotation with respect to , and
where . Under the assumption of and , the non-local mode B is decoupled to the system, and we have
Now we obtain an effective model as in Reference [31], where a pair of two-level atoms are simultaneously driven by a quantum field and a classical field. The difference is that and are the ground states and mode A is non-local. It should be noted that Stevenson et al. have also derived a similar model with two Raman three-level systems in the same cavity [36], but we will see below that the coupled-cavity array system is much useful for stabilizing different Bell states. The dissipative dynamics of the whole system is characterized by the Markovian master equation
where the terms characterizing the spontaneous emission of atom has been neglected, since the atom is restricted in the subspace spanned by , . By virtue of the standard adiabatic elimination of the non-local cavity mode A in the regime of , the master equation of the reduced density operator for the atomic degrees of freedom becomes (the detail has been shown in the Appendix A)
where represents the cavity-loss induced collective decay operator of atoms with decay rate , and the superoperater is defined as .
3. Stabilization of Different Bell States via Quantum Feedback Control
Quantum feedback control is a compelling method to make the system evolve to the desired state by suitable regulation of relevant parameters. In our scheme, the loss of cavities equivalent to the collective decay of atoms can be monitored by a photondetector D. Once the photons out of cavities are detected by the photondetector, a feedback operator will be applied to the first atom. In this situation the master equation Equation (8) can be modified to [31]
In the following numerical simulations, we will characterize the long-time dynamics of system by solving Equation (9) from different initial states instead of direct solving the steady master equation, because there is not always a unique steady solution to Equation (9).
In Figure 2a, we first plot the concurrence of the evolution of the system governed by Equation (9) from an initial state . We find that the concurrence is equal to unity in most of the region except for the point or , and it is also consistent with the result of Reference [31]. A simple inspection shows that the final density matrix is:
which just corresponds to the density matrix of entanglement .
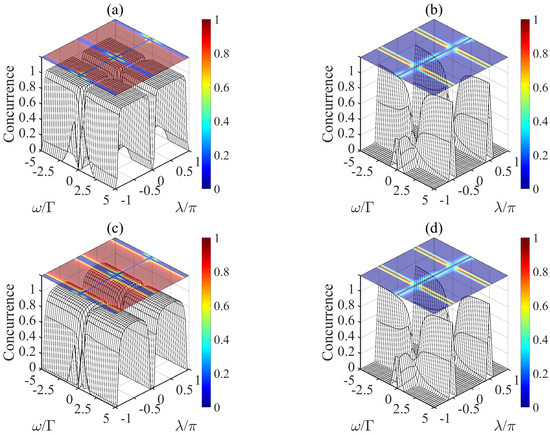
Figure 2.
The concurrence of the system at the time as a function of and as initial state is , without (a,b) or with (c,d) a large decay rate of atomic spontaneous emission ().
In order to produce other Bell states, we now change the phase of the microwave field acting on the second atom and the corresponding master equation for this case is derived as:
where .
Then we plot the concurrence of the system governed by Equation (11) in Figure 2b. The concurrence is almost vanished except for the particular point with a large , where the concurrence is near to unity, and the final density matrix is described as:
According to Equation (12), we find that the state of system is not pure at this time but it is similar to the density matrix of entanglement , where the fidelity of the state is . Thus the final state can be regarded as . This state has not been created using quantum dissipation before and the mechanism of our scheme can be explained in the following. In the absence of the feedback , the steady state of the system is mixed by . The state may radiate to the state and , which will be further transferred to . When a feedback operation with is introduced, the transitions of and will occur, which means that or is unstable in the presence of feedback. Therefore a non-equilibrium mixed state is generated which has a large overlap with the Bell state .
Then we consider the effect of atomic spontaneous emission. The formula for the damping operators of the effective atomic spontaneous emission takes the form of
and the corresponding master equations reads
with different phases (0 and ) of microwave field for the second atom. We then plot the concurrence of in Figure 2c and in Figure 2d with . In Figure 2c, the maximum value of concurrence can reach in the region of , . Similarly, in Figure 2d, when , , the concurrence may achieve at . It adequately demonstrated the robustness of the scheme against the atomic spontaneous emission.
In Figure 3, we consider another initial state as , and illustrate the concurrence of the system with atomic spontaneous emission effects (Figure 3c,d) and without atomic spontaneous emission (Figure 3a,b), respectively. For Figure 3a (or Figure 3c), in the region of , , the fidelity of arrives at (or ). Similarly, in Figure 3b (or in Figure 3d), the fidelity of is () for , . Combined with the previous analysis, we can conclude that the preparation of entangled state of our current proposal is independent of the initial state. It is also worth mentioning that in Figure 3b (or Figure 3d), when removing the classical driving field and the feedback coefficient satisfies , we get the density matrix different from Equation (12):
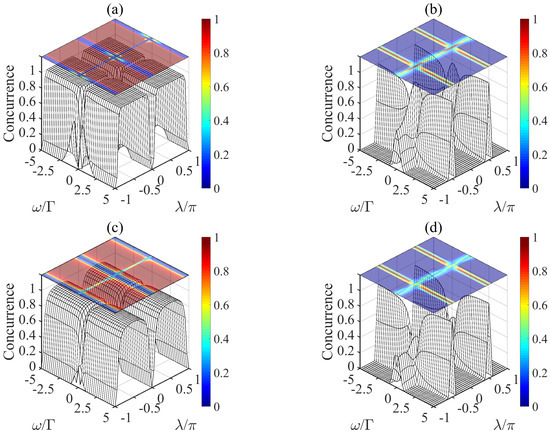
Figure 3.
The concurrence of the system in the case of changing the initial state only () without (a,b) or with (c,d) a large decay rate of atomic spontaneous emission ().
It means that when the microwave field is absent and we select and , the entangled state can also be produced. Furthermore, the present scheme can be also used to prepare the states and , which has been discussed in the Appendix B in detail.
Then it is significant to discuss the experimental feasibility of our program. The atomic configuration involved can be realized with Cs atoms. Since the achievement of trapping atoms in cavities has been demonstrated by several groups [37,38,39,40], we can accurately manipulate trapped atoms [37], microwave fields [38] and laser beams [39] to achieve the desired Rabi frequency and atom-cavity coupling. The full master equation of the system is written as
where the feedback control is carried out once the photon leaking out of the cavities is detected. In an optical cavity with a coupling coefficient MHz, the cavity mode and atomic decay rate can be chosen as MHz [36,41]. Substituting these parameters and into Equation (16), we acquire the time evolution for fidelities of the target states with different initial states in Figure 4. The purple dashed lines and dotted triangle lines represent the fidelities of the state with and without atomic spontaneous emission, respectively. The other two curves describe the fidelity of state with (signed empty circles line) and without (blue dashed line) atomic spontaneous emission. Although the atomic dissipation is chosen as MHz, the fidelities still arrive at 96.01% for and 98.21% for in a short time . It manifests the robustness of our protocol against decoherence once again.
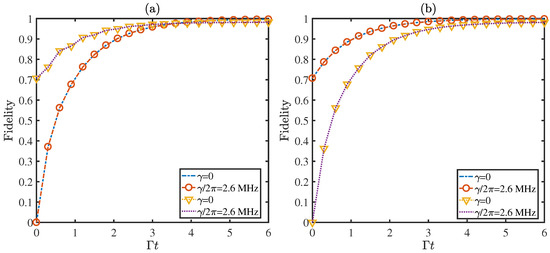
Figure 4.
The fidelities for the states and under different initial states (a) , (b) with the full master equation. The selection of related parameters is , , , and the driving frequency is set at .
4. Summary
In summary, we have put forward an efficient scheme to generate different maximal entanglements by two -type atoms trapped into an array of cavities. After a systematic analysis with the relevant parameters, we confirm the availability of quantum-jump-feedback control to improve the fidelity of entangled states. And our approach is robust against atomic spontaneous emission since the excited states are adiabatically eliminated. In addition, we can obtain all kinds of Bell states by changing the detuning parameter and the relative phase of microwave field operated on two atoms. We hope that our scheme will inspire the future preparation of entangled states with quantum feedback.
Author Contributions
X.-Q.S. put forward the idea. B.L. performed the calculations and prepared the figures. The main manuscript written by B.L. and D.-X.L. examined the calculations and improved the manuscript. All authors contributed to the discussion and reviewed the final manuscript.
Funding
This research was funded by National Natural Science Foundation of China (NSFC) grant number 11774047.
Acknowledgments
The authors acknowledge the support by National Natural Science Foundation of China (NSFC) under Grants No. 11774047.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Derivation of the Effective Master Equation
The dissipative dynamics of the whole system is characterized by the Markovian master equation
The density operator in the photon number representation is given by [42]
where are the density matrix elements based on photon number states. When the relation is achieved, the highly excited mode of the cavities can be neglected. So the cavity is in the single-photon state at most and the density matrix can be expressed in a small low-photon-number condition to a good approximation, i.e.,
where represents the state of the cavity mode with n photons. Substituting Equation (A3) into Equation (A1), we can get a series of coupled equations:
The photon-independent items are included in the superoperator , where is written as . In the regime of , it is reasonable to suppose that and then get the value of the operator as
By substituting Equation (A7) into the representation of and , we can get a diagonal density matrix whose matrix elements are:
Because of , these two terms explain the evolutionary nature of the atomic dynamics. We add these two terms together and adiabatically eliminate the term of , the master equation of the simplified density operator for the atomic degrees of freedom becomes:
where denotes the collective decay rate of atoms.
Appendix B. Generation of the Other Two Triplet States
In order to generate the state , we can choose the of Equation (5) as , which leads to the non-local mode B preserved and A dropped. Then we have
Defining , , the corresponding master equation of the system becomes
and the final density matrix is described as:
It is equal to the density matrix of the target state and the preparation of state is finished.
Similarly, we can set of Equation (5) and change the phase of the microwave field for the second atom to generate the state . The associated master equation can be rewritten as
and the final density matrix is
The overlap between this density operator and the ideal state is , which means we have successfully obtained the state .
References
- Bruß, D.; Macchiavello, C. Multipartite entanglement in quantum algorithms. Phys. Rev. 2011, 83, 052313. [Google Scholar] [CrossRef]
- Deng, F.G.; Ren, B.C.; Li, X.H. Quantum hyperentanglement and its applications in quantum information processing. Sci. Bull. 2017, 62, 46–68. [Google Scholar] [CrossRef]
- Ye, S.Y.; Zhong, Z.R.; Zheng, S.B. Deterministic generation of three-dimensional entanglement for two atoms separately trapped in two optical cavities. Phys. Rev. 2008, 77, 014303. [Google Scholar] [CrossRef]
- Yang, C.P.; Su, Q.P.; Zheng, S.B.; Nori, F.; Han, S. Entangling two oscillators with arbitrary asymmetric initial states. Phys. Rev. 2017, 95, 052341. [Google Scholar] [CrossRef]
- Long, G.L.; Liu, X.S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. 2002, 65, 032302. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef]
- Vinay, S.E.; Kok, P. Practical repeaters for ultralong-distance quantum communication. Phys. Rev. 2017, 95, 052336. [Google Scholar] [CrossRef]
- Felicetti, S.; Fedortchenko, S.; Rossi, R.; Ducci, S.; Favero, I.; Coudreau, T.; Milman, P. Quantum communication between remote mechanical resonators. Phys. Rev. 2017, 95, 022322. [Google Scholar] [CrossRef]
- Niu, P.H.; Zhou, Z.R.; Lin, Z.S.; Sheng, Y.B.; Yin, L.G.; Long, G.L. Measurement-device-independent quantum communication without encryption. Sci. Bull. 2018, 63, 1345–1350. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F. Entangled light from white noise. Phys. Rev. Lett. 2002, 88, 197901. [Google Scholar] [CrossRef]
- Yi, X.X.; Yu, C.S.; Zhou, L.; Song, H.S. Noise-assisted preparation of entangled atoms. Phys. Rev. 2003, 68, 052304. [Google Scholar] [CrossRef]
- Lambert, N.; Aguado, R.; Brandes, T. Nonequilibrium entanglement and noise in coupled qubits. Phys. Rev. B 2007, 75, 045340. [Google Scholar] [CrossRef]
- Galve, F.; Pachón, L.A.; Zueco, D. Bringing entanglement to the high temperature limit. Phys. Rev. Lett. 2010, 105, 180501. [Google Scholar] [CrossRef] [PubMed]
- Fischbach, J.; Freyberger, M. Steady-state entanglement enhanced by a dissipative ancilla. Phys. Rev. 2015, 92, 052327. [Google Scholar] [CrossRef]
- Li, D.X.; Shao, X.Q.; Wu, J.H.; Yi, X.X. Engineering steady-state entanglement via dissipation and quantum Zeno dynamics in an optical cavity. Opt. Lett. 2017, 42, 3904–3907. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.Q.; Wu, J.H.; Yi, X.X.; Long, G.L. Dissipative preparation of steady Greenberger-Horne-Zeilinger states for Rydberg atoms with quantum Zeno dynamics. Phys. Rev. 2017, 96, 062315. [Google Scholar] [CrossRef]
- Tacchino, F.; Auffèves, A.; Santos, M.F.; Gerace, D. Steady state entanglement beyond thermal limits. Phys. Rev. Lett. 2018, 120, 063604. [Google Scholar] [CrossRef] [PubMed]
- Paz, J.P.; Zurek, W.H. Continuous error correction. Proc. R. Soc. Lond. Ser. A 1998, 454, 355–364. [Google Scholar] [CrossRef]
- Ahn, C.; Doherty, A.C.; Landahl, A.J. Continuous quantum error correction via quantum feedback control. Phys. Rev. 2002, 65, 042301. [Google Scholar] [CrossRef]
- Fujii, K.; Negoro, M.; Imoto, N.; Kitagawa, M. MeasurementFree Topological Protection Using Dissipative Feedback. Phys. Rev. X 2014, 4, 041039. [Google Scholar]
- Leghtas, Z.; Touzard, S.; Pop, I.M.; Kou, A.; Vlastakis, B.; Petrenko, A.; Sliwa, K.M.; Narla, A.; Shankar, S.; Hatridge, M.J.; et al. Confining the state of light to a quantum manifold by engineered two-photon loss. Science 2015, 347, 853–857. [Google Scholar] [CrossRef] [PubMed]
- Kapit, E. Hardware-efficient and fully autonomous quantum error correction in superconducting circuits. Phys. Rev. Lett. 2016, 116, 150501. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Noh, K.; Albert, V.V.; Krastanov, S.; Devoret, M.H.; Schoelkopf, R.J.; Girvin, S.M.; Jiang, L. Quantum channel construction with circuit quantum electrodynamics. Phys. Rev. B 2017, 95, 134501. [Google Scholar] [CrossRef]
- Reiter, F.; Sørensen, A.S.; Zoller, P.; Muschik, C.A. Dissipative quantum error correction and application to quantum sensing with trapped ions. Nat. Commun. 2017, 8, 1822. [Google Scholar] [CrossRef] [PubMed]
- Li, D.X.; Shao, X.Q. Unconventional Rydberg pumping and applications in quantum information processing. Phys. Rev. 2018, 98, 062338. [Google Scholar] [CrossRef]
- Wang, C.; Gertler, J.M. Autonomous quantum state transfer by dissipation. arXiv, 2019; arXiv:1809.03571. [Google Scholar]
- Matsuzaki, Y.; Bastidas, V.M.; Takeuchi, Y.; Munro, W.J.; Saito, S. One-way transfer of quantum states via decoherence. arXiv, 2019; arXiv:1810.02995. [Google Scholar]
- Li, D.X.; Shao, X.Q. Directional quantum state transfer in a dissipative Rydberg-atom-cavity system. Phys. Rev. A 2019, 99, 032348. [Google Scholar] [CrossRef]
- Wang, J.; Wiseman, H.M.; Milburn, G.J. Dynamical creation of entanglement by homodyne-mediated feedback. Phys. Rev. 2005, 71, 042309. [Google Scholar] [CrossRef]
- Mancini, S. Markovian feedback to control continuous-variable entanglement. Phys. Rev. 2006, 73, 010304. [Google Scholar] [CrossRef]
- Carvalho, A.R.R.; Hope, J.J. Stabilizing entanglement by quantum-jump-based feedback. Phys. Rev. 2007, 76, 010301. [Google Scholar] [CrossRef]
- Carvalho, A.R.R.; Reid, A.J.S.; Hope, J.J. Controlling entanglement by direct quantum feedback. Phys. Rev. 2008, 78, 012334. [Google Scholar] [CrossRef]
- Stevenson, R.N.; Hope, J.J.; Carvalho, A.R.R. Engineering steady states using jump-based feedback for multipartite entanglement generation. Phys. Rev. 2011, 84, 022332. [Google Scholar] [CrossRef]
- Li, D.X.; Shao, X.Q.; Wu, J.H.; Yi, X.X. Noise-induced distributed entanglement in atom-cavity-fiber system. Opt. Express 2017, 25, 33359–33378. [Google Scholar] [CrossRef]
- Rafiee, M.; Nourmandipour, A.; Mancini, S. Universal feedback control of two-qubit entanglement. Phys. Rev. A 2017, 96, 012340. [Google Scholar] [CrossRef]
- Stevenson, R.N.; Carvalho, A.R.R.; Hope, J.J. Production of entanglement in Raman three-level systems using feedback. Eur. Phys. J. D 2011, 61, 523–529. [Google Scholar] [CrossRef][Green Version]
- Leibfried, D.; Blatt, R.; Monroe, C.; Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 2003, 75, 281. [Google Scholar] [CrossRef]
- Trupke, M.; Hinds, E.A.; Eriksson, S.; Curtis, E.A.; Moktadir, Z.; Kukharenka, E.; Kraft, M. Microfabricated high-finesse optical cavity with open access and small volume. Appl. Phys. Lett. 2005, 87, 211106. [Google Scholar] [CrossRef]
- Miroshnychenko, Y.; Alt, W.; Dotsenko, I.; Förster, L.; Khudaverdyan, M.; Meschede, D.; Rauschenbeutel, A. Quantum engineering: An atom-sorting machine. Nature 2006, 442, 151. [Google Scholar] [CrossRef]
- Metz, J.; Beige, A. Macroscopic quantum jumps and entangled-state preparation. Phys. Rev. 2007, 76, 022331. [Google Scholar] [CrossRef]
- Khudaverdyan, M.; Alt, W.; Kampschulte, T.; Reick, S.; Thobe, A.; Widera, A.; Meschede, D. Quantum jumps and spin dynamics of interacting atoms in a strongly coupled atom-cavity system. Phys. Rev. Lett. 2009, 103, 123006. [Google Scholar] [CrossRef] [PubMed]
- Ficek, Z.; Tanaś, R. Entangled states and collective nonclassical effects in two-atom systems. Phys. Rep. 2002, 372, 369–443. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).