Robust Variable Selection and Estimation Based on Kernel Modal Regression
Abstract
1. Introduction
- We formulate a new RGVS method by integrating the RMR in RKHS and the model-free strategy for variable screening. This algorithm can be implemented via the half-quadratic optimization [32]. To our knowledge, this algorithm is the first one for robust model-free variable selection.
- In theory, the proposed method enjoys statistical consistency on regression estimator under much general conditions on data noise and hypothesis space. In particular, the learning rate with polynomial decay is obtained, which is faster than in [20] for linear RMR. It should be noted that our work is established under the MRC, while all previous model-free methods are formulated under the MSE criterion. In addition, variable selection consistency is obtained for our approach under a self-calibration condition.
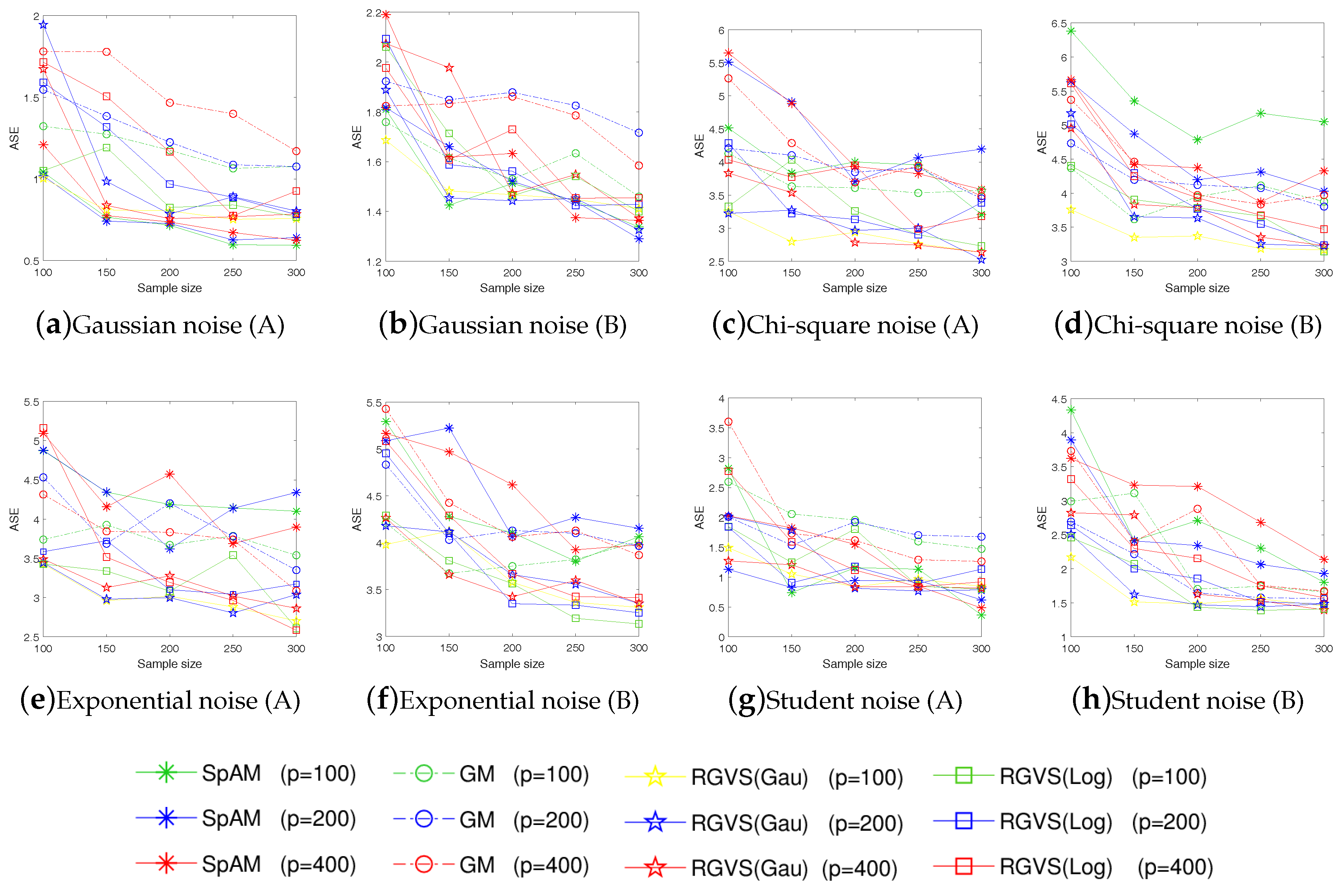
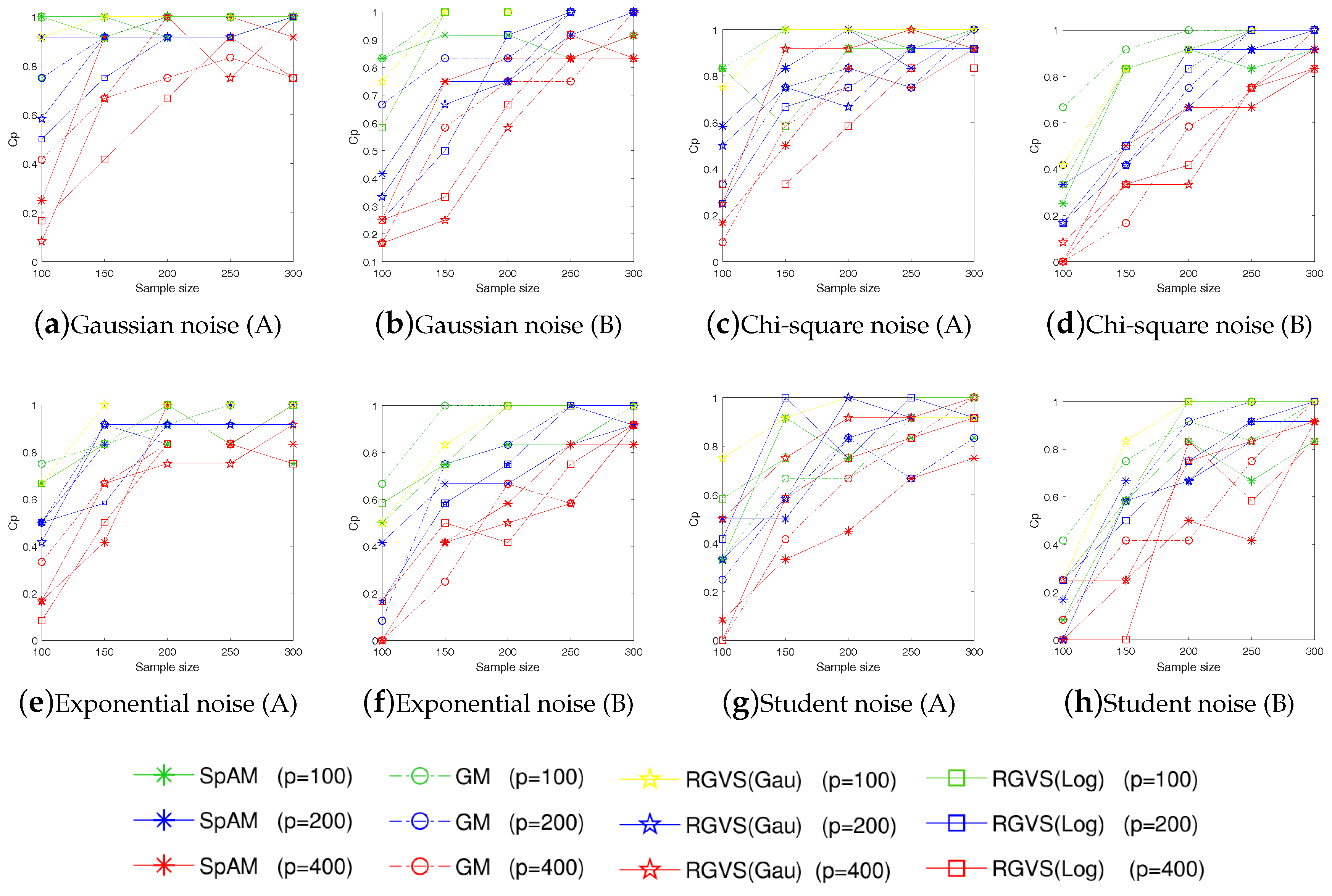
- In application, the proposed RGVS shows the empirical effectiveness on both simulated and real-world data sets. In particular, our approach can achieve much better performance than the model-free algorithm in [12] for complex noise data, e.g., containing Chi-square noise, Exponential noise, and Student noise. Experimental results together with theoretical analysis support the effectiveness of our approach.
2. Gradient-Based Variable Selection in Modal Regression
2.1. Gradient-Based Variable Selection Based on Kernel Least-Squares Regression
2.2. Robust Gradient-Based Variable Selection Based on Kernel Modal Regression
3. Generalization-Bound and Variable Selection Consistency
4. Optimization Algorithm
| Algorithm 1: Optimization algorithm of RGVS with Logistic kernel |
| Input: Samples , the modal representation (Logistic kernel), Mercer kernel K; |
| Initialization: , , bandwidth , Max-iter , ; |
| Obtain in RKHS: |
| While not converged and Max-iter; |
| 1. Fixed , update ; |
| 2. Fixed , update ; |
| 3. Check the convergence condition: ; |
| 4. ; |
| End While |
| Output: ; |
| Variable Selection: }. |
| Output: |
5. Empirical Assessments
5.1. Simulated Data
5.2. Real-World Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tibshirani, R. Regression shrinkage and delection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Stone, C.J. Additive regression and other nonparametric models. Ann. Stat. 1985, 13, 689–705. [Google Scholar] [CrossRef]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Chapman and Hall: London, UK, 1990. [Google Scholar]
- Kandasamy, K.; Yu, Y. Additive approximations in high dimensional nonparametric regression via the SALSA. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Kohler, M.; Krzyżak, A. Nonparametric regression based on hierarchical interaction models. IEEE Trans. Inf. Theory 2017, 63, 1620–1630. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Huang, H. Group sparse additive machine. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 198–208. [Google Scholar]
- Ravikumar, P.; Liu, H.; Lafferty, J.; Wasserman, L. SpAM: Sparse additive models. J. R. Stat. Soc. Ser. B 2009, 71, 1009–1030. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, H.H. Component selection and smoothing in multivariate nonparametric regression. Ann. Stat. 2007, 34, 2272–2297. [Google Scholar] [CrossRef]
- Yin, J.; Chen, X.; Xing, E.P. Group sparse additive models. In Proceedings of the International Conference on Machine Learning (ICML), Edinburgh, UK, 26 June–1 July 2012. [Google Scholar]
- He, X.; Wang, J.; Lv, S. Scalable kernel-based variable selection with sparsistency. arXiv 2018, arXiv:1802.09246. [Google Scholar]
- Yang, L.; Lv, S.; Wang, J. Model-free variable selection in reproducing kernel Hilbert space. J. Mach. Learn. Res. 2016, 17, 1–24. [Google Scholar]
- Ye, G.; Xie, X. Learning sparse gradients for variable selection and dimension reduction. Mach. Learn. 2012, 87, 303–355. [Google Scholar] [CrossRef]
- Gregorová, M.; Kalousis, A.; Marchand-Maillet, S. Structured nonlinear variable selection. arXiv 2018, arXiv:1805.06258. [Google Scholar]
- Mukherjee, S.; Zhou, D.X. Analysis of half-quadratic minimization methods for signal and image recovery. J. Mach. Learn. Res. 2006, 7, 519–549. [Google Scholar]
- Rosasco, L.; Villa, S.; Mosci, S.; Santoro, M.; Verri, A. Nonparametric sparsity and regularization. J. Mach. Learn. Res. 2013, 14, 1665–1714. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Feng, Y.; Fan, J.; Suykens, J.A.K. A statistical learning approach to modal regression. arXiv 2017, arXiv:1702.05960. [Google Scholar]
- Wang, X.; Chen, H.; Cai, W.; Shen, D.; Huang, H. Regularized modal regression with applications in cognitive impairment prediction. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 1448–1458. [Google Scholar]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Chernoff, H. Estimation of the mode. Ann. Inst. Stat. Math. 1964, 16, 31–41. [Google Scholar] [CrossRef]
- Yao, W.; Lindsay, B.G.; Li, R. Local modal regression. J. Nonparametr. Stat. 2012, 24, 647–663. [Google Scholar] [CrossRef]
- Chen, Y.C.; Genovese, C.R.; Tibshirani, R.J.; Wasserman, L. Nonparametric modal regression. Ann. Stat. 2014, 44, 489–514. [Google Scholar] [CrossRef]
- Collomb, G.; Härdle, W.; Hassani, S. A note on prediction via estimation of the conditional mode function. J. Stat. Plan. Inference 1986, 15, 227–236. [Google Scholar] [CrossRef]
- Lee, M.J. Mode regression. J. Econom. 1989, 42, 337–349. [Google Scholar] [CrossRef]
- Sager, T.W.; Thisted, R.A. Maximum likelihood estimation of isotonic modal regression. Ann. Stat. 1982, 10, 690–707. [Google Scholar] [CrossRef]
- Li, J.; Ray, S.; Lindsay, B. A nonparametric statistical approach to clustering via mode identification. J. Mach. Learn. Res. 2007, 8, 1687–1723. [Google Scholar]
- Liu, W.; Pokharel, P.P.; Príncipe, J.C. Correntropy: Properties and applications in non-Gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Príncipe, J.C. Information Theoretic Learning: Rényi’s Entropy and Kernel Perspectives; Springer: New York, NY, USA, 2010. [Google Scholar]
- Feng, Y.; Huang, X.; Shi, L.; Yang, Y.; Suykens, J.A.K. Learning with the maximum correntropy criterion induced losses for regression. J. Mach. Learn. Res. 2015, 16, 993–1034. [Google Scholar]
- Nikolova, M.; Ng, M.K. Analysis of half-quadratic minimization methods for signal and image recovery. SIAM J. Sci. Comput. 2005, 27, 937–966. [Google Scholar] [CrossRef]
- Aronszajn, N. Theory of Reproducing Kernels. Trans. Am. Math. Soc. 1950, 68, 337–404. [Google Scholar] [CrossRef]
- Cucker, F.; Zhou, D.X. Learning Theory: An Approximation Theory Viewpoint; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Yao, W.; Li, L. A new regression model: Modal linear regression. Scand. J. Stat. 2013, 41, 656–671. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y. Kernel-based sparse regression with the correntropy-induced loss. Appl. Comput. Harmon. Anal. 2018, 44, 144–164. [Google Scholar] [CrossRef]
- Sun, W.; Wang, J.; Fang, Y. Consistent selection of tuning parameters via variable selection stability. J. Mach. Learn. Res. 2012, 14, 3419–3440. [Google Scholar]
- Zou, B.; Li, L.; Xu, Z. The generalization performance of ERM algorithm with strongly mixing observations. Mach. Learn. 2009, 75, 275–295. [Google Scholar] [CrossRef]
- Guo, Z.C.; Zhou, D.X. Concentration estimates for learning with unbounded sampling. Adv. Comput. Math. 2013, 38, 207–223. [Google Scholar] [CrossRef]
- Shi, L.; Feng, Y.; Zhou, D.X. Concentration estimates for learning with ℓ1-regularizer and data dependent hypothesis spaces. Appl. Comput. Harmon. Anal. 2011, 31, 286–302. [Google Scholar] [CrossRef]
- Shi, L. Learning theory estimates for coefficient-based regularized regression. Appl. Comput. Harmon. Anal. 2013, 34, 252–265. [Google Scholar] [CrossRef]
- Chen, H.; Pan, Z.; Li, L.; Tang, Y. Error analysis of coefficient-based regularized algorithm for density-level detection. Neural Comput. 2013, 25, 1107–1121. [Google Scholar] [CrossRef]
- Zou, B.; Xu, C.; Lu, Y.; Tang, Y.Y.; Xu, J.; You, X. k-Times markov sampling for SVMC. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 1328–1341. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Li, W.; Zou, B.; Wang, Y.; Tang, Y.Y.; Han, H. Learning with coefficient-based regularized regression on Markov resampling. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 4166–4176. [Google Scholar]
- Steinwart, I.; Christmann, A. Support Vector Machines; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Wu, Q.; Ying, Y.; Zhou, D.X. Multi-kernel regularized classifiers. J. Complex. 2007, 23, 108–134. [Google Scholar] [CrossRef]
- Steinwart, I.; Christmann, A. Estimating conditional quantiles with the help of the pinball loss. Bernoulli 2011, 17, 211–225. [Google Scholar] [CrossRef]
- Belloni, A.; Chernozhukov, V. ℓ1-penalized quantile regression in high dimensional sparse models. Ann. Stat. 2009, 39, 82–130. [Google Scholar] [CrossRef]
- Kato, K. Group Lasso for high dimensional sparse quantile regression models. arXiv 2011, arXiv:1103.1458. [Google Scholar]
- Lv, S.; Lin, H.; Lian, H.; Huang, J. Oracle inequalities for sparse additive quantile regression in reproducing kernel Hilbert space. Ann. Stat. 2018, 46, 781–813. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, Y.Y.; Li, L. Correntropy matching pursuit with application to robust digit and face recognition. IEEE Trans. Cybern. 2017, 47, 1354–1366. [Google Scholar] [CrossRef] [PubMed]
- Rockafellar, R.T. Convex Analysis; Princeton Univ. Press: Princeton, NJ, USA, 1997. [Google Scholar]
| Lasso [1] | RMR [20] | SpAM [9] | COSSO [10] | GM [12] | Ours | |
|---|---|---|---|---|---|---|
| Learning criterion | MSE | MRC | MSE | MSE | MSE | MRC |
| Model assumption | linear | linear | additive | additive | model-free | model-free |
| Noise | Method | SIZE | TP | FP | Up | Op | Cp | ASE | SIZE | TP | FP | Up | Op | Cp | ASE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (100, 150) | Lasso | 3.92 | 3.92 | 0.00 | 0.36 | 0.00 | 0.64 | 1.369 | 4.40 | 4.28 | 0.12 | 0.44 | 0.12 | 0.44 | 5.112 | |
| SpAM | 4.12 | 3.92 | 0.20 | 0.08 | 0.16 | 0.76 | 1.075 | 5.02 | 4.98 | 0.04 | 0.04 | 0.04 | 0.92 | 1.611 | ||
| GM | 4.12 | 3.88 | 0.24 | 0.12 | 0.16 | 0.72 | 1.123 | 5.14 | 4.98 | 0.16 | 0.04 | 0.12 | 0.84 | 1.775 | ||
| 4.00 | 3.92 | 0.08 | 0.08 | 0.04 | 0.88 | 1.003 | 5.12 | 5.00 | 0.12 | 0.00 | 0.08 | 0.92 | 1.565 | |||
| 3.84 | 3.80 | 0.04 | 0.20 | 0.04 | 0.76 | 1.131 | 5.12 | 4.92 | 0.20 | 0.08 | 0.16 | 0.76 | 1.914 | |||
| (150, 150) | Lasso | 4.20 | 3.92 | 0.04 | 0.16 | 0.12 | 0.72 | 1.245 | 4.48 | 4.28 | 0.20 | 0.40 | 0.16 | 0.44 | 4.794 | |
| Gaussian Noise | SpAM | 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.804 | 5.00 | 5.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.612 | |
| GM | 3.96 | 3.92 | 0.04 | 0.08 | 0.04 | 0.88 | 1.011 | 5.04 | 5.00 | 0.04 | 0.00 | 0.04 | 0.96 | 1.627 | ||
| 3.96 | 3.96 | 0.00 | 0.04 | 0.00 | 0.96 | 0.899 | 5.00 | 5.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.500 | |||
| 3.96 | 3.80 | 0.04 | 0.08 | 0.04 | 0.88 | 1.083 | 5.02 | 5.00 | 0.02 | 0.00 | 0.03 | 0.97 | 1.622 | |||
| (200, 150) | Lasso | 4.00 | 3.92 | 0.08 | 0.20 | 0.00 | 0.80 | 1.252 | 4.52 | 4.52 | 0.00 | 0.40 | 0.00 | 0.60 | 2.507 | |
| SpAM | 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.829 | 5.04 | 5.00 | 0.04 | 0.00 | 0.02 | 0.98 | 1.497 | ||
| GM | 3.96 | 3.96 | 0.00 | 0.04 | 0.00 | 0.96 | 1.012 | 5.06 | 5.00 | 0.06 | 0.00 | 0.04 | 0.96 | 1.528 | ||
| 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.813 | 5.00 | 5.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.485 | |||
| 3.96 | 3.96 | 0.00 | 0.04 | 0.00 | 0.96 | 0.915 | 5.00 | 5.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.453 | |||
| (100, 150) | Lasso | 3.72 | 3.64 | 0.08 | 0.36 | 0.04 | 0.60 | 5.854 | 4.32 | 3.72 | 0.60 | 0.68 | 0.12 | 0.20 | 6.888 | |
| SpAM | 4.24 | 3.76 | 0.48 | 0.24 | 0.28 | 0.48 | 4.342 | 5.52 | 5.00 | 0.52 | 0.00 | 0.40 | 0.60 | 4.328 | ||
| GM | 4.24 | 3.80 | 0.44 | 0.20 | 0.36 | 0.44 | 4.012 | 4.48 | 4.44 | 0.04 | 0.30 | 0.05 | 0.65 | 3.611 | ||
| 4.16 | 3.96 | 0.20 | 0.04 | 0.20 | 0.76 | 2.937 | 5.08 | 4.92 | 0.16 | 0.06 | 0.16 | 0.78 | 3.486 | |||
| 4.18 | 3.90 | 0.28 | 0.16 | 0.12 | 0.72 | 2.681 | 5.08 | 4.84 | 0.24 | 0.08 | 0.18 | 0.74 | 3.968 | |||
| (150, 150) | Lasso | 5.32 | 3.84 | 1.48 | 0.16 | 0.48 | 0.36 | 5.392 | 5.16 | 4.16 | 1.00 | 0.60 | 0.16 | 0.24 | 4.503 | |
| Chi-square Noise | SpAM | 4.04 | 3.96 | 0.08 | 0.04 | 0.08 | 0.88 | 2.765 | 5.32 | 5.00 | 0.32 | 0.00 | 0.24 | 0.76 | 3.748 | |
| GM | 4.00 | 3.88 | 0.12 | 0.12 | 0.08 | 0.80 | 2.873 | 4.98 | 4.92 | 0.06 | 0.05 | 0.05 | 0.90 | 4.173 | ||
| 3.96 | 3.92 | 0.04 | 0.08 | 0.04 | 0.88 | 2.809 | 5.02 | 5.00 | 0.02 | 0.00 | 0.02 | 0.98 | 2.929 | |||
| 4.08 | 3.96 | 0.12 | 0.04 | 0.12 | 0.84 | 2.097 | 5.04 | 5.00 | 0.04 | 0.00 | 0.04 | 0.96 | 3.519 | |||
| (200, 150) | Lasso | 4.24 | 4.00 | 0.24 | 0.00 | 0.28 | 0.72 | 5.805 | 4.36 | 4.32 | 0.04 | 0.52 | 0.04 | 0.44 | 3.754 | |
| SpAM | 4.08 | 4.00 | 0.08 | 0.00 | 0.08 | 0.92 | 2.463 | 5.04 | 5.00 | 0.04 | 0.00 | 0.04 | 0.96 | 3.634 | ||
| GM | 4.04 | 4.00 | 0.04 | 0.00 | 0.04 | 0.96 | 2.523 | 5.18 | 5.00 | 0.18 | 0.00 | 0.20 | 0.80 | 3.816 | ||
| 3.96 | 3.96 | 0.00 | 0.04 | 0.00 | 0.96 | 2.449 | 5.00 | 5.00 | 0.00 | 0.00 | 0.00 | 1.00 | 2.989 | |||
| 3.96 | 3.96 | 0.00 | 0.04 | 0.00 | 0.96 | 1.738 | 5.00 | 5.00 | 0.00 | 0.00 | 0.00 | 1.00 | 3.457 | |||
| (100, 150) | Lasso | 3.46 | 3.46 | 0.00 | 0.60 | 0.00 | 0.40 | 4.631 | 4.64 | 4.00 | 0.64 | 0.60 | 0.20 | 0.20 | 4.567 | |
| SpAM | 4.28 | 3.88 | 0.40 | 0.12 | 0.28 | 0.60 | 4.599 | 5.84 | 5.00 | 0.84 | 0.00 | 0.44 | 0.56 | 4.224 | ||
| GM | 4.20 | 3.64 | 0.56 | 0.36 | 0.36 | 0.28 | 3.941 | 5.36 | 4.68 | 0.68 | 0.32 | 0.28 | 0.40 | 4.528 | ||
| 4.20 | 3.88 | 0.32 | 0.12 | 0.20 | 0.68 | 3.274 | 5.06 | 4.82 | 0.24 | 0.14 | 0.14 | 0.72 | 3.907 | |||
| 3.96 | 3.80 | 0.16 | 0.20 | 0.16 | 0.64 | 2.775 | 5.12 | 4.92 | 0.20 | 0.04 | 0.16 | 0.80 | 3.667 | |||
| (150, 150) | Lasso | 5.30 | 3.66 | 1.64 | 0.20 | 0.44 | 0.36 | 4.747 | 5.64 | 4.16 | 1.48 | 0.48 | 0.28 | 0.24 | 4.786 | |
| Exponential Noise | SpAM | 4.04 | 3.96 | 0.08 | 0.04 | 0.08 | 0.88 | 3.403 | 5.28 | 5.00 | 0.28 | 0.16 | 0.00 | 0.84 | 4.969 | |
| GM | 4.08 | 3.96 | 0.12 | 0.04 | 0.12 | 0.84 | 3.177 | 4.98 | 4.92 | 0.06 | 0.08 | 0.04 | 0.88 | 4.129 | ||
| 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 2.724 | 5.02 | 4.98 | 0.04 | 0.02 | 0.04 | 0.94 | 2.964 | |||
| 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 2.643 | 5.00 | 4.96 | 0.04 | 0.04 | 0.04 | 0.92 | 3.918 | |||
| (200, 150) | Lasso | 3.80 | 3.80 | 0.00 | 0.20 | 0.00 | 0.80 | 4.291 | 4.68 | 4.60 | 0.08 | 0.28 | 0.08 | 0.64 | 3.669 | |
| SpAM | 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 2.988 | 5.24 | 5.00 | 0.24 | 0.00 | 0.20 | 0.80 | 4.808 | ||
| GM | 3.96 | 3.96 | 0.00 | 0.04 | 0.00 | 0.96 | 3.016 | 4.98 | 4.98 | 0.00 | 0.04 | 0.00 | 0.96 | 3.878 | ||
| 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 2.884 | 5.00 | 5.00 | 0.00 | 0.00 | 0.00 | 1.00 | 3.041 | |||
| 3.96 | 3.92 | 0.04 | 0.09 | 0.00 | 0.91 | 3.113 | 4.96 | 4.96 | 0.00 | 0.04 | 0.00 | 0.96 | 3.771 | |||
| (100, 150) | Lasso | 4.92 | 3.80 | 1.12 | 0.28 | 0.32 | 0.40 | 2.301 | 6.52 | 3.92 | 2.60 | 0.64 | 0.20 | 0.16 | 6.971 | |
| SpAM | 4.90 | 3.80 | 1.1 | 0.24 | 0.20 | 0.56 | 1.698 | 7.92 | 4.72 | 3.20 | 0.24 | 0.44 | 0.32 | 4.658 | ||
| GM | 5.00 | 3.64 | 1.36 | 0.32 | 0.32 | 0.36 | 1.551 | 5.68 | 4.32 | 1.32 | 0.40 | 0.32 | 0.28 | 3.561 | ||
| 4.14 | 3.94 | 0.20 | 0.05 | 0.10 | 0.85 | 0.822 | 5.00 | 4.84 | 0.16 | 0.08 | 0.16 | 0.76 | 2.308 | |||
| 4.14 | 3.88 | 0.26 | 0.12 | 0.16 | 0.72 | 1.208 | 4.96 | 4.80 | 0.16 | 0.16 | 0.12 | 0.72 | 2.339 | |||
| (150, 150) | Lasso | 5.08 | 3.72 | 1.36 | 0.24 | 0.40 | 0.36 | 1.793 | 6.32 | 3.80 | 2.52 | 0.68 | 0.20 | 0.12 | 6.020 | |
| Student Noise | SpAM | 4.30 | 4.00 | 0.30 | 0.00 | 0.32 | 0.68 | 0.955 | 5.44 | 5.00 | 0.44 | 0.00 | 0.28 | 0.72 | 2.739 | |
| GM | 4.04 | 3.80 | 0.24 | 0.16 | 0.16 | 0.68 | 1.046 | 5.56 | 4.60 | 0.96 | 0.28 | 0.08 | 0.64 | 2.557 | ||
| 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.757 | 4.98 | 4.98 | 0.00 | 0.08 | 0.00 | 0.92 | 1.716 | |||
| 3.92 | 3.88 | 0.04 | 0.12 | 0.04 | 0.84 | 1.169 | 4.96 | 4.96 | 0.00 | 0.04 | 0.00 | 0.96 | 1.723 | |||
| (200, 150) | Lasso | 5.00 | 3.92 | 1.08 | 0.32 | 0.20 | 0.48 | 1.262 | 5.44 | 4.36 | 1.08 | 0.44 | 0.28 | 0.28 | 2.976 | |
| SpAM | 4.10 | 4.00 | 0.10 | 0.00 | 0.27 | 0.73 | 1.060 | 5.64 | 5.00 | 0.64 | 0.00 | 0.28 | 0.72 | 2.427 | ||
| GM | 4.00 | 3.96 | 0.04 | 0.04 | 0.04 | 0.92 | 1.011 | 5.20 | 4.72 | 0.48 | 0.20 | 0.04 | 0.76 | 2.350 | ||
| 4.04 | 4.00 | 0.04 | 0.00 | 0.10 | 0.90 | 0.681 | 5.00 | 5.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.517 | |||
| 4.04 | 4.00 | 0.04 | 0.00 | 0.04 | 0.96 | 0.884 | 4.96 | 4.96 | 0.00 | 0.04 | 0.00 | 0.96 | 1.672 |
| Noise | Method | SIZE | TP | FP | Up | Op | Cp | ASE | |
|---|---|---|---|---|---|---|---|---|---|
| (300, 500) | Lasso | 1.98 | 1.98 | 0.00 | 1.00 | 0.00 | 0.00 | 1.98 | |
| GM | 4.04 | 4.00 | 0.04 | 0.00 | 0.04 | 0.96 | 0.80 | ||
| 4.06 | 4.00 | 0.06 | 0.00 | 0.06 | 0.94 | 0.63 | |||
| 4.14 | 3.98 | 0.16 | 0.01 | 0.03 | 0.96 | 0.88 | |||
| (500, 500) | Lasso | 1.92 | 1.92 | 0.00 | 1.00 | 0.00 | 0.00 | 1.35 | |
| Gaussian Noise | GM | 4.06 | 4.00 | 0.06 | 0.00 | 0.06 | 0.94 | 0.78 | |
| 4.02 | 4.00 | 0.02 | 0.00 | 0.02 | 0.98 | 0.59 | |||
| 4.04 | 4.00 | 0.04 | 0.00 | 0.02 | 0.98 | 0.74 | |||
| (700, 500) | Lasso | 1.88 | 1.88 | 0.00 | 1.00 | 0.00 | 0.00 | 1.55 | |
| GM | 4.04 | 4.00 | 0.04 | 0.00 | 0.04 | 0.96 | 0.77 | ||
| 4.02 | 4.00 | 0.02 | 0.00 | 0.02 | 0.98 | 0.62 | |||
| 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.73 | |||
| (300, 500) | Lasso | 1.80 | 1.80 | 0.00 | 1.00 | 0.00 | 0.00 | 4.45 | |
| GM | 4.18 | 4.00 | 0.18 | 0.00 | 0.14 | 0.86 | 2.92 | ||
| 4.09 | 4.00 | 0.09 | 0.00 | 0.11 | 0.89 | 2.39 | |||
| 4.06 | 3.88 | 0.18 | 0.12 | 0.14 | 0.74 | 1.95 | |||
| (500, 500) | Lasso | 1.74 | 1.74 | 0.00 | 1.00 | 0.00 | 0.00 | 4.62 | |
| Chi-square Noise | GM | 4.14 | 4.00 | 0.14 | 0.00 | 0.14 | 0.86 | 3.01 | |
| 4.08 | 4.00 | 0.08 | 0.00 | 0.06 | 0.94 | 2.22 | |||
| 4.04 | 3.98 | 0.06 | 0.02 | 0.06 | 0.92 | 1.82 | |||
| (700, 500) | Lasso | 1.86 | 1.86 | 0.00 | 1.00 | 0.00 | 0.00 | 4.37 | |
| GM | 4.28 | 4.00 | 0.28 | 0.00 | 0.24 | 0.76 | 2.96 | ||
| 4.02 | 4.00 | 0.02 | 0.00 | 0.02 | 0.98 | 2.13 | |||
| 4.02 | 4.00 | 0.02 | 0.00 | 0.02 | 0.98 | 1.72 | |||
| (300, 500) | Lasso | 2.04 | 2.04 | 0.00 | 1.00 | 0.00 | 0.00 | 4.25 | |
| GM | 3.94 | 3.87 | 0.07 | 0.13 | 0.05 | 0.82 | 3.14 | ||
| 4.02 | 4.00 | 0.02 | 0.00 | 0.02 | 0.98 | 2.36 | |||
| 3.98 | 3.94 | 0.04 | 0.06 | 0.02 | 0.92 | 1.92 | |||
| (500, 500) | Lasso | 1.94 | 1.94 | 0.00 | 1.00 | 0.00 | 0.00 | 4.34 | |
| Exponential Noise | GM | 4.12 | 4.00 | 0.12 | 0.00 | 0.10 | 0.90 | 2.35 | |
| 3.99 | 3.96 | 0.03 | 0.04 | 0.03 | 0.93 | 2.37 | |||
| 4.02 | 4.00 | 0.02 | 0.00 | 0.02 | 0.98 | 1.71 | |||
| (700, 500) | Lasso | 1.90 | 1.90 | 0.00 | 1.00 | 0.00 | 0.00 | 4.67 | |
| GM | 4.08 | 4.00 | 0.08 | 0.00 | 0.06 | 0.94 | 2.33 | ||
| 3.99 | 3.99 | 0.00 | 0.01 | 0.00 | 0.99 | 1.74 | |||
| 4.05 | 4.00 | 0.05 | 0.00 | 0.05 | 0.95 | 1.92 | |||
| (300, 500) | Lasso | 1.96 | 1.96 | 0.00 | 1.00 | 0.00 | 0.00 | 4.63 | |
| GM | 3.50 | 3.46 | 0.04 | 0.24 | 0.04 | 0.72 | 2.48 | ||
| 4.14 | 3.94 | 0.20 | 0.06 | 0.10 | 0.84 | 0.82 | |||
| 4.00 | 3.98 | 0.02 | 0.02 | 0.00 | 0.98 | 0.90 | |||
| (500, 500) | Lasso | 1.76 | 1.76 | 0.00 | 0.98 | 0.00 | 0.02 | 3.83 | |
| Student Noise | GM | 4.30 | 4.00 | 0.30 | 0.00 | 0.16 | 0.84 | 1.96 | |
| 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.76 | |||
| 4.02 | 4.00 | 0.02 | 0.00 | 0.01 | 0.99 | 0.75 | |||
| (700, 500) | Lasso | 1.96 | 1.96 | 0.00 | 0.96 | 0.00 | 0.04 | 2.46 | |
| GM | 4.06 | 4.00 | 0.06 | 0.00 | 0.04 | 0.96 | 1.95 | ||
| 4.04 | 4.00 | 0.04 | 0.00 | 0.06 | 0.94 | 0.68 | |||
| 4.00 | 4.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.74 |
| Variable | CyL | DISP | HPOWER | WEIG | ACCELER | YEAR | ORIGN | RSSE(std) |
|---|---|---|---|---|---|---|---|---|
| Lasso | - | - | - | ✔ | - | ✔ | - | 0.5918(0.3762) |
| SpAM | ✔ | ✔ | - | ✔ | - | - | - | 0.2754(0.0191) |
| GM | ✔ | ✔ | ✔ | ✔ | - | ✔ | ✔ | 0.2547(0.0313) |
| RGVS | ✔ | ✔ | ✔ | ✔ | - | ✔ | - | 0.1425(0.0277) |
| RGVS | ✔ | ✔ | ✔ | ✔ | - | ✔ | ✔ | 0.1379(0.0183) |
| Variable | RC | SA | WA | RA | OH | ORIENT | GA | GAD | RSSE(std) |
|---|---|---|---|---|---|---|---|---|---|
| Lasso | - | - | - | - | ✔ | - | ✔ | - | 0.1739(0.0801) |
| SpAM | - | - | - | ✔ | ✔ | - | - | - | 0.1684(0.0045) |
| GM | ✔ | ✔ | ✔ | ✔ | ✔ | - | - | - | 0.1244(0.0383) |
| RGVS | - | ✔ | ✔ | ✔ | ✔ | - | ✔ | - | 0.0935(0.0099) |
| RGVS | - | - | ✔ | ✔ | ✔ | - | ✔ | - | 0.1110(0.0066) |
| Lasso | - | - | ✔ | - | ✔ | - | ✔ | - | 0.2119(0.0926) |
| SpAM | - | - | - | ✔ | ✔ | - | - | - | 0.1910(0.0131) |
| GM | ✔ | ✔ | ✔ | ✔ | ✔ | - | - | - | 0.1515(0.0120) |
| RGVS | - | ✔ | ✔ | ✔ | ✔ | - | ✔ | - | 0.1339(0.0116) |
| RGVS | ✔ | ✔ | ✔ | ✔ | ✔ | - | - | - | 0.1368(0.0077) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Song, B.; Wang, Y.; Chen, H.; Xiong, H. Robust Variable Selection and Estimation Based on Kernel Modal Regression. Entropy 2019, 21, 403. https://doi.org/10.3390/e21040403
Guo C, Song B, Wang Y, Chen H, Xiong H. Robust Variable Selection and Estimation Based on Kernel Modal Regression. Entropy. 2019; 21(4):403. https://doi.org/10.3390/e21040403
Chicago/Turabian StyleGuo, Changying, Biqin Song, Yingjie Wang, Hong Chen, and Huijuan Xiong. 2019. "Robust Variable Selection and Estimation Based on Kernel Modal Regression" Entropy 21, no. 4: 403. https://doi.org/10.3390/e21040403
APA StyleGuo, C., Song, B., Wang, Y., Chen, H., & Xiong, H. (2019). Robust Variable Selection and Estimation Based on Kernel Modal Regression. Entropy, 21(4), 403. https://doi.org/10.3390/e21040403




