Abstract
To understand the accelerating universe discovered observationally in 1998, we develop the scalar-tensor theory of gravitation originally due to Jordan, extended only minimally. The unique role of the conformal transformation and frames is discussed particularly from a physical point of view. We show the theory to provide us with a simple and natural way of understanding the core of the measurements, for the observed values of the cosmological constant and today’s age of the universe both expressed in the Planckian units. According to this scenario of a decaying cosmological constant, is this small only because we are old, not because we fine-tune the parameters. It also follows that the scalar field is simply the pseudo Nambu–Goldstone boson of broken global scale invariance, based on the way astronomers and astrophysicists measure the expansion of the universe in reference to the microscopic length units. A rather phenomenological trapping mechanism is assumed for the scalar field around the epoch of mini-inflation as observed, still maintaining the unmistakable behavior of the scenario stated above. Experimental searches for the scalar field, as light as eV, as part of the dark energy, are also discussed.
1. Introduction and Summary
More than a decade has passed since the accelerating universe was indicated strongly from the analysis of Type Ia supernovae in 1998 [1,2]. Also combining these breakthrough studies with other corroborating observations, including WMAP, baryon acoustic oscillation, large-scale structure, resulted in an overall determination of the cosmological constant Λ [3,4,5],
where the critical density is defined by , also choosing a spatially flat Robertson–Walker (RW) metric, assumed throughout the article, while the Hubble parameter is determined by
Note that we use the Planckian units in which , or in the conventional units, also throughout this article. In units of the Planck time, today’s age of the universe is re-expressed by
Also by using we may re-express (1) by
From a view aiming at Unification, on the other hand, we naturally expect a theoretical estimate in the Planckian units;
Comparing this with (4) appears to invite a fine-tuning problem to as much as 120 orders of magnitude. In addition, we might also ask ourselves why we are so lucky to witness a truly rare event of the onset of an acceleration near the present era, which is supposed to be none of the distinct epochs throughout the entire history of the universe. This seems to add another riddle, to be referred to as a coincidence problem.
This issue is acute as long as the ordinary matter density falls off uniformly as a function of the cosmic time, while stays constant, so that they cross each other yielding as in (1), only once for all. Too much accidentally! Probably the only way out is to relinquish the notion of a truly constant . In this way we are naturally led to imagining to be time-dependent, likely of some dynamical nature. As one of the simplest approaches, we may start with expecting to come from a scalar field that has never been established before, but occupies as much as 3/4 of the entire cosmological energy, called dark energy, as derived from the value in (1). Moreover, the apparent absence of the coupling with other components of the universe with any significant strength indicates this field to be part of gravitation. In this sense, we are going to appeal to the scalar-tensor theory of gravity as a well-known alternative to Einstein’s General Relativity, but with a natural extension to live a new life in the era of the accelerating universe.
Unfortunately, however, we are still left with too much arbitrariness in fixing more of the theoretical details. Variety of theoretical models have been attempted under various names, like quintessence, k-essence, and theories, and so on, still away from a final conclusion. See [6] for an overview. As it appears, on the other hand, few attentions have been paid to the first part of (4), which, to be accepted beyond a mere numerical coincidence, is by itself so simple yet something of profound theoretical implication. A simple result deserves a simple reasoning. Based on this faith in simplicity, we may start with re-interpreting an “instantaneous” relation (4), confirmed observationally only for , as part of a more general relation
expected to be true in the time span over a major part of the entire history of the expanding universe, at least to a first approximation. Under this “scenario of a decaying cosmological constant,” today’s Λ is small only because we are old cosmologically, but not due to any of the fine-tuning of the theoretical parameters.
Rather unexpectedly, we come to finding as if the simplest type of the scalar-tensor theory originally due to Jordan [7] could have been prepared for implementing the above-mentioned scenario, for the globally overall behavior of our intuitive desire, as long as some portions of the theory are to be revised rather drastically. As we admit, we are still left with locally subtle behaviors, particularly near the present epoch, which will be dealt with by what we call a trapping mechanism later in Section 6. But the Scenario in overall behaviors is so successful that we have no other choice but to keep it alive at any cost.
As we also recall, the relation (4) or (6) had been foreseen in 1980s [8,9], when only the upper bound was available for the cosmological constant. With the renewed observational results on the accelerating universe, we decided to re-formulate the theory.
Throughout this attempt we have faced many unprecedented issues. By carefully following the way of astronomers and astrophysicists in measuring the cosmological expansions, we have found it unavoidable to replace the additional theoretical requirement due to Brans and Dicke (BD), often called the BD model, or even the BD theory [10], by what we call the scale-invariance model [11], reaching eventually to the conclusion that the scalar field is identified with the dilaton, a Nambu–Goldstone (NG) boson [12,13] of spontaneously broken global scale invariance. This is a highly remarkable aspect of the Unification program, trying to bridge two vastly different sizes, the cosmological and microscopic scales. Also to be noticed, our approach might be a rediscovery of the earlier theoretical efforts to accept a realistic dilaton [14,15].
Following the above overall context in this article, we start Section 2 with presenting Jordan’s simplest version of the scalar-tensor theory [7], upgraded only by including the cosmological constant, with other features listed briefly for the later use.
In Section 3, we then review briefly the important elements of the conformal transformation and frames, which are unique to the scalar-tensor theory. We then discuss the Jordan and Einstein frames, abbreviated by J frame and E frame, respectively, in what follows, each characterized by the variable and the truly constant gravitational constant.
Section 4 is for simple cosmology, particularly radiation-dominated universe in J frame and E frame, in Subsection 4.1 and Subsection 4.2, respectively. Without entering into detailed derivations, we show the attractor and asymptotic solutions in J frame to reach an unrealistic static universe, at the same time, with constant mass of microscopic particles according to the BD model [10], in which they demanded the gravitational scalar field decoupled from the matter Lagrangian, originally to save the idea of Weak Equivalence Principle (WEP). The universe corresponding to the solutions in E frame is, on the other hand, now shown to expand, fortunately in conformity with the realistic universe. Also to be emphasized, the falling-off behavior shown by (6) follows naturally and automatically in spatially-flat RW spacetime in the same way as we derive a critical density in the ordinary sense, .
In spite of this encouraging sign, a serious flaw is pointed out, however, that the scale factor of the universe expands in the same rate as the inverse mass of the electron, as a typical example of microscopic particles. In other words, the universe should look static if measured in reference to the units provided by the mass of the electron, for example. We argue the BD requirement to be blamed, as will be the main subject in Subsection 4.3.
A rescue attempt is made in Section 5. First in Subsection 5.1, we propose to introduce the so far forbidden coupling of the gravitational scalar field, denoted by the symbol ϕ, to the matter fields, with dimensionless coupling constants, h, thus implementing global scale invariance except for the term of Λ, hence what is called the scale-invariance model. In moving to E frame, we pick up the constant part, or the vacuum expectation value, of ϕ, eventually providing with constant particle masses, as we had anticipated, to be acceptable in the physical frame, at least to a good approximation. This is precisely the way of a spontaneously broken global scale invariance, or dilatation symmetry. Also this global transformation is described in terms of a globalized version of the conformal transformation used before. This allows us to apply the analysis to curved spacetime.
The nature of this spontaneous breaking is further developed in Subsection 5.2, first deriving the dilatation current explicitly. Most remarkably, we come to finding that the field σ, a renewed name of the gravitational scalar field in E frame, is a massless NG boson of dilatation symmetry, thus called a dilaton. We also show briefly that this σ might play a crucial role in generating the Higgs field in the Standard Model, hence the masses of all the fundamental particles.
As an ensuing development discussed in Subsection 5.3, the way of breaking scale invariance is now upgraded further from being spontaneous to being explicit due to the loops in the context of relativistic quantum field theory. We exploited the mathematical technique, dimensional regularization, in terms of continuous spacetime dimension D, which is sent back to the physical value 4 only at the end of the calculation. We then find a quantum-anomaly-type effect in which σ, once decoupled from the ordinary matter, thus contributing only to the acceleration of the universe, is brought back to coupling again with matter particles through the mass terms as well as the coupling constants, with the strength nearly as weak as gravity, also WEP violating to a relatively small amount. Furthermore the dilaton itself acquires a nonzero mass, as had been suggested [12] that the massive pion might be a theoretical descendant of an ideally massless NG boson. We expect a value as light as , with the corresponding force-range . In this way we reach a finite-range force mediated by this pseudo NG boson, suggested first in the early 1970s [16], now to be rediscovered in the new light of the accelerating universe. A question might arise if the emergence of this type of force can be understood in a manner consistent with the way of accelerating the universe, as will be discussed affirmatively later in Section 6.
Subsection 5.4 discusses briefly how the physical frame consequently deviates from the pure E frame slightly. The E frame can be still accepted as a physical frame to a good approximation in practice.
We are now in Section 6 in showing what the realistic results on the accelerating universe looks like. We start with discussing a confrontation between an intrinsically discrete nature of the cosmological “constant” and the Scenario of its continuous decay. In Subsection 6.1 we find that our theory is already equipped with a built-in mechanism for a step-like behavior, but finding its insufficiency in practice. To overcome this defect, we propose in Subsection 6.2 an ad hoc mechanism for trapping, which, in terms of another scalar field χ with its contrived potential, is designed to provide with a short-time push to induce a mini-inflation of the scale factor, as is observed probably for a relatively short duration of the cosmic time around the present era. At this moment, the trapping mechanism is a phenomenological superstructure placed on top the substructure laid down at a more fundamental level. Through a veil of the former we may peep unmistakably into the latter supposed to sustain the Scenario, the basic law of the accelerating universe, as was emphasized particularly in [17].
Some of the marked features of the results are itemized. Among them we focus particularly upon a small oscillatory behavior of the trapped σ, suggesting possible experimental measurements on the time-dependent fine-structure constant also the ratio of the electron mass to the proton mass.
In the following, Section 7 will be devoted to a brief account of the proposed experimental search for the massive pseudo NG boson, through the photon-photon scattering processes [18,19]. In this laboratory experiment, we rely heavily on the use of strong laser beams, unlike in the past similar attempts.
In the final Section 8, we summarize what we have done very briefly, also adding what is yet to be done.
Before closing this first section, we admit that some of the contents of the present article are taken from our past publications, particularly from [11]. However, our renewed emphases will be placed on how we have been motivated, stated in as intuitive and hopefully plain languages as possible and to be conveyed to experts and non-experts alike. For this purpose some of the details are left, in favor of the major messages, to the interested readers to consult the original references.
2. Scalar-Tensor Theory Due to Jordan
Jordan proposed the scalar-tensor theory with the Lagrangian
where ϕ is the scalar field. We are going to list the related remarks.
- The first term with , multiplied with R, is called a nonminimal coupling term, designed to give an effective gravitational “constant” represented by allowing it to be spacetime-dependent, obviously intended to implement Dirac’s idea of the time-dependent gravitational constant [20]. Note the continued use of the Planckian unit system.
- In the sign factor , the positive choice corresponds to a positive kinetic energy of ϕ, though the negative choice is not excluded immediately because ϕ at the level of (7) is not a fully diagonalized field. See Section 2.6 of [11] for details on the mixing interaction between ϕ and the spinless part of the metric, taking place in the nonminimal coupling term.
- We also use the parameter , instead of the original , excluding repulsive gravity.
- We have the ordinary type of the matter Lagrangian , specifically representing the fundamental fields in the microscopic world.
- Also to be added beyond Jordan is the cosmological constant introduced to expect the theory now to provide us with a new way of understanding the accelerating universe. Respecting the arguments on the Unification program, we assume Λ of the order unity in the Planckian unit system, or .
We find it appropriate to add an important remark for the scalar-tensor theory to be discussed in our context. Jordan appeared to have assumed tacitly ϕ to be massless, implemented by the absence of the term , probably only for simplicity. We point out, however, that this is not the way we exclude the additional long-range force. The expected masslessness or its proximity, particularly for σ in E frame, will be discussed later from another point of view for the role of dilaton. We emphasize that, unlike the authentic gauge fields, such as the photon and graviton, a scalar field has no immunity against the field-theoretical self-energy. It acquires a nonzero mass likely of the order of , as was already pointed out. The corresponding force-range is probably of the order of 100 m, which is much smaller than the solar radius. As a result, we are now free from the past constraints obtained from the Shapiro delay of the lights in the solar-system experiments, like [10], or more recent result [21]. See also [22].
3. Conformal Transformation/Frames
As was pointed out by Pauli, the theory features a unique role played by the conformal transformation defined by
together with a few of immediate consequences
with an arbitrary spacetime function . Equation (8) can be interpreted as a local scale transformation, sometimes called Weyl re-scaling. As we point out, the transformation makes sense even if we have no invariance under this transformation, unlike the gauge transformation that had evolved somehow from Weyl’s initial attempt. The situation might be compared with the notion of inertial frame, without invariance in classical Newtonian dynamics, resulting in different physical processes, presence or absence of inertial forces, like a centrifugal force, for example. Note how different physics looks like on the orbiting International Space Station (ISS) compared with what we experience on the Earth.
It is crucially important to notice that, by substituting described by the inverse of (8) into (7), we now re-express the same Lagrangian in terms of the new metric . More profoundly, we have no way to write down a Lagrangian without choosing a frame. It is true that it might be sufficient to keep it in our mind that any of the measurements are made in reference to certain units. But we recognize how convenient a tool is provided by the notion of the conformal frame. Thanks to the non-invariance we reach a different dependence on the metric, hence describing different physical processes. One of the most useful results is obtained by choosing Ω by
resulting in
where , re-expressed by , is now multiplied by a pure constant, representing the conventional Einstein–Hilbert (EH) term, in other words, the time-independent constant .
Also the new canonical scalar field σ is related to the original ϕ by
where the new constant ζ is defined by
For later use, it might be convenient to combine (10) with (12) to derive
Also the “constant” term Λ in (7) has been converted to the potential of the scalar field;
In connection with the quintessence approach [23,24], we recall that an exponential potential has been one of the favorite candidates because it shows asymptotically a rather flat behavior, sometimes called a run-away behavior, hence allowing a slow rolling of σ. We find it even fascinating to arrive at the same potential as a transformation factor, also traced back to the simplest imaginable choice of a constant Λ added to (7).
We emphasize that we continue to use the Planckian unit system, implying that ϕ in (10) also σ in (15) are interpreted always to be multiplied by a constant , for example. Notice that σ is now a diagonalized field, according to the analysis in Section 2.6 of [11], hence the positivity of its kinetic energy should be assured by the requirement shown in (11), or
according to (13), which implies
or either an arbitrary ξ for or for , as exhibited in Figure 1.
Since Ω is an arbitrary function, we have infinitely many conformal transformations, hence infinitely many Lagrangians. Out of them, however, there are two special ones, represented by (7) and (11), respectively. The second one is characterized by a pure EH term, while the first one is by the absence of ϕ except for the nonminimal coupling term and the kinetic term of ϕ.
Strictly speaking the last point is unique to what is called the BD model, which features the absence of ϕ in the matter Lagrangian . Revising this point will be made later as a crucial step toward application to the modern cosmology. At the present time, however, we assume the BD model to define (7) as one of the possible ways ϕ comes into the Lagrangian, which is then called the one in the Jordan (conformal) frame. On the other hand, (11) is the Lagrangian defined in the Einstein (conformal) frame. By the conformal transformation with Ω defined by (10), we say we have moved from J frame to E frame.
Given the truly constant in (11), we learn that whether a quantity is constant or not depends on what conformal frame we choose. This is part of the arguments we discussed before; the Lagrangian can be written down only after the conformal frame is chosen. This also shows how physics looks different from frame to frame. In this sense, a question is then what conformal frame we live in, or what the physical conformal frame is.
After these precautionary remarks, we now discuss explicit examples of simplified cosmology.
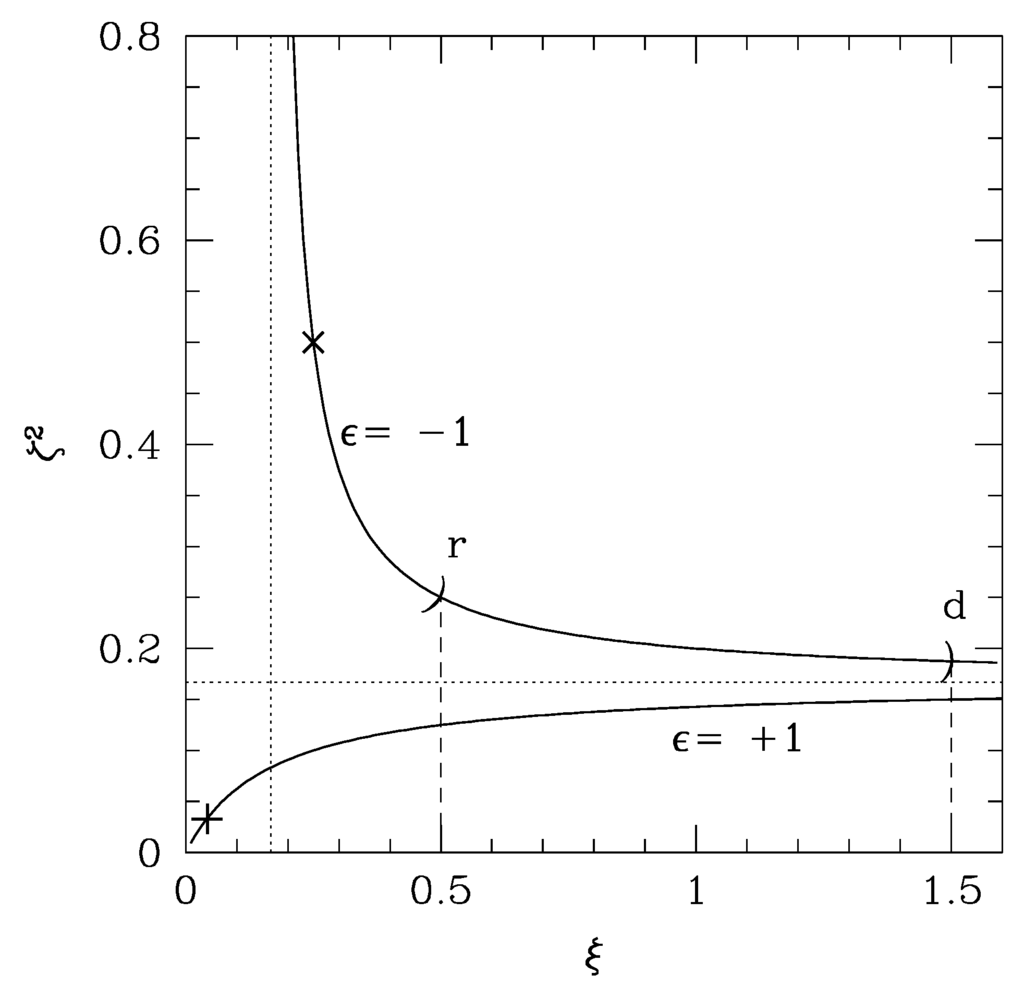
Figure 1.
given by (13) restricted to be positive is plotted against , taken from Figure 1 of [25]. There are two branches for bounded by the two (dotted) straight lines and . The results from the solar-system experiments correspond to the points, like the one marked by +, converging toward the origin with . The symbol ) also marked with r at the point naturally with provides with the boundary of selecting the portion of the curve to the upper-left, arising from the positive radiation-dominated matter energy both in J frame, (26) and (27), and E frame, (38). The same marked by d is for the dust-dominated universe. The symbol × shows a prediction of string theory in higher-dimensional spacetime, thus , and , based on (4.1) of [25], taken originally from (3.4.58) of [26].
4. Simple Cosmology
4.1. Radiation Dominance in J Frame
Consider first J frame in the radiation-dominated universe in spatially flat Robertson–Walker (RW) metric. The line element is given by
We naturally assume the scalar field to be spatially uniform, depending only on the cosmic time t. Skipping all the details on the derivation, the cosmological equations from the Lagrangian (7) are obtained;
where
We then present the asymptotic and attractor solutions for the scale factor a, scalar field ϕ, and the matter density ρ;
We are also going to present Figure 2, illustrating how an example of the numerical solutions tends to the asymptotic behaviors shown above, though leaving more details of the analyses in [28].
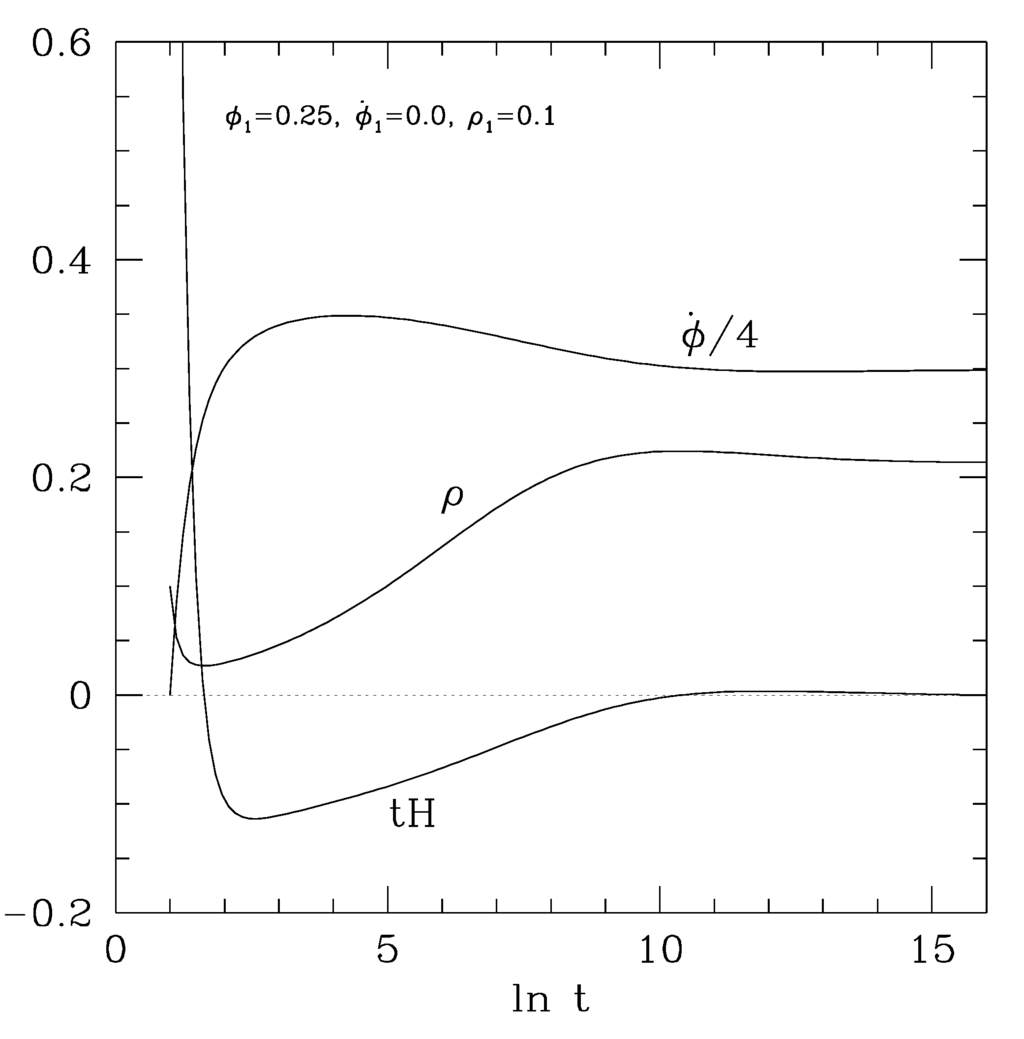
Figure 2.
An example of a numerical integration, corresponding to the initial values at the initial time , taken from Figure 4.1 of [11], originally from [27].
We first notice that the constant scale factor, as shown in (23), describes the static universe that is totally unrealistic, simply implying that J frame is not the conformal frame we live in. This solution is in fact appreciated only for the simplest way to look for other frames. Nevertheless studying this frame from an overall theoretical point of view is useful, as will be argued.
We may impose a physical requirement . On the other hand, we have some reason why , which turns out to be fitted to the observation, as will be shown later in E frame. Combining these two requirements, also including , which otherwise would have ultimately implied a repulsive gravity from (7), we come to conclude
and hence
thus selecting the portion of the curve in Figure 1 to the upper-left of the point marked as ) and r.
These properties in the fundamental parameters of the theory should be taken over to other frames, including E frame in particular. We also point out that the sign of the matter energy density remains unchanged through the conformal transformation.
Now with the first of (26), the “wrong” sign before the kinetic energy of ϕ tends to cancel the sum of ρ and Λ on RHS of (19). As it is known, the presence of with , or in the absence of ϕ, usually brings about an exponential growth of the scale factor;
thus causing an “inflation,” also known as de Sitter universe. The above solution with , on the other hand, allows a complete cancellation, resulting in an asymptotically static universe, magically without fine-tuning any of the continuous parameters, as was demonstrated first by Dolgov [29]. This remarkable finding is certainly related to the absence of the inflationary behavior in E frame, as will be shown shortly.
4.2. Radiation Dominance in E Frame
In order to land on the promised physical frame, it appears necessary to search for infinitely many Ω. Fortunately, however, faith in the simplicity principle turns out to be rewarding. Being guided by the constant , we first try E frame.
Under (8) we have now
where
We have a comment that the first term of RHS of (29) would have been , with if we insisted that the conformal transformation is different from a general coordinate transformation. We have, however, an obvious advantage that using as obtained by a general coordinate transformation represented by the first equation in (30) plays the role of the cosmic time , a proper time in the new freely-falling coordinate system.
We then obtain the cosmological equations now in the form;
where
with the dot everywhere for a differentiation with respect to . We find that is nothing but the dark-energy density, or the effective cosmological constant , which might be identified with .
The attractor and asymptotic solutions are obtained either directly from (31)–(33), or by re-expressing (23)–(25) based on (14), (30) and (34);
We may impose for and hence , in agreement with (26) and (27). An example of the behavior of the solution in the detailed phase-diagrams is shown in Figure 3.
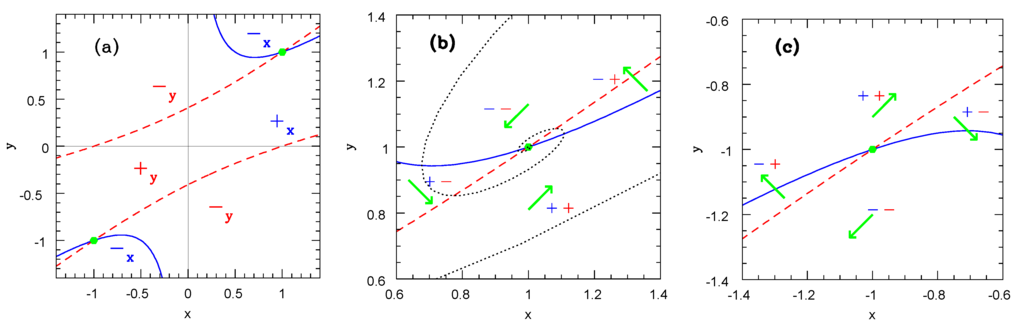
Figure 3.
An example of the phase-diagrams in E frame taken from Figure 3 of [28]. The evolution variable is chosen to be , while the coordinates are defined by and , which satisfy the self-autonomous equations (3.15) and (3.16) of [28]. The solid and dashed curves in (a) are for the null curves of and , respectively, bounding the area of marked by , for example. The fixed points are and for an attractor and repeller, respectively, as shown in the close-up views in (b) and (c). The trajectory shown by a dotted curve enters the frame of (b), with thus , near the lower-left corner, going out across the right edge, re-entering again at the top, spiraling finally into the attractor at . No such trajectory is shown naturally in (c).
It appears as if we have achieved a two-fold success;
- According to (35), the universe not only expands but also does so in conformity with the assumed radiation-dominance.
- Equation (37) can be interpreted as implementing the scenario of a decaying cosmological constant, represented by (6) supposed to apply to quite wide a time span, as a first step toward understanding the numerical relation (4), which we have focused upon as the simplest yet probably the most important achievement arising from the discovery of the acceleration of the universe. As we also add, the behavior of the inverse-square of time is simply a standard result deriving a critical density. As we recall, this nearly desired behavior is a consequence of the exponential potential (15), also traced back to the simplest imaginable choice, Λ, added to (7). We notice, however, that multiplying Λ by results only in replacing ζ in by .
Too much optimism, however, turns out to be too early before more careful analysis is needed on the microscopic world. It might sound as if such details are irrelevant for the radiation-dominated universe; the behavior of the particle masses hardly affects the evolution of the universe. It nevertheless does indirectly because the astronomers measure the patterns of atomic spectra of the observed lights to be compared with the same measured in the Earth-bound laboratories. An underlying assumption is that the atomic spectra are the same here and there, distant astronomical objects, interpreting the observed difference in terms of the redshift due to the receding speeds of galaxies.
The separations between the atomic levels are given basically by the Rydberg constant where e is the elementary charge while is for the reduced mass of the electron and the nucleus. In what follows we simplify the equations by using , the electron mass, rather than . This is a unique way, as we emphasize from a practical point of view, that the modern cosmology of the expanding universe is tied so closely with the physics of the microscopic world, another strong indication for the need of the Unification approach, aiming at bridging two vastly different sizes in Nature.
Before entering into details of this type, it might be convenient to present a quick derivation of the result (35). By first substituting (24) with (12) and (14) into the first of (30), we obtain
which is then substituted into the second of (30) also using (23), hence
without use of the equation of state of radiation, (33). The last point might also be supported by the less important role of ρ compared with as shown by (24) asymptotically. In this sense the exponent in (35) is only accidentally.
4.3. The Brans–Dicke Requirement
Now to make a crucial point of the microscopic mass term in a model as simple as possible, we consider an example of the matter Lagrangian consisting only of a free massive real spinless field Φ in J frame, at this moment;
From (8) and (9) we readily derive
which leaves the kinetic term “nearly invariant,”
where
also with the use of (14). Notice that (43) keeps the same form as the first term of (41) to the approximation in which is ignored.
Then we face a question what the mass term is like. We begin with requiring the absence of ϕ in , proposed by Brans and Dicke [10] originally to save WEP. The mass term in J frame is then simply
The absence of ϕ implies only a purely constant m; we have none of the ways in which m varies depending on the spacetime position. Quite unexpectedly, however, we then come across a tumbling block, as will be discussed.
Substituting the second of (9) and first of (44), we re-express (45) as
where as a local mass is defined by
which might be accepted as a nearly constant mass only up to likely slow variation due to global spacetime dependence. This is something like a slow change of as was discussed in (7) in accordance with Dirac’s conjecture.
Now the problem is that the rate of change of the mass due to is the same as that of as noticed in the second of (30). In fact eliminating Ω from the second of (30) and (47) yields the relation
as was verified also in [25] in the wider class of fields. This relation implies that , representing the change of the intergalactic distances, measured relatively to the unit of length , remains unchanging. This is an entirely unacceptable situation, according to the current view on the cosmological expansion, as we emphasized before, toward the near end of the preceding subsection. The source of this inconvenient feature can be traced back to J frame, in which the static universe implied by (23) happens to be precisely in accordance with the constant mass chosen under the BD requirement, which has to be revised.
In a slightly different language, we might say that a quantity that is constant in a given conformal frame can be used as a unit or a standard. This is also in conformity with an intuitive view that a unit itself is a constant by definition, allowing no variability, as was discussed under the name of Own-Unit-Insensitivity-Principle (OUIP) in [25]. We also add that constancy of a in J frame is a consequence of the solution of dynamical equations, whereas m is constant simply due to the BD requirement prepared at the outset. Following these lessons, we try to replace the BD requirement by some other mechanism in which the particle mass in E frame, favored by the two advantages emphasized by the itemized remarks in the preceding subsection, emerges as a constant.
5. Scale-Invariance Model
5.1. Leaving the Brans–Dicke Model
For this purpose we may start with E frame with an assumed constant going back to J frame. Skipping this heuristic procedure, however, we show the result. In place of the conventional mass term (45), we introduce the interaction term
with h a dimensionless coupling constant. On the RHS we use the first of (44) and (12) together with (14) finding
where the obtained coefficient can be interpreted as the truly constant mass in E frame, as expected. Note that the Ω’s have cancelled out each other. The resulting constancy of has been reached without use of the dynamical equations, thus leaving the solutions (35)–(38) unaffected. This allows us to use as a unit in reference to which we measure . Since ξ is basically of the order unity, we must choose h to be as small as if . The small number like this causes what is called a hierarchy problem, a core of the Unification program, basically the issue of the same nature as what urged Dirac to propose his time-dependent G [20]. At this moment, however, we are content with these numbers simply as they are.
As we notice, on the other hancd, the true length unit in practice is the inverse of the Rydberg constant, , with e the electric charge, which does depend on time, as will be shown in Subsection 5.3 later, hence affecting the constancy of the unit itself. In principle, the physical conformal frame is such that it keeps the product constant. At this moment, however, we may start reasonably with giving the first priority to the mass, which is fully responsible for providing with the length dimension, unlike the charge. Detailed behaviors of such complicated objects as units should be subjects of more realistic analyses in the future.
More importantly, we emphasize that the way deriving the mass from the interaction term, also with ϕ acquiring a constant part interpreted as a vacuum expectation value as in (12), suggests a spontaneous breaking with σ as an NG boson of a global scale invariance, often called dilaton, due to the dimensionless h, as will be confirmed explicitly in what follows.
The global scale invariance to be discussed here might be formulated in terms of the globalized version of the conformal transformation given by (8), but now with a spacetime-independent ;
Note that the transformation considered at present has nothing to do with moving to another conformal frame, like E frame. The above transformation can be considered in any of the conformal frames. Other relations like
may also turn out to be useful in the following analyses. This transformation might be conveniently called a dilatation transformation, if we find it necessary to differentiate from what has been known traditionally as a scale transformation,
which applies only to flat spacetime.
As an illustration, we now consider the kinetic term of ϕ;
as represented by the second term on RHS of (7) in J frame. By combining this with the last equation in (52), we find an invariance
if
On RHS, we have with the choice of the exponent to be accepted as minus of the dilatation scaling of 1 for the scalar field ϕ. This happens to be the same as the mass dimension 1 of ϕ in the traditional scale transformation, in which the role of the two derivative and is replaced by . Advantage in using in curved spacetime is obvious.
We then move on to discuss the nonminimal coupling term, the first term on RHS of (7);
Through a rather complicated computation, as shown in Appendix G of [11], simplified by spacetime-independence of , we derive
which turns out to be the same as the transformation of in , as shown by (52). This immediately implies an invariance;
demonstrating again the usefulness of the dilatation transformation applied to curved spacetime. We emphasize that this invariance is unique to the simplest version due to [7], not maintained by unless .
5.2. Spontaneously Broken Scale Invariance
After these preparations, we are now ready to give an explicit equation of the dilatation current that generates all of the global dilatation transformations, including (51), (56) together with the same transformation of Φ, as a simplified matter field, to be distinguished from the gravitational scalar field ϕ. This field Φ can be a matter scalar field that might be expected to play important roles in the Standard Model, particularly by creating its vacuum expectation value. But at this moment, we first start with explicit equations only for free and massless Φ, also chosen to be a real field for simplicity.
We now re-express in the infinitesimal transformation;
then computing the Noether current as defined by
where
We then find
leaving the detailed derivation in Appendix M of [11]. We further obtain
The far right equality, showing the conservation of the , is justified explicitly by a rather tedious calculation starting from (7) with the Λ term removed. See also (2.20) or (6.11) of [11].
In the first term on RHS of (64), we first substitute , as shown by (12) and (14), reaching
Comparing this with (63), we easily find that contains , which is linear with respect to σ. This is a clear signal of a spontaneous symmetry breaking with σ an NG boson, as will be shown more explicitly shortly.
Now with the constant according to (50) we are going to have
up to terms of the spacetime-dependent σ assumed to be small. We then derive
which is nonzero, particularly due to a nonzero mass . Substituting this together with (65) into (64), we obtain
We find, rather unexpectedly in this formulation, that the role of σ is indispensable even if . It appears as if the term , the trace of the energy-momentum tensor of a massless , was a springboard prepared for the later application to a nonzero . With this reservation in mind, the dilatation current remains conserved in spite of a nonzero mass , implying the dilatation symmetry broken spontaneously, by means of the NG boson σ. The above equation in (68) may also be considered to be a differential equation for σ. The presence of the massless operator shows that σ is in fact a massless field, corresponding to the statement that a nonzero mass term of is counterbalanced by a nonzero contribution of σ, with a momentum space representation of cancelled by a massless pole [12,13], corresponding to the presence of σ in (68).
We point out further that the present formulation in terms of Φ can be extended immediately to the mass generation mechanism in terms of the Higgs boson in the Standard Model, details of which might be found in [30] particularly in Section 87, for example, also in the analysis in 6.1 to 6.3 in [11]. Here we are going to sketch briefly how the J frame field Φ can be used as a simplified way of describing the Higgs field with the required nonzero vacuum expectation value, ignoring, for the moment, complications related to internal symmetries.
For this purpose, we consider (49) with replaced by for a negative squared-mass, also adding the scale-invariant term , hence the E frame Lagrangian,
instead of (50), representing a double-well potential of . We further re-express this in terms of in such a way that no term linear in is present, thus
where
for the characteristic vacuum expectation value v of and the vacuum energy due to the phase transition , respectively. The positive squared-mass of is finally obtained by
which happens to be twice as large as in (69).
In this way we find that our model, called the scale-invariance model, to be capable of generating the Higgs field in the Standard Model.
It is generally understood that the Higgs field, with its nonzero vacuum expectation value, provides with the universal origin of the masses of all the fundamental particles, including fermions and gauge fields. As an example, the mass of a quark field is given by the product
where is the coupling constant of the assumed Yukawa interaction between and to which we substitute its vacuum expectation value v. Obviously is a pure constant, like with any other fields.
In this way we may reach the view that the origin of the masses in this world can be traced back finally to the gravitational scalar field with its vacuum expectation value together with the nature of an NG boson. We re-emphasize that the whole argument is based on the current view on the modern cosmology with its size measured obviously in reference to the microscopic length units.
So far we disregarded the presence of Λ, which violates the dilatation invariance. In a sense the invariance is only partial. The effect of Λ, however, can be included first by re-writing RHS of (64) as with T the trace of the matter energy-momentum tensor. Further on replacing T by , we arrive at the non-conservation due to Λ;
where we have used (36). This much of non-invariance can be ignored in most of the time range around today. We then accept the massless σ at the present stage of relativistic quantum field theory realized on tangential Minkowski spacetime. In other words, σ is accepted massless as far as local physics is concerned with the cosmological acceleration as a whole being ignored.
The vacuum component in (70) might be a problem estimated to be around 60 orders of magnitude too large compared with (4), for corresponding to . This might be cancelled by another scale-invariant term included in (69). We might also expect that the new vacuum with respect to had been defined at such an early an epoch that it had likely been absorbed into the classical component , leaving us with no noticeable remnant near today.
As one of the noticeable aspects of the present approach, we point out that the series of the arguments is not derived from the Mexican-hat potential. For this reason, we can no longer discuss the stability of the solution in the true vacuum. Nevertheless we reach a spontaneous nature in a sense that we find the solution characterized by the initial, final or boundary conditions, not by the parameters prepared in the Lagrangian. The spontaneous compactification that we have met in higher-dimensional spacetime is another example of basically the same nature.
It is even surprising to find that the new model, featuring the dimensionless coupling constants, is miraculously as simple as the BD model, characterized by the absence of the matter fields. On the other hand, allowing the matter fields implies WEP to be broken, in principle, but with the physical results largely suppressed, as will be discussed shortly.
At the end of this subsection, we also note that we did not include the fermion explicitly in (61). This is partly because the mass of fermions, like quarks and leptons, emerges from the Yukawa coupling of the Higgs field, with its vacuum expectation value, and the spinor fields in the standard model, but is also because the spinor field fails to contribute to the Noether current of dilatation. On the RHS of (61) a cancellation takes place between the terms of the spinor field ψ and its conjugate field , having the same relations and . Probably relevant is that the mass of a fermion is generated from a spontaneously broken chiral invariance rather than dilatation symmetry. We simply suspect that the two reasons likely share the same theoretical basis.
5.3. Quantum Loop Effects
Another theoretically intriguing point is that the results of the above scale-invariance model is subject to the quantum loop effects coming from the relativistic quantum field theory realized on the tangential Minkowski spacetime. For some details, see Section 6 together with Appendix N of [11]. Remarkably, the effects show themselves first through what is known as quantum anomalies, in combination explicitly with the regularization technique, implemented particularly by continuous spacetime dimension D, which is finally sent to the physical value 4.
We start with the obvious relation
even with the same transformation rule as (8). Leaving details in Appendix G of [11], we derive
where , , and . We do not intend to go into any details at present, but only emphasize that the exponent 2 of Ω in the first term on RHS is always true; most of the remaining terms exhibit no critical behavior of D near . Combined this with (75) we have the factor in the first term on RHS of (7), which affects the derivation of (14) replaced by
where shows none of the critical behaviors near the physical value . At the same time we find the condition for E frame to be with constant;
in place of (12) combined with (14), where
On the other hand, requiring a near invariance of (43) replaces the first of (44) by
Substituting (78) and (80) into (50) yields, with re-denoted by ,
where we have expanded the exponential into a power series with respect to σ, only up to the linear term at this moment. Noticing the first of (71) and replacing v in (73) by the correspoding result for (81), we obtain
including the coupling to σ, but with the coefficient , where d is still off the physical value 2, also corresponding to (a) of Figure 4.
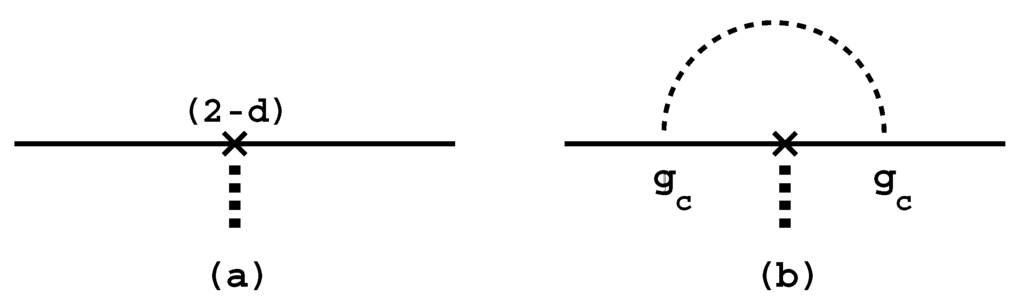
Figure 4.
The simple Yukawa interaction with the coefficient as in (a), but now with a non-gravitational radiative correction included, like in (b), where the dashed curve is for a non-gravitational field with the associated coupling constant . Heavy dotted lines drawn vertically are for σ.
Now as illustrated in (b) of the same figure, we apply a radiative correction due to some non-gravitational field, dashed curve, with the coupling constant . Apparently logarithmic loop integral will be expressed by the Gamma function , which develops a pole as ;
where and hence are constants. This is the way we regularize the divergent loop integral by making it finite for , as far as d is kept rather close to the physical value 2. We have also simplified the result by skipping some of the complications with mass renormalization process, still keeping the consistency with the perturbative expansion. We thus re-express (82) into
showing how the second term in the far RHS of (81) is salvaged from vanishing by the pole in (83), to yield a nonzero finite contribution, a typical way in which a quantum-anomaly-type effect is generated.
In this way our field now couples to σ, hence the WEP violation is going to be resurrected. This coupling is going to be used as a basis in deriving the one-σ exchange force between two matter objects.
Note also that the strength of the σ coupling is proportional to the mass , also to , which is understood to be multiplied with σ in the current Planckian unit system. It thus follows that the scalar field σ couples to the matter through the mass nearly as weakly as gravity, as expected.
As we point out, however, the pole structure emerges only for such fundamental particles, like quarks and leptons, which are supposed to exhibit a point-like nature in the short-distance limit. It then follows that no salvaging effect occurs as in (84) for composite objects, like ordinary nucleons or hadrons. Combining this with the fact that the quark mass is much smaller than the nucleon mass, we find it likely that the WEP violating effects are relatively small, perhaps somewhat below the available observational upper bounds, as shown in our analysis in Section 6.4 in [11]. It should nevertheless be worth contemplating the experiments for a force mediated by exchanging σ, sometimes called non-Newtonian gravity [16] or the fifth force [31,32]. This will eventually be the search for at least a component of dark energy. An important point is that the mediated force is most likely of a finite force-range, as will be briefly discussed.
As we discussed toward the end of Subsection 5.2, we have been dealing with a massless σ in the area of local physics. Extending the loop corrections, we find this σ also being subject to the loop correction of the self-energy type as in Figure 5;
with , for the mass of quarks and leptons, and supersymmetric mass scale, respectively, though a latitude of a few orders of magnitude might be unavoidable. Note also the above mass corresponds to the force-range much smaller than the solar radius. In this way we are now going to substantiate the argument at the end of Section 2.
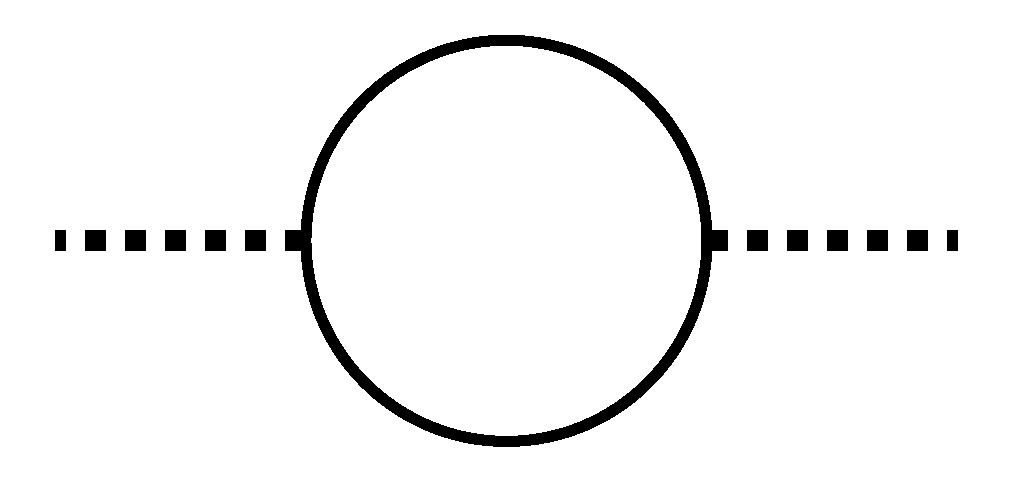
Figure 5.
A loop diagram generating a mass of the field σ (heavy dotted lines), while solid lines inside a loop represent quarks or leptons, with the coupling strength proportional to their own masses divided by . We also assume the integral to be cut off roughly around , the mass scale of supersymmetry breaking.
As another comment to be added, we notice that we deal mostly with the results with nonzero mass dimensions, which are always supplied by in the present analyses. We may write it as with . If ς were to pass a zero, like , it would have been salvaged again by the pole , giving another type of terms , like the anomalous dimensions in the renormalization-group approaches. Absence of this kind of contribution marks a unique difference from what have been discussed in renormalizable theories.
We add another reason for our departure from the BD model. To be discussed is the behavior of the solution for dust dominance in E frame. Following precisely the same way as obtaining (35)–(38), we reach particularly instead of the standard result . Although this result of the scale factor in E frame independent of the equation of state has been derived in [28], we have presented a brief account already at the end of Subsection 4.2. Still for some more details of the precise analysis, see Section 4.4.3, particularly around (4.118) in [11]. In Section 3 of [25] we derived explicitly together with basically the same results as (37) and (38), but with somewhat different coefficients based on the scale-invariance model, hence curing a disease of the BD model.
Before closing this subsection, we add a brief discussion of the same kind of effect on the electric charge e in addition to the mass. We start with the Maxwell Lagrangian
In D dimensions we find the conformal transformation
By requiring the invariance, we derive the transformation rule
ignoring the contribution from the derivatives of σ, as was pointed out following (43) and (44) with the spinless field Φ.
On the other hand, the minimal electromagnetic interaction of the matter field is constrained by the gauge invariance, which leads eventually to the conformal invariance of the product . We combine this with (88) to derive
which happens to agree with the ratio in (82) for the mass. In other words, the charge will be modified by the presence of σ if combined with radiative corrections, with the non-σ term absorbed simply into the ordinary charge renormalization.
As a 1-loop diagram we discuss the photon self-energy diagram , in which the loop contains the contribution from all the fundamental quarks and leptons, shown as (a) in Figure 6, while the attached σ line comes from the second term of (89). In D dimensions we find a logarithmic divergence regularized by
where e in the following is for the charge in E frame. We multiply (90) with twice the second term of (89), also using as , thus obtaining the γ-γ-σ coupling;
corresponding to the diagram (a) of Figure 6 with
where is the electric charge of each quark and lepton. An experimental proposal will be made later based on (91).
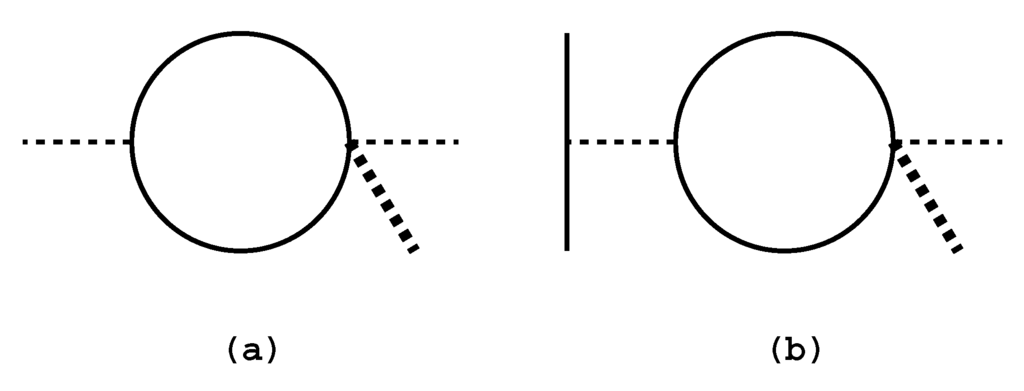
Figure 6.
(a) 1-loop photon self-energy part with σ (heavy dotted line) attached to two of the vertices. (b) The same but one of the photon lines (thin dotted lines) attached to another charged field (vertical solid line), with σ attached to three of the vertices.
Another application, corresponding to Figure 6b, is the change of the charge of a charged field due to the change of σ as represented by
For on RHS we may use the changing σ, which occurs in the trapping process of the accelerating universe, as will be shown later in connection with Figure 11 of Subsection 6.2, particularly with the related measurements.
5.4. A Slight Deviation from E Frame
As we presented in (84), the mass of a microscopic particle in E frame is given by
within the one-loop approximation. This depends on σ, hence varies with time, according to (36);
We then move to another conformal frame designated by the symbol ♮ in which is a constant chosen to be equal to at the present time , hence
This mass ratio can be identified with the ratio , so that
with the condition at the present time.
Substituting from (96) thus gives a differential equation for as a function . This provides us with an illustration on what the required frame is like, supposed to be valid for a neighborhood of the present time also justifying the use of the one-loop approximation. A rather weak dependence on shown in (96) does indicate that the new frame remains in fact rather close to E frame.
6. Trapping Mechanism
In Section 5 we argued in favor of E frame to be identified with the physical frame to a good approximation. In addition to the concomitant assumption of the scale-invariance model in place of the BD model, one of the most important ingredients was the uniformly falling behavior , (37), re-interpreted as the Scenario of a decaying cosmological constant, which is expected to understand the core result, , as shown in (4). But how do we compromise this approach of smooth behaviors with something discrete implied by a cosmological “constant”? A possible reply will be offered by an expected step-like behavior superimposed on the smooth background. To our another surprise, this is already prepared largely in a more rigorous solution of the E frame equations, though still short of reaching reality.
6.1. Hesitation Behavior
In order to show this, we first go one step further by integrating the Equations (31)–(33) numerically, beyond the purely asymptotic solutions. Leaving the details again to Section 5.4.1 of [11], we show a typical example in Figure 7. We choose the initial time at probably somewhat after the end of the primordial inflation period. In the current article, we limit ourselves to the epochs after the primordial inflation, for which another distinct kind of mechanism had been responsible.
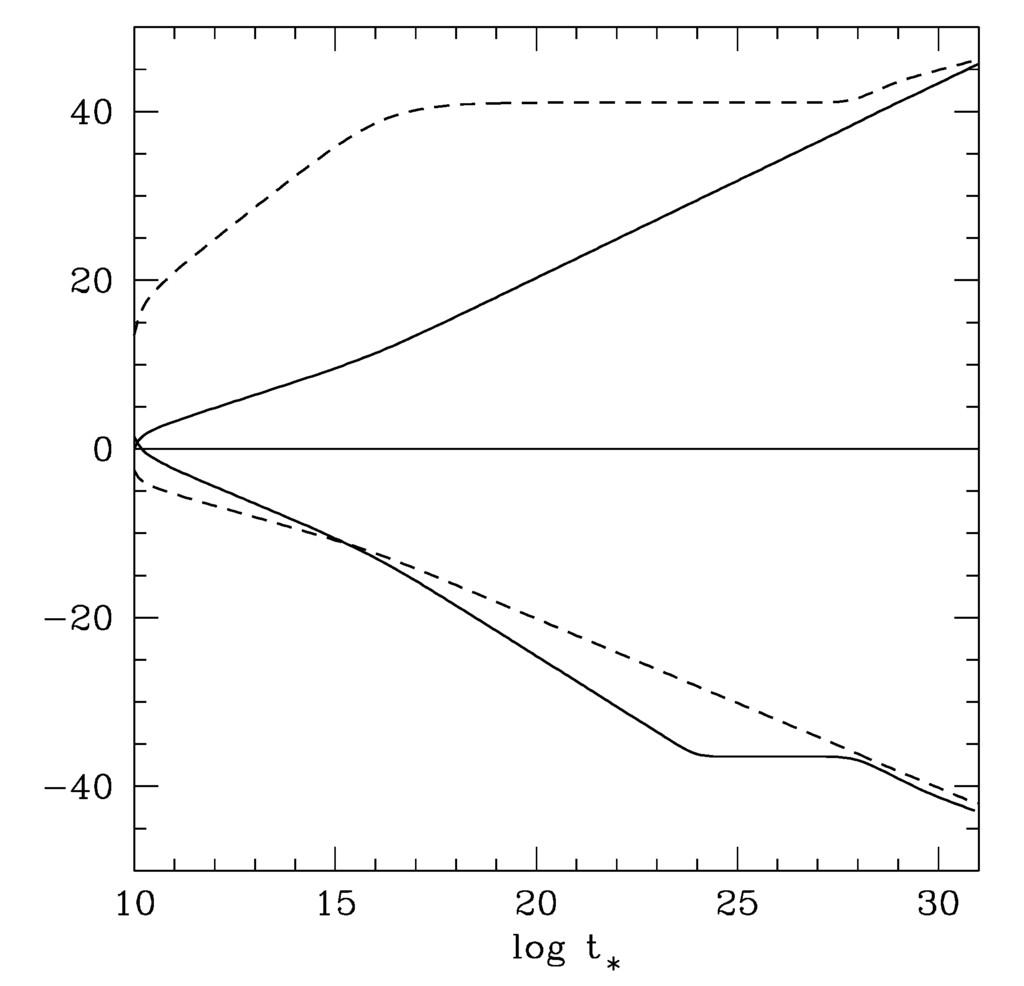
Figure 7.
An example of hesitation behavior, taken from Figure 5.6 of [11]. The solid curve in the upper-half of the plot shows , while the dashed curve represents . In the lower-half of the plot, the dashed and the solid curves are for and , respectively. We chose , the same as will be used in the next subsection. The initial values at is given by , while the matter density assumed to be radiation-dominated is .
We also assume the initial value for simplicity, but still σ begins to proceed as it naturally falls off the potential slope. The dashed curve in the upper panel represents how σ increases before it reaches a near plateau toward for the “present" era, just as a toy calculation. This increase results in a rapid decrease of the exponential potential , which yields the kinetic-energy dominance . During this K-dominated period, we find K to fall off like at its steepest. In this way nearly settles down finally at a very small value, a plateau to be called a hesitation behavior. This is what is going to be a built-in mechanism for a step-like behavior, as we mentioned before. We add that the same type of behavior had been discussed in [33,34,35], but the latter with an inverse-power potential.
This typically nonlinear behavior might be better understood by applying a well-known analytic method to each of the small local time regions, as was shown in detail in 5.4.1 of [11]. We might inquire if this plateau extends itself to cross the ordinary matter density , which comes closer to from above. If the crossing were to occur, it would have derived the value or beyond according to (1). As we find from many of the numerical exercises, however, this is far from being the case. We find a general trend in which starts bending itself downward, as if it had its own strong will to avoid a collision with , hence keeping . In the example of Figure 7, the system appears to end up with the type of the asymptotic behavior with corresponding to , as derived from a comparison of (37) with (38). We further find that even with choosing , actually as in Figure 7, the real result remains basically unchanged.
In accordance with this, the effective cosmological constant is short of pushing up the scale factor , as also illustrated by the solid curve in the upper panel, in disagreement with the observation. We have to do something.
6.2. Mini-Inflation(s)
From now on we are going to follow a phenomenological approach. In order to curb the downward flight of , we assume some other interaction to keep σ from going forward, encouraging the plateau to last longer, acting like a truly time-independent cosmological constant, corresponding to what was stated as the tracking behavior, rather than the scaling one. We also wish that this is not a single event throughout the entire history of the universe. After some efforts on the try-and-error bases, we came to introducing another scalar field χ with a potential [36,37,38];
This is designed to keep σ trapped near one of the local minima of with , the trapping mechanism. Figure 8 shows what (98) looks like. The field equations are also derived;
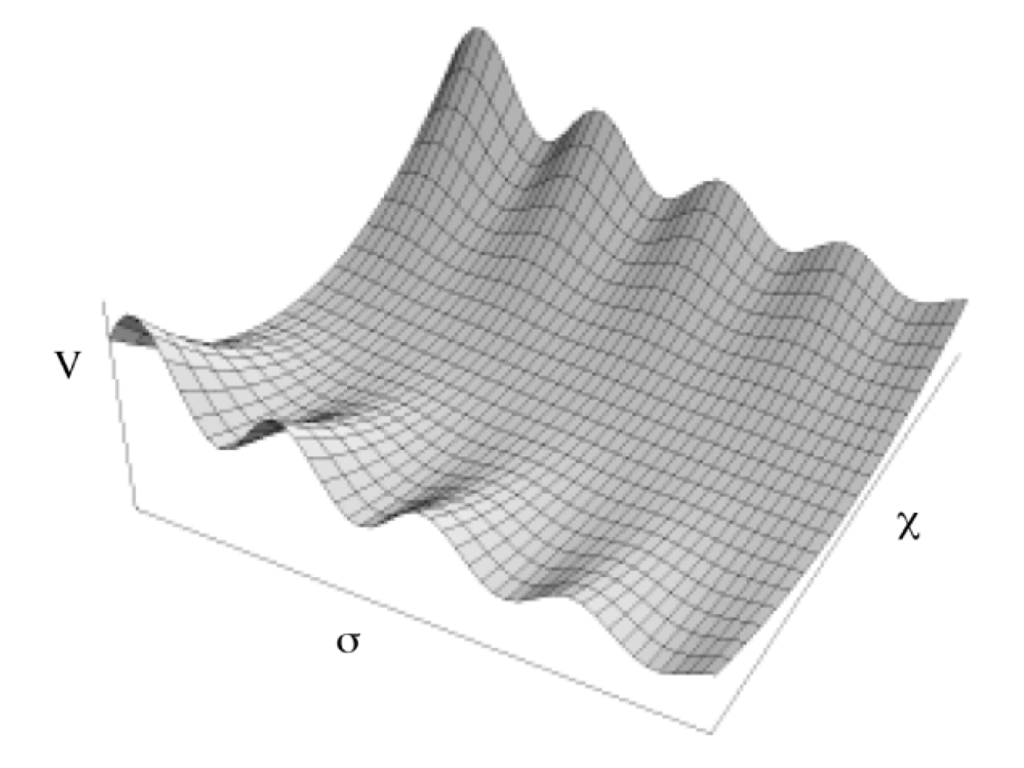
Figure 8.
The potential given by (98), taken from Figure 5.7 of [11]. Along the central valley with , the potential reduces back to the simpler behavior , but with , it shows an oscillation in the σ direction. The configuration of σ and χ is represented by a point, which is trapped in one of the valleys in the χ direction stays there, hence contributing a lasting that acts like a cosmological “constant”. As the time elapses, however, the force in the χ direction towards the central valley becomes strong, because of the increase of in the last term on LHS of (101), eventually releasing the point in the positive σ direction, the end of the mini-inflation. For more details, see also Figure 5.14 of [11].
As the time variable we use , with the prime for differentiation with respect to τ. As a result we have
In the similar manner we find explicit occurrences of in (99)–(101).
As we admit, this potential with χ has been introduced in an ad hoc manner in E frame, without inquiring its origin at this moment. With the sinusoidal behavior as a function of σ in the coupling with χ, we intend to evade a coincidence problem, as we find shortly. Without entering the details, we believe it useful to show an example of the solutions, as in Figure 9.
We look at first the portion , where we took over basically the same step-like behavior as in the lower panel of Figure 7. The hesitation behavior can be seen as part of an interlacing falling off of and represented by the dashed and solid curves, respectively, in the lower panel. Notice, however, that we have replaced by defined by
which includes the contribution from χ as well. We have chosen the parameters in such a way that the plateau of thrusts its way through , hence reaching , also resulting in a temporary and extra acceleration of , as represented by the dotted curve in the upper panel. This behavior, which is followed by a subsequent resumption back to the normal increase, might be referred to as a mini-inflation.
As we find in the upper panel, the field χ (dashed curve) stays nearly dormant most of the time. It does its job only when time is ripe; it traps σ for some duration of time before it moves to the other side of the central valley; . In this way χ helps to cross , allowing to shoot upward, a mini-inflation. After this relatively short period, χ starts again to be dormant. falls down sharply coming back nearly to the “initial” stage as in Figure 7, hence repeating the process for another mini-inflation again. But depending on the parameters, χ’s help might be limited, leaving , with the two densities going down simply side by side, as shown by Figure 10. This example illustrates that even with the presence of at the present epoch, the eternal inflation is by no means a uniquely determined fate of the universe.
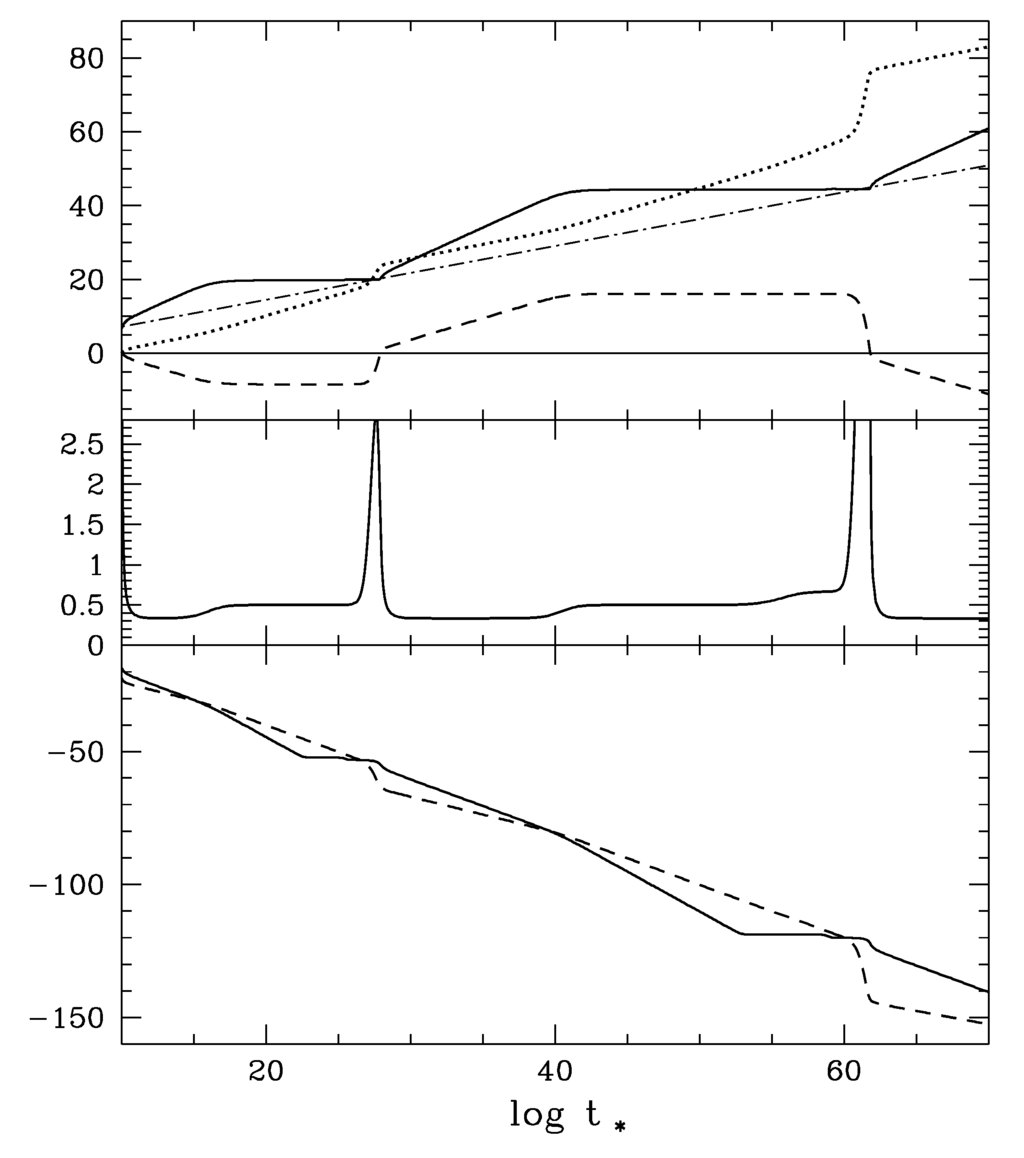
Figure 9.
An example of the solution, taken from Figure 5.8 of [11]. In accordance with the argument following (102), we chose , without much affecting the result around today. Upper diagram: (dotted), σ (solid) and (dashed) are plotted against . The present epoch corresponds to , while the primordial nucleosynthesis must have taken place at . The parameters are . The initial values at are (a prime implies differentiation with respect to ), . The dashed-dotted straight line represents the asymptote of σ given by . Notice long plateaus of σ and χ, and their rapid changes during relatively “short” periods. Middle diagram: for an effective exponent in the local power-law expansion of the universe. Notable leveling-offs can be seen at 0.333, 0.5 and 0.667 corresponding to the epochs dominated by the kinetic terms of the scalar fields, the radiation matter and the dust matter, respectively. Lower diagram: (solid), the total energy density of the σ-χ system, and (dashed), the matter energy density. Notice an “interlacing" pattern of and , still obeying as an overall behavior. Nearly flat plateaus of precede before it overtakes , hence with passing through 0.5.
We also point out that Figure 9 is an example in which we adjusted the parameters and the initial values in such a way that we had experienced another mini-inflation but left the primordial nucleosynthesis, for , unaffected by .
It is important to notice that our trapping mechanism is activated only when comes close to . In this respect the present mechanism is different from the model [39], with two exponential potentials resulting in a single minimum of the entire potential, for example.
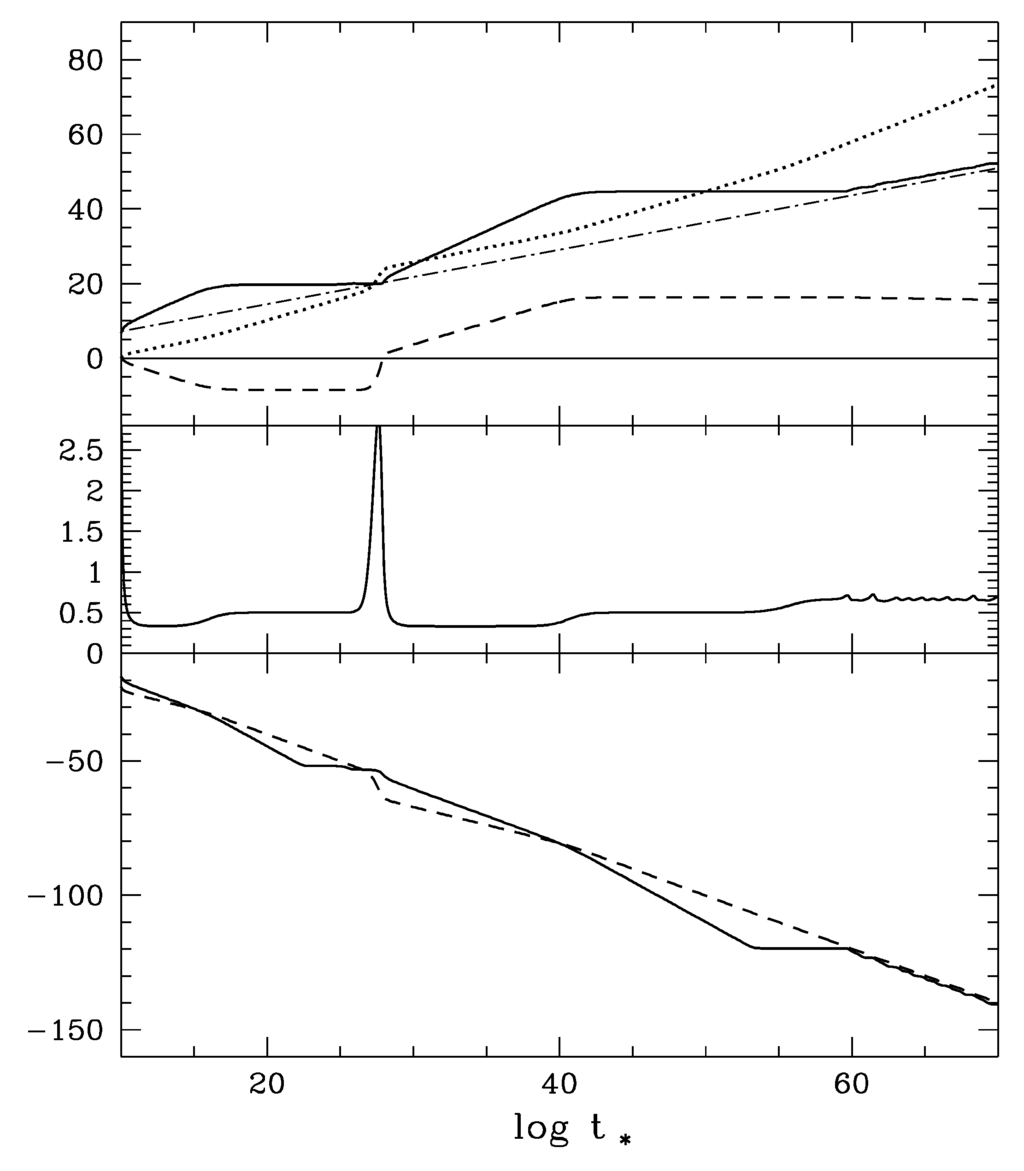
Figure 10.
An example of the solution, taken from Figure 5.11 of [11], showing no mini-inflation around the present epoch, though another mini-inflation at is still present. Symbols and initial values are the same as explained in Figure 9, except for , which is different form 6.7544 in Figure 9 only slightly. This indicates how sensitively the result might depend on the choice of some of the parameters.
In what follows we list some of other unique features;
- Generally speaking, the accelerating universe we are now watching might be one of the repeated events, in the past or the future. Due to this feature, we may expect to lessen the weight of the coincidence problem, though by a little bit, not entirely.
- The mini-inflations do occur as step-like behavior superimposed on the smooth and overall behaviors , as expected. The values of the height of each plateau, essentially for , are given basically by , with the times at which the mini-inflation occurred. This is because and falling off interlacingly with a common overall behavior as . The exact time of a mini-inflation is obviously determined by the height of the plateau, which depends critically on the parameter values at preceding times. For this reason exact timing of mini-inflations are hard to be determined theoretically. But once determined, the relation always follows, no matter when it occurs. This is what is truly meant by (4).
- At this point we take up again the question we asked ourselves toward the end of Section 1: Can we include the presence of a finite-range force between matter objects in a manner consistent with the cosmological evolution in terms of σ, which rolls slowly down the smooth slope of an exponential potential? The key of the points lies in noticing that we found the solution, as in the upper panel of Figure 9 in which σ varies in a range of the order unity in the Planckian units. Even the initial value is overwhelmingly larger than the value corresponding to the resonance; in the Planckian units. This implies that is completely outside the range corresponding to the entire history of the universe. In this sense a massive pseudo dilaton exerts a force nearly independent of the accelerating universe, in conformity with the former phenomenon belonging to the local physics, as we remarked.
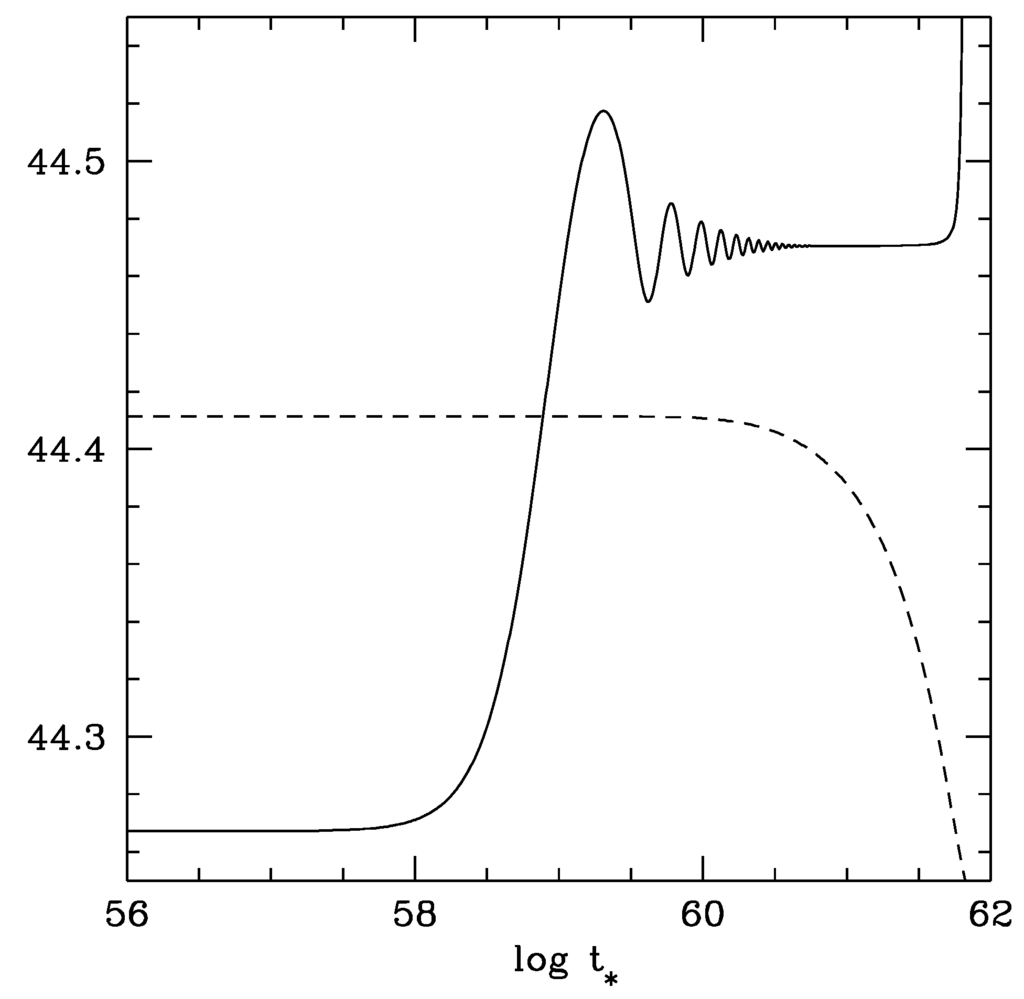
- There are so many different fine details as were discussed in Section 5.4.2. of [11]. We will make a comment particularly on Figure 11, in which the vertical scale is enlarged by more than 300 times of Figure 9, also with the horizontal scale by more than 10 times. Around the present time, what appears to be a little upward kink of σ (solid curve) in the upper panel of Figure 9 is magnified to reveal a small oscillatory structure unique to the trapping dynamics. This small variation of σ may be substituted to the RHS of the second equation of (93) to predict an oscillatory time-variation of the fine-structure constant, to be tested by near-future experiments [40,41,42,43,44]. In order to give an example, we are going to show a set of plots in Figure 12 calculated based on Figure 9 to be compared with the observation [46,47]. We expect that future experiments with improved accuracy will probe the proposed trapping mechanism probably with even better precision than in measuring the way of accelerating universe itself. It seems important to emphasize that we do provide with this way of observational verification, though our trapping mechanism implemented in terms of the potential (98) is not yet necessarily proved unique at present. For more recent observations on the ratio of the electron to the proton masses, see [49,50], and papers cited therein.
- The equations are highly nonlinear, as was discussed in [48] and also in 5.4.3 of [11]. As an example, an apparently repeated occurrence of mini-inflations, particularly its separations, or “frequencies”, are determined by the initial values or the parameters, in the presence of the cosmological friction, but not prepared in the starting Lagrangian like a harmonic oscillator, for example. Consequently, some of the final results may depend sharply on the choice of the initial values or the parameters. This might even be at odds with a traditional attitude that the cosmologically computed results on the present era should be as insensitive as possible to the initial states of the universe. But is anything wrong if certain aspect of the universe is as chaotic as what is happening daily around us? Some of the parameters have been fine-tuned, but not to the extreme extent of 120 orders of magnitude. We have obtained Figure 9, for example, after a few days of working on Mathematica. It might be still worth quoting, among others, that the occurrence of another mini-inflation around was a consequence of requiring none of the significant presence of in the era of primordial nucleo-synthesis around .
Summarizing, we conclude that the theory on the physical processes is of a two-layer structure. In this respect, we differ from those attempts trying to fit everything by a single function , for example, in the non-minimal coupling term. We have the fundamental theory based on the simple scalar-tensor theory combined with the scale-invariance model to deal with the asymptotic behaviors described by (35)–(38), also scrutinized to the hesitation behavior with the interlacing falling-off of the two densities sharing the common overall behavior . On top of this substructure, we need a superstructure for an additional push to extend the plateau to thrust into to implement a mini-inflation. This part of the theory, specifically applied to a rather short time span around each mini-inflation, is simply contrived in terms of another scalar field χ and the potential (98), expected to simulate possible complications from string theory or Standard Model. In spite of this tentative nature of the current trapping mechanism, we nevertheless attempt to fit the observational results with reasonable accuracies, as shown by Figures 5.9 and 5.14 of [11] and also by figures in [40,41,42,43,44], including Figure 11 and Figure 12 of the current article, which cannot be expected without the theoretical basis formulated in the substructure. This is in contrast with other more conventional quintessence approaches, for example, in which complications are distributed more or less evenly among components of the entire theory.
This is the way we want to probe the fundamental theory; simplicity through complication!
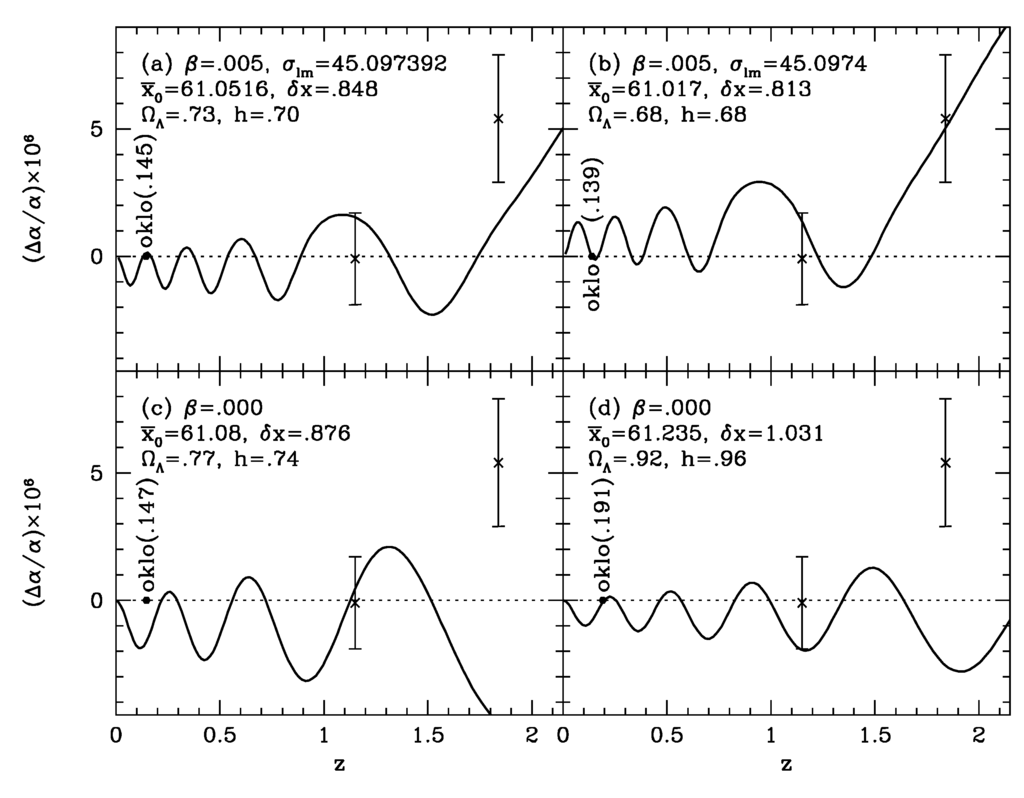
Figure 12.
Typical plots of the theoretical curves for as a function of redshift z, translated from the same of , taken from Figure 1 of [40]. See also [41,42,43,44]. The Oklo phenomenon having occurred ago corresponds to [45], while two QSO data [46,47] are shown; and for and , also for the fractional look-back time 0.59 and 0.73, respectively. We commonly choose the initial values at in the reduced Planckian unit system, as in Figure 5.8 of [11]; , where the prime is for the derivative with respect to .
7. Proposed Experimental Search for the Scalar Field
Since the early suggestions of a possible gravitational scalar field [16], many attempts have been made to discover it experimentally, as a due course of the development. Most conventionally, we measure the force between two massive objects. In order to overcome the weakness of the force as weak as gravity, however, we had often no other choice but to use the objects that are heavy and hence huge, sometimes appealing even to natural environments, like reservoirs, cliffs or polar ice, etc. See [32,51], for example, for summarizing such activities, including a somewhat similar suggestion of the fifth force [31]. In this way we faced many of the uncontrollable uncertainties in the measurements. In order to be free from such inaccuracies, we now propose to measure the force between two massless photons, implemented by a laboratory experiment on photon-photon scattering now by appealing to very intense laser beams to be available thanks to the state-of-the-art technology [18,19]. We are going to sketch only the new basic ideas.
We consider the tree diagrams as depicted in Figure 13. At each vertex we substitute from (91). Only in the s-channel process, the scalar field will act as a resonance at .
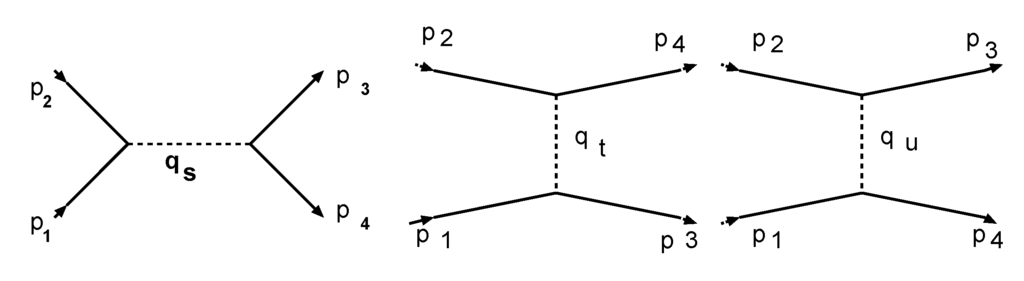
Figure 13.
σ-dominated tree diagrams for the photon-photon scattering process, taken from Figure 3 of [18]. Solid lines are for the photons with the attached momenta p’s while the dashed lines for σ, in the s-, t-, and u-channels, respectively.
The experimental setup will be the one illustrated as in Figure 14. We have a laser beam injected from the left, to be bent by a lens focusing the photons into the focal point O, where the two photons are supposed to collide to each other. After the scattering process, one of the final photons is expected to emerge to the right.
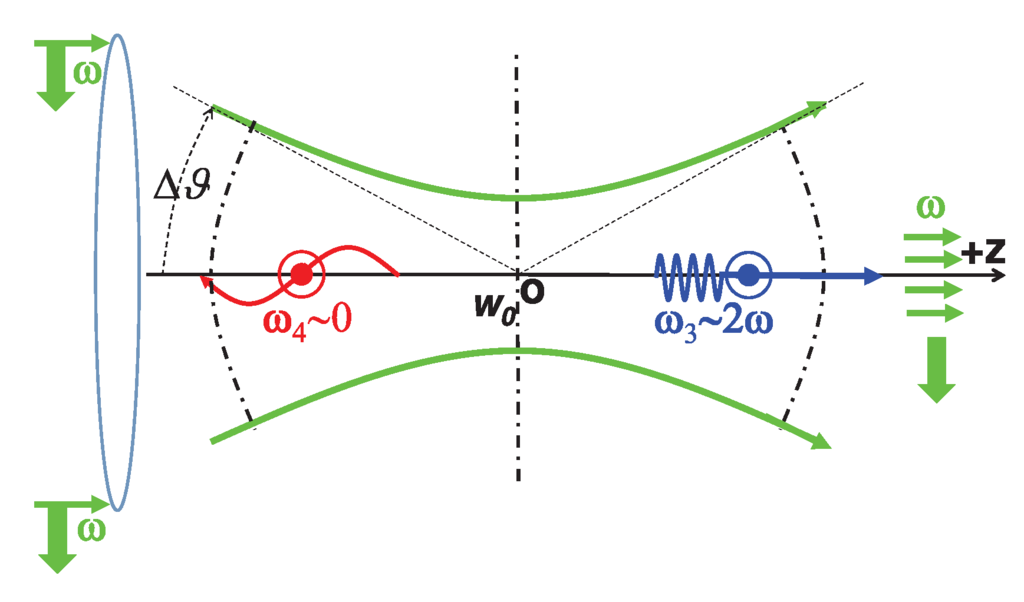
Figure 14.
A single Gaussian laser beam focused by an ideal lens where a scalar field exchange entails a frequency-upshifted photon in the forward direction, taken from Figure 5 of [18]. The frequency of the incident laser beam is assumed to be within a narrow band, while the incident angle varies largely including the value .
Corresponding to this configuration, we propose to use what is called a quasi-parallel-frame (QPF) as shown in Figure 15, in which the two incident photons share the same frequency ω making the angle , with the central line defining the z axis. We use the photons typically of the frequency .
The invariant amplitude in the s-channel is then given by
where the subscripts 1111, for example, indicate one of the possible polarization states. We may approximate this by a Breit–Wigner formula;
where the resonance frequency is defined by
With and , both of the RHS equations can be satisfied only with ϑ as small as . For this reason we always use this size of the frequency as a typical energy scale in what follows. In a sense, QFP is a convenient tool to achieve a lower CM energy starting from the incident frequency for which we maintain a sufficiently strong intensity.
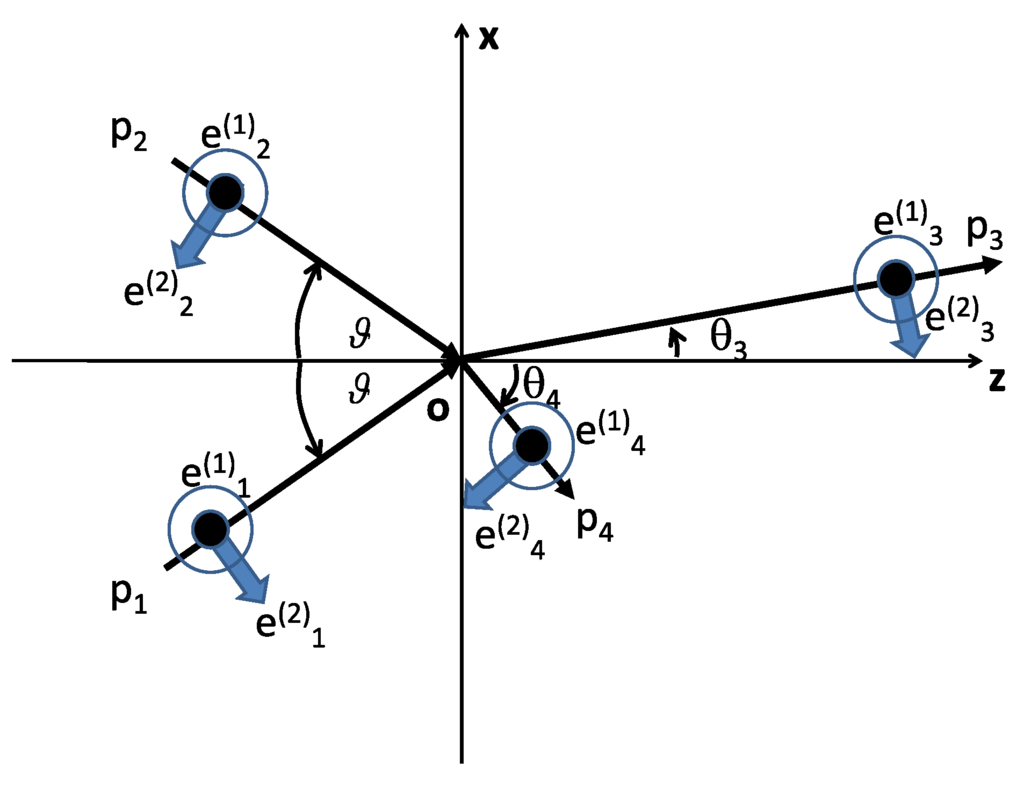
Figure 15.
Definitions of kinematical variables, taken from Figure 1 of [18], in the Quasi-Parallel-Frame.
We also introduced the imaginary part a given by
We notice that the peak-value of is independent of the strength of the coupling, hence giving , which might be interpreted as a consequence of an enhancement from the cross section expected naively to be , where comes from (105), while eV in the numerator corresponds to the typical energy scale of the experiment, as we noted. On the other hand, however, the width squared a is too narrow to be measured in practice. We should be satisfied with an average taken over the range with ;
Probably fortunately, we are still left with even after averaging. Before discussing further enhancement factors, we look at a practical experimental setup. With our current experiments, we discuss a bit of experimental details.
With a nearly fixed value of the frequency , the incident angle distributes within the range less than , where d and f are for the lens radius and the focal length, respectively. The angle
is the resonance angle, as defined by (107). For this reason the cross section is sizable only within a very small range of the angles around . Now the averaged squared amplitude in (109) is re-expressed by
where .
In computing the final cross sections, we find factors arising from the phase-space volume and the normalized initial photon state, but two of them are going to be consumed for other purposes, leaving a margin of . More effective, however, will be the intensities of the laser beams themselves. According to the quantum coherent states discussed by Glauber [52], one of the incident photons annihilates not into the vacuum at the first vertex in the s-channel diagram of Figure 13, but into the sea of incident photons of nearly the same frequency and phase. This contributes a factor multiplied to the strength of the coupling at the vertex, where N is an average number of photons contained in a pulse of the laser beam. This corresponds to the well-known induced process rather than the spontaneous process, derived from the commutation relations of creation and annihilation operators of the photons.
The same analysis applies obviously to another of the incident photons, hence producing multiplied to the amplitude, thus to the whole cross section. We know that the beams are now going to be available reaching , or to be called the kilojoule beam, hence the enhancement of , still short of the deficiency of , as mentioned above.
A still advanced suggestion is made to add another beam supposed to create one of the final photons with a very small frequency from the prepared sea of photons rather than from the vacuum at the second vertex of the same diagram as discussed above, culminating into the enhancement of as a whole. More detailed and careful analyses of the experimental circumstance are under way. We still believe that with our proposed laboratory experiment of fully controlled conditions [53], we can overcome most of the defects that haunted past experiments.
8. Concluding Remarks
We have shown the following:
- The overall Scenario of a decaying cosmological constant is shown to be implemented naturally in E frame in terms of the simplest version of the scalar-tensor theory with the term of added in J frame, a model much simpler than any of those discussed by [54,55], for example. With the help of a rather phenomenological trapping mechanism, we reproduce a mini-inflation, with , undoubtedly a core of the message of the observed accelerating universe, leaving us free from the fine-tuning problem. This E frame is close to the physical conformal frame in which we have a constant unit of length/time provided by microscopic particles, with reference to which an expansion/acceleration of the universe is measured. We must be ready, however, to leave the long-held idea of the Brans–Dicke requirement, replacing it by another model of global scale invariance, thus allowing WEP violation expected to be somewhere below the directly available observational upper bounds.
- It is crucially important to recognize that the invariance just mentioned is broken spontaneously in which the gravitational scalar field plays a role of a dilaton, a pseudo NG boson, allowing us to understand two vastly different scales of size, cosmological and microscopic, in an entirely new perspective. Remarkably enough, this dilaton mediates a WEP violating force, likely with the finite range around the order of 100 m, or so. In order to search for it, we propose two types of the experiment; photon-photon scattering using strong laser beams, and time-dependent variation of the fine-structure constant and the ratio of the masses of electron and proton. As we also point out, the dilaton is responsible for providing us with the Higgs field in the Standard Model. It then follows that all the masses in the world have their common origin ultimately in the scalar field of the scalar-tensor theory, re-formulated to understand the observed accelerating universe.
- In this connection we recall a comic drawn by Sato [56] in 1983, when he symbolized a then new era of Unification inspired particularly by GUT (Grand Unified Theories), as reproduced in Figure 16. Decades later, we still appreciate the same comic, but this time reminding us of how strongly the cosmology is tied with the microscopic physics, specifically in terms of the choice of the physical conformal frame, a unique concept of the scalar-tensor theory, with the role of a dilaton.
- Also noteworthy is the importance of J frame, although it is not a physical frame. Above-mentioned scale-invariance is made visible in J frame, in which the radiation-dominated universe turns out to be static asymptotically. Obviously, J frame is an indispensable ingredient from a theoretical point of view. In this connection we point out that a string-theory model in higher-dimensional spacetime was shown in J frame, with , as indicated in Figure 1.
- We still know little about how various masses and other coupling constants vary with time beyond the lowest-order perturbation estimates. This might be a problem if we look deeper into the early universe. In the more practical side, on the other hand, we already have examples of “composite” units, like the Rydberg constant, the reduced mass multiplied with the electric charge, as pointed out in Subsection 5.1. Even different reduced masses might depend on time differently, if the leptons and quarks yield different variations. The presence by itself of a number of different units in this sense might be an issue from a more general point of view. The exercises attempted in Subsection 5.4 are expected to provide us with a first step toward possible complications. We should be prepared with other types of complications arising both from theoretical and phenomenological aspects.
- One of the aspects we failed to discuss from a truly more significant view is another possible origin of the cosmological constant; the vacuum energy expected from the relativistic quantum field theory, as was emphasized in [57], for example. In view of our success in understanding the scenario of a decaying cosmological constant as a theoretical goal, probably an entirely different approach appears to be called for. See, however, [58], for example.

Figure 16.
Fumitaka Sato’s image of Unification in 1983. His original caption in Japanese goes like “Understanding microscopic world now provides us with a powerful tool to understand the hyper-macroscopic world”. In his own drawing, a guy is looking into a microscope instead of a telescope, yelling “Look, I got the universe!”.
Acknowledgments
I thank Kei-ichi Maeda, Mamoru Doi, Kazuharu Bamba and Kensuke Homma for useful discussions. My gratitude is also due to Fumitaka Sato for his generosity allowing me to use his drawing shown in Figure 16 in the text.
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurement of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the baryon acoustic peak in the large-scale correlation of SDSS luminous red galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Tegmark, M.; Eisenstein, D.; Strauss, M.; Weinberg, D.; Blanton, M.; Frieman, J.; Fukugita, M.; Gunn, J.; Hamilton, A.; Knapp, G.; et al. Cosmological constraints from SDSS Luminous Red Galaxies. Phys. Rev. 2006, D74, 123507. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy—Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Jordan, P. Schwerkraft und Weltall (in German); Friedrich Vieweg und Sohn: Braunschweig, Germany, 1955. [Google Scholar]
- Fujii, Y. Origin of the gravitational constant and particle masses in a scale-invariant scalar-tensor theory. Phys. Rev. 1982, D26, 2580–2588. [Google Scholar] [CrossRef]
- Bertolami, O. Time dependent cosmological term. Nuovo Cim. 1986, B93, 36–42. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Fujii, Y.; Maeda, K. The Scalar-Tensor Theory of Gravitation; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nambu, Y. Axial vector current conservation in weak interactions. Phys. Rev. Lett. 1960, 4, 380–382. [Google Scholar] [CrossRef]
- Goldstone, J. Field theories with superconductor solutions. Nuovo Cim. 1961, 19, 154–164. [Google Scholar] [CrossRef]
- Mack, G. Partially conserved dilatation current. Nucl. Phys. 1968, B5, 499–507. [Google Scholar] [CrossRef]
- Chiu, C.B.; Fujii, Y.; Wada, W.W. Scale invariance, Goldstone boson and f’ trajectory. Lett. Nuovo Cim. 1971, 1, 110–115. [Google Scholar] [CrossRef]
- Fujii, Y. Dilaton and possible non-Newtonian gravity. Nature Phys. Sci. 1971, 234, 5–7. [Google Scholar] [CrossRef]
- Fujii, Y. How successful can the scalar-tensor theory be in understanding the accelerating universe? In Presented at IPMU international conference Dark Energy, Kashiwa, Japan, 22–26 June 2009. arXiv:0908.4324.
- Fujii, Y.; Homma, K. An approach toward the laboratory search for the scalar field as a candidate of drak energy. Prog. Theor. Phys. 2011, 126, 531–553. [Google Scholar] [CrossRef]
- Fujii, Y.; Homma, K. Probing dark energy with high-intensity laser field. In Proceedings of XLI Int. Symp. Multiparticle Dynamics, Miyajima, Japan, 26–30 September 2011. Prog. Theor. Phys. Suppl. 2012, 193, 230–234. [Google Scholar] [CrossRef]
- Dirac, P.A. A new basis for cosmology. Proc. Roy. Soc. 1938, A165, 199–208. [Google Scholar] [CrossRef]
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using a radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Fujii, Y.; Sasaki, M. Gravitational scalar field coupled directly to the Maxwell field and its effect to solar-system experiments. Phys. Rev. 2007, D75, 064028. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equationn of state. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Wang, L.; Caldwell, R.R.; Ostriker, J.P.; Steinhardt, P.J. Cosmic concordnce of quintessence. Astroph. J. 2000, 530, 17–35. [Google Scholar] [CrossRef]
- Fujii, Y. Conformal transformation in the scalar-tensor theory applied to the acceleraing universe. Prog. Theor. Phys. 2007, 118, 983–1018. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Fujii, Y. Choosing a conformal frame in scalar-tensor theories of gravity with a cosmological constant. Prog. Theor. Phys. 1998, 99, 599–621. [Google Scholar] [CrossRef]
- Maeda, K.; Fujii, Y. Attractor universe in the scalar-tensor theory of gravitation. Phys. Rev. 2009, D79, 084026. [Google Scholar]
- Dolgov, D. An attempt to get rid of the cosmological constant. In The Very Early Universe, Proceedings of Nuffield Workshop; Gibbons, G.W., Siklos, S.T., Eds.; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Srednick, M. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Fischbach, E.; Sudarsky, D.; Szafer, A.; Talmadge, C.; Aronson, H. Reanalysis of the Eötvös experiment. Phys. Rev. Lett. 1986, 56, 3–6. [Google Scholar] [CrossRef] [PubMed]
- Fischbach, E.; Talmadge, C. The Search for Non-Newtonian Gravity; AIP Press, Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
- Nishioka, T.; Fujii, Y. Inflation and the decaying cosmolgical constant. Phys. Rev. 1992, D45, 2140–2143. [Google Scholar]
- Fujii, Y.; Omote, M.; Nishioka, T. Time-dependent coupling constant in unfied theories? Prog. Theor. Phys. 1994, 92, 521–534. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. 1999, D59, 123504. [Google Scholar] [CrossRef]
- Fujii, Y.; Nishioka, T. Reconciling a small density parameter to inflation. Phys. Lett. B 1991, 254, 347–354. [Google Scholar] [CrossRef]
- Fujii, Y. How natural is a small but nonzero cosmological constant? Astropart. Phys. 1996, 5, 133–138. [Google Scholar] [CrossRef]
- Fujii, Y. Two-scalar model for a small but nonzero cosmological constant. Phys. Rev. 2000, D62, 064004. [Google Scholar] [CrossRef]
- Barreiro, T.; Copeland, E.J.; Nunes, N.J. Quintessence arising from exponential potentials. Phys. Rev. 2000, D61, 127301. [Google Scholar] [CrossRef]
- Fujii, Y. Revised fits to Δα/α in consistency with the accelerating universe. Phys. Lett. B 2009, 671, 207–210. [Google Scholar] [CrossRef]
- Fujii, Y.; Mizuno, S. Δα/α from QSO absorption lines. Int. J. Mod. Phys. 2005, D14, 677–885. [Google Scholar] [CrossRef]
- Fujii, Y. A possible new interpretation of the result of Δα/α from QSO absorption lines. Phys. Lett. B 2005, 616, 141–144. [Google Scholar] [CrossRef]
- Fujii, Y. Possible time variability of the fine-structure constant expected from the accelerating universe. Phys. Lett. B 2008, 660, 87–92. [Google Scholar] [CrossRef]
- Fujii, Y. Accelerating universe and the time-dependent fine-structure constant. In Proceedings of IAU General Assembly 2009, JD9 conference, Rio de Janeiro, Brazil, 3–14 August 2009; Molaro, P., Vangioni, E., Eds.; arXiv:0910.5090.
- Fujii, Y.; Iwamoto, A.; Fukahori, T.; Ohnuki, T.; Nakagawa, M.; Hidaka, H.; Oura, Y.; Möller, P. The nuclear interaction at Oklo 2 billion years ago. Nucl. Phys. 2000, B573, 377–401. [Google Scholar] [CrossRef]
- Levshakov, S.A.; Molaro, P.; Lopez, P.; D’Odorico, S.; Centurión, M.; Bonifacio, P.; Agafonova, I.I.; Reimers, D. A new measure of Δα/α at redshift z=1.84 from very high resolution spectra of Q1101-264. Astron. Astrophys. 2007, 466, 1077–1082. [Google Scholar]
- Porsev, S.G.; Koshelef, K.V.; Tupisyn, I.I.; Kozlov, M.G.; Reimers, D.; Levshakov, S.A. Transition frequency shifts with fine structure constant variation for Fe II: Breit and core-valence correlation corrections. Phys. Rev. 2007, A76, 052507. [Google Scholar] [CrossRef]
- Fujii, Y. Nonzero ΩΛ and a new type of the dissipative structure. In Proceedings of XXXIIIrd Rencontre de Moriond, Fundamental Parameters in Cosmology, Les Arcs, France, 17–24 January 1998. arXiv:gr-qc/9806089.
- Beloy, K.; Borschevsky, A.; Flambaum, V.V.; Schwerdfeger, P. Effect of α variation on a prospective experiment to detect variation of me/mp in diatomic molecules. Phys. Rev. 2011, A84, 042117. [Google Scholar] [CrossRef]
- Ilyushin, V.V.; Jansen, P.; Mikhail, J.; Kozlov, G.; Levshakov, S.A.; Kleiner, I.; Ubacks, W.; Bethlem, H.L. Sensitivity to a possible variation of the proton-to-electron mass ratio of torsion-wagging-rotation transition in Methylamine (CH3NH2). Phys. Rev. 2011, A84, 032505. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.-Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the equivalence principle using a rotating torsion balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef] [PubMed]
- Glauber, R.J. Coherent and incoherent states of the radiation field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Homma, K. Sensitivity to Dark Energy candidates by searching for four-wave mixing of high-intensity lasers in the vacuum. Prog. Theor. Exp. Phys. 2012. submitted for publication. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D.; Faraoni, V. A bird’s eye view of f(R)-gravity. The open astronomy juournal. arXiv2009. arXiv:0909.0895.
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144, arXiv:1011.0544. [Google Scholar] [CrossRef]
- Sato, F. Observing Universe Through a Microscope (in Japanese); Iwanami: Tokyo, Japan, 1983. [Google Scholar]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Fujii, Y. Mass of the dilaton and the cosmological constant. Prog. Theor. Phys. 2003, 110, 433–439. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).