Abstract
The aim of this paper is to present the use of an innovative approach based on MCDM methods as the main component of a consumer Decision Support System (DSS) by recommending the most suitable products among a given set of alternatives. This system provides a reliable recommendation to the consumer in the form of a compromise ranking constructed from the five MCDM methods: the hybrid approach TOPSIS-COMET, COCOSO, EDAS, MAIRCA, and MABAC. Each of the methods used contributes significantly to the final compromise ranking built with the Copeland strategy. Chosen MCDM methods were combined with the objective CRITIC weighting method, and their performance was presented on the illustrative example of choosing the most suitable mobile phone. A sensitivity analysis involving the and correlation coefficients was performed to determine the match between the compromise ranking of the candidates and the rankings provided by each MCDM method. Sensitivity analysis demonstrated that all investigated compromise candidate rankings show high convergence with the rankings provided by the particular MCDM methods. Thus, the performed study proved that the proposed approach shows high potential to be successfully used as a central component of DSS for recommending the most suitable product. Such DSS could be a universal and future-proof solution for e-commerce sites and websites, providing advanced product comparison capabilities in delivering a recommendation to the user as a final ranking of alternatives.
1. Introduction
At present, customer expectations of manufactured products are constantly growing. High demands of clients often make it difficult for producers to offer a product that would satisfy them completely. As a consequence, it is increasingly difficult to maintain a stable position in the market. In free-market economies, companies are challenged to continuously improve their products and introduce new ones that will meet customer requirements and have a strong position in the market [1]. The need to improve service standards and innovation in order to keep or raise a profit level in an intensely competitive marketplace is particularly relevant to online commerce and service sites. A significant factor in the effective realization of this goal is introducing customer enhancements that will support their decision-making process in choosing the products they purchase. This goal could be achieved by providing consumers with the ability to use the Decision Support System with advanced decision-making tools, including multi-criteria decision-making methods [2]. Trading through e-commerce sites is a standard these days. These websites also provide price and performance comparison services for products available at various stores. These services use heuristics to detect differences between product specifications. Customers confront difficulties when trying to identify the most appropriate product given their preferences and the multiple selection criteria that the specifications represent. Additionally, changes in salesmans’ policies and product offerings available on websites often confuse decision-makers trying to select the most appropriate products. The field of multi-criteria decision-making (MCDM) explores these problems [3].
The increasing sophistication of the parameters of products and devices available on the market causes that a wide extension characterizes the decision problem related to their purchase. It is important to take into account all selection criteria, make compromises, and reconcile conflicting goals. Consumers facing the complexity of decision-making situations need decision support methods and systems. In order to support decision-makers in making informed and satisfactory choices, many tools have been created that are both generally applicable and domain specific [4].
1.1. Nature, Significance, and Commonness of the Mobile Phone Selection Problem
The continuous advancement of technology is causing people to focus their attention increasingly on electronic gadgets. As a result, technologies are being progressed a lot by researchers all over the world. In recent years, electronic devices, such as mobile phones, laptops, and tablets, have become a significant part of everyday life [5]. One of the commonly purchased products today, in which many criteria need to be taken into account in the selection, is the mobile phone. Mobile phones, today named smartphones, are mobile electronic devices with the advantages of mobile phones and personal computers. Mobile phones are used not only for phone calls. With powerful processors embedded and running on multiple open platforms, smartphones play the role of multimedia devices, providing users with many functions, such as email, web browsing, multimedia entertainment, document processing, mobile video communication, global positioning applications, and financial services. It is now used to organize and entertain everyday life, such as sending and receiving text messages, taking pictures, entertainment, browsing the Internet, reading business emails, keeping a calendar, and making appointments [6]. It is precisely because this device is used for different tasks that the decision-making process of selecting is so important and laborious.
In today’s digital world, the smartphone plays a fundamental role in people’s lives because of its mobility, ability and portability [7]. Currently, smartphones are used to organize almost all our issues, both personal and professional [8]. The advancement of mobile phones technology and their simplicity of usage has caused them to become an inseparable component of the consumer’s life. Thus, owning a mobile phone is now among the basic needs and is an integral part of people’s daily lives. There are so many activities for which it can be used. The fact that the smartphone has become one of the global trends is evidenced by people’s intense buying of mobile phones [9].
As a result of decreasing charges of the telecommunications services and increasing competition in the mobile phones market due to the emergence of new manufacturers offering top quality phones with various desirable features at lower prices to attract customers, the number of mobile phone users is steadily increasing. Currently, smartphones are one of the most widely available and cost-effective solutions that practically everyone can afford. Every year new models of these phones, upgraded with additional features, enter the market. Moreover, mobile devices are being equipped with increasingly improved software and hardware to satisfy the expectations and requirements of the market [10]. The described situation in the market causes an increase in the expectations of users.
An important step performed before buying a new mobile phone is to evaluate specifications, such as features, hardware capabilities, and performance, for a particular model. A quick analysis of specifications and prices is often not enough to accurately identify the most suitable model from among the many alternatives [3]. The wide selection of mobile phones available in different price ranges makes it complicated to choose the most beneficial phone. The price of mobile phones, the features and specifications for types of mobile phones are also increasingly varied. Considering only product ratings to select the best smartphone carries the risk of unclear and inconsistent interpretation of these ratings and does not ensure that the best smartphone is selected. The requirements and preferences of mobile phone users differ, so there is no universal and single solution to the mobile phone selection problem.
Choosing the most suitable mobile phone is challenging and requires the consumer to compare different models, often with similar configurations, and consider many different, often opposing principles. Hence, the multi-criteria decision-making strategy looks very useful in mobile phone selection. Priority, mobile phone selection criteria, include elements [7,11,12,13,14], such as quantitative criteria:
- Product price—gross price of the phone.
- Random Access Memory (RAM) size—RAM size is a parameter of mobile phones that determines the capacity to install various applications on them.
- Processor (CPU) type—the processor is a powerful built-in device in smartphones that provides flexible access to applications. Almost all mobile phones have different processors by speed and type. A higher number of cores and higher processor speed are the preferred features.
- Built-in memory size—internal memory is a mobile phone feature that allows storing data on it with a defined capacity.
- The camera quality—the camera in a smartphone is used to take pictures and videos. The camera is responsible for resolution image quality.
- Screen dimension.
- Battery capacity—duration of a rechargeable battery of a product.
- Weight—body’s relative mass.
Qualitative criteria contain:
- Operating System (OS). Provides user interface and interaction functions. Smartphones run on different operating systems: Android (e.g., Huawei P30 Pro 6, Xiaomi Mi 9), Windows Phone, and iOS (all Apple models).
- Chipset. Manages the data flow between the processor, memory, and peripherals.
- Apps. Application services to consumers.
- Durability.
- User-friendliness.
- Brand. A brand is associated with a company’s name and its services that distinguish it from other companies. The market analysis results show that ease of use of the device, access to spare parts and customer support are essential in attracting the customer to the product. High-quality service and the level of customer support can increase a company’s profit exponentially.
- Basic and extended in-built function. Basic built-in features are indispensable in all mobile phones. However, they are specific to particular phone models. For example, it is already a standard that every smartphone is equipped with a camera and a video camcorder. In addition, a smartphone also comes with GPS, a voice recorder, and a media player for video and audio files.
- Prominence, product reputation.
- Quality of the screen. There are smartphones on the market that are almost all screen, such as the Apple iPhone Xs. Super Retina HD OLED screens allow seeing color depth, such as the Apple iPhone Xs. Widespread and trusted by customers are SUPER AMOLED screens (an improved version of OLED screens). They are distinguished by energy efficiency and good contrast. In addition, they are ultra-thin and respond much faster to touch. High-end smartphones are often equipped with a protective layer of glass to protect against mechanical damage.
The rising variety of products available on the market and the associated increasing amount of information can overwhelm consumers and confuse them, resulting in non-optimal decision-making. Given the complexity of the multi-criteria problem of choosing the best mobile phone model, there is a need to provide a decision support system to help minimize customer trouble when selecting a smartphone.
E-commerce websites are increasingly popular and widely used in the minds of customers. They give the possibility to find a product in different stores, compare its price, and do virtual shopping. These sites also often provide customer opinions about products. The constantly growing number of Internet users and the development of the e-commerce market cause these websites to develop very quickly, introducing new solutions and improvements for their users. A system based on MCDM methods offering customers a ranking of products selected by them according to the desired criteria and a recommendation of the best choice for them could be a helpful tool significantly supplementing the functionalities of e-commerce sites. The proposed system is personalized and allows for user interaction in the form of possible pre-selection of alternatives within user-selected value ranges, selection of relevant criteria, and a weighting method that can be subjective or objective, depending on user preferences.
Many studies have been reported in the literature using DSSs based on different MCDM methods applied to decision-making problems for purchasing mobile phones and other devices. However, most of them consider the study of a single method. It is a limitation of the studies because particular MCDM methods have various methodological assumptions, resulting in different solutions for the same problem. Most studies also lack a proposal for a compromise solution that reliably integrates the results provided by the different methods studied. A sensitivity analysis is also needed to determine the reliability of the obtained solutions. In many works on the multi-criteria mobile phones selection problem, the set of alternatives is insufficient because it contains only a few models. Moreover, the number of evaluation criteria considered is also insufficient. The presented shortcomings are limitations of the research. The authors’ goal was to design a DSS in which the research gaps mentioned above are completed. For this purpose, a set of alternatives consisting of 1039 mobile phones models was collected, and 12 evaluation criteria were identified. Furthermore, to obtain a reliable solution, the authors have selected five state-of-the-art MCDM methods based on which a compromise ranking is constructed. Finally, the study is supplemented by a sensitivity analysis confirming the reliability of the solution.
1.2. Aim of the Study
This paper aims to present a universal system based on innovative MCDM methods of recent years that are characterized by high accuracy, efficiency, and delivery of objective results while maintaining ease of application, designed for giving to recommend the most advantageous product. Furthermore, an attempt was made to select methods in which problems, such as the ranking reversal phenomenon and high computational complexity, whose usefulness in selecting the most advantageous alternative, have been confirmed in the literature.
In order to generate more relevant rankings, the authors use as a final ranking the compromise ranking resulting from the evaluation of alternatives by the selected set of MCDM methods. It was assumed that the hybrid approach combining COMET with TOPSIS, COCOSO, EDAS, MAIRCA, and MABAC, because of the advantages presented in the literature review, represent an appropriate set of MCDM methods that will make a significant contribution to the final recommendation for consumer decision support in shopping on e-commerce sites. Furthermore, the system could become an engine for future Internet services providing the possibility of comparing products and services automatically and intuitively and considering many selection criteria. The final result of such a system would be a complete and understandable ranking of products of interest to the customer. MCDM methods are effective tools for solving problems that require consideration of many often conflicting criteria. These types of problems include purchase decisions for electronic devices, such as mobile phones. MCDM methods, due to their different methodological basis, may produce different results for the same real-world problem. Thus, the results provided by different methods should be interpreted carefully. For this reason, this paper proposes a framework integrating five MCDM methods and the Copeland method, providing a reliable compromise ranking based on their results.
To illustrate the application of the proposed system, the authors of this paper performed a descriptive case study of selecting the most advantageous product using mobile phone data collected from various websites. In the following step of this survey, the final rankings of alternatives are compared using two ranking correlation coefficients: symmetrical and asymmetrical . In the next step, to present a reliable solution based on the applied MCDM methods, a compromise ranking was determined using the Copeland ranking strategy. Then, a sensitivity analysis was performed for the compromise rankings candidates constructed after excluding one from each applied MCDM method. Finally, the correlation coefficients of the and rankings were used to measure the match between the compromise rankings candidates and the rankings provided by each MCDM method.
The proposed framework can be used as a basis for a DSS supporting detailed purchasing decisions. The DSS, which is the subject of the study, will enable customers to make more knowledgeable decisions when selecting products, devices and services based on the current market. Furthermore, the suggested system demonstrates its usefulness as a decision support tool for the most suitable mobile phone recommendation.
The rest of the paper is organized as follows. In Section 2, a literature review from which the applicability and usefulness of MCDM methods in decision support systems are confirmed is provided. Section 3 introduces the background and main assumptions of the methods and techniques used in the study. Section 4 illustrates the case study. The outcomes of the performed research are given in Section 5. Discussion of obtained results is included in Section 6. Finally, Section 7 provides conclusions and summary.
2. Literature Review
2.1. Characteristics and Applicability of Decision Support System
The early beginning of Computer Decision Support Systems (DSSs) dates back to the 1970s. Their goal is to improve various fields of people’s lives by supporting decisions with the increasing use of information technology to improve the quality of decisions by recommending solutions [15]. Decision Support Systems (DSS) were defined by Little in 1970 as computer information systems that help people solve different issues in a semi-structured or unstructured way involving data and judgment [9,16]. The modeling strategy is provided by DSS frameworks by integrating knowledge discovery and automated decision-making. In the early 1970s, DSSs were introduced as an innovative kind of tool that combines Data Mining (DM) with artificial decision-making. DSSs are described as an interactive computer-based system or subsystem used to support decision-makers in using communication techniques, data, documents, cognition, and patterns to identify and solve problems, perform decision-making tasks, and make judgments [17].
Decision support is based on the necessary data collected and processed accordingly. Decision support systems can be based on expert knowledge to support decision-making in a given focus area effectively. A characteristic element of decision support systems is the presence of a mechanism that generates recommendations [18]. Recommender systems solve the problem of the large amount of information that e-commerce platforms generate. They provide personalized information to improve user satisfaction. Recommender systems are used in many fields, such as e-commerce, health, industry, and e-learning. Generating personalized recommendations in RS can be done automatically using Machine Learning (ML) models, big data, Artificial Neural Network (ANN) models, Deep Neural Networks (DNN) models, Reinforcement Learning (RL), rules, and multi-criteria decision analysis methods (MCDA), and other methods, such as linear regression, decision trees, and logic rules [19,20,21,22].
More and more advanced algorithms are used to improve the accuracy of RS, such as fuzzy sets and genetic algorithms [23]. Fuzzy set theory is becoming an increasingly popular approach in problems requiring data representation and user interaction, and information extraction from the user. An example is the Operations Research-based Intelligent Decision Support System (OR-IDSS) [24]. Systems based on fuzzy rules are soft computing techniques introduced based on a fuzzy set theory proposed by Zadeh [25]. Fuzzy sets are based on degrees of membership to represent uncertainty. In these techniques, membership functions and fuzzy rules are generated, which build the system’s knowledge base, and, based on it, prediction is possible. The fuzzy rules are discovered from the data provided to the system [26].
RS are important in e-commerce development by implementing personalized and intelligent services. They provide recommendations based on information extracted from data and placed in a model that allows interactions and models user preferences. As a result, RSs minimize customer search costs and suggest products based on explicit and implicit feedback about customer behavior and preferences [27]. Recommendation systems increase turnover by offering customized products and services to the client, suggesting additional products, helping to improve customer loyalty [28]. In e-commerce, recommendation accuracy leads to increased sales and customer loyalty.
Recommender systems depend on consumer feedback and information about their shopping behavior. There are recommender systems that use agents to determine user interests and preferences based on historical transaction data. However, these systems have several problems, such as over-fitting the data of systems based on artificial neural networks and machine learning, and the difficulty of extracting from the available data that would represent human preferences accurately and objectively. Therefore, developing an objective and accurate recommendation system is necessary to provide personalized recommendations in e-commerce [27].
As it can be noticed, there are many DSSs based on different algorithms, but for an accurate representation of human preferences, an approach based on Multi-Criteria Decision-Making seems to be more important. This approach allows the personalization of recommendations in the form of integrating multiple selected criteria and prioritizing them. In order to implement multi-criteria decision support systems (MCDSS), these systems were supplemented with MCDM tools. The decision-making process requiring aggregation of multiple incommensurable and conflicting dimensions is complex and requires commitment. The technology used in the DSS is supposed to simplify the decision-making process for decision-makers by combining their priorities and using data with models to handle multi-criteria decision-making problems [29].
The use of MCDM in DSS increases their efficiency [30]. DSSs consist of three main components: data integration, Data Mining (DM), and MCDM. In the third module, MCDM methods are used to evaluate the currently available alternatives, find the most satisfactory options, and make appropriate reactions in a timely manner [31]. The performance of MCDM-based DSS requires a defined fixed set of criteria that presents the decision-maker with a clear representation of all available alternatives. The task essentially is to calculate the score of each alternative, thereby creating a ranking and selecting the one that maximizes that value [32].
2.2. Overview of Various MCDM Methods Applied to Decision-Making Problems
Multi-criteria decision-making (MCDM) is the process by which the most suitable solution is selected from a set of alternatives considering evaluation criteria [33]. Studies that consider MCDM methods are widely reported in the operations research (OR) literature. MCDM methods are used in solving multi-criteria problems to indicate to decision-makers the best alternative from a set of other options [8]. The use of algorithms in MCDM models is now a standard in modern approaches to understanding some types of human thinking and decision-making process [34]. Alternatives and criteria are the two main parameters considered in any multi-criteria problem. MCDM methods aim to provide a ranking of alternatives taking into account the criteria weights. The TOPSIS technique, which involves ranking the results in terms of similarity to the ideal solution, belongs to the methods of comparing and prioritizing alternatives [35,36].
MCDM methods are being developed all the time to be able to cope with the challenges that are specific to their domain. One such phenomenon is the rank reversal (RR) paradox. It consists of a change in the ranking of alternatives when an alternative is added or removed from their set. It results in a change in the order of priorities of decision-makers regarding two alternatives and is against the principle of independence of irrelevant alternatives. Research directions to develop methods resistant to the RR phenomenon are evident in the development of methods, such as Ranking of Alternatives through Functional mapping of criterion sub-intervals into a Single Interval (RAFSI) [37], Stable Preference Ordering Towards Ideal Solution (SPOTIS) [38], and the Characteristic Objects Method (COMET) [39]. Other advantages of the COMET method worth noting are the high accuracy and the absence of the requirement for arbitrary weights [40]. In literature, there are descriptions of studies in the successful application of this method to choose the most advantageous product, for example, electric scooters [41], electric bikes [42], and electric-powered cars [43,44].
Combined Compromise Solution (COCOSO) is another innovative and relevant MCDM method [34]. Combined compromise solution (COCOSO) was first introduced initially by Yazdani et al. in 2019 [45]. This method is among the most recent techniques of MCDM. In its performance, the comparability sequence is used in three ways. This method is effective in dealing with the ranking or selection of alternatives. Furthermore, they are assessed against specific criteria [46]. It integrates simple additive weighting (SAW), step-wise weight assessment ratio analysis (WASPAS), and Exponentially Weighted Product (EWP) methods. Combining three different aggregation strategies distinguishes COCOSO from other MCDM methods and provides stable and reliable results [47]. The literature reports a successful application of the COCOSO method in the selection of manufacturing technology [48], personnel selection [49], and sustainable supplier selection [50].
Today, MCDM approaches are extensively applied to elucidate the problems, namely the mobile phone selection problem. However, MCDM problems differ according to the solution status and the approaches’ implementation. In recent literature, many research papers are available in which the solution of the multi-criteria problem of selecting the best mobile phone using MCDM based approach is presented. In the study of Aggarwal et al., the MCDM method called EDAS is used to select the most favorable mobile phone model from some previously selected mobile phones available in the Indian market [10]. The result obtained from the averaged solution, which reduces the risk of expert bias against the alternative, is the main advantage that distinguishes EDAS from other MCDM methods. Additionally, the result obtained from the average solution already normalizes the data, significantly reducing the chances of deviation from the best solution. It follows that this method gives more reliable and more precise results for real-world multi-criteria problems, such as choosing the best mobile phone, than other well-known MCDM methods, such as TOPSIS or VIKOR.
Mishra et al., in 2021, applied an innovative procedure employing the multi-attribute boundary approximation area comparison (MABAC) to solve the smartphone selection problem [12]. MABAC has an easy computational process, organized procedure, and an innovative direction that determines the foundation of real-world decision-making problems. Over the past few years, the MABAC approach is used by many scholars in different application areas. Furthermore, the outcomes of the analysis of the results demonstrate that the introduced method is well-ordered and effective with the existing ones. Therefore, MABAC appears to be an attractive explorative way to implement the MABAC in mobile phone selection.
MAIRCA is a technique recently proposed by Pamucar et al. This method is based on the definition of the difference between theoretical and actual results. It means that this method is based on the gap between ideal and empirical priorities [51]. The main advantage of this method is related to the dissimilar linear normalization algorithm used. The described approach to linear normalization allows this method to achieve more efficient results [52]. Stability of the solution, a well-structured analytical framework for ranking alternatives, the number of steps independent of the number of criteria, and suitability for cases with a large number of alternatives and criteria provide an appropriate ranking depending on a predefined dominance threshold [51].
The MAIRCA method performs calculations given their proximity to ideal solutions, so it is the preferred method for evaluating decision alternatives. Furthermore, considering the studies in which this method has been applied, this study is expected to contribute to the literature as it is a novel method, and surveys using the MAIRCA method for evaluating mobile phones have not been evidenced yet. Finally, compared with some other MCDM methods, such as ELECTRE, MAIRCA was chosen due to its relative novelty and ease of use, as well as its requiring less computing time [53].
Rankings provided by MCDM methods that require weights depend significantly on their determined values. Criteria weights have a direct impact on the final results of MCDM methods. The weights can be established by both objective and subjective methods. Weights determined by subjective methods require the active participation of the expert and are assigned by the expert based on knowledge and experience. Examples of subjective weighting methods include BWM (Best-Worst Method) [51], AHP (Analytic Hierarchy Process) [5,54]. Objective methods set weights based on the data structure, taking into account each evaluation criterion’s actual degree of dominance.
The evaluation criteria in this study are quantitative measurement data. In such a case, the CRITIC method gets all the information included in the criteria of assessment. Therefore, CRITIC’s objective weighting methods may demonstrate more realistic results due to varying weights to criteria. This method, similar to Mean Weight (MW), Entropy method, Standard Deviation (SD), and Statistical Variance procedure, belongs to objective methods that calculate weights by solving mathematical equations omitting to take into account the decision-maker preferences [55]. The use of subjective methods to determine weights raises questions about the reliability of the results obtained. Objective weighting techniques are used to overcome this problem. For this purpose, the CRITIC method was proposed by Diakoulaki et al. in 1995 [56]. This method takes into consideration the intensity of the contrast occurring in the structure of the decision problem. Determination of contrasts between criteria is possible after performing fundamental statistical operations, such as correlation analysis [57]. During the weighting process, both the standard deviation of a criterion and its correlation with other criteria are considered [58]. The CRITIC method belongs to the class of correlation techniques. In this method, the intensity of contrast and conflict in the decision problem structure is considered. In addition, the decision matrix is examined to determine the information included in the criteria for assessing the alternatives [59]. In the literature, many examples of the use of the CRITIC method for weights computation in combination with MCDM methods can be found, both known for many years and developed in recent times, employed to obtain the rankings of the assessed alternatives in multi-criteria problems, for example, TOPSIS [58], VIKOR [55,60], MAUT [61], WASPAS [57,62], AHP [63], EDAS [64], COCOSO [65,66], MULTIMOORA [67], and CODAS [60].
In Table 1, the MCDM approaches used in the problem of selecting the most advantageous mobile phone model found in the most recent literature are listed. According to the recent literature, various MCDM strategies have been implemented to identify the most desirable mobile phone. Moreover, hybrid strategies of MCDM methods demonstrate high efficiency in analyzing real-world problems [8]. It can be noticed that, for better results, a combined approach involving more than one method is often used in research. For example, in several publications from recent years, a combined MCDM procedure was adopted to select the best mobile phone model, where the weights are computed applying the Analytic Hierarchy Process (AHP). In the final stage, a set of alternatives was assessed employing the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) MCDM method to give an appropriate reference to the customer [7,8,68]. Therefore, in the research presented in many publications, several MCDM methods are used to analyze in terms of comparison and conformity [11,34,69]. Another approach described includes using AHP adopted to find out the criteria weights. In the next stage, two MCDM methods, named COPRAS and ARAS, are applied to obtain the rankings of the evaluated alternatives [5].

Table 1.
MCDM methods used to evaluate mobile phones in recent literature.
Only one MCDM method, AHP, was used in Reference [70], which is a subjective method. So, there is a lack of comparative analysis with other MCDM methods, which could give a different final ranking. Besides, only four mobile phones were evaluated in this study with five criteria. The situation is similar in Reference [3], which also used only the AHP method to evaluate three criteria for mobile phone models. In Reference [69], only five alternatives of mobile phones were evaluated. Many works dedicated to evaluating mobile phones using MCDM have used only one method [6,10,12,13,71,72]. In Reference [5], 10 alternatives were evaluated with four criteria. Two MCDM approaches, AHP-COPRAS and AHP-ARAS, were used as methods to evaluate the alternatives, resulting in two rankings that were not identical. However, their similarity was not measured using an objective correlation coefficient. In addition, no strategy was proposed to present a consensus solution considering both rankings. Similar approaches considering no more than two MCDM methods for ranking alternatives can be observed in References [11,13,14,69]. In the case of the mobile phones evaluation problem, the small set of evaluated alternatives containing only 3–5 alternatives is a limitation of the study because it insufficiently represents the diversity specific to these devices. The same is true for the criteria, as their small number insufficiently represents consumer preferences. The use of one or two MCDM methods is also a limitation because different MCDM methods may give different solutions to the same problem. Thus, selecting an MCDM method to make a reliable decision is a challenge. In turn, using multiple MCDM methods may result in different rankings. Thus, a framework is needed that integrates the results of different methods and builds a reliable compromise ranking based on them. In Reference [75], a set of six MCDM methods, including TOPSIS, VIKOR, PROMETHEE II, COPRAS, COMET, and SPOTIS, were used to evaluate electric bus alternatives. Based on the rankings obtained using the voting approach, compromise rankings were constructed and then compared with the rankings provided by the six MCDM methods using correlation coefficients. The compromise ranking was also used in the battery electric vehicles (BEVs) evaluation problem [47]. It was generated from the SECA, MARCOS, ARAS, COCOSO, MAIRCA, and COPRAS rankings by applying the Borda technique and Copeland strategy.
The AHP method uses a scale to determine the importance of each criterion and a pairwise comparison matrix to scale the importance of each criterion [54]. The requirement to perform only a pairwise comparison for all alternatives simplifies the decision-making process. Unfortunately, this method is not rank reversal-free [76]. The AHP (Analytic Hierarchy Process) method is from the American school, similar to TOPSIS, VIKOR. Methods from the American school are based on the utility or value function. These methods use two types of relationships between the alternatives being evaluated: indifference and preference. However, they do not consider the incomparability of the options. It results in undesirable substitution effects (linear compensation) that occur even in their fuzzy extensions. The most popular methods from the European School include ELECTRE family and PROMETHEE II. Methods from the European school consider relations, the most common of which is indifference and weak or strong preference. They have a reduced linear compensation effect and are more oriented toward modeling user preferences. Methods from European school utilize outranking relations in the preference aggregation process. The described relationship is not transitive between pairs of evaluated alternatives. Researchers from European school point out that American school methods do not consider variability or uncertainty of expert judgements [77]. The PROMETHEE II method results in numerical values calculated for each evaluated alternative. In contrast, the result of the ELECTRE family of methods is not quantitative, so the application of this method is limited depending on the results expected by the decision-maker, the need to combine different methods, or comparative analysis [78]. The methods mentioned above are not resistant to the rank reversal paradox, evidenced by a change in rankings when some alternatives are added or removed. The problem of the occurrence of rank reversal paradox has been evidenced in studies for TOPSIS [79,80], AHP [76,81], PROMETHEE II [82], and ELECTRE [83]. Rank reversal paradox is a problem in the automation of decision-making processes [76].
The COCOSO method, unlike the approaches mentioned above, considers three different aggregation strategies, Simple Additive Weighting (SAW), step-wise weight assessment ratio analysis (WASPAS), and Exponentially Weighted Product (EWP) methods, to obtain a stable and reliable solution [34]. The main advantage of the ARAS method is that it has a utility function that enables an alternative to be proportioned to the optimal alternative. The COPRAS method helps find the similarity between each alternative and the optimal alternative by using degrees of utility [5,47]. The WASPAS method is a unique combination of the Weighted Sum Model (WSM) and Weighted Product Model (WPM). The main objective of the WASPAS method is to achieve the highest estimation accuracy by using weighted aggregate function optimization [57].
The Characteristic Objects METhod (COMET) is an innovative method based on fuzzy set theory that successfully addresses the limitations in the previously mentioned approaches. The main advantage of this method is its resistance to the rank reversal paradox [84]. This phenomenon consists in changing the ranking order when some alternatives are removed from the set under evaluation [76]. The algorithm of the COMET method is based on a set of characteristic objects, which are reference points in the problem space. The characteristic objects are independent of the evaluated alternatives, so, even if an alternative is removed or added, there will never be a swap of places in the resulting ranking [85]. In contrast to the previously mentioned methods, the algorithm of the COMET method has a complexity independent of the number of alternatives evaluated. This method provides accurate results, and operating on fuzzy numbers reflects adequately realistic problems where uncertainty and fluctuation are common. In this approach, the knowledge-dependent step for the decision-maker is a pairwise comparison of characteristic objects, the number of which depends on the number of criteria considered in the evaluation and their characteristic values. The possibility of creating a hierarchical model with an arbitrary structure in the decomposition process significantly reduces the number of comparisons required [86]. However, the expert pairwise comparison stage is always the most laborious step of this method. In order to eliminate this subjective and time-consuming step, a novel hybrid approach named TOPSIS-COMET, combining another MCDA method, TOPSIS, with the COMET method, is proposed. TOPSIS is used in this case to evaluate a set of characteristic objects instead of a laborious pairwise comparison by an expert to fill in the Matrix Expert Judgement (MEJ). The proposed method is still rank reversal-free, just as in its classical version because TOPSIS, unlike its traditional application, is used here to evaluate characteristic objects instead of alternatives. The described approach was first presented in Reference [87]. The decision to combine TOPSIS with COMET is justified by the fact that the TOPSIS method has many advantages, such as a simple, understandable, and widely used algorithm and returning the result in the form of a vector of numbers [88], which plays the role of the SJ vector created in the classical version of the COMET method based on MEJ. The modular approach of the COMET method allows for further development and modification of the method, which is a significant advantage when considering this method as a DSS engine. Different MCDM methods may generate divergent solutions to the same problem due to their various methodological bases. The differences in results do not mean that the solutions are wrong. There is no complex or single method that is better than its equivalents. Although all MCDM methods are based on sound theoretical foundations, each technique has its advantages and disadvantages. Thus, a model must be proposed to achieve the compromise score and, thus, increase its reliability. In the approach presented in Reference [47], the results from six different MCDM techniques are aggregated using the Borda and Copeland compromise ranking counting method. With this model, a consensus result can be achieved, and the reliability of the results is increased.
Due to the several advantages of the COMET method proved above, the authors of this work propose the TOPSIS-COMET hybrid approach as an engine of novelty DSS, which will be presented on an illustrative example of the problem of selecting the most advantageous mobile phone model. The authors propose an innovative DSS that recommends the compromise ranking that considers rankings from several relevant methods. Therefore, as a set of additional methods complementary for the innovative TOPSIS-COMET approach, the authors of this paper have chosen four MCDA methods: COCOSO, EDAS, MAIRCA, and MABAC. Based on the methods used, the Copeland strategy for constructing compromise ranking was applied, allowing multiple ranking lists to be combined into one. A sensitivity analysis was then performed on the compromise rankings candidates to calculate their match to the rankings provided by the methods used in the study. Correlation coefficients and were chosen as measures of matching.
3. Materials and Methods
This section introduces the MCDM methods selected based on the performed literature review as the main component of a DSS designed to provide customers with recommendations in ranking a selected range of products on e-commerce websites. The fundamentals, main assumptions and stages of TOPSIS-COMET, COCOSO, EDAS, MAIRCA, and MABAC methods are provided here.
3.1. The TOPSIS-COMET Method
COMET (Characteristic Objects METhod) method uses the basics of fuzzy logic and triangular fuzzy sets [89]. The main advantages of the COMET method are its high accuracy, lack of requirement for weights, and its complete resistance to rank reversal paradox [87]. It happens because the alternatives are evaluated in the COMET method using a model identified based on characteristic objects independent of the set of evaluated decision alternatives. Thus, it ensures that there is no comparison of the evaluated decision alternatives among themselves, unlike many other multi-criteria decision analysis methods, and the result of their evaluation is obtained solely based on the identified model. It guarantees that the evaluation values for the alternatives will not change when the same decision model is used, so the paradox never occurs [90].
Step 1. The dimensionality of the problem is defined by the expert by choosing the number r of criteria, . In the next stage, the set of fuzzy numbers for each criterion is chosen, i.e., . Each fuzzy number defines the value of the membership for a particular linguistic concept for particular crisp values [91,92]. Therefore, it is also useful for variables that are not continuous. In this way, the following outcome is achieved (1).
where are numbers of the fuzzy numbers for all criteria.
Step 2. Characteristic objects are named generated objects that define reference points in n-dimensional space. Their role may be played by real or idealized objects, which do not exist [93]. The characteristic objects () are received from the Cartesian product of fuzzy numbers cores for each criteria [43]. As the result, the ordered set of all is obtained (2):
where t means a number of (3):
Step 3. The Matrix of Expert Judgement () is determined by the expert. It is a result of pairwise comparison of the characteristic objects to the knowledge of the expert [94]. The structure is represented by (4):
where is a result of comparing and by the expert. The characteristic object which is more preferred gets one point, and the second object which is less preferred is given zero points. If the preferences are equal, both objects get half point [44]. It depends only on the knowledge of the expert and can be illustrated as (5):
where is an expert mental judgement function. In this study, however, the TOPSIS method was used as an expert function. This approach is presented in Reference [87].
Then, the vertical vector of the Summed Judgements () is received as provided by Equation (6):
The number of query is equal because, for each element , we can observe that .
In the result, the vector P is obtained, where i-th row includes the accurate value of preference for .
In the proposed hybrid TOPSIS-COMET approach, in this step, the characteristic objects are not compared pairwise by the expert, and the MEJ matrix is not constructed. Instead of these procedures, the set of characteristic objects is evaluated by the TOPSIS method, which returns a vertical preference vector as the SJ vector. The following steps are identical to the classic version of the COMET method.
Step 4. Each characteristic object is converted into a fuzzy rule, where the degree of membership of each criterion is the premise for activating the inference in the form . Each characteristic object and preference value is converted into a fuzzy rule in the following detailed form (7). In this way, a complete fuzzy rule base is obtained, which approximates the mental evaluation function of the expert [95].
Step 5. Each one of the alternatives is a set of crisp numbers corresponding to criteria . It can be displayed as follows (8):
3.2. The COCOSO Method
Using many methods to explain multi-criteria problems, the outcome ranking produced by specific methods may change significantly, corresponding to the change of weight distributions of criteria. To improve this limitation, the COCOSO (Combined Compromise Solution) method, a newly proposed algorithm, was introduced by Yazdani et al. The recommended procedure is based on combined, simple additive weighting and exponentially weighted product model [45]. It can represent a summary of compromise solutions [96]. It integrates the SAW [97], WASPAS (Weighted Aggregated Sum Product Assessment) [98], and MEW (Multiplicative Exponential Weighting) methods [99] with aggregation strategies. By this method, decision-makers can get a multi-faceted compromise solution, which is compatible with the solution received by other MCDM methods, such as the VIKOR [100], WASPAS [98], and MOORA (Multi-Objective Optimization on the basis of Ratio Analysis) methods [101]. Moreover, the optimal solution screened by the COCOSO method is not simply influenced by the changes of criteria’s weight distribution or the deletion/addition of alternatives. These imply that the COCOSO method is a robust method, which has advantages in reliability and stability of the decision-making results. In addition, the COCOSO method is easy to understand and has wide applicability and, thus, has been extended to different circumstances to solve decision-making problems in different domain [65,102]. To solve a decision problem with COCOSO, after determining the alternatives and the related criteria, the following steps are validated [45]:
Step 1. Definition of a decision matrix of dimension , where n is the number of alternatives, and m is the number of criteria (9).
Step 2. Normalization the decision matrix, where, for profit criteria, use the Equation (10), and for cost criteria, use the Equation (11). In this study, The Minimum-Maximum normalization method was used.
Step 3. Calculation of the weighted sum of the comparison sequence and the total power weight of the comparison sequences for each alternative. The values of are based on the grey relationship generation method (12), and for the values are achieved according to the multiplicative WASPAS setting (13).
Step 4. Computation of the relative weights of alternatives using aggregation strategies. The formulas determine the strategies (14)–(16), where the first strategy expresses the average of the sums of WSM and WPM scores (14), the second strategy expresses the sum of WSM and WPM scores over the best (15), and the third strategy expresses the compromise strategy of WSM and WPM by using the value (16). In this study, a value of 0.5 was used.
Step 5. Establish the final ranking of alternatives based on values defined using Formula (17). The higher the value, the higher the ranking.
3.3. The EDAS Method
EDAS (Evaluation based on Distance from Average Solution) is a newly proposed method proposed by Ghorabaee et al. in 2015 [103]. Ghorabaee et al. also developed a fuzzy extension of this method [104]. The EDAS method uses two distance measures in the calculation: the positive distance from the mean (PDA) and the other being the negative distance from the mean (NDA). Alternatives are evaluated according to higher PDA values and lower NDA values. The subsequent stages of the EDAS procedure for a decision-making problem with the m criteria and the n alternatives can accurately be shown as follows [33]:
Step 1. Define a decision matrix of dimension , where n is the number of alternatives, and m is the number of criteria (18).
Step 2. Calculate the average solution for each criterion according to Formula (19).
Step 3. Calculating the positive distance from the mean solution and the negative distance from the mean solution for the alternatives. When the criterion is of profit type, the negative distance and the positive distance are calculated using Equations (21) and (20), while, when the criterion is of cost type, the distances are calculated using Formulas (23) and (22).
Step 4. Calculate the weighted sums of PDA and NDA for each decision variant using Equations (24) and (25).
Step 5. Normalize the weighted sums of negative and positive distances using Equations (26) and (27).
Step 6. Calculate the evaluation score () for each alternative using Formula (28). A higher point value determines a higher ranking alternative.
3.4. The MAIRCA Method
The MAIRCA (MultiAttributive Ideal-Real Comparative Analysis) method is a procedure that is easy to use because it maintains a high degree of stability even when the criteria change [105]. The Center for Logistics Research at the University of Defence in Belgrade developed MAIRCA in 2014 [52]. The performance of the MAIRCA method requires the determination of the gap between the ideal and empirical weights. Then, the sum of the gaps for each criterion provides the total gap for each observed alternative. In the final step, a final ranking of alternatives is provided, in which the best-ranked alternative is the one with the smallest value of the total gap. The alternative having the smallest total gap value has values that are closest to the ideal weights according to the largest number of criteria (ideal criteria values). The MAIRCA method is performed in six steps, described as follows [106]:
Step 1. Define a decision matrix of dimension , where n is the number of alternatives, and m is the number of criteria (29).
Step 2. Determine the preference for choosing alternatives using the vector using Formula (30).
If the decision-maker is neutral in choosing an alternative, the vector should have the same values (31).
Step 3. Create a theoretical ranking matrix . The elements of this matrix are the multiplied priorities of alternatives by the criteria weights. The form of this matrix can be represented by Formula (32).
When the preferences determined for the alternatives by the decision-maker are equal, the theoretical ranking matrix is represented by a theoretical ranking vector using Formula (33).
Step 4. Create the real rating matrix, which is shown by Formula (34).
The values of the real rating matrix are determined depending on the criterion of profit type or cost type, sequentially, according to Formulas (35) and (36).
Step 5. Calculate the total gap matrix (G) by taking the difference between the theoretical grade matrix () and the actual grade matrix () using Formula (37).
Step 6. Calculate the final values of the criterion functions () for the alternatives using the sum of the rows of the gap matrix (G) using Formula (38). The alternative with the lowest value of has the highest ranking.
3.5. The MABAC Method
The MABAC (Multi-Attributive Border Approximation Area Comparison) is a new method of multi-criteria decision-making. The MABAC method was worked out just as in MAIRCA by the research center at the University of Defence in Belgrade. Pamučar and Ćirović first implemented this approach in 2015 [12,107]. It determines the distance measures between each possible alternative and the boundary approximation area (BAA) [108]. The fundamental objective of the MABAC method is to determine the distance of the criterion function of each alternative from the approximation region of the boundary. The following section presents the implementation process of the MABAC method, which consists of 6 stages [107]:
Step 1. Define a decision matrix of dimension , where n is the number of alternatives, and m is the number of criteria (39).
Step 2. Normalization of the decision matrix, where, for criteria of type profit, Equation (40) is used, and, for criteria of type cost, Equation (41) is used.
Step 3. Create a weighted matrix based on the values from the normalized matrix according to Formula (42).
Step 4. Boundary approximation area (G) matrix determination. The Boundary Approximation Area () for all criteria can be determined using Formula (43).
Step 5. Distance calculation of alternatives from the boundary approximation area for matrix elements (Q) by Equation (44).
Step 6. Rank the alternatives according to the sum of the distances of the alternatives from the areas of approximation of the borders (46).
3.6. The CRITIC Weighting Method
The CRITIC method (CRiteria Importance Through Intercriteria Correlation) is an objective weighting method introduced by Diakoulaki et al. in 1995 [56]. This method is used to establish the values of the assessment criteria weights. The CRITIC method gains all information included in the evaluation criteria [55]. This method allows the weights to be determined by omitting the preferences of the decision-maker. The weights are calculated in this procedure using mathematical formulas This method appears to be appropriate for determining the criteria weights because it determines them by considering both contrast and conflict intensity in the structure of the decision problem. The described algorithm is founded on an analytical examination of the evaluation matrix aimed at obtaining all the information included in the evaluation criteria. Objective weight values are obtained through the process of quantifying the internal information of each evaluation criterion. In this method, determining criteria weights considers both the standard deviation of a criterion and its correlation among other criteria. An initial decision matrix for the described procedure has the form given by the equation and consists of m alternatives and n criteria, where is the metric of performance of ith alternative with regard to jth criterion. Weights of the jth criterion are obtained with using of the following notations: , means the quantity of information included in jth criterion, means the standard deviation of the jth criterion, and indicates the correlation coefficient among the jth and kth criteria. Based on the assumptions presented above, the calculation stages of the CRITIC method are as follows [109]:
Step 1. Normalization of the initial decision matrix using Equation (47) for benefit criteria:
Step 2. Calculation of the correlation among criteria pairs by using Equation (48):
3.7. Ranking Similarity Coefficients
Employing various MCDM methods to solve the identical decisional problem may give different rankings. For examining their similarity, several correlation measures are used. Two similarity coefficients were applied to compare the outcomes received from the various methods and determine how strong they were consistent. For this purpose, symmetrical weighted Spearman’s rank correlation coefficient and asymmetrical rank similarity coefficient were used.
Weighted Spearman’s Rank Correlation Coefficient
For a samples of size N, the rank values and is defined as (51). In this approach, the positions at the top of both rankings are more significant. The relevance weight is computed for each comparison.
3.8. Rank Similarity Coefficient
For a sample of size N, the rank values and is defined as (52) [110]. It is an asymmetrical measure. The weight of each comparison is determined by the importance of the items in the first ranking. In turn, the first ranking is used as the reference ranking during the calculation [111].
3.9. The Copeland Method
The Copeland method is used to construct a compromise ranking based on the rankings provided by different approaches. It uses the well-known technique of aggregating the rankings of Borda count. The subsequent stages of this strategy are presented in Reference [47].
The stages of the Borda count are as follows:
Step 1. Evaluation of the alternatives. This technique first assigns points to the alternative which is most preferred by the decision-maker and zero points for the least preferred. This stage is performed for each MCDM method.
Step 2. Calculation of the Borda score. The Borda score of each alternative is received by summing up the scores.
Step 3. Rank the options. The best alternative has the highest Borda score.
The steps of the Copeland strategy are as follows:
Step 1. Calculation of the wins score. First of all, the wins score of each alternative is calculated. The win score is calculated as the sum of the ranking order of the alternatives according to different methods.
Step 2. Calculation of the losses score. The wins score of each option are subtracted from the majority wins score. In this way, the losses scores of the options are received.
Step 3. Determination of the final scores and ranking. The difference between the wins score and the losses score provides the final score of each option. Finally, the best option is this one, which has the highest overall score.
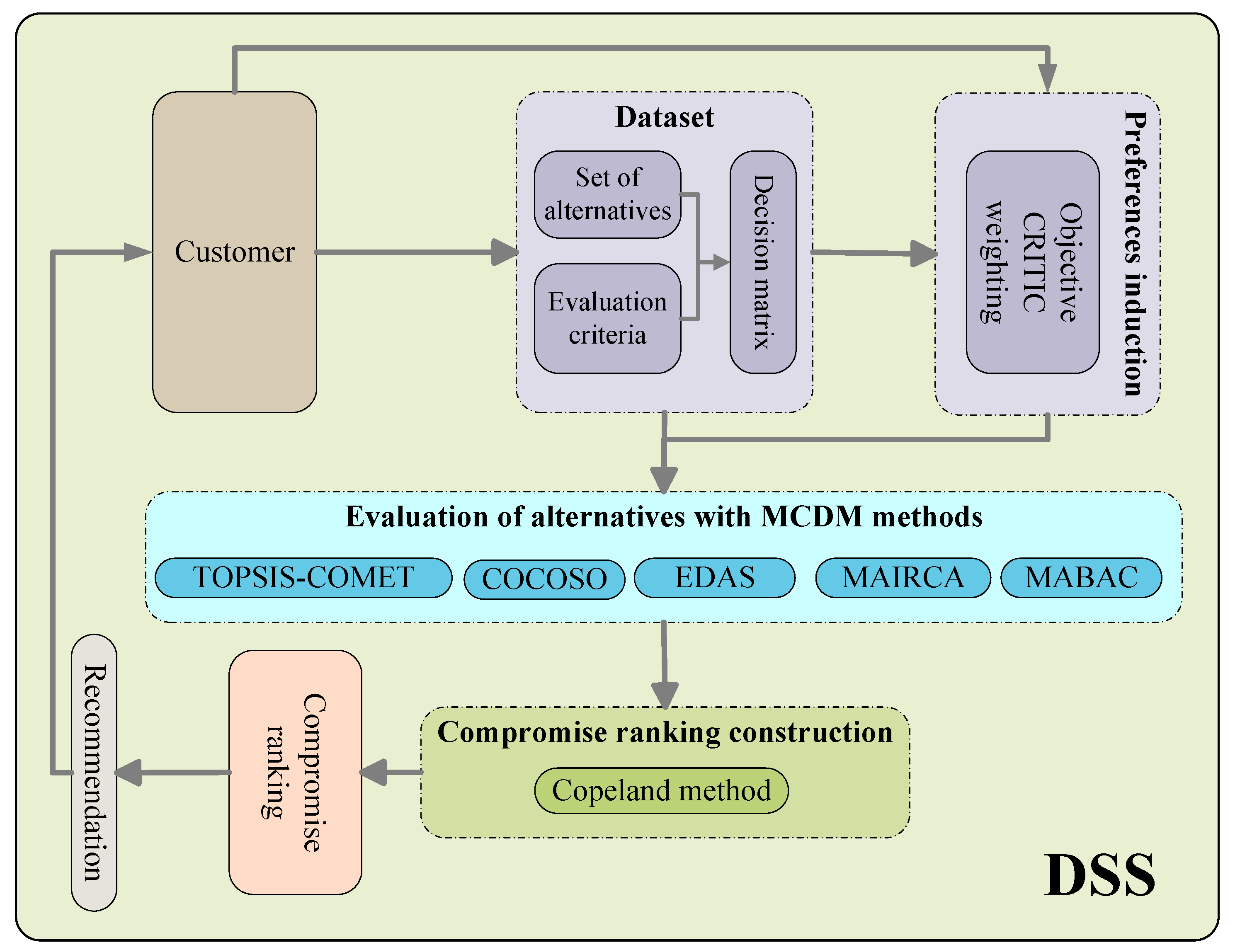
A flow chart visualizing the presented DSS designed on the basis of methods presented in this section is displayed in Figure 1. The user chooses the criteria relevant in selecting the most advantageous alternative from the available dataset. The next step is to determine the importance of the criteria using a user-selected weighting technique, either objective or subjective. In the example presented here, the objective CRITIC weighting technique is used. Then, the decision matrix with alternatives and criteria and the vector of criteria importance are taken by a set of MCDM methods to evaluate the alternatives. Finally, based on the obtained solutions, a compromise ranking is constructed as a recommendation for the user.
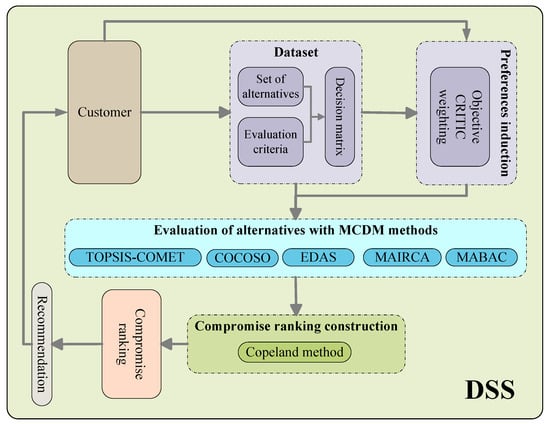
Figure 1.
The flow chart of the DSS with component based on MCDM methods.
4. An Illustrative Case Study of a Multi-Criteria Mobile Phones Selection Problem with Proposed DSS
In this study, a Decision Support System founded on MCDM methods is presented on the evaluation of selected mobile phone models. This DSS could be applied in the Internet services industry, such as e-commerce. The system recommendation is provided as a compromise ranking based on the recommendation of each method used. The compromise ranking is calculated by aggregating the result rankings of all the MCDM methods used according to the Copeland strategy, which involves the Borda method. For the TOPSIS-COMET method, minimum and maximum values were used as characteristic values for each criterion.
The system proposed by the authors of this study includes three main stages, which can be presented as follows:
- In the first step, data from various online platforms are analyzed to recognize a list of relevant criteria used to assess mobile phones.
- The second step includes the calculation of the weights, which represent user preferences. In this illustrative example, the weights are determined using an objective weighting method named CRITIC, introduced in Section 3.6. However, it is also possible to customize to the decision-maker’s preference and use a vector of weights determined independently, or using another method, also subjective, such as AHP.
- Finally, a set of alternatives is evaluated using the MCDM methods, and a recommendation of the most advantageous product in the form of compromise ranking based on the used set of MCDMs is provided to a user.
Additionally, a comparative analysis of the rankings obtained using all MCDM methods considered in this study is presented. It was followed by a sensitivity analysis performed for compromise rankings candidates calculated from all methods used and for the compromise rankings candidates obtained by excluding one each from all MCDM methods used. In other words, the compromise ranking candidate Rank 1 was calculated with all MCDM methods used in this study, while Rank 2 was created without TOPSIS-COMET, Rank 3 without COCOSO, Rank 4 without EDAS, Rank 5 without MAIRCA, and Rank 6 without MABAC. In the lack of having a reference ranking, the goal is to select the reference ranking that shows the most significant similarity to the rankings provided by the MCDM methods included in the study. The next stage of the sensitivity analysis is to calculate the correlation coefficients and between the compromise ranking candidates and the rankings provided by each MCDM method. This step determines the match between the compromise ranking candidates and the rankings from the MCDM methods. The final stage is to compute the and between the compromise ranking candidates.
In this study, 1039 mobile phone models were selected and evaluated using the implemented DSS. Data on selected mobile phones models, including values of selected evaluation criteria, were collected from various websites, i.e., online stores posting sales offers for various phone models, along with parameters of selected evaluation criteria. In Table 2, 12 selected criteria considered in the evaluation of mobile phones, with their names, types of profit or cost and units, are listed. The selected criteria represent sample parameters of mobile phones. However, the system allows selecting any evaluation criteria relevant to the customer, whose values will be expressed in numbers.

Table 2.
Selected criteria –, their name, type, and unit.
In the example simulation presented in this article, criteria weights were established applying the sample objective CRITIC method introduced in Section 3.6. For the TOPSIS-COMET method, each considered criterion’s minimum and maximum values were used as characteristic values.
In the next step, the similarity of the received rankings is investigated. For this purpose, two ranking correlation coefficients are calculated, symmetrical and asymmetrical , for each pair of rankings obtained applying various MCDM methods. The fundamentals of these coefficients are detailed in Section 3.7.
The data for the complete set of alternatives and a set containing 20 models selected randomly from it, their normalized values, the preference values obtained for the MCDM methods used in the study, and the resulting rankings are available at https://github.com/kiziebar/Phones_data (accessed on 15 July 2021).
5. Results
5.1. A Small Set Containing 20 Sample Randomly Selected Alternatives from the Complete Set
The first stage of the study presents the practical implication of applying the proposed DSS using an example of 20 alternatives randomly selected from the whole set. They represent a small set of alternatives. This step aims to simulate a situation in which the user selects from a set of alternatives constrained by factors, such as pre-selection of alternatives within specific ranges of criteria values acceptable to the user or are available at the time. Weights determined with the CRITIC weighting method are included in Table 3.

Table 3.
Criteria weights determined for a small set of alternatives using the CRITIC method.
The decision matrix, including the criteria values for the evaluated randomly selected alternatives, is contained in Table 4. The decision matrix normalized with using the Minimum-Maximum normalization method is contained in Table 5.

Table 4.
Decision matrix for a small set of alternatives.

Table 5.
Normalized decision matrix for a small set of alternatives.
Table 6 provides the final rankings obtained in the evaluation process of 20 randomly selected mobile phones models using five MCDM methods.

Table 6.
Final rankings obtained with MCDM methods for a small set of alternatives.
A comparative analysis of the results obtained demonstrated that the four MCDM methods, including TOPSIS-COMET, EDAS, MAIRCA, and MABAC, identified alternative (Zenfone 3 Deluxe 5.5 ZS550KL) as the rankings leader. This model is characterized by very high, attractive and distinctive values of 7 profit criteria, such as (256 GB of the memory card), (64 GB of internal memory), (4096 MB of RAM), (Resolution of primary camera equal to 16 ), (Resolution of secondary camera equal to 8 ), (Version 4 of Bluetooth), and (Version 2 of USB), among other evaluated alternatives. Very favorable values for most of the relevant evaluation criteria resulted that the large majority of MCDA methods used in this study indicated this mobile phone as the best alternative despite the highest price among all evaluated models. Only in the ranking received by the COCOSO method, the alternative achieved fourth place.
In the ranking provided by the COCOSO method, alternative (Idol 4) was ranked first. This mobile phone has very favorable and high values of 5 profit criteria, such as (256 GB of the memory card), (resolution of primary camera equal to 13 ), (resolution of secondary camera equal to 8 ), (version 4 of Bluetooth), and (version 2 of USB), except that the value of criterion C8 is lower in the case of the model than for , which is the leader of the rankings provided by the other methods used in this study. The Idol 4 () has an advantage over the Zenfone 3 Deluxe 5.5 ZS550KL () on three cost criteria. The first and second are (weight in g) and (weight in ), which is lower for the . The third cost criterion whose value is more attractive for is (price). It is equal to 250 € for , while it is equal to 440 € for . Model ranked second in the rankings obtained with the other MCDM methods applied in this study.
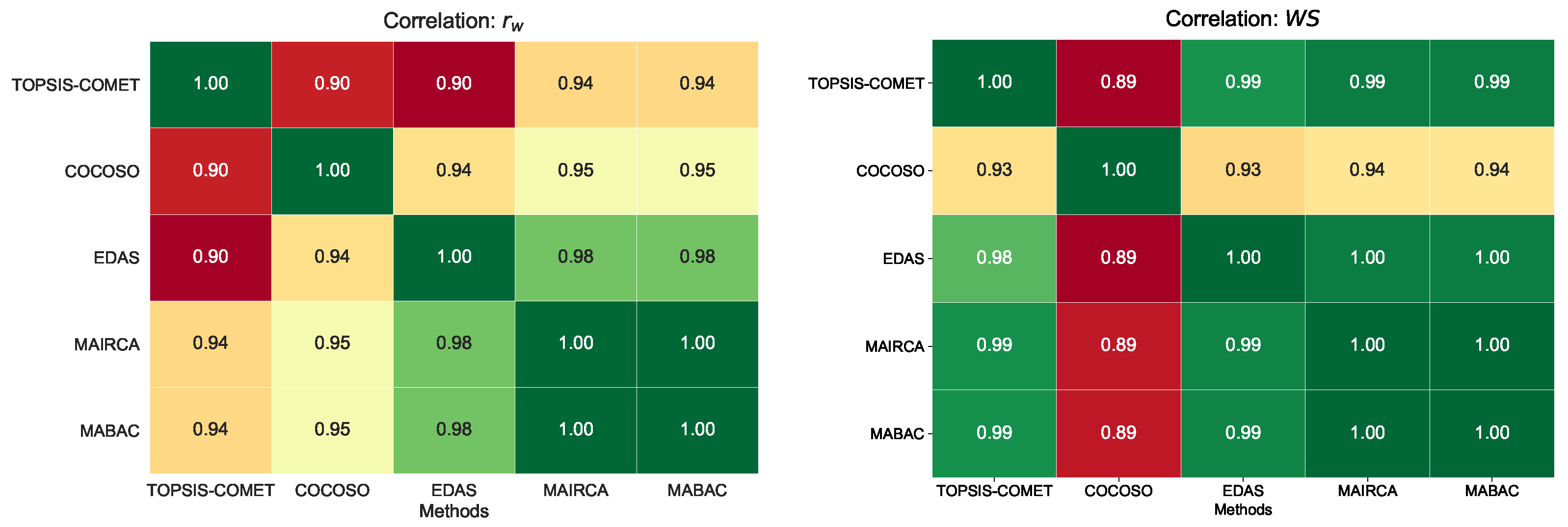
There was a tie in the resulting rankings for alternatives (1110i) and (Honor 6A), which have identical values for all criteria. In the COCOSO rankings, these models came in second, while in the other rankings, they came in third. In Figure 2 are visualized values of the ranking similarity coefficients and used to determine the convergence of the rankings provided by all MCDM methods used in this study.
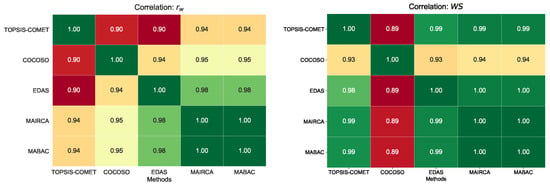
Figure 2.
Visualization of rankings correlation coefficients and for each pair of MCDM method for a small set of alternatives.
For the symmetrical coefficient, the highest correlation values were observed between the rankings provided by MAIRCA and EDAS and MABAC and EDAS (0.98). On the other hand, the lowest correlation values were observed between the COCOSO and TOPSIS-COMET rankings and EDAS and TOPSIS-COMET methods (0.90). The matrix with rank correlation scores measured by is symmetrical because this coefficient gives the same result regardless of the order of the two rankings being compared.
The asymmetric correlation coefficient is different because its value is affected by order of the rankings being compared. The values of the asymmetrical rank similarity coefficient are high for most of the compared rankings. Their values are in the range of 0.98–1.00. The exception is the ranking obtained by the COCOSO method. The calculated values for COCOSO and the other methods are contained in the range of 0.93–0.94. The values of the asymmetrical coefficient calculated for the cases of the other MCDM methods used in this study and COCOSO are even lower, as they are 0.89. In the correlation analysis of the rankings using and shown in Figure 2, symmetry in the results for both coefficients is observed in lower correlation values when comparing the obtained rankings with the ranking provided by the COCOSO method. values are higher than in most cases.
For , the best compromise rankings among the rankings determined by MCDM methods are the rankings obtained by MAIRCA and MABAC methods because they have the highest value of the minimum and average ranking similarity, which are 0.94 and 0.97, respectively. For , the situation is similar. MAIRCA and MABAC rankings have the highest average ranking similarity values of 0.97, accompanied by minimum values of 0.89.
Compromise Rankings Candidates and Their Sensitivity Analysis for the Little Set
The six compromise rankings candidates that were generated based on the proposed approach are displayed in Table 7. The first ranking is a compromise ranking created using the Copeland technique based on the rankings provided by all the MCDM methods used in this study. Subsequent compromise rankings were also created using the Copeland technique but excluding one following MCDM method each. The names of the excluded methods are included in the headings of the following columns of Table 7. It can be observed that, in the compromise ranking constructed from all the MCDM methods used, is the leader. is ranked second, and is ranked third. These alternatives took the same positions in the rankings of four of the five methods used, TOPSIS-COMET, EDAS, MAIRCA, and MABAC.

Table 7.
Rank values for compromise ranking candidates with consideration of the little set.
Table 8 and Table 9 display the values of the correlation coefficients between the candidate compromise rankings and the particular MCDM method rankings. The best match to the rankings expressed by , provided by the methods used in the study, was obtained for Rank 3 after eliminating the COCOSO ranking. Therefore, this candidate’s rounded mean and minimum match values are 0.97 and 0.94, respectively.

Table 8.
Values of similarity coefficient for compromise ranking candidates with consideration of sample smartphones.

Table 9.
Values of similarity coefficient for compromise ranking candidates with consideration of sample smartphones.
For , the best match to all MCDM rankings in the form of the highest average value of this coefficient was observed for the compromise ranking created from all rankings (Rank 1) and the compromise ranking built excluding COCOSO (Rank 3).
Table 10 and Table 11 display the correlation values between all the compromise rankings candidates created. All the calculated correlation values for each ranking combination are high and similar to each other. It proves that the choice of methods to construct the compromise rankings is not a problem in the presented case.

Table 10.
Correlation matrix for values for compromise ranking candidates with consideration of sample smartphones.

Table 11.
Correlation matrix for values for compromise ranking candidates with consideration of sample smartphones.
5.2. A Complete Set of 1039 Mobile Phones
The second stage of the study involved evaluating a complete set of alternatives containing criteria values for 1093 selected mobile phone models. As in stage one, rankings were prepared using the five MCDM methods used in this study. Then, the values of correlation coefficients and were calculated for the received rankings. Comparative similarity analysis of the rankings of the different methods was then undertaken. The next step was to determine candidate compromise rankings and perform sensitivity analysis for them. Criteria weighting values for the complete set of evaluated alternatives determined by the CRITIC method are included in Table 12.

Table 12.
Criteria weights determined for the whole set of alternatives using the CRITIC method.
The decision matrix with the criteria values for each alternative is provided in Table 13. However, due to the large size of the matrix containing 1039 alternatives, only the first 20 records of this matrix are displayed.

Table 13.
Decision matrix for the whole set of alternatives.
The decision matrix was normalized using the Minimum-Maximum normalization technique. For example, Table 14 displays the 20 head records of the normalized decision matrix.

Table 14.
Normalized decision matrix for the whole set of alternatives.
Table 15 contains sample rankings for the complete set of alternatives derived using the five MCDM methods.

Table 15.
Final rankings obtained with MCDM methods for the whole set of alternatives.
In the rankings provided by TOPSIS-COMET, COCOSO, MAIRCA, and MABAC, two alternatives, (Zenfone 3 Deluxe ZS570KL) and (KF510), came as the leaders. Both models have the same values for all criteria considered in the evaluation process. In addition, they have attractive and distinctive values of criteria (256 GB of the memory card), (64 GB of internal memory), (resolution of primary camera equal to 23 ), (version 4 of Bluetooth), and (version 3 of USB), among other alternatives available in the evaluated set.
The EDAS method identified alternatives (Pop C3) and (Phab Plus) as ranking leaders. Both alternatives have favorable low cost criteria values of (weight in g) and (weight in ). Both phones have a desirable, highest value of gain criterion (resolution of secondary camera equal to 4033 ) and a favorable value of (version 4 of Bluetooth) among all evaluated alternatives. In addition, both mobile phones have an extremely low price compared to the other alternatives (80 €). Figure 3 visualizes the values of the rank correlation coefficients for the complete set of mobile phones obtained using the MCDM methods used in the study.
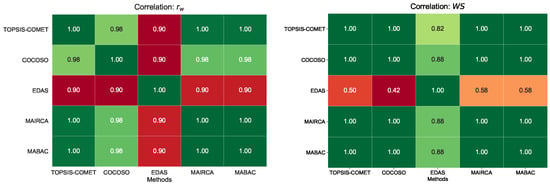
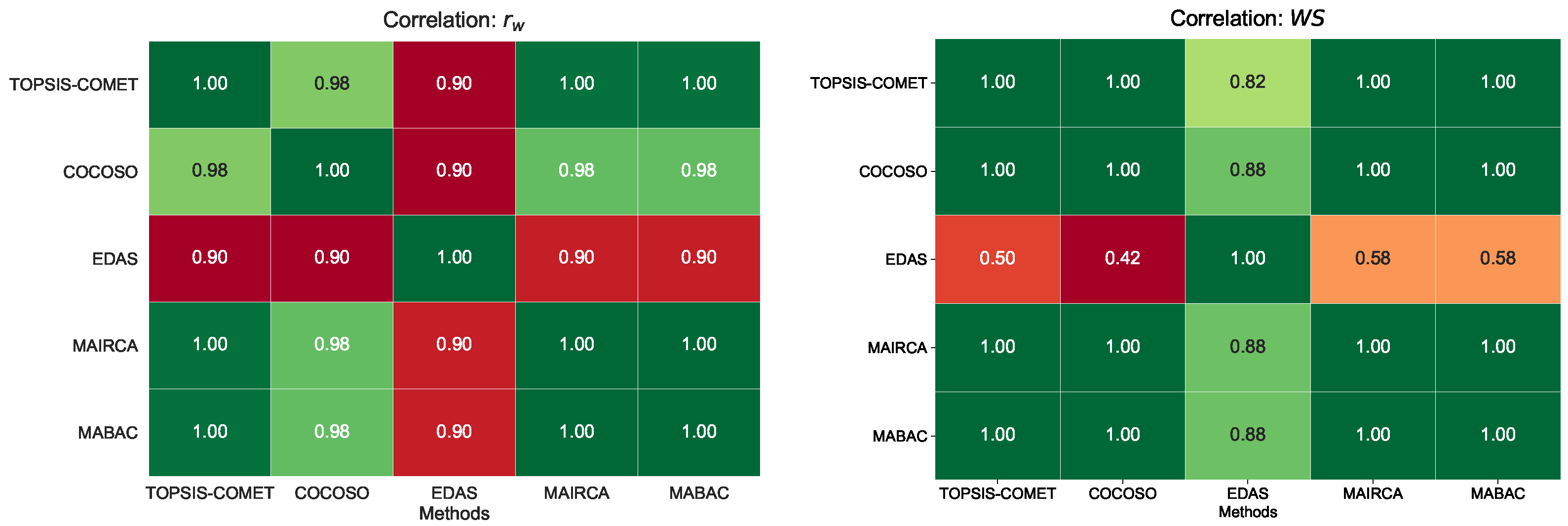
Figure 3.
Visualization of rankings correlation coefficients and for each pair of MCDM method for the whole set of alternatives.
For the symmetrical correlation coefficient , the lowest correlation values were observed for rank comparisons obtained by the EDAS method (0.90). However, the correlation values were much higher for comparisons between the other MCDM methods, between 0.98 and 1.00.
The lowest correlation values (0.42–0.58) noticed in comparisons of the ranking received using the EDAS method with the other rankings were also noted for the asymmetrical Rank Similarity Coefficient . However, for the remaining comparisons between rankings, the value was 1.00, indicating a linear correlation.
In the correlation study of the MCDM rankings considering the complete set of alternatives, it can be clearly observed that, for both and , the lowest similarity values occur for the comparison of EDAS results with other methods.
Compromise Rankings Candidates and Their Sensitivity Analysis for the Whole Set
Table 16 lists the six rankings that are candidates for the compromise ranking created analogously to the small phones dataset. The alternative was indicated as the most advantageous mobile phone model by five compromise ranking candidates. However, it received third place only in the compromise ranking candidate constructed without EDAS.

Table 16.
Rank values for compromise ranking candidates with consideration of the whole dataset.
Table 17 and Table 18 contain the values of the similarity coefficients between compromise ranking candidates and the rankings obtained using the particular MCDM methods.

Table 17.
Values of similarity coefficient for candidate compromise rankings with consideration of the whole dataset.

Table 18.
Values of similarity coefficient for candidate compromise rankings with consideration of the whole dataset.
For the correlation coefficient , the best matches to rankings from particular MCDM methods were recorded for the candidate rankings, excluding the TOPSIS-COMET (Rank 2), MAIRCA (Rank 5), and MABAC (Rank 6) methods. In the mentioned cases, the average and minimum match values for the rankings obtained from each MCDM method were 0.98 and 0.95, respectively. For the similarity coefficient value, the best match to rankings from particular MCDM methods was demonstrated by as many as five rankings: Rank 1, in which a candidate compromise ranking was created considering all the MCDM methods used in the study, Rank 2, Rank 3, Rank 5, and Rank 6. In their case, the average matching value for the rankings from each MCDM method is 0.995, and the minimum is 0.991. On the other hand, the worst matching in terms of lowest average (0.972) and minimum value (0.864) was recorded for Rank 4, in which EDAS was excluded.
Table 19 and Table 20 contain the correlation values between all the candidate compromise rankings constructed. It can be observed that the correlation values between the compromise rankings are high and similar to each other, which means that all the MCDM methods used in this study are suitable for compromise ranking.

Table 19.
Correlation matrix for values for candidate compromise rankings with consideration of the whole dataset.

Table 20.
Correlation matrix for values for candidate compromise rankings with consideration of the whole dataset.
6. Discussion
An essential aspect of this paper was to develop an approach that would provide a ranking recommendation of products with selected criteria in an objective and completely automated way, without involving the decision-maker in the evaluation process. In general, subjective estimates of criteria importance are established following the opinions of decision-makers. The resulting weights are, thus, subjective inputs in analyses such as. There are several methods (e.g., Simple Multi-Attribute Rating Technique (SMART), SIMOS, Revised SIMOS, SWING, Analytic Hierarchy Process (AHP), Best-Worst Method (BWM), Pairwise Comparison Method, and Delphi method) that establish the weights solely following the choices of the decision-makers. When subjective weighting methods determine weights, the results of the analysis or the rankings of the evaluated alternatives are affected by the level of knowledge and experience of the decision-maker in the field because then the weights represent the subjective evaluation of the decision-maker [55]. Weights determined subjectively can lead to concerns about the reliability of the results obtained [58]. The CRITIC method guarantees that the weights of the criteria determined in an entirely objective manner are obtained, eliminating the problem of the subjective viewpoint of the decision-maker. Although the types of criteria are not considered in the CRITIC method, MCDM methods separately consider profit and cost criteria in the problem.
The MCDM methods used in this work are characterized by ease of use, clarity of algorithms, and good adaptation to real-world problems [47]. So, they can be easily applied to many solutions of real choice problems. They are based on a decision matrix that is simple and intuitive to create from most data sets. The number of criteria and alternatives is not limited in any way [57]. Thus, the proposed approach fulfils the requirements of objectivity, automatic performance and simplicity of application that a consumer decision support DSS should characterize. The designed DSS is effective, as proven by its ability to be simple and smoothly applied to both a small (20 alternatives) and many evaluated alternatives, such as 1039.
The rankings obtained using the methods presented in the paper show that, in most cases, the recommendation of a particular mobile phone model is determined by distinctive functionalities and high-level parameters. This observation is consistent with the fact that, today, phones are not only used for calling. Generally, following trends, people will also want to choose the most recent models. Therefore, they can also look for models with parameters similar to flagship models of famous brands, but with a more affordable price [34]. As a result of being equipped with high-resolution cameras, multiple ways of communication, music, games and business applications, mobile phones have become an indispensable part of people’s lives. However, the comfort of their use and functionality depends on the high level of technical parameters [69]. Besides, a mobile phone is bought with a view to its long-term use. Therefore, the amount invested in a better model will profit from its advantages.
Investigating the correlation of rankings for the whole set of alternatives and the 20 alternatives randomly selected from it generated different results. For the complete set, the lowest correlation values were observed for the rank comparisons provided by the EDAS method. These values were lower for the coefficient than . For a small set of random alternatives, the differences in both correlation coefficients values were not as significant. Thus, it can be deduced that the coefficient is characterized by higher volatility concerning the ranking size. This phenomenon can be justified because the highest positions in the rankings are, therefore, more influenced by their similarity than the more distant ones, which is valid in decision problems [44]. Thus, the value of the coefficient is related strictly to the position at which the ranking divergence appeared [110]. This occurrence is reasoned because rankings are established to select the best possible solution, i.e., the one at the top of the ranking [112]. The values decrease in correspondence with a progressive decrease in the quality of the rankings as the best solution moves away from the top of the rankings. This variability for the coefficient is not as significant. It is evidenced by the lower range of changes in its value for the rankings compared in this study. The results derived from the rank correlation study confirm that coefficient is asymmetrical instead of [78].
Even if all MCDM methods have proven robustness and algorithmic efficiency, their application may lead to different solutions to the same problem. For this reason, a framework that integrates the rankings obtained using several MCDM methods into a reliable compromise ranking is recommended. Each of the MCDM methods then contributes significantly to the final compromise ranking. As a result, a DSS recommending a compromise solution helps make more considered decisions than relying on the ranking provided by a single method [47,75].
7. Conclusions and Future Research Directions
This paper aimed to present a developed future-proof MCDM based universal decision support system for the e-commerce sector and product comparison websites to recommend the most advantageous product considering multiple selection criteria. A unique advantage of the designed system is the complete automation of the assessment process, the application of innovative MCDM methods: TOPSIS-COMET, COCOSO, EDAS, MAIRCA, and MABAC, whose effectiveness, literature studies confirm adequacy and usefulness in the product selection problem, the objectivity of the provided results, the possibility of using them to evaluate any products. The rankings provided by the MCDM methods used are then integrated by the Copeland strategy, which results in a reliable compromise ranking created from the MCDM methods applied. By incorporating MCDM methods based on different methodological assumptions into the solution, the proposed DSS recommends a solution that is a real compromise and is compatible with all methods involved in its determination. A sensitivity analysis based on two measures of match compromise rankings candidates, and , confirms the high match of each candidate to the rankings given by each MCDM.
Results are presented first on a sample set of twenty mobile phones randomly selected from a set containing 1039 alternatives and then on the whole set. As a result, for a set of twenty alternatives, as many as four of the five MCDM methods used indicated the best alternative the same mobile phone model, Zenfone 3 Deluxe 5.5 ZS550KL (). One of the methods used, COCOSO, identified another model as the ranking leader. That alternative was the Idol 4 (), which came in second in the rankings of the other four methods. In the compromise ranking created from the results from all the MCDM methods used, is the leader of the ranking, followed by in second place and (Honor 6A) in third place. When evaluating the complete set of alternatives, the leader of the trade-off ranking considering solutions from all MCDM methods is (GM730 Eigen), followed by (Diamond 2 Plus) in second place and (6085) in third place.
The obtained outcomes demonstrate that selecting the most suitable mobile phone is a challenging task. One has to face many alternatives that are characterized by different parameters. Therefore, direct comparisons would take too long and might not be meaningful due to different value scales and parameter units. However, the performed study proved that MCDM methods show potential to be successfully used to solve this problem. With a proper selection of criteria, they can provide a reliable ranking.
For the rankings provided by the methods used in the study, the values of correlation coefficients and are high. However, only for the whole set of evaluated alternatives, the ranking obtained by the EDAS method shows low values of correlation with the other rankings in terms of the value of asymmetrical coefficient. This phenomenon results from the properties of the coefficient, which is featured by a higher variability, depending on the ranking size.
The final recommendation in the form of a compromise ranking created from the solutions of the five MCDM methods solves the problem of inconsistent results caused by the different methodological assumptions of each method. The resulting DSS recommendation helps make more informed purchasing decisions that require consideration of multiple criteria.
The results presented make it easier to choose among the many alternatives available in the market. Furthermore, the MCDM methods, despite the presence of inequalities among the criterion values, finally enabled the generation of a reliable ranking. The obtained outcomes indicate that a consumer decision support system based on MCDM methods could be a valuable and useful option to support online e-commerce and product comparison services. It could also help increase the competitiveness and technological sophistication of the outlets offering them and differentiate themselves in the market. The DSS presented in this paper is a prototype, so the practical benefits for e-commerce sites and customers could be investigated after its implementation by measuring the number of transactions and questionnaires as a measure of customer satisfaction. Directions for further work may include exploring other MCDM methods to select a set of methods that produce the most similar results, especially at the top of the rankings. Other directions for additional research should include exploring other strategies that provide a compromise solution and investigating other methods for selecting the best candidate for the compromise solution.
Author Contributions
Conceptualization, A.B., B.K., A.S., J.W. and W.S.; methodology, A.B., B.K., A.S., J.W. and W.S.; software, A.B., B.K., A.S., J.W. and W.S.; validation, A.B., B.K., A.S., J.W. and W.S.; formal analysis, A.B., B.K., A.S., J.W. and W.S.; investigation, A.B., B.K., A.S., J.W. and W.S.; resources, A.B., B.K., A.S., J.W. and W.S.; data curation, A.B., B.K., A.S., J.W. and W.S.; writing—original draft preparation, A.B., B.K., A.S., J.W. and W.S.; writing—review and editing, A.B., B.K., A.S., J.W. and W.S.; supervision, A.B., B.K., A.S., J.W. and W.S.; project administration, A.B., B.K., A.S., J.W. and W.S.; funding acquisition, A.B., B.K., A.S., J.W. and W.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Science Center, Decision number UMO-2018/29 /B/HS4/02725 (B.K., A.S. and W.S.) and by the project financed within the framework of the program of the Minister of Science and Higher Education under the name “Regional Excellence Initiative” in the years 2019–2022, Project Number 001/RID/2018/19; the amount of financing: PLN 10.684.00000 (A.B. and J.W.).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the editor and the anonymous reviewers, whose insightful comments and constructive suggestions helped us to significantly improve the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AHP | Analytic Hierarchy Process |
| ANN | Artificial Neural Network |
| ARAS | Additive Ratio Assessment |
| BWM | Best-Worst Method |
| COCOSO | COmbined COmpromise SOlution |
| CODAS | COmbinative Distance-based ASsessment |
| COMET | Characteristic Objects METhod |
| CPU | Central Processing Unit |
| CRITIC | Criteria Importance Through Inter-criteria Correlation |
| DNN | Deep Neural Networks |
| DSS | Decision Support Systems |
| EDAS | Evaluation based on Distance from Average Solution |
| ELECTRE | ÉLimination et Choix Traduisant la REalité |
| EWP | Exponentially Weighted Product |
| MABAC | Multiattribute Boundary Approximation Area Comparison |
| MARICA | Multi-Attributive Real- Ideal Comparative Analysis |
| MAUT | MultiAttribute Utility Theory |
| MCDM | Multiple Criteria Decision-Making |
| ML | Machine Learning |
| MULTIMOORA | full Multiplicative form Multiple Objective Optimization |
| on the basis of Ratio Analysis | |
| OR-IDSS | Operations Research-based Intelligent Decision Support System |
| OS | Operating System |
| PROMETHEE | Preference Ranking Organization Method for Enrichment Evaluations |
| RAM | Random Access Memory |
| RS | Recommender Systems |
| SAW | Simple Additive Weighting |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
| VIKOR | Vise Kriterijumska Optimizacija I Kompromisno Resenje |
| WASPAS | step wise Weight assessment ratio analysis |
| WS coefficient | Weighted Similarity coefficient |
References
- Efe, B.; Yerlikaya, M.A.; Efe, Ö.F. Mobile phone selection based on a novel quality function deployment approach. Soft Comput. 2020, 24, 15447–15461. [Google Scholar] [CrossRef]
- Lei, N.; Moon, S.K. A Decision Support System for market-driven product positioning and design. Decis. Support Syst. 2015, 69, 82–91. [Google Scholar] [CrossRef]
- Deb, K.; Chatterjee, R.P.; Banerjee, S.; Bag, R.; Das, A. Mobile Phone Ranking by Analytical Hierarchical Process: A Case Study. Int. J. Inf. Eng. Electron. Bus. 2018, 11, 52. [Google Scholar] [CrossRef]
- Wątróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Zioło, M. Generalised framework for multi-criteria method selection. Omega 2019, 86, 107–124. [Google Scholar] [CrossRef]
- Goswami, S.; Mitra, S. Selecting the best mobile model by applying AHP-COPRAS and AHP-ARAS decision making methodology. Int. J. Data Netw. Sci. 2020, 4, 27–42. [Google Scholar] [CrossRef]
- Chen, I.F.; Tsaur, R.C.; Chen, P.Y. Selection of Best Smartphone using revised ELECTRE-III method. Int. J. Inf. Technol. Decis. Mak. 2018, 17, 1915–1936. [Google Scholar] [CrossRef]
- Singh, R.; Avikal, S.; Rashmi, R.; Ram, M. A Kano model, AHP and TOPSIS based approach for selecting the best mobile phone under a fuzzy environment. Int. J. Qual. Reliab. Manag. 2020, 37, 837–851. [Google Scholar] [CrossRef]
- Kumar, G.; Parimala, N. An integration of sentiment analysis and MCDM approach for smartphone recommendation. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 1037–1063. [Google Scholar] [CrossRef]
- Natasya, W.A.G.; Kusnawi, K. Decision support system design to decide on the latest smartphone using analytical hierarchy process. In Proceedings of the 2017 2nd International conferences on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 1–2 November 2017; pp. 456–461. [Google Scholar]
- Aggarwal, A.; Choudhary, C.; Mehrotra, D. Evaluation of smartphones in Indian market using EDAS. Procedia Comput. Sci. 2018, 132, 236–243. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, T.A.; Agrawal, S.; Singh, S.K. Research Methodology: Prioritization of New Smartphones Using TOPSIS and MOORA. In Proceedings of the International Conference of Advance Research & Innovation (ICARI), Delhi, India, 19 January 2020. [Google Scholar]
- Mishra, A.R.; Garg, A.K.; Purwar, H.; Rana, P.; Liao, H.; Mardani, A. An extended intuitionistic fuzzy multi-attributive border approximation area comparison approach for smartphone selection using discrimination measures. Informatica 2021, 32, 119–143. [Google Scholar] [CrossRef]
- Musrini, M.; Umaroh, S.; Al Arifin, A. Desicion support system using topsis method for smartphone selection. In Proceedings of the 2nd Faculty of Industrial Technology International Congress International Conference (FoITIC 2020), Bandung, Indonesia, 28–30 January 2020; pp. 270–276. [Google Scholar]
- Okfalisa, O.; Rusnedy, H.; Iswavigra, D.U.; Pranggono, B.; Haerani, E.; Saktioto, T. Decision support system for smartphone recommendation: The comparison of fuzzy AHP and fuzzy ANP in multi-attribute decision making. SINERGI 2021, 25, 101–110. [Google Scholar] [CrossRef]
- Sutton, R.T.; Pincock, D.; Baumgart, D.C.; Sadowski, D.C.; Fedorak, R.N.; Kroeker, K.I. An overview of clinical decision support systems: Benefits, risks, and strategies for success. NPJ Digit. Med. 2020, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Acosta, M.; Corral, S. Multicriteria decision analysis and participatory decision support systems in forest management. Forests 2017, 8, 116. [Google Scholar] [CrossRef]
- Alyoubi, B.A. Decision support system and knowledge-based strategic management. Procedia Comput. Sci. 2015, 65, 278–284. [Google Scholar] [CrossRef] [Green Version]
- Vertakova, Y.; Mkrtchyan, V.; Leontyev, E. Information provision of decision support systems in conditions of structural changes and digitalization of the economy. J. Appl. Eng. Sci. 2019, 17, 74–80. [Google Scholar] [CrossRef] [Green Version]
- Cánovas-Segura, B.; Campos, M.; Morales, A.; Juarez, J.M.; Palacios, F. Development of a clinical decision support system for antibiotic management in a hospital environment. Prog. Artif. Intell. 2016, 5, 181–197. [Google Scholar] [CrossRef]
- Lahav, O.; Mastronarde, N.; van der Schaar, M. What is interpretable? using machine learning to design interpretable decision-support systems. arXiv 2018, arXiv:1811.10799. [Google Scholar]
- Shoja, B.M.; Tabrizi, N. Customer reviews analysis with deep neural networks for e-commerce recommender systems. IEEE Access 2019, 7, 119121–119130. [Google Scholar] [CrossRef]
- Baryannis, G.; Dani, S.; Validi, S.; Antoniou, G. Decision support systems and artificial intelligence in supply chain risk management. In Revisiting Supply Chain Risk; Springer: Berlin/Heidelberg, Germany, 2019; pp. 53–71. [Google Scholar]
- Jahani, A.; Feghhi, J.; Makhdoum, M.F.; Omid, M. Optimized forest degradation model (OFDM): An environmental decision support system for environmental impact assessment using an artificial neural network. J. Environ. Plan. Manag. 2016, 59, 222–244. [Google Scholar] [CrossRef]
- Zong, K.; Yuan, Y.; Montenegro-Marin, C.E.; Kadry, S.N. Or-based intelligent decision support system for e-commerce. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 1150–1164. [Google Scholar] [CrossRef]
- Goguen, J. LA Zadeh. Fuzzy sets. Information and control, vol. 8 (1965), pp. 338–353.-LA Zadeh. Similarity relations and fuzzy orderings. Information sciences, vol. 3 (1971), pp. 177–200. J. Symb. Log. 1973, 38, 656–657. [Google Scholar] [CrossRef]
- Yadegaridehkordi, E.; Nilashi, M.; Shuib, L.; Asadi, S.; Ibrahim, O. Development of a SaaS adoption decision-making model using a new hybrid MCDM approach. Int. J. Inf. Technol. Decis. Mak. 2019, 18, 1845–1874. [Google Scholar] [CrossRef]
- Zhang, Y.; Abbas, H.; Sun, Y. Smart e-commerce integration with recommender systems. Electron. Mark. 2019, 29, 219–220. [Google Scholar] [CrossRef] [Green Version]
- Alamdari, P.M.; Navimipour, N.J.; Hosseinzadeh, M.; Safaei, A.A.; Darwesh, A. A systematic study on the recommender systems in the E-commerce. IEEE Access 2020, 8, 115694–115716. [Google Scholar] [CrossRef]
- Razmak, J.; Aouni, B. Decision Support System and Multi-Criteria Decision Aid: A State of the Art and Perspectives. J. Multi-Criteria Decis. Anal. 2015, 22, 101–117. [Google Scholar] [CrossRef]
- Bączkiewicz, A.; Watrobski, J.; Sałabun, W. Towards MCDA Based Decision Support System Addressing Sustainable Assessment. 2021. Available online: https://aisel.aisnet.org/isd2014/proceedings2021/sustainable/6/ (accessed on 1 September 2021).
- Kizielewicz, B.; Więckowski, J.; Shekhovtsov, A.; Wątróbski, J.; Depczyński, R.; Sałabun, W. Study Towards The Time-based Mcda Ranking Analysis—A Supplier Selection Case Study. In Facta Universitatis, Series: Mechanical Engineering; University of Niš: Niš, Serbia, 2021. [Google Scholar]
- Khademolqorani, S.; Hamadani, A.Z. An adjusted decision support system through data mining and multiple criteria decision making. Procedia-Soc. Behav. Sci. 2013, 73, 388–395. [Google Scholar] [CrossRef] [Green Version]
- Stanujkic, D.; Zavadskas, E.K.; Ghorabaee, M.K.; Turskis, Z. An extension of the EDAS method based on the use of interval grey numbers. Stud. Inform. Control 2017, 26, 5–12. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P.; Montero-Simo, M.J.; Araque-Padilla, R.A. An integrated multi-attribute model for evaluation of sustainable mobile phone. Sustainability 2019, 11, 3704. [Google Scholar] [CrossRef] [Green Version]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Kuo, T. A modified TOPSIS with a different ranking index. Eur. J. Oper. Res. 2017, 260, 152–160. [Google Scholar] [CrossRef]
- Žižović, M.; Pamučar, D.; Albijanić, M.; Chatterjee, P.; Pribićević, I. Eliminating rank reversal problem using a new multi-attribute model—The RAFSI method. Mathematics 2020, 8, 1015. [Google Scholar] [CrossRef]
- Dezert, J.; Tchamova, A.; Han, D.; Tacnet, J.M. The SPOTIS rank reversal free method for multi-criteria decision-making support. In Proceedings of the 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020; pp. 1–8. [Google Scholar]
- Sałabun, W. The Characteristic Objects Method: A New Distance-based Approach to Multicriteria Decision-making Problems. J. Multi-Criteria Decis. Anal. 2015, 22, 37–50. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Dobryakova, L. MCDA based approach to sports players’ evaluation under incomplete knowledge. Procedia Comput. Sci. 2020, 176, 3524–3535. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Dobryakova, L. How to choose the optimal single-track vehicle to move in the city? Electric scooters study case. Procedia Comput. Sci. 2020, 176, 2243–2253. [Google Scholar] [CrossRef]
- Sałabun, W.; Palczewski, K.; Wątróbski, J. Multicriteria approach to sustainable transport evaluation under incomplete knowledge: Electric bikes case study. Sustainability 2019, 11, 3314. [Google Scholar] [CrossRef] [Green Version]
- Sałabun, W.; Karczmarczyk, A. Using the comet method in the sustainable city transport problem: An empirical study of the electric powered cars. Procedia Comput. Sci. 2018, 126, 2248–2260. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Kołodziejczyk, J.; Sałabun, W. Fuzzy Model Identification Using Monolithic and Structured Approaches in Decision Problems with Partially Incomplete Data. Symmetry 2020, 12, 1541. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A Combined Compromise Solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Khan, S.; Haleem, A. Investigation of circular economy practices in the context of emerging economies: A CoCoSo approach. Int. J. Sustain. Eng. 2021, 1–11. [Google Scholar] [CrossRef]
- Ecer, F. A consolidated MCDM framework for performance assessment of battery electric vehicles based on ranking strategies. Renew. Sustain. Energy Rev. 2021, 143, 110916. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P. Intelligent decision making tools in manufacturing technology selection. In Futuristic Composites; Springer: Berlin/Heidelberg, Germany, 2018; pp. 113–126. [Google Scholar]
- Wen, Z.; Liao, H.; Mardani, A.; Al-Barakati, A. A hesitant fuzzy linguistic combined compromise solution method for multiple criteria decision making. In Proceedings of the International Conference on Management Science and Engineering Management, Chisinau, Moldova, 30 July–2 August 2020; Springer: Berlin/Heidelberg, Germany, 2019; pp. 813–821. [Google Scholar]
- Zolfani, S.H.; Chatterjee, P.; Yazdani, M. A structured framework for sustainable supplier selection using a combined BWM-CoCoSo model. In Proceedings of the International Scientific Conference in Business, Management and Economics Engineering, Vilnius, Lithuania, 9–10 May 2019; Vilnius Gediminas Technical University: Vilnius, Lithuania, 2019. [Google Scholar] [CrossRef] [Green Version]
- Zolfani, S.H.; Ecer, F.; Pamučar, D.; Raslanas, S. Neighborhood selection for a newcomer via a novel BWM-based revised MAIRCA integrated model: A case from the Coquimbo-La Serena conurbation, Chile. Int. J. Strateg. Prop. Manag. 2020, 24, 102–118. [Google Scholar] [CrossRef]
- Pamučar, D.; Vasin, L.; Lukovac, L. Selection of railway level crossings for investing in security equipment using hybrid DEMATEL-MAIRCA model. In Proceedings of the XVI International Scientific-Expert Conference on Railway, Railcon, Niš, Serbia, 9–10 October 2014; pp. 89–92. [Google Scholar]
- Aksoy, E. An Analysis on Turkey’s Merger and Acquisition Activities: MAIRCA Method. Gümüşhane Üniversitesi Sos. Bilim. Enstitüsü Elektron. Derg. 2021, 12, 1–11. [Google Scholar]
- Sari, F.; Kandemir, İ.; Ceylan, D.A.; Gül, A. Using AHP and PROMETHEE multi-criteria decision making methods to define suitable apiary locations. J. Apic. Res. 2020, 59, 546–557. [Google Scholar] [CrossRef]
- Yalcin, N.; Ünlü, U. A multi-criteria performance analysis of Initial Public Offering (IPO) firms using CRITIC and VIKOR methods. Technol. Econ. Dev. Econ. 2018, 24, 534–560. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The CRITIC method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Tuş, A.; Adalı, E.A. The new combination with CRITIC and WASPAS methods for the time and attendance software selection problem. Opsearch 2019, 56, 528–538. [Google Scholar] [CrossRef]
- Kazan, H.; Ozdemir, O. Financial performance assessment of large scale conglomerates via TOPSIS and CRITIC methods. Int. J. Manag. Sustain. 2014, 3, 203–224. [Google Scholar]
- Madic, M.; Radovanović, M. Ranking of some most commonly used nontraditional machining processes using ROV and CRITIC methods. UPB Sci. Bull. Ser. D 2015, 77, 193–204. [Google Scholar]
- Zandi, I.; Pahlavani, P.; Bigdeli, B. Combining CRITIC Objective Weighting Method with CODAS and VIKOR Methods for Selecting Prospect Hospital Sites (Case Study: District 5 of Tehran). Geogr. Urban Space Dev. 2021. [Google Scholar] [CrossRef]
- Adalı, E.A.; Işık, A.T. CRITIC and MAUT methods for the contract manufacturer selection problem. Eur. J. Multidiscip. Stud. 2017, 2, 93–101. [Google Scholar] [CrossRef] [Green Version]
- Keshavarz Ghorabaee, M.; Amiri, M.; Kazimieras Zavadskas, E.; Antuchevičienė, J. Assessment of third-party logistics providers using a CRITIC–WASPAS approach with interval type-2 fuzzy sets. Transport 2017, 32, 66–78. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Zhou, X.; Xie, R.F.; GU, J.H.; Gu, X.J. Application of Analytic Hierarchy Process (AHP) Combined with CRITIC to Studying Weighted Coefficient of Multiple Criteria for Optimization of Extraction Technology of Compound Zishenqing Granules. Pharm. Care Res. 2009, 1. Available online: https://en.cnki.com.cn/Article_en/CJFDTotal-YXFY200901012.htm (accessed on 15 July 2021).
- Mishra, A.R.; Rani, P.; Pandey, K. Fermatean fuzzy CRITIC-EDAS approach for the selection of sustainable third-party reverse logistics providers using improved generalized score function. J. Ambient. Intell. Humaniz. Comput. 2021, 1–17. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, X.; Luo, Z. Pythagorean fuzzy MCDM method based on CoCoSo and CRITIC with score function for 5G industry evaluation. Artif. Intell. Rev. 2019, 1–35. [Google Scholar] [CrossRef]
- Peng, X.; Huang, H. Fuzzy decision making method based on CoCoSo with CRITIC for financial risk evaluation. Technol. Econ. Dev. Econ. 2020, 26, 695–724. [Google Scholar] [CrossRef] [Green Version]
- Baidya, J.; Garg, H.; Saha, A.; Mishra, A.R.; Rani, P.; Dutta, D. Selection of third party reverses logistic providers: An approach of BCF-CRITIC-MULTIMOORA using Archimedean power aggregation operators. Complex Intell. Syst. 2021, 1–28. [Google Scholar] [CrossRef]
- Goswami, S.S.; Behera, D.K. An Analysis for Selecting Best Smartphone Model by AHP-TOPSIS Decision-Making Methodology. Int. J. Serv. Sci. Manag. Eng. Technol. (IJSSMET) 2021, 12, 116–137. [Google Scholar]
- Rani, P.; Mishra, A.R.; Ansari, M.D. Analysis of smartphone selection problem under interval-valued intuitionistic fuzzy ARAS and TOPSIS methods. In Proceedings of the 2019 Fifth International Conference on Image Information Processing (ICIIP), Shimla, India, 15–17 November 2019; pp. 509–514. [Google Scholar]
- Ansari, N. Smartphone Selection Using Analytic Hierarchy Process. 2016. Available online: http://dspace.sfit.co.in:8004/jspui/handle/123456789/1449 (accessed on 15 July 2021).
- Goswami, S.S.; Behera, D.K. Evaluation of the best smartphone model in the market by integrating fuzzy-AHP and PROMETHEE decision-making approach. Decision 2021, 48, 71–96. [Google Scholar] [CrossRef]
- Mishra, A.R.; Singh, R.K.; Motwani, D. Intuitionistic fuzzy divergence measure-based ELECTRE method for performance of cellular mobile telephone service providers. Neural Comput. Appl. 2020, 32, 3901–3921. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P. Shapley divergence measures with VIKOR method for multi-attribute decision-making problems. Neural Comput. Appl. 2019, 31, 1299–1316. [Google Scholar] [CrossRef]
- Mishra, A.R.; Singh, R.K.; Motwani, D. Multi-criteria assessment of cellular mobile telephone service providers using intuitionistic fuzzy WASPAS method with similarity measures. Granul. Comput. 2019, 4, 511–529. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Więckowski, J.; Kizielewicz, B.; Sałabun, W. Towards Reliable Decision-Making in the Green Urban Transport Domain; University of Niš: Niš, Serbia, 2020. [Google Scholar] [CrossRef]
- Sałabun, W.; Ziemba, P.; Wątróbski, J. The rank reversals paradox in management decisions: The comparison of the ahp and comet methods. In International Conference on Intelligent Decision Technologies; Springer: Berlin/Heidelberg, Germany, 2016; pp. 181–191. [Google Scholar]
- Faizi, S.; Rashid, T.; Sałabun, W.; Zafar, S.; Wątróbski, J. Decision making with uncertainty using hesitant fuzzy sets. Int. J. Fuzzy Syst. 2018, 20, 93–103. [Google Scholar] [CrossRef] [Green Version]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are MCDA methods benchmarkable? A comparative study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- García-Cascales, M.S.; Lamata, M.T. On rank reversal and TOPSIS method. Math. Comput. Model. 2012, 56, 123–132. [Google Scholar] [CrossRef]
- Yang, W. Ingenious solution for the rank reversal problem of TOPSIS method. Math. Probl. Eng. 2020, 2020, 9676518. [Google Scholar] [CrossRef] [Green Version]
- Barzilai, J.; Golany, B. AHP rank reversal, normalization and aggregation rules. INFOR Inf. Syst. Oper. Res. 1994, 32, 57–64. [Google Scholar] [CrossRef]
- Verly, C.; De Smet, Y. Some results about rank reversal instances in the PROMETHEE methods. Int. J. Multicriteria Decis. Mak. 71 2013, 3, 325–345. [Google Scholar] [CrossRef]
- Liu, X.; Ma, Y. A method to analyze the rank reversal problem in the ELECTRE II method. Omega 2021, 102, 102317. [Google Scholar] [CrossRef]
- Sałabun, W.; Piegat, A.; Wątróbski, J.; Karczmarczyk, A.; Jankowski, J. The COMET Method: The First MCDA Method Completely Resistant to Rank Reversal Paradox; European Working Group “Multiple Criteria Decision Aiding” Printemps 2019, Series 3, No. 39; EWG-MCDA: Cracow, Poland, Spring; 2019; Available online: http://www.cs.put.poznan.pl/ewgmcda/newsletter/Spr19.pdf (accessed on 15 July 2021).
- Piegat, A.; Sałabun, W. Identification of a multicriteria decision-making model using the characteristic objects method. Appl. Comput. Intell. Soft Comput. 2014, 2014, 536492. [Google Scholar] [CrossRef] [Green Version]
- Sałabun, W. Fuzzy Multi-Criteria Decision-Making Method: The Modular Approach in the Characteristic Objects Method. Stud. Proc. Pol. Assoc. Knowl. Manag. 2015, 77, 54–64. [Google Scholar]
- Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. A New Approach to Eliminate Rank Reversal in the MCDA Problems. In Proceedings of the International Conference on Computational Science, Cracow, Poland, 16–18 June 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 338–351. [Google Scholar]
- Jiří, M. The robustness of TOPSIS results using sensitivity analysis based on weight tuning. In World Congress on Medical Physics and Biomedical Engineering 2018; Springer: Singapore, 2019; pp. 83–86. [Google Scholar]
- Shekhovtsov, A.; Kizielewicz, B.; Sałabun, W. New Rank-Reversal Free Approach to Handle Interval Data in MCDA Problems. In Proceedings of the International Conference on Computational Science, Cracow, Poland, 16–18 June 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 458–472. [Google Scholar]
- Sałabun, W.; Karczmarczyk, A.; Wątróbski, J.; Jankowski, J. Handling data uncertainty in decision making with COMET. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1478–1484. [Google Scholar]
- Faizi, S.; Sałabun, W.; Rashid, T.; Wątróbski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Sałabun, W.; Karczmarczyk, A.; Wątróbski, J. Decision-making using the hesitant fuzzy sets COMET method: An empirical study of the electric city buses selection. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1485–1492. [Google Scholar]
- Sałabun, W. Reduction in the number of comparisons required to create matrix of expert judgment in the comet method. Manag. Prod. Eng. Rev. 2014, 5, 62–69. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Kołodziejczyk, J. Effects of the selection of characteristic values on the accuracy of results in the COMET method. Procedia Comput. Sci. 2020, 176, 3581–3590. [Google Scholar] [CrossRef]
- Wątróbski, J.; Sałabun, W.; Karczmarczyk, A.; Wolski, W. Sustainable decision-making using the COMET method: An empirical study of the ammonium nitrate transport management. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, Czech Republic, 3–6 September 2017; pp. 949–958. [Google Scholar]
- Lai, H.; Liao, H.; Wen, Z.; Zavadskas, E.K.; Al-Barakati, A. An Improved CoCoSo Method with a Maximum Variance Optimization Model for Cloud Service Provider Selection. Eng. Econ. 2020, 31, 411–424. [Google Scholar] [CrossRef]
- Afshari, A.; Mojahed, M.; Yusuff, R.M. Simple additive weighting approach to personnel selection problem. Int. J. Innov. Manag. Technol. 2010, 1, 511. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of weighted aggregated sum product assessment. Elektron. Ir Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Zanakis, S.H.; Solomon, A.; Wishart, N.; Dublish, S. Multi-attribute decision making: A simulation comparison of select methods. Eur. J. Oper. Res. 1998, 107, 507–529. [Google Scholar] [CrossRef]
- Wei, J.; Lin, X. The multiple attribute decision-making VIKOR method and its application. In Proceedings of the 2008 4th international conference on wireless communications, networking and mobile computing, Dalian, China, 12–14 October 2008; pp. 1–4. [Google Scholar]
- Brauers, W.K.; Zavadskas, E.K. The MOORA method and its application to privatization in a transition economy. Control Cybern. 2006, 35, 445–469. [Google Scholar]
- Yazdani, M.; Wen, Z.; Liao, H.; Banaitis, A.; Turskis, Z. A grey combined compromise solution (CoCoSo-G) method for supplier selection in construction management. J. Civ. Eng. Manag. 2019, 25, 858–874. [Google Scholar] [CrossRef] [Green Version]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Turskis, Z. Extended EDAS method for fuzzy multi-criteria decision-making: An application to supplier selection. Int. J. Comput. Commun. Control 2016, 11, 358–371. [Google Scholar] [CrossRef] [Green Version]
- Pamučar, D.; Mihajlović, M.; Obradović, R.; Atanasković, P. Novel approach to group multi-criteria decision making based on interval rough numbers: Hybrid DEMATEL-ANP-MAIRCA model. Expert Syst. Appl. 2017, 88, 58–80. [Google Scholar] [CrossRef] [Green Version]
- Gigović, L.; Pamučar, D.; Bajić, Z.; Milićević, M. The combination of expert judgment and GIS-MAIRCA analysis for the selection of sites for ammunition depots. Sustainability 2016, 8, 372. [Google Scholar] [CrossRef] [Green Version]
- Pamučar, D.; Ćirović, G. The selection of transport and handling resources in logistics centers using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
- Wei, G.; Wei, C.; Wu, J.; Wang, H. Supplier selection of medical consumption products with a probabilistic linguistic MABAC method. Int. J. Environ. Res. Public Health 2019, 16, 5082. [Google Scholar] [CrossRef] [Green Version]
- Jahan, A.; Mustapha, F.; Sapuan, S.; Ismail, M.Y.; Bahraminasab, M. A framework for weighting of criteria in ranking stage of material selection process. Int. J. Adv. Manuf. Technol. 2012, 58, 411–420. [Google Scholar] [CrossRef]
- Sałabun, W.; Urbaniak, K. A new coefficient of rankings similarity in decision-making problems. In Proceedings of the International Conference on Computational Science, Amsterdam, The Netherlands, 3–5 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 632–645. [Google Scholar]
- Shekhovtsov, A.; Sałabun, W. A comparative case study of the VIKOR and TOPSIS rankings similarity. Procedia Comput. Sci. 2020, 176, 3730–3740. [Google Scholar] [CrossRef]
- Shekhovtsov, A.; Kozlov, V.; Nosov, V.; Sałabun, W. Efficiency of Methods for Determining the Relevance of Criteria in Sustainable Transport Problems: A Comparative Case Study. Sustainability 2020, 12, 7915. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).