PyMossFit: A Google Colab Option for Mössbauer Spectra Fitting
Abstract
1. Introduction
1.1. Isomer Shift, or
1.2. Quadrupole Splitting, or
1.3. Magnetic Hyperfine Field,
1.4. Statement of Need
2. Mössbauer Spectra and Curve Shapes
Curve Fitting and Least Squares Method
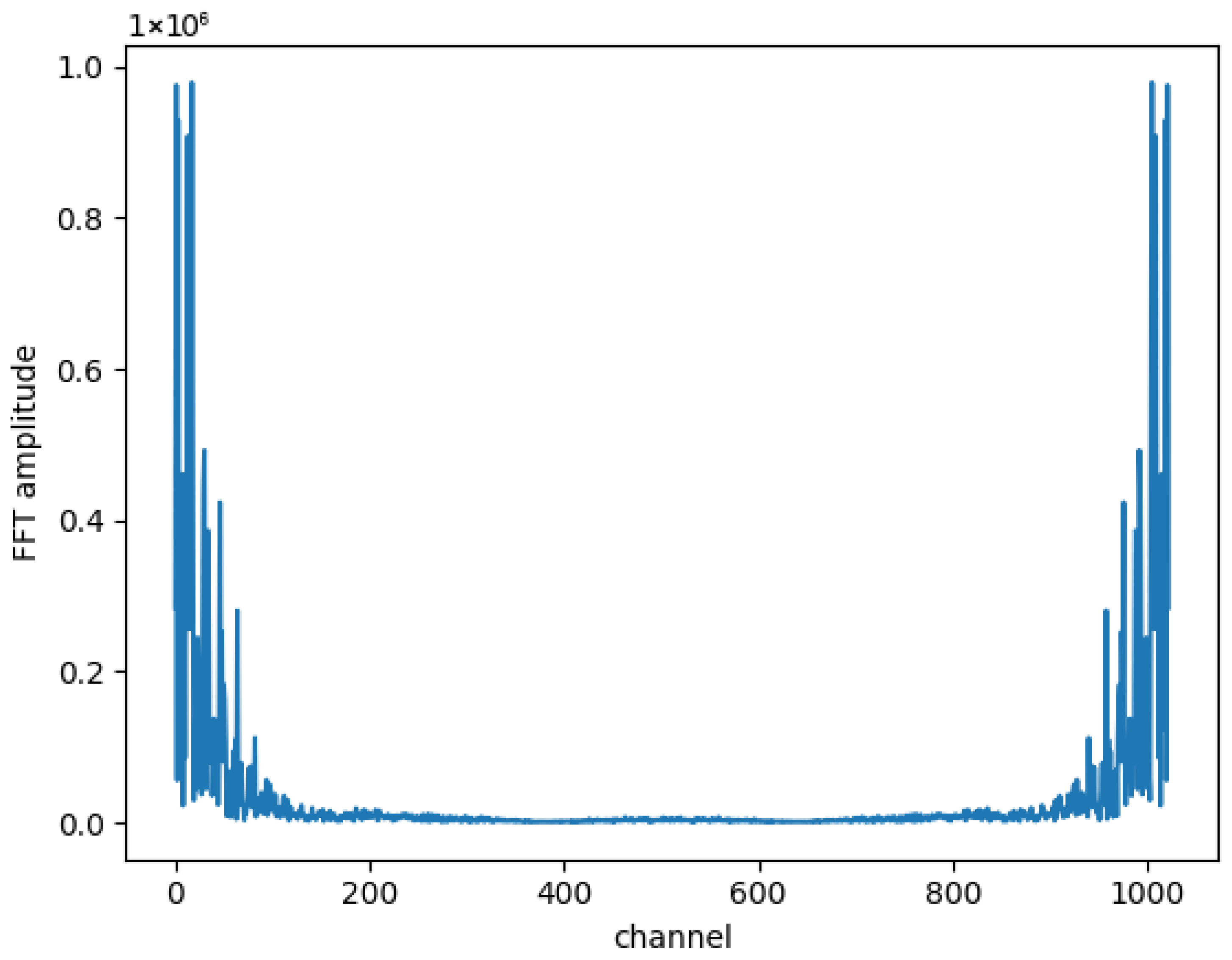
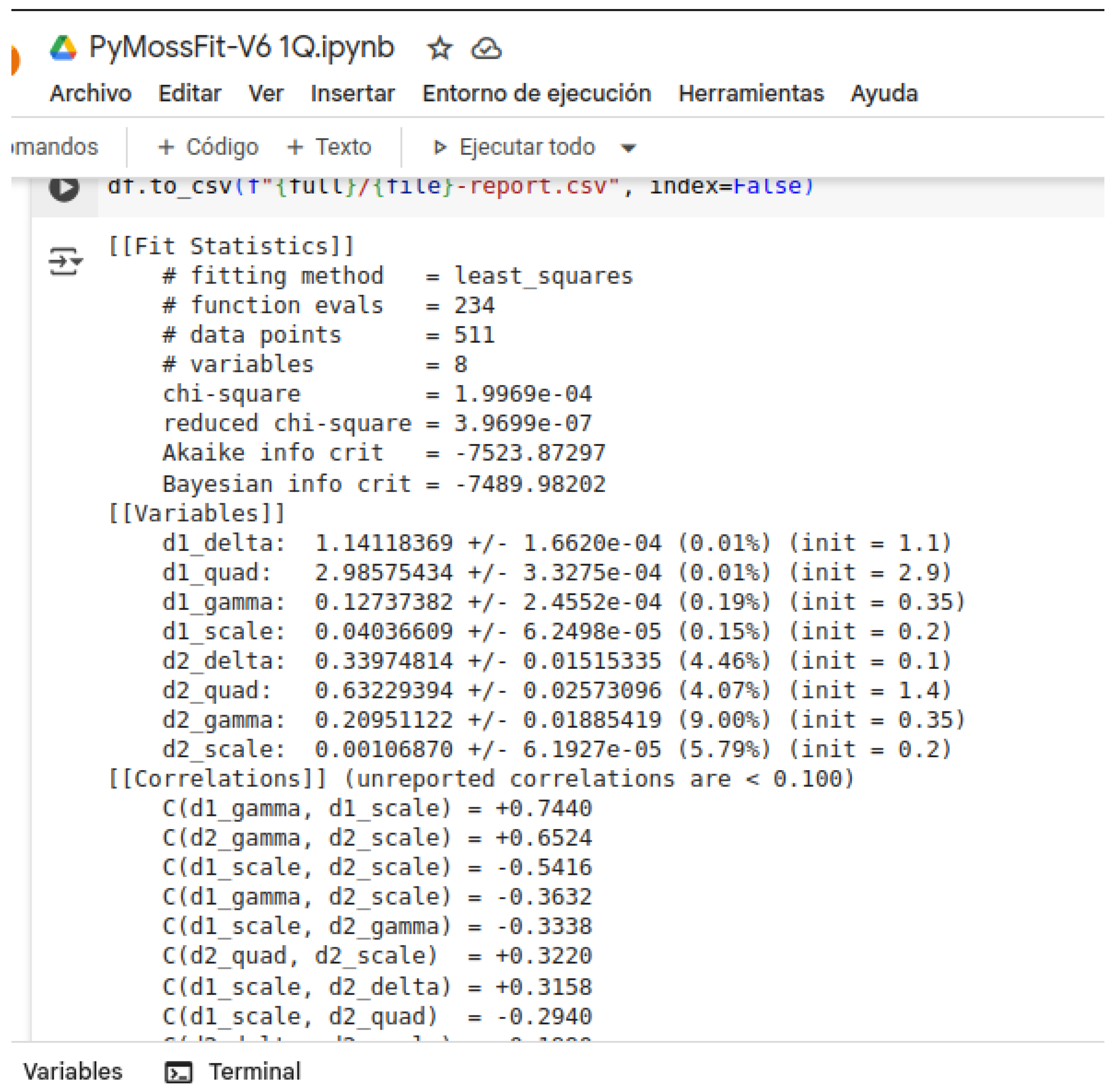
3. Description of the Python Code for Google Colab (PyMossFit)
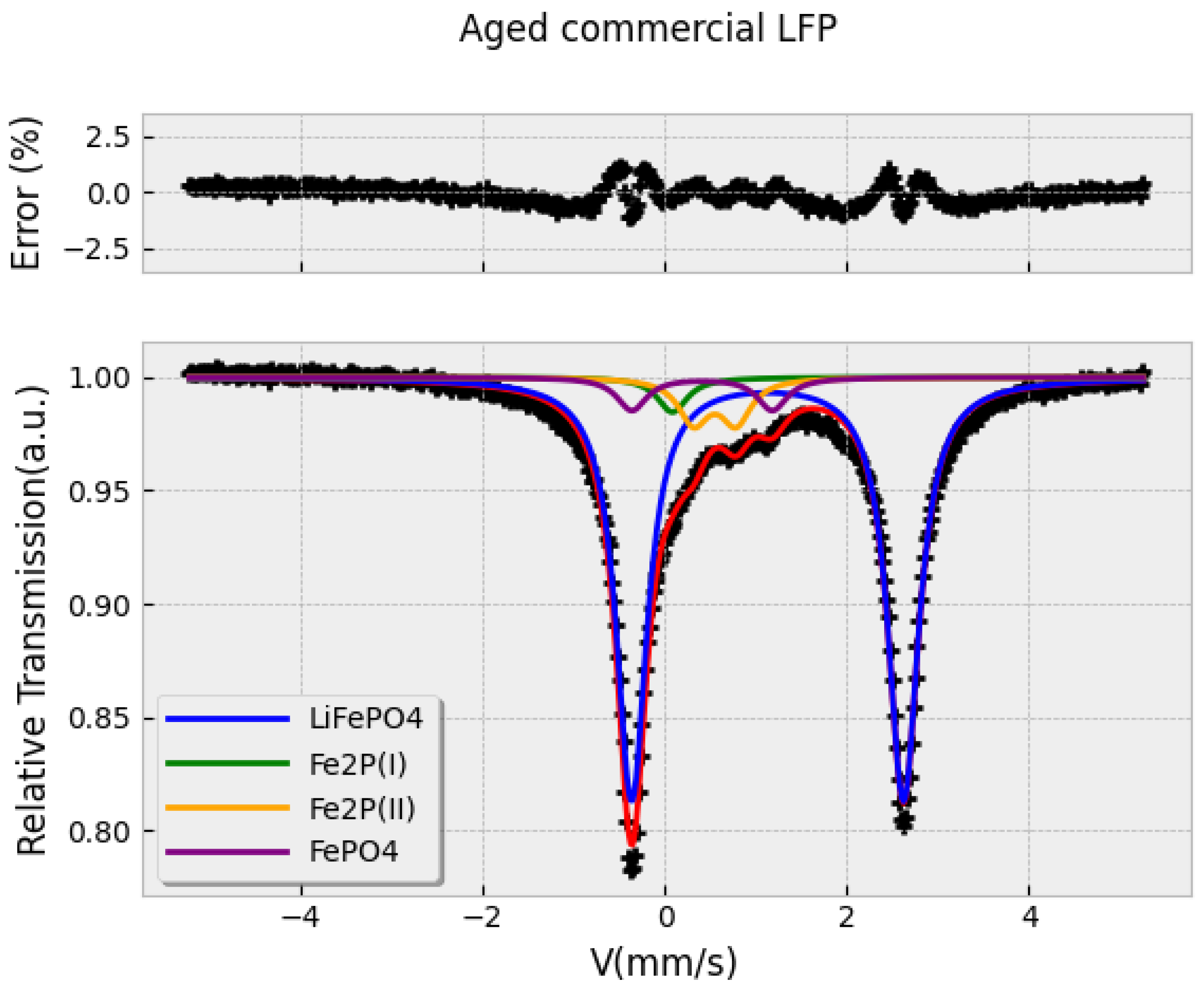
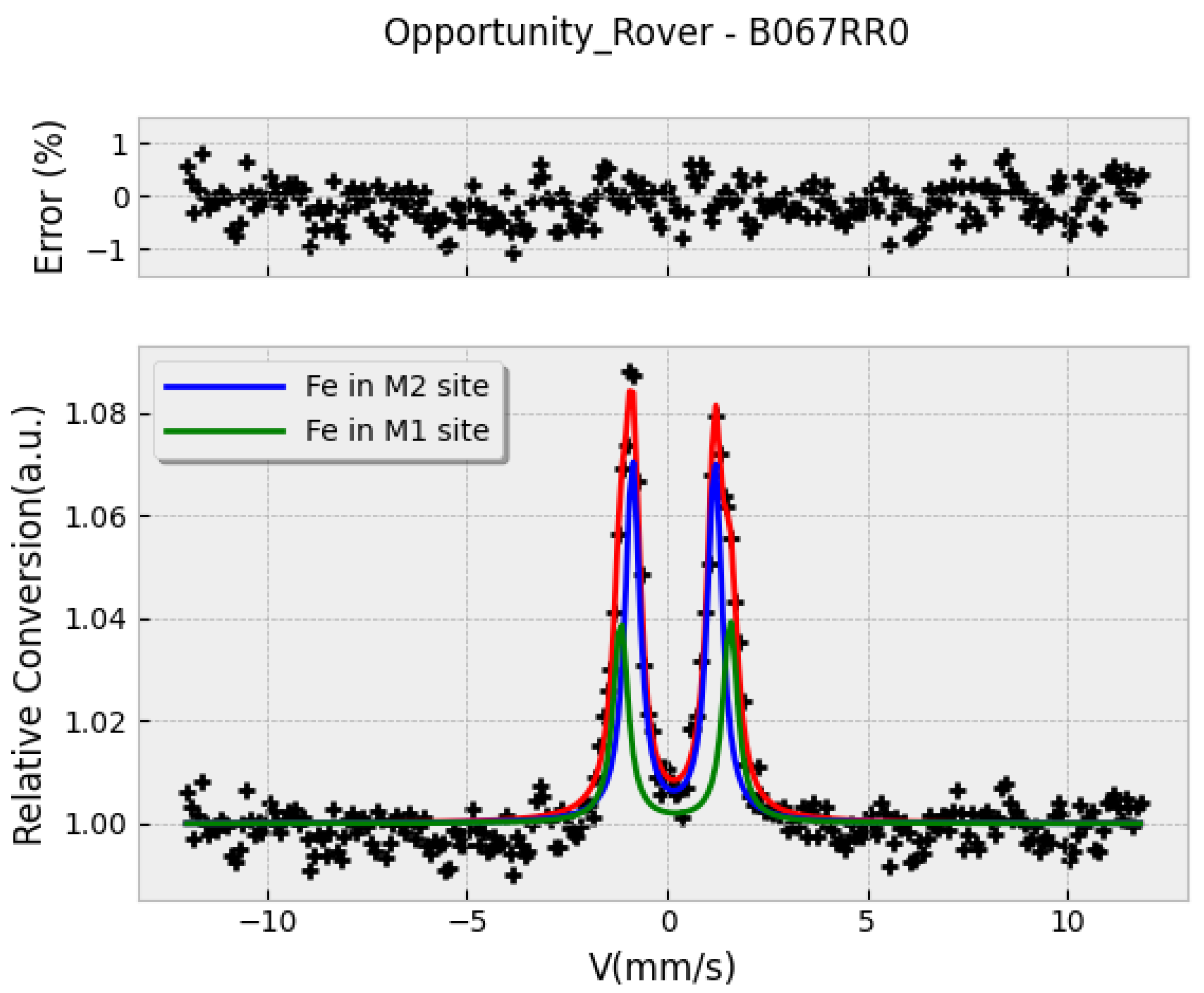
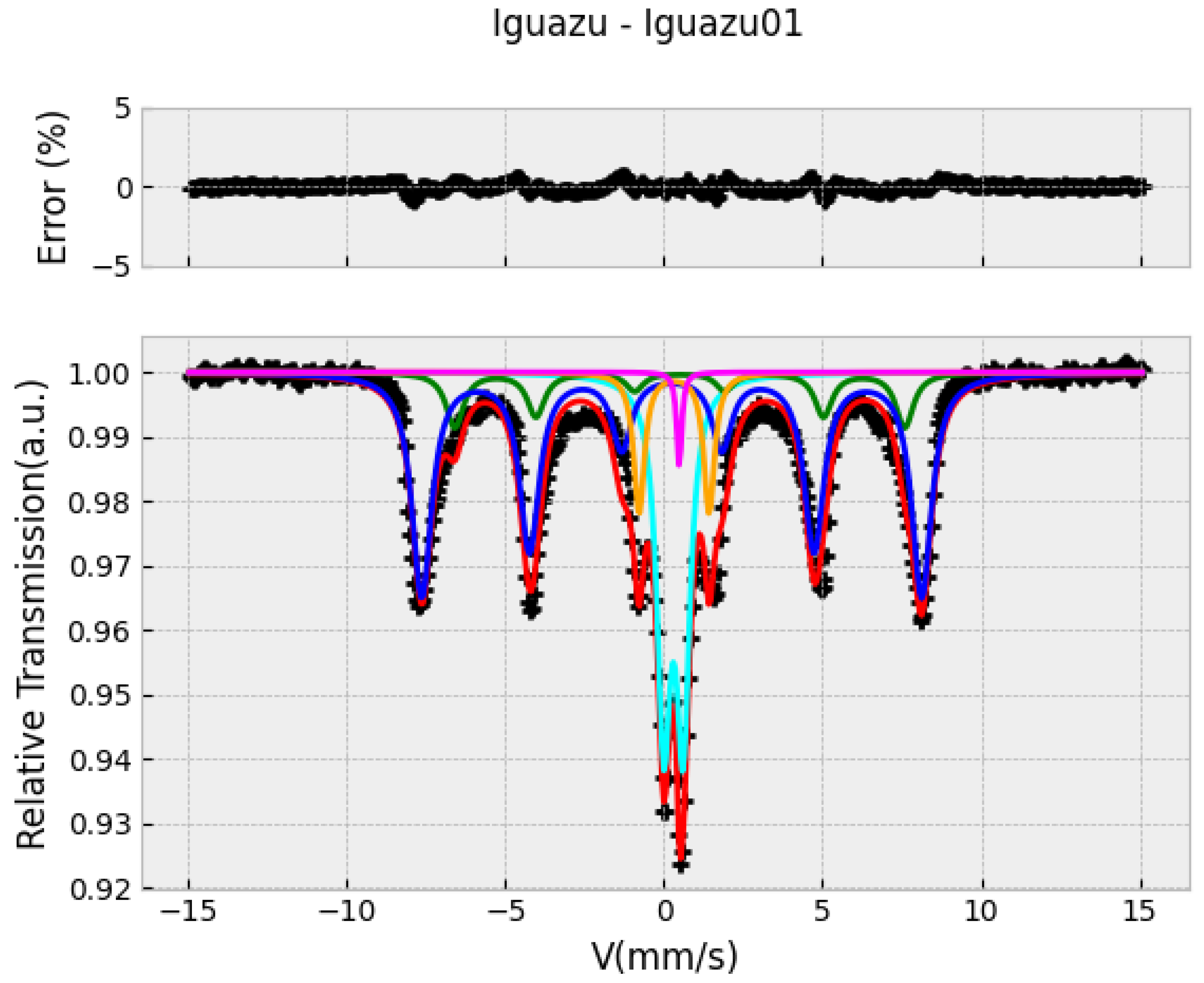
3.1. Some Examples
3.2. Matching of Fitted Parameters with a Local Database
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gütlich, P. Fifty Years of Mössbauer Spectroscopy in Solid State Research—Remarkable Achievements, Future Perspectives. Z. Anorg. Allg. Chem. 2012, 638, 15–43. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, J. The Mössbauer Effect Data Center. Available online: https://medc.dicp.ac.cn/ (accessed on 25 October 2025).
- Martinho, M.; Münck, E. 57Fe Mössbauer Spectroscopy in Chemistry and Biology. In Physical Inorganic Chemistry; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2010; Chapter 2; pp. 39–67. [Google Scholar] [CrossRef]
- Dyar, M.D.; Agresti, D.G.; Schaefer, M.W.; Grant, C.A.; Sklute, E.C. Mössbauer spectroscopy of earth and planetary materials. Annu. Rev. Earth Planet. Sci. 2006, 34, 83–125. [Google Scholar] [CrossRef]
- Gao, Y.; Xu, W.; Zhang, H. A Mössbauer scheme to probe gravitational waves. Sci. Bull. 2024, 69, 2795–2798. [Google Scholar] [CrossRef] [PubMed]
- Walker, L.R.; Wertheim, G.K.; Jaccarino, V. Interpretation of the Fe57 Isomer Shift. Phys. Rev. Lett. 1961, 6, 98–101. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Yang, D.-P. Synchrotron Mössbauer Spectroscopy. In Mössbauer Effect in Lattice Dynamics; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2007; Chapter 7; pp. 253–304. [Google Scholar] [CrossRef]
- Grandjean, F.; Long, G.J. Best Practices and Protocols in Mössbauer Spectroscopy. Chem. Mater. 2021, 33, 3878–3904. [Google Scholar] [CrossRef]
- Lagarec, K.; Rancourt, D.G. RECOIL, Mössbauer Spectral Analysis Software for Windows, Version 1.0; University of Ottawa: Ottawa, ON, Canada, 1998. [Google Scholar]
- Klencsár, Z.; Kuzmann, E.; Vértes, A. User-friendly software for Mössbauer spectrum analysis. J. Radioanal. Nucl. Chem. 1996, 210, 105–118. [Google Scholar] [CrossRef]
- Newville, M.E.A. LMFIT: Non-Linear Least-Squares Minimization and Curve-Fitting for Python, version 1.3.4; Zenodo: Geneva, Switzerland, 2025. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Saccone, F.D. Fitting Code for Mössbauer Spectroscopy Running in Jupyter Colab; Zenodo: Geneva, Switzerland, 2025. [Google Scholar] [CrossRef]
- Kong, Q.; Siauw, T.; Bayen, A. Discrete Fourier Transform (DFT). 2020. Available online: https://pythonnumericalmethods.studentorg.berkeley.edu/notebooks/chapter24.02-Discrete-Fourier-Transform.html (accessed on 25 October 2025).
- Ferrari, S.; Apehesteguy, J.C.; Saccone, F.D. Structural and magnetic properties of Zn doped magnetite nanoparticles obtained by wet chemical method. IEEE Trans. Magn. 2015, 51, 2900206. Available online: https://ieeexplore.ieee.org/document/6975229/ (accessed on 25 October 2025). [CrossRef]
- Opportunity (MERB) Analyst’s Notebook. 2025. Available online: https://an.rsl.wustl.edu/merb/AN/an3.aspx (accessed on 25 October 2025).
- Corke, P.; Haviland, J. Mössbauer mineralogy of rock, soil, and dust at Meridiani Planum, Mars: Opportunity’s journey across sulfate-rich outcrop, basaltic sand and dust, and hematite lag deposits. J. Geophys. Res. Planets 2006, 111. [Google Scholar] [CrossRef]
- Oshtrakh, M.I.; Petrova, E.; Grokhovsky, V. Determination of quadrupole splitting for 57Fe in M1 and M2 sites of both olivine and pyroxene in ordinary chondrites using Mössbauer spectroscopy with high velocity resolution. Hyperfine Interact. 2007, 177, 65–71. [Google Scholar] [CrossRef]
- Tao, W.; Junhu, Z. Mössbauer Effect Data Reference Journal. Available online: https://merdj.dicp.ac.cn/indexen.htm (accessed on 25 October 2025).
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saccone, F.D. PyMossFit: A Google Colab Option for Mössbauer Spectra Fitting. Spectrosc. J. 2025, 3, 29. https://doi.org/10.3390/spectroscj3040029
Saccone FD. PyMossFit: A Google Colab Option for Mössbauer Spectra Fitting. Spectroscopy Journal. 2025; 3(4):29. https://doi.org/10.3390/spectroscj3040029
Chicago/Turabian StyleSaccone, Fabio D. 2025. "PyMossFit: A Google Colab Option for Mössbauer Spectra Fitting" Spectroscopy Journal 3, no. 4: 29. https://doi.org/10.3390/spectroscj3040029
APA StyleSaccone, F. D. (2025). PyMossFit: A Google Colab Option for Mössbauer Spectra Fitting. Spectroscopy Journal, 3(4), 29. https://doi.org/10.3390/spectroscj3040029






