Abstract
The effect of nuclear quadrupole coupling of a single nucleus on the rotational spectra of diatomic molecules is given. By careful selection of examples, procedures are given for the analysis of successively more complicated spectra. The microwave spectra of some alkali halides, interhalogen diatomics, and deuterium halides provide excellent examples for analysis and for student exercises.
1. Introduction
In Part I, the basic theory of microwave spectroscopy for diatomic molecules was given [1]. The photon energies correspond to transitions between states with different angular momenta, and information about the dipole moment and moments of inertia of a gas-phase molecule can be gleaned [2]. By analysis of the microwave spectra of the molecules CO, CsI, CsBr, CsCl, CsF, RbI, RbBr, KI, KCl, and NaCl with a suitable model, once the rotational quantum number J is determined, the rotational constant may be determined. The models expand on the basic formula of Equation (1) (Model 0):
The techniques presented in Part I [1] show us how to analyze multiple isotopologues and account for the effects of centrifugal distortion (De) and vibration–rotation interaction (αe, γe) via Equations (2)–(5) (Models 1–4):
While these models suffice for the molecules listed above, at higher resolution or for other molecules, it will be shown that the effect of nuclear quadrupole coupling (hyperfine splitting) must be taken into account.
2. Materials and Methods
The aim below is to present simpler spectra from the literature and analyze them using the models above, followed by progressively more complicated spectra, in order to introduce concepts and tools on an as-needed basis. Microsoft Excel [3] is used with Solver [4] to analyze the spectrum in each case, with the spreadsheets given as supporting information. In the older literature, often only the frequency and not the intensity is reported, so the simulated spectra are necessarily one-dimensional. Another approach is to use specialized programs to predict and/or fit spectra [5], but these often have a steep learning curve that might deter some students and/or instructors.
3. Results
Sodium Iodide (NaI)
Both sodium and iodine are monoisotopic (Appendix E, Table A1). The predicted value of 2B from the electron diffraction [6] distance is 6200 MHz (see Supplementary Materials, Excel file NaI.xlsx). The spectrum of sodium iodide in the region 20.6–21.2 GHz was measured [7] at 650 °C, and the frequencies observed (error 0.2 MHz) are given in Figure 1. Inspection of the 25 frequencies demonstrates that there appear to be five major groupings of frequencies, as determined by cluster analysis [8]. Cluster analysis is an automated method to assign each datum to a cluster average. If there are N data, then if you pick the number of clusters (or groupings) 1 ≤ k ≤ N, the method assigns each datum to a cluster j = 1, …, k with cluster average xjk. If k = 1, then the cluster average is just the average itself. If k = N, then each datum forms its own cluster and is equal to its cluster average. Typically, the optimal number of clusters corresponds to a break in slope of a plot of the sum of squared errors (difference between each datum and its assigned cluster average) versus the number of clusters.
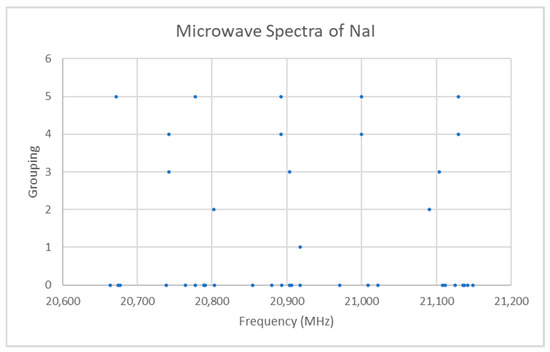
Figure 1.
The spectrum of sodium iodide (Grouping 0), and the cluster averages for k = 1–5.
The range is too narrow to permit more than one possible value of J. The value of J + 1 may be estimated by taking the maximum frequency (or group frequency) and dividing it by the estimated 2B, which gives 3.4. The estimated 2B from electron diffraction measurements is typically too small, giving an estimate for J + 1 that is too large. We can therefore surmise that J = 2, and that each cluster corresponds to a vibrational progression of a single isotopic species. We assign these clusters as v = 0–4 and suppose that there is some additional structure. The residuals of the fits to Models 1 and 2 are shown in Figure 2. It is clear that adding γe only slightly improves the agreement (sum of squared errors (MHz2), SSE decreases by <10%, Table 1), and that most of the splitting from the average is still unaccounted for. The residuals in both models form a series of parabolic curves that seem to be consistently spaced. We must return to the theory to explain this.
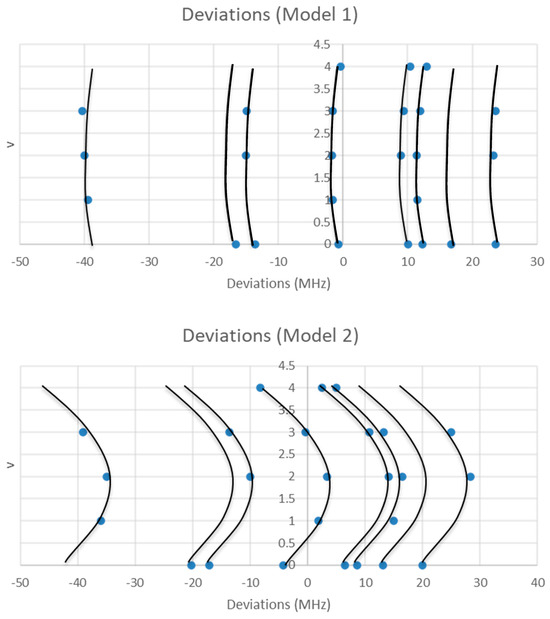
Figure 2.
The residual plots of Models 1 and 2 for the microwave spectrum of sodium iodide.

Table 1.
Model parameters for sodium iodide (MHz) (23Na127I, n = 25). Be is the rotational constant at the equilibrium distance, αe and γe are the first two terms of the rotation-vibration interaction, eQq is the nuclear electric quadrupole moment, and SSE is the sum of squared errors for the model. n/a = not applicable.
4. Basic Theory of Nuclear Quadrupolar Coupling
In much the same way that the electron orbital angular momentum l couples with the electron spin angular momentum s to give the total electron angular momentum j, the rotational angular momentum J may couple with the nuclear spin angular momentum I of a given single nucleus to give a total angular momentum F, which can range from |J − I| to J + I. No effect is observed if I = 0, 0.5. If we let:
then we can define Casimir’s function f [2,9] as:
The energy levels are then split (to first order) by:
where e is the electronic charge, Q is the nuclear quadrupole moment, and q is the average second derivative of the potential energy (the electric field gradient) at the nucleus along the internuclear axis [2,10]. The term eQq is collectively called the nuclear quadrupole coupling constant. The selection rules are ΔJ = ±1; ΔF = 0, ±1.
The nuclear quadrupole interaction is a result of a nonspherical distribution of nuclear charge (i.e., the nucleus cannot be treated as a point charge Ze) combined with a nonspherical distribution of electronic (and other nuclear) charge, giving rise to an electric field gradient at the nucleus [2,11,12]. It can be shown classically that assuming a uniform distribution of nuclear charge in a small spheroid of volume gives an intrinsic nuclear quadrupole moment , and . The intrinsic nuclear quadrupole moment is a measure of the deviation of the nuclear shape from spherical symmetry. If , then the nucleus is elongated along the spin axis z (prolate spheroid), whereas if , then the nucleus is flattened along the spin axis z (oblate spheroid). If , the nucleus is spherical.
The electric field gradient (because it is the second partial derivative of the potential which already has an inverse dependence on the electron-nuclear distance) is proportional to 1/r3 and is therefore a sensitive probe of electron density near a nucleus. For example, it can be used to help predict the solid-state 51V-NMR of vanadate compounds, which possess a very diverse structural chemistry [13].
5. Results
5.1. Sodium Iodide (NaI, Reprise)
For 23Na, I = 1.5, and for 127I, I = 2.5. Both nuclei could potentially couple. The residual pattern suggests that there are at least eight sub-bands of this J = 2 transition. Which nucleus is responsible for the observed quadrupole splitting?
We examine the possible splitting patterns to decide (Figure 3). It is clear that for I = 1.5, there are not enough predicted sub-bands to account for the (at least) eight sub-bands observed. However, for I = 2.5, the eight smallest sub-bands predict the splitting pattern very well. We therefore conclude that the nucleus responsible for the splitting has spin I = 2.5 (i.e., 127I). We can modify Models 1 and 2 by adding the nuclear quadrupole coupling term (Equations (9) and (10), Models 1-1 and 2-1, respectively):
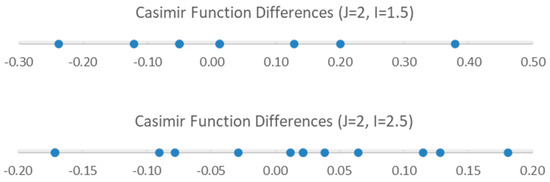
Figure 3.
The Casimir function differences for J = 2 and I = 1.5 and 2.5.
The residuals for models 1-1 and 2-1 are plotted in Figure 4. By including the nuclear quadrupole coupling, the SSE is reduced by three orders of magnitude (Table 1), and the individual residuals are reduced to about 1 MHz. The quadratic pattern in the error is still visible in Model 1-1 but disappears in Model 2-1. However, in both models, the residual range seems to follow an hourglass shape. What this suggests is that q may be a function of vibrational quantum number v, which is reasonable due to anharmonicity giving slightly larger bond lengths for larger v. This would slightly affect the average electric field gradient at the iodine nucleus. Further improvement to the models can be realized by incorporating this dependence (Equations (11) and (12); Models 1-2 and 2-2, respectively).
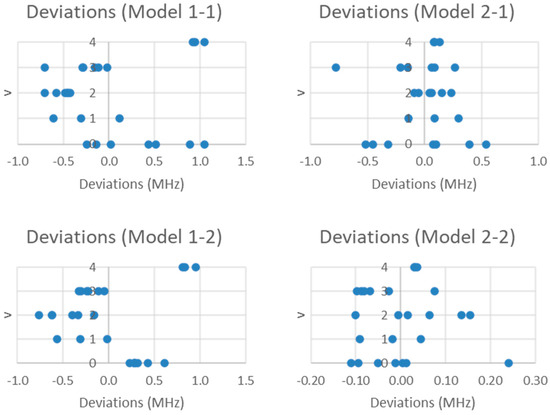
Figure 4.
The residual plots of Models 1-1, 1-2, 2-1, and 2-2 for the microwave spectrum of sodium iodide.
The SSE is not reduced much on going from Model 1-1 (8.099) to 1-2 (5.596), because the quadratic error is still present. However, it is reduced a further order of magnitude on going from 2-1 (2.033) to 2-2 (0.187). For Model 2-2, the residual errors are now on the order of the error of the experiment. The predicted re is 2.711456 Å.
The pedagogical goals achieved here are showing that for NaI, calculating effective molecular constants using only Models 1 and 2 cannot reproduce the spectrum and that a model of the quadrupole coupling is required. Two models for nuclear quadrupole coupling are introduced, one in which eQq is constant and another in which it depends (weakly) on the vibrational state.
5.2. Lithium Iodide (LiI)
Lithium has two isotopes in approximately a 12:1 ratio, so two isotopologues should be observable in natural samples. The predicted value of 2B of the most abundant isotope from the electron diffraction distance is 24,500 MHz (see Supplementary Materials, Excel file LiI.xlsx). The spectrum of lithium iodide in the region 25–31 GHz was measured [7] at 600 °C, and the frequencies observed (error 0.1–0.4 MHz) are given in Figure 5. Inspection of the 14 frequencies demonstrates that there appears to be two major groupings of frequencies centered at 26,209 and 30,498 MHz. The difference of these is 4289 MHz. The clustering could be due either (a) to different values of J for a single isotopologue or (b) to the same value of J for two isotopologues.
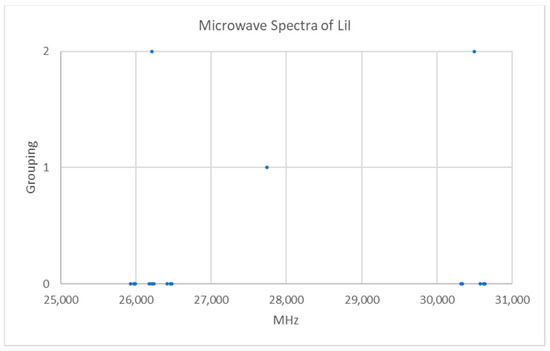
Figure 5.
The microwave spectrum of lithium iodide (Grouping 0), and the cluster averages for k = 1–2.
If the groupings were due to different values of J of the heavier isotopologue, then division of the cluster averages by the difference gives J + 1 values of 6.111 and 7.111, suggesting that the groupings are due to transitions from J = 5 and J = 6, respectively. Using the highest frequency in each cluster, and dividing by that difference (4160 MHz), gives values of 6.364 and 7.364. Using highest cluster frequency instead of average cluster frequency is usually more accurate (closer to integers), not less. The nearly six-fold difference in the predicted 2B (24,500 MHz) and either the cluster difference (4289 MHz) or highest frequency difference (4160 MHz) is cause for alarm. We may, however, continue the analysis under this assumption (Model 0, Be = 2181.675 MHz, SSE = 476,090). Within each cluster, there appears to be a vibrational progression, assigned as v = 0–2 for the lower frequency cluster and v = 0, 1 for the higher frequency cluster (Model 1, Be = 2201.097 MHz, αe = 15.642 MHz, SSE = 157,984). The deviations for the two clusters (values of J) are predominantly opposite in sign (Figure 6), suggesting that there must be a huge centrifugal distortion constant (Model 3, Be = 2201.097 MHz, αe = 15.642 MHz, De = −0.865 MHz, SSE = 8113). Further splitting is due to nuclear quadrupole effects. The lack of agreement between the predicted 2B and difference between clusters, along with the huge centrifugal distortion constant needed to fit the data (about 105 too big) suggests that the clustering is not due to different values of J.
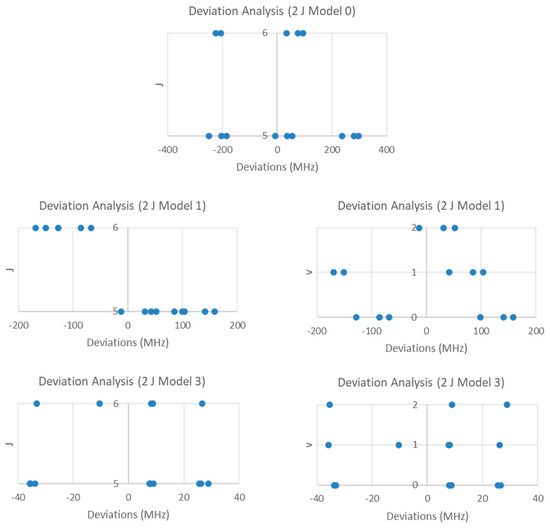
Figure 6.
The residual plots for LiI (one isotopologue, two J).
If the groupings were due to two different isotopologues but the same value of J, then comparison of the predicted 2B with the measured spectrum strongly suggests that J = 0. The ratio between the two highest frequencies of each cluster is 1.1571 (the underline indicates the significant figure agreement with the predicted value), whereas the predicted isotopologue mass ratio should be 1.157679. These ratios are strong evidence for this hypothesis. Fitting to Model 1 gives a Be ratio of 1.15736, SSE = 6050 (7Li127I) + 2058 (6Li127I), with a residual pattern suggesting that nuclear quadrupole effects are the next major source of variation (Figure 7). For lithium, I = 1 (6Li) or 1.5 (7Li), but it is iodine (127I, I = 2.5) that is responsible for the observed splitting, as the Casimir function differences for J = 0, I = 2.5 support this assignment. Model 1-1 gives a Be ratio of 1.157702, SSE = 7.820 (7Li127I) + 0.203 (6Li127I), approximately three orders of magnitude smaller. Comparisons of Models 2-1, 1-2, and 2-2 indicate that improving the description of the nuclear quadrupole model first is most advantageous (Table 2). The values for re are 2.391920 (7Li127I, Model 2-2) and 2.391956 Å (6Li127I, Model 1-2), which is excellent agreement.
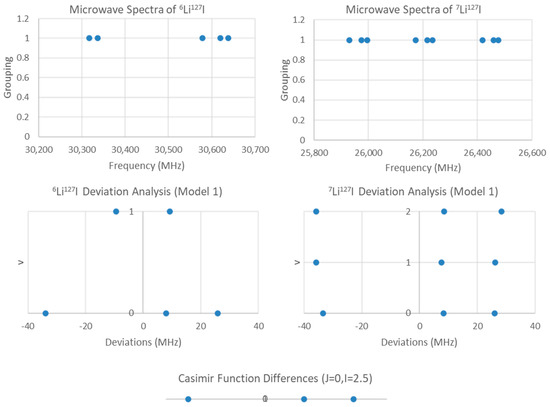
Figure 7.
The residual plots for LiI (two isotopologues, one J).

Table 2.
Model parameters for lithium iodide (MHz) (6Li127I, n = 5; 7Li127I, n = 9).
The pedagogical goals achieved here show that for LiI, two models for the primary variation can be entertained and that the two-isotopologue, one-J model is better.
5.3. Interhalogen Diatomics
Table 3 gives the internuclear distances in the known crystal structures of the interhalogen diatomic molecules. In most cases, the X-ray crystal structure determination of these reactive species was carried out after the gas-phase microwave spectra were measured and serve as an independent check.

Table 3.
The internuclear distance in interhalogen diatomics.
5.4. Chlorine Monofluoride (ClF)
Fluorine is monoisotopic. Chlorine has two isotopes in approximately a 3:1 ratio, so two isotopologues should be observable in natural samples. The spectrum of chlorine monofluoride is given in Figure 8 [19]. The spectrum forms four clusters (see Supplementary Materials, Excel file ClF.xlsx). The range is too narrow to be due to be due to multiple values of J. We assume that the spectrum is due to J = 0, which would give a predicted Cl-F distance of 1.63 Å, which is very close to the observed X-ray structure (Table 3). Are these four clusters due to (a) one isotopologue, vibrational progression v = 0–3 or (b) two distinct isotopologues with a vibrational progression v = 0, 1?
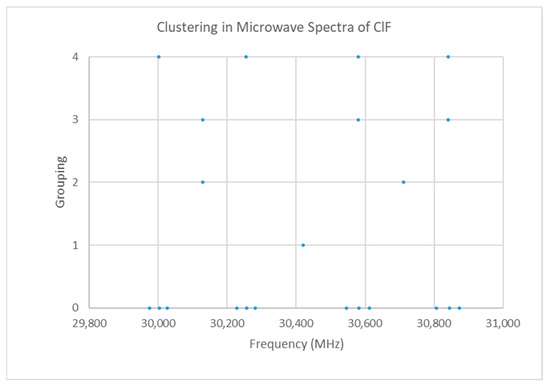
Figure 8.
The microwave spectrum of ClF (Grouping 0) and the cluster averages for k = 1–4.
The four clusters are not quite evenly spaced, which one would expect if they formed a vibrational progression. One can carry out an analysis assuming that the four clusters correspond to v = 0–3, but a zig-zag pattern is obvious in the residuals (Figure 9). The cluster frequency ratios are 1.00854, 1.01937, 1.02800, 1.01074, 1.01929, and 1.00846. Two of these are close to the expected isotopologue mass ratio of 1.01938, which strongly suggests that the clusters at 30,580 and 30,841 are due to 35Cl19F, whereas those at 30,001 and 30,255 are due to 37Cl19F (due to a v = 0, 1 progression). The reduction in error on going from the one isotopologue and four vibrational states (SSE = 9777) to two isotopologue anf two vibrational states (SSE = 2687.4 + 4332.3 = 7020) is not large, however.
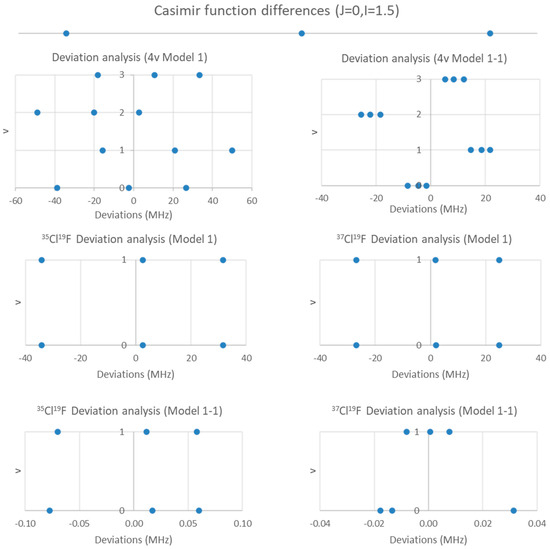
Figure 9.
Residual analysis of ClF.
The isotope 19F will not give a nuclear quadrupole coupling because I = 0.5, but both 35Cl and 37Cl will because I = 1.5. For J = 0, F = 1.5 (one level), but for J = 1, F = 2.5, 1.5, and 0.5 (three levels). For each transition, a triplet of signals should be observed, consistent with experiment. The spacing of the triplets allows for unambiguous assignment (F’). The values for re (Model 1-1), 1.628314 (35Cl19F) and 1.628313 Å (37Cl19F) are in excellent agreement with each other (Table 4) and the X-ray result of 1.628 Å. This makes an excellent student exercise (see Appendix A).

Table 4.
Model parameters for chlorine monofluoride (MHz) (35Cl19F, n = 6; 37Cl19F, n = 6).
The pedagogical goals achieved here are to demonstrate that for ClF, it is difficult but not impossible, to distinguish between a single-isotopologue, four-vibrational-state model and a two-isotopologue, two-vibrational state model by examining patterns in the residuals.
5.5. Bromine Monofluoride (BrF)
Bromine has two isotopes in approximately a 1:1 ratio, so two isotopologues should be observable in natural samples. The spectra of bromine monofluoride is given in Figure 10 [20]. There is no obvious pattern, although the narrow range suggests that only a single value of J is being observed. Assuming J = 0 gives an re = 1.77 Å, which is slightly shorter than the observed X-ray structure (Table 3), so this is a safe assumption (see Supplementary Materials, Excel file BrF.xlsx). Through trial and error, the spectrum of 12 frequencies can be assigned (Figure 10), but there is a more systematic way to assign this using knowledge of theory. Because of the lack of an obvious pattern, it is clear that splitting effects due to isotope shifts, vibrational progressions, and nuclear quadrupole effects are about the same.
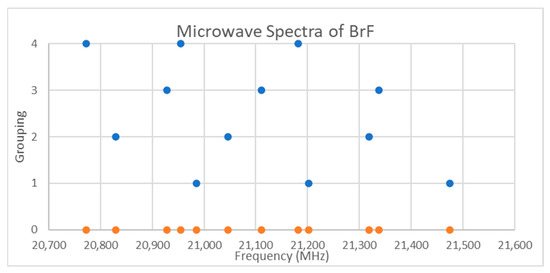
Figure 10.
The microwave spectrum of bromine monofluoride (Grouping 0), and the assignment via trial and error. Each grouping corresponds to a different isotopologue and vibrational state.
The first step is to create a list of all of the possible frequency differences (12 × 13/2 = 69 differences) and then plot a series of histograms with narrowing bin ranges. For this spectrum, the largest difference is just over 700, so we take the total range as 720 and then subdivide. No patterns are noticed for bin size 360 (N = 2), 180 (N = 4), and 100 (N = 8), but deviations from a monotonic decrease in frequency begin to appear for bin sizes 50 (N = 15), 40 (N = 18), 30 (N = 24), 20 (N = 36), and 10 (N = 71). For bin size 10 (Figure 11), prominent peaks for bin ranges [90,100], [130,140], [150,160], [210,220], and [270,280] are noted. For bin range [150,160] with a frequency of 6, the differences correspond to all twelve frequencies (no overlap) with a range 155.8–157.0. This is the pattern that one would expect for bands with the same F but different v. The higher frequency of each difference corresponds to v = 0, whereas the lower frequency corresponds to v = 1. Analysis of frequency ratios gave no discernible pattern.
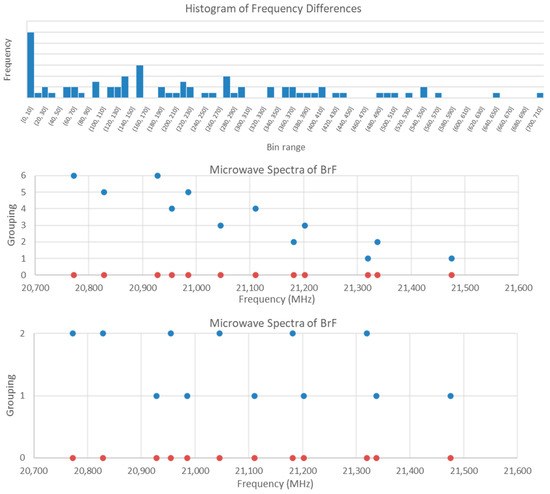
Figure 11.
Tools for the assignment of bromine monofluoride. In the top plot, a histogram of frequency differences is shown, with 6 differences in the [150,160] bin. In the middle plot, the v = 0, 1 pairs are grouped together. In the lower plot, the v = 0 frequencies are grouped together along with the v = 1 frequencies.
Now that the vibrational quantum number has been assigned and the spectrum separated into two groups (v = 0 and v = 1), these can be analyzed separately. Nuclear quadrupole splitting into three frequencies is expected because both isotopes of bromine have I = 1.5. The ratio of the splitting is 1.00, 2.25, and 1.25 (dividing by the smallest splitting) or 0.444, 1.000, and 0.556 (dividing by the largest splitting). If we take the differences above and calculate their ratios, we find that difference ratios of states with the same J but different F will match the patterns above, allowing us to assign F. Division by an unrelated state will not give a matching pattern. In this way, we can determine which differences correspond to the same J of the same species and reproduce what can be found through trial and error (Figure 10). Because we have already broken the problem into v = 0 and v = 1, we only have to deal with 6 × 6 matrices of difference ratios instead of 12 × 12 matrices.
All that remains is to assign the frequencies to specific isotopologues. Within each of the six frequencies for constant v (assumed to be two Casimir triplets from each isotopologue), it is the central frequency of the triplet that would be least affected by nuclear quadrupole coupling. Examining the frequency ratios and comparing with the expected isotopologue mass ratio of 1.004814, the closest values are 1.00436, 1.00434, and 1.00478, corresponding to the frequency pairs at {21,110.4, 21,202.6}, {20,954.6, 21,045.6}, and {20,828.9, 20,928.4}, respectively. The last pair can be excluded because they correspond to different values of v. Of the first two pairs, the higher frequency should belong the lighter isotope. We have thus finished the assignment. Referring to Figure 10, Grouping 1 is 79Br19F, v = 0; Grouping 2 is 79Br19F, v = 1; Grouping 3 is 81Br19F, v = 0; and Grouping 4 is 81Br19F, v = 1. The nuclear quadrupole splitting is somewhat smaller for the heavier 81Br19F isotopologue. The values for re (Model 1-2, Table 5) of 1.758940 (79Br19F) and 1.758933 Å (81Br19F) are in excellent agreement with each other and in good agreement with the X-ray result of 1.822 Å (Table 3).

Table 5.
Model parameters for bromine monofluoride (MHz) (79Br19F, n = 6; 81Br19F, n = 6).
The pedagogical goals achieved here are that for BrF, (a) a spectrum with no obvious pattern can appear; (b) by examining a histogram of frequency differences and looking for higher than normal occurrences, the vibrational structure can be assigned; (c) by comparing ratios of frequency differences to the predicted Casimir function differences, the F quantum number can be assigned; and (d) by comparing the frequency ratios of the frequencies least affected by nuclear quadrupole coupling, the isotopologues can be assigned.
5.6. Iodine Monofluoride (IF)
Only one isotopologue should be observable in natural samples. The spectra of iodine monofluoride is given in Figure 12 [21]. There are two groupings centered at 16,754 and 33,258 MHz. The difference between the groupings is 16,503 MHz, which is close to the center of the first grouping, so these may confidently be assigned to J = 0 and J = 1 transitions (see Supplementary Materials, Excel file IF.xlsx). The predicted re is approximately 1.93 Å, which falls in line with the expected crystal structure distance of approximately 2.0 Å.
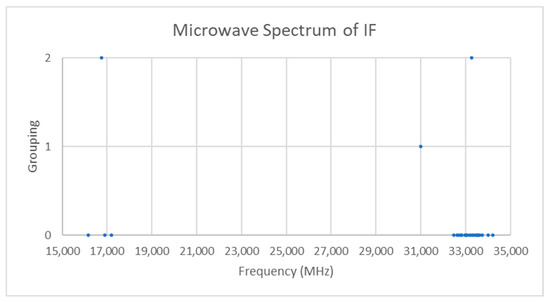
Figure 12.
The microwave spectrum of iodine monofluoride (Grouping 0) and the cluster averages for k = 1–2.
The plot of the Model 0 residuals is given in Figure 13. The J = 0 frequency deviations match the expected Casimir function difference pattern quite nicely. The value of eQq is large and approximately equal to −3400 MHz (Table 6). Because eQq should not strongly depend on J, we may use the same value for J = 1 to assign the spectrum. Clearly, most of the deviation is due to the nuclear quadrupole coupling. However, the 19 frequencies must belong to at least three vibrational progressions (at most 9 frequencies per v). These can be assigned by overlaying the Casimir function difference plot for J = 1 onto the spectra. The SSE is reduced by an order of magnitude upon going from Model 0 to Model 0-1 amd less than 10% upon going from Model 0 to Model 1, but three additional orders of magnitude upon going from Model 0-1 to 1-1. The estimated error in each frequency is only 0.04–0.08 MHz, but the residuals for Model 1-1 are still on the order of 0–10 MHz. Some minor improvement in SSE is achieved by including De and/or γe (Models 2-1, 3-1, and 4-1), but the lack of pattern in the variation of the residual with J and v indicates that there is a bigger reason for the discrepancy. The reason is evident when one compares the magnitude of eQq and B. The quadrupolar coupling can no longer be regarded as a small perturbation.
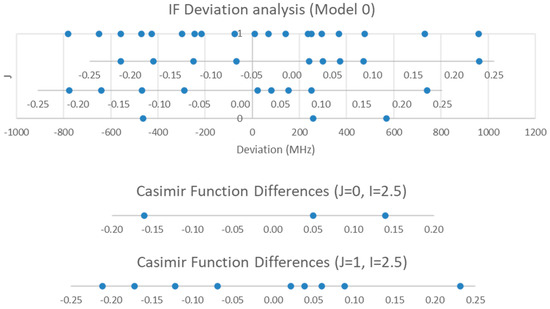
Figure 13.
Model 0 residuals for IF, and the assignment of F and v. Only v = 0, 1 are shown.

Table 6.
Model parameters for iodine monofluoride (MHz) (127I19F, n = 22). De is the centrifugal distortion constant.
The pedagogical goals achieved here are that for IF, (a) a spectrum with quadrupolar coupling and multiple values of J and v can be analyzed, and (b) even though the quadrupolar coupling is ~40% of the value of B, the assignments can still be made even if the residuals are large and the spectroscopic parameters thus derived would not be as accurate.
5.7. Deuterium Iodide (DI)
The spectrum of deuterium iodide (2H127I) was measured [22] and given in Figure 14 (Grouping 1). If we assume that J = 0, then the predicted r is 1.62 Å, in excellent agreement with the liquid neutron diffraction result [23] of 1.625 ± 0.015 Å (see Supplementary Materials, Excel file HI.xlsx). It is not immediately obvious whether the splitting around the average of 195,083 MHz is due to nuclear quadrupole effects or to a vibrational progression, v = 0, 1, 3 (with v = 2 missing). Fitting to Model 1 gives Be = 97,708, αe = 91 MHz, SSE = 114. Model 2 exactly reproduces the spectrum (Be = 97,699.5, αe = 77.3, γe = −3.3 MHz, SSE = 0) but gives a negative γe. Model 0-1 fits the spectrum to within the error but only requires two parameters (B0 = 97,532.3, eQq = −1809.3 MHz, SSE = 14.58, r0 = 1.61664 Å). A more precise spectrum was also measured [24] (Figure 14, Grouping 2) and the same gap for the purported v = 2 was noticed, suggesting that the splitting is actually due to nuclear quadrupole effects. The same models with the more precise spectrum gave: Model 1, Be = 97,711.4, αe = 91.8 MHz, SSE = 229; Model 2, Be = 97,698.8, αe = 72.2, γe = −4.72 MHz, SSE = 0; Model 0-1, B0 = 97,534.1, eQq = −1822.6 MHz, SSE = 0.264, r0 = 1.61662 Å. These make excellent student exercises (Appendix B and Appendix C).
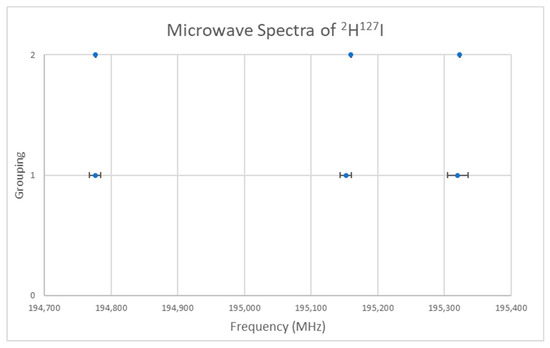
Figure 14.
The microwave spectrum of deuterium iodide from two sources.
The pedagogical goal achieved here is to show that that, for HI, (a) the nuclear quadrupole coupling can sometimes appear to be a vibrational progression with a missing v, (b) proper model fitting can support one model over the other, (c) a lower residual does not necessarily mean a better physical model.
5.8. Deuterium Bromide (DBr)
The spectrum of deuterium bromide (2HBr) was measured [25] and given in Figure 15. If we assume that J = 0, then the predicted r is 1.44 Å, in excellent agreement with the liquid neutron diffraction result [26] of 1.446 ± 0.002 Å (see Supplementary Materials, Excel file HBr.xlsx). Because the bromine isotopes are in nearly equal abundance, both isotopologues should be observable. While the isotopologues can be separated by trial and error, the calculated frequency ratios are instructive as well. The predicted reduced mass ratio is 1.000614. Of the frequency ratios, four are close: 1.000687 (254,812/254,638), 1.000527 (254,812/254,678), 1.000597 (254,678/254,526), and 1.000522 (254,572/254,439). Of these, the first, third, and fourth encompass all of the data points, and we can provisionally separate the higher and lower frequencies of these sets as belonging to two different isotopologues: 254,812, 254,678, and 254,678 MHz (Grouping 1) belong to 2H79Br, and 254,638, 254,526, and 254,439 (Grouping 2) belong to 2H81Br. In this case, the magnitude of the remaining splitting is small enough to keep the frequency ratios close to the mass ratio.
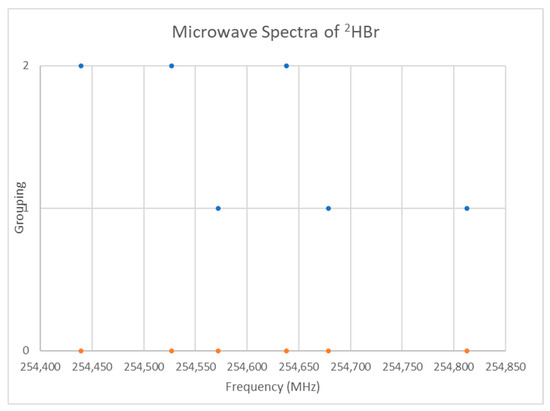
Figure 15.
The microwave spectrum of deuterium bromide (Grouping 0), and its grouping into isotopologues.
The splitting in each of these is not quite even, so each triplet could be assigned to a vibrational progression of v = 0, 1, 2, if γ was sufficiently large or to nuclear quadrupole splitting. All of these models are presented in Table 7. The B ratios of the four models are Model 0, 1.000601; Model 1, 1.000725; Model 2, 1.000738; and Model 0-1, 1.000614. Only Models 0 and 0-1 give the correct B ratios. Although Model 2 is exact, the γ values are quite large, and there are three parameters, whereas Model 0-1 is quite good, but only has two parameters. We therefore choose Model 0-1 over Models 1 and 2. Analysis of the ratios of the frequency differences and comparison with the expected Casimir triplet pattern confirms the analysis, but there are many false positive matches as well. This makes an excellent student exercise (Appendix D).

Table 7.
Model parameters for deuterium bromide (MHz) (2H79Br, n = 3; 2H81Br, n = 3).
The pedagogical goals achieved here is that, for HBr, (a) if the hyperfine splitting is small, then frequency ratios can be used to separate spectra into isotopologues, and (b) the hyperfine splitting can look like a normal vibrational progression with a large value of γ.
5.9. Sodium Bromide (NaBr)
The spectrum of sodium bromide (NaBr) was measured [7] at 780 °C and given in Figure 16. There are two main groupings, centered at 17,886 and 26,720 MHz (difference 8835 MHz). The predicted value of 2B from the electron diffraction distance is 8200–8300 MHz (see Supplementary Materials, Excel file NaBr.xlsx). This suggests that the observed transitions correspond to J = 1 and J = 2, as does dividing the cluster averages by the cluster difference. There does appear to be one frequency that is too low (17,082.50 MHz). Based on an analysis of the effective rotational constants (Figure 17), we believe that this is a misprint and that the correct value is 17,982.50 MHz. Upon first glance, the grouping into five clusters appears to be a vibrational progression of v = 0–4 of a single isotopologue (Be~4534.2 MHz, αe~27.3 MHz), with some fine structure.
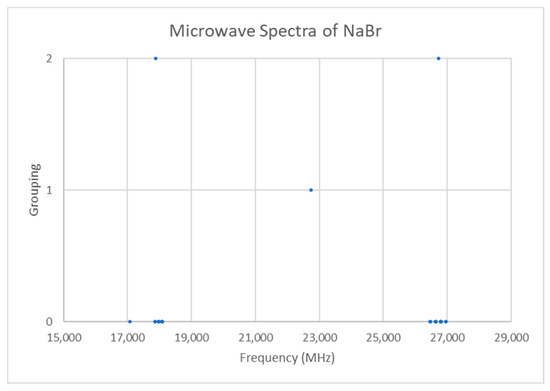
Figure 16.
The microwave spectrum of sodium bromide (Grouping 0), and the cluster averages for k = 1–2.
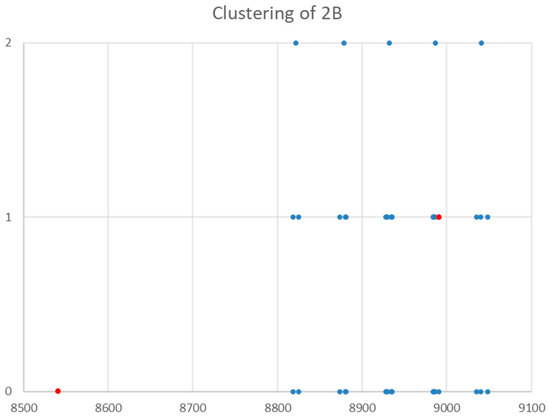
Figure 17.
The clustering of the effective rotational constants (MHz) of sodium bromide. Grouping 0 is the original, Grouping 1 corrects the bad point (red), and Grouping 2 shows the clustering into 5 groups.
We now fit our data to Model 1 (one isotope), with the understanding that there is some unexplained fine structure that could be due to a combination of isotopologues and nuclear quadrupole coupling (Be = 4534.177, αe = 27.286 MHz, SSE = 1445). Examination of the residuals reveals no obvious pattern as a function of J, but there does seem to be a clustering of positive and negative residuals as a function of v. When the points corresponding to these residual clusters are fit to two separate models with the same J, v assignments (Be = 4533.367, αe = 27.529 MHz, SSE = 107; Be = 4537.004, αe = 27.698 MHz, SSE = 37.8), the error is reduced by an order of magnitude, but the Be ratio (1.0008) is too small for it to be due to isotopologues (1.0056).
Our next step is to calculate all possible frequency ratios (common J) to see if any match the expected Be ratio of 1.005601. For J = 1, there are six ratios within a 0.0002 tolerance, but at most, three of them correspond to isotopic pairs because three of the frequencies are common. There are four possible ways to do this (reassigning v of 23Na81Br is required); the one with the lowest combined SSE is taken. This gives 18,080.13, 18,070.07, and 17,968.42 for 23Na79Br, and 17,980.48, 17,971.00, and 17,868.49 for 23Na81Br. The isotopic separation is about the same as the vibration–rotation interaction, which is what makes the assignment so difficult. When this is done, we try to assign the remaining J = 1 frequencies. Clearly the high frequency at 18,095.95 MHz belongs to 23Na79Br, establishing it as part of a Casimir triplet v = 0. Similarly, the frequency at 17,982.50 MHz must belong to the same species for v = 1. The assignment of the lower frequency at 17,856.57 could arise from a Casimir grouping for 23Na81Br, v = 1 or for 23Na79Br, v = 2. The latter assignment is preferred because of the slightly lower SSE. Fortunately, the nuclear quadrupole coupling is small enough not to affect the frequency ratios too much. We carry out a similar procedure for the J = 2 frequencies and can assign 10 of the 11 frequencies. Fitting to the same model, starting with J = 1 Be and αe, resulted in no change to these parameters. The low frequency at 26,455.80 MHz could be assigned to either 23Na81Br v = 3, or to 23Na79Br, v = 4, with the latter giving a much better residual.
Now that we have assigned all frequencies to the specific isotopologues v and J, all that remains is to assign the hyperfine splitting. This is initially challenging because only 1–3 frequencies are observed of the possible seven. Fortunately, consideration of which signals should be most intense allows for the assignment of the frequencies to specific F, which can be checked against the splitting pattern. The Be ratio for all models with hyperfine splitting included is 1.00560 ± 0.00002, in excellent agreement with experiment, whereas without hyperfine splitting included, the values are slightly too high (1.0059–1.0063, Table 8). The equilibrium bond distances re are 2.502037 (23Na79Br) and 2.502035 Å (23Na81Br), in excellent agreement.

Table 8.
Model parameters for sodium bromide (MHz) (23Na79Br, n = 12; 23Na81Br, n = 8).
The pedagogical goals achieved here for NaBr are (a) that the spectrum is rather difficult to analyze because the isotopic separation is about the same as the vibrational dependence and many possible models may need to be examined before settling on just one, starting with the simplest models and building from there and (b) that it is sometimes a good idea to analyze a single value of J first and then expand the model.
5.10. Lithium Bromide (LiBr)
The spectrum of lithium bromide (LiBr) was measured [7] at 680 °C and given in Figure 18. There are two main groupings, a single frequency at 38,113 MHz and a cluster centered at 32,876 MHz (difference 8835 MHz). The predicted value of 2B from the (estimated) electron diffraction distance is 31,000 MHz (for the lighter isotope). This suggests that the observed transitions correspond to J = 0 and that the clustering is due to the large isotope effect of lithium (see Supplementary Materials, Excel file LiBr.xlsx). Because of the natural abundance of lithium, mostly 7Li isotopologues should be observed.
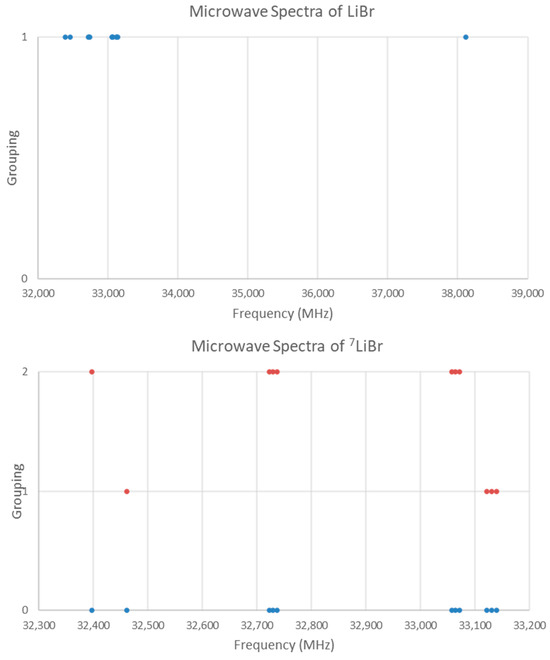
Figure 18.
The microwave spectrum of lithium bromide. The original spectrum is in blue, and the separation into two isotopologues is in orange.
There are four possible isotopologues: 6Li79Br, 6Li81Br, 7Li79Br, and 7Li81Br. Examination of frequency ratios suggests that the frequency at 38,113 MHz is from 6Li81Br (r0 = 2.176390 Å), the three-frequency cluster at 33,130 MHz is due to 7Li79Br, and the three-frequency cluster at 33,065 MHz is due to 7Li81Br. Similarly, the bands at 32,462 and 32,397 MHz can be assigned to 7Li79Br, and 7Li81Br. The final cluster at 32,730 MHz is nearly in the middle of the two clusters due to 7Li81Br, and these form a vibrational progression (the corresponding v = 1 cluster of 7Li79Br was not observed, Figure 18 lower panel). The hyperfine structure is easily assigned, giving re (Model 1-1) of 2.170483 Å (7Li79Br) and 2.170487 Å (7Li81Br). An order of magnitude SSE improvement is gained by including γ (Model 2-1), and the vibrational dependence of eQq, (Model 2-2), but these are somewhat dependent on one another.
The pedagogical goal achieved here is, for LiBr (in the absence of additional data) the variation of eQq with vibrational quantum number and the effect of γ can mimic each other, making these parameters somewhat dependent on each other during fitting procedures.
6. Conclusions
The microwave spectra of NaI, LiI, ClF, BrF, IF, HI, HBr, NaBr, and LiBr are presented and procedures for their analysis discussed. By the use of either additional information (electron or X-ray diffraction) or cluster analysis of the spectra, the approximate value of 2B can be determined, followed by the assignment of the frequencies to rotational quantum number J (Model 0). Once J has been assigned, a combination of comparing the spectra to Casimir function differences, comparing frequency ratios, comparing frequency difference ratios, and statistical analysis of frequency differences is applied, which allows assignment to isotopologues, v, and F’. Then, the spectra are fitted to models to determine the rotational constant Be, bond length re, vibration–rotation interaction constant αe, and the nuclear quadrupole splitting eQq. (Model 1-1). In some cases, other spectroscopic constants (De, γe) can be determined.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/spectroscj2030006/s1, Microsoft Excel spreadsheets Isotopes.xlsx, NaI.xlsx, LiI.xlsx, ClF.xlsx, BrF.xlsx, IF.xlsx, HI.xlsx, HBr.xlsx, NaBr.xlsx, and LiBr.xlsx.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used in this article can be found in either the references cited or in the Supplementary Materials.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Analysis of the Microwave Spectrum of Chlorine Monofluoride (ClF)
The microwave spectrum of chlorine monofluoride in the range 29.8–31.0 GHz has transitions at 29,974.47, 30,003.218, 30,026.195, 30,228.369, 30,257.159, 30,280.107, 30,545.994, 30,582.614, 30,611.761, 30,807.413, 30,843.948, and 30,873.004 MHz, corresponding to transitions from J = 0 to J = 1. These transitions correspond to two isotopologues in the ground and the first excited vibrational state. (a) Assign these bands to isotopologue and vibrational states. (b) Assign the hyperfine structure (F’). (c) Calculate (in MHz) Be, αe, and eQq. (d) Give a precise value of re.
[Ans: (a) In order of increasing frequency, the four triplets are: 19F37Cl, v = 1; 19F37Cl, v = 0; 19F35Cl, v = 1; 19F35Cl, v = 0 (b) Within each triplet, in order of increasing frequency, F’ = 1.5, 2.5, 0.5 (c) 19F37Cl: Be = 15,189.169, αe = 126.959, eQq = −114.964; 19F35Cl: Be = 15,483.628, αe = 130.666, eQq = −145.968 (d) re = 1.62831 Å].
Appendix B. Analysis of the Microwave Spectrum of Deuterium Iodide (DI)
A low-resolution microwave spectrum of deuterium iodide in the range 194.7–195.4 GHz has transitions at 194,776 ± 8, 195,152 ± 8, and 195,320 ± 15 MHz, corresponding to transitions from J = 0 to J = 1. These transitions correspond to the v = 0 vibrational state. (a) Assign the hyperfine structure (F’). (b) Calculate B0 and eQq. (c) Give a precise value of r0.
[Ans: (a) F’ = 2.5, 3.5,1.5 (b) B0 = 97,532.3, eQq = −1809.3 MHz (c) r0 = 1.61664 Å].
Appendix C. Analysis of the Microwave Spectrum of Deuterium Iodide (DI)
A medium-resolution microwave spectrum of deuterium iodide in the range 194.7–195.4 GHz has transitions at 194,776.40, 195,159.68, and 195,323.02 (±0.3) MHz, corresponding to transitions from J = 0 to J = 1. These transitions correspond to the v = 0 vibrational state. (a) Assign the hyperfine structure (F’). (b) Calculate B0 and eQq. (c) Give a precise value of r0.
[Ans: (a) F’ = 2.5, 3.5,1.5 (b) B0 = 97,534.1, eQq = −1822.6 MHz (c) r0 = 1.61662 Å].
Appendix D. Analysis of the Microwave Spectrum of Deuterium Bromide (DBr)
A medium-resolution microwave spectrum of deuterium bromide in the range 254.4–254.9 GHz has transitions at 254,439.4, 254,526.7, 254,572.2, 254,638.0, 254,678.6, and 254,812.9 (±0.5–1.5) MHz, corresponding to transitions from J = 0 to J = 1. These transitions correspond to the v = 0 vibrational state of two isotopologues. (a) Assign each frequency to an isotopologue (b) Assign the hyperfine structure (F’). (c) Calculate B0 and eQq. (d) Give a precise value of r0.
[Ans: (a) 2H79Br, 254,572.2, 254,678.6, 254,812.9; 2H81Br, 254,439.4, 254,526.7, 254,638.0 (b) F’ = 0.5, 2.5, 1.5 (c) 2H79Br, B0 = 127,352.87, eQq = +534.87; 2H81Br, B0 = 127,274.71, eQq = 441.49 (d) r0 = 1.421464 Å].
Appendix E. Some Relevant Isotopic Data

Table A1.
Some relevant isotopic data. Z = atomic number, m = atomic mass, I = nuclear spin, Q = nuclear quadrupole.
Table A1.
Some relevant isotopic data. Z = atomic number, m = atomic mass, I = nuclear spin, Q = nuclear quadrupole.
| Isotope | Z | m (amu) | Abundance (%) | I | Q (barn) |
|---|---|---|---|---|---|
| 2H | 1 | 2.014101777844 | 0.03 | 1 | +0.0028578 |
| 6Li | 3 | 6.015122795 | 7.59 | 1 | −0.000806 |
| 7Li | 3 | 7.016004550 | 92.41 | 1.5 | −0.0400 |
| 19F | 9 | 18.998403220 | 100.00 | 0.5 | −0.0942 |
| 23Na | 11 | 22.989769281 | 100.00 | 1.5 | +0.104 |
| 35Cl | 17 | 34.968852721 | 75.76 | 2.5 | −0.0817 |
| 37Cl | 17 | 36.965902590 | 24.24 | 2.5 | −0.0644 |
| 79Br | 35 | 78.9183371 | 50.69 | 1.5 | +0.3087 |
| 81Br | 35 | 80.9162906 | 49.31 | 1.5 | +0.2579 |
| 127I | 53 | 126.904473 | 100.00 | 2.5 | −0.688 |
References
- Pye, C.C. Interpreting the Microwave Spectra of Diatomic Molecules. Spectrosc. J. 2023, 1, 3–27. [Google Scholar] [CrossRef]
- Townes, C.H.; Schawlow, A.L. Microwave Spectroscopy; Dover: New York, NY, USA, 1975. [Google Scholar]
- Microsoft Office Professional Plus (Excel); Microsoft Corporation: Redmond, DC, USA, 2016.
- Solver, Microsoft Office Add-In; Frontline Systems: Incline Village, NV, USA, 2016.
- Available online: http://info.ifpan.edu.pl/~kisiel/prospe.htm (accessed on 4 June 2024).
- Maxwell, L.R.; Hendricks, S.B.; Mosley, V.M. Interatomic Distances of the Alkali Halide Molecules by Electron Diffraction. Phys. Rev. 1937, 52, 968–972. [Google Scholar] [CrossRef]
- Honig, A.; Mandel, M.; Stitch, M.L.; Townes, C.H. Microwave Spectra of the Alkali Halides. Phys. Rev. 1954, 96, 629–642. [Google Scholar] [CrossRef]
- Pye, C.C. One-Dimensional Cluster Analysis and its Application to Chemistry. Chem. Educ. 2020, 25, 50–57. [Google Scholar]
- Casimir, H.B.G. On the Interaction between Atomic Nuclei and Electrons; Springer: Dordrecht, NL, USA, 1936; pp. 201–283. [Google Scholar]
- Bardeen, J.; Townes, C.H. Calculation of Nuclear Quadrupole Effects in Molecules. Phys. Rev. 1948, 73, 97–105. [Google Scholar] [CrossRef]
- Gordy, W.; Cook, R.L. Microwave Molecular Spectra; Wiley: New York, NY, USA, 1984; Ch. 9; pp. 392–449. [Google Scholar]
- Lucken, E.A.C. Nuclear Quadrupole Coupling Constants; Academic Press: London, UK, 1969; Ch. 1-3b; pp. 1–34. [Google Scholar]
- Lo, A.Y.H.; Hanna, J.V.; Schurko, R.W. A Theoretical Study of 51V Electric Field Gradient Tensors in Pyrovanadates and Metavanadates. Appl. Magn. Reson. 2007, 32, 691–708. [Google Scholar] [CrossRef]
- Boese, R.; Boese, A.D.; Blaser, D.; Antipin, M.Y.; Ellern, A.; Seppelt, K. The Surprising Crystal Packing of Chlorinefluoride. Angew. Chem. Int. Ed. 1997, 36, 1489–1492. [Google Scholar] [CrossRef]
- Drews, T.; Seppelt, K. Bromine Monofluoride. Z. Anorg. Allg. Chem. 2012, 638, 2106–2110. [Google Scholar] [CrossRef]
- Boswijk, K.H.; van der Heide, J.; Vos, A.; Wiebenga, E.H. The Crystal Structure of α-ICl. Acta Cryst. 1956, 9, 274–277. [Google Scholar]
- Carpenter, G.B.; Richards, S.M. The Crystal Structure of β-Iodine Monochloride. Acta Cryst. 1962, 15, 360–364. [Google Scholar] [CrossRef]
- Swink, L.N.; Carpenter, G.B. The Crystal Structure of Iodine Monobromide. Acta Cryst. B 1968, 24, 429–433. [Google Scholar] [CrossRef]
- Gilbert, D.A.; Roberts, A.; Griswold, P.A. Nuclear and Molecular Information from the Microwave Spectrum of FCl. Phys. Rev. 1949, 76, 1723. [Google Scholar] [CrossRef]
- Smith, D.F.; Tidwell, M.; Williams, D.V.P. The Microwave Spectrum of Bromine Monofluoride. Phys. Rev. 1950, 77, 420–421. [Google Scholar] [CrossRef]
- Tiemann, E.; Hoeft, J.; Torring, T. Das Rotationsspektrum des JF. Z. Naturforsch. A 1973, 28, 1405–1407. [Google Scholar] [CrossRef][Green Version]
- Klein, J.A.; Nethercot, A.H., Jr. Microwave Spectrum of DI at 1.5-mm Wavelength. Phys. Rev. 1953, 91, 1018. [Google Scholar] [CrossRef]
- Andreani, C.; Nardone, M.; Ricci, F.P.; Soper, A.K. Neutron-diffraction study of liquid hydrogen iodide. Phys. Rev. A 1992, 46, 4709–4716. [Google Scholar] [CrossRef]
- Burrus, C.A.; Gordy, W. One-to-Two Millimeter Wave Spectroscopy. III. NO and DI. Phys. Rev. 1953, 92, 1437–1439. [Google Scholar] [CrossRef]
- Gordy, W.; Burrus, C.A. Spectrum of DBr in the One-Millimeter Wave Region. Phys. Rev. 1954, 93, 419–420. [Google Scholar] [CrossRef]
- Andreani, C.; Menzinger, F.; Ricci, M.A.; Soper, A.K.; Dreyer, J. Neutron-diffraction from liquid hydrogen bromide: Study of the orientational correlations. Phys. Rev. B 1994, 49, 3811–3820. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).