Automatic Modeling and Object Identification in Radio Astronomy ^†

Abstract

Building appropriate models is crucial for imaging tasks in many fields but often challenging due to the richness of the systems. In radio astronomy, for example, wide-field observations can contain various and superposed structures that require different descriptions, such as filaments, point sources or compact objects. This work presents an automatic pipeline that iteratively adapts probabilistic models for such complex systems in order to improve the reconstructed images. It uses the Bayesian imaging library NIFTy, which is formulated in the language of information field theory. Starting with a preliminary reconstruction using a simple and flexible model, the pipeline employs deep learning and clustering methods to identify and separate different objects. In a further step, these objects are described by adding new building blocks to the model, allowing for a component separation in the next reconstruction step. This procedure can be repeated several times for refinement to iteratively improve the overall reconstruction. In addition, the individual components can be modeled at different resolutions allowing us to focus on important parts of the emission field without getting computationally too expensive.

1. Introduction

With modern and future radio interferometers such as the Australian Square Kilometre Array Pathfinder (ASKAP), MeerKAT, and the Square Kilometer Array (SKA), radio astronomy is starting to produce large volumes of data containing high-sensitivity sky maps over wide fields-of-view (FOV). These large area observations can contain various and superposed structures such as filaments, point sources, and compact objects. Imaging of these rich systems is a challenging task due to several reasons: firstly, the exact locations of the objects are unknown beforehand; secondly, the individual objects may need different model descriptions for a successful reconstruction; and finally, the imaging should be achieved in an automated way due to the large volumes of data.

In order to determine the locations of the individual objects, called source finding in radio astronomy, there exist plenty of different tools in the literature, summarized and compared in [1]. Recent advances in machine learning have set the stage for further improvements in the source-finding process. In particular, deep learning in the form of convolutional neural networks (CNNs) has been successfully used to detect point sources [2,3,4] or classify radio galaxy morphologies [5,6,7,8,9,10,11,12]. However, most of these source-finding algorithms have the problem that they are performed on images reconstructed using the CLEAN algorithm [13,14]. Although being the commonly employed imaging algorithm in radio interferometry, CLEAN has a couple of shortcomings and can produce imaging artifacts, which often need to be excluded manually before or during the source finding process.

We circumvent this problem by using the Bayesian imaging algorithm resolve instead, which has shown enhancements compared to CLEAN and provides uncertainty quantification of the results [15]. Moreover, being based on the Numerical Information Field Theory (NIFTy) library [16], it allows the creation and combination of complex forward models to separate components while reconstructing images from noisy input data.

In this work, we now combine the modeling and optimization capabilities of NIFTy with deep learning methods like CNNs in an automated way. But we do not only want to identify objects within a reconstructed image but rather use the gained information to further improve the reconstruction itself. By detecting and separating objects in the data, we aim to adjust our initial model in order to improve the overall reconstruction. To evaluate our method, we will test it on synthetic image data, which is based on real radio data and contains several compact objects and point sources. This should set the stage for its application to wide-field radio observations.

The paper is organized as follows. Section 2 describes the modeling and optimization process with NIFTy. Section 3 provides deep learning and clustering frameworks used for object identification and separation. Section 4 then combines these two parts into an iterative method and shows its application to a simple imaging problem, the reconstruction of synthetic image data.

2. Model and Optimization

For a general imaging task with additive noise the measurement equation reads

$$d=Rs+n,$$

(1)

where d is the observed data, s is the to-be-reconstructed image or signal, R is the signal response mapping the image to the data, and n is an additive noise realization. The response function depends on the particular instrument.

At this point we do not use a response that describes a radio observation. Instead we work on synthetic image data and use $R=\mathbb{1}$. However, we generate this synthetic image data based on real radio observations. In general, signal and image data can have different resolutions, yielding a response that interpolates between the two grids.

We approach this inverse problem as a Bayesian inference problem: we express the posterior distribution $P\left(s\right|d)$, the probability distribution of the signal conditioned on the measured data, in terms of a likelihood $P\left(d\right|s)$ and a prior distribution $P\left(s\right)$ via Bayes’ Theorem

$$P\left(s\right|d)={\displaystyle \frac{P\left(d\right|s\left)P\right(s)}{P\left(d\right)}}.$$

(2)

The evidence $P\left(d\right)$ does not depend on s and acts as a normalization constant. The likelihood contains all information about the measurement process and the noise. It will be discussed in Section 2.3. The prior model encodes all general knowledge and assumptions about the signal before taking the data into account.

2.1. Prior Model

In this work, we consider two main prior models, one for diffuse emission and one for point sources. They are encoded as standardized generative models [17], which map a set of uniformly distributed Gaussian random variables $\left\{\xi \right\}$ to the desired target distribution.

Nearly all continuous quantities, in our case filaments, galaxies, or large-scale background emission, can be described as smooth functions. We model them using Gaussian processes, which assume correlations between nearby pixels. Assuming homogeneity and isotropy allows us to describe the correlation structure as a diagonal matrix in the harmonic domain [18], the power spectrum. As the correlation of a component is not known a priori, we extend our model by including a nonparametric model for this power spectrum and infer it jointly with the Gaussian process. We only assume that the spectrum is falling and a smooth function of the Fourier frequencies. Further details of this correlation model can be found in [19].

Another assumption the model has to fulfill is positivity, since the observed flux in radio astronomy is strictly positive and usually varies over several orders of magnitude. We can achieve this by exponentiating the correlated Gaussian process model, $s_d=exp\left(F_d\left({\xi }_d\right)\right)$, to encode a correlated log-normal distribution.

The correlation model has problems describing point sources, as they are completely different in their behavior. In this work, we aim to predict the exact pixel locations of point sources from previous reconstructions. Moreover, we are able to determine the flux of each detected point source from the previous reconstruction. Thus, we use a lognormal distribution for each identified point source, $s_{p_i}=exp\left(\mathcal{N}({\mu }_i,{\sigma }_i^2)\left({\xi }_{p_i}\right)\right)$, with prior mean ${\mu }_i$ and standard deviation ${\sigma }_i$ derived from the previous image.

2.2. Sky Description

These two models combined allow for generic descriptions of radio skies. However, different diffuse structures might exhibit different correlation properties. For this purpose, we introduce the so-called tiles $t_i$, pointing to specific sub-parts of the signal field. We furthermore add a diffuse background component $s_b$ to catch any unrepresented structure. The full forward model reads

$$s=s_b+\sum _i{s}_{t_i}+\sum _i{s}_{p_i}.$$

(3)

Now, we can express each compact object with its individual correlation structure and, as the tile models can have different resolutions, focus the high resolution on important parts of the emission field without getting computationally too expensive. Since the correlation model is quite flexible, we can utilize it to describe both the background and the tiles by soft adjustments of its hyperparameters.

Again, the different components have to be added together to build the full prior model. Due to the potentially different resolution, there are two possible ways how this can be achieved: First, one can map all components to a full, high-resolution grid, add them together and then apply the response to the full signal s. As a second option, one can apply the response to each component individually and then build the sum of the responses in the data space,

$$Rs=R_b{s}_b+\sum _i{R}_{t_i}{s}_{t_i}+\sum _i{R}_{p_i}{s}_{p_i}.$$

(4)

If the tiles are much higher resolved than the background field; the full signal can become a very large array. Thus, option two is usually faster and more efficient, especially for the computationally expensive radio response.

2.3. Likelihood

With the full signal prior model from above and the respective response function, we can compute the model data using Equation (1). Similarily to [15], we assume independent Gaussian noise. With this, the likelihood becomes a Gaussian, given by

$$P\left(d\right|s,N)=\mathcal{G}(d-Rs,N).$$

(5)

Note that $Rs$ is the response sum we specified in Equation (4). For simplicity, we start with a fixed diagonal noise covariance.

2.4. Posterior Estimation

To actually obtain the individual sub-signals from the data, we need to obtain the posterior distribution $P\left(s\right|d)$ in Equation (2). Since our model is highly nonlinear and high-dimensional, we cannot compute the posterior directly, but we will rather obtain an approximation of it. In this work, we utilize the following two optimization algorithms:

Either we compute the maximum a posteriori (MAP) solution of the signal components by maximizing the joint probability $P(d,s)=P\left(d\right|s\left)P\right(s)$ of the data and the signal. This yields a decent and fast reconstruction of the signals but lacks a reliable uncertainty quantification.

In order to obtain a more accurate approximation of the posterior probability distribution with reliable uncertainty maps, we use geometric variational inference (geoVI), an accurate but also more costly variational inference technique [20]. GeoVI is able to capture non-Gaussian posterior statistics and intercorrelation between the posterior parameters. It outputs a set of posterior samples, from which the mean of the signals and their standard deviation can be computed.

3. Object Identification

Having obtained a reconstruction of the data, we now aim to identify objects within this reconstruction using deep learning. There are two major challenges in this detection task: firstly, the presence of numerous different objects whose exact number is unknown beforehand; and secondly, the need for precise localization of the individual objects, especially of the point sources. To tackle these problems, we use semantic segmentation, which assigns a label to every pixel and thus provides a detailed understanding of the image’s content at the pixel level. In addition, we utilize a clustering algorithm to discriminate between the different identified objects.

3.1. Semantic Segmentation

We aim to distinguish between two basic types of objects: point sources and extended objects. For our predicting network, we choose the U-Net architecture [21], which has emerged as a powerful tool for semantic segmentation tasks. The U-Net is based on CNNs and features an encoder-decoder structure with skip connections, enabling precise localization of features while maintaining spatial details. Applying it to a reconstruction, our network produces two output segmentation maps, indicating whether a pixel represents a point source or not and if it belongs to an extended object or not.

As with all supervised learning tasks, the quality of the prediction depends on the training data. In our case, the training data should be as close as possible to an actual reconstruction. To achieve this, we use random initializations of the log-normal correlation model introduced in Section 2.1 to generate the background field. For each training image, a variable number of point sources is added at random locations to this background. They can be blurred out, as our correlation model cannot perfectly represent point sources. In order to obtain realistic-looking extended objects, we use a part of the RadioGalaxyDataset (https://zenodo.org/records/7692494, accessed on 2 March 2023), which is a collection of several radio catalogs [22,23,24,25,26,27,28,29]. We generate the corresponding segmentation maps containing the locations of the different objects and, finally, train the U-Net on the data images and output maps.

3.2. Clustering

While our neural network directly outputs the locations of the point sources, it only provides one map containing all the extended objects. In order to discriminate between them, we utilize DBSCAN (Density-Based Spatial Clustering of Applications with Noise) [30], which searches for core samples of high density and expands clusters from them. Unlike other clustering algorithms, it does not require the number of clusters as input and works well for data that contains clusters of similar density.

Besides the localization of the extended objects, the clustering has a regulating role. By setting a minimum number of points needed to form a cluster, we avoid that blurred-out point sources are miss-classified as small extended objects.

4. Iterative Method and Application

By combining Section 2 and Section 3, we can construct an iterative method to step-by-step improve the reconstruction of the data. This automatic pipeline can be effectively managed using the snakemake tool [31]. We showcase the general workflow on a simple imaging problem, the reconstruction of the synthetic image data introduced in Section 2. The first two iterations of the pipeline are depicted in Figure 1.

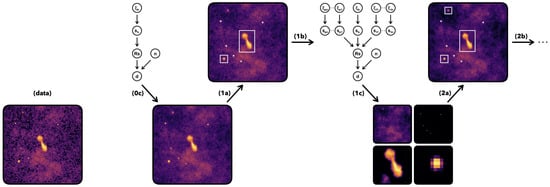
Figure 1. Visualization of the iterative pipeline applied to a simple imaging problem (synthetic, noisy data on the left). Using a single component model (upper left graph), it generates a preliminary reconstruction (0c), in which it identifies point sources and objects (1a), marked with crosses and boxes, respectively. Adding them (represented as side branches) to the existing model (1b) yields separate reconstructions for each component (1c), which are composed into a full sky image, allowing for another object detection in this composite image (2a). This procedure can be repeated for further refinement.

To initiate the process, we load the data and specify the desired resolution as well as the FOV we wish to reconstruct. On the model site, we start with a single component: the background signal. The full forward model is represented by the upper left graph in Figure 1. The employed correlation model should be initialized with wide and flexible hyperparameter priors. Using geoVI, we obtain a preliminary reconstruction of the data, shown in step (0c). The pipeline then iterates over the following steps:

(a)

First, the trained U-Net is utilized to detect objects within this preliminary reconstruction. For the point sources, we determine the position from the output segmentation map and extract the mean and standard deviation for the log-normal prior from the reconstruction. For the extended objects, we use the clustering technique introduced in Section 3.2 to discriminate between the different objects.

(b)

The next step involves writing all predicted components to the model configuration file, which defines the subsequent reconstruction iteration. For each cluster, we determine the FOV and center of this signal component. Furthermore, we can decide how finely the tiles should be resolved compared to the background field. Having specified all the model components, we can start the next reconstruction step.

(c)

Before continuing the optimization on the data, we first fit the new, advanced model on the previous reconstructed image. For this step, it is usually sufficient to use MAP estimation. This transition saves computation time and should ensure that the components get separated properly. The model then serves as a starting point to continue the geoVI optimization with the data. We now obtain one reconstruction for each model component, which we add together to compose an image of the full sky, allowing for object detection in this composite image.

The process can be stopped when the reconstruction does not improve anymore. Alternatively, one can increase the resolution of individual model components to further improve the quality of the overall reconstruction and potentially resolve smaller objects that could not be captured before.

For the imaging problem shown in Figure 1, the pipeline only needs a few iterations to identify all objects and build an improved model. It successfully detects all noticeable point sources and compact objects, allowing for a separate modeling in the next reconstruction step. For further investigation, we compare the initial model (M0) of step (0c) and the advanced, multi-component one (MC) of step (2c) by optimizing them with geoVI until convergence. We plot the reconstructed full sky images in Figure 2, the individual model components of MC in Figure 3, and the corresponding learned power spectra of all diffuse model components in Figure 4. We observe that M0 is already sufficient to achieve a good reconstruction of the data. However, using MC further improves the overall reconstruction and, in particular, the modeling of the point sources and the tile components. The individual components are well separated from each other and from the point sources. Moreover, the plotted power spectra differ significantly; whereas the spectrum of M0 shows many small-scale features, those are captured by the individual tile components and point sources in MC, leading to a smoother and steeper background power spectrum. Furthermore, the spectra of the individual tile components show different correlation properties.

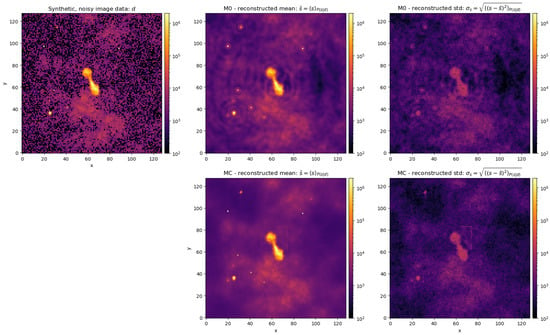
Figure 2. Comparison of the reconstructed full-sky images (mean and standard deviation) between the initial model (M0) and the advanced, multi-component model (MC) of synthetic, noisy image data. The latter improves the overall reconstruction as well as the modeling of the individual components.

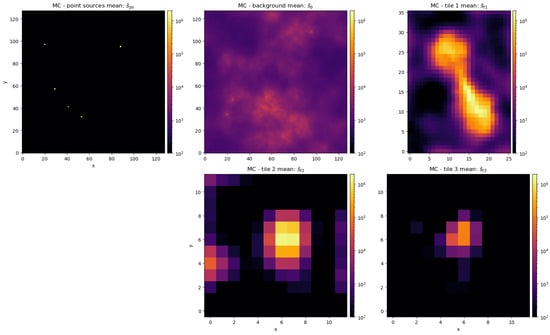
Figure 3. Reconstructed model component images (mean) of the advanced, multi-component model (MC). The individual tile components and the point sources are well separated from each other and from the background, which captures all remaining structures.

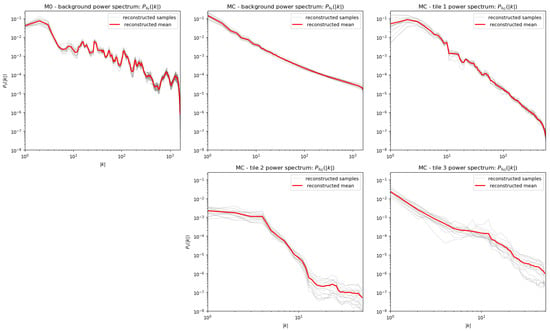
Figure 4. Comparison of the reconstructed power spectra between the initial model (M0) and the advanced, multi-component model (MC). In the latter, the background and the individual tile components exhibit different correlation properties.

We conclude this section with a short comment: Performing a transition from the old model to the new model in step (c) offers several benefits: it ensures that the components are separated properly by first fitting them individually on the corresponding part of the old reconstruction, and we do not need to start the reconstruction from scratch, which saves computation time as we do not have to apply the response function during the transition. This becomes particularly relevant when dealing with radio datasets, where a large fraction of the computing time is spent on evaluating the response.

5. Conclusions

In this work, we presented an automatic pipeline that should improve imaging for wide-field radio observations, which contain various different objects. We introduced the individual parts of this pipeline, namely modeling, optimization, and object detection, as well as separation, and then combined them into an iterative method. To evaluate the method, a simple and generic, yet still sufficiently complex, imaging problem was set up and solved for. Within a few iterations, the pipeline was able to detect and separate all relevant compact objects and point sources from the background. By using individual model components for each object, it successfully improved the overall reconstruction of the data. Detailed plots of the reconstructed sky maps and power spectra showed the benefits of the multi-component model compared to the initial model. It separated point sources from diffuse flux and introduced individual models and power spectra for the compact objects and the background, enabling detailed reconstructions of all components.

This sets the stage for real data applications on various wide-field radio observations. For this step, the simple response function needs to be exchanged with the radio response, leading to a harder and computationally more expensive optimization task. The transitions from the old model to the new model now become particularly relevant to ensure the component separation and save computation time.

Of course, further testing of the method is required; for example, to actually use higher resolutions for the tile components than the background field. This should further improve the reconstructions of extended objects like galaxies. When going to higher resolutions, one also could think of implementing an advanced point source model, which, instead of having fixed locations, can learn the exact locations of the sources in a similar way as the brightness. In total, testing and further developments remain to be conducted; at the same time, the current state of the presented method enables a precise detection of point sources and compact objects followed by a successful component separation during the reconstruction.