Bayesian Regularization for Dynamical System Identification: Additive Noise Models †
Abstract
1. Introduction
2. Theoretical Foundations
3. Application
4. Results
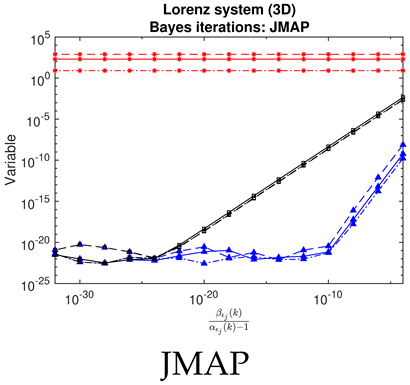
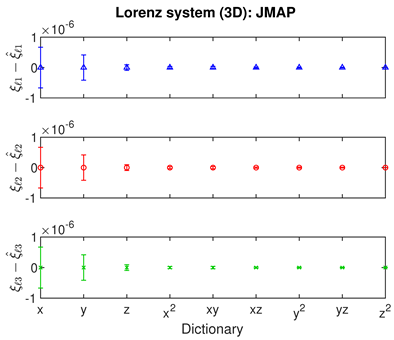
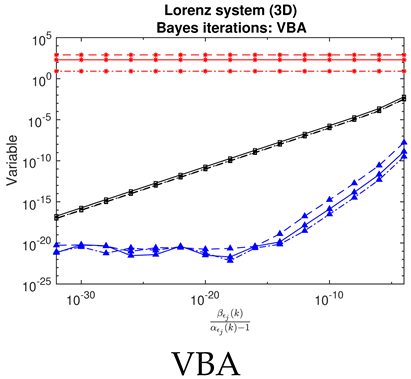
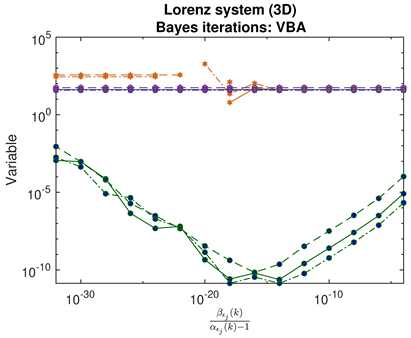
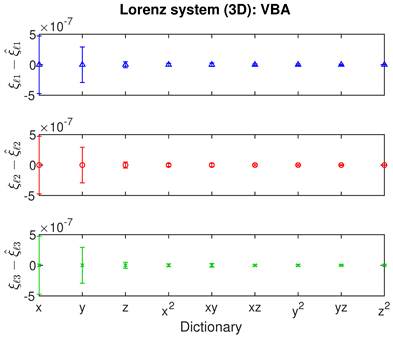
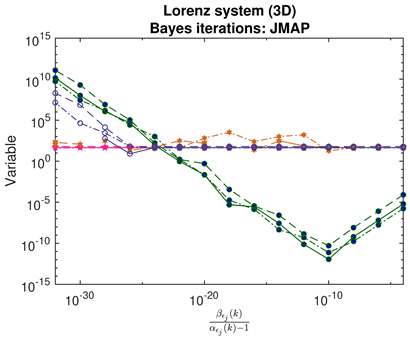
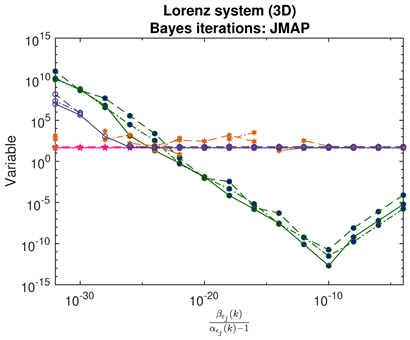
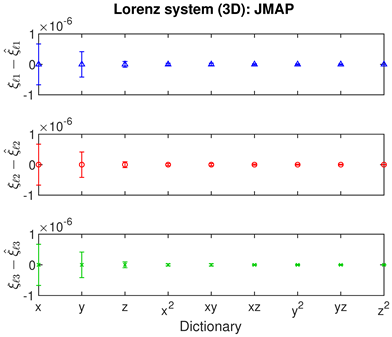
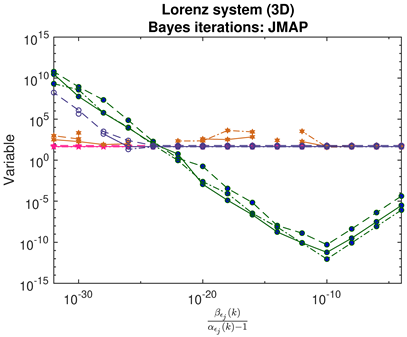
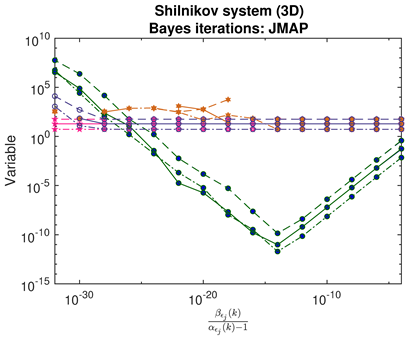
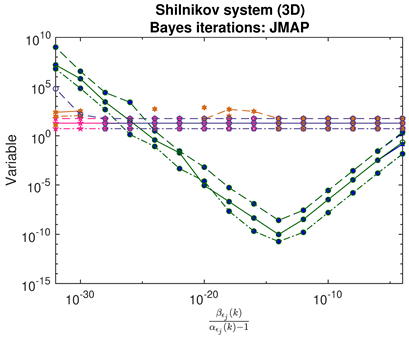
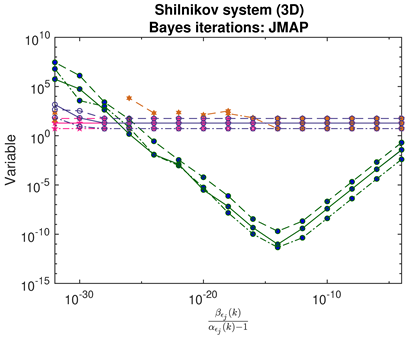
- For JMAP and VBA, the optimum in is identified by a minimum in the posterior Gaussian norm (green curves, column 1 of Table 2; column 2 of Table 3 and Table 4). This optimum corresponds to the maximum in the posterior (14), and is distinct in all examples considered. Both algorithms are fairly efficient in finding the optimum (∼5–10 iterations).
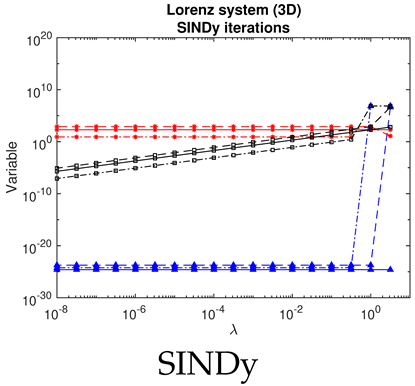
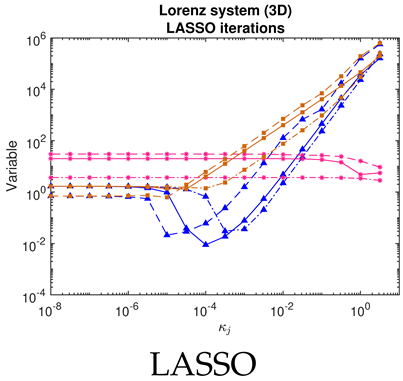
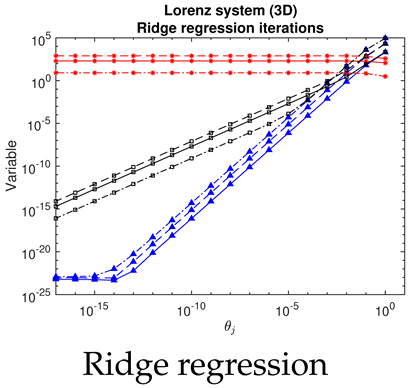
- For SINDy and ridge regression, the optimum in the threshold or regularization parameter is identified by a turning point in the residual (blue curves, column 1 of Table 2). In contrast, for LASSO, the residuals follow strange curves; the optimum is instead identified by a turning point in the objective function (brown curves, column 1 of Table 2). The SINDy method is very efficient (∼4–5 iterations) in finding the optimum, while LASSO and ridge regression require many more iterations.
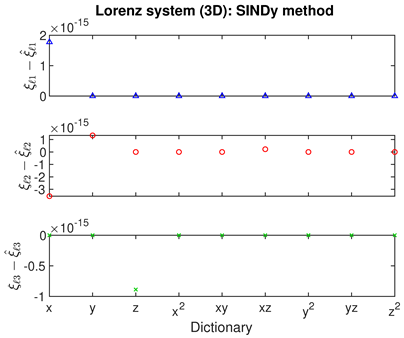
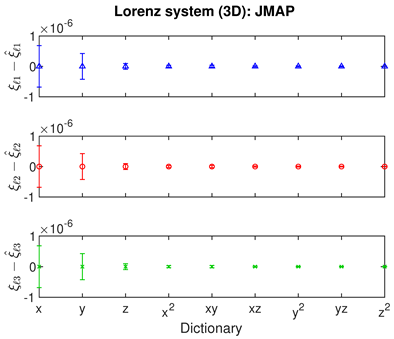
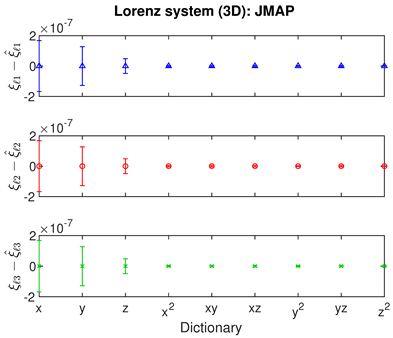
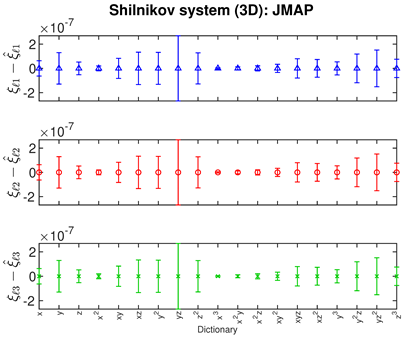
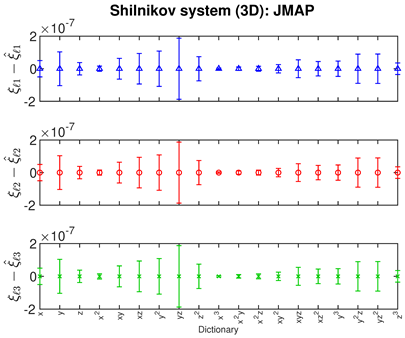
- The Bayesian methods provide standard deviations on the predicted coefficients, extracted from the posterior covariance in (14) (error bars, column 3 of Table 2, Table 3 and Table 4). These are of order ∼– in all examples. In contrast, SINDy and ridge regression report a coefficient precision of ∼–. The inconsistency with JMAP and VBA suggest that this high precision is artificial. LASSO was unsuccessful in all examples examined, with a precision of ∼ and poor recovery of the dynamical system.
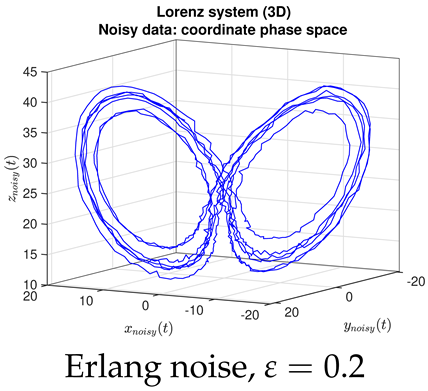
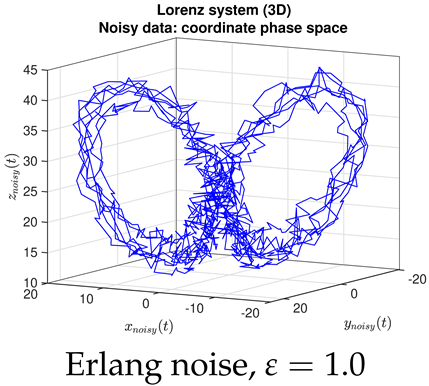
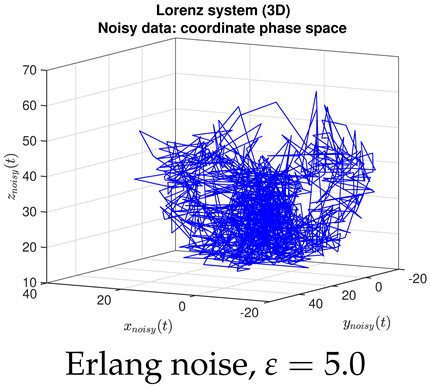
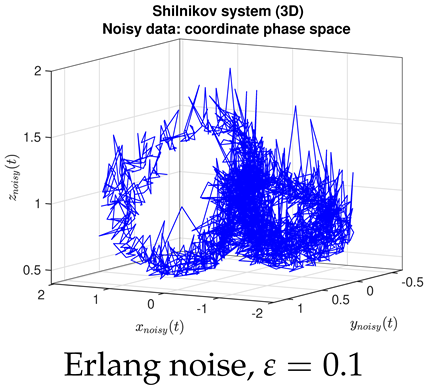
- Contrary to our expectations, JMAP and VBA based on Gaussian noise (13) were highly robust to different choices of additive noise, for all dynamical systems, noise models, and parameter choices examined. Little difference was observed between the symmetric or non-negative noise models, even for such high magnitudes of added noise that the dynamical system becomes overwhelmed by noise (column 1 of Table 2 and Table 3).
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Mangan, N.M.; Kutz, J.N.; Brunton, S.L.; Proctor, J.L. Model selection for dynamical systems via sparse regression and information criteria. Proc. R. Soc. Proc. A 2017, 473, 20170009. [Google Scholar] [CrossRef] [PubMed]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef] [PubMed]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Santosa, F.; Symes, W.W. Linear inversion of band-limited reflection seismograms. SIAM J. Sci. Stat. Comput. 1986, 7, 1307–1330. [Google Scholar] [CrossRef]
- Mohammad-Djafari, A. Inverse problems in signal and image processing and Bayesian inference framework: From basic to advanced Bayesian computation. In Proceedings of the Scube Seminar, L2S, CentraleSupelec, Gif-sur-Yvette, France, 27 March 2015. [Google Scholar]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Mohammad-Djafari, A.; Dumitru, M. Bayesian sparse solutions to linear inverse problems with non-stationary noise with Student-t priors. Digit. Signal Proc. 2015, 47, 128–156. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Shil’nikov, A.L.; Shil’nikov, L.P.; Turaev, D.V. Normal forms and Lorenz attractors. Int. J. Bifurc. Chaos 1993, 3, 1123–1139. [Google Scholar] [CrossRef]
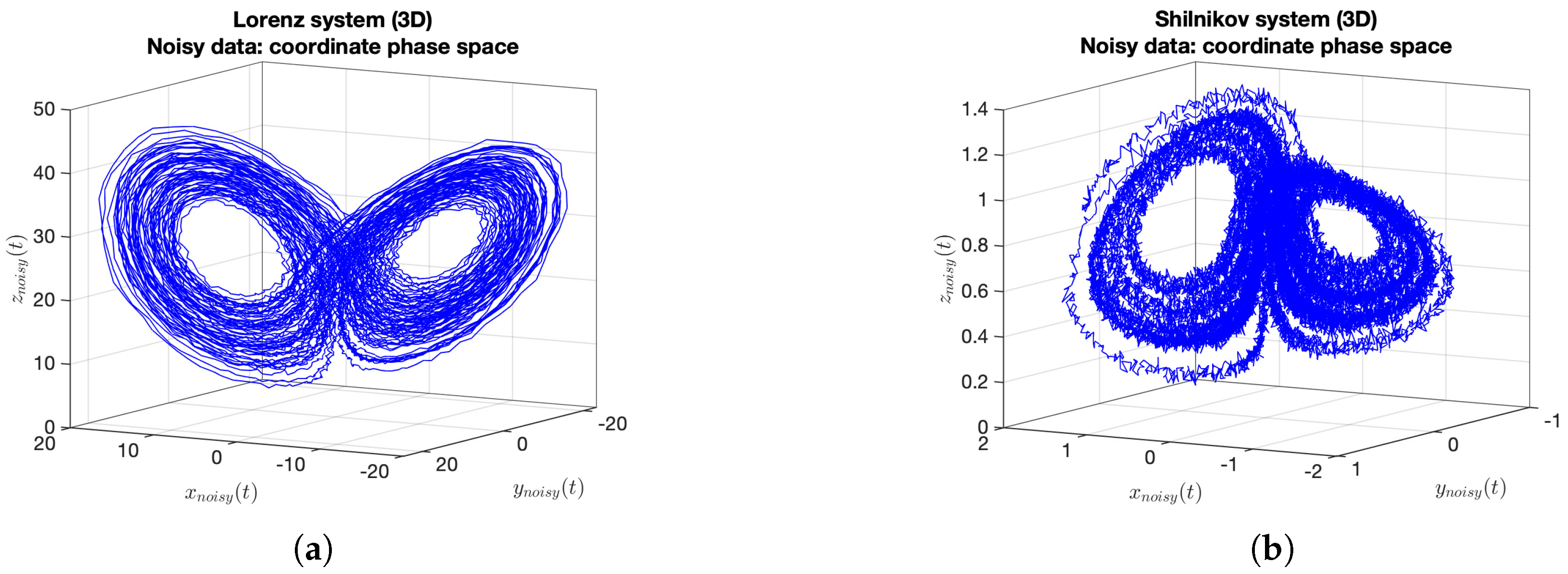
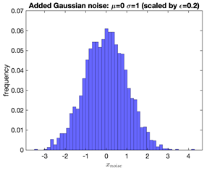 | 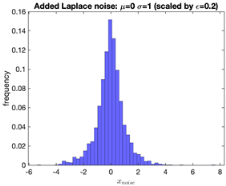 |  | 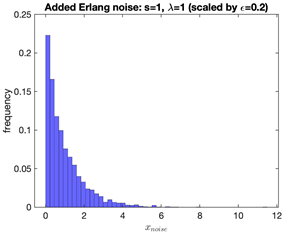 |
| Gaussian noise | Laplace noise | Rayleigh noise | Erlang noise |
| for | for | ||
| mean , standard deviation | mean , scale | scale | shape s, rate |
| 2-Norm Plots | Gaussian Norm Plots | Coefficient Plots |
|---|---|---|
 |  |  |
 | Not applicable | 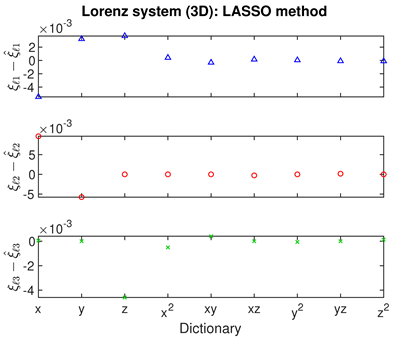 |
 | Not applicable | 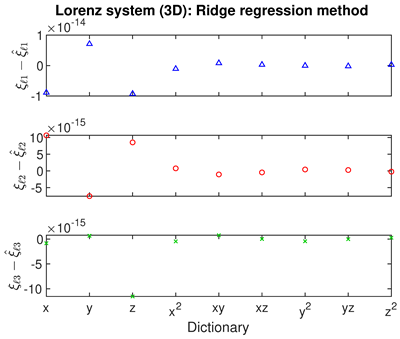 |
 |  |  |
 |  |  |
| Phase Plots | Gaussian Norm Plots | Coefficient Plots |
|---|---|---|
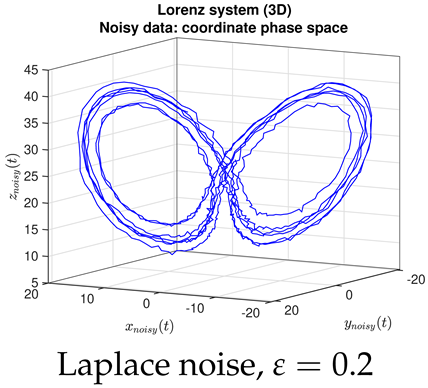 | 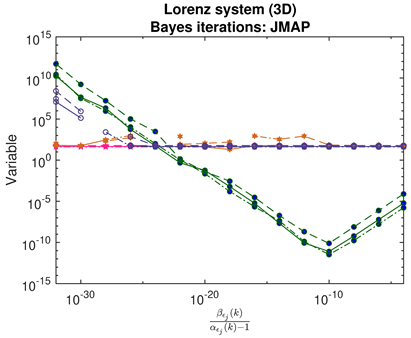 | 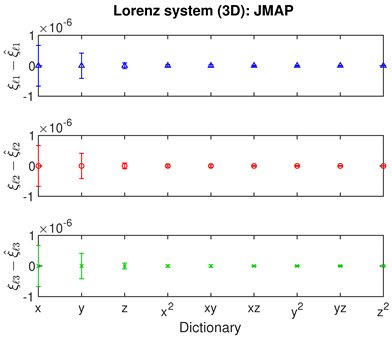 |
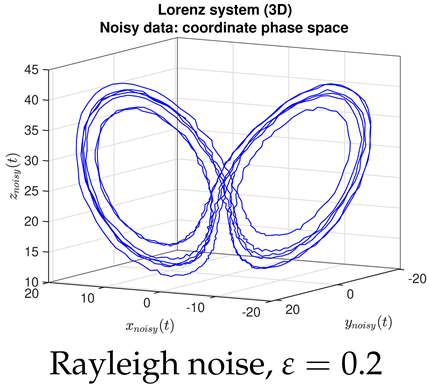 |  |  |
 |  |  |
 |  |  |
 |  |  |
| Phase Plots | Gaussian Norm Plots | Coefficient Plots |
|---|---|---|
 |  |  |
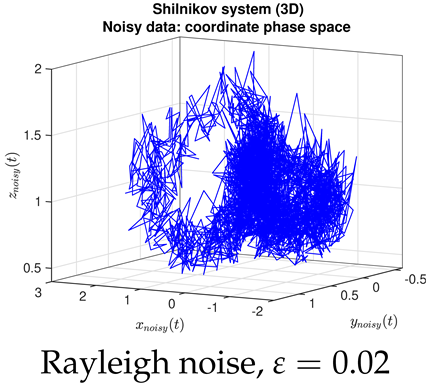 | 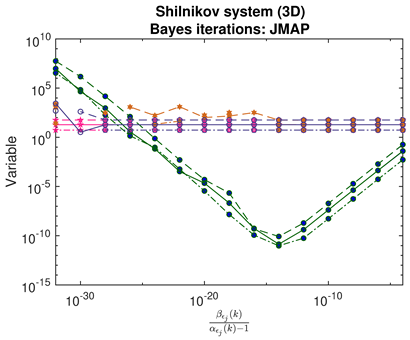 | 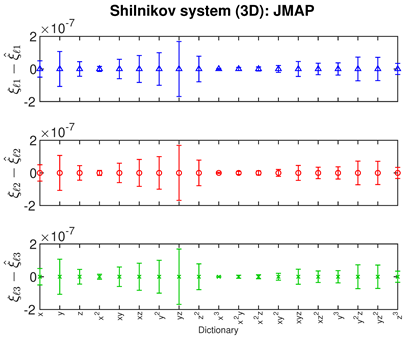 |
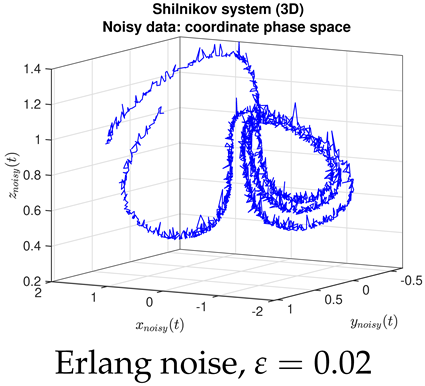 |  |  |
 |  |  |
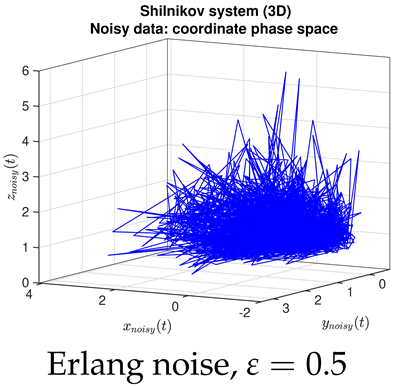 | 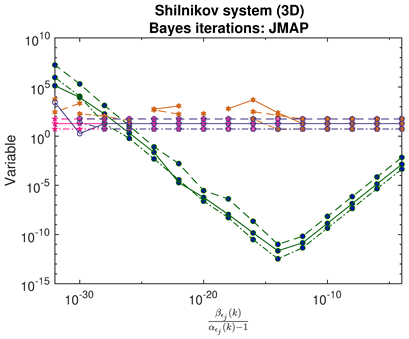 | 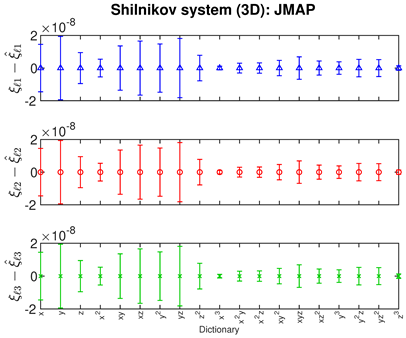 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niven, R.K.; Cordier, L.; Mohammad-Djafari, A.; Abel, M.; Quade, M. Bayesian Regularization for Dynamical System Identification: Additive Noise Models. Phys. Sci. Forum 2025, 12, 17. https://doi.org/10.3390/psf2025012017
Niven RK, Cordier L, Mohammad-Djafari A, Abel M, Quade M. Bayesian Regularization for Dynamical System Identification: Additive Noise Models. Physical Sciences Forum. 2025; 12(1):17. https://doi.org/10.3390/psf2025012017
Chicago/Turabian StyleNiven, Robert K., Laurent Cordier, Ali Mohammad-Djafari, Markus Abel, and Markus Quade. 2025. "Bayesian Regularization for Dynamical System Identification: Additive Noise Models" Physical Sciences Forum 12, no. 1: 17. https://doi.org/10.3390/psf2025012017
APA StyleNiven, R. K., Cordier, L., Mohammad-Djafari, A., Abel, M., & Quade, M. (2025). Bayesian Regularization for Dynamical System Identification: Additive Noise Models. Physical Sciences Forum, 12(1), 17. https://doi.org/10.3390/psf2025012017





