Detecting Homoclinic Points in Nonlinear Discrete Dynamical Systems via Resurgent Analysis

Abstract

We present a novel and completely deterministic method to model chaotic orbits in nonlinear discrete dynamics, taking the quadratic map as an example. This method is based on the resurgent analysis developed by Écalle to perform the resummation of divergent power series given by asymptotic expansions in linear differential equations with variable coefficients. To determine the long-term behavior of the dynamics, we calculate the zeros of a function representing the unstable manifold of the system using Newton’s method. The asymptotic expansion of the function is expressed as a kind of negative power series, which enables the computation with high accuracy. By use of the obtained zeros, we visualize the set of homoclinic points. This set corresponds to the Julia set in one-dimensional complex dynamical systems. The presented method is easily extendable to two-dimensional nonlinear dynamical systems such as Hénon maps.

1. Introduction

In 1890, Poincaré proved that the three-body problem in celestial mechanics is non-integrable and the solution cannot be described by any existent function [1]. He introduced a geometrical concept called homoclinic points for the proof and showed that, if a dynamical system has one (transverse) homoclinic point, then an infinite number of homoclinic points exist in the system. Mathematically, homoclinic points are represented as intersections of the stable and unstable manifolds emerging from fixed or periodic points in a given dynamics [2]. The set of homoclinic points is a geometrical representation of chaos that yields a corresponding configuration in the phase space, which possesses a fractal structure [3,4]. If one can detect the set of homoclinic points, all the quantities of a given dynamical system such as the entropy, Hausdorff (fractal) dimension, Lyapunov exponent, etc., can be obtained whenever the dimension of the phase space is less than three.

Following the discovery of homoclinic points by Poincaré, the ergodic theory was developed by Birkhoff, von Neumann, and Sinai et al. [5,6,7], which is also a geometrical construct. Smale, Ruelle, and Bowen formulated a stochastic analysis technique for chaos, which is based on a geometrical representation [8,9,10]. Barreira and Pesin proved that an abstract concept known as Kolmogorov–Sinai entropy is equivalent to the Lyapunov exponent in chaotic regions, and connected this purely mathematical concept to the corresponding physical quantity [11]. Recently, Koda, Hanada, and Shudo provided the relationship between Kolmogorov–Sinai entropy on Julia sets of polynomial maps and quantum tunneling [12]. These studies are all essentially stochastic and were constructed under the assumption that the integral manifold does not exist, as this characteristic indicates the appearance of chaos. To date, the deterministic approach to chaos has involved the time-series analysis technique only [13,14]; however, this approach is suitable for short-term analysis only, and the accuracy of the time-series analysis deteriorates significantly for long-term calculations.

In contrast to the time-series analysis, the set of homoclinic points involves every event extending from the past to the future in a dynamical system, and therefore, one can calculate chaotic trajectories deterministically provided that all homoclinic points are found. The sea of chaos following the collapse of the KAM torus is a well-known and typical example of the set of homoclinic points [15,16]. Usually, homoclinic points are obtained by perturbing the integrable Hamiltonian systems such that the stable manifold coincides with the unstable one. Detection of homoclinic points has been performed only by qualitative methods as Melnikov integral [15,16]. This method is effective to show the existence of homoclinic points mathematically; however, it is unsuitable for numerical computations and inapplicable to physics.

Tovbis was the first to estimate quantitatively a homoclinic point [17]. He succeeded in calculating the splitting angle between the stable and unstable manifolds in the Hénon map for the case in which the system becomes the Hamiltonian system and showed the transversality at a homoclinic point numerically by using the Borel–Laplace transform. In the same dynamical system, Gelfreich and Sauzin have found a homoclinic point with higher accuracy than that given by Tovbis [18] using the resurgent analysis [19,20,21]. Anastassiou, Bountis, and Bäcker [22] calculated a few homoclinic points using the classical linearizing function presented by Poincaré [23,24,25,26]. This linearizing function is given by the Taylor expansion around a fixed point, and the accuracy rapidly deteriorates when we consider points far from the fixed point. Therefore, it is not suitable for quantitative calculations.

Biham and Wenzel proposed a computational method for unstable periodic orbits with long period [27,28]. Their method has enabled the detection of a large number of unstable periodic points, opening up a research field for the quantitative study of chaotic dynamical systems, such as Hénon maps, since the 1990s [29,30,31]. Note that the sets of periodic points and homoclinic points are mutually disjoint. We emphasize that the set of homoclinic points is a purely mathematical concept that provides all three elements of chaos from the qualitative viewpoint: sensitive dependence on initial conditions, regularity provided by periodic points, and indecomposability [3]. Therefore, the difficulty in detecting homoclinic points is not surprising. The purpose of this paper is not to detect periodic points, but to propose a method for detecting homoclinic points, which overcomes this difficulty and opens up a new field of research for the quantitative study of chaotic dynamical systems.

Here, we present a method for calculating homoclinic points in a dynamical system, using an analytic function that represents the stable and unstable manifolds of the system and taking a quadratic map as an example. The method adopted here, which is an extension of the resurgent analysis described above, is mathematically rigorous, and no approximation is required. We also provide a numerical scheme that permits visualization of the set of homoclinic points, so that it can be treated as an ordinary function. The set of obtained points represents the solution to a non-integrable system and corresponds to an integral manifold in integrable systems. Identification of the set of homoclinic points indicates that every event extending from the past into future can be determined. If one can calculate all homoclinic points concretely, it becomes possible to model chaos and to make long-term predictions. In one-dimensional dynamical systems, the closure of the set of homoclinic points coincides with the Julia set [32], where the trajectories of dynamical systems are chaotic [33,34,35,36]. We verify this fact by an experimental mathematical approach (multiple-precision calculation) and discuss the extensibility to higher-dimensional dynamical systems where the configuration of homoclinic points is unknown.

In the current study, Newton’s method is used for the computation of homoclinic points, in which we need to converge Newton’s method for a function $x\left(t\right)$ with extremely large absolute values (refer to Section 4 and Section 5). The convergence of the conventional Newton’s method for this function is very poor, and the method does not work well in calculating the roots of $x\left(t\right)=0$. We present a new geometrical acceleration method in Newton’s method, which is effective for functions whose convergence is extremely slow (refer to Section 4).

This paper is organized as follows. In Section 2, we introduce the difference equation derived from the quadratic map and present the solution to the difference equation in an asymptotic expansion form. This solution can describe the unstable manifold of the quadratic map. In Section 3, we estimate the number of zeros of the function adopted to capture the homoclinic points. In Section 4, we present an algorithm for the detection of zeros of the function describing the unstable manifold. Numerical results, including error estimates for the distribution of the zeros and the configuration of the set of homoclinic points, are provided in Section 5. Section 6 is devoted to concluding remarks.

2. Basic Concepts of Homoclinic Points and Governing Equations

We consider a state $x=x\left(t\right)$ that is parameterized by a parameter t ($t\in \mathbb{C}$) and denote the stable and unstable manifolds as $x=x_s$ and $x=x_u$, respectively [23,24,25]. Then, the set of homoclinic points, which is the intersection of $x=x_s$ and $x=x_u$, is generally represented by the equation

$$x_s\left(t_s\right)-x_u\left(t_u\right)=0,$$

where $t=t_s$ and $t=t_u$ are complex parameters parameterizing $x=x_s$ and $x=x_u$, respectively. When the system is one-dimensional, $x_s\left(t_s\right)=0$ and, therefore, the above equation is reduced to

$$x_u\left(t_u\right)=0,$$

which indicates that, in order to obtain the set of homoclinic points, the zeros of $x_u$ must be calculated. From now on, we drop the subscript u in $x_u\left(t_u\right)$.

We now introduce a nonlinear map f that describes a physical phenomenon, and consider a transform such that the n-th iteration ($n\ge 0$, $n\in \mathbb{Z}$) of f is given by a shift in the t plane [37]:

$$\begin{array}{c}\hfill f^n\circ x\left(t\right)=x(t+n),\end{array}$$

(1)

where $f\left(x\right)$ is assumed to be a polynomial for x. We emphasize that time evolution as a dynamical system is described by n, which is related to the parameter t through relation (1).

As a prototype of chaotic dynamical systems, we adopt the quadratic map

$$\begin{array}{c}\hfill f\circ x\left(t\right)=1-ax{\left(t\right)}^2,\end{array}$$

(2)

where a is a dynamical parameter. One of the (hyperbolic) fixed points

$$x_f={\displaystyle \frac{-1+\sqrt{1+4a}}{2a}}$$

is shifted to the origin according to $x\mapsto x+x_f$, and the quadratic map is then given by

$$\begin{array}{c}\hfill f\circ x\left(t\right)=-2a{x}_{f}x\left(t\right)-ax{\left(t\right)}^2.\end{array}$$

(3)

From (1) and (3), we obtain the difference equation

$$\begin{array}{c}\hfill x(t+1)=-2a{x}_{f}x\left(t\right)-a{\left[x\left(t\right)\right]}^2.\end{array}$$

(4)

By performing the Laplace transform of $x\left(t\right)$, which is based on the resurgent analysis [18,19,20,21], we obtain the following asymptotic expansion representation as a global solution to Equation (4) [37,38]:

$$\begin{array}{c}\hfill x\left(t\right)=\sum _{N=1}^{\infty }{\displaystyle \frac{b_N(N-1),{\mathrm{e}}^{N{\zeta }_{1}t}}{{(t+n_0)}^N}}\left[1+O\left(\right|t+n_0{|}^{-1})\right],\end{array}$$

(5)

where $n_0$, a large positive integer, is an artificial parameter used to increase the accuracy of the asymptotic expansion, ${\zeta }_1=ln\left|\alpha \right|-\pi i$, $\alpha$ ($\alpha \ne 0$) is the eigenvalue of the map that satisfies $\left|\alpha \right|>1$ (hyperbolic, $\alpha <0$ here), i is the imaginary unit, and the coefficient $b_N$ satisfies the recurrence formula

$$\begin{array}{c}\hfill b_N=-{\displaystyle \frac{2a}{D_N}}\sum _{k=1}^{N-1}\sum _{r=0}^{N-k-1}{b}_k{b}_{N-k}{\displaystyle \frac{(N-k-1)!{(-1)}^r{\left(k/N\right)}^{k+r}}{(N-k-1-r)!r!(k+r)}},\end{array}$$

(6)

in which $D_N={\alpha }^N+2a{x}_f$ and the initial value $b_1$ is selected as $b_1=x_f/2$. Here, the coefficient $b_N$ is estimated as [38]

$$|b_N|\le {\displaystyle \frac{C^N{\left|\alpha \right|}^{-NlogN}}{N!}}$$

for $\left|\alpha \right|>1$, where $C>1$ is a constant. This estimate guarantees the suppression of divergence of the factor ${\mathrm{e}}^{N{\zeta }_{1}t}(N-1)!$ for $\Re \left({\zeta }_{1}t\right)>0$ in (5).

Since the function $x\left(t\right)$ in (5) is represented by an asymptotic expansion, it describes the stable and unstable manifolds realized at $t=\pm \infty$ very accurately [38]. The value $t=-n_0$ in (5) is merely a cosmetic singularity, and it is possible to expand $x\left(t\right)$ for any value of t ($t\in \mathbb{C}$). The asymptotic expansion (5) can describe various dynamical quantities in nonlinear systems very precisely [37,39]. Further, expansion (5) is a mathematically rigorous solution to the difference Equation (4), and no approximation is applied to derive the former expression [38]. The only equation used to calculate the set of homoclinic points is (5), which incorporates the deterministic coefficient given in (6). We calculate the set of homoclinic points as zeros of the function $x\left(t\right)$ as accurately as possible and visualize the results via a computational representation. In the following, we set the positive integer $n_0={10}^5$ and drop the higher order term of $O\left(|t+n_0{|}^{-(N+1)}\right)$ from (5).

3. Distribution of Zeros in the Complex Plane

The equation $f\circ x\left(t\right)=0$ in (3) [or (2)] has two roots corresponding to simple zeros, from which we see that the zeros of $f^n\circ x\left(t\right)=x(t+n)=0$ are given by $2^n$ points

$$\begin{array}{c}\hfill x=x_1,x_2,\cdots ,x_{2^n}.\end{array}$$

(7)

When $\left|t\right|$ is large, the function $x\left(t\right)$ oscillates very rapidly [37], which provides as many zeros as the number of oscillations. We estimate the values of t that provide these zeros.

Theorem 1. 

Let $J\left(f\right)$ be the Julia set of the nonlinear map f. Then, there exists some constant $M>0$ ($M\in \mathbb{R}$) such that

$$\begin{array}{c}\hfill \left\{x\right(t\left)\right||\Re (t\left)\right|,|\Im (t\left)\right|\le M\}\supset J(f)\end{array}$$

(8)

holds.

Proof. 

The Julia set $J\left(f\right)$ is an infinite set and therefore, there exists some constant $t_0\in \mathbb{C}$ such that $x\left(t_0\right)\in J\left(f\right)$ holds. Let U be an open neighborhood of $t_0$. Then, $x\left(U\right)$ is an open set intersecting $J\left(f\right)$ and there exists $n\in \mathbb{N}$ such that $f^n\left(x\left(U\right)\right)\supset J\left(f\right)$ holds [32,35]. Since $f^n\circ x\left(t\right)=x(t+n)$, we have

$$\begin{array}{c}\hfill x(U+n)\supset J\left(f\right).\end{array}$$

(9)

Choose $M>0$ such that

$$U+n\subset \{t\in \mathbb{C}\mid |\Re \left(t\right)|,|\Im \left(t\right)|\le M\}.$$

Then, the theorem is obtained.

□

For $M>0$ and $n\ge 0$ ($n\in \mathbb{Z}$), we define

$$\begin{array}{ccc}\hfill B(n,M)& =& \{t\in \mathbb{C}\mid |\Re (t-n)|,|\Im (t-n)|\le M\},\hfill \\ \hfill z(n,M)& =& \{t\in B(n,M)\mid x(t)=0\}.\hfill \end{array}$$

Let ♯ denote the cardinality. For the number of zeros of $x\left(t\right)$, the following theorem holds.

Theorem 2.

There exists a constant $M>0$ such that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\displaystyle \frac{1}{n}}log♯z(n,M)=log2\end{array}$$

(10)

holds.

Proof. 

Let M be as in Theorem 1. Since 0 is an expanding fixed point of f, we have $0\in J\left(f\right)$. Note that the Julia set $J\left(f\right)$ is completely invariant under f; i.e.,

$$f\left(J\left(f\right)\right)=f^{-1}\left(J\left(f\right)\right)=J\left(f\right).$$

As $f^{-n}\left(J\left(f\right)\right)=J\left(f\right)$, we have $x_1^n,x_2^n,\cdots x_{2^n}^n$ such that

$$f^{-n}\left(0\right)=\{x_1^n,x_2^n,\cdots x_{2^n}^n\}\subset J\left(f\right).$$

From Theorem 1, there exist $t_1^n,t_2^n,\cdots t_{2^n}^n$$\in B(0,M)$ such that

$$x\left(t_i^n\right)=x_i^n(i=1,2,\cdots 2^n),$$

which satisfy

$$\begin{array}{c}\hfill f^n\circ x\left(t_i^n\right)=x(t_i^n+n)=0.\end{array}$$

Therefore,

$$t_i^n+n\in z(n,M).$$

The multiple root $x_i^n=a{x}_f^2$ [refer to (17)] occurs at most once in $i=1,2,\cdots 2^n$ and all n. Then, the number of roots $2^n$ reduces to at most $2^{n-1}$. Therefore,

$$\begin{array}{c}\hfill ♯z(n,M)\ge 2^n-2^{n-1}.\end{array}$$

(11)

The number of $t_i^n$ that satisfies $x\left(t_i^n\right)=x_i^n$ is at most $p\in \mathbb{N}$ for a fixed M when t is restricted on $B(0,M)$. Thus, we obtain

$$\begin{array}{c}\hfill ♯z(n,M)\le p{2}^n.\end{array}$$

(12)

From (11) and (12), the theorem is obtained. □

In the current study, we detect these zeros with the assistance of a computer.

Remark 1.

The number of zeros in well-known classical entire functions that appear as solutions to the linearization of nonlinear maps [22,23,24,25,26] is usually of polynomial growth. Therefore, detecting the roots in the complex t-plane is not easy. On the other hand, the number of zeros of the function x(t) represented by (5) exponentially increases with n as found in (12). The fact that the number of zeros is of exponential growth enables us to compute homoclinic points.

4. Properties of the Adopted Function and Algorithm for Computations

By Theorem 2, we see that the number of zeros of $x\left(t\right)$, which provides the homoclinic points, increases with exponential order as the increase in $\Re \left(t\right)$ in the complex t plane, and the more of these zeros we calculate, the better we can approximate the true Julia set. In this section, we detect the zeros of $x\left(t\right)$ using Newton’s method accompanied by a geometric acceleration method.

As stated in Theorem 2, the number of zeros increases as $\Re \left(t\right)$ becomes large. Therefore, it is desirable to select the value of $\Re \left(t\right)$ as large as possible to capture more homoclinic points. However, almost all values of $\left|x\right(t\left)\right|$ for $\Re \left(t\right)\gg 1$ are extremely large [$\sim O\left({10}^{1000}\right)$ for selected t [refer to Figure 1a], while the ratio between $\left|x\right(t\left)\right|$ and its derivative $d\left|x\right(t\left)\right|/dt$; $|x\left(t\right)/x^{\prime }\left(t\right)\left|\right)$, is exponentially small [refer to Figure 1b]. This indicates that the value of t hardly moves and the convergence of Newton’s method [refer to Equation (13)] is extremely slow. Therefore, it is difficult to capture the homoclinic points (zeros of $x\left(t\right)$) only by the conventional Newton’s method. We show this in Section 4.1. In Section 4.2, we present an acceleration scheme to converge Newton’s method in the fewest times as possible.

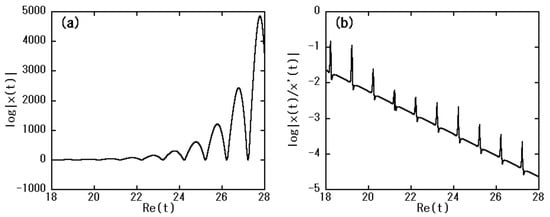
Figure 1. (a) The initial amplitude of $x\left(t\right)$ and (b) the ratio $\left|x\left(t\right)\right|/|x^{\prime }\left(t\right)|$ plotted by log (${\log }_{10}$) scale, where the horizontal axis denotes the real part of t and we select a as $a=1.9408$. Here, the imaginary part of t is fixed as $\Im \left(t\right)=1$.

4.1. Initial Values for Newton’s Method

In this subsection, we estimate the initial magnitude of the function $x\left(t\right)$ and the number of initial zeros prior to implementing Newton’s method. The roots of

$$x\left(t\right)=0,\left(t\in \mathbb{C}\right)$$

are calculated by using Newton’s method:

$$\begin{array}{c}\hfill t_{k+1}=t_k-{\displaystyle \frac{x\left(t_k\right)}{x^{\prime }\left(t_k\right)}},\end{array}$$

(13)

where $t_k\in \mathbb{C}$ ($k=1,2,\cdots$) is the discretized variable of t and the prime denotes the differentiation with respect to t. Since $x\left(t\right)$ is Laplace transformable (and hence $x^{\prime }\left(t\right)$ is also Laplace transformable), it is guaranteed that the growth at $t=\infty$ is at most exponential order [40].

We show the properties of the function $x\left(t\right)$ in Figure 1 to which Newton’s method is applied. The parameter range $18\le \Re \left(t\right)\le 28$ is selected based on the computations of the topological entropy and Lyapunov exponent for the quadratic map (4) [37]. In Figure 1a, we numerically show an example of the initial amplitude of $x\left(t\right)$ before implementing Newton’s method, where we select the dynamical parameter a as $a=1.9408$. This parameter value is located at the left edge of the window in Figure 2.

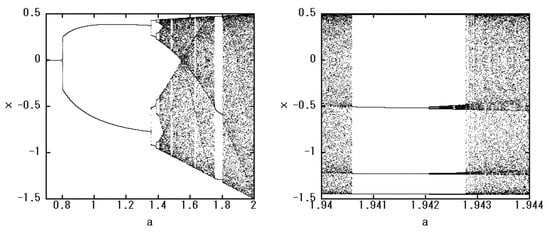
Figure 2. Bifurcation diagrams of the quadratic map (3), where the right figure enlarges the parameter region $1.940\le a\le 1.944$ in the left figure. The value of x moves in the range $-1.5\le x\le 0.5$ in our normalization.

The magnitude of the ratio $|x\left(t\right)/x^{\prime }\left(t\right)|$ on the right hand side of (13) is shown in Figure 1b. Using (1), we have

$$\begin{array}{c}\hfill [f^{\prime }\circ x\left(t\right)]x^{\prime }\left(t\right)=x^{\prime }(t+1).\end{array}$$

(14)

Figure 1a denotes that the difference between $\left|x\right(t_{k+1}\left)\right|$ and $\left|x\right(t_k\left)\right|$ is extremely large (e.g., more than ${10}^{10}$) when $\Re \left(t_k\right)$ is large. From this figure, we can estimate the growth of $x\left(t\right)$ as

$$\begin{array}{c}\hfill \left|x\left(t\right)\right|\sim {10}^{c_0\left|t\right|}(c_0>0,c_0\in \mathbb{R}).\end{array}$$

(15)

From (3), (14), and (15), we can estimate the ratio $|x\left(t\right)/x^{\prime }\left(t\right)|$ as

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{x\left(t\right)}{x^{\prime }\left(t\right)}}\right|\sim \left|{\displaystyle \frac{x^{\prime }(t+1)}{{\left[x^{\prime }\left(t\right)\right]}^2}}\right|\sim c_1{10}^{-c_2\left|t\right|},\end{array}$$

(16)

for some constants $c_1>0$ and $c_2>0$. Figure 1b supports this estimate. Estimate (16) shows that $|t_{k+1}-t_k|=O\left({10}^{-4}\right)$ holds for the distance $|t_{k+1}-t_k|$ in (13) when $26\le \Re \left(t\right)\le 28$, while $\left|x\left(t\right)\right|=O\left({10}^{1000}\right)$ [refer to Figure 1a]. This fact remarkably deteriorates the convergence of Newton’s method. In the neighborhood of cusps in Figure 1b where the derivative $|x^{\prime }\left(t\right)|$ is very small compared to $\left|x\right(t\left)\right|$, the difference $|t_{k+1}-t_k|$ in (13) is relatively large. The candidates of first zeros (“seeds”, refer to Section 4.2) appear after a few implementations of Newton’s method.

From the fact that the value of $log\left|x\right(t\left)\right|$ in Figure 1a and $log|x\left(t\right)/x^{\prime }\left(t\right)|$ in Figure 1b are finite, we find that there is no zero in $x\left(t\right)$ before the implementations of Newton’s method. There exist various acceleration methods in the conventional Newton’s method, such as the Aitken acceleration [41] to speed up the convergence; however, these methods can only apply to the case that $|x\left(t_k\right)/x^{\prime }\left(t_k\right)|$ in (13) is not so small and of polynomial order with respect to t [42]. They do not work for extremely small values of $|x\left(t_k\right)/x^{\prime }\left(t_k\right)|$ as represented by Figure 1. Therefore, another way is required to accelerate the convergence of Newton’s method in the current study. We present the method in the next subsection.

4.2. Algorithm for Detecting Zeros

The set of homoclinic points is the set of points that are at the fixed point at $t=-\infty$ (distant past) and that return to the fixed point at $t=\infty$ (distant future). The behavior of $x\left(t\right)$ given by (5) is violent for $\left|t\right|\gg 1$ (distant future), where a large number of zeros exist [37]. We define the parameter corresponding to the distant future as $t=t_r+i{t}_i$ ($27\le t_r\le 28$), where the imaginary part $t_i$ is selected appropriately depending on the value of a. As regards the value of $t_r$, the larger the better, as described in the previous subsection. Here, we select $27\le t_r\le 28$ in consideration of Figure 1 and referring to the previous computations for the entropy and Lyapunov exponent [37]. The range $27\le t_r\le 28$, where we detect the zeros of $x\left(t\right)$, is purely the limit of our computation, and that is not the mathematical one. In order to find the zeros of $x\left(t\right)$, we adopt Newton’s method with a certain geometrical acceleration. Generally, the values of $\left|x\right(t\left)\right|$ are very large when $t_i>0$, and the typical values of $\left|x\right(t\left)\right|$ calculated here are within $\left|x\left(t\right)\right|>O\left({10}^{100}\right)\sim O\left({10}^{5000}\right)$ for almost all a $(\ge 1.0)$. The conventional Newton’s method and the typically applied double-precision calculation do not work in determining the zeros for such large values of $x\left(t\right)$. In this subsection, we present an acceleration scheme to converge Newton’s method for a function such that its absolute value is very large and the difference $|t_{k+1}-t_k|$ in (13) is exponentially small.

The following acceleration method (processes 3–7 in the algorithm) enables a significant reduction in the number of implementations in Newton’s method. Using this method, typical initial values of $\left|x\left(t\right)\right|=O\left({10}^{100}\right)-O\left({10}^{5000}\right)$ can be converged to $\left|x\left(t\right)\right|<O\left({10}^{-22}\right)$ after a few dozen iterations. The algorithm to find the zeros of $x\left(t\right)$ is as follows.

• Calculate the coefficient $b_N$ given by (6) in advance. Set the upper limit N in (6) as $N=300$ in consideration of the CPU time.
• Divide the region $t=t_r+i{t}_i$ ($27\le t_r\le 28$, $t_i$, fixed) into $1/K_0$ ($K_0>0$ an integer) parts and calculate the value of $x\left(t\right)$ for each t. The initial number of partitions $K_0$ is selected so that it almost coincides with the number of oscillations of $x\left(t\right)$ in the $27\le t_r\le 28$ region, where the number of oscillations corresponds to the zeros of $x\left(t\right)$. Here, we set $K_0$ to e.g., $K_0=2000$. For $x\left(t\right)$, we implement Newton’s method once only for each t.
• Set the initial values before and after Newton’s method is implemented once as $t=t_0\left(k\right)$ and $t=t_1\left(k\right)$ ($k=1,2,\cdots K$), respectively. During Newton’s method calculation, we remove the values of t such that they satisfy $|x\left(t_1\right)|>|x\left(t_0\right)|$. Therefore, the value of K (the number of partitions after the implementation of Newton’s method) is always smaller than $K_0$.
• Detect the values of $t_1={\tilde{t}}_1\left(m\right)$ ($m=1,2,\cdots M_s$) in $t_1\left(k\right)$ ($k=1,2,\cdots K$) such that $\left|x\right({\tilde{t}}_1\left(m\right)\left)\right|<L$ is satisfied, where L is a relatively small integer ($L=100$ here). The value of $M_s$ is generally small ($M_s\ll K$) after Newton’s method is implemented for the first time. We refer to the ${\tilde{t}}_1\left(m\right)$ ($m=1,2,\cdots M_s$) as “seeds”.
  As mentioned in Section 4.1, the seeds are the candidates of zeros of $x\left(t\right)$ and appear in the neighborhood of cusps in Figure 1b, where the values $|x\left(t\right)/x^{\prime }\left(t\right)|$ are relatively small compared to other values of t. The above integer L ($L=100$) is selected as a value that can converge to find the first seeds, even with the conventional Newton’s method without any accelerations. According to Theorem 2, if one root of $x\left(t\right)=0$ is found, there are many roots in the vicinity of its shifted value $t-n$. Therefore, if a seed is a true root of $x\left(t\right)=0$, there must be many roots around it. The (geometrical) acceleration method described above is based on that expectation and developed to capture a large number of those roots.
• Calculate the distance between the seeds as $d(k,m)\equiv |t_1\left(k\right)-{\tilde{t}}_1\left(m\right)|$ for all k ($k=1,2,\cdots K$) and m ($m=1,2,\cdots M_s$) and detect the minimum value with respect to each k, $d_{min}\left(k\right)$, for all m.
• Calculate the acceleration coefficient $\beta \left(k\right)\equiv d_{min}\left(k\right)/|t_1\left(k\right)-t_0\left(k\right)|$ ($k=1,2,\cdots K$), where we set $\beta \left(k\right)=1$ when $d_{min}\left(k\right)=0$.
• Calculate the next initial values $t=t_2$ as $t_2\left(k\right)=\beta \left(k\right)[t_1\left(k\right)-t_0\left(k\right)]+t_0\left(k\right)$, reset to $t_0\left(k\right)=t_2\left(k\right)$, and perform the next Newton’s method calculation.

The processes 1–2 are initial settings. We repeat the above processes 3–7 until each value of $x\left(t\right)$ tends to zero [less than $O\left({10}^{-22}\right)$; the tolerance level adopted here]. In process 7, we consider a vector obtained by multiplying $t_1\left(k\right)-t_0\left(k\right)$ by a large scalar $\beta \left(k\right)$ and set $t_2\left(k\right)$ to be the endpoint of that vector, with $t_0\left(k\right)$ the starting point. The solution is expected to lie on the extension of that vector. We refer to processes 4–6 as the “acceleration”. The acceleration coefficient $\beta \left(k\right)$ satisfies $\beta \left(k\right)>1$ when the points are far from the seeds. The number of seeds $M_s$ increases as repeatedly implement both Newton’s method and the acceleration, and finally, $M_s=K$ holds as a result of the acceleration after the final implementation of Newton’s method. The final $M_s$, defined as $M_{final}$ here, provides the number of zeros (refer to Figure 3 and Remark 2) of $x\left(t\right)$.

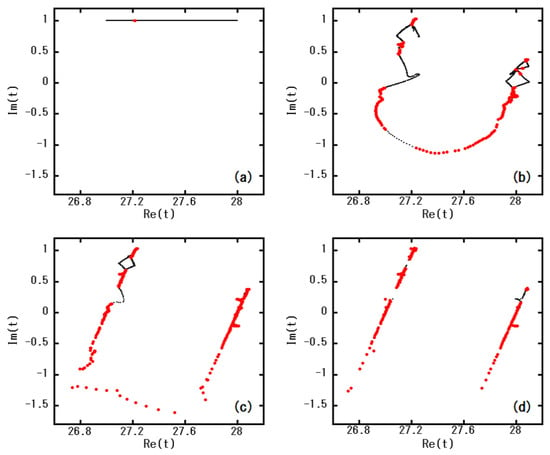
Figure 3. Results of Newton’s method and acceleration technique for $a=1.9408$ in the complex t plane, where the black points denote (a) the initial distribution, the distributions after (b) 5 and (c) 10 implementations of Newton’s method, and (d) the final distribution. The red points depict the “seeds” (the points satisfying $\left|x\right(t\left)\right|<100$) obtained by the acceleration after each implementation of Newton’s method. All seeds in (d) coincide with the zeros of $x\left(t\right)$ ($\left|x\left(t\right)\right|<{10}^{-22}$).

The number of implementations of Newton’s method required to reach $\left|x\left(t\right)\right|<O\left({10}^{-22}\right)$ depends on the value of the dynamical parameter a in (2) and the value of t, and becomes larger as a increases. By adopting the acceleration, almost all values of $\left|x\right(t\left)\right|$ with $O\left({10}^{1000}\right)$ decrease up to the level of $O\left(1\right)$ after 10–15 implementations of Newton’s method. If the acceleration process is not employed, the value of $\left|x\right(t\left)\right|$ with $O\left({10}^{1000}\right)$ remains at the level of $O\left({10}^{400}\right)\sim O\left({10}^{500}\right)$, even after 20 implementations of Newton’s method, and this value decreases only slightly, even though we continue to implement Newton’s method. This is the reason why we require powerful acceleration methods for the computations. All calculations in processes 2–7 are performed with multiple precision (150 digits here) to avoid the round-off error.

5. Numerical Results

As stated in the introduction, it is mathematically known that the set of homoclinic points coincides with the Julia set in one-dimensional dynamical systems. In this section, we show this fact numerically by calculating the homoclinic points of the function $x\left(t\right)$.

The chaotic region is specified by the bifurcation diagram of the nonlinear map f. Iterative calculation of the quadratic map (3) provides Figure 2, where $a\ge 1.4$ is fully chaotic region, at least, as long as we consider the real x. There exist non-chaotic regions called “windows” in this fully chaotic region. These window regions exhibit events that rarely occur but are physically important and it is known to be difficult to calculate dynamical quantities such as the entropy or Lyapunov exponent in those regions because there exists no physically observable measure in the window regions. We show one of the window regions in the right figure of Figure 2. The orbit realized in the real space is not chaotic in this region; however, the same complexity as the chaotic region ought to exist there. The set of homoclinic points can capture the complexity precisely. We show that in the subsequent subsections, taking $a=1.9408$ (a point in the window of fully chaotic region) as an example. When $a<1.4$, the orbit is non-chaotic in the real space. However, the behavior in the complex plane is completely different. We also present the complexity in the complex plane of the dynamical system such that it is periodic in the real space, taking $a=1.0$ (a point in the periodic region) as an example.

5.1. Results of Newton’s Method: Effects of Acceleration

In this subsection, we estimate the acceleration method stated in Section 4.2. Figure 3 shows the distribution of t such that the value of $x\left(t\right)$ tends to $x\left(t\right)=0$ for Newton’s method with acceleration stated in Section 4.2, where we select $a=1.9408$. This value of a belongs to a window in the fully chaotic region (refer to Figure 2). The initial parameter range (distant future) $t=t_r+i{t}_i$ is selected as $27\le t_r\le 28$ and $t_i=1.0$ for this value of a, where almost all values of $\left|x\right(t\left)\right|$ for this parameter region are within ${10}^{1000}$–${10}^{5000}$ initially [refer to Figure 1a]. The distribution is finally integrated into the neighborhood of two parallel lines with some inclination in the complex t plane. For t on these two parallel lines, $x\left(t\right)\in \mathbb{R}$ and small branches extending from the lines provide a tree-like structure in the complex plane.

No zero exists in $x\left(t\right)$ before the implementation of Newton’s method. Only eight seeds (red points, the points satisfying $\left|x\right(t\left)\right|<100$) after the first implementation of Newton’s method (a) gradually increase upon repetition of Newton’s method with the acceleration technique (processes 3–7 in the algorithm described in Section 4.2). Finally, the number of seeds $M_s$ in process 4 in Section 4.2 coincides with the whole zeros $M_{final}$ [Figure 3d], where $M_{final}=1154$ for the initial number of detecting points $K_0=2000$ when $a=1.9408$. The required number of implementations of Newton’s method for the convergence [$\left|x\left(t\right)\right|<O\left({10}^{-22}\right)$] is 14–35 for almost all t (this number depends on the initial value of $\left|x\right(t\left)\right|$ and, generally, a greater number of implementations is required for a larger value of $\left|x\right(t\left)\right|$).

The effect of the acceleration is depicted in Figure 4. Although the number of implementations of Newton’s method (four times here) is identical for (a) and (b), the distribution configurations are quite different. When we compare Figure 4b with Figure 3b, it is apparent that the t distribution (black points) remains almost unchanged before and after implementations of Newton’s method. This indicates that the solution of the conventional Newton’s method without the acceleration does not converge in the system such that $|x\left(t\right)/x^{\prime }\left(t\right)|$ is exponentially small.

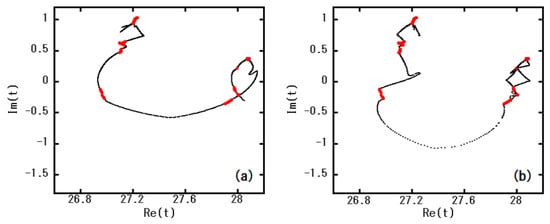
Figure 4. (a) Before and (b) after acceleration for the same number of implementations (four times) of Newton’s method, where the dynamical parameter a is the same as in Figure 3. The red points (seeds) have the same positions in (a,b).

Remark 2.

The solution $t=t_r+i{t}_i$ of $x\left(t\right)=0$ by Newton’s method presented here was obtained in the range $27\le t_r\le 28$ and $0.35<t_i<1.05$ when $a=1.9408$ (refer to Figure 3), and $27\le t_r\le 28$ and $2.55<t_i<3.01$ when $a=1.0$. Within the above parameter ranges, we obtained 1154 roots for $a=1.9408$ and 560 roots for $a=1.0$ as the solution to $x\left(t\right)=0$. The homoclinic sets for these two values of a are calculated in Section 5.2.

5.2. Comparison with Julia Set Obtained by Backward Iteration

In this subsection, we show that it is possible to capture the set of homoclinic points by the method mentioned above and the obtained homoclinic points coincide with the Julia set obtained by the conventional backward iteration of the nonlinear map f with a very good approximation.

Figure 5a and Figure 6a show the set of homoclinic points for $a=1.9408$ and $a=1.0$, respectively. These figures are calculated using the zeros of $x\left(t\right)$ obtained via the asymptotic expansion given in (5). In Figure 6a, the initial value of $t=t_r+i{t}_i$ (distant future) is selected as $27\le t_r\le 28$ and $t_i=3.0$. The number of obtained zeros $M_{final}=560$ (for the initial number of detecting points $K_0=2000$) at the acceleration after the final implementation of Newton’s method, where the typical initial values of $\left|x\right(t\left)\right|$ for the above parameter region are within the range ${10}^{100}-{10}^{5000}$, and the number of implementations of Newton’s method required for the convergence [$\left|x\left(t\right)\right|<O\left({10}^{-22}\right)$] is 12–20 for almost all points; i.e., the convergence of Newton’s method for $a=1.0$ was faster than that for $a=1.9408$.

Figure 5. Homoclinic points for $a=1.9408$ obtained by using (a) the zeros of function $x\left(t\right)$ given by (5) and (b) the backward iteration of the original quadratic Equation (17). The horizontal and vertical axes denote the real and imaginary parts of $x\left(t\right)$, respectively.

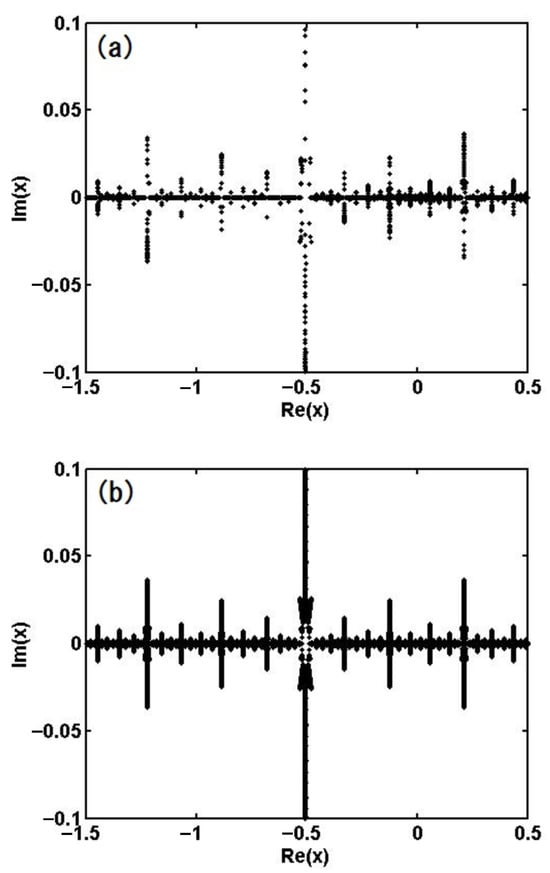
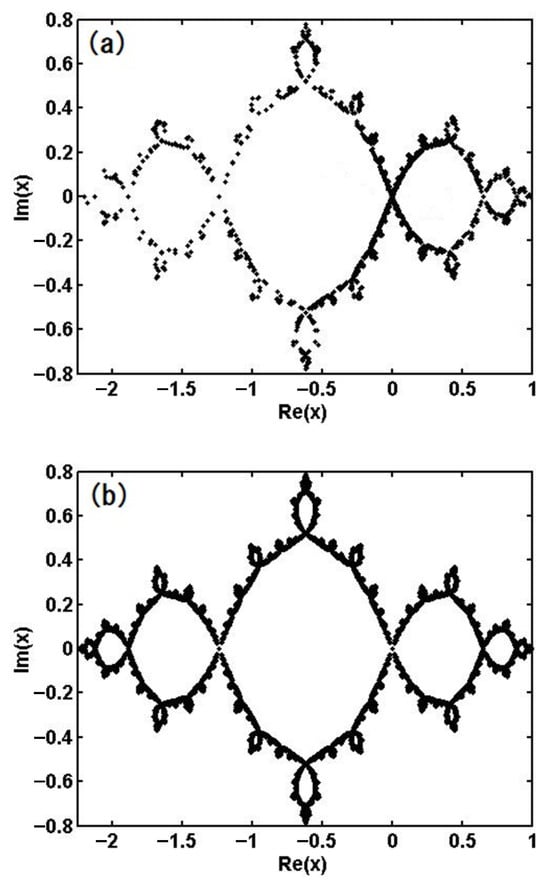
Figure 6. Homoclinic points for $a=1.0$ obtained by using (a) the zeros of function $x\left(t\right)$ and (b) the backward iteration (17).

In Figure 5a and Figure 6a, we shift the obtained values of t that provide $x\left(t\right)=0$ (for the specific values of t, refer to Remark 2) as $t-1,t-2,t-3,\cdots ,t-27$, and plot $(\Re [x(t-n)],\Im [x(t-n)\left]\right)$ for all of these $t-n$ ($n=1,2,\cdots 27$) together, where $1154\times 27=\mathrm{31,158}$ points are plotted in Figure 5a and $560\times 27=\mathrm{15,120}$ points are plotted in Figure 6a in total.

All points correspond to the homoclinic points. For $n=1-3$ and $n=22-27$, the value of $\left|x\right(t-n\left)\right|$ is very small and almost all points are located in the neighborhood of the fixed point $x=0$ for both $a=1.9408$ and $a=1.0$.

Figure 5b and Figure 6b are the corresponding Julia sets calculated via the backward iteration of the quadratic map given in (3). Here, the backward iteration is given by

$$\begin{array}{c}\hfill x_{n+1}={\displaystyle \frac{-a{x}_f\pm \sqrt{a^2{x}_f^2-a{x}_n}}{a}}(n=0,1,2,\cdots ),\end{array}$$

(17)

starting from the initial condition $x_0=0$ (fixed point), in which the calculation is performed with 64 digits and the number of iteration (i.e., the number of plotted points) is $2^{18}=\mathrm{262,144}$ for both Figure 5 and Figure 6.

Obviously, figures (a) and (b) in Figure 5 and Figure 6 are identical, which guarantees the accuracy of the present method. Indeed, the Hausdorff distance $d_H$ between the set of obtained homoclinic points and the Julia set is approximately $d_H=0.0905$ for $a=1.0$ and $d_H=0.0148$ for $a=1.9408$. The Hausdorff distance $d_H$ is defined as a measure of the degree of coincidence between two shapes [43]. If two shapes are perfectly identical, the Hausdorff distance $d_H$ is zero, and the greater the deviation between the two shapes, the larger the value of $d_H$. In the present study, the Hausdorff distance $d_H$ for $a=1.0$ is larger than the one for $a=1.9408$. This suggests that the dynamical system of $a=1.9408$ is less disordered than that of $a=1.0$.

The set of homoclinic points has a fractal structure for both dynamical parameters $a=1.9408$ and $a=1.0$. As we see from Figure 2, the value $a=1.0$ in map (3) belongs to the periodic region for $x\in \mathbb{R}$ and the chaotic behavior is not observed in the real space. However, the behavior of x in the complex plane is very complicated. This exhibits the essential complexity that the dynamical system (3) possesses.

It seems that the figures of Julia sets, Figure 5b and Figure 6b, are more accurate than those depicted in Figure 5a and Figure 6a. However, we cannot extract any physically meaningful quantities from the backward iteration of map (3). On the other hand, each point in Figure 5a and Figure 6a corresponds to a real physical event given by a deterministic function. The points included in the set of homoclinic points cannot escape and be physically meaningful, i.e., the observable events are all confined to this set. This result indicates that determination of the set of homoclinic points and identification of the orbit of each point allows every event from the past to the future to be determined; i.e., the dynamical systems given in Figure 5a and Figure 6a are no longer chaotic but deterministic. The number of points that appear on the real axis increases as the dynamical parameter a becomes large, which is reflected in the complexity of the real dynamics, although the two sets of homoclinic points for $a=1.0$ and $1.9408$ have the same degree of complexity in the complex plane.

5.3. Accuracy of Computations

In this subsection, we discuss the error in the computation in Section 5.1 and Section 5.2 using relation (1). As described in Remark 2, the solutions to $x\left(t\right)=0$, which give the homoclinic points, are calculated in $27\le t_r\le 28$ and $0.35<t_i<1.05$ when $a=1.9408$, and $27\le t_r\le 28$ and $2.55<t_i<3.01$ when $a=1.0$. Therefore, the errors of the obtained values of t in these regions could be expected to be extremely small to the exact solutions to $x\left(t\right)=0$. In the following, we observe how each error increases with the map iteration. Since the map f on the Julia set is locally expanding [33,34,35,36], the forward iteration of f should increase the error. Here, we verified that by examining how large values of n the relation (1) holds for.

First, we calculate the forward iteration

$$x(t-27+m),f\circ x(t-27+m),f^2\circ x(t-27+m),\cdots ,f^{27-m}\circ x(t-27+m)$$

for all integers m that satisfy $0\le m\le 27$, where t is selected as the solution to $x\left(t\right)=0$ obtained by Newton’s method ($27\le t_r\le 28$, for $t_i$, refer to Remark 2). Next, we compare the above forward iterations with

$$x(t-27+m),x(t-26+m),x(t-25+m),\cdots ,x\left(t\right),$$

calculated by asymptotic expansion (5) for each value of m ($m=0,1,2,\cdots ,27$). The value $f^m\circ x(t-M)$, M an integer, should coincide with $x(t-M+m)$ when relation (1) holds without errors, where $0\le m\le M\le 27$. We calculated $f^m\circ x(t-M)-x(t-M+m)$ for all values of m ($0\le m\le M$). We choose M as the largest integer satisfying

$$\begin{array}{c}\hfill |f^m\circ x(t-M)-x(t-M+m)|=O\left({10}^{-22}\right),(0\le m\le M).\end{array}$$

(18)

We refer to this M as the maximum iteration number.

Figure 7 shows the homoclinic points that satisfy (18). The points in the figure are depicted by using the forward iteration $x(t-M)$, $f\circ x(t-M)$, …, $f^M\circ x(t-M)=x\left(t\right)$, where $M=9$ for $a=1.9408$, and $M=7$ for $a=1.0$. A total of $1154\times 9=\mathrm{10,386}$ points for $a=1.9408$ and $560\times 7=3920$ points for $a=1.0$ are plotted in the figure.

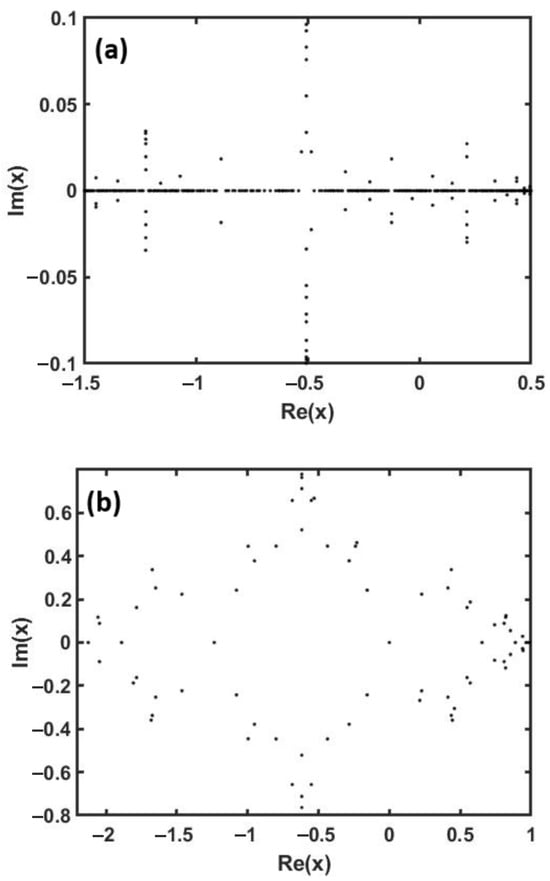
Figure 7. Homoclinic points by the computation with high accuracy, where $a=$ (a) 1.9408 and (b) 1.0. The maximum iteration number M is given as $M=$ (a) 9 and (b) 7, respectively.

Figure 8 shows the points by the further forward iteration of $x\left(t\right)$:

$$x\left(t\right),,f\circ x\left(t\right),f^2\circ x\left(t\right),\cdots ,f^{M_f}\circ x\left(t\right),$$

where $M_f$ is selected as the maximum integer satisfying

$$|f^{M_f}\circ x\left(t\right)-x(t+M_f)|=O\left({10}^{-20}\right),$$

for the roots of $x\left(t\right)=0$ ($27\le t_r\le 28$). Here, the maximum integer $M_f$ is given as $M_f=3$ for $a=1.9408$ and $M_f=12$ for $a=1.0$. The value of $M_f$ is larger for $a=1.0$ than for $a=1.9408$. This indicates that the solution by Newton’s method is more accurate for $a=1.0$.

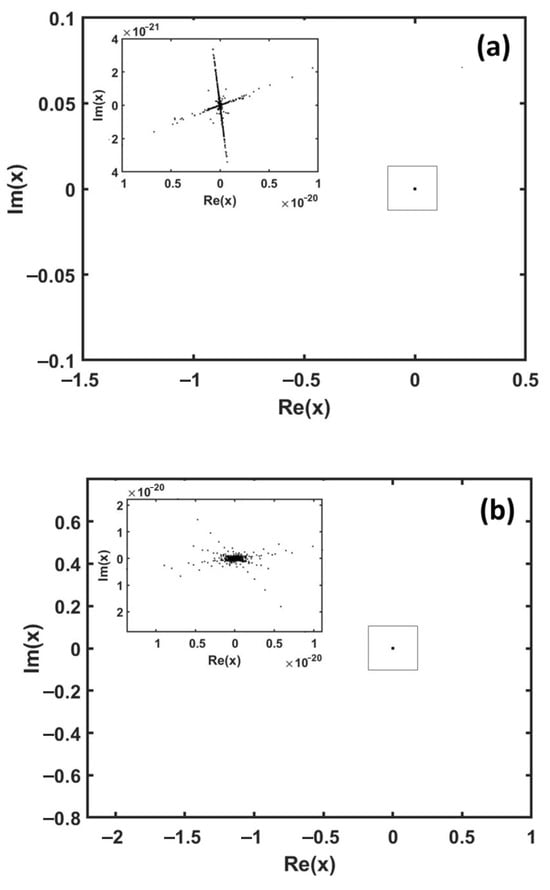
Figure 8. Errors from the fixed point (the exact solution), where $a=$ (a) 1.9408 and (b) 1.0. The boxed region surrounding the origin, the fixed point, is enlarged in the upper left corner of each figure.

Remark 3.

For $a=1.9408$, the other eigenvalue, which is not adopted in the current study, is −1.0203, which is close to 1. For $a=1.0$, the other eigenvalue that is not used here is −1.6180, which is far from 1. As the eigenvalue approaches 1, the dynamical system transitions from hyperbolic to parabolic. We remark that the accuracy of the current calculations deteriorates as the dynamical system deviates from hyperbolic. The larger iteration number $M_f$ for $a=1.0$ than for $a=1.9408$ in the calculation of Figure 8 indicates that the computation by Newton’s method for $a=1.0$ is more accurate than for $a=1.9408$, although the case of $a=1.9408$ yields more roots than that of $a=1.0$ by Newton’s method. The dynamical system with $a=1.0$ is a uniform hyperbolic system. On the other hand, the value of $a=1.9408$ is located near the edge of the window in Figure 2, suggesting a non-uniform hyperbolic system; i.e., there may be a large number of tangencies at this value of a.

6. Concluding Remarks

We have successfully calculated the set of homoclinic points concretely, using the quadratic map as an example. This enables us to capture the chaos deterministically. The obtained results coincide with those defined mathematically, confirming the accuracy of our calculations. The sets of homoclinic points provided in Figure 5 and Figure 6 involve numerical errors; however, our method itself is mathematically rigorous, and it is possible to decrease those errors through the use of higher-performance computers or higher-precision computations. In the current study, we have calculated the sets of homoclinic points for the dynamical systems such that the dynamical parameter a is in the windows. The convergence of Newton’s method in the fully chaotic region without windows (e.g., the region of $a\ge 1.943$ in Figure 2) deteriorates significantly even if the acceleration scheme is applied. This fact suggests the existence of numerous points of homoclinic tangency between the stable and unstable manifolds in the corresponding dynamical systems. The results in Section 5 suggest that the presented Newton’s method works well for uniformly hyperbolic cases, but it is slightly less accurate for non-uniformly hyperbolic (with tangencies) cases.

We emphasize that the calculation of a large number of homoclinic points was made possible by using the asymptotic expansion (5), and chaotic sets such as Julia sets could be detected. It is difficult to capture so many homoclinic points when we adopt the classical linearization function [22,23,24,25,26] for the calculation. This is due to the number of zeros of $x\left(t\right)$ in the complex t plane, where the former is exponential and the latter is polynomial.

Finally, we mention that almost all calculations in the present study do not work with double-precision calculations. The method presented in this study is applicable to two-dimensional nonlinear dynamical systems such as Hénon maps and can be used to determine the set of homoclinic points, provided the dynamical system is Laplace transformable. For the case where the stable and unstable manifolds are higher-dimensional (greater than one), mathematical development is required.