Abstract
Above-ground outdoor swimming pools are increasingly popular due to their affordability and ease of installation, yet maintaining optimal water temperature under variable climate conditions remains challenging. Our study develops a theoretical and mathematical modeling framework to quantify heat gains and losses in residential frame pools, focusing on convection, radiation, and evaporation as dominant mechanisms. The analysis demonstrates that daytime water circulation enhances solar heat gains but increases nighttime losses, while opaque covers reduce evaporation at the expense of solar input. Heating during colder months in Central and Eastern Europe is highly energy-intensive due to low ambient temperatures, strong winds, and reduced solar radiation. Based on these findings, the paper proposes cost-effective strategies, including optimized pool geometry, wind protection, transparent covers, and operational adjustments such as daytime-only circulation. The model provides a foundation for advanced simulations and supports the design of sustainable heating solutions, aiming to extend the swimming season and reduce operational costs.
1. Introduction
Above-ground outdoor swimming pools, especially frame pools, have become increasingly popular worldwide. They are affordable, easy to install, and adaptable to different terrain conditions. Their modular design allows quick assembly at the start of the summer season and easy disassembly at the end, making them an attractive alternative to traditional in-ground pools. Open-air pools also provide a unique recreational experience. Swimming outdoors combines physical activity with relaxation and contact with nature [1]. Additional benefits include lower noise levels and reduced exposure to chemical odors compared to indoor facilities [2,3].
Maintaining a comfortable water temperature is one of the most important factors affecting user satisfaction. The optimal temperature depends on several factors: the swimmer’s age, type of activity, intended use of the pool, and environmental conditions such as air temperature, solar radiation, and wind speed. In practice, water temperature usually ranges from 25 °C to 37 °C. Keeping water warm, especially at the higher end of this range, is challenging for outdoor pools exposed to significant heat losses [4]. This problem is particularly relevant in Central and Eastern Europe, where the swimming season is short and weather conditions are variable [5,6].
To extend the swimming season and ensure thermal comfort, users increasingly adopt active water heating methods. Available solutions include solar mats, electric heaters, heat pumps, and systems using renewable energy [7,8,9,10]. The choice of technology depends on local climate, energy availability, operating costs, and ease of use. Many ready-to-install kits allow users to implement heating systems without specialized technical knowledge. However, regardless of the chosen technology, heating water is costly due to water’s high thermal capacity and substantial heat losses. These losses occur mainly through convection, radiation, and evaporation, and their intensity increases with low ambient temperatures and strong winds [4,11,12,13]. For systems powered by electricity or fossil fuels, this means higher operating costs. For renewable systems, heat losses must be considered during design, as they affect the required size and cost of the installation.
Reducing heat loss requires understanding the mechanisms responsible for it. Losses depend on pool design and external conditions, and they strongly influence energy efficiency and operating costs. Therefore, before designing a heating system, it is essential to analyze when and how heat losses occur and identify measures to minimize them. Such knowledge supports the selection of technical solutions that improve efficiency and user comfort.
The global market for above-ground pools is expected to grow by USD 592.7 million between 2024 and 2029 [14]. This growth is driven by urbanization and rising disposable incomes. Above-ground pools are more affordable and easier to maintain than in-ground pools. They are also available in various shapes and materials, making them suitable for limited spaces in urban areas. Their flexibility, easy assembly, disassembly, and relocation, further increases their attractiveness.
The main challenge in maintaining optimal water temperature is the high cost of heating, which depends heavily on weather conditions. In colder regions such as Central and Eastern Europe, the short swimming season further increases costs. A detailed understanding of heat gain and loss mechanisms is therefore crucial for improving energy efficiency.
Therefore, the aim of this study is to develop a theoretical and mathematical model for analyzing heat gains and losses in a residential above-ground frame pool under conditions typical of Central and Eastern Europe. The model supports effective water temperature management, minimizes heat losses, and optimizes energy consumption. This paper provides a theoretical analysis of the dominant heat exchange mechanisms and the factors influencing them. The goal is to improve understanding of thermodynamic processes in outdoor pools and offer practical recommendations for energy-efficient design and operation.
The novelty of this work lies in the development of a dedicated modeling framework for above-ground outdoor swimming pools, i.e., a category that has received considerably less attention in the literature compared to in-ground pools, whether indoor or outdoor [4,7,8,9,10,11,12,13]. Whereas most of these previous studies have typically emphasized empirical audits or simplified representations of individual heat transfer mechanisms, our approach integrates convection, radiation, and evaporation within a single analytical model. This unified treatment allows for more reliable predictions of the overall thermal balance under variable climatic conditions, particularly in regions characterized by pronounced seasonal fluctuations and significant wind exposure.
Finally, this study bridges the gap between theory and practice. It provides design and operational guidelines to improve energy efficiency and reduce costs. Unlike prior works that rely on site-specific correlations, our model offers a generalizable, physics-based foundation. It can support advanced simulations and optimization strategies for sustainable pool heating solutions. By combining theoretical rigor with practical relevance, this research contributes to both scientific understanding and real-world energy management in residential aquatic environments.
2. Energy Balance Modeling of an Outdoor Above-Ground Pool
In this section, an energy balance model for an outdoor above-ground swimming pool is developed, considering the various heat and mass exchange mechanisms between the pool and its surroundings. While most existing literature focuses on the thermal balance of indoor (and, less frequently, outdoor) in-ground pools, relatively little attention has been paid to outdoor above-ground installations, especially frame pools. Therefore, this study proposes a mathematical framework that describes the distinct pathways of energy exchange, with an emphasis on a detailed analysis specifically tailored to above-ground pool configurations. This approach aims to highlight the key differences in heat balance resulting from the unique placement and exposure conditions of this pool type.
In the energy balance analysis of outdoor pools, the main factors influencing heat and mass transfer include:
- Evaporation losses;
- Condensation gains;
- Convective heat transfer;
- Conductive heat transfer;
- Long-wave (infrared) radiation;
- Short-wave solar radiation;
- Heat gains from auxiliary heating systems;
- Heat input from pool users;
- Heat and mass influx from make-up water.
Most of these factors are further affected by environmental and operational conditions, which can significantly alter both the nature and magnitude of energy exchanges between the pool and its surroundings. These complex interactions require a robust and physically realistic mathematical model to reliably estimate the thermal performance of an outdoor above-ground pool under real operating conditions.
2.1. Analyzed Cases
The following subsections present the configurations analyzed in this study, including an uncovered pool, a pool equipped with a cover, and other practical scenarios relevant to residential above-ground installations.
2.1.1. Outdoor Above-Ground Swimming Pool
In this configuration, illustrated in Figure 1, the pool is assumed to be an above-ground structure with an exposed water surface. Heat exchange occurs primarily through the water surface; however, mechanisms such as convection, solar radiation absorption, and thermal radiation also affect the side walls of the pool. The dominant heat transfer processes include the absorption of solar radiation by the pool water and shell, convection at the water surface, and long-wave thermal radiation. Additional processes include heat exchange due to the presence of swimmers, phase changes such as evaporation and condensation, heat input from auxiliary heating systems, heat flux due to external water inflow (e.g., precipitation or make-up water), and thermal conduction through the pool bottom into the ground.
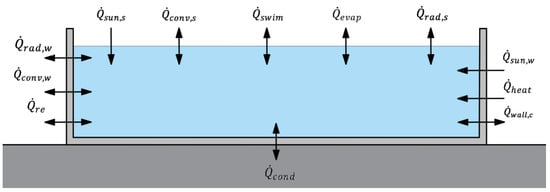
Figure 1.
Heat and mass transfer pathways in an outdoor above-ground swimming pool.
The heat flux balance for this variant can be expressed as:
where
is the resultant heat flux;
is the heat flux due to solar radiation absorbed by the horizontal surface;
is the convective heat flux at the horizontal surface;
is the heat flux caused by the presence of people in the pool;
is the heat flux due to evaporation or condensation;
is the heat flux from long-wave radiation interacting with the horizontal surface;
is the heat flux by thermal conduction through the pool floor;
is the heat flux through the side walls in direct contact with the water;
is the heat flux due to the inflow of external water;
is the heat flux supplied by the heating system.
In the literature, the most analyzed configuration is the in-ground swimming pool with an uncovered water surface [15,16]. Unlike this typical scenario, an above-ground pool has distinct thermal behavior: conduction occurs mainly through the pool bottom, while convection, solar absorption, and long-wave radiation also influence the side walls. Accordingly, an additional element appears in the heat balance, i.e., , which can be expressed as:
where
is the heat flux due to long-wave radiation at the side walls;
is the convective heat flux at the side walls;
is the heat flux due to solar radiation absorbed by the side walls.
The side walls enable energy transfer between the water and the environment through conduction, given by:
where
is the thermal conductivity of the wall;
is wall thickness;
is the temperature of the outer surface of the side walls in contact with water;
is the temperature of the water;
is the surface area of the side wall in contact with water.
2.1.2. Outdoor Above-Ground Swimming Pool with a Non-Contact Cover
This model assumes that the above-ground pool’s water surface is covered by a pool cover that does not come into direct contact with the water, as shown in Figure 2. It should be noted that above-ground pools are typically not filled to their maximum capacity. Manufacturers generally recommend filling only 80–90% of the tank’s volume. Consequently, the cover does not rest directly on the water surface, leaving an air gap between the cover and the water, i.e., a situation rarely described in the literature.
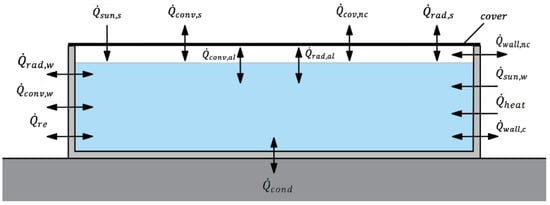
Figure 2.
Heat and mass transfer pathways in an outdoor above-ground swimming pool covered with a non-contact cover.
The heat flux balance for this variant is given by:
where in addition to the previously defined terms:
is the heat flux through the non-contact cover;
is the heat flux through the side walls not in direct contact with water.
Figure 1 and Figure 2 illustrate the two main configurations considered: an uncovered pool with direct heat and mass exchange through the exposed water surface, and a pool with a non-contact cover that creates an insulating air layer. This insulating layer modifies the dominant heat transfer mechanisms by adding resistance to convective and radiative losses, which is significant for improving energy efficiency under real conditions.
Developing an accurate energy balance for this case is more complex due to the air gap between the water surface and the cover. When the cover is installed, evaporation initially causes heat loss; however, these losses are short-lived. The air space soon becomes saturated with water vapor, effectively stopping further evaporation. Depending on conditions, cycles of condensation and evaporation may occur, but the net heat flux from these processes within the closed pool-cover system is negligible.
Since the cover does not come directly into contact with the water, conduction through the air layer can be neglected due to air’s low thermal conductivity. Instead, energy exchange between the water and the cover occurs mainly through convection and radiation. Thus, can be expressed as:
where
is the convective heat flux in the air layer;
is the heat flux from long-wave radiation in the air layer.
The cover also enables conduction between the air layer and the external environment:
where
is the thermal conductivity of the cover;
is the cover thickness;
is the outer surface temperature of the cover;
is the air layer temperature;
is the cover area.
Additionally, the portion of the side wall above the water surface exchanges energy with the air layer mainly through convection and radiation:
and conduction through the wall enables heat exchange with the external environment:
where
is the temperature of the side wall not in contact with water,
is the surface area of the side wall above the water line.
2.2. Heat Transfer Mechanisms
To develop an accurate thermal balance model for an outdoor above-ground swimming pool, it is essential to identify and describe the primary mechanisms responsible for heat and mass exchange with the surrounding environment. Each mechanism contributes differently to the overall energy balance, depending on weather conditions, pool design, operational scenarios, and user behavior.
This section provides a detailed overview of the key physical processes governing energy exchange in such installations, including phase change phenomena, convection, conduction, long-wave and solar radiation, external water inflow, heat input from auxiliary heating systems, and the impact of users.
2.2.1. Phase Change Processes
Evaporation is a phase change phenomenon in which water molecules transition from the liquid to the gaseous state, resulting in both heat and mass transfer. This process occurs at the liquid surface, where water vapor diffuses into the surrounding unsaturated air due to molecular motion.
The intensity of evaporation primarily depends on the difference in the partial pressure of water vapor between the ambient air and the boundary layer—a thin film of air saturated with water vapor at a temperature close to the water surface temperature and with relative humidity near 100%. Evaporation occurs when the partial pressure of water vapor in the ambient air is lower than that in the boundary layer.
This process is naturally limited by molecular diffusion, making spontaneous evaporation relatively slow. However, it is significantly enhanced when the thin saturated layer above the water surface is replaced with drier air due to air movement. This can occur through:
- Natural convection, driven by buoyancy forces arising from temperature and density differences between the warm water surface and cooler ambient air;
- Forced convection, caused by external air flows, such as wind.
The greater the difference in partial vapor pressures between the ambient air and the boundary layer, the more intense the evaporation becomes.
In uncovered outdoor pools, evaporation is typically the dominant mechanism of heat loss [17]. It should also be noted that evaporation leads to a continuous reduction in the pool’s water volume.
Evaporation can be modeled by the following relationship [4,15]:
where
is the mass transfer coefficient for free convection;
is the vapor density at the water surface;
is the vapor density in the free stream.
It is assumed that the air directly above the pool surface is saturated with water vapor ( = 100%) at a temperature approximately equal to the water temperature . Thus, corresponds to the saturated vapor density at , while is calculated based on the ambient air temperature and free stream relative humidity [15].
The mass transfer coefficient for free convection, derived using the analogy between heat and mass transfer, can be expressed as [18]:
where
is the Sherwood number;
is the molecular diffusion coefficient for air-water at the film temperature ;
is the characteristic length of the pool.
The Sherwood number for free convection over a flat horizontal surface, for both laminar and turbulent regimes, can be approximated by [4,19]:
where the Rayleigh mass transfer number is defined as:
where
is gravitational acceleration;
is the density of moist air in the free stream;
is the density of moist air at the water surface;
is the dynamic viscosity of air at the film temperature.
The film temperature is given by:
while the characteristic length for a horizontal surface is approximated by [4]:
where
is the pool’s water surface area.
is the pool’s circumference.
The molecular diffusion coefficient at the film temperature is estimated as [4]:
where is the total atmospheric pressure.
To describe evaporation under forced convection, the empirical correlation by İnan and Atayılmaz [20] is used, which Poós and Varju [21] identified as the most accurate among ten tested models. It corrects the vapor pressure difference using an exponential factor:
where
is the wind speed;
is the vapor pressure at the water surface;
is the vapor pressure in the free stream;
is the latent heat of vaporization.
The vapor pressures are calculated as:
where is the saturated vapor pressure at the given temperature.
To capture the combined effect of forced and free convection, Lovell et al. [4] applied the following power law relationship [19]:
Once the evaporation rate per unit area, , is known, the associated heat loss for an uncovered pool is given by:
Condensation, in contrast, occurs when the relative humidity of the ambient air exceeds the saturation level at the water surface temperature. Under such conditions, excess water vapor condenses, transferring latent heat to the pool water. This typically happens at night or early in the morning, when air temperatures are higher than the pool water temperature and relative humidity is high. It is especially pronounced in humid climates or after heavy rainfall, when the air is nearly saturated.
However, it should be emphasized that in the present thermal balance analysis only evaporation-induced heat losses (Equation (20)) are considered, while condensation is disregarded, as it would formally represent a heat gain rather than a loss.
Condensation may also occur on the outer pool walls, or the inner surface of a pool cover if present.
It is important to emphasize that phase change processes involve both heat and mass transfer. In the energy balance framework of this study, only evaporation is treated as a source of heat loss, whereas possible condensation phenomena are not included in the calculations.
Various computational approaches exist for estimating the amount of water evaporated under specific conditions. The water loss rate can be directly estimated by comparing the heat lost through evaporation with the latent heat of vaporization.
Actual water loss can also be measured by monitoring changes in the pool water level. However, due to the relatively low evaporation rate compared to the total pool volume, accurate short-term tracking is challenging. Additionally, the water balance is influenced by splashing, water carried away by swimmers, and precipitation or condensation. In practice, precisely determining evaporation by monitoring the water level is impractical unless performed under strictly controlled conditions.
2.2.2. Convection
Convection occurs when fluid particles move and mix due to flow, resulting in heat transfer between surfaces and the surrounding fluid. Fluid motion may be induced mechanically, for example, by a pump, fan, or wind (forced convection), or it may result from buoyancy forces caused by density differences due to temperature or concentration gradients (natural convection).
In the context of swimming pools, convection refers primarily to the heat exchange process between the pool water surface (or the cover surface) and the surrounding air. For above-ground pools, it also includes heat exchange between the external side walls and the outdoor environment. Depending on ambient conditions and the thermal state of the water, convection can lead to heat gains or losses.
Modeling convection is challenging because it involves complex fluid flows around surfaces with specific roughness, temperatures, and changing boundary layers. Due to the many variables involved, natural convection coefficients are typically estimated using empirical correlations based on experimental or numerical studies rather than purely theoretical models.
For convective heat losses from the water surface, the Bowen ratio approach is commonly used and has proven effective for predicting temperature changes in outdoor pools [16,22]. According to this method, convective heat loss—both natural and forced—can be expressed as:
where is the Bowen coefficient, defined as:
where is the specific heat of air at .
When the relative humidity of the surrounding air is lower than the saturation humidity at the water surface temperature, a positive Bowen coefficient indicates that heat is lost through both evaporation and convection—maximizing the cooling effect. As the ambient temperature approaches the water temperature, the Bowen coefficient approaches zero, and convective heat transfer diminishes, although evaporation may still occur.
A negative Bowen coefficient means that convection opposes evaporation. If the coefficient is between 0 and −1, evaporation still dominates; if it equals −1, the net heat exchange is zero; if it is less than −1, convective heat gains exceed evaporation losses, resulting in a net heat gain for the water.
When ambient humidity exceeds the saturation level at the water surface temperature, both condensation and convection supply heat to the pool water. In such cases, the Bowen coefficient must be positive, as this scenario does not occur if the air temperature is lower than the water temperature [16].
For pools covered with a contact cover, convective heat loss can be defined as a function of the temperature difference between the cover and the ambient air [23]:
where is the average convective heat transfer coefficient.
To estimate for a covered pool at night, the method by Lovell et al. [4], based on principles by Bergman et al. [19], can be used:
where
is the heat transfer coefficient for free convection;
is the heat transfer coefficient for forced convection.
To define the heat transfer coefficient for free convection it can be presented using equation [19]:
The heat transfer coefficient for free convection, , can be expressed as [19]:
where
is the thermal conductivity of air at film temperature;
is the average Nusselt number.
If , the mean Nusselt number for the upper surface of a horizontal hot plate is approximated by:
For , the following correlation for a horizontal cold plate applies [19]:
The Rayleigh number is defined as [19]:
where
is the Prandtl number;
is the kinematic viscosity of air.
For forced convection in turbulent flow, Sartori [24] derived:
where . Wind direction effects are typically neglected.
These equations apply to covered pools only at night (without solar radiation). Using them for daytime conditions may lead to significant errors. Possible condensation on the cover is not included.
For covered pools with a non-contact cover, convective heat exchange between the cover and ambient air is as above, but heat exchange between the water and the cover is mainly due to free convection inside the air gap:
where is the air temperature in the gap.
Convection at the side walls may differ due to local airflows. However, if the ratio of the horizontal cover area to the inner side wall area is large (e.g., 90% filled), wall effects are often neglected.
For the external pool walls, convection occurs on vertical or inclined surfaces, what requires different treatment. The BLAST (Building Loads Analysis and System Thermodynamics) model can be used to determine the convection coefficient for the vertical walls of an above-ground pool [18]. This model, based on wind tunnel studies by Sparrow et al. [25] and earlier findings [26,27,28], is more versatile than most others. The total convection coefficient is the sum of forced and natural convection:
where
is the forced convection coefficient;
is the natural convection coefficient.
The forced convection component is calculated as [25]:
where
is the wind direction factor (1 for windward, 0.5 for leeward [26]);
is the surface roughness factor;
is the perimeter of the surface;
is the area;
is the wind speed.
The natural convection component is given by [28]:
For vertical surfaces, both expressions reduce to:
The BLAST model does not account for shielding, geometry, or radiative effects, so careful interpretation is required for different pool designs.
2.2.3. Thermal Conduction
Thermal conduction involves energy transfer through a material due to a temperature gradient. In fluids, this occurs through particle collisions; in solids, it results from free electron motion and lattice vibrations.
In the case of in-ground swimming pools, conduction occurs through the side walls and the pool bottom, whereas for above-ground pools, conduction occurs primarily through the bottom surface. To calculate heat loss by conduction, Fourier’s law is used. This law describes the heat flow through a material as a function of the temperature gradient and the thermal properties of the material. For a swimming pool, conduction through the walls and the bottom can be described by the following relationship:
where
is the thermal conductivity of the wall/bottom material;
is the surface area of conduction;
is the water temperature;
is the external temperature;
is the wall or bottom thickness.
The soil’s high thermal inertia means that short-term pool temperature changes have minimal impact on ground temperature. Thus, the ground temperature is generally assumed to be constant. Because the resulting conduction losses are typically less than 1–2% of total heat losses [29], they are often neglected in detailed energy balance models [16].
2.2.4. Long-Wave Radiation
Long-wave radiation, often referred to as thermal or infrared radiation, involves the transfer of energy through electromagnetic waves emitted by the pool water sur-face (or cover) and, in the case of above-ground pools, also by the external side walls. Unlike conduction or convection, this mode of heat transfer does not require a material medium and can occur in a vacuum. The exchange of long-wave radiation with the surroundings is a continuous process in outdoor swimming pools, but under typical conditions its contribution to the overall thermal balance is relatively small compared to evaporation and convection.
All surfaces, whether liquid or solid, constantly emit long-wave radiation. However, radiation in this wavelength range (approximately 740 nm to 1 mm) is invisible to the human eye under typical ambient temperatures because it lies in the infrared spectrum. When the surface temperature rises significantly, the emission spectrum shifts towards shorter wavelengths, eventually becoming visible, as in the case of glowing hot objects. Otherwise, specialized instruments, such as infrared cameras, are needed to detect and quantify thermal radiation.
In the context of swimming pools, long-wave radiation exchange is commonly described using the concept of effective sky temperature, which simplifies the complex radiative interaction between the pool, the semi-transparent atmosphere, and outer space to a net exchange between the pool surface and an equivalent “sky” surface at a representative temperature.
The net long-wave heat flux from the pool surface to the sky can be modeled using the Stefan–Boltzmann law [30,31]:
where
is the Stefan–Boltzmann constant;
is the longwave emissivity of the pool surface;
is the pool water surface area;
is the sky view factor;
is the temperature of the pool surface;
is the effective sky temperature.
If the pool is uncovered, the pool surface temperature equals the water temperature ; if the pool is covered, it equals the cover temperature . Similarly, the pool surface emissivity equals the water emissivity or the emissivity of the cover material . The longwave emissivity of water is commonly assumed to be about 0.95 [30,32,33,34].
For outdoor pools with a free upper surface, the sky view factor is typically assumed to be 1, as the pool surface exchanges radiation directly with the open sky. The sky temperature can be related to the ambient air temperature by [26,27]:
where is the sky emissivity.
Numerous empirical models exist for calculating sky emissivity [30,31,35,36]. One commonly used approach is based on the formulation by Martin and Berdahl [37], further developed by Crawford and Duchon [38] and Carmona et al. [36]:
where
is the clear-sky emissivity;
is the fractional cloud cover.
The clear-sky emissivity can be estimated using the expression adapted by Guo et al. [35]:
where is the relative humidity of the ambient air.
Cloud cover fraction () can be determined through visual observation, solar radiation measurements, or satellite data [36]. For example, Carmona et al. [36] used the expression proposed by Crawford and Duchon [38] to estimate cloud fraction from measured global horizontal solar irradiance:
where is the theoretical global horizontal irradiance under clear-sky conditions.
At night, visual estimation of cloud cover can be challenging but possible using methods such as star visibility or observation of the Moon. Satellite and local meteorological data may also provide estimates of nighttime cloud fraction for a given location.
For longwave radiation exchange from the external side walls of an above-ground pool, an analogous relationship applies:
where
is the wall area;
is the wall surface temperature;
is the longwave emissivity of the wall material.
For vertical walls, the sky view factor is often approximated as 0.5 to account for surrounding obstructions [31].
In the case of covered above-ground pools with a non-contact cover, the non-submerged inner side walls must also be considered. These walls can radiate and absorb heat on both sides because they are exposed to the humid air layer under the cover. Long-wave radiation exchange within this enclosed space is a multidirectional process involving the water surface, inner pool walls, the cover, and the humid air layer. The water surface, with high emissivity, acts as a strong emitter, while the walls and the cover reflect and absorb radiation. The humid air, rich in water vapor, can also absorb and emit radiation, complicating the balance.
Due to this complexity, practical models often apply simplifying assumptions, such as treating the enclosed air as a gray medium with average absorptivity and emissivity. Alternatively, a radiative equilibrium can be assumed, or an effective average temperature can be used to approximate net radiation exchange within the air gap.
It should be emphasized that, although the long-wave radiation term is retained in the present model for completeness, its relative contribution to the overall heat exchange of the pool is typically minor under ordinary operating conditions. Nonetheless, it may become more pronounced during clear nights with large sky–water temperature differences.
2.2.5. Solar Radiation
Solar radiation is the energy emitted by the Sun that reaches the Earth’s surface in the form of electromagnetic waves, primarily within the visible light, ultraviolet, and near-infrared ranges. The Sun’s total irradiance at the outer edge of the Earth’s atmosphere is known as the solar constant, with an approximate value of . However, due to scattering and absorption by the atmosphere, only a fraction of this energy, i.e., approximately , actually reaches the Earth’s surface under clear-sky conditions [39].
The total solar radiation reaching the ground consists of:
- Direct radiation, which arrives at the surface on a straight path from the sun;
- Diffuse radiation, which has been scattered by air molecules, aerosols, and clouds, reaching the surface from all directions.
Geographical factors such as latitude, the distribution of land and sea, ocean currents, altitude, and terrain shape play a crucial role in determining the final value of shortwave solar radiation at a given location. The solar energy flux density is not evenly distributed worldwide, depending heavily on sunny days and the total number of sunshine hours. The state and composition of the atmosphere, fog, cloud cover, and the inclination of the receiving surface also have significant impacts.
Some portion of solar radiation is reflected, while part is absorbed by the Earth’s surface and objects on it. Multiple reflections can deliver additional energy to surfaces, increasing their temperature and turning them into sources of longwave thermal radiation.
In the case of outdoor swimming pools, solar radiation is the main natural factor influencing heat gains. The pool water and its walls absorb solar radiation, resulting in an increase in temperature. During the day, the pool water surface is exposed to solar radiation, contributing to heat gains, which can be estimated using the following equation:
where
is the global horizontal irradiance (GHI);
is the absorptivity of the pool;
is the surface area absorbing solar radiation.
This expression holds true if the pool is not shaded by nearby structures. Otherwise, shading must be assessed for each hour through on-site inspection and solar path analysis, considering the geographical location, season, and simulation period.
Regarding the parameter , the literature suggests a typical value of 0.85 for an uncovered pool [30,33,34,40], although other studies indicate that this value can exceed 0.85, even for surfaces with low absorption capacity [41]. Conversely, some studies report values as low as 0.56, while another experimental study found an average of 0.77 [23]. These discrepancies likely result from the complexity of modeling this phenomenon. Wu et al. [42] presented a methodology for assessing variations in solar absorption by shallow water considering factors such as the solar incidence angle, pool depth, the spectral distribution of direct and diffuse radiation components, and the optical properties of the pool bottom.
For covered pools, the total solar absorption by the pool surface (cover) is always lower than for uncovered pools, because absorbed heat from the cover can be lost to the surroundings through convection and thermal emission [38]. If the cover is transparent, part of the solar radiation is absorbed by the cover and part by the pool:
where
is the heat flux of solar radiation absorbed by the cover;
is the heat flux of solar radiation absorbed by the pool through the cover;
is the absorptivity of the cover;
is the absorptivity of the covered pool.
The value of will always be lower than due to the presence of the cover. If for an uncovered pool is assumed and the transparent cover has , then the absorptivity for the covered pool should be assumed at = 0.4 [23]. The air gap between the cover and the water can be neglected in this context.
If the cover is opaque, then = 0 and the cover absorptivity is [23].
Estimating the heat flux from solar radiation on the water surface or cover is relatively straightforward because these surfaces are uniformly illuminated. The situation is more complex for sidewalls, since solar radiation reaches them primarily from one side, meaning only part of their surface is directly exposed. For simplicity, it is assumed that only a portion of the sidewalls is exposed to direct solar radiation, while the remaining area receives mainly diffuse and reflected radiation:
where
is the sidewall area exposed to direct solar radiation;
is the sidewall area exposed to diffuse and reflected radiation;
is the direct solar exposure coefficient.
For a circular pool, may be assumed, implying that half of the sidewall area is exposed to direct solar radiation. For rectangular or other shapes, the sun’s orientation, relative to the pool, must be considered at each moment. A detailed energy analysis should therefore account for the time-varying coefficient.
The heat flux absorbed by the sidewalls is given by:
is the heat flux absorbed by sidewalls exposed to direct solar radiation;
is the heat flux absorbed by sidewalls exposed to diffuse and reflected solar radiation.
The direct absorption by a vertical surface is expressed as:
and analogously for the diffuse and reflected part:
where
is the global tilted irradiance;
is the absorptivity of the pool wall.
The global solar irradiance on tilted surfaces varies significantly depending on whether the surface is predominantly exposed to direct solar radiation or to diffuse and reflected components. In the energy analysis of solar systems and buildings, it is essential to distinguish between the direct normal irradiance (DNI) and the diffuse horizontal irradiance (DHI).
In engineering practice, direct measurements of the total global tilted irradiance, including both direct and diffuse components, are rarely available. Therefore, when only the global horizontal irradiance GHI is measured, decomposition into its direct and diffuse components is required. Although GHI is the most recorded parameter, its decomposition into DNI and DHI typically relies on empirical models. One of the most widely accepted approaches is the correlation developed by Erbs, Klein, and Duffie [43].
The Erbs model uses empirical relationships between the hourly diffuse fraction and the hourly clearness index. The first step is to estimate the extraterrestrial horizontal irradiance , which represents the solar radiation incident on a horizontal surface at the top of the atmosphere. It depends on the day of the year and the geographic latitude and can be calculated based on standard astronomical relations [44].
The solar constant, , represents the average solar irradiance on a unit area normal to the rays at the mean Earth–Sun distance. The eccentricity correction factor is given by:
where denotes the day of the year.
The solar declination angle is:
The hour angle, describing the solar position east–west relative to local solar noon, is:
where is the local solar time [h]. The solar zenith angle is computed as:
where φ is the observer’s latitude.
The extraterrestrial horizontal irradiance is then:
The atmospheric clearness index is defined as:
where is the measured GHI. Typical values of range from 0 (overcast) to 1 (clear sky).
Given , the hourly diffuse fraction can be derived from the Erbs correlation:
The DHI can then be estimated as:
The DNI is subsequently determined by:
valid only for .
To estimate the solar radiation incident on tilted surfaces, transposition models are employed. One widely accepted anisotropic model is the Perez model [45], which accounts for the anisotropic nature of diffuse radiation, yielding more accurate results than isotropic models.
The direct component on a tilted surface is:
where is the incidence angle, calculated as:
where is the tilt angle and is the surface azimuth angle. The solar azimuth is determined from:
The diffuse component on the tilted surface is:
where and are the Perez anisotropy factors, and:
Finally, the reflected component is given by:
where is the ground albedo.
The total global tilted irradiance is then:
2.2.6. External Water Inflow
During the operation of a swimming pool, gradual water losses occur due to physical processes and routine maintenance. The main factors contributing to the reduction in the pool’s working volume include evaporation, water displacement by bathers, and losses during backwashing of the filtration system. In addition to these unavoidable losses, partial renewal of the pool water is recommended (especially in public facilities) to maintain the required hygiene and microbiological standards. Periodic replacement of a portion of the pool water improves overall water quality and enhances the effectiveness of disinfection and treatment processes.
Fresh makeup water is typically supplied at a temperature lower than the operating temperature of the pool water. Under these conditions, the thermal losses associated with the replacement water can be estimated using the following relation [15]:
where
is the volume of supplied water;
is the density of water;
is the specific heat capacity of water;
is the temperature of fresh water.
In the freshwater balance, precipitation must also be considered. Rainfall entering the pool contributes additional water, usually at a temperature lower than the ambient air temperature. It is commonly assumed that the temperature of rainwater can be approximated by , where is the air temperature. In the case of snow, the temperature is generally assumed to be equal to the ambient air temperature, unless the snow is falling at an air temperature above −0.5 °C, in which case the snow temperature is assumed to be −0.5 °C [46].
2.2.7. Heat Gains from the Heating System
The swimming pool heating system is typically a combination of multiple cooperating components that together form an integrated unit ensuring continuous water heating. Depending on the system type, it may include, among others, a circulation pump responsible for water flow, a heat exchanger (e.g., water-to-water or air-to-water), and a filtration system that maintains water cleanliness and quality.
The fundamental operating principle of such a system remains unchanged: water at a lower temperature is drawn from the pool, heated within the system, and then returned to the pool through appropriate diffusers as warm water. The net heat flux delivered to the pool, accounting for thermal losses during water circulation and heat exchange, can be expressed as:
where
is the volumetric flow rate of pool water through the heating system;
is the temperature of heated water;
represents thermal losses due to conduction, radiation from system components, and hydraulic effects.
Due to possible water stagnation phenomena and non-uniform temperature distribution within the pool basin, the optimal point for measuring the temperature of the supply water is directly before it enters the heating circuit. Measuring at this point ensures the most representative value of the cold medium, enabling precise control of the heating process. For the temperature of the heated water , it is recommended to measure it immediately at the outlet to the pool. This sensor location allows real thermal losses occurring during flow through the system to be accounted for, providing a more accurate evaluation of the thermal efficiency and ensuring that the water is delivered to the pool with the required temperature parameters.
In real operating conditions, heating systems are not perfectly efficient; part of the supplied energy is dissipated due to conduction, radiation, and hydraulic effects within the installation. The inclusion of in Equation (65) allows these losses to be explicitly considered in the pool’s thermal balance.
2.2.8. Presence of Users
The presence of bathers in a swimming pool significantly affects the facility’s energy demand, influencing both heat gains and losses. Heat gains result from the transfer of body heat from swimmers to the surrounding water, which locally increases the water temperature. Simultaneously, users disturb the water surface, intensifying evaporation and convective heat exchange, which leads to higher energy losses.
Quantifying the heat exchange between bathers and pool water is complex and depends on multiple dynamic factors. Key parameters include:
- The difference between skin temperature and water temperature (which varies with blood circulation and body region);
- The heat transfer coefficient;
- The degree of body immersion;
- The duration of bathing, and;
- The type and intensity of physical activity.
Skin temperature itself depends on the water temperature and the level of activity. Marino and Booth [47] reported that the average skin temperature remains approximately 3 °C higher than the water temperature during the first 60 min of immersion (with no significant movement). A typical bather who starts with about 8587 kJ of stored body heat can transfer around 473 kJ to the water in three minutes and 545 kJ within an hour. This results in an average heat output of about 2.6 kW during the first three minutes and approximately 151 W after an hour. During intense swimming, the amount of heat transferred is higher, especially initially when heat comes mainly from stored body energy and later also from metabolic heat production due to physical effort [48].
Consequently, the heat gains due to bathers in the overall thermal balance of a swimming pool is particularly complex due to these many variables. There were attempts to estimate this effect—for example, Molineaux et al. [49] propose adding about 400 calories per bather per hour, which can significantly affect the water temperature in heavily used pools.
Additionally, the presence of users increases the evaporation rate due to wave formation, splashing, and direct contact with the water, which enlarges the effective evaporation surface area [50]. However, once a certain occupancy level is reached, the intensification of evaporation and convective losses stabilizes, meaning it no longer increases proportionally with the number of users [15,50]. According to Marín and Garcia-Cascales [50], under full outdoor pool occupancy, the evaporation rate may increase by up to 50% compared to an unoccupied pool.
To account for the impact of bathers on evaporation, a correction factor can be used to calculate the actual evaporation rate for an occupied pool, expressed as:
The factor can be derived from the original model by Marín and Garcia-Cascales [50], neglecting the wetted deck effect:
where is the pool surface utilization factor [−], calculated as:
where
is the maximum pool surface area per user at full occupancy;
is the number of users.
Marín and Garcia-Cascales [50] suggest that a typical value for is about 4.5 m2 per user.
2.2.9. Boundary Conditions for Heat Transfer Model
The heat transfer model can assume the following boundary conditions for the pool system:
Water–air interface:
The water surface can be modeled using a convective boundary condition based on Newton’s law of cooling:
where is the convective heat transfer coefficient, which depends on wind speed and air properties, is the water surface temperature, and is the ambient air temperature.
Pool walls:
External wall surfaces are exposed to ambient air and modeled with combined convective and radiative heat exchange:
where accounts for wind-enhanced convection, and represents longwave radiation exchange. Internally, walls can be assumed to be in thermal contact with the water, enabling conductive heat transfer.
Pool bottom:
The bottom boundary can be treated as adiabatic () because ground-related heat losses in above-ground pools are negligible compared to surface and wall losses [16,41,51].
These assumptions provide a simplified yet physically representative framework for analyzing the thermal balance of above-ground pools under variable climatic conditions.
Moreover, environmental parameters such as solar radiation, wind speed, and ambient temperature are quantitatively incorporated into the boundary conditions of the heat transfer model. These variables are treated as dynamic inputs based on meteorological data and physical laws, allowing for precise simulation of their impact on the pool’s thermal balance under varying climatic conditions.
2.3. Summary of the Heat Balance
The thermal balance of a swimming pool is determined by the combined effects of various heat exchange mechanisms acting simultaneously. These include both heat losses and gains, which must be considered together to maintain the desired water temperature and to ensure energy-efficient operation.
A precise prediction of the pool’s energy performance requires:
- Accurate estimation of each mechanism using empirical correlations or measurement data;
- Consideration of local climate conditions (temperature, humidity, wind, solar radiation, and cloud cover);
- The effect of pool occupancy and its variation throughout operation;
- The presence and properties of covers or enclosures.
Optimizing these heat balance components, for example, by using thermal covers to reduce evaporation and longwave losses, or by managing user occupancy and heating schedules, is essential for improving the energy efficiency of pool facilities and minimizing operational costs.
3. Discussion
Accurately determining the heat balance in systems such as swimming pools requires considering a range of dynamically changing environmental parameters. Practical measurements and accurate representation of real-world conditions pose significant challenges [15]. That is why his section aims to discuss the main measurement difficulties and sources of variability in thermal and environmental parameters that can hinder the accurate determination of heat losses and gains in swimming pools. Limitations of our study were discussed as well.
3.1. Additional Factors
3.1.1. Wind Speed and Its Impact on Convective and Evaporative Heat Losses
Heat losses in swimming pools, resulting primarily from evaporation and convection, are strongly dependent on the wind speed in the immediate vicinity of the pool surface. It is important to note that correlations for forced convection are calibrated using wind speed measurements taken at various heights, typically ranging from 0.3 to 2 m above the pool water surface [41]. In contrast, meteorological stations generally record wind speed at a standard height of 10 m [52], which can lead to significant discrepancies when directly applying these measurements to pool heat loss analyses. Moreover, local site-specific conditions such as buildings, fences, or surrounding vegetation can substantially modify the airflow distribution and intensity over the pool area [53]. Given that evaporation and convection are the dominant mechanisms of heat loss in outdoor pools, properly accounting for wind speed variability at different heights is essential for accurately modeling the pool’s energy balance [15].
For outdoor pools, it is common practice to use the power law expression [52,54,55], which adjusts the wind speed measured at the meteorological station to reflect local site conditions [56]:
where
is the wind speed measured at the reference height;
is the height at which the wind speed measurement was taken;
is the zero-plane displacement height due to nearby obstacles;
is the wind shear exponent.
The displacement parameter accounts for modifications to the undisturbed wind profile caused by obstacles in the pool’s surroundings [15]. If obstacles are present (), the approach [15] assumes that:
- the reference wind speed , measured at height in an unobstructed area, would occur at an increased height () near the pool;
- the wind speed calculated at the height where the forced convection correlation (e.g., Equation (16)) is calibrated will be lower in the vicinity of the pool compared to an unobstructed area.
The wind shear exponent depends on both the terrain roughness and the atmospheric stability class. It is assumed that can be interpolated between the value for smooth terrain and that for rough terrain using the following relation [15]:
where
is the average surface roughness of the area;
is the exponent for smooth surfaces (e.g., rural areas);
is the exponent for rough surfaces (e.g., urban areas).
The roughness parameter is assumed to be 0 for smooth surfaces and 1 for rough surfaces. The values of and are determined according to the Pasquill atmospheric stability classes [57], using the respective values listed in Table 1. The atmospheric stability class is defined based on the reference wind , the global horizontal solar radiation , and the total sky cover , following the criteria given in Table 2.

Table 1.
Wind shear exponents by stability class and terrain type [52].

Table 2.
Pasquill atmospheric stability classes based on wind speed, solar radiation, and sky cover [57].
This method introduces two additional degrees of freedom into the pool heat loss analysis, namely the outer radius (ro) and wall thickness (d). These parameters were selected to capture the most influential geometric factors affecting lateral heat transfer, while maintaining analytical tractability. Expanding the model to include further degrees of freedom, such as multi-layer wall structures, material heterogeneity, or dynamic insulation properties, would significantly increase its complexity and necessitate numerical methods like finite element analysis. Given the theoretical nature of this study, our aim was to develop a simplified yet physically representative framework that supports preliminary energy assessments and design optimization without requiring extensive computational resources. Alternatively, these parameters can be refined using local wind speed measurements at a specific height over an extended period, which allows for calibration to minimize discrepancies between measured and calculated wind speeds. In the absence of local wind data, if the pool’s energy consumption or long-term water temperature changes are known, these parameters can be adjusted to minimize the deviation between actual and modeled heat demand or water temperature [15].
3.1.2. Thermal Stratification and Mixing Assumptions
It is important to note that all heat transfer equations presented in Section 2.2 assume a uniform water temperature throughout the entire pool volume. However, as emphasized by Schramek et al. [58], even a very thin surface layer (e.g., approximately 1 mm thick) can exhibit a temperature drop of several degrees compared to deeper water layers. A reduced temperature gradient between the pool water and the surrounding air lowers the thermal conductivity at the interface, thereby decreasing the overall heat exchange rate between the pool and its environment [59].
Accurately determining a representative pool water temperature is therefore a critical challenge for precise modeling of heat losses, as real pools often exhibit com-plex and dynamic temperature profiles influenced by multiple interacting factors. One such phenomenon is thermal stratification, which refers to the formation of stable fluid layers with different temperatures and densities arranged vertically. This occurs naturally due to the temperature-dependent density of water—warmer water is less dense and tends to rise to the surface, while cooler, denser water sinks to the bottom.
Thermal stratification is a well-known phenomenon across disciplines such as geophysics (e.g., atmospheric and lake stratification) and engineering (e.g., HVAC systems, thermal energy storage). In swimming pools, it is particularly relevant because the warmer, lower-density surface layers enhance evaporation at the water–air inter-face [60], significantly accelerating heat loss and affecting the pool’s overall energy balance. Specifically, stratification can reduce vertical mixing, which limits heat trans-fer from the warmer surface to cooler bottom layers. While this may slow down heat loss from deeper layers, it also creates inefficiencies in heating, as additional energy is required to achieve uniform water temperature for thermal comfort. Moreover, uneven temperature distribution can lead to localized “hot spots” and “cold spots,” com-plicating thermal management and energy optimization.
In outdoor pools, intense solar radiation during the day often leads to pronounced heating of the upper water layers, while deeper layers remain relatively cooler. More-over, temperature gradients may develop not only vertically (with depth) but also horizontally. For example, water near sun-exposed walls may be warmer than water in shaded areas or near surfaces in contact with cooler structures such as the pool floor or walls. Additionally, poorly circulated regions can form stagnant zones that either retain heat or remain cooler, creating localized thermal anomalies.
Despite these complexities, theoretical analyses and thermal balance models often rely on simplifying assumptions. A common simplification is the assumption of a uniform water temperature throughout the pool volume. To justify this assumption, it is typically presumed that adequate water circulation is provided by a pump system with sufficient flow capacity. Such forced circulation continuously mixes the water, theoretically homogenizing the temperature distribution. Studies on hydraulic efficiency in pools, often supported by computational fluid dynamics (CFD) simulations, have shown that the proper placement and capacity of return inlets are crucial for minimizing stagnant zones and ensuring uniform flow patterns [61]. In residential pools, particularly those with shallow depths, bather activity also plays a significant role in mixing water layers. Movements such as swimming, diving, and general play generate turbulence that mechanically disrupts thermal gradients. This natural mixing effect can, in many cases, effectively complement or even partially substitute the function of circulation pumps, resulting in an approximately uniform temperature distribution throughout the pool.
3.1.3. Variability of Solar Radiation
Solar radiation is a primary source of heat gain in swimming pools, particularly in outdoor facilities [15]. However, its intensity and characteristics are highly variable, posing a significant challenge for accurately modeling the thermal balance of such systems. Solar irradiance fluctuates continuously throughout daily and seasonal cycles and is strongly influenced by atmospheric conditions such as cloud cover, fog, and airborne particulates. Additionally, local environmental factors—such as nearby buildings, trees, or landscape features—can create dynamic shading effects on the pool surface, altering the effective solar absorption area throughout the day [39].
Given the complexity of these influences, it is common practice to use average daily or hourly values of solar irradiance on a horizontal plane for practical calculations. These data can be sourced from local meteorological stations, derived from long-term climate datasets for the specific location, or obtained through direct measurement using a calibrated pyranometer installed near the facility.
Nevertheless, due to the inherent difficulty in precisely capturing dynamic shading effects and local variations in ground albedo, simplifying assumptions are often necessary. While these introduce a degree of uncertainty, they enable the development of practical and usable models for engineering applications [15].
3.1.4. Atmospheric Precipitation and Extreme Weather Events
Atmospheric precipitation affects the thermal behavior of swimming pools in several ways beyond simply altering the water level. In addition to introducing water at a potentially different temperature, precipitation in the form of snow or hail can significantly impact on the thermal balance due to the latent heat absorbed during melting [46]. This phase change can extract substantial thermal energy from the pool water. Moreover, precipitation can modify heat exchange processes on surfaces such as pool walls or covers (if present). The formation of a water film on these surfaces alters the dominant heat transfer mechanisms; for example, standard correlations for forced convection may no longer apply due to changes in boundary conditions and airflow behavior over wetted surfaces.
Sudden weather events, such as thunderstorms or strong gusty winds, can also have a pronounced impact on the pool’s heat balance. These events are typically characterized by rapid air temperature fluctuations, intense precipitation (including hail), and high wind speeds—all of which can dramatically increase heat losses over a short period. Models based on time-averaged weather data may fail to capture the magnitude of such transient effects, potentially underestimating actual heat losses during extreme conditions. Accurately accounting for these phenomena in thermal balance models is challenging without access to high-resolution meteorological data, both temporally and spatially, which is rarely available in practical applications [62,63].
3.2. Complexity of the Swimming Pool Heat Balance and Practical Implications
Determining the heat balance of a swimming pool is a complex task due to the large number of interrelated parameters involved in the modeling process. These variables fluctuate continuously throughout the day and night, and their actual values are strongly influenced by the installation site—whether the pool is indoor or outdoor, in-ground or above-ground.
According to various literature sources, evaporation is the dominant mechanism of heat loss in in-ground pools, typically accounting for 40% to 70% of total heat losses. The second most significant contributor is longwave radiation, responsible for approximately 20% to 40% losses, while convective losses are generally less impactful, ranging from 2% to 19% [15,16,64].
In contrast, above-ground pools exhibit a different distribution of heat losses. Heat exchange occurs not only through the water surface but also through the pool walls, which are fully exposed to external factors such as wind and solar radiation. Unlike in-ground pools, where lateral surfaces are insulated by soil, the exposed walls of above-ground pools act as additional heat transfer surfaces. Solar radiation absorbed by the walls can increase their temperature, leading to conductive heat transfer to the water during the day, while at night, these same walls lose heat through longwave radiation and convective cooling. Wind flowing across the external wall surfaces further enhances convective heat losses, particularly under turbulent conditions. This exposure makes heat losses more sensitive to local wind speeds and solar intensity. Consequently, air circulation around the pool structure can significantly increase convective losses compared to scenarios where heat exchange is limited to the water surface. Additionally, the larger exposed surface area affects the distribution of solar heat gains throughout the day, and longwave radiation losses increase due to the expanded radiating surface. However, reliable data quantifying the breakdown of heat losses specifically for above-ground pools remain scarce.
Swimming during colder months remains popular, particularly in hotel and resort settings. As a result, the hospitality and tourism industries invest heavily in outdoor pools and spas designed for year-round operation, including winter. Maintaining comfortable water temperatures in such facilities requires substantial energy input, especially since the target temperature is typically higher than in summer. This leads to increased energy demand. Moreover, average wind speeds during autumn, winter, and spring are higher and more variable than in summer [65,66]. Studies show that reducing the operating water temperature by just 1 °C can lower energy consumption by approximately 7–11% [15,50,67], while covering the pool at night can yield energy savings of up to 30% [15,67].
Neglecting the presence of users in energy consumption models, common in studies of outdoor in-ground pools, can introduce an error of about 10% in annual energy estimates [15]. However, these studies typically focus on public facilities with continuous use. In contrast, private above-ground pools used occasionally are less affected by user activity, which can be considered negligible for modeling purposes, simplifying energy forecasts without significantly compromising accuracy.
Literature also indicates that surface roughness (represented by the parameter r0) influences heat loss. A decrease in r0, assuming a constant displacement parameter d (representing surrounding structures), leads to increased heat loss. In areas with lower surface roughness (typically more exposed to wind) heat losses rise with distance from urbanized zones [15]. This suggests that variability in annual energy consumption among different pools may be attributed to local environmental conditions rather than solely to poor energy management.
Human activity also modifies environmental parameters, particularly in urban areas. Cities exhibit distinct microclimates due to the urban heat island effect, where solar radiation absorbed by buildings, roads, and pavements is re-emitted as heat. As a result, urban air temperatures are often significantly higher than in rural or forested areas [68,69]. Additionally, surrounding infrastructure alters local air circulation, typically reducing wind speeds. These localized conditions, such as surface and air temperatures, wind direction, and speed, become unique characteristics of each urban environment [39].
It is important to emphasize that all equations presented in this article assume a homogeneous water temperature () throughout the pool volume. However, as noted in the literature [58], even a thin surface layer (approximately 1 mm) can exhibit a temperature drop of several degrees compared to deeper water. A reduced temperature gradient between the water and the environment limits thermal conductivity, thereby decreasing the intensity of heat exchange [59].
This observation leads to the concept of optimizing circulation pump operation [59]. When the water temperature is lower than the ambient temperature, running the pump enhances the temperature gradient, promoting heat gains. Conversely, when the water is warmer than the surroundings, turning off the pump helps retain heat by maintaining cooler surface and wall layers, thus reducing heat exchange. Extending pump operation during the day can increase solar heat gains, while shutting it off at night can limit heat losses.
To account for this effect, the following expression is proposed in [59]:
where is the temperature of the water layer in contact with the environment.
Direct solar energy transmission is also highlighted as the most effective method for heating pool water, as energy is absorbed directly by the water and pool shell. In contrast, heating via solar absorption by a pool cover is less efficient. All covers absorb some solar energy and re-emit it as longwave radiation, which is partially transferred to the pool. Transparent covers are the most effective, while opaque covers perform worse. Covering the pool eliminates evaporation losses, significantly reducing nighttime heat loss. However, during the day, covers reduce solar heat gains by limiting direct absorption by the water and shell. For in-ground pools, transparent covers compensate for reduced absorption by eliminating evaporation, resulting in solar efficiency comparable to uncovered pools. In contrast, opaque covers rely solely on re-radiation, leading to approximately 27 ± 4% lower solar efficiency compared to transparent covers [23].
These considerations clearly demonstrate that accurate modeling of swimming pool heat balance requires not only the integration of meteorological and structural data but also flexible approaches that account for operational practices and local environmental conditions.
3.3. Study Limitations
It should be noted that under real operating conditions, the pool cover is often not sufficiently tensioned to maintain a uniform air gap between its underside and the water surface. This can result in local variations in the thickness of the air layer and, in extreme cases, even direct contact between the central portion of the cover and the water. Such non-uniform and potentially intermittent contact conditions introduce nonlinearities that can significantly influence local heat and mass transfer processes. Therefore, advanced thermal models should account for these effects to improve the accuracy of heat loss predictions.
A further limitation of the proposed heat transfer model concerns the treatment of conduction through the pool walls. In the present formulation, the convective resistances at the water–wall and wall–air interfaces are not resolved explicitly but are included in the overall heat transfer coefficient. This modeling choice is consistent with many simplified energy balance approaches applied to swimming pools and building envelopes [17,28,29]. The rationale behind this simplification is twofold. First, the pool analyzed in this study is an above-ground structure with relatively thin walls (most often it is PVC lining), where the conductive resistance of the wall itself is negligible compared with the convective resistances at the fluid–surface boundaries. Second, the aim of this work is to provide a practically applicable heat balance framework that can be used for comparative analyses and operational assessments rather than for detailed local temperature field predictions.
We acknowledge that the assumption of bulk water and ambient air temperatures in conduction equations may introduce a degree of inaccuracy in specific scenarios, especially for pools with thick concrete walls or with layered insulation systems, where the conductive resistance becomes significant. In such cases, resolving the thermal resistances separately and accounting for wall surface temperatures on both sides would improve the accuracy of the model. However, for the type of pool considered in this study, the potential error is marginal and does not affect the overall conclusions. This simplification is therefore considered acceptable, while more detailed formulations may be pursued in future studies focusing on thermally massive or insulated pool structures.
4. Conclusions
Our study provides a theoretical and mathematical framework for analyzing heat gains and losses in above-ground outdoor swimming pools under climatic conditions typical of Central and Eastern Europe. The results highlight several key findings and practical implications:
- Dominant heat transfer mechanisms—evaporation remains the primary source of heat loss, strongly influenced by wind speed and air temperature. Convection and longwave radiation also play significant roles, particularly during cooler periods;
- Impact of operational strategies—daytime water circulation enhances solar heat gains but increases nighttime losses, emphasizing the need for time-controlled pump operation;
- Effectiveness of covers—transparent covers offer the best trade-off between reducing evaporation and maintaining solar gains, while opaque covers, although effective in limiting evaporation, significantly reduce solar heating;
- Seasonal challenges—heating pools during colder months is highly energy-intensive due to low ambient temperatures, turbulent winds, and reduced solar radiation, making passive measures and wind protection critical for cost control.
4.1. Practical Recommendations
Based on the findings, the following recommendations are organized into three categories to support pool designers and operators in improving thermal performance and cost-efficiency:
Design recommendations:
- Optimize pool geometry—select a design with a favorable surface-to-volume ratio to reduce evaporation losses. Deeper pools with smaller surface areas are more thermally efficient;
- Choose sheltered locations—position the pool in areas protected from wind by natural or artificial barriers (e.g., vegetation, fences, buildings) without obstructing sunlight;
- Orient non-circular pools—align the longest sidewall toward the south to maximize solar exposure;
- Consider sidewall insulation—it reduces lateral heat losses, especially for pools used beyond the summer season.
Operational strategies:
- Use transparent covers—these reduce evaporation while allowing solar radiation to heat the water, offering a good balance between energy retention and gain;
- Control pump operation—run circulation pumps during sunny daytime hours to enhance solar heat absorption and switch them off at night to minimize heat loss;
- Maintain optimal temperature—keep water temperature between 25 and 28 °C to balance thermal comfort and energy efficiency.
Cost-efficiency measures:
- Install windbreaks—strategic placement of fences or hedges can reduce convective losses without shading the pool;
- Avoid insulating the pool floor—ground-related heat losses are minimal in above-ground pools, making floor insulation generally not cost-effective;
- Evaluate solar mats cautiously—unglazed solar collectors may offer supplemental heating but often have limited efficiency and durability.
To support practical implementation, Table 3 presents a practical guidance matrix, summarizing the recommended measures.

Table 3.
Recommendation priority matrix for pool energy efficiency.
This matrix organizes key recommendations into categories and evaluates them based on implementation complexity, cost–benefit priority, and suggested practical relevance. It is designed to support decision-making by pool designers and operators, helping them prioritize actions that offer the greatest impact with feasible effort.
4.2. Additional Considerations
- Sidewall insulation can reduce lateral heat losses, though its cost-effectiveness depends on usage duration;
- Innovative solutions, such as placing pools inside greenhouses, can significantly reduce heat losses but require careful design to avoid overheating and humidity issues.
4.3. Future Research Directions
Accurate prediction of pool energy demand requires advanced modeling techniques, such as finite element analysis and computational fluid dynamics (CFD), to capture local wind effects, stratification, and dynamic weather conditions. These tools offer actionable benefits for both designers and operators. For example, CFD simulations can help optimize heating cycles by identifying zones of thermal stratification and guiding pump operation schedules to improve temperature uniformity. Finite element analysis can be used to evaluate the impact of wind exposure and insulation strategies, enabling more effective placement of windbreaks or selection of materials. Additionally, both methods support the design of pool geometries and orientations that maximize solar gains and minimize convective losses under specific climatic conditions.
Future studies should also incorporate experimental validation and explore the integration of renewable energy systems, such as solar thermal collectors, to develop sustainable and cost-effective heating strategies.
5. Patents
This article is related to the following patent: Chwietczuk, P.; Dziubiński, Ł. A system for controlling the heating and filtration of water in a garden pool. News of the RP Patent Office 2024, 38, 8 [70].
The above patent describes a practical implementation of a system for managing the heating and filtration processes in above-ground outdoor swimming pools. The patent solution complements the theoretical analysis presented in this paper by providing an applied method for efficient management and operational control of residential pools.
Author Contributions
Conceptualization, Ł.D. and S.L.; methodology, Ł.D. and P.C.; formal analysis, Ł.D. and S.L.; investigation, Ł.D.; resources, Ł.D., P.C. and S.L.; writing—original draft preparation, S.L. and Ł.D.; writing—review and editing, Ł.D. and P.C.; visualization, Ł.D. and P.C.; supervision, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Middlestadt, S.E.; Anderson, A.; Ramos, W.D. Beliefs about using an outdoor pool: Understanding perceptions of place in the context of a recreational environment to improve health. Health Place 2015, 34, 1–8. [Google Scholar] [CrossRef]
- Bernard, A.; Nickmilder, M.; Voisin, C. Outdoor swimming pools and the risks of asthma and allergies during adolescence. Eur. Respir. J. 2008, 32, 979–988. [Google Scholar] [CrossRef] [PubMed]
- Ramos, W.D.; Anderson, A.R.; Middlestadt, S.E.; Bhurosy, T. An examination of an outdoor pool’s contributions to well-Being: Predicting different dimensions of well-Being from the use of an outdoor community pool. Ann. Leis. Res. 2021, 24, 414–429. [Google Scholar] [CrossRef]
- Lovell, D.; Rickerby, T.; Vandereydt, B.; Do, L.; Wang, X.; Srinivasan, K.; Chua, H.T. Thermal performance prediction of outdoor swimming pools. Build. Environ. 2019, 160, 106167. [Google Scholar] [CrossRef]
- Ilona, J.; Bartók, B.; Dumitrescu, A.; Cheval, S.; Gandhi, A.; Tordai, Á.V.; Weidinger, T. Using long-term historical meteorological data for climate change analysis in the Carpathian region. Atmosphere 2022, 13, 1751. [Google Scholar] [CrossRef]
- Karamushka, V.; Boychenko, S.; Kuchma, T.; Zabarna, O. Trends in the environmental conditions, climate change and human health in the southern region of Ukraine. Sustainability 2022, 14, 5664. [Google Scholar] [CrossRef]
- Cardemil, J.M.; Schneider, W.; Behzad, M.; Starke, A.R. Thermal analysis of a water source heat pump for space heating using an outdoor pool as a heat source. J. Build. Eng. 2021, 33, 101581. [Google Scholar] [CrossRef]
- Gomez-Guillen, J.J.; Arimany-Serrat, N.; Tapias Baqué, D.; Giménez, D. Water and energy sustainability of swimming pools: A case model on the Costa Brava, Catalonia. Water 2024, 16, 1158. [Google Scholar] [CrossRef]
- Ilgaz, R.; Yumrutaş, R. Heating performance of swimming pool incorporated solar assisted heat pump and underground thermal energy storage tank: A case study. Int. J. Energy Res. 2022, 46, 1008–1031. [Google Scholar] [CrossRef]
- Liebersbach, J.; Żabnieńska-Góra, A.; Polarczyk, I.; Sayegh, M.A. Feasibility of grey water heat recovery in indoor swimming pools. Energies 2021, 14, 4221. [Google Scholar] [CrossRef]
- Pomorski, M.; Kołodko, Z. An analysis of heat losses from an all-year outdoor swimming pool. Instal 2022, 9, 37–42. [Google Scholar]
- Ratajczak, K.; Szczechowiak, E.; Pobudkowska, A. Energy-Saving Scenarios of an Existing Swimming Pool with the Use of Simple in Situ Measurement. Energies 2023, 16, 5886. [Google Scholar] [CrossRef]
- Smith, C.C.; Löf, G.; Jones, R. Measurement and analysis of evaporation from an inactive outdoor swimming pool. Sol. Energy 1994, 53, 3–7. [Google Scholar] [CrossRef]
- Above Ground Swimming Pools Market Analysis, Size, and Forecast 2025-2029: North America (US, Canada, and Mexico), Europe (France, Germany, Italy, Spain, and UK), APAC (Australia and China), and Rest of World (ROW). Available online: https://www.technavio.com/report/above-ground-swimming-pools-market-analysis (accessed on 1 July 2025).
- Buscemi, A.; Biondi, A.; Catrini, P.; Guarino, S.; Brano, V.L. A novel model to assess the energy demand of outdoor swimming pools. Energy Conv. Manag. 2024, 302, 118152. [Google Scholar] [CrossRef]
- Woolley, J.; Harrington, C.; Modera, M. Swimming pools as heat sinks for air conditioners: Model design and experimental validation for natural thermal behavior of the pool. Build. Environ. 2011, 46, 187–195. [Google Scholar] [CrossRef]
- Tarrad, A.H. Heating mechanism and energy analyses for over-ground outdoor swimming pool technology. Asian J. Appl. Sci. Technol. 2017, 1, 8–22. [Google Scholar]
- Mirsadeghi, M.; Costola, D.; Blocken, B.; Hensen, J.L. Review of external convective heat transfer coefficient models in building energy simulation programs: Implementation and uncertainty. Appl. Therm. Eng. 2013, 56, 134–151. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Inan, M.; Atayılmaz, Ş.Ö. Experimental investigation of evaporation from a horizontal free water surface. Sigma J. Eng. Nat. Sci. 2017, 35, 118–131. [Google Scholar]
- Poós, T.; Varju, E. Mass transfer coefficient for water evaporation by theoretical and empirical correlations. Int. J. Heat Mass Transf. 2020, 153, 119500. [Google Scholar] [CrossRef]
- Irmak, S.; Skaggs, K.E.; Chatterjee, S. A review of the Bowen ratio surface energy balance method for quantifying evapotranspiration and other energy fluxes. Trans. ASABE 2014, 57, 1657–1674. [Google Scholar] [CrossRef]
- Waché, R.; Fielder, T.; Dickinson, W.E.; Hall, J.L.; Adlington, P.; Sweeney, S.J.; Clowes, S.K. Selective light transmission as a leading innovation for solar swimming pool covers. Sol. Energy 2020, 207, 388–397. [Google Scholar] [CrossRef]
- Sartori, E. Convection coefficient equations for forced air flow over flat surfaces. Sol. Energy 2006, 80, 1063–1071. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Ramsey, J.W.; Mass, E.A. Effect of finite width on heat transfer and fluid flow about an inclined rectangular plate. J. Heat Transf. 1979, 101, 204–210. [Google Scholar] [CrossRef]
- Cole, R.J.; Sturrock, N.S. The convective heat exchange at the external surface of buildings. Build. Environ. 1977, 12, 207–214. [Google Scholar] [CrossRef]
- Gliah, O.; Kruczek, B.; Etemad, S.G.; Thibault, J. The effective sky temperature: An enigmatic concept. Heat Mass Transf. 2011, 47, 1171–1180. [Google Scholar] [CrossRef]
- Koehn, A. 2021 Ashrae Handbook–Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Peachtree Corners, GA, USA, 2021. [Google Scholar]
- Root, D.E. Designing and Installing Solar Commercial Pool Heating Systems; Florida Solar Energy Center: Cape Canaveral, FL, USA, 1983. [Google Scholar]
- Buonomano, A.; De Luca, G.; Figaj, R.D.; Vanoli, L. Dynamic simulation and thermo-economic analysis of a PhotoVoltaic/Thermal collector heating system for an indoor–outdoor swimming pool. Energy Conv. Manag. 2015, 99, 176–192. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Asdrubali, F. On the sky temperature models and their influence on buildings energy performance: A critical review. Energy Build. 2019, 183, 607–625. [Google Scholar] [CrossRef]
- Katsaprakakis, D.A. Comparison of swimming pools alternative passive and active heating systems based on renewable energy sources in Southern Europe. Energy 2015, 81, 738–753. [Google Scholar] [CrossRef]
- Ruiz, E.; Martínez, P.J. Analysis of an open-air swimming pool solar heating system by using an experimentally validated TRNSYS model. Sol. Energy 2010, 84, 1917–1928. [Google Scholar] [CrossRef]
- Zsembinszki, G.; Farid, M.M.; Cabeza, L.F. Analysis of implementing phase change materials in open-air swimming pools. Sol. Energy 2012, 86, 708–718. [Google Scholar] [CrossRef]
- Guo, Y.; Cheng, J.; Liang, S. Comprehensive assessment of parameterization methods for estimating clear-sky surface downward longwave radiation. Theor. Appl. Climatol. 2019, 135, 1045–1058. [Google Scholar] [CrossRef]
- Carmona, F.; Rivas, R.; Caselles, V. Estimation of daytime downward longwave radiation under clear and cloudy skies conditions over a sub-humid region. Theor. Appl. Climatol. 2014, 115, 509–519. [Google Scholar] [CrossRef]
- Martin, M.; Berdahl, P. Characteristics of infrared sky radiation in the United States. Sol. Energy 1984, 33, 321–336. [Google Scholar] [CrossRef]
- Crawford, T.M.; Duchon, C.E. An improved parameterization for estimating effective atmospheric emissivity for use in calculating daytime downwelling longwave radiation. J. Applied Meteorol. 1999, 38, 1424–1430. [Google Scholar] [CrossRef]
- Dylla, A. Thermal Physics of Buildings in Practice: Heat and Moisture Calculations; PWN: Warsaw, Poland, 2015. [Google Scholar]
- Lam, J.C.; Chan, W.W. Life cycle energy cost analysis of heat pump application for hotel swimming pools. Energy Conv. Manag. 2001, 42, 1299–1306. [Google Scholar] [CrossRef]
- Hahne, E.; Kübler, R. Monitoring and simulation of the thermal performance of solar heated outdoor swimming pools. Sol. Energy 1994, 53, 463–469. [Google Scholar] [CrossRef]
- Wu, H.; Tang, R.; Li, Z.; Zhong, H. A mathematical procedure to estimate solar absorptance of shallow water ponds. Energy Conv. Manag. 2009, 50, 1438–1444. [Google Scholar] [CrossRef]
- Erbs, D.G.; Klein, S.A.; Duffie, J.A. Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy 1982, 28, 293–302. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, Photovoltaics and Wind, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Perez, R.; Stewart, R.; Seals, L.; Gueymard, R. An anisotropic hourly diffuse radiation model for sloping surfaces. Sol. Energy 1987, 39, 461–469. [Google Scholar]
- Pająk, L. Heat and mass exchange for year-long open swimming pools-mathematical model of occurring processes. Part I. Dist. Heat. Heat. Vent. 2008, 39, 37–42. [Google Scholar]
- Marino, F.; Booth, J. Whole body cooling by immersion in water at moderate temperatures. J. Sci. Med. Sport. 1998, 1, 73–81. [Google Scholar] [CrossRef]
- Teległów, A.; Bilski, J.; Marchewka, A.; Głodzik, J.; Jaśkiewicz, J.; Staszek, P. Cechy reakcji organizmu na wysiłek fizyczny w niskiej temperaturze wody. Med. Sport. Pract. 2008, 9, 66–72. [Google Scholar]
- Molineaux, B.; Lachal, B.; Guisan, O. Thermal analysis of five outdoor swimming pools heated by unglazed solar collectors. Sol. Energy 1994, 53, 21–26. [Google Scholar] [CrossRef]
- Marín, J.; García-Cascales, J. Dynamic simulation model and empirical validation for estimating thermal energy demand in indoor swimming pools. Energy Effic. 2020, 13, 955–970. [Google Scholar] [CrossRef]
- Li, Y.; Nord, N.; Huang, G.; Li, X. Swimming pool heating technology: A state-of-the-art review. Build Simul. 2021, 14, 421–440. [Google Scholar] [CrossRef]
- Ying, M.; Wang-Li, L.; Stikeleather, L.F.; Edwards, J. Measurements and visualization of the fluid field of the plume from an animal housing ventilation fan. J. Environ. Prot. 2017, 8, 867–877. [Google Scholar] [CrossRef]
- Rakopoulos, C.D.; Vazeos, E. A model of the energy fluxes in a solar heated swimming pool and its experimental validation. Energy Conv. Manag. 1987, 27, 189–195. [Google Scholar] [CrossRef]
- Gualtieri, G. Improving investigation of wind turbine optimal site matching through the self-organizing maps. Energy Convers. Manag. 2017, 143, 295–311. [Google Scholar] [CrossRef]
- Nakajima, K.; Yamanaka, T.; Ooka, R.; Kikumoto, H.; Sugawara, H. Observational assessment of applicability of Pasquill stability class in urban areas for detection of neutrally stratified wind profiles. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104337. [Google Scholar] [CrossRef]
- Abubaker, A.; Kostić, I.; Kostić, O. Numerical modelling of velocity profile parameters of the atmospheric boundary layer simulated in wind tunnels. IOP Conf. Ser. Mater. Sci. Eng. 2018, 393, 012025. [Google Scholar] [CrossRef]
- Pasquill, F. The estimation of the dispersion of windborne material. Meteorogy Mag. 1961, 90, 20–49. [Google Scholar]
- Schramek, E.R.; Recknagel, H.; Sprenger, E. Pocket Book for Heating and Air Conditioning Technology 05/06 Including Warm Water and Refrigeration Technology, 72nd ed.; Oldenbourg Wissenschaftsverlag: Munchen, Germany, 2005. [Google Scholar]
- Pająk, L. Heat and mass exchange for year-long open swimming pools-mathematical model of occurring processes. Part II. Dist. Heat. Heat. Vent. 2008, 39, 15–17. [Google Scholar]
- Sekine, M.; Tsukamoto, N.; Masuhara, Y.; Furuya, M. Experimental study on thermal stratification in water pool with vertical heat source. Ann. Nucl. Energy 2024, 207, 110681. [Google Scholar] [CrossRef]
- Zhang, J.; Sinha, N.; Ross, M.; Tejada-Martínez, A.E. Computational fluid dynamics analysis of the hydraulic (filtration) efficiency of a residential swimming pool. J. Water Health 2018, 16, 750–761. [Google Scholar] [CrossRef]
- Prokhorova, U.V.; Terekhov, A.V.; Demidov, V.E.; Romashova, K.V.; Barskov, K.V.; Chechin, D.G.; Vasilevich, I.I.; Tretiakov, M.V.; Ivanov, B.V.; Repina, I.A.; et al. Impact of Extreme Weather Events on the Surface Energy Balance of the Low-Elevation Svalbard Glacier Aldegondabreen. Water 2025, 17, 274. [Google Scholar] [CrossRef]
- Newman, A.J.; Kalb, C.; Chakraborty, T.C.; Fitch, A.; Darrow, L.A.; Warren, J.L.; Strickland, M.J.; Holmes, H.A.; Monaghan, A.J.; Chang, H.H. The High-resolution Urban Meteorology for Impacts Dataset (HUMID) daily for the Conterminous United States. Sci. Data 2024, 11, 1321. [Google Scholar] [CrossRef]
- Bernhard, M.; Marc, O.; Quilichini, E.; Castaing-Lasvignottes, J. Sensitivity analysis of an outdoor swimming pool under dynamic conditions. Procedia Manuf. 2019, 35, 124–129. [Google Scholar] [CrossRef]
- Hadjipetrou, S.; Kyriakidis, P. High-Resolution Wind Speed Estimates for the Eastern Mediterranean Basin: A Statistical Comparison Against Coastal Meteorological Observations. Wind 2024, 4, 311–341. [Google Scholar] [CrossRef]
- Hoxha, B.; Kuriqi, A.; Filkoski, R.V. Influence of seasonal air density fluctuations on wind speed distribution in complex terrains in the context of energy yield. Energy Ecol. Environ. 2024, 9, 175–187. [Google Scholar] [CrossRef]
- Mousia, A.; Dimoudi, A. Energy performance of open air swimming pools in Greece. Energy Build. 2015, 90, 166–172. [Google Scholar] [CrossRef]
- Garvey, S.M.; Templer, P.H.; Pierce, E.A.; Reinmann, A.B.; Hutyra, L.R. Diverging patterns at the forest edge: Soil respiration dynamics of fragmented forests in urban and rural areas. Glob. Change Biol. 2022, 28, 3094–3109. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Lan, X.; Lian, Y.; Zhao, F.; Li, T. Estimation of Urban–Rural Land Surface Temperature Difference at Different Elevations in the Qinling–Daba Mountains Using MODIS and the Random Forest Model. Int. J. Environ. Res. Public Health 2022, 19, 11442. [Google Scholar] [CrossRef] [PubMed]
- Chwietczuk, P.; Dziubiński, Ł. A system for controlling the heating and filtration of water in a garden pool. News RP Pat. Off. 2024, 38, 8. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).