A Multi-Output Ensemble Learning Approach for Multi-Day Ahead Index Price Forecasting

Abstract

The stock market index future price forecasting is one of the imperative financial time series problems. Accurately estimated future closing prices can play important role in making trading decisions and investment plannings. This work proposes a new multi-output ensemble framework that integrates the hybrid systems generated through importance score based feature weighted learning models through a continuous multi-colony ant colony optimization technique (MACO-LD) for multi-day ahead index future price forecasting. Importance scores are obtained through four different importance score generation strategies (F-test, Relief, Random Forest, and Grey correlation). Multi-output variants of three baseline learning algorithms are brought in to address multi-day ahead forecasting. This study uses three learning algorithms namely multi-output least square support vector regression (MO-LSSVR), multi-output proximal support vector regression (MO-PSVR) and multi-output $\epsilon$-twin support vector regression (MO-$\epsilon$-TSVR) as the baseline methods for the feature weighted hybrid models. For the purpose of forecasting the future price of an index, a comprehensive collection of technical indicators has been taken into consideration as the input features. The proposed study is tested over eight index futures to explore the forecasting performance of individual hybrid predictors obtained after incorporating importance scores over baseline methods. Finally, multi-colony ant colony optimization algorithm is employed to construct the ensemble results from the feature weighted hybrid models along with baseline algorithms. The experimental results for all the eight index futures established that the proposed ensemble of importance score based feature weighted models exhibits superior performance in index future price forecasting compared to the baseline methods and that of importance score based hybrid methods.

1. Introduction

The stock market is a convoluted sector due to the chaotic and non-linear nature of the stock price. Thus, the precise forecasting of future stock index prices is a stimulating yet demanding task. It is observed that many factors, both economic and non-economic factors, influence the behavior of a stock price [1,2]. Closing prices always appear to be an important measure in stock market decision-making. A better approximation of the closing price beforehand enables investors to make trading decisions. A number of statistical models (AR, ARMA, ARIMA) [3] have been introduced to solve this encounter. However, the evolution of machine learning techniques and their high generalization capabilities have been proven efficient in financial time series forecasting [4]. Artificial Neural Networks (ANNs) and Support Vector Machines (SVMs) have been widely used in financial market price forecasting problems.

Drucker et al. [5] developed Support Vector Machine for regression problem (SVR), which opened the gateway for future research perspectives in time series forecasting using SVM networks. Early research shows the efficient application of SVR in financial time series forecasting. Tay et al. [6] first examined the possibility of using SVR in financial forecasting. The experiments were performed over five future contracts which shows the efficiency of SVR over BPNN (Back Propagation Neural Networks) in financial time series forecasting. Kim [7] uses SVR in index price forecasting and shows SVR as a possible alternative in index price forecasting. Pai et al. [8] developed a hybrid structure that assimilates the linear prediction power of ARIMA with the non-linear forecasting merits of SVR in stock price forecasting. The presented work displayed improvement in the forecasting performance after the use of hybrid techniques.

The evolution of Deep Neural Networks stimulated the research on the application of DNNs in financial time series forecasting [9]. Recent studies have witnessed vast productive developments in the stock market price forecasting using Neural Networks. Tsang et al. [10] implemented a back-propagation neural network version (NN5) for stock market price forecasting. The proposed method experimented on Hong Kong Stock and HSBC holdings, which suggested improvement over earlier works. Yu et al. [11] proposed a meta learning approach to produce a nonlinear meta-learning model based on neural networks for financial time series forecasting. This meta modeling approach first generates different base models over feed forward neural networks for different input sets produced from different initial setups and later integrates these base models to get the final meta model. An integration proposal for combining Genetic fuzzy systems with self organizing ANN was proposed by [12]. The proposed approach uses step-wise regression to select the influencing input features for the stock price. Later, it used self organizing ANN to create clusters from the stock historical data. Furthermore, the clusters used as genetic fuzzy system feeds to generate future stock price. A hybrid stock price forecasting model using deep learning algorithms is presented in [13]. The model uses CEEMD, SE, ICA, PSO, and LSTM to simplify data and boost statistical efficiency. The model is tested on four Chinese stock prices and found it accurate and robust. The proposed work integrate granular computing with decomposition and ensemble to build non-stationary data forecasting models. By integrating BPNN with ensemble empirical mode decomposition (EEMD), a new hybrid model is constructed in [14], improving prediction accuracy and robustness. The new hybrid model outperforms the existing EEMD-LSTM model in international gold price series forecasting. A detailed literature review for financial time series forecasting using Deep NNs is found in [9]. The article explores over a period of 15 years from 2005 to 2019 to investigate the applications of DNNs in Financial time series forecasting. Ray et al. [15] presents a hybrid algorithm for forecasting multiple correlated time-series data using a multivariate Bayesian structural time series approach and an M-TCN. The algorithm accurately predicts stock price movements, COVID-19 pre-lockdown data from Nifty stock sectoral indices, and newspaper and social media sentiment. The hybrid model predicts pandemic stock market trends better than benchmark models.

Traditional methods have limitations toward nonlinear high fluctuations in financial price data. Conventional forecasting models, including Autoregressive Integrated Moving Average (ARIMA) and Support Vector Regression (SVR), are proficient for short-term predictions but frequently encounter difficulties with long-term dependencies and nonlinear patterns. Therefore, Zhipeng et al. [16] use candlestick patterns to implement a noise removal process on financial data. Later, a Cooperative Co-evolution infused SVR was used to predict financial time series. Gupta et al. [17] proposed a Twin-SVR based approach for forecasting financial time series to deal with non-stationary noisy data. Lahmir [18] presented a hybrid approach, VMD-PSO-BPNN, for intraday stock price forecasting. Proposed approach first uses Variational Mode Decomposition to generate different variation modes of the price data for input features and later uses Back Propagation Neural Network as predictive learning system with the Particle Swarm Optimization technique is used for initial initial weights optimization of BPNN.

Traditional approaches are based on the assumption that all the features have equal contributions toward the target variable. Nevertheless, the assumption is not always sufficient in the practical world, and individual features have their own importance toward the output variables. Thus, the performance of a learning technique can be improved by assigning different weights to the input features. For instance, Wang et al. [19] showed that the generalization capability and performance of SVM can be improved by assigning different weights to different input features. Following this study, Zhang et al. [20] used rough set theory based information gain to determine the feature weights of a SVM classifier. Liu et al. [21] investigated the application of Grey correlation based feature weighted SVR model for stock price forecasting. The proposed hybrid feature weighted SVR method and the baseline SVR were tested over the stock data from China and the experiments indicated improvements in forecasting performance after incorporating weighted features with support vector regression. Yu et al. [22] presents an LSSVR ensemble learning framework for predicting crude oil prices, taking into account user-defined parameters as uncertain variables. The methodology employs a grid technique for estimating a low upper bound, generates stochastic parameters, and integrates the outcomes.

A review of the literature suggests that it is not possible to develop an individual standalone model that can be appropriate for every stock market. Earlier research less explores the possibility of multi-day ahead forecasting. An alternative proposal is to use diverse techniques as individual forecasting models. Recent works have focused on hybrid combined ensemble models in time series forecasting. The ensemble models make use of the merits of all individual forecasting results to produce one improved ensemble result [23,24,25]. The motivation behind all ensemble models is to consider all the individual models as independent contributors and to intelligently integrate the responses to produce ensemble forecast results. Traditional ensemble models, such as bagging and boosting, apply static weights to base learners, optimizing for a single-step forecast [26]. These methods often struggle with multi-day forecasting, where error propagation is significant. Ensemble learning frameworks address single-output forecasting, where models predict only the next day’s price. For multi-day forecasts, recursive strategies are used, leading to cumulative error. Recursive forecasting, where single-step predictions are iteratively used to predict multi-day ahead prices, introduces cumulative errors [27]. These errors compound over time, reducing accuracy for multi day ahead forecasting. Multi-output forecasting, which predicts multiple future points simultaneously, remains under-explored in ensemble architectures. Although metaheuristic algorithms like Particle Swarm Optimization (PSO) and Genetic Algorithms (GA) have been utilized for hyperparameter tuning [28], their application in dynamic weight optimization for ensemble learning is still constrained. Although Ant Colony Optimization (ACO) has demonstrated promise in combinatorial optimization and path-finding tasks, it is underutilized in financial forecasting.

Inspired from the previous works, this study proposes a new ensemble framework that integrates the importance scores with learning algorithms through a Multi-colony Ant Colony Optimization techniques. This ensemble approach incorporates different importance score generation strategies to determine the importance of an input feature and later uses it to build new feature weighted input spaces. Afterward, it uses three multi-output improved variants of Support Vector Regression as baseline learning algorithms. The three baseline algorithms incorporated in this work (i.e., MO-LSSVR, MO-PSVR and MO-$\epsilon$-TSVR) have computational advantages over SVR, and earlier research shows improvement in performance toward price forecasting problems [29,30,31,32]. In the final stage, a multi-colony variant of ACO-LD (MACO-LD) [33] is used to combine the hybrid models generated by integrating importance score based weighted features with baseline methods to construct the final multi-output ensemble model. The proposed framework dynamically adjusts the contributions of base learners for each forecast horizon. This ensures that model weights are optimized based on real-time performance, enhancing adaptability to market conditions. The multi-output framework generates multi-day ahead future values in a single pass, thus minimizes error propagation, a critical issue in recursive forecasting. This increases the accuracy of multi-day ahead predictions without relying heavily on iterative processes. The exploration-exploitation mechanism of ACO dynamically fine-tunes ensemble weights, preventing local optima and ensuring that the ensemble evolves with changing market dynamics. This metaheuristic-driven optimization differentiates the framework from traditional ensemble learning methods that rely on static weight assignments.

The main contributions of this proposed study are summarized as follows:

• This work proposes a new importance score based feature weighted ensemble model for index future price forecasting. The merits of Importance scores, multi-output baseline algorithms, and the intelligent multi colony ACO-LD [33] technique are integrated for index future price forecasting. This method suggests an ensemble alternative for price forecasting problems in an efficient way.
• Four different types of importance score generation methods (F-test, Relief, Random Forest, and Grey Correlation) are incorporated to generate new feature weighted input feature spaces.
• Three baseline algorithms (LSSVR, PSVR and $\epsilon$-TSVR) are integrated with the new input spaces to generate twelve hybrid feature weighted models. Multi-output versions of the baseline learning algorithms are introduced to address multi-day ahead index price forecasting problem.
• To construct the ensemble model from the hybrid feature weighted models, a multi colony version of ACO-LD optimization technique is introduced to aggregate the hybrid models.
• To illustrate the performance characteristics, experiments have been performed over eight historical index futures price datasets and the input features for forecasting the future price of an index have been chosen from a vast array of technical indicators.
• A detailed discussion is performed for both, on improvements of baseline algorithms after integrating importance scores and the comparison of individual forecasting results with the ensemble forecasting results.

The remainder of the paper is organized as follows. Section 2 briefly reviews the related studies. Different feature importance score generation strategies are introduced in Section 3.1. The baseline forecasting algorithms are explained in Section 3.2 and the complete architecture of the proposed ensemble technique is described in Section 4. Section 4.1 gives details about the input feature space and Section 4.2 describes hybrid models, and finally, Section 4.4 explains the construction of proposed ensemble model. Section 5 comprises the experiments over the index future and the detailed discussion for both hybrid feature weighted models and the ensemble model. Finally, the conclusions from the empirical findings are presented in Section 6.

2. Related Works

Recent works demonstrate the prodigious application of models based on support vector machines in financial time series forecasting. Ince et al. [34] used heuristic models of principal component analysis (PCA) and non-parametric hybrid models with SVR for stock price prediction [35]. The presented works use factor analysis and kernel principal components to find the most important input features. Lu et al. [36] propose a two-stage approach for financial forecasting. They first use independent component analysis to deal with high noise in a financial time series and then use support vector regression in forecasting future prices. Hsu et al. [37] introduced a two-stage hybrid design by using a self-organizing map to decompose the input space with a similar statistical distribution and then using SVR in the later stage in forecasting index prices. A multi-kernel learning based hybrid approach is introduced in [38] for price forecasting. It uses semi-definite programming to derive kernel parameters and Lagrange multipliers simultaneously. Kazem et al. [39] proposed a different forecasting model incorporating the firefly algorithm with SVR and chaotic mapping to forecast the stock market prices. The proposed three staged algorithm first reconstructs phase space dynamics of input space, then it uses the firefly algorithm to tune SVR hyper-parameters and later it uses the optimal SVR model in the prediction of the stock market price. A hybrid $\mu$-SVR model is introduced for stock index price forecasting in [40]. The proposed approach uses PCA for input feature selection, and the Brain-Storm Optimization technique is used to select the optimal parameters of $\mu$-SVR. Pai et al. [30] incorporate LSSVR for stock market price forecasting with different causality scenarios, where historical trading data and social media influences are taken as input features, and correlation is used for feature pruning to obtain independent variables.

Hybrid learning methods incorporating heuristic optimization techniques with Support Vector Machine are being introduced by researchers to increase the performance of price forecasting techniques. Rustam et al. [41] investigated the application of SVR and particle swarm optimization together in forecasting stock prices with several technical indicators as input. PSO is used to select appropriate inputs, and later, SVR is used as the prediction model. Zhang et al. [28] proposed a modified Firefly algorithm to increase the convergence speed. The later stage of the proposed work uses this modified FA with SVR as a hybrid structure for stock price forecasting, where the modified FA is used for the optimal selection of parameters for SVR. Recent works indicate that hybrid combined models are proven to be effective and also improve the forecasting performance of single baseline models. Kumar et al. [31] proposed a hybrid system for market trend forecasting. The proposed method uses different importance scores to build hybrid classification models. The performance comparison implied the superiority of hybrid models over baseline methods. Meng et al. [42] introduced a continuous ACO based ensemble approach with SVR for forecasting the price in cloud manufacturing. The efficacy of the methodology is validated using real-world data in the proposed contribution. Significant generalization performance and dependable outcomes in ensemble learning randomness are achieved by the proposed method, as demonstrated by the experimental outcomes. Chen et al. [13] presents a hybrid model for stock price forecasting using machine learning algorithms, including decomposition and ensemble, independent component analysis, particle swarm optimization, and long short-term memory. The model’s accuracy and robustness were tested on four stock prices from the China stock market. Wang et al. [40] introduces a hybrid v-SVR model for forecasting stock price indexes that incorporates principal component analysis and brain storm optimization. The model, which uses correlation analysis and PCA, accurately approximates the actual CSI300 stock price index. Xu et al. [43] explores stock closing price forecasting using clustering and ensemble learning. K-means clustering and SVR based ensemble model is proposed. The proposed hybrid prediction model obtains the best predicting accuracy of the stock price.

A brief description of supporting studies that built the motivation for the proposed work is summarized in Table 1. These findings validate that ensemble methods, which integrate multiple baseline methods, can produce more precise predictions in comparison to individual methods. The findings indicate that utilizing a diverse ensemble is an appropriate method for forecasting the movement of stock prices in the banking industry of South Africa.

Table 1. Related works.

Author(s)	Data Set	Period (Data Points)	Attributes	Predictor	Comparisons	Performance Metrics	Observations
Hsu et al. [37]	7 Stock Index data	1997–2002	OHLC + TIs	SOM-SVR	SVR	NMSE, DS, MAE	The two-stage hybrid SVR approach can improve the performance of SVR on non-stationary financial time series data.
Lu et al. [36]	Nikkei 225 and TAIEX	1999–2004 (1144)	OLHC + 7TIs	ICA-SVR	Random walk, SVR	RMSE, NMSE, MAD and DS	The proposed ICA–SVR is efficient in finding and removing noise in financial time series data and improving the forecasting capability of baseline SVR.
Yeh et al. [38]	TAIEX	2002-2005	OHLC + TIs	MKSVR	SVR, ARIMA, FNN	RMSE	The proposed two-stage multi-kernel SVR gives superior performance over single-kernel SVR. Moreover, it increases computational complexities.
Kazem et al. [39]	NASDAQ	2007–2011 (670)	OLHC + reconstructed phase space matrix	SVR-FA	SVR, ANN and ANFIS	MSE and MAPE	The proposed hybrid SVR-FA approach suggests that the performance of baseline algorithms can be improved by considering metaheuristics algorithms with learning models.
Meng et al. [42]	cloud manufacturing	2016 (55)	23 Value Measures and Metrics (VMMs)	ACO-based SVR	SVR, BPNN	MSE	ACO-based SVR ensemble learning is efficient for price forecasting problems.
Pai et al. [30]	DJI, SP500 and total 8 index and stock data	2016–2017 (270)	OHLC, Google trend search, news	LSSVR	NA	MAE and MAPE	The proposed work suggests the use of LSSVR, along with news and social sentiments as attributes, performs better than the traditional learning models.
Sedighi et al. [44]	DJI, NASDAQ, SP500	2008–2018 (3000)	OHLC + 20 TIs	ABC-ANFIS-SVM	SVR, NN, ARIMA	RMSE, MAE and MAPE	The proposed ensemble approach uses metaheuristics algorithms along with the traditional SVR model to improve forecasting accuracy when considering high fluctuations in the financial market.
Zhang et al. [28]	Shanghai StockExchange	2015–2017(500)	OHLC	MFA-SVR	SVR, GA-SVR, FA-SVR, PSO-SVR, LSTM	MSE, MAPE and MAE	The proposed MFA-SVR hybrid learning approach suggests the use of metaheuristics-integrated hybrid learning methods can improve the forecasting capability of the baseline SVR learning method.
Rustam et al. [41]	JKSE and real estate stock data	2016–2018 (650)	OHLC + 10TIs	PSO-SVR	SVR	NMSE	The proposed work uses a two-stage hybrid approach that uses PSO for feature selection and, later, SVR as a learning algorithm. Experimental results suggest the use of a metaheuristic-based hybrid approach for price forecasting problems.
Parvini1 et al. [45]	Cryptocurrency	2015–2019 (1372)	OHLC + Volume	PSO-SVR	SVR, LSTM, MLP	RMSE, MAPE and $R^2$	The hybrid PSO-SVR performed better than the baseline algorithms. This work suggests improvement in forecasting capability by adopting a hybrid approach.
Chen et al. [13]	Shanghai Stock Exchange (SSE) 50	2001-2021	OHLC + IMFs	CEEMD-ICA-LSTM	ARIMA, BP, SVM, LSTM, CNN	MAPE, MAE, and RMSE	The decomposition and ensemble-based hybrid forecasting models have proved to be efficient in handling non-stationary data and improving the forecasting capability of baseline models.
Wang et al. [40]	CSI300 and SZSE	2011	OLHC + 20 TIs	v-SVR-BSO	GA-SVR, GA-SVR and PSO-SVR	MSE, MAE and MAPE	The proposed work addresses the feasibility of integrating learning models with metaheuristic algorithms to deliver better forecasting capability.
Xu et al. [43]	Chinese Stock	2008–2019 (2600)	OLHC	E-SVR-RF	SVR and RF-SVR	MAPE, MAE and RMSE	The proposed study makes use of a Random forest-based ensemble SVR model for stock price forecasting problems. The study considers a clustering approach to identify similar technical indicators to reduce complexity and further improve forecasting accuracy.
Liu et al. [21]	China Shenzhen A-share market	2006–2008	OLHC + Tis	FWSVR	Classical SVR	NMSE, MAE and DS	The work suggests the use of Grey Correlation-based hybrid feature weighted learning models can improve the forecasting performance of the baseline algorithms.

Acronyms: OHLC: Open, High, Low, Close, TIs: Technical Indicators, RMSE: Root Mean Square Error, DS: Directional Symmetry, SOM: Self Organizing Map, NMSE: Normed Mean Square Error, MAE: Mean Absolute Error, MAPE: Mean Absolute Percentage Error, MAD: Mean Absolute Deviation, MKSVR: Multi-Kernel SVR, MFA: Modified Firefly Algorithm, ABC: Artificial Bee Colony, GA: Genetic Algorithm, PSO: Particle Swarm Optimization, BSO: Brain Storm Optimization, CEEMD: Complementary ensemble empirical mode decomposition.

3. Methodology

3.1. Feature Importance Score Generation Strategy

A classical regression learning problem $(\left\{\chi ,y\right\},\mathrm{where}\chi =\left\{{\varkappa }_1,{\varkappa }_2,\dots ,{\varkappa }_m\right\},$$y\in \mathbb{R})$ assumes that all the input features $\left({\varkappa }_i\in \chi \right)$ have equal contribution toward response variables. In practice, this is not always followed in real scenarios. Thus the performance of learning methods can be upgraded by weighting the input features according to their importance toward predicting the target variables. In this section, various importance score generation methods presented in this study for forecasting stock index prices are briefly described.

3.1.1. F-Test

One of the simplest means to decide the importance scores of input features is by observing their statistical significance toward the target variables. This can be performed by ANOVA F-statistics or the F-test, where the F-test investigates the null hypothesis that the target values and corresponding values of an input feature are taken from sample populations having the same mean versus the alternative hypothesis is that the sample population means are different. The p-values of the test statistics represent the importance of the corresponding input feature. That is, a small p-value implies that the corresponding feature has important contributions. Thus, the importance scores $I_{f{t}_i}$ for input feature ${\varkappa }_i$ can be calculated as

$$\begin{array}{c}\hfill I_{f{t}_i}=-log{p}_i,i=1,2,\dots ,m\end{array}$$

(1)

3.1.2. Relief Algorithm

Robnik-Sikonja et al. [46] proposed an extension of the ReliefF algorithm [47] for regression. The ReliefF algorithm uses a nearest neighbor algorithm to determine important scores of input features in a classification problem based on proximal class for input samples. In regression ReliefF, proximity is considered according to the comparative distance among forecasted values of two input samples. The importance score $I_{r{l}_i}$ for input feature ${\varkappa }_i$ is described as

$$\begin{array}{c}\hfill I_{r{l}_i}={\displaystyle \frac{{\delta }_{yi}}{{\delta }_y}}-{\displaystyle \frac{{\delta }_i-{\delta }_{yi}}{m-{\delta }_y}},i=1,2,\dots ,m\end{array}$$

(2)

where ${\delta }_y$, ${\delta }_i$ and ${\delta }_{yi}$ are intermediate weights that define the probability of the prediction values being different. ${\delta }_y$ for different predictions y, ${\delta }_i$ for different input featured ${\varkappa }_i$ and ${\delta }_{yi}$ different targeted y and different input featured ${\varkappa }_i$ respectively. m is the number of iterations. Intermediate weights at j-th iteration are calculated as

$$\begin{array}{cc}\hfill {\delta }_y^j=& {\delta }_y^{j-1}+{\Delta }_y\left({\varkappa }_k{\varkappa }_l\right)·d\left({\varkappa }_k{\varkappa }_l\right)\hfill \\ \hfill {\delta }_i^j=& {\delta }_i^{j-1}+{\Delta }_i\left({\varkappa }_k{\varkappa }_l\right)·d\left({\varkappa }_k{\varkappa }_l\right)\hfill \\ \hfill {\delta }_{yi}^j=& {\delta }_{yi}^{j-1}+{\Delta }_y\left({\varkappa }_k{\varkappa }_l\right)·{\Delta }_i\left({\varkappa }_k{\varkappa }_l\right)·d\left({\varkappa }_k{\varkappa }_l\right)\hfill \end{array}$$

(3)

where ${\Delta }_y\left({\varkappa }_k{\varkappa }_l\right)$ is the difference in target y for two features ${\varkappa }_k$ and ${\varkappa }_l$ and $d\left({\varkappa }_k{\varkappa }_l\right)$ is the distance between ${\varkappa }_k$ and ${\varkappa }_l$ [46].

3.1.3. Random Forest

Random Forest [48] is a widely used learning technique for regression and classification problems. Random Forest constructs decision trees with bootstrapped training-data from a subset of selected input features. The present work uses Random Forest to obtain the importance scores by following the procedure described in [31]. In this work, two-thirds of bootstrapped samples are used for the training of decision trees, and the rest of the samples (called as Out-of-a-Bag(OOB)) then utilized for determining feature importance scores. First, all the decision trees ${\mathrm{\Gamma }}_i,i=1,2,\dots ,m$ are trained and then tested using respective OOB samples, and the corresponding error rate ${\epsilon }_{{\mathrm{\Gamma }}_i}$ is obtained. Then, OOB samples are generated through random permutation of features for each decision tree, and the error rates for perturbed OOB samples error rate ${\epsilon }_{{\mathrm{\Gamma }}_i}^{\prime }$ are recorded for each tree ${\mathrm{\Gamma }}_i$. Then the importance score $I_{r{f}_i}$ for input feature ${\varkappa }_i$ is calculated as

$$\begin{array}{c}\hfill I_{r{f}_i}={\displaystyle \frac{1}{m}}\sum _{{\mathrm{\Gamma }}_i}({\epsilon }_{{\mathrm{\Gamma }}_i}-{\epsilon }_{{\mathrm{\Gamma }}_i}^{\prime }),i=1,2,\dots ,m\end{array}$$

(4)

3.1.4. Grey Correlation

Grey system theory [49] was first introduced by Julong Deng in 1982. An integral part of Grey system theory is Grey correlation analysis, which describes the information carried by an input feature toward the target variable. In practical applications, an input feature carries partial information that contributes to generating target variables. Grey correlation thus focuses on those partial information and determines the relational degree between the target y and feature ${\varkappa }_i\in \chi$ through the similarity in their geometric shapes. A higher Grey Correlation Degree indicates the high similarity of the corresponding feature, thus implying more importance of that feature. In this proposed work, the Grey Correlation Degree of an input feature is considered the importance score of the corresponding feature. Let $\chi =({\varkappa }_1,\dots ,{\varkappa }_m)$ be the input feature space, $Y={(y_1,\dots ,y_n)}^T$ be target variables and ${\varkappa }_i={(x_{i1},x_{i2},\dots ,x_{in})}^T$ be an input feature. Then, the importance score through Grey correlation $I_{g{r}_i}$ for input feature ${\varkappa }_i$ is computed as

$$\begin{array}{c}\hfill I_{g{r}_i}={\displaystyle \frac{1}{n}}\sum _{j=1}^n\gamma (y_j,x_{ij}),i=1,2,\dots ,m\end{array}$$

(5)

where the importance score $I_{g{r}_i}$ is actually the Grey correlation degree of ${\varkappa }_i$. $\gamma (y_j,x_{ij})$ is the relation coefficient that can be calculated as

$$\gamma (y_j,x_{ij})={\displaystyle \frac{m_{min}+\eta m_{max}}{\left(|y_j-x_{ij}|\right)+\eta m_{max}}}$$

where $\eta \in (0,1)$ and $m_{min}$ and $m_{max}$ are the minimal and maximal difference values, respectively.

$$m_{min}={min}_i{min}_j\left(|y_j-x_{ij}|\right) \mathrm{a}\mathrm{n}\mathrm{d} m_{max}={max}_i{max}_j\left(|y_j-x_{ij}|\right)$$

3.1.5. Importance Scores Based Feature Weights Generation

In this section, the importance scores obtained from Section 3.1 are used to determine the corresponding feature weight matrices. In general, to obtain the weight matrix, first, let $I=(I_{{\varkappa }_1},\dots ,I_{{\varkappa }_m})$, where I is any one from ($I_{ft},I_{rl},I_{rf},I_{gr}$) and $I_{{\varkappa }_i}$ is the corresponding feature importance score of feature ${\varkappa }_i$. Then, we first normalize the importance score set I, $I^{\prime }=\left({\displaystyle \frac{I_{{\varkappa }_1}}{\left|I\right|}},\dots ,{\displaystyle \frac{I_{{\varkappa }_m}}{\left|I\right|}}\right)$. The weight matrix $V_{m\times m}$ is constructed as a diagonal matrix, where $I_{{\varkappa }_i}^{\prime }\left(\mathrm{i}.\mathrm{e}.,{\displaystyle \frac{I_{{\varkappa }_1}}{\left|I\right|}}\right)$ are the corresponding diagonal elements ${\nu }_{ii}$. The feature weighted new input feature ${\chi }^{\prime }$ is constructed as

$${\chi }^{\prime }=\chi ·V=[{\varkappa }_1{\varkappa }_2\dots {\varkappa }_m]\left[\begin{array}{ccccc}{I}_{{\varkappa }_1}^{\prime }& 0& 0& \dots & 0\\ 0& I_{{\varkappa }_2}^{\prime }& 0& \dots & 0\\ ·& ·& ·& \dots & 0\\ ·& ·& ·& \dots & 0\\ 0& 0& 0& \dots & I_{{\varkappa }_m}^{\prime }\end{array}\right]$$

3.2. Learning Algorithms

3.2.1. Multi-Output Least Square Support Vector Regression

Suykens et al. [50] proposed Least Squares Support Vector Regression (LSSVR) that uses equality constraint in place of inequality constraints of the Support Vector Regression. Thus, the complexity is reduced by solving a linear system of equations.

MO-LSSVR is an extension of the standard LSSVR designed to handle multiple output variables $y_i\in {\mathbb{R}}^m$, by solving a series of optimization problems, one for each output dimension as follows,

$$\underset{(W,b,\zeta )}{min}\left\{{\displaystyle \frac{1}{2}}\sum _{j=1}^m{\parallel {\omega }_j\parallel }^2+{\displaystyle \frac{\gamma }{2}}\sum _{i=1}^k\sum _{j=1}^m{\zeta }_{ij}^2\right\}$$

(6)

subject to the constraints for each training example i and each output dimension j:

$$y_{ij}-({\omega }_j\varphi \left(x_i\right)+b_j)={\zeta }_{ij}$$

(7)

Using Karush-Kuhn-Tucker (KKT) condition, training and testing process of MO-LSSVR is made possible by solving the dual in the form of a system of linear equations. The complete process is described in Algorithm 1.

Algorithm 1 Multi-output Least Square Support Vector Regression (MO-LSSVR)

Require:  Training data ${\left\{(x_i,y_i)\right\}}_{i=1}^N$ where $x_i\in {\mathbb{R}}^d$ and $y_i\in {\mathbb{R}}^m$ Require:  Regularization parameter $\gamma$ Require:  RBF kernel parameter $\sigma$   1: function MO-LSSVR-Training($X,Y,\gamma ,\sigma$)   2:     $N\leftarrow \mathrm{number}\mathrm{of}\mathrm{samples}$   3:     $d\leftarrow \mathrm{dimension}\mathrm{of}\mathrm{input}$   4:     $m\leftarrow \mathrm{dimension}\mathrm{of}\mathrm{output}$   5:     Compute the kernel matrix K: $K_{ij}=exp\left(-{\displaystyle \frac{\parallel x_i-x_j{\parallel }^2}{2{\sigma }^2}}\right)\forall i,j\in \{1,\dots ,N\}$   6:     Construct the block matrix $\Omega =\left[\begin{array}{cc}{\gamma }^{-1}{I}_N& K\\ K^T& 0\end{array}\right]$       where $I_N$ is the $N\times N$ identity matrix.   7:     Construct the target matrix $E=\left[\begin{array}{c}Y\\ 0\end{array}\right]$       where Y is the $N\times m$ output matrix and 0 is an $N\times m$ zero matrix.   8:     Solve the linear system $\Omega \alpha =E$ for $\alpha ={\Omega }^{-1}E$   9:     Extract $\alpha$ and b from the solution: ${\alpha }_{train}\leftarrow \alpha [1:N],$ $b\leftarrow \alpha [N+1:2N]$ 10:     return ${\alpha }_{train},b$ 11: end function 12: function MO-LSSVR-Predict($X_{\mathrm{new}},X,{\alpha }_{train},b,\sigma$) 13:     Compute the kernel matrix $K_{\mathrm{new}}$: $K_{\mathrm{new},ij}=exp\left(-{\displaystyle \frac{\parallel x_{\mathrm{new},i}-x_j{\parallel }^2}{2{\sigma }^2}}\right)$ $\forall i\in \{1,\dots ,\text{num\_new\_samples}\},\forall j\in \{1,\dots ,N\}$ 14:     Predict the output for new inputs: $\widehat{Y}=K_{\mathrm{new}}{\alpha }_{train}+b$ 15:     return $\widehat{Y}$ 16: end function

3.2.2. Multi-Output Proximal Support Vector Regression

Similar to LSSVR, Fung et al. [51] proposed Proximal Support Vector Regression (PSVR). The term in the objective function of LSSVR Section 3.2.1 ${\displaystyle \frac{1}{2}}{\parallel \omega \parallel }^2$ is later replaced with $({\displaystyle \frac{1}{2}}\parallel \omega {\parallel }^2+{\displaystyle \frac{1}{2}}{b}^2)$. This addition of bias makes the above optimization problem a strong convex problem, and PSVR can be interpreted as regularized LSSVR.

PSVR can be extended to Multi-output PSVR to manage multiple target responses $y_i\in {\mathbb{R}}^m$. The optimization problem for PSVR can be modified to deal with multi-output case as follows,

$$\begin{array}{cc}\hfill \underset{W,B,\xi ,{\xi }^{*}}{min}& \left({\displaystyle \frac{1}{2}}\sum _{j=1}^m{\parallel w_j\parallel }^2+C\sum _{i=1}^N\sum _{j=1}^m({\xi }_{ij}+{\xi }_{ij}^{*})\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& y_{ij}-(w_j^T\varphi \left(x_i\right)+b_j)\le ϵ+{\xi }_{ij},\hfill \\ \hfill & (w_j^T\varphi \left(x_i\right)+b_j)-y_{ij}\le ϵ+{\xi }_{ij}^{*},\hfill \\ \hfill & {\xi }_{ij},{\xi }_{ij}^{*}\ge 0,\forall i\in \{1,\dots ,N\},\forall j\in \{1,\dots ,m\}\hfill \end{array}$$

(8)

Using the Karush-Kuhn-Tucker (KKT) condition in (8), solving the dual problem is also equivalent to finding the solution of the linear systems. The complete process can be realized using Algorithm 2.

Algorithm 2 Multi-Output Proximal Support Vector Regression (MO-PSVR)

Require:  Training data ${\left\{(x_i,y_i)\right\}}_{i=1}^N$ where $x_i\in {\mathbb{R}}^d$ and $y_i\in {\mathbb{R}}^m$ Require:  Regularization parameters C, Epsilon margin $ϵ$   1: function MOPSVR-Train($X,Y,C,ϵ$)   2:     $N\leftarrow \mathrm{number}\mathrm{of}\mathrm{samples}$   3:     $m\leftarrow \mathrm{number}\mathrm{of}\mathrm{outputs}$   4:     $K\leftarrow \mathrm{Compute}\mathrm{kernel}\mathrm{matrix}(X,X)$   5:     Initialize $A\in {\mathbb{R}}^{2N\times 2N}$, $b\in {\mathbb{R}}^{2N}$   6:     for $j=1$ to m do   7:         Construct block matrices for output j: $A_j=\left[\begin{array}{cc}0& K+{\displaystyle \frac{1}{C}}{I}_N\\ K+{\displaystyle \frac{1}{C}}{I}_N& 0\end{array}\right],$ $b_j=\left[\begin{array}{c}ϵ{\mathbf{1}}_N+Y_j\\ ϵ{\mathbf{1}}_N-Y_j\end{array}\right]$   8:         Solve ${\alpha }_j=A_j^{-1}{b}_j$   9:         Extract support vectors and coefficients ${\alpha }_j$ 10:     end for 11:     return Model parameters ${\left\{{\alpha }_j\right\}}_{j=1}^m$ 12: end function 13: function MOPSVR-Predict($X_{\mathrm{new}},X,{\left\{{\alpha }_j\right\}}_{j=1}^m$) 14:     $K_{\mathrm{new}}\leftarrow \mathrm{Compute}\mathrm{kernel}\mathrm{matrix}(X_{\mathrm{new}},X)$ 15:     Initialize predictions $Y_{\mathrm{new}}$ 16:     for $j=1$ to m do 17:         $Y_{\mathrm{new},j}\leftarrow K_{\mathrm{new}}{\alpha }_j$ 18:     end for 19:     return $Y_{\mathrm{new}}$ 20: end function

3.2.3. Multi-Output $\epsilon$-Twin Support Vector Regression

Different from LSSVR and PSVR, Shao et al. [52] introduced a twin SVM method, i.e., $\epsilon$-Twin Support Vector Regression ($\epsilon$-TSVR). Unlike LSSVR, $\epsilon$-TSVR uses two pair $\epsilon$-insensitive decision functions [53].

Multi-Output Epsilon Twin SVR (MO-$\epsilon$-TSVR) can be achieved from $\epsilon$-TSVR through the following modification of the optimization problem,

$$\begin{array}{cc}\hfill \underset{(W_1,b_1,\zeta )}{min}& {\displaystyle \frac{1}{2}}{a}_3(\parallel W_1{\parallel }^2+b_1^2)+{\displaystyle \frac{1}{2}}{\zeta }^T{\zeta }^{*}+a_1{e}^T\zeta \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& y_{ij}-(w_j^{+}\varphi \left(x_i\right)+b_j^{+})\le ϵ+{\xi }_{ij}^{+},\hfill \\ \hfill & (w_j^{+}\varphi \left(x_i\right)+b_j^{+})-y_{ij}\le ϵ+{\xi }_{ij}^{+*},\hfill \\ \hfill & {\xi }_{ij}^{+},{\xi }_{ij}^{+*}\ge 0\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \underset{(W_2,b_2,\eta )}{min}& {\displaystyle \frac{1}{2}}{a}_4(\parallel {\omega }_2{\parallel }^2+b_2^2)+{\displaystyle \frac{1}{2}}{\eta }^T{\eta }^{*}+a_2{e}^T\eta \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& y_{ij}-(w_j^{-}\varphi \left(x_i\right)+b_j^{-})\le ϵ+{\xi }_{ij}^{-},\hfill \\ \hfill & (w_j^{-}\varphi \left(x_i\right)+b_j^{-})-y_{ij}\le ϵ+{\xi }_{ij}^{-*},\hfill \\ \hfill & {\xi }_{ij}^{-},{\xi }_{ij}^{-*}\ge 0\hfill \end{array}$$

(10)

Algorithm 3 describes the solution process of MO-$\epsilon$-TSVR by solving dual problem using system of linear equations using matrix operations, emphasizing the kernel methods’ role in simplifying the problem.

Algorithm 3 Multi-Output $\epsilon$ Twin Support Vector Regression (MO-$\epsilon$-TSVR)

Require:  Training data ${\left\{(x_i,y_i)\right\}}_{i=1}^N$ where $x_i\in {\mathbb{R}}^d$ and $y_i\in {\mathbb{R}}^m$ Require:  Regularization parameters $C_1,C_2$, Epsilon $ϵ$   1: function MO-$\epsilon$-TSVR_Train($X,Y,C_1,C_2,ϵ$)   2:     $N\leftarrow \mathrm{number}\mathrm{of}\mathrm{samples}$   3:     $m\leftarrow \mathrm{number}\mathrm{of}\mathrm{outputs}$   4:     $W^{+}\leftarrow$ Empty list, $W^{-}\leftarrow$ Empty list   5:     $B^{+}\leftarrow$ Empty list, $B^{-}\leftarrow$ Empty list   6:     $K\leftarrow \mathrm{Kernel}\mathrm{Matrix}\left(\varphi \right(X),\varphi (X\left)\right)$   7:     for $j=1$ to m do   8:         Formulate the dual problems for the j-th output:   9:         Solve for ${\alpha }_j^{+},{\alpha }_j^{-}$: $\left[\begin{array}{ccc}0& Y_j& K+{\displaystyle \frac{1}{2C_1}}I\\ -Y_j^T& 0& {\mathbf{1}}^T\\ K+{\displaystyle \frac{1}{2C_1}}I& \mathbf{1}& -ϵI\end{array}\right]\left[\begin{array}{c}{\alpha }_j^{+}\\ b_j^{+}\\ {\xi }_j^{+}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ϵ\mathbf{1}\end{array}\right],$ $\left[\begin{array}{ccc}0& Y_j& K+{\displaystyle \frac{1}{2C_2}}I\\ -Y_j^T& 0& {\mathbf{1}}^T\\ K+{\displaystyle \frac{1}{2C_2}}I& \mathbf{1}& -ϵI\end{array}\right]\left[\begin{array}{c}{\alpha }_j^{-}\\ b_j^{-}\\ {\xi }_j^{-}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ϵ\mathbf{1}\end{array}\right]$ 10:         Compute $w_j^{+}$ and $w_j^{-}$ from ${\alpha }_j^{+}$ and ${\alpha }_j^{-}$ respectively 11:         Store $w_j^{+},b_j^{+},w_j^{-},b_j^{-}$ to $W^{+},B^{+},W^{-},B^{-}$ 12:     end for 13:     return $W^{+},B^{+},W^{-},B^{-}$ 14: end function 15: function MO-$\epsilon$-TSVR_Predict($X_{\mathrm{new}},X,W^{+},B^{+},W^{-},B^{-}$) 16:     Initialize $Y_{\mathrm{new}}\leftarrow$ Empty matrix 17:     for $j=1$ to m do 18:         Compute predictions using upper and lower models: $f_j^{+}\left(x_{\mathrm{new}}\right)=w_j^{+}\varphi \left(x_{\mathrm{new}}\right)+b_j^{+},f_j^{-}\left(x_{\mathrm{new}}\right)=w_j^{-}\varphi \left(x_{\mathrm{new}}\right)+b_j^{-}$ 19:         Average predictions for output j: $Y_{\mathrm{new},j}={\displaystyle \frac{f_j^{+}\left(x_{\mathrm{new}}\right)+f_j^{-}\left(x_{\mathrm{new}}\right)}{2}}$ 20:     end for 21:     return $Y_{\mathrm{new}}$ 22: end function

3.3. Multi-Colony Ant Colony Optimization

Ant Colony Optimization (ACO) is a well-known metaheuristic that is employed to solve combinatorial optimization problems. It is inspired by the foraging behavior of ants. Traditional ACO is typically employed to address single-objective problems; however, numerous real-world problems involve multiple objectives. In order to resolve this issue, a multi-colony ACO approach is suggested for this work. This approach capitalizes on the strengths of multiple ant colonies, each of which has distinct objectives, and periodically exchanges information to identify high-quality solutions that balance the different objectives. To enhance the interaction scheme among the ants, the ACO-LD algorithm is incorporated, which uses a Laplace distribution-based interaction scheme as described by [33]. In the Multi-colony ACO (MACO-LD), multiple colonies are initialized, where each colony optimizes a different objective function. The overall process can be summarized in Algorithm 4.

Algorithm 4 Multi-colony ACO with laplace distribution (MACO-LD)

Require:  C (number of colonies), $N_k$ (number of ants per colony), T (maximum number of iterations), $\rho$ (pheromone evaporation rate), $\alpha$ (influence of pheromone), $\beta$ (influence of heuristic), $\lambda$ (scaling parameter), b (diversity parameter), $t_e$ (exchange interval) Ensure:  Best solution for each colony   1: Initialize pheromone matrices ${\tau }_{ij}^{\left(c\right)}$ for each colony c and heuristic information ${\eta }_{ij}^{\left(c\right)}$   2: for $iteration=1$ to T do   3:     for each colony $c=1$ to C do   4:         for each ant $k=1$ to $N_k$ do   5:            Initialize an empty solution $S_k$   6:            while solution $S_k$ is incomplete do   7:                Select next component j for current position i based on probability: $$p_{ij}^{\left(c\right)}={\displaystyle \frac{{\left({\tau }_{ij}^{\left(c\right)}\right)}^{\alpha }{\left({\eta }_{ij}^{\left(c\right)}\right)}^{\beta }}{{\sum }_{l\in \mathrm{allowed}}{\left({\tau }_{il}^{\left(c\right)}\right)}^{\alpha }{\left({\eta }_{il}^{\left(c\right)}\right)}^{\beta }}}$$   8:                Add component j to solution $S_k$   9:            end while 10:            Evaluate solution $S_k$ based on objective function $f^{\left(c\right)}\left(S_k\right)$ 11:         end for 12:         Update pheromone matrix for colony c 13:         for each ant $k=1$ to $N_k$ do 14:            for each edge $(i,j)$ used in $S_k$ do 15:                Update pheromone: ${\tau }_{ij}^{\left(c\right)}\leftarrow (1-\rho ){\tau }_{ij}^{\left(c\right)}+Q/f^{\left(c\right)}\left(S_k\right)$ 16:                Apply Laplace distribution-based interaction scheme: $${\tau }_{ij}^{\left(c\right)}\leftarrow {\tau }_{ij}^{\left(c\right)}+\lambda exp\left(-{\displaystyle \frac{|f^{\left(c\right)}\left(S_k\right)-f^{\left(c\right)}\left(S_{\mathrm{best}}\right)|}{b}}\right)$$ 17:            end for 18:         end for 19:     end for 20:     if $iteration\%t_e==0$ then 21:         for each colony pair $(c_1,c_2)$ do 22:            Exchange best solutions $S_{\mathrm{best}}^{\left(c_1\right)}$ and $S_{\mathrm{best}}^{\left(c_2\right)}$ 23:            Update pheromone matrices: $${\tau }_{ij}^{\left(c_1\right)}\leftarrow {\tau }_{ij}^{\left(c_1\right)}+\Delta {\tau }_{ij,\mathrm{best}}^{\left(c_2\right)}$$ $${\tau }_{ij}^{\left(c_2\right)}\leftarrow {\tau }_{ij}^{\left(c_2\right)}+\Delta {\tau }_{ij,\mathrm{best}}^{\left(c_1\right)}$$ 24:         end for 25:     end if 26: end for 27: Select best solutions for each output node from dedicated colony

The parameter C determines the number of ant colonies participating in the optimization process. Higher C increases solution diversity by enabling parallel searches across multiple objectives. Number of colonies can increase computational cost but improve multi-objective coverage. $N_k$ is the number of ants operating within each colony during an iteration. Higher $N_k$ allows for more extensive exploration of the solution space, improving solution quality. Pheromone Evaporation Rate ($\rho$) ranges between 0 and 1, that controls the rate at which pheromone trails decay over time. The parameter $\alpha$ (influence of pheromone) controls how much the existing pheromone levels influence the path selection process and the parameter $\beta$ (influence of heuristic) controls how much heuristic information affects the path selection. The scaling parameter $\lambda$ is scaling factor used in the Laplace distribution-based pheromone update scheme (ACO-LD). b is the diversity parameter of ACO-LD that controls the width of the Laplace distribution in the pheromone update process. Parameters $\alpha$ and $\beta$ directly control the balance between exploration and exploitation. The diversity parameter b prevents the ACO-LD in converging to a local optima.

The proposed Multi-colony ACO-LD (MACO-LD) approach offers several advantages over ACO. Each colony operates in parallel, allowing simultaneous exploration of different regions in the solution space. Periodic information exchange between colonies helps in leveraging the strengths of different colonies, improving convergence rates. Each colony focuses on a specific objective, ensuring a balanced approach to multi-objective optimization.

4. Proposed Forecasting Model

In this section, the research design is explained in detail. The overall architecture of the proposed forecasting model is shown in Figure 1. The presented forecasting model can be realized in four stages, which are explained in Section 4.1–Section 4.4.

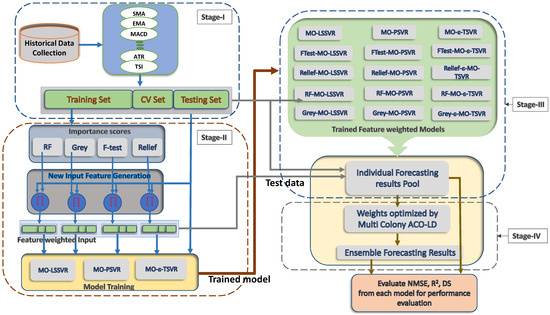
Figure 1. Overall architecture of the proposed ensemble strategy.

4.1. Stage-I: Data Preprocessing and Input Features

The first important step, in developing the forecasting model, is to determine the input features. Historical closing prices of index futures along with technical indicators and oscillators are traditionally considered by researchers in index future closing price forecasting [54,55]. Basic descriptive statistics for all the dataset are presented in Table 2. A large collection of technical indicators and oscillators are introduced as input features. Along with OLHC (Open, Low, High, Close) historical prices, other technical indicators and oscillators considered in this work are listed in Table 3. A detailed explanation and formulation of the indicators and oscillators used in this work may be found in [7,54,56].

Table 2. Basic descriptive statistics of datasets.

Dataset	Data Points	Missing Values	Min	Max	Mean	Standard Deviation	ADF p-Value
DJI	2765	0	9686.50	30,303.00	18,438.00	5625.50	0.97
NASDAQ	2765	0	2091.80	12,808.00	5231.70	2408.70	0.99
NIFTY 50	2691	25	4544.20	13,761.00	8059.60	2353.90	0.98
SP500	2765	0	1022.60	3722.50	2074.90	672.25	0.99
HSI	2701	11	16,250.00	33,154.00	23,896.00	3117.60	0.66
RUSSELL	2764	1	586.49	2007.10	1169.00	324.27	0.96
TSEC	2691	10	6633.30	14,390.00	9264.70	1485.20	0.96
KOSPI	2698	12	1457.60	2806.90	2050.40	206.00	0.90

Table 3. Indicators used as input features.

O: Open	SMA: Moving Average	EMA: Exponential Moving Average
H: High	RSI: Relative Strength Index	CCI: Commodity Channel Index
L: Low	%K: Stochastic $\%K$	MACD: Moving Average Convergence Divergence
C: Close	%D: Moving average of $\%K$	KST: Know Sure Thing
Bias	%R: Larry William’s $\%R$	ATR: Average True Range
MOM: Momentum	ROC: Rate of Change	TSI: True Strength Index
UI: Ulcer Index	OSC: Price Oscillator	ADX: Average Directional Movement Index

4.2. Stage-II: Construction of Feature Weighted Hybrid Models

In this work, the importance scores ($I_{ft},I_{rl},I_{rf},I_{gr}$) obtained from Section 3.1 are used to determine the corresponding feature weight matrices, i.e., $V_{ft},V_{rl},V_{rf}$ and $V_{gr}$. The corresponding feature weighted input feature sets are generated as ${\chi }_{ft}^{\prime },{\chi }_{rl}^{\prime },{\chi }_{rf}^{\prime }$ and ${\chi }_{gr}^{\prime }$, respectively following Section 3.1.5. Thus, the importance score based feature weighted input sets are combined with the baseline forecasting methods Section 3.2 to construct hybrid models. Tweleve hybrid models are obtained and denoted by Ftest-MO-LSSVR, Relief-MO-LSSVR, RF-MO-LSSVR, Grey-MO-LSSVR, Ftest-MO-PSVR, Relief-MO-PSVR, RF-MO-PSVR, Grey-MO-PSVR, Ftest-MO-$\epsilon$-TSVR, Relief-MO-$\epsilon$-TSVR, RF-MO-$\epsilon$-TSVR and Grey-MO-$\epsilon$-TSVR.

4.3. Stage-III: Training and Individual Forecasting

The proposed system uses walk forward (sliding window) methodology [56,57] for the training and forecasting of hybrid models along with baseline algorithms. The input data set is first split into ten overlapping groups of training-testing set pairs. For importance score based feature weights generation and forecasting purposes, the first 1500 consecutive days are used as the training set, and the next 50 days of data are taken as the testing set. The next overlapping training set-testing set pair is obtained by sliding the data window to 50 days forward, and the initial 50 data points are discarded to maintain the training set-testing set size as same as the previous window. A similar structure is followed to obtain the corresponding 10 overlapping pairs. The trade-off between forecasting accuracy and generalization ability are taken into consideration to find the optimal regularization parameter $\nu$.

4.4. Stage-IV: Ensemble Forecasting

The proposed study incorporates importance score generation strategies to generate different weighted input feature spaces. The new weighted feature is then integrated with baseline algorithms to make hybrid models. The proposed strategy then combines individual results to reach the required ensemble prediction results, which aims to use full advantage of the merits of the individual models to improve the ensemble predictive performance. At certain trading day $(t-1)$, consider p individual forecast results of day t, as $({\widehat{y}}_{1t},{\widehat{y}}_{2t},\dots ,{\widehat{y}}_{pt})$, then the ensemble forecast result can be generated by

$${\widehat{y}}_t^{en}=\sum _{i=1}^p{W}_i{\widehat{y}}_{it}$$

(11)

where $W_i$ is the weight for the ith individual model. In general, the integration of individual forecasting results with equal weights is not suitable to obtain the desired output. Thus this paper employs a continuous Multi-colony Ant Colony Optimization algorithm (MACO-LD) to obtain the optimal allocated weights to combine the individual forecast outcomes. The procedure to predict the ensemble results from the individual forecasting results for each colony is described in Figure 2. The procedure integrates baseline and hybrid learners through Ant Colony Optimization (ACO-LD), which determines the optimal combination of model outputs by assigning dynamic weights to each learner. The iterative process described in in Figure 2 and in Algorithm 4 of MACO-LD ensures that the ensemble adapts over time, minimizing error and improving predictive performance. In this study, ACO-LD in Figure 2 uses the normalized mean square error ($NMSE$) as the fitness function for the continuous series of actual and predicted closing prices, and it uses a probabilistic tour construction approach based on the Laplace distribution. Ants are deployed in a search space where each dimension corresponds to a model’s weight and initial weight configurations are randomly distributed. New ant tour selection and shifting is processed according to weight configurations with higher fitness and to avoid local optima, small percentage of ants explore new set of weights through Laplace Distribution. Iterative weight adjustments continue until convergence or the maximum iteration limit is reached. The ensemble prediction uses Equation (11) to forecast the final ensemble results. A detailed explanation of the ACO-LD approach is found in [33].

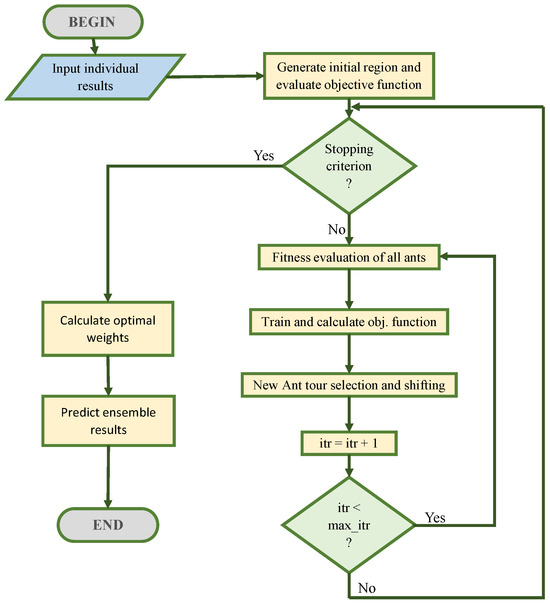
Figure 2. Flowchart to get ensemble results from individual results for each colony.

5. Experiment & Discussion

To facilitate the comparative analysis of the proposed importance score based feature weighted hybrid ensemble model, three baseline algorithms (i.e., LSSVR, PSVR, $\epsilon$-TSVR), and their hybrid models (see Section 4.2), are taken into consideration along with the proposed ensemble model. The inclusion of feature weighted hybrid methods is primarily to observe the effectiveness of importance scores based feature weighted models over baseline methods.

5.1. Data-Set Description

To demonstrate the effectiveness of the proposed ensemble model, eight index future historical price data have been considered for the experiment (viz: DJI, NASDAQ, NIFTY 50, SP500, Hangseng-HSI, RUSSELL-Chicago, TSEC-Taiwan, KOSPI). Daily price data for every index future (Open, Low, High, Close) have been imported over a time period of 10 years (January 2010 to December 2020) from yahoo-finance (https://finance.yahoo.com, accessed on 1 January 2021). To cover all possible market scenarios (Up Trend, Down Trend, and Sideways) and to observe the effectiveness of the proposed strategy in recent pandemic situations, the data sets have been imported carefully following the current timeline. Overall 2700 trading days of each index future data have been taken for the experiments. The missing values are replaced using mean imputation technique, where the mean of the four closest data points of the corresponding missing value is used for the imputation. The Augmented Dickey-Fuller (ADF) test [58] is used to determine whether a time series is stationary or not stationary. ADF p values in Table 2 explains the non-stationary nature of financial time series data. The Partial Autocorrelation (PACF) and first-order differenced closing price are presented in Figure 3. Where PACF represent the direct correlation between the series and its lag values, after removing the effects of other lags and the differenced closing price represents the day-to-day change in the closing price. That demonstrates long-term trends and volatility of financial time series data. The Input feature set Section 4.1 first constructed for each data-set then following the walk forward procedure described in Section 4.3 corresponding training-testing set pairs have been obtained from the imported data.

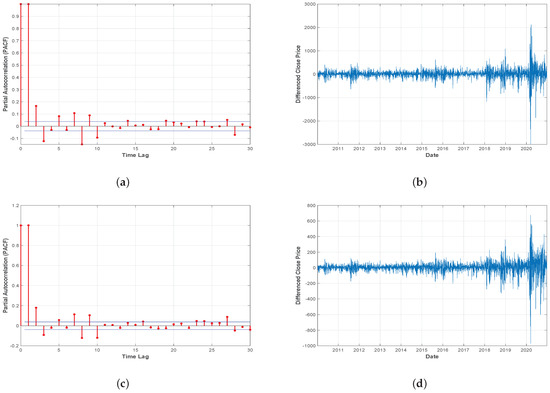
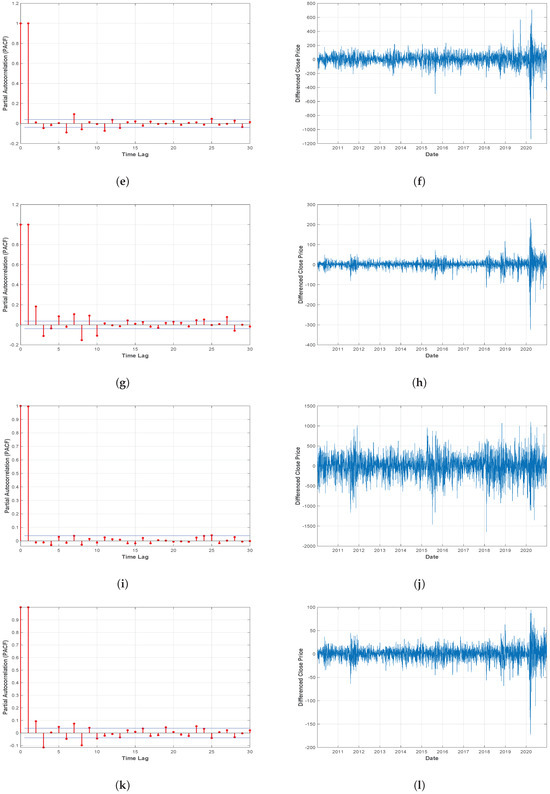
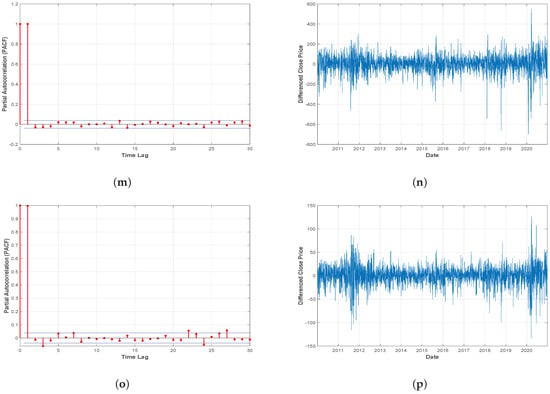
Figure 3. (a). PACF and (b). Differenced closing price for Dow Jones Index. (c). PACF and (d). Differenced closing price for NASDAQ. (e). PACF and (f). Differenced closing price for NIFTY 50. (g). PACF and (h). Differenced closing price for SP500. (i). PACF and (j). Differenced closing price for HSI. (k). PACF and (l). Differenced closing price for RUSSELL. (m). PACF and (n). Differenced closing price for TSEC. (o). PACF and (p). Differenced closing price for KOSPI.

A multi-day ahead forecasting method is carried out to validate the performance of the proposed approach over multi-day ahead forecasting performance. In this work, a direct strategy [27] has been implemented for multi-day ahead forecasting. In this strategy, the target is to predict the next h day closing prices for the h-day ahead model with input of w days historical price and indicators. Where it assumes that the h-day ahead response solely depends on current input features. Thus, the learning algorithm treats each day as an independent model and training is performed accordingly for each target, i.e., the proposed approach builds h independent model for h day ahead forecasting but takes the same input feature set. The forecasting problem can be formulated as follows:

$$\begin{array}{cc}\hfill \left[C_{t+1}\right]& ={\widehat{f}}_{t+1}(C_t,C_{t-1},\dots ,C_{t-(w-1)},T{I}_1,T{I}_2,\dots ,T{I}_k)\hfill \\ \hfill [C_{t+2}]& ={\widehat{f}}_{t+2}(C_t,C_{t-1},\dots ,C_{t-(w-1)},T{I}_1,T{I}_2,\dots ,T{I}_k)\hfill \\ \hfill \dots & \dots \dots \dots \dots \dots \dots \dots \dots \dots \hfill \\ \hfill [C_{t+h}]& ={\widehat{f}}_{t+h}(C_t,C_{t-1},\dots ,C_{t-(w-1)},T{I}_1,T{I}_2,\dots ,T{I}_k)\hfill \end{array}$$

(12)

where $T{I}_i,i=1,\dots ,k$ are technical indicators at day t, and $C_i$ is the closing price of day i and ${\widehat{f}}_i$ is the independent model to be learnt for $C_i$ by the forecasting method in the training phase.

5.2. Performance Metrics

A number of statistical measures are considered to estimate the performance of the forecasting methods. In this study, three performance metrics are utilized to evaluate the performance as follows:

Normalized Mean Square Error (NMSE) measures the deviation between the predicted response and the actual response. A small NMSE value indicates the closeness of the predicted response with the actual value. It can be computed from true responses ($y_{act}$) and forecasted responses ($y_{pred}$) as:

$$NMSE={\displaystyle \frac{{\sum }_{i=1}^k{(y_{act}-y_{pred})}^2}{{\sum }_{i=1}^k{(y_{act}-{\overline{y}}_{act})}^2}}$$

(13)

Coefficient of multiple determinations ($R^2$), which determines the degree of variation of predicted response from the actual response. It measures the goodness of fit of the proposed model. An $R^2$ value near to 1 represents a better fit of the model to the response data. $R^2$ is defined as:

$$R^2={\displaystyle \frac{{\sum }_{i=1}^k{(y_{pred}-{\overline{y}}_{act})}^2}{{\sum }_{i=1}^k{(y_{act}-{\overline{y}}_{act})}^2}}$$

(14)

Directional Symmetry (DS), which describes the trend predicting capacity of the proposed model. That is, correctly predicted directions of the closing price in terms of percentage. Thus, it can be considered as accuracy of prediction and it is formulated as:

$$\begin{array}{cc}\hfill DS=& {\displaystyle \frac{100}{k}}\times \sum _{i=1}^k{d}_i,\hfill \end{array}$$

(15)

where $d_i=1$ for $({y_{act}}_i-{y_{act}}_{i-1})({y_{pred}}_i-{y_{pred}}_{i-1})\ge 0$ and 0 otherwise.

5.3. Discussion

As described earlier, the proposed ensemble technique first uses importance scores to determine weighted input features and later uses these input feature sets to generate hybrid models. Thereafter, it combines the individual forecasting responses to obtain the ensemble response. Figure 4 shows the assigned weight values for different input features concerning different importance scores obtained from the F-test, Relief, RF, and Grey correlation respectively. The significant difference in weight values in Figure 4 implies the diverse computational structures of the methods (i.e., F-test, Relief, RF, and Grey) to determine importance scores. The forecasting performance of all the baseline algorithms (i.e., MO-LSSVR, MO-PSVR, MO-$\epsilon$-TSVR) along with their hybrid feature weighted models and the final ensemble model in terms of the three performance metrics (i.e., $NMSE$, $R^2$, and $DS$) are presented in Table 4, Table 5 and Table 6. Thus, the proposed study is assessed through two different set-ups. First, we considered the performance of the hybrid models obtained from baseline algorithms after incorporating importance scores with the baseline algorithms. In the second scenario, we investigate the superiority of the ensemble model over parent models. The proposed work also investigates the same set-up for multi-day ahead forecasting. Where all the experiments has been performed for 1-day, 3-day and 5-day ahead forecasting. The performance metrics results are produced in Table 4, Table 5 and Table 6, and the corresponding $NMSE$ and $R^2$ changes can be verified from Figure 5. The multi-day ahead foresting of the closing price with actual price are presented in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.

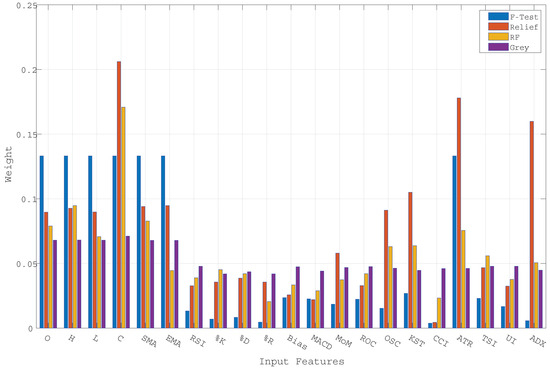
Figure 4. Weights assigned to distinct input features, listed in Table 3, according to different importance scores obtained from the F-test, Relief, RF, and Grey correlation. The difference in weight values implies the distinct computational approach of the methods (i.e., F-test, Relief, RF, and Grey) to determine importance scores.

Table 4. Performance metrics for 1-day ahead forecasting.

Dataset	DJI	NASDAQ	NIFTY 50	SP500	HSI	RUSSELL	TSEC	KOSPI
Methods	NMSE
LSSVR	0.2931	0.2525	0.2173	0.2068	0.2057	0.2647	0.2001	0.1796
PSVR	0.2455	0.2669	0.2511	0.2337	0.2112	0.2944	0.2408	0.1910
$\epsilon$-TSVR	0.3079	0.3386	0.4190	0.2434	0.2158	0.3570	0.2907	0.1408
Grey-MO-LSSVR	0.2099	0.2043	0.2083	0.1954	0.1874	0.2728	0.1947	0.1699
RF-MO-LSSVR	0.2010	0.2025	0.2176	0.1911	0.1114	0.2349	0.1782	0.1638
Relief-MO-LSSVR	0.2046	0.2040	0.2050	0.1130	0.1717	0.2387	0.1835	0.1538
Ftest-MO-LSSVR	0.2115	0.2135	0.2085	0.1963	0.1838	0.2588	0.1924	0.1629
Grey-MO-PSVR	0.2363	0.2235	0.2346	0.2288	0.2036	0.2711	0.2201	0.1803
RF-MO-PSVR	0.2123	0.2028	0.2141	0.1983	0.1795	0.2315	0.1808	0.1575
Relief-MO-PSVR	0.2144	0.2193	0.2248	0.2042	0.1842	0.2501	0.1944	0.1697
Ftest-MO-PSVR	0.2293	0.2281	0.2226	0.2209	0.1844	0.2522	0.2249	0.1676
Grey-MO-$\epsilon$-TSVR	0.2211	0.2262	0.2089	0.2037	0.2058	0.2110	0.1716	0.1537
RF-MO-$\epsilon$-TSVR	0.2160	0.1901	0.2054	0.1865	0.1769	0.2413	0.1741	0.1622
Relief-MO-$\epsilon$-TSVR	0.2416	0.2417	0.2440	0.2271	0.2045	0.2906	0.2228	0.1873
Ftest-MO-$\epsilon$-TSVR	0.2077	0.2236	0.2358	0.2035	0.1855	0.2488	0.1885	0.1818
ENSEMBLE	0.1474	0.1104	0.1230	0.1292	0.1363	0.1265	0.1148	0.1225
	$R^2$
LSSVR	0.7540	0.9367	0.9677	0.9861	0.9428	0.9874	0.9789	0.9962
PSVR	0.8076	0.9198	0.9340	0.9602	0.9758	0.9194	0.9856	0.9767
$\epsilon$-TSVR	0.9299	0.8486	0.8166	0.9653	0.9945	0.8167	0.9443	0.9934
Grey-MO-LSSVR	0.9203	0.9681	0.9693	0.9500	0.9887	0.9254	0.9737	0.9763
RF-MO-LSSVR	0.9065	0.9417	0.9632	0.9772	0.9241	0.9448	0.9595	0.9423
Relief-MO-LSSVR	0.9587	0.9676	0.9956	0.9812	0.9416	0.9408	0.9875	0.9712
Ftest-MO-LSSVR	0.9211	0.9542	0.9669	0.9012	0.9647	0.8779	0.9765	0.9891
Grey-MO-PSVR	0.9214	0.8401	0.9557	0.9114	0.9916	0.9534	0.9325	0.9966
RF-MO-PSVR	0.8820	0.9359	0.9539	0.9201	0.9394	0.9200	0.9392	0.9338
Relief-MO-PSVR	0.9245	0.9421	0.9485	0.9444	0.9976	0.8776	0.9303	0.9336
Ftest-MO-PSVR	0.8928	0.9357	0.9773	0.9023	0.9881	0.9252	0.9165	0.9821
Grey-MO-$\epsilon$-TSVR	0.9474	0.9353	0.9715	0.9427	0.9862	0.9748	0.9952	0.9323
RF-MO-$\epsilon$-TSVR	0.7696	0.8542	0.8437	0.8321	0.8951	0.9234	0.8595	0.9481
Relief-MO-$\epsilon$-TSVR	0.9728	0.8517	0.8953	0.8064	0.9035	0.9342	0.8873	0.9460
Ftest-MO-$\epsilon$-TSVR	0.8278	0.7638	0.8815	0.8415	0.9072	0.9174	0.8772	0.9434
ENSEMBLE	0.9764	0.9872	0.9979	0.9635	0.9732	0.9980	0.9992	0.9265
	DS
LSSVR	59.4311	54.1213	60.1553	51.6170	52.7840	53.5437	59.7056	58.3732
PSVR	52.3285	53.6758	59.9911	54.3243	52.6770	55.7608	58.5376	58.6238
$\epsilon$-TSVR	55.3339	54.5744	57.3383	59.5882	55.3566	53.9873	58.2780	58.8343
Grey-MO-LSSVR	50.1214	53.8966	60.1434	52.3339	50.5568	52.4205	58.7103	57.4988
RF-MO-LSSVR	49.8886	54.7754	58.5375	51.6770	52.2249	52.6418	58.1477	55.9108
Relief-MO-LSSVR	53.2394	57.2156	62.3361	55.2657	51.2249	52.3692	59.0797	59.8973
Ftest-MO-LSSVR	52.1258	54.4657	60.5579	54.5686	53.5675	56.3621	59.0763	59.7398
Grey-MO-PSVR	53.5648	55.0341	61.2647	53.8988	56.9570	51.9977	58.1870	58.7894
RF-MO-PSVR	52.4385	54.4656	60.8002	52.5691	51.8448	52.6816	56.8837	56.1495
Relief-MO-PSVR	53.8876	57.3356	59.2743	55.4546	52.1858	50.4699	58.7974	59.5036
Ftest-MO-PSVR	54.1303	56.3224	61.0825	53.0407	52.3585	52.9098	59.1804	59.1837
Grey-MO-$\epsilon$-TSVR	51.9931	56.3454	54.3943	52.5784	51.6804	52.2365	58.4232	55.6445
RF-MO-$\epsilon$-TSVR	51.8961	54.4343	60.3456	60.3256	51.8931	52.8183	57.5456	57.0469
Relief-MO-$\epsilon$-TSVR	52.7844	58.1329	59.9511	57.0316	54.1203	53.5531	58.2437	59.3636
Ftest-MO-$\epsilon$-TSVR	53.0127	55.2563	62.1381	56.5770	53.0067	52.1719	57.2841	57.9788
ENSEMBLE	60.3430	63.5744	64.9109	61.1203	58.4477	57.6748	59.2528	60.9065

Table 5. Performance metrics for 3-day ahead forecasting.

Dataset	DJI	NASDAQ	NIFTY 50	SP500	HSI	RUSSELL	TSEC	KOSPI
Methods	NMSE
LSSVR	0.6253	0.5408	0.7296	0.5159	0.6231	0.6444	0.6075	0.5552
PSVR	0.5812	0.5628	0.7892	0.5525	0.7073	0.6149	0.6086	0.5678
$\epsilon$-TSVR	0.6005	0.5077	0.6007	0.4686	0.6123	0.5928	0.6088	0.5086
Grey-MO-LSSVR	0.6020	0.4878	0.7425	0.4867	0.5896	0.5714	0.5488	0.5138
RF-MO-LSSVR	0.5514	0.4887	0.6797	0.4974	0.6512	0.4328	0.5093	0.4879
Relief-MO-LSSVR	0.5617	0.4790	0.7275	0.4956	0.5405	0.5317	0.6278	0.6269
Ftest-MO-LSSVR	0.5611	0.4882	0.6971	0.4916	0.5754	0.5454	0.5386	0.5178
Grey-MO-PSVR	0.6275	0.4926	0.7623	0.5336	0.6399	0.6440	0.6094	0.5431
RF-MO-PSVR	0.5555	0.4866	0.8037	0.4870	0.5609	0.5578	0.5474	0.5009
Relief-MO-PSVR	0.5850	0.5073	0.7417	0.4986	0.6035	0.5683	0.5191	0.5370
Ftest-MO-PSVR	0.5976	0.5354	0.7118	0.5410	0.6240	0.5659	0.5769	0.5301
Grey-MO-$\epsilon$-TSVR	0.6241	0.5400	0.7002	0.6233	0.5158	0.7072	0.5652	0.4849
RF-MO-$\epsilon$-TSVR	0.4874	0.3825	0.6210	0.4358	0.5210	0.5208	0.4381	0.4697
Relief-MO-$\epsilon$-TSVR	0.6804	0.5116	0.6389	0.4489	0.5822	0.6603	0.5223	0.5054
Ftest-MO-$\epsilon$-TSVR	0.4710	0.4376	0.5521	0.4125	0.5816	0.5604	0.4139	0.4728
ENSEMBLE	0.1997	0.1205	0.1514	0.1420	0.1761	0.1728	0.1362	0.1604
	$R^2$
LSSVR	0.7939	0.9272	0.9009	0.8142	0.9633	0.8733	0.9326	0.9519
PSVR	0.7058	0.9498	0.9451	0.8101	0.9132	0.8038	0.9499	0.9652
$\epsilon$-TSVR	0.7426	0.8313	0.6610	0.8864	0.5513	0.6173	0.8228	0.9501
Grey-MO-LSSVR	0.9310	0.9281	0.9229	0.9125	0.9719	0.8450	0.9556	0.9939
RF-MO-LSSVR	0.9753	0.9449	0.9231	0.8050	0.8654	0.9086	0.8548	0.7646
Relief-MO-LSSVR	0.9854	0.8865	0.9726	0.9636	0.8691	0.8600	0.9613	0.8766
Ftest-MO-LSSVR	0.9598	0.8735	0.9926	0.9760	0.9814	0.8160	0.9724	0.8886
Grey-MO-PSVR	0.9002	0.9136	0.8544	0.9221	0.9961	0.7168	0.8304	0.9535
RF-MO-PSVR	0.9510	0.9069	0.8985	0.8998	0.8578	0.7398	0.8912	0.9453
Relief-MO-PSVR	0.9894	0.9011	0.9785	0.9387	0.9903	0.7800	0.9055	0.9665
Ftest-MO-PSVR	0.9576	0.8989	0.9228	0.9687	0.8781	0.8678	0.9528	0.9226
Grey-MO-$\epsilon$-TSVR	0.9085	0.8855	0.9006	0.9633	0.9142	0.9130	0.9558	0.7625
RF-MO-$\epsilon$-TSVR	0.6003	0.6519	0.6658	0.6973	0.8656	0.6282	0.7219	0.8033
Relief-MO-$\epsilon$-TSVR	0.9275	0.7904	0.6864	0.7750	0.9230	0.5562	0.7770	0.7994
Ftest-MO-$\epsilon$-TSVR	0.5595	0.5886	0.7287	0.6329	0.8758	0.7461	0.7127	0.7890
ENSEMBLE	0.9944	0.9927	0.8879	0.9948	0.9238	0.9504	0.9868	0.9864
	DS
LSSVR	56.5800	59.6460	55.0774	57.9253	56.8909	55.8153	57.7743	53.3665
PSVR	59.3639	59.4767	54.8721	60.1092	53.6313	60.3077	56.3401	53.9864
$\epsilon$-TSVR	59.8452	62.8185	57.0790	61.5235	54.3210	55.2711	58.4249	56.2799
Grey-MO-LSSVR	59.0396	59.3385	58.1856	57.0291	54.8481	56.0986	55.6482	57.2302
RF-MO-LSSVR	52.2174	61.8333	57.5396	55.1364	56.0026	56.3770	56.8088	59.5289
Relief-MO-LSSVR	56.8647	56.3558	58.6376	54.9249	55.7579	56.4651	55.9271	57.4726
Ftest-MO-LSSVR	59.1420	58.1882	56.9988	54.8744	56.3098	58.0775	55.7235	57.9911
Grey-MO-PSVR	57.8445	57.8157	55.9765	59.0024	54.4720	58.8434	58.2983	55.2811
RF-MO-PSVR	55.8595	59.0527	60.2583	56.1865	57.2610	57.0493	55.9325	56.8429
Relief-MO-PSVR	57.4142	57.8306	57.5567	57.0395	54.8778	60.4622	56.2506	56.5947
Ftest-MO-PSVR	57.5298	58.4326	53.8453	60.4091	56.8027	59.0999	57.7471	57.4845
Grey-MO-$\epsilon$-TSVR	58.7853	58.6528	55.5940	57.3293	57.6161	53.5882	53.3467	59.1400
RF-MO-$\epsilon$-TSVR	58.7038	59.3189	58.3892	53.9706	57.3374	57.7962	56.9101	57.1992
Relief-MO-$\epsilon$-TSVR	61.2435	61.6267	58.3661	60.4721	57.8261	57.4148	55.6421	56.8297
Ftest-MO-$\epsilon$-TSVR	60.6752	59.5454	58.7259	58.5210	56.6734	59.0232	59.5556	59.8323
ENSEMBLE	63.5746	64.0156	66.9020	63.6837	60.8018	65.8243	61.9065	64.1156

Table 6. Performance metrics for 5-day ahead forecasting.

Dataset	DJI	NASDAQ	NIFTY 50	SP500	HSI	RUSSELL	TSEC	KOSPI
Methods	NMSE
LSSVR	1.1254	0.7922	1.1673	0.7996	1.1995	0.7717	0.8962	0.9531
PSVR	1.0864	0.8260	1.1448	0.8405	1.1884	0.8333	0.8241	0.9440
$\epsilon$-TSVR	0.6469	0.5806	0.7170	0.5913	0.7191	0.6481	0.7337	0.7241
Grey-MO-LSSVR	0.9384	0.6880	1.1748	0.7614	1.0628	0.7962	0.7910	0.8613
RF-MO-LSSVR	0.8363	0.6683	1.1287	0.6718	0.9783	0.7781	0.7318	0.7447
Relief-MO-LSSVR	0.9596	0.6843	1.1348	0.7012	0.9833	0.7820	0.8019	0.7761
Ftest-MO-LSSVR	0.9175	0.7122	1.1197	0.6977	0.9876	0.7895	0.7789	0.7831
Grey-MO-PSVR	0.9964	0.7249	1.0729	0.7870	1.0462	0.8190	0.8276	0.8978
RF-MO-PSVR	0.8911	0.7213	1.0348	0.7439	1.0215	0.7551	0.7519	0.7673
Relief-MO-PSVR	0.9740	0.7579	1.1177	0.7826	1.0801	0.8457	0.7621	0.8237
Ftest-MO-PSVR	0.9544	0.8035	1.1008	0.8135	1.0137	0.7929	0.8040	0.9242
Grey-MO-$\epsilon$-TSVR	0.9545	0.8105	1.1556	1.1295	0.7896	1.1284	0.9431	0.7470
RF-MO-$\epsilon$-TSVR	0.6154	0.5501	0.8176	0.5723	0.8906	0.6573	0.5767	0.6941
Relief-MO-$\epsilon$-TSVR	0.7082	0.7212	0.9213	0.6813	1.0974	0.7268	0.6955	0.7516
Ftest-MO-$\epsilon$-TSVR	0.6103	0.4994	0.7167	0.5876	1.0292	0.7265	0.5409	0.7312
ENSEMBLE	0.2325	0.1288	0.1751	0.1730	0.2289	0.1953	0.1452	0.1792
	$R^2$
LSSVR	0.3445	0.5448	0.5847	0.9972	0.9416	0.8650	0.9518	0.9747
PSVR	0.6047	0.4858	0.6070	0.9829	0.8432	0.7415	0.8791	0.7692
$\epsilon$-TSVR	0.4590	0.5721	0.5802	0.7677	0.4768	0.5531	0.8251	0.9791
Grey-MO-LSSVR	0.8913	0.9870	0.7877	0.9422	0.8545	0.9537	0.9478	0.9163
RF-MO-LSSVR	0.9630	0.8918	0.8231	0.9852	0.9057	0.9144	0.8707	0.6620
Relief-MO-LSSVR	0.8515	0.9504	0.8247	0.9786	0.9048	0.9204	0.9841	0.9418
Ftest-MO-LSSVR	0.9963	0.9047	0.8616	0.9846	0.9089	0.7475	0.9823	0.9463
Grey-MO-PSVR	0.9351	0.9769	0.9901	0.9391	0.8199	0.7056	0.9746	0.7341
RF-MO-PSVR	0.9721	0.9546	0.9575	0.9654	0.8972	0.7613	0.8872	0.8220
Relief-MO-PSVR	0.9187	0.9155	0.9129	0.9659	0.8133	0.7035	0.7894	0.8765
Ftest-MO-PSVR	0.8431	0.9381	0.9210	0.9674	0.7159	0.7854	0.7816	0.8261
Grey-MO-$\epsilon$-TSVR	0.9358	0.9484	0.7297	0.9567	0.9955	0.8411	0.9722	0.6601
RF-MO-$\epsilon$-TSVR	0.5583	0.9799	0.7387	0.6031	0.8376	0.4388	0.6081	0.6689
Relief-MO-$\epsilon$-TSVR	0.8618	0.9723	0.8144	0.6953	0.8589	0.4577	0.6591	0.7273
Ftest-MO-$\epsilon$-TSVR	0.4924	0.7622	0.9769	0.5433	0.7295	0.3769	0.6699	0.7096
ENSEMBLE	0.8631	0.9878	0.9701	0.9188	0.9131	0.9815	0.9036	0.8009
	DS
LSSVR	58.0700	60.3676	60.2049	57.7617	60.2044	60.1433	57.8327	58.4286
PSVR	58.1316	60.2741	57.6338	60.3363	55.3824	59.6590	55.6883	62.8429
$\epsilon$-TSVR	58.4448	59.8523	59.7778	60.7077	58.6231	67.1277	55.2160	56.1258
Grey-MO-LSSVR	58.6447	58.0352	63.1802	60.6918	56.1706	61.1813	56.8215	59.7555
RF-MO-LSSVR	57.7330	59.9115	62.2352	59.5668	56.8132	62.2204	57.2818	57.8210
Relief-MO-LSSVR	57.7419	61.5447	61.6231	57.9304	56.4677	62.0244	55.1108	58.8135
Ftest-MO-LSSVR	60.1358	58.5939	59.6847	58.1818	59.5260	60.4033	55.1058	59.4438
Grey-MO-PSVR	58.0611	56.9976	57.2014	60.9316	58.9071	59.9488	57.3803	60.2125
RF-MO-PSVR	57.0552	59.9853	56.9117	59.1940	56.5887	62.1629	57.0650	61.4195
Relief-MO-PSVR	58.5231	58.9068	60.9323	59.1834	56.3702	60.0373	53.7563	60.8550
Ftest-MO-PSVR	58.2764	60.7653	57.2756	60.7214	56.8877	62.1794	58.7154	59.2486
Grey-MO-$\epsilon$-TSVR	57.0219	61.0035	59.0672	60.1444	58.0360	55.3490	58.0789	57.9337
RF-MO-$\epsilon$-TSVR	58.2750	59.2444	61.3787	60.9625	57.5862	60.3737	55.7226	59.5894
Relief-MO-$\epsilon$-TSVR	54.8718	61.4864	62.9311	60.8309	58.8847	60.5386	54.9060	62.2353
Ftest-MO-$\epsilon$-TSVR	56.0494	59.0931	63.9663	60.4763	59.8874	62.1240	57.8534	61.1203
ENSEMBLE	60.5791	64.9107	66.4697	64.2383	60.1336	65.2561	64.9020	64.1425

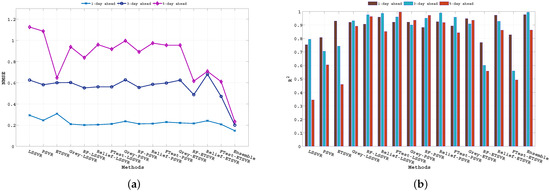
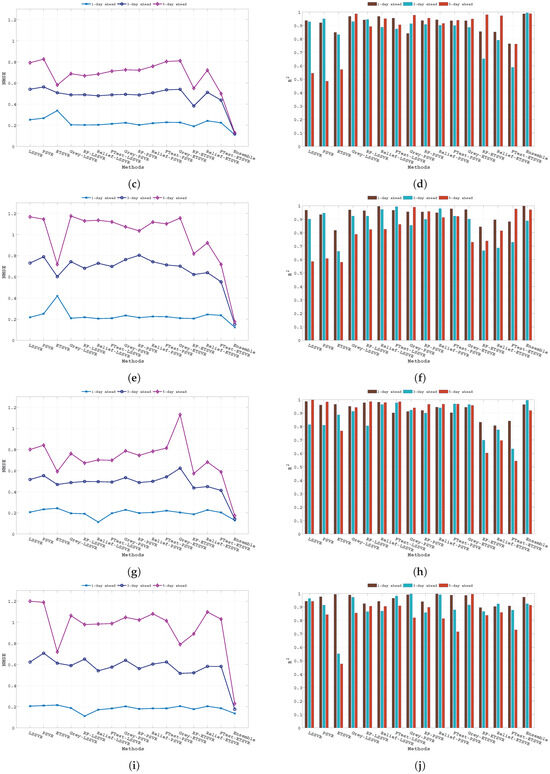
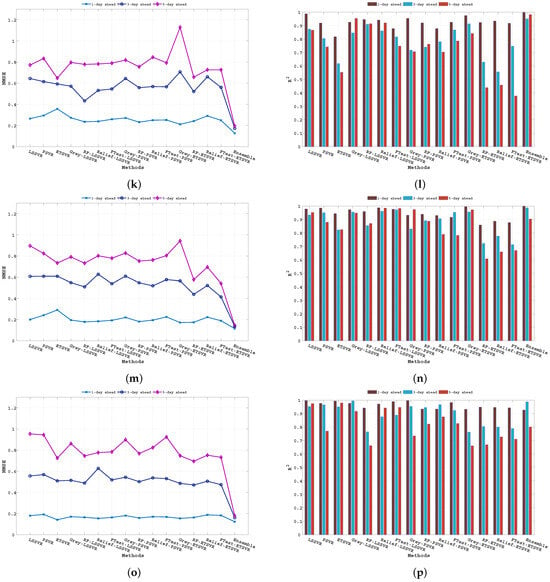
Figure 5. (a). NMSE and (b). $R^2$ comparison of different baseline models along with hybrid models and the proposed ensemble model for DJI. (c). NMSE and (d). $R^2$ comparison of different baseline models along with hybrid models and the proposed ensemble model for NASDAQ. (e). NMSE and (f). $R^2$ comparison of different baseline models along with hybrid models and the proposed ensemble model for NIFTY 50. (g). NMSE and (h). $R^2$ comparison of different baseline models along with hybrid models and the proposed ensemble model for S&P 500. (i). NMSE and (j). $R^2$ comparison of different baseline models along with hybrid models and the proposed ensemble model for HSI. (k). NMSE and (l). $R^2$ comparison of different baseline models along with hybrid models and the proposed ensemble model for RUSSELL. (m). NMSE and (n). $R^2$ comparison of different baseline models along with hybrid models and the proposed ensemble model for TSEC. (o). NMSE and (p). $R^2$ comparison of different baseline models along with hybrid models and the proposed ensemble model for KOSPI.

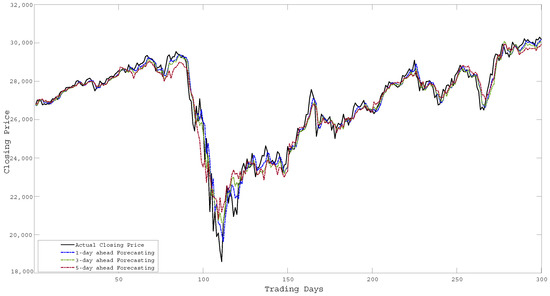
Figure 6. Forecasting of Closing Price over 300 days for DJI.

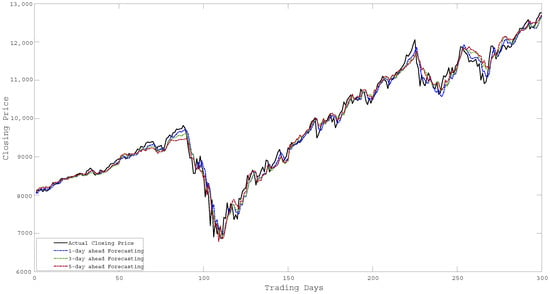
Figure 7. Forecasting of Closing Price over 300 days for NASDAQ.

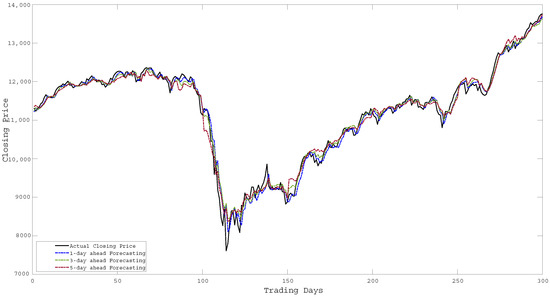
Figure 8. Forecasting of Closing Price over 300 days for NIFTY 50.

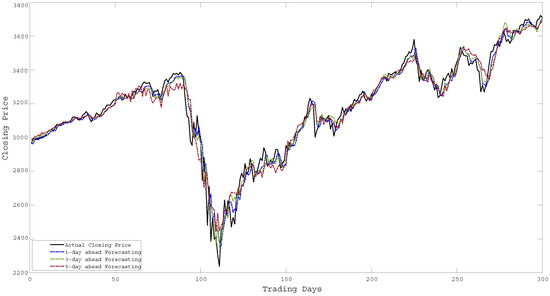
Figure 9. Forecasting of Closing Price over 300 days for SP500.

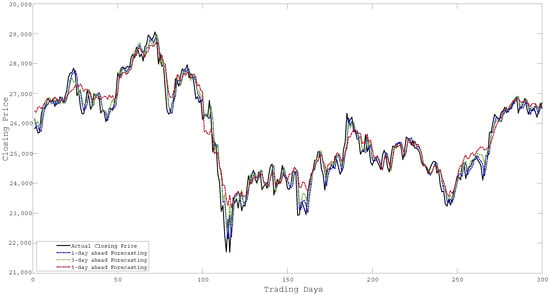
Figure 10. Forecasting of Closing Price over 300 days for HSI.

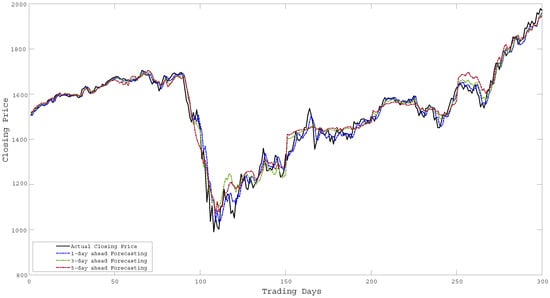
Figure 11. Forecasting of Closing Price over 300 days for RUSSELL.

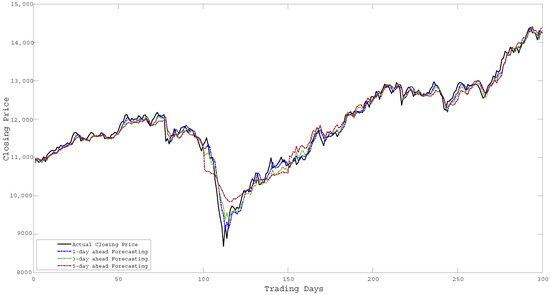
Figure 12. Forecasting of Closing Price over 300 days for TSEC.

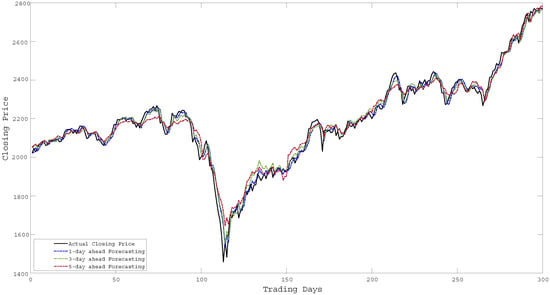
Figure 13. Forecasting of Closing Price over 300 days for KOSPI.

Following the result metrics presented in Table 4, Table 5 and Table 6, it is suggested that the proposed ensemble model outperforms all the hybrid models along with baseline models in all performance metrics for all index futures. The results imply that the proposed importance score based feature weighted models ensemble through the MACO-LD strategy can enhance the forecasting accuracy. Further, the detailed discussion can proceed through two different criteria. Firstly, to verify the significance of importance score based hybrid methods over baseline methods and secondly, to observe the efficiency of ensemble forecasting results obtained by combining the individual forecasting results through ACO-LD.

5.3.1. Comparison of Individual Forecasting Results

The result metrics presented in Table 4, Table 5 and Table 6 demonstrate that the incorporation of importance scores based feature weighted models improves the forecasting accuracy of the baseline methods. For 1-day ahead forecasting of closing price (Table 4), it is observed that RF-MO-$\epsilon$-TSVR has better NMSE values for NASDAQ, NIFTY 50, and TSEC-TAIWAN, where RF-MO-LSSVR has lower NMSE for DJI and HSI. Furthermore, for S&P 500 and RUSSEL, the NMSE values are comparatively lower for Relief-MO-LSSVR and Grey-MO-$\epsilon$-TSVR, respectively. The 3-day ahead and 5-day ahead forecasting of closing price (Table 5 and Table 6) demonstrate that RF-MO-$\epsilon$-TSVR and Ftest-MO-$\epsilon$-TSVR have lower deviation between the actual closing price and forecasted price in terms of NMSE for most of the index futures, except HSI and RUSSEL where Grey-MO-$\epsilon$-TSVR and $\epsilon$-TSVR have lower NMSE values respectively. The $R^2$ values presented in Table 4, Table 5 and Table 6 explain the goodness of fit of the forecast values of all the individual learning methods with actual values. The values imply that the importance scores based hybrid models have better $R^2$ than the baseline methods for most of the index futures. The hybrid model may be overfitting to the training data, capturing noise rather than the underlying trend in multi-day ahead forecasting. thus, the baseline algorithms are performing better in those data set. The results suggest that the Grey correlation based feature weighted hybrid models have better $R^2$ in most of the index futures in multi-day ahead foresting. Where Relief based feature weighted models show better $R^2$ values second after Grey correlation based method. Although there are few improvements observed in terms of DS after incorporating importance scores (i.e., NASDAQ, NIFTY 50, HSI, RUSSEL, KOSPI), still the improvements are not much higher, and in some cases, baseline algorithms are able to produce better DS percentages (i.e., DJI, SP500, and TSEC-Taiwan). In multi-day ahead forecasting, the DS results show that in most of the index futures, hybrid models perform better in terms of following the same direction as actual price movements. Table 4, Table 5 and Table 6 shows that there are improvements observed after incorporating feature weights obtained from proposed importance score determination strategies. Table 4, Table 5 and Table 6 imply that the importance scores contributed to better the forecasting performance of baseline algorithms. Importance score-based feature-weighted hybrid models outperform baseline algorithms by leveraging the strengths of dynamically assigning greater influence to features that contribute more significantly to prediction accuracy.

5.3.2. Comparison of Proposed Ensemble Forecasting with Individual Forecasting

This study proposes a hybrid ensemble model based on importance score based hybrid models. The proposed strategy has been successfully developed based on the framework described in Figure 1. First, consideration has been given to a vast assortment of technical indicators as input characteristics in the preprocessing module. Later, the present work introduced four different importance score generation strategies that use the input feature sets to determine the importance score of each feature. These scores are further used to produce feature weighted hybrid models. Section 5.3.1 demonstrates the effectiveness of hybrid models and shows that the results failed to choose a single hybrid model that can be applied globally for index future price prediction. Thus, to employ the full advantage of the individual hybrid models, the presented technique makes use of the hybrid models along with baseline methods aggregated by ACO-LD to produce the ensemble results. The results presented in Table 4, Table 5 and Table 6 established that the proposed approach improves the performance effectively in index future price forecasting.

In a broad perspective, the proposed ensemble model is an intelligent fusion of forecasting models. Associated with individual models, the importance score based ensemble model receipts the benefits of the data preprocessing module i.e., Technical indicators and Oscillators, Importance scores based hybrid learning models, and intelligent optimization algorithm, i.e., ACO-LD, all together to produce the ensemble output. The framework improves overall accuracy by dynamically adjusting weights for every forecast horizon, which lowers bias-variance trade-offs. This yields more dependable predictions, essential for portfolio managers, algorithmic traders, and risk analysts. By reducing error propagation in long-term forecasting, the framework can be utilized for multi-day trading strategies. Financial markets are characterized by fluctuating patterns and sudden shifts. The ACO-LD driven weight adjustment mechanism allows the ensemble to adapt changing market conditions, outperforming static models that often fail during periods of high volatility. The improvements and experimental benefits have already been analyzed and discussed, however, in terms of disadvantage, the proposed approach faces the computational complexity problem due to the fusion of hybrid methods. The iterative nature of the algorithm introduces computational overhead, particularly with large datasets or extensive model ensembles. This can make real-time forecasting challenging, limiting the scalability in high-frequency trading environments. Moreover, the detailed procedure of experiment in fabricating the final ensemble model is accomplished to produce a better forecasting accuracy over baseline models for index future price forecasting. Different adaption and experimentation of the proposed approach can be done in future research. Testing the framework across diverse markets, including forex, commodities, and emerging financial instruments, will provide insights into its generalization and robustness. Future iterations could integrate external macroeconomic indicators, geopolitical risk factors, and sentiment analysis from news and social media.

6. Conclusions

In this work, a new ensemble approach is proposed for multi-day ahead index future price forecasting problem. The proposed approach uses different importance score generation methods to obtain feature-weighted hybrid learning models. multi-out support vector regression approaches are developed for multi-day ahead forecasting. Finally, the individual feature weighted hybrid forecast models are combined through a continuous multi colony ant colony optimization model (MACO-LD) to construct the ensemble model.

Eight index futures price data are considered to evaluate the performance. A comprehensive array of technical indicators and oscillators have been utilized as the input features in this study. The data sets are trained and tested through a walk forward sliding window approach. First, the experimental findings are investigated to compare importance score based hybrid models with the baseline models, and then the ensemble forecasting model is compared with the parent models. The numerical results, achieved based on different performance metrics, show the superiority of the proposed ensemble model over baseline algorithms and the hybrid feature weighted models. The empirical findings establish that the proposed ensemble model is a promising price forecasting tool and should be applied for the index future price forecasting problem.

The proposed framework signifies a substantial improvement in financial forecasting, overcoming critical shortcomings of conventional ensemble learning via dynamic weight optimization and hybrid model integration. Despite the limitations in computational complexity and hyperparameter sensitivity, future research may refine and augment the model, thereby improving its robustness and applicability across various financial markets. This study establishes a basis for more flexible, interpretable, and precise multi-day forecasting models, enhancing the development of financial time series analysis.