Real-Time Handover in LEO Satellite Networks via Markov Chain-Guided Simulated Annealing

Abstract

This paper presents a real-time handover and link assignment framework for low-Earth-orbit (LEO) satellite networks operating in dense urban canyons. The proposed Markov chain-guided simulated annealing (MCSA) algorithm optimizes user-to-satellite assignments under dynamic channel and capacity constraints. By incorporating Markov chains to guide state transitions, MCSA achieves faster convergence and more effective exploration than conventional simulated annealing. Simulations conducted in Ku-band urban canyon environments show that the framework achieves an average user satisfaction of about 97%, providing an approximately 10% improvement over genetic algorithm (GA) results. It also delivers 10–15% higher resource utilization, lower blocking rates comparable to integer linear programming (ILP), and superior runtime scalability with linear complexity $O(k·|U|·|S\left|\right)$. These results confirm that MCSA provides a scalable and robust real-time mobility management solution for next-generation LEO satellite systems.

1. Introduction

Recent advances in wireless technologies have driven the need for reliable, wide-area connectivity. While terrestrial networks perform well in populated areas, they fall short in remote, rural, and maritime regions due to deployment limitations. Satellite communications, especially those based on low-Earth-orbit (LEO) satellites, offer a promising alternative with global coverage, low latency, and energy-efficient links. Due to their proximity to Earth, LEO satellites play a central role in the vision of seamless global 6G connectivity [1,2,3].

While LEO satellite systems enhance coverage and communication, they also pose significant challenges, most notably, frequent handovers. Unlike fixed terrestrial base stations, LEO satellites move rapidly (∼7 km/s), causing user links to change frequently, even within short sessions [4,5,6], typically every 20–40 s for users under LEO constellations operating near 550 km altitude, resulting in dynamic user-satellite connectivity. The growth of mega-constellations like Starlink and OneWeb intensifies this issue by increasing both the number of handovers and the complexity of real-time user-satellite assignment [7,8,9], making it essential to develop resilient handover strategies. In response to these challenges, early research explored a range of handover strategies, which are typically categorized based on whether the serving satellite changes, either as beam handovers (within the same satellite) or satellite handovers (between different satellites) [10]. In this context, earlier studies focused on beam handovers due to the relatively small number of satellites in legacy systems [11,12,13]. However, the rise of mega-constellations has shifted focus toward satellite handovers. To this end, graph-based handover models have gained attention [14,15,16]. For instance, ref. [14] modeled satellite coverage and handover intervals as graph nodes and directed edges to apply path optimization techniques. The authors of [15] extended them to MIMO systems for energy-efficient switching, while [16] incorporated user priority into the optimization model.

While graph-based methods show promise, their scalability becomes a concern in large-scale LEO networks due to increasing computational complexity because of ever-increasing satellite numbers. To overcome this, reinforcement learning (RL) has emerged as a viable alternative. Unlike traditional optimization, RL learns optimal policies through interaction with dynamic environments, making it well suited to the variability of LEO networks [17]. Once trained, it can be deployed with low computational overhead, and it has shown effectiveness in related satellite tasks such as beam hopping [18,19,20], power control [21,22,23], and routing optimization [24,25,26].

Despite RL’s growing role in satellite network optimization, its practical use in LEO environments remains limited. RL frameworks often entail substantial training overhead and require relatively stable environments for convergence, conditions that are difficult to meet in highly dynamic orbital geometries with rapidly changing satellite visibility and user mobility [27]. Recent studies further emphasize the difficulty of maintaining policy generalization under non-stationary topologies, where convergence instability and retraining cost degrade real-time feasibility [28,29]. Centralized training also introduces latency and communication overhead, especially in large-scale constellations [30], while defining realistic state representations and reward functions remains an open challenge [31,32]. These constraints highlight the need for lightweight, stable, and scalable optimization strategies that maintain responsiveness under stochastic and time-sensitive LEO conditions.

In practical deployments, static propagation assumptions are unrealistic. Satellite-to-user links, particularly for ground mobile users, are affected by dynamic and unpredictable conditions. In urban areas, obstacles such as buildings and vegetation intermittently block signals, causing fluctuations in channel quality [33]. Maintaining a continuous quality of service (QoS) in such scenarios requires responsive switching to links with a better line of sight (LOS). However, the unpredictable propagation dynamics and high satellite density of mega-constellations pose significant challenges for real-time decision-making. The resulting increase in handover frequency and signaling complexity demands reactive, propagation-aware mechanisms that are both low-latency and scalable. These mechanisms must quickly detect link degradation and dynamically reassign users based on real-time connectivity and resource availability.

Beyond reinforcement learning approaches, heuristic optimization methods have also been investigated for LEO satellite management. For instance, Zhou et al. [34] proposed the MOLM algorithm, which employs multi-objective simulated annealing for congestion-aware routing in LEO networks. While such methods demonstrate the potential of annealing for global optimization, they typically address static routing or load-balancing problems. In contrast, the proposed Markov chain-guided simulated annealing (MCSA) introduces a probabilistic exploration mechanism that adapts in real time to dynamic handover conditions, enabling both scalability and stability under mobility-induced uncertainty.

To address these challenges, we propose an adaptive real-time handover framework for LEO satellite networks based on Markov chain-guided simulated annealing (MCSA). The approach formulates user-satellite association as a constrained optimization problem that maximizes instantaneous preference scores while satisfying connectivity and resource constraints. Unlike predictive approaches, it relies on real-time metrics such as the elevation angle, data rate, and resource availability, for fast, data-driven decisions. MCSA employs a Markov Chain to guide probabilistic transitions and incorporates a dynamic cooling schedule to balance exploration and convergence in large-scale and time-sensitive scenarios. The main contributions are summarized as follows:

• A real-time, propagation-aware handover framework tailored to LEO networks, capturing the stochastic link dynamics due to user mobility and urban obstructions.
• An MCSA algorithm that optimizes user-satellite associations under real-time resource and connectivity constraints with adaptive probabilistic transitions.
• A dynamic exploration–exploitation balance through real-time annealing factor adjustment, improving convergence in dynamic environments.
• A resource- and preference-aware assignment strategy that ensures scalability and user satisfaction in LEO mega-constellations.

In addition, the proposed framework aligns with emerging 6G Non-Terrestrial Network (NTN) directions and the standardization efforts of ITU-R M.2150-0 [35] and M.2514 [36], which emphasize intelligent, adaptive mobility management across integrated terrestrial–satellite infrastructures.

The remainder of this paper is organized as follows. Section 2 outlines the system model and channel characteristics. Section 3 presents the problem formulation and the proposed MCSA algorithm; Section 3.4 details the implementation of the reactive handover strategy. Section 4 presents simulation results and performance evaluation. Finally, Section 5 concludes the paper and suggests future research directions.

2. System Model

This study categorizes network nodes by altitude into space-based, aerial, and terrestrial. The focus is on LEO satellites at altitudes of 500–1200 km, operating in dense urban canyons with high-rise buildings (over 50 m) and narrow streets (under 30 m wide). Channel modeling and non-terrestrial network (NTN) analyses are based on Ku-band frequencies (10.7–21.2 GHz downlink, 29.5–30.0 GHz uplink), aligned with ITU-R P.618-13 recommendations [37]. Terminal deployment considers fully outdoor, fully indoor, and mixed scenarios to support realistic evaluation under diverse propagation conditions.

This study focuses on ground mobile users in dense urban canyons, aiming to design handover mechanisms that integrate real-time satellite positioning, elevation angle, and user-specific service-level agreements (SLAs) into decision-making. Geostationary (GEO) and medium-Earth-orbit (MEO) systems, non-urban environments, and inter-satellite optimization are excluded to maintain scope.

To address these challenges, we propose a real-time handover framework that dynamically assigns users to satellites based on instantaneous link quality and network load. It integrates satellite position data, 3D urban mapping, live network feedback, and user session requirements to enable reactive, propagation-aware handover decisions. This ensures continuous connectivity and resource-efficient allocation in complex, fast-changing environments. The framework illustrated in Figure 1 comprises three main components: Real-Time Monitoring, the Scoring Engine, and the Assignment Module, detailed in Section 3.

Figure 1. Real-time handover and link assignment framework. AR (available resources), RT (remaining time), EA (elevation angle), DR (achievable data rate).

2.1. LEO Satellite Channel Model for Dense Urban Canyons

This study adopts a conventional 3D geometric multiple-input, multiple-output (MIMO) channel model to characterize the LEO satellite downlink to the user terminal. Geometric relationships among scatterers and transceivers define the channel properties. Handover is modeled as an inter-satellite event, with the communication channel assumed to be established beforehand. It targets dense urban canyon environments, characterized by high-rise buildings, trees, and narrow streets, as shown in Figure 2. In these settings, non-line-of-sight (NLoS) conditions are highly probable, with scatterers around the user terminal assumed to be uniformly distributed.

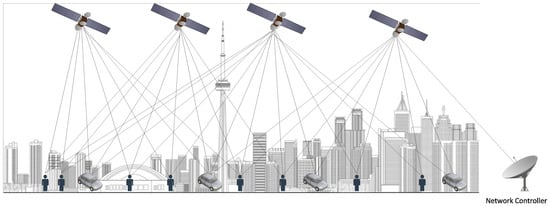
Figure 2. System model for LEO downlink in urban canyon.

Total path loss, $P{L}_{\mathrm{total}}$, is modeled as the sum of free-space path loss (FSPL) and atmospheric absorption from oxygen (${\alpha }_{\mathrm{O}2}$) and water vapor ($\alpha {\mathrm{H}}_2\mathrm{O}$) [38], with other gases considered negligible above ${30}^{°}$ elevation angles [39].

$$P{L}_{\mathrm{total}}=FSPL+\Theta$$

(1)

$$\Theta =\alpha ·d$$

(2)

where $\alpha$ is the atmospheric attenuation (dB/km), and d is the distance in kilometers.

2.1.1. Free-Space Path Loss (FSPL)

The LoS probability is modeled as a function of the elevation angle:

$$P_{\mathrm{LoS}}={\displaystyle \frac{1}{1+a·exp\left[-b\left(\frac{180}{\pi }arctan\left(\frac{h_s}{d_{s,u}}\right)-a\right)\right]}}$$

(3)

where a and b are environment-specific parameters, $h_s$ is the satellite altitude, and $d_{s,u}$ is the slant distance between the satellite and user. The NLoS probability is defined as follows:

$$P_{\mathrm{NLoS}}=1-P_{\mathrm{LoS}}$$

(4)

The slant distance, $d_{s,u}$, illustrated in Figure 3, is geometrically derived from the satellite altitude, Earth’s curvature, and user elevation angle, expressed as follows:

$$d_{s,u}=\sqrt{R_E^2{sin}^2\varphi +h_s^2+2R_E{h}_s}-R_{E}sin{\varphi }_{u,s}$$

(5)

where $R_E$ is the Earth’s radius, $h_s$ the satellite altitude, and ${\varphi }_{u,s}$ the elevation angle from the user’s perspective.

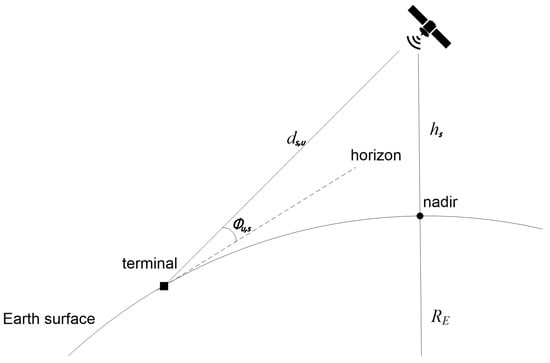
Figure 3. Slant distance, $d_{s,u}$, between satellite and ground user.

The LoS and NLoS path loss components are defined as follows:

$$P{L}_{\mathrm{LoS}}=20{log}_{10}\left({\displaystyle \frac{4\pi f_c{d}_{s,u}}{c}}\right)+{\eta }_{\mathrm{LoS}}$$

(6)

$$P{L}_{\mathrm{NLoS}}=20{log}_{10}\left({\displaystyle \frac{4\pi f_c{d}_{s,u}}{c}}\right)+{\eta }_{\mathrm{NLoS}}$$

(7)

The expected FSPL is computed as follows:

$$FSPL=P_{\mathrm{LoS}}·P{L}_{\mathrm{LoS}}+P_{\mathrm{NLoS}}·P{L}_{\mathrm{NLoS}}$$

(8)

Expanding this, we define the following:

$$A={\eta }_{\mathrm{LoS}}-{\eta }_{\mathrm{NLoS}},B=20{log}_{10}\left({\displaystyle \frac{4\pi f_c}{c}}\right)+{\eta }_{\mathrm{NLoS}}$$

(9)

$$\begin{array}{ccc}FSPL={\displaystyle \frac{A}{1+a·exp\left[-b\left(\frac{180}{\pi }arctan\left(\frac{h_s}{d_{s,u}}\right)-a\right)\right]}}\hfill & & \\ & & \hfill +10{log}_{10}(h_s^2+r_{ik}^2)+B\end{array}$$

(10)

Atmospheric Absorption 

Atmospheric attenuation is the sum of specific attenuations due to oxygen and water vapor,

$$\alpha ={\alpha }_{{\mathrm{O}}_2}+{\alpha }_{{\mathrm{H}}_2\mathrm{O}}$$

(11)

Signal-to-Noise Ratio and Data Rate 

The received signal-to-noise ratio (SNR) under additive white Gaussian noise is,

$$SNR(h_s,d_{s,u})=P_t-P_n-P{L}_{\mathrm{total}}(h_s,d_{s,u})$$

(12)

where $P_t$ and $P_n$ is the transmit power and noise power in dBm. The achievable data rate is as follows:

$$D{R}_{s,u}=BW·{log}_2\left(1+{10}^{{\displaystyle \frac{SNR(h_s,d_{s,u})}{10}}}\right)$$

(13)

2.2. Handover Process

Building on the channel model, handovers in the proposed system are triggered on-demand, based on real-time detection of link quality fluctuation. Figure 4 illustrates the handover process, with three main stages. In Stage 1: Real-Time Context Monitoring, the system continuously tracks link-level metrics such as the elevation angle and the achievable data rate, to evaluate connection quality. “Real-time context” includes user-specific parameters (e.g., location, mobility, SLA), satellite attributes (e.g., visibility window, resource availability), and channel conditions (e.g., signal quality). This data is periodically gathered from the user terminal, satellite telemetry using satellite ephemeris, and urban geometry. Upon detecting degradation, such as falling elevation angles or reduced data rates, the system initiates stage 2.

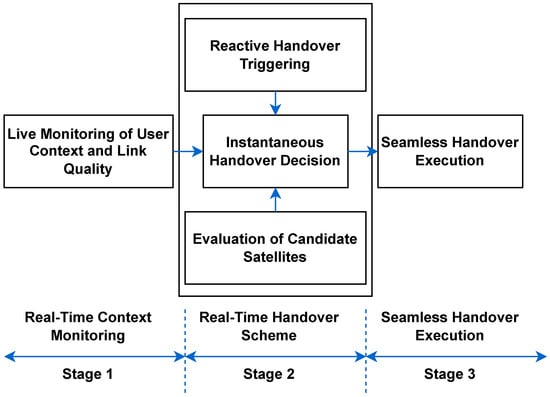
Figure 4. Real-time handover process.

Stage 2: Real-Time Handover Decision begins once degradation is detected, such as signal quality drops and SLA violations. The system then evaluates candidate satellites based on current conditions and selects the most suitable target in real time to maintain service continuity. Finally, Stage 3: Seamless Handover Execution ensures fast and efficient switching with minimal service interruption. The transition utilizes previously gathered context and live measurements to sustain QoS throughout the session.

Section 3 introduces the Real-Time Handover and Link Assignment Framework, which formalizes decision-making and resource allocation for efficient user-to-satellite associations in multi-LEO environments.

3. Real-Time Handover and Link Assignment Framework

To support real-time, resource-aware mobility management, the proposed system introduces a Reactive Handover and Link Assignment Framework that dynamically assigns users to the most suitable satellites based on instantaneous conditions, measured data rates, and resource availability.

The process starts with the Context Acquisition Module, which continuously monitors real-time parameters including user equipment (UE) location, achievable data rate, SLA requirements, and link-specific metrics such as available resources (AR), remaining visibility time (RT), and elevation angle (EA). These measurements are passed to the Metrics Weight Adjuster (MWA), which dynamically tunes metric weights based on network conditions and operator policies, ensuring that the scoring process remains responsive to real-time network dynamics.

The Scoring Engine then uses these weights and real-time inputs to compute a score for each satellite-user pair, reflecting the satellite’s ability to meet user requirements while ensuring overall network efficiency. After that, the computed scores are forwarded to the Assignment Module, which evaluates candidate pairings under real-time constraints such as satellite capacity, SLA compliance, and load conditions. It then selects the best assignment to maximize user satisfaction and overall network performance.

By integrating real-time monitoring, adaptive scoring, and resource-aware assignment, the proposed framework offers a scalable and responsive management solution. It maintains continuous service quality while promptly adapting to link degradation and mobility-induced changes.

The following subsection presents the problem formulation, modeling handover and link assignment as a real-time optimization problem constrained by user SLA and satellite resources. Subsequent subsections describe the scoring mechanism and assignment strategy that enable responsive and efficient decision-making within the proposed framework.

3.1. Problem Formulation

The real-time handover and link assignment problem is modeled as a binary combinatorial optimization problem. The objective is to determine the optimal assignment of users to satellites at time t, considering real-time user context, link quality, and resource availability. A binary decision variable, $x_{ij}$, is defined, where $x_{ij}=1$ if user i is assigned to satellite j, and 0 otherwise, as shown in Equation (14).

$$x_{ij}=\left\{\begin{array}{cc}1\hfill & \text{if user}i\text{is assigned to satellite}j,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(14)

The objective is to maximize user satisfaction by selecting assignments that yield the highest user-satellite scores, $Scor{e}_{ij}^t$, subject to user SLA constraints and satellite capacity.

$$\begin{array}{cc}\hfill \max & \sum _{i=1}^I\sum _{j=1}^J{x}_{ij}Scor{e}_{ij}^t\hfill \end{array}$$

(15)

$$\begin{array}{cccc}\hfill \mathrm{s}.\mathrm{t}.\mathrm{C}1:& D{R}_{min,u}^t\le D{R}_{u,s}^t,\hfill & \hfill & \forall u\in U,\forall s\in S\hfill \end{array}$$

(16)

$$\begin{array}{cccc}\hfill \mathrm{C}2:& D{R}_{max,u}^t\ge D{R}_{u,s}^t,\hfill & \hfill & \forall u\in U,\forall s\in S\hfill \end{array}$$

(17)

$$\begin{array}{cccc}\hfill \mathrm{C}3:& \sum _{u=1}^{U}m\times l_{u,s}^t\le L_s^t,\hfill & \hfill & \forall s\in S\hfill \end{array}$$

(18)

$$\begin{array}{cccc}\hfill \mathrm{C}4:& \sum _{s=1}^S{x}_{u,s}\le 1,\hfill & \hfill & \forall u\in U\hfill \end{array}$$

(19)

$$\begin{array}{cccc}\hfill \mathrm{C}5:& {\varphi }_{u,s}^t\ge {\varphi }_0,\hfill & \hfill & \forall s\in S,\forall u\in U\hfill \end{array}$$

(20)

Here, constraints (16) and (17) enforce that each user’s data rate remains within SLA-defined bounds. Constraint (18) ensures satellite resource limits are respected based on the current load, while (19) restricts each user to at most one satellite. Finally, constraint (20) guarantees that the elevation angle exceeds the minimum threshold for LOS connectivity.

It is worth noting that the weighting coefficients in the objective function (15) are not static. As formulated in Equation (22), each metric’s contribution is adaptively scaled through an entropy-based weighting factor $w_{u_i,m_j}^t$, which evolves with the temporal variability of the corresponding metric (e.g., data rate, resource availability, elevation). This mechanism enables the optimization process to dynamically emphasize metrics that show higher discriminative power or volatility at time t, allowing the objective in (15) to remain responsive to real-time network conditions.

Rather than using conventional integer programming, the problem is solved with the proposed MCSA method. MCSA enables efficient solution space exploration and avoids premature convergence by allowing probabilistic transitions governed by a Markov Chain and accepting suboptimal solutions via an annealing schedule. This approach offers a scalable, adaptive solution that is well suited to the dynamic and time-sensitive nature of handover and link assignment in LEO networks.

3.2. Satellite Scoring Module

As part of the decision process, a scoring mechanism evaluates the suitability of each candidate satellite, $s_j$, for user $u_i$ at time t. The score ($Scor{e}_{u_i,s_j}^t$) reflects the satellite’s ability to meet the user’s requirements while satisfying network constraints. It is computed using three measured metrics, AR, RT, and Achievable DR, each weighted according to its real-time impact on service quality.

3.2.1. Weight Calculation

To dynamically determine metric importance, an entropy-based approach is employed to quantify the variability of each metric across candidates, allowing data-driven weight adjustment in response to evolving network conditions. The entropy of metric $m_j$ for user $u_i$ is given as follows:

$$E_{u_i,m_j}^t=-\sum _{k=1}^K{P}_k{log}_2{P}_k$$

(21)

where $P_k$ is the probability of the $k\mathrm{th}$ cluster within metric $m_j$, and K is the number of clusters determined using the elbow method with KMeans clustering.

To address scale differences (e.g., Mbps, seconds, percentage), metrics are normalized. Once entropy is computed, the normalized weight $w_{u_i,m_j}^t$ of metric $m_j$ for user $u_i$ is defined as follows:

$$w_{u_i,m_j}^t={\displaystyle \frac{E_{u_i,m_j}^t}{{\sum }_{j=1}^M{E}_{u_i,m_j}^t}}$$

(22)

where M is the total number of considered metrics.

3.2.2. Satellite Scoring

Using the computed weights, the score for satellite $s_j$ with respect to user $u_i$ at time t is given as follows:

$$Scor{e}_{ij}^t=w_{rt}^{t}R{T}_{ij}^t+w_{dr}^{t}D{R}_{ij}^t+w_{ar}^t(1-U_j^t)$$

(23)

where $R{T}_{ij}^t$ is the visibility time, $D{R}_{ij}^t$ is the achievable data rate, and $U_j^t$ is satellite j utilization. The weights $w_{rt}^t$, $w_{dr}^t$, and $w_{ar}^t$ correspond to RT, DR, and AR, respectively. Each component is normalized as follows:

$$R{T}_{ij}^t={\displaystyle \frac{R{T}_{ij}^t-R{T}_{\min }^t}{R{T}_{\max }^t-R{T}_{\min }^t}}$$

(24)

$$D{R}_{ij}^t={\displaystyle \frac{D{R}_{ij}^t-D{R}_{i,s}^{\min ,t}}{D{R}_{i,s}^{\max ,t}-D{R}_{i,s}^{\min ,t}}}$$

(25)

where $R{T}_{\min }^t$ and $R{T}_{\max }^t$ are the minimum and maximum visibility durations across all satellite–user pairs at time t. Similarly, $D{R}_{i,s}^{\min ,t}$ and $D{R}_{i,s}^{\max ,t}$ define the range of achievable data rates for user $u_i$ across candidate satellites.

The resulting score, $Scor{e}_{ij}^t$, serves as input to the optimization problem in Equations (15)–(20), guiding user-to-satellite assignments. These scores are then passed to the Assignment Module, which selects the best satellite for each user based on the defined constraints and service quality.

3.3. Real-Time Handover and Assignment Strategy

The proposed real-time handover strategy integrates reactive mobility management with dynamic user-to-satellite assignment. By utilizing satellite position data, urban geometry, live user context, and satellite load metrics, the system enables on-demand handovers to ensure seamless connectivity and efficient resource use. A key challenge here is the user admission under rapidly changing conditions due to mobility and link variability. To address this, we introduce an enhanced Simulated Annealing algorithm guided by a Markov Chain model, offering an adaptive solution for real-time assignment.

In this framework, each state represents a user-to-satellite assignments at a given time. Transitions between states are guided by preference $Scor{e}_{ij}^t$ (Section 3.2.2), which reflects the real-time suitability of satellites for individual users and influences the likelihood of moving toward higher utility configurations. This probabilistic structure enhances both user satisfaction and system performance.

A transition matrix derived from these scores directs the search process. Integrating the Markov Chain model strengthens Simulated Annealing’s capacity to explore the solution space effectively, balancing global exploration and local exploitation and enabling convergence to near-optimal solutions within the tight latency and performance bounds of LEO networks.

The next subsection presents the Adaptive MCSA algorithm, detailing the optimization procedures that support responsive, efficient, and SLA-compliant user-to-satellite assignments in real time.

3.4. Adaptive Handover via Markov Chain-Guided Simulated Annealing Algorithm

This section introduces the proposed adaptive handover framework, which reactively assigns users to the most suitable satellites by continuously assessing real-time network conditions and optimizing user associations. It combines a context-aware module with a metaheuristic optimization strategy to enhance handover decisions in dynamic, resource-constrained LEO environments, it consists of two components:

• Real-time handover algorithm: Acquires real-time user context, satellite visibility, and resource availability. It computes user-satellite preference scores based on SLAs and observed network conditions.
• MCSA Assignment: A search-based algorithm that iteratively explores and improves user-to-satellite assignments. It employs a Markov chain to guide state transitions and a temperature-based acceptance criterion to balance exploration and exploitation.

The adaptive handover strategy is outlined in Algorithm 1.

Algorithm 1 Real-time handover algorithm

Require: Set of users $\left|U\right|$, and satellites $\left|S\right|$ 1: for all user $i\in \left|U\right|$ do 2:       Retrieve SLA profile for user i 3:       Determine candidate satellites $j\subseteq \left|S\right|$ visible to user i 4:       Acquire elevation angle ${\varphi }_{ij}^t$ and available resources $A{R}_j^t$ for all $j\in \left|S\right|$ 5:       Measure achievable data rate $D{R}_{ij}^t$ 6: end for 7: Compute real-time scores $Scor{e}_{ij}^t$                 ▹ Algorithm 2 8: Perform user-to-satellite assignment               ▹ Algorithm 3 9: return Optimal user-to-satellite assignment

Algorithm 2 Real-time satellite-scoring engine

Require: Real-time metrics for users U and satellites S: 1:    $D{R}_{ij}^t$—Measured achievable data rate 2:    $A{R}_j^t$—Available satellite resources 3:    $R{T}_{ij}^t$—Remaining visibility time Ensure: Real-time scores $Scor{e}_{ij}^t$ for all $i\in U,j\in S$ 4: for each metric $m_j\in \{DR,RT,AR\}$ do 5:       Apply KMeans clustering to standardize values 6: end for 7: for all user $i\in U$ do 8:       for each metric $m_j$ do 9:              Compute entropy $E_{i,m_j}^t$                 ▹ Equation (21) 10:            Compute weight $w_{i,m_j}^t$                ▹ Equation (22) 11:      end for 12: end for 13: for all user $i\in U$ do 14:      for all satellite $j\in S$ do 15:            Compute score $Scor{e}_{ij}^t$                   ▹ Equation (23) 16:      end for 17: end for 18: return All $Scor{e}_{ij}^t$ values

Algorithm 3 Markov chain-guided simulated annealing

Require: 1: U, S—Set of users and satellites 2: $Scor{e}_{ij}^t$—Calculated score of satellite j for user i 3: $L_{s_j}^t$—Available capacity on satellite $s_j$ 4: $l_{ij}^t$—Required capacity if user i connects to satellite j 5: $T_0$—Initial annealing temperature 6: ${\alpha }_{\min },{\alpha }_{\max }$—Bounds for adaptive decay rate 7: N—Total number of iterations Ensure: 8: $best\_state$—Final user-to-satellite assignment 9: $best\_score$—Maximum total score achieved 10: Initialize $current\_state$ with a random valid assignment 11: Evaluate $current\_score$ based on total $Scor{e}_{ij}^t$ 12: Set $best\_state\leftarrow current\_state$ 13: Set $best\_score\leftarrow current\_score$ 14: Set $T\leftarrow T_0$, $\alpha \leftarrow {\alpha }_{\max }$ 15: Set $no\_improvement\leftarrow 0$ 16: Set $max\_no\_improvement\leftarrow 0.1·N$ 17: for $i=1$ to N do 18:     Generate $new\_state$ by modifying $current\_state$ 19:     if $new\_state$ violates any constraints then 20:         continue 21:     end if 22:     Compute $new\_score$ based on $Scor{e}_{ij}^t$ 23:     Compute transition probability:        $$P=\min \left(1,exp\left({\displaystyle \frac{new\_score-current\_score}{T}}\right)\right)$$ 24:     if $new\_score>current\_score$ or $rand\left(\right)<P$ then 25:         $current\_state\leftarrow new\_state$ 26:         $current\_score\leftarrow new\_score$ 27:         if $new\_score>best\_score$ then 28:            $best\_state\leftarrow new\_state$ 29:            $best\_score\leftarrow new\_score$ 30:         end if 31:         $\alpha \leftarrow \min ({\alpha }_{\max },\alpha ·{\displaystyle \frac{best\_score}{current\_score}})$ 32:         $no\_improvement\leftarrow 0$ 33:     else 34:         $no\_improvement\leftarrow no\_improvement+1$ 35:         $\alpha \leftarrow \max ({\alpha }_{\min },\alpha ·{\displaystyle \frac{best\_score}{current\_score}})$ 36:     end if 37:     $T\leftarrow \alpha ·T$ 38:     if $no\_improvement\ge max\_no\_improvement$ then 39:         break 40:     end if 41: end for 42: return $best\_state$, $best\_score$

3.5. Real-Time Satellite Scoring Engine

Algorithm 2 outlines the satellite scoring process used to compute $Scor{e}_{u_i,s_j}^t$ for all user–satellite pairs, reflecting the satellite’s ability to serve users based on real-time link metrics. The algorithm relies solely on live measurements, ensuring responsiveness to current network conditions.

Required inputs defined in (Lines 1–3) include the achievable data rate, $D{R}_{ij}^t$, available resources, $A{R}_j^t$, and visibility time, $R{T}_{ij}^t$, for all relevant pairs. At the beginning (Lines 4–6), KMeans clustering is applied to standardize metric scales, enabling fair entropy computation and avoiding scale dominance. After which, (Lines 7–12) computes entropy for each metric (Line 9) and normalizes the results into user-specific weights (Line 10), capturing the relative metrics importance under current conditions. Finally, (Lines 13–17), $Scor{e}_{ij}^t$ are computed using the utility function in Equation (23) (Line 15). Afterward, the resulting score is passed to the assignment module (Algorithm 3) to find the best user-to-satellite mappings.

The matching process is handled in the following subsection using the MCSA algorithm, detailed in Algorithm 3.

3.6. Markov Chain-Guided Simulated Annealing Assignment

To address the handover and link assignment problem under SLA and resource constraints, we adopt a metaheuristic optimization strategy based on simulated annealing (SA). To enhance convergence and guide the search process, the SA procedure is integrated with a Markov chain framework, which biases transitions toward higher-scoring user-satellite configurations. This subsection outlines the problem formulation, the relaxation strategy, and the algorithmic structure of the proposed assignment method.

Let $U=\{1,2,\dots ,i\}$ be the set of users and $S=\{1,2,\dots ,j\}$ be the set of satellites. The following definitions are used:

• $x_{ij}$: binary variable equal to 1 if user i is assigned to satellite j, and 0 otherwise.
• $D{R}_{ij}^t$: current data rate between satellite j and user i.
• $D{R}_{\min ,i}^t$, $D{R}_{\max ,i}^t$: SLA-defined minimum and maximum data rates for user i, such that $D{R}_{\min ,i}^t\le D{R}_{ij}^t\le D{R}_{\max ,i}^t$.
• $c_j$: satellite j capacity.
• $Scor{e}_{ij}^t$: utility score for assigning user i to satellite j.

3.6.1. Objective Function

The assignment problem aims to maximize the overall score while satisfying user requirements and resource constraints, as formulated in OP (15)–(20).

3.6.2. Continuous Relaxation and Penalty Method

To enable continuous optimization, the binary variable $x_{ij}$ is relaxed to the interval $[0,1]$. A penalty term is introduced to enforce SLA and capacity constraints:

$$\min f\left(\mathbf{x}\right)=-\sum _{i=1}^n\sum _{j=1}^{m}Scor{e}_{ij}^t·x_{ij}+P\left(\mathbf{x}\right)$$

(26)

where the penalty function, $P\left(\mathbf{x}\right)$, penalizes violations of SLA and capacity constraints:

$$P\left(\mathbf{x}\right)=\alpha \sum _{i=1}^n\left[\max {\left(0,\underset{i}{\min }-\sum _{j=1}^m{r}_{ij}{x}_{ij}\right)}^2\right]+\beta \sum _{j=1}^m\left[\max {\left(0,\sum _{i=1}^n{r}_{ij}{x}_{ij}-c_j\right)}^2\right]$$

where $\alpha$ and $\beta$ are large positive constants penalizing constraint violations.

3.6.3. Dual Annealing Algorithm

To minimize $f\left(\mathbf{x}\right)$ (Equation (26)), we adopt dual annealing, a hybrid global-local optimization strategy combining global exploration with local refinement, allowing the algorithm to iteratively improve solutions and escape local optima.

3.6.4. Adaptive Decay Mechanism

To improve convergence, an adaptive decay mechanism is applied to the cooling rate, $\alpha$, adjusting its value dynamically based on the objective progress:

$${\alpha }_{n+1}=\left\{\begin{array}{cc}\min ({\alpha }_{\max },{\alpha }_n·{\displaystyle \frac{f\left({\mathbf{x}}_n\right)}{f\left({\mathbf{x}}_{n+1}\right)}})\hfill & \mathrm{if}f\left({\mathbf{x}}_{n+1}\right)<f\left({\mathbf{x}}_n\right),\hfill \\ \max ({\alpha }_{\min },{\alpha }_n·{\displaystyle \frac{f\left({\mathbf{x}}_n\right)}{f\left({\mathbf{x}}_{n+1}\right)}})\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(27)

where ${\alpha }_{\min }$ and ${\alpha }_{\max }$ are the lower and upper bounds of the cooling rate $\alpha$. This adaptive mechanism dynamically balances exploration and exploitation based on the optimization progress, encouraging a broader search in the early stages and promoting convergence as the algorithm evolves.

3.7. Markov Chain-Guided Simulated Annealing Assignment

The assignment procedure is detailed in Algorithm 3, which implements the MCSA algorithm for real-time user-to-satellite assignment. Inspired by the annealing process in metallurgy, MCSA uses probabilistic state transitions to explore the solution space and approximate the global optimum. The objective is to maximize the total satisfaction score, $Scor{e}_{ij}^t$, subject to satellite resource constraints. The algorithm begins by defining the required input parameters (Lines 1–7), namely user and satellite sets $\left|U\right|$ and $\left|S\right|$, user-satellite scores $Scor{e}_{ij}^t$ (Algorithm 2), satellite capacity $L_{s_j}^t$, user resource demands $l_{ij}^t$, initial temperature $T_0$, adaptive decay bounds ${\alpha }_{\min }$, ${\alpha }_{\max }$, and maximum iterations N. The initial temperature, $T_0$, was empirically set to the mean absolute change in the scoring function between random neighboring states, ensuring an initial acceptance probability of approximately 0.8 for uphill moves, following common simulated-annealing heuristics.

The process initializes with a valid random assignment (Line 10) and score evaluation (Line 11), both stored as the current and best-known solution (Lines 12–13). The temperature T and decay factor $\alpha$ are initialized (Line 14), along with a counter to monitor stagnation (Lines 15–16). The initial temperature, $T_0$, was empirically set to the mean absolute change in the scoring function between random neighboring states, ensuring an initial acceptance probability of approximately 0.8 for uphill moves, following common simulated-annealing heuristics.

The main loop runs for up to $N=k·\left|U\right|·\left|S\right|$ iterations (Line 17), where k is a tunable scaling constant that controls the depth of exploration and scales with problem size. The impact of k is analyzed in Section 4. At each iteration, a new candidate assignment is generated (Line 18) by modifying the current state (e.g., reassigning a user), where invalid configurations are discarded (Lines 19–21). For valid candidates, the new score is computed (Line 22) and evaluated using the Metropolis criterion (Lines 23–24). If accepted, the current state is updated (Lines 25–26). If the new score improves upon the best-known solution, the best state is updated (Lines 27–30), $\alpha$ is increased to encourage exploration (Line 31), and the stagnation counter is reset (Line 32). Otherwise, the counter is incremented (Line 34), and $\alpha$ is decreased to promote exploitation (Line 35) and the temperature is updated (Line 37). Early termination occurs if no improvement is observed over a predefined threshold (Lines 38–40). Upon completion, the best assignment and score are returned (Line 42). This adaptive mechanism balances exploration and exploitation, making it well suited for dynamic LEO environments with user mobility and real-time service demands. The effectiveness of MCSA depends on the accuracy of the calculated $Scor{e}_{ij}^t$, which is generated via the scoring engine. This engine evaluates satellite suitability based on user- and link-specific metrics and is further described in the next subsection, building on in [40].

Parameter Sensitivity

To ensure the robustness of the proposed algorithm, a brief sensitivity analysis was conducted on the key parameters governing exploration and convergence. The cooling decay rate, $\alpha$, was varied in the range of $[0.9,0.95]$, where lower values caused premature convergence, while higher values delayed stabilization. An intermediate setting of $\alpha =0.92$ offered the best trade-off between runtime and convergence quality. Similarly, the exploration depth, k, was tuned between 5 and 20, with $k=10$ providing consistent convergence behavior and solution diversity, as will be detailed in Section 4.3. These parameter choices were retained for all subsequent simulations.

3.8. Discussion on MCSA Convergence and Effectiveness

We argue that the proposed algorithm with adaptive decay demonstrates strong convergence behavior and yields high-quality solutions within practical constraints. This is supported by the following key characteristics:

• Adaptive cooling for balanced search: The annealing schedule dynamically adjusts based on optimization progress. When improvements stall, cooling accelerates to promote convergence; when improvement is detected, cooling slows to allow deeper exploration of promising regions, maintaining a balance between exploration and exploitation.
• Probabilistic acceptance: At higher temperatures, the algorithm probabilistically accepts suboptimal solutions, enabling escape from local minima. As the temperature declines, acceptance becomes more selective, guiding the search toward optimal configurations.
• Score-guided Markov transitions: unlike purely random transitions, state changes are biased by a Markov Chain structured around utility scores, encouraging movement toward higher-quality solutions and enhancing convergence stability.
• Periodic local refinement: Global transitions are complemented by local search, enabling rapid exploitation of promising states. This hybrid approach improves convergence speed and solution quality.
• Empirical convergence within finite iterations: although theoretical convergence requires infinite time, empirical results show consistent convergence to near-optimal solutions within a practical number of iterations, regardless of initialization.
• Stochastic completeness and ergodicity: assuming ergodicity, the Markov chain allows non-zero probability transitions to all feasible states, ensuring comprehensive exploration and robustness against local entrapment.

These properties confirm that MCSA provides a scalable and effective optimization framework for real-time user-to-satellite assignment in dynamic LEO environments.

The next section presents simulation results, evaluation metrics, and a comparative analysis that validate the framework’s effectiveness under realistic deployment scenarios.

4. Numerical Results

This section evaluates the performance of the proposed MCSA framework using key metrics, including computational complexity, assignment quality, user satisfaction, and resource utilization. Each subsection examines a specific aspect and compares MCSA with benchmark approaches such as integer linear programming (ILP) and a genetic algorithm (GA). For fair comparison, GA parameters were configured following standard convergence-balanced settings (population size = 50, crossover rate = 0.8, mutation rate = 0.1), providing a similar computational budget and termination condition to MCSA.

The effectiveness of the real-time handover and link assignment framework is demonstrated through comprehensive simulations tailored to dense urban canyon environments characterized by high user density and severe signal scattering caused by tall buildings and vegetation. The main simulation parameters are listed in Table 1. Several values are derived from Starlink specifications, while others reflect current trends in LEO satellite network design [41,42]. To capture urban propagation challenges, elevated values for the path loss parameters, A and B, are adopted, following 3GPP guidelines [43]. A relatively high minimum elevation angle, ${\varphi }_{\min }$, is also enforced to ensure sufficient LOS probability, in line with 3GPP Release 15 recommendations [44].

Table 1. Simulation parameters.

Symbol	Parameter Description	Value
$f_c$	Carrier frequency	10.7 GHz
$h_s$	Satellite altitude	550 km
T	Noise temperature	285 K
e	Water vapor pressure	9.36 hPa
$P_t$	Transmit power	85.89 dBm
$BW$	Communication bandwidth	120 Mbps
A	LOS path loss exponent	2.5
B	NLOS path loss exponent	20
${\varphi }_{\min }$	Minimum elevation angle	${20}^{°}$

4.1. Simulation Setup

The MCSA algorithm was implemented in Python 3.12, and the simulation dataset was generated using STK 17.1 by analyzing Starlink constellation coverage, as summarized in Table 2. At the time of evaluation, the study area was covered by 10 LEO satellites; however, not all were capable of meeting the required data rates, especially when the elevation angle dropped below 20 degrees.

Table 2. Satellite access report.

Acc.	Access Start–End	Duration (s)	High EV (°)	Range (km) Min–Max
1	16:22:34–16:35:03	749	46.55	732.91–2713.43
2	16:23:20–16:31:31	491	6.24	2097.13–2709.33
3	16:20:50–16:31:40	650	15.38	1496.30–2711.10
4	16:25:55–16:38:38	763	74.29	570.11–2713.65
5	16:16:10–16:28:16	726	27.42	1059.90–2713.52
6	16:26:48–16:38:37	709	22.36	1212.77–2712.25
7	16:28:42–16:41:15	753	44.35	758.80–2713.83
8	16:14:24–16:24:46	622	13.24	1594.62–2692.18
9	16:27:03–16:39:39	756	75.31	560.08–2694.93
10	16:22:02–16:34:05	723	28.12	1029.27–2694.92

Although satellite visibility durations ranged from 491 to 763 s, the periods during which data rate constraints were satisfied were significantly shorter. To emulate a group handover scenario, the dataset comprises 1000 users, enabling a comprehensive assessment of the proposed handover and assignment framework.

In addition to orbital and ephemeris computation, STK 17.1 was also used to model the three-dimensional urban propagation environment, including terrain elevation and building obstruction effects. This ensured that user–satellite visibility and handover dynamics accurately reflected realistic urban canyon conditions. To complement the empirical evaluation, we analyze MCSA time complexity to assess its scalability and suitability for real-time execution.

4.2. Time Complexity Analysis

To evaluate the computational efficiency of the MCSA, we analyze its time complexity and compare it with benchmark methods: GA and ILP. Figure 5 shows a log-scaled comparison of runtime growth with respect to the number of users U.

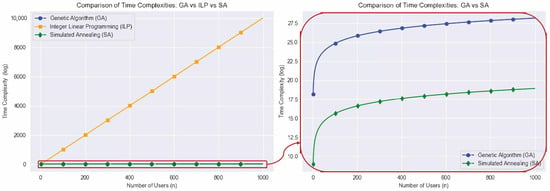
Figure 5. Comparison of time complexity for ILP, GA, and SA with an increasing number of users.

In the left subfigure, ILP shows exponential growth in runtime as the user population increases, an expected outcome due to the exhaustive search space involved, which limits its scalability for large-scale assignment problems (e.g, at 1000 users, ILP becomes computationally infeasible). The right subfigure compares the performance of the proposed framework with GA. Although GA exhibits a near-logarithmic trend, its runtime remains consistently higher than that of SA. This is attributed to GA’s population-based operations, which require evolving multiple candidate solutions per generation. It is noted that these runtime trends are empirical and depend on the parameter settings used for GA and MCSA (e.g., population size, mutation rate, and initial temperature); thus, the comparison reflects observed behavior under equivalent computational budgets, rather than universal asymptotic bounds.

The time complexity of the integrated framework (Algorithm 1–3) is $\mathcal{O}(k·|U|·|S\left|\right)$, where k is a tunable constant controlling the depth of exploration, $\left|U\right|$ the set of users, and $\left|S\right|$ is their candidate satellites. This overall complexity stems from three main components:

• Satellite filtering (Algorithm 1): operates over all users and their candidate satellites, contributing $\mathcal{O}\left(\right|U|·|S\left|\right)$.
• Satellite scoring (Algorithm 2): processes all user-satellite pairs, contributing $\mathcal{O}\left(\right|U|·|S\left|\right)$.
• MCSA assignment (Algorithm 3): dominates the overall cost with $\mathcal{O}(k·|U|·|S\left|\right)$.

While classical simulated annealing can exhibit exponential time complexity in its unrestricted form, the proposed MCSA operates under a bounded iteration schedule $N=k·\left|U\right|·\left|S\right|$, which constrains runtime growth to linear scaling with respect to the number of users and satellites. This bounded design explains the polynomial runtime trend observed in Figure 5. Compared to ILP’s exponential complexity and GA’s higher per-iteration cost, MCSA offers superior scalability with near-optimal performance, confirming its suitability for real-time use in large-scale LEO networks.

4.3. Effect of Exploration Depth, k, on Assignment Quality

The exploration depth k significantly influences the performance of the MCSA assignment framework, as it determines the total number of iterations ($N=k·\left|U\right|·\left|S\right|$). This subsection analyzes the impact of varying k on assignment quality, stability, and consistency. Two key metrics are evaluated: maximum assignment score and the distribution of user satisfaction, providing practical insights for selecting an optimal k that balances performance with computational cost.

For instance, Figure 6 illustrates the impact of the exploration parameter k on assignment quality. Specifically, Figure 6a illustrates how increasing k from 1 to 20 results in a rapid rise in the assignment score, highlighting the benefits of deeper exploration. Beyond 20, improvements plateau, indicating diminishing returns and unnecessary computational overhead. These results suggest that setting k between 10 and 20 achieves an effective trade-off between solution quality and runtime.

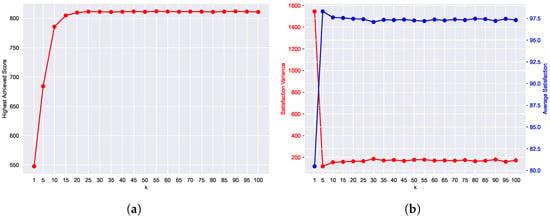
Figure 6. Effect of k on (a) highest achieved score and (b) average satisfaction and variance.

Moreover, Figure 6b presents average user satisfaction and its variance as functions of k. Satisfaction increases sharply up to $k=5$, stabilizing around 97%, while variance decreases significantly until $k=5$, indicating more consistent service quality. Beyond this point, both metrics level off, confirming that the solution space has been sufficiently explored. These findings confirm that moderate values of k not only improve assignment but also enhance fairness across users.

In summary, moderate exploration values ($k=10$ to 20) deliver the highest quality, improved satisfaction, and reduced variance with manageable computational cost. Higher values yield marginal gains at the expense of runtime, while lower values risk suboptimal convergence. The next subsection examines how these gains influence resource utilization.

4.4. Satellite Resource Utilization Comparison

This subsection analyzes satellite resource utilization across different methods, namely SA, ILP, and GA, under both normal- and high-load conditions. The evaluation focuses on load balancing efficiency and the adaptability of each method to growing network demands.

4.4.1. Simulated Annealing (SA)

Figure 7 illustrates the resource utilization achieved through the SA method under both normal and high load conditions. At normal load, Figure 7a, SA achieves a balanced utilization across most satellites. Resource usage is evenly distributed, avoiding both bottlenecks and underutilization. Satellite 6 shows notably lower utilization due to its inability to meet user data rate requirements during the simulation, making it less favorable for assignment. Overall, the results demonstrate SA’s ability to optimize assignments while promoting fairness in resource consumption. Under high load, Figure 7b, SA continues to perform effectively. While overall utilization increases, the load remains evenly distributed across satellites, with no instance of critical overload. This confirms SA’s strong load-balancing capability, even under increased network demand.

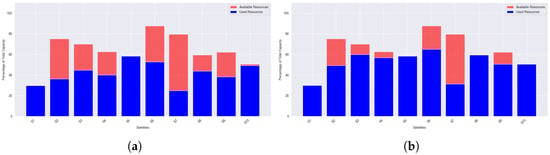
Figure 7. Satellite resource utilization under (a) normal- and (b) high-load conditions using SA.

4.4.2. Integer Linear Programming (ILP)

Figure 8 illustrates ILP satellite utilization under normal- and high-load conditions. Under normal load, Figure 8a, ILP exhibits a relatively uneven distribution. Satellites 1, 6, and 10 are heavily utilized, while others retain substantial unused capacity. This imbalance stems from ILP’s deterministic behavior, where score maximization may override fair load distribution. At high loads, Figure 8b, the imbalance becomes more pronounced. Several satellites approach saturation, while others remain underutilized. Although ILP meets overall demand, the skewed distribution may cause service bottlenecks and increased handover frequency in practical scenarios.

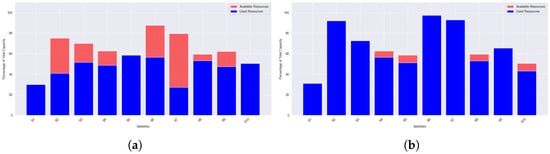
Figure 8. Satellite resource utilization under (a) normal- and (b) high-load conditions using ILP.

4.4.3. Genetic Algorithm (GA)

Figure 9 shows GA satellite utilization under normal- and high-load conditions. At a normal load, Figure 9a, GA shows moderate variability in satellite utilization. While some satellites are used efficiently, others display noticeable imbalances due to the stochastic nature of GA’s evolutionary process. Under high load, Figure 9b, GA struggles to maintain balanced allocations. Resource usage becomes more erratic, with some satellites underutilized and others congested, indicating reduced reliability in convergence compared to SA and ILP.

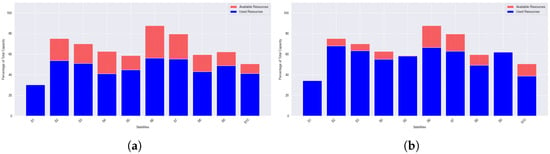
Figure 9. Satellite resource utilization under (a) normal- and (b) high-load conditions using GA.

In summary, the SA approach consistently outperforms ILP and GA in satellite resource utilization. Under both normal- and high-load conditions, it achieves a more balanced load distribution across the constellation, minimizing severe underutilization and overload. These results underscore the effectiveness of the proposed framework in adapting to dynamic network conditions while maintaining operational efficiency. All reported results represent the average of 20 independent STK-based simulation runs with randomized user and satellite positions. The observed variance across runs remained below 3%, confirming consistency at the 95% confidence level and supporting the statistical reliability of the presented comparisons.

4.5. Assigned vs. Required Data Rate Analysis

This subsection evaluates the accuracy of each assignment strategy in meeting user requirements under both normal- and high-load conditions. Performance is assessed by plotting assigned versus required data rates, using an equality line as the ideal reference for perfect assignment.

4.5.1. Simulated Annealing (SA)

Figure 10a,b show assigned versus required data rates using SA-based assignment under normal and high loads. In both cases, assigned rates align closely with the equality line, indicating high precision. While slight dispersion appears at higher data rates under heavy load, SA consistently maintains strong assignment accuracy. A few users remain unserved at high load due to resource constraints, but overall, SA effectively balances performance and feasibility across conditions.

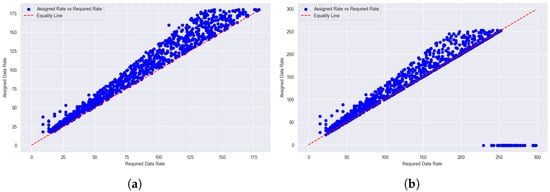
Figure 10. Assigned vs. required data rates under (a) normal- and (b) high-load conditions for SA.

4.5.2. Integer Linear Programming (ILP)

Figure 11 shows ILP-based results. Under normal load (Figure 11a), ILP aligns well with user demands. However, at a high load (Figure 11b), deviations increase, especially for users with higher data rate demand. A notable number of users were blocked due to limited satellite resources, highlighting the limitations of hard optimization approaches, such as ILP under heavy-load conditions.

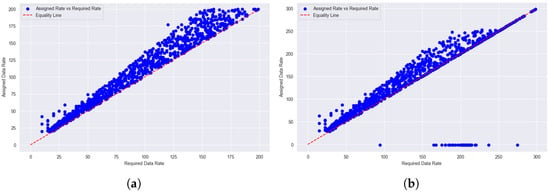
Figure 11. Assigned vs. required data rates under (a) normal- and (b) high-load conditions for ILP.

4.5.3. Genetic Algorithm (GA)

Figure 12 shows GA-based results. Under normal load (Figure 12a), GA follows the equality line, but with greater dispersion than SA and ILP. At high load (Figure 12b), assignment quality declines further, with many users underserved and a higher blocked users. GA’s stochastic nature results in less consistent performance, particularly in resource-constrained scenarios.

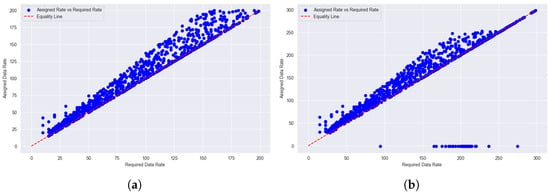
Figure 12. Assigned vs. required data rates under (a) normal- and (b) high-load conditions for GA.

Overall, these findings confirm that all methods perform well under normal load. However, under high load, resource scarcity leads to increased user blocking, most notably with ILP and GA. The SA-based framework demonstrates the most consistent and resilient performance, maintaining high satisfaction levels and superior adaptability to resource constraints.

4.6. User Satisfaction Distribution

Beyond performance, it is essential to assess the distribution of user satisfaction, especially in multi-user satellite networks where fairness and consistency are crucial. This subsection compares individual user satisfaction across the three methods using violin plots to illustrate the distribution density and heatmaps to visualize per-user satisfaction.

4.6.1. Simulated Annealing (SA)

Figure 13 and Figure 14 shows the user satisfaction distribution under the SA-based assignment strategy for both normal and high load conditions.

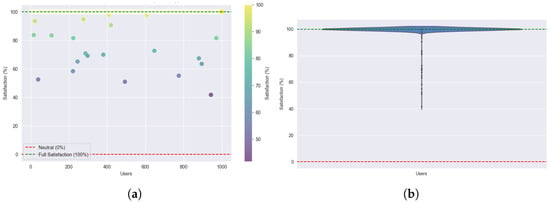
Figure 13. User satisfaction under normal load: (a) Individual user satisfaction. (b) User satisfaction density using SA.

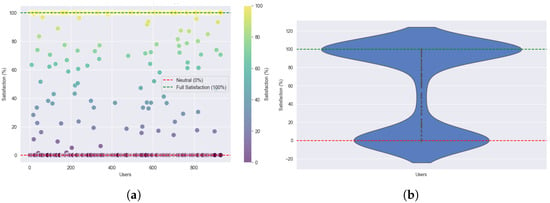
Figure 14. User satisfaction under high load: (a) Individual user satisfaction. (b) User satisfaction density using SA.

Under normal load (Figure 13a,b), most users achieve near-complete satisfaction, as indicated by the dense clustering around 100%. The violin plot reveals a narrow peak with minimal variance, confirming consistent service quality across users.

In high-load scenarios (Figure 14a,b), satisfaction remains high for a large portion of users, though a secondary cluster near 0% emerges, corresponding to users who were blocked due to resource constraints. Despite these limitations, served users maintain high satisfaction levels, demonstrating SA’s ability to prioritize quality under stress.

These trends reflect the design philosophy of the SA-based strategy: rather than spreading limited resources thinly, it maximizes overall satisfaction by fully serving as many users as capacity allows. In high-load conditions, this results in selective admission, blocking users whose demands would significantly degrade overall performance. This resource-aware approach ensures high and consistent QoS for connected users, balancing service coverage with user experience.

4.6.2. Integer Linear Programming (ILP)

Figure 15 and Figure 16 illustrates the user satisfaction distribution under the ILP-based assignment strategy for both normal- and high-load conditions.

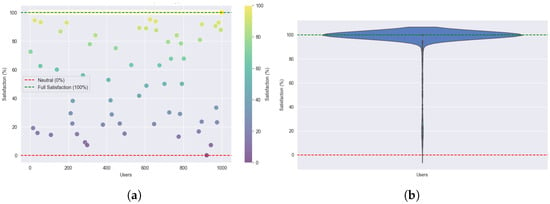
Figure 15. Users’ satisfaction under normal load: (a) Individual user satisfaction. (b) User satisfaction density using ILP.

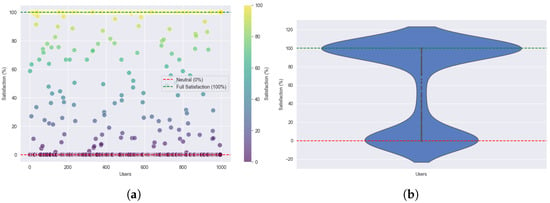
Figure 16. Users’ satisfaction under high load: (a) Individual user satisfaction. (b) User satisfaction density using ILP.

Under a normal load (Figure 15a,b), most users achieve high satisfaction levels near 100%. However, compared to SA, slightly higher variance is observed. The violin plot shows a broader peak, indicating less uniform satisfaction across users. A small subset experiences lower satisfaction, reflecting ILP’s deterministic yet less flexible handling of resource allocation.

In high-load scenario (Figure 16a,b), the number of users with near-zero satisfaction increases, reflecting those blocked due to capacity constraints. Among the served users, satisfaction remains high, at nearly 100%, although the distribution is slightly more dispersed than in the SA-based results.

These trends stem from ILP’s strict optimization behavior. While ILP seeks to maximize the global objective, it does not account for users’ fairness. Consequently, it may achieve high satisfaction for many users but leave others underserved, especially under high-demand conditions. This highlights ILP’s rigid yet precise resource allocation, which can lead to uneven user experiences when resources are constrained.

4.6.3. Genetic Algorithm (GA)

Figure 17 and Figure 18 show user satisfaction distribution for the GA-based assignment under normal- and high-load conditions. With a normal load (Figure 17a,b), most users achieve high satisfaction, though with slightly greater variability than ILP. The violin plot reveals a strong peak near 100% satisfaction, accompanied by a modest spread toward lower values, suggesting occasional inconsistencies in service allocation. With a high load (Figure 18a,b), a substantial portion of users are still fully satisfied. However, a noticeable rise in users with near-zero satisfaction is observed, reflecting increased resource contention. This suggests that, under limited capacity, some users are either blocked or receive poor assignments.

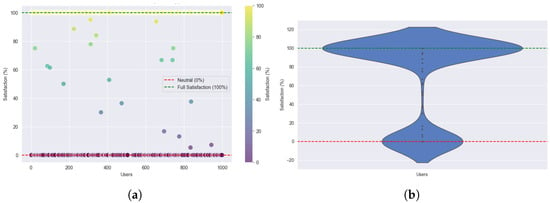
Figure 17. User satisfaction under normal load: (a) Individual user satisfaction. (b) User satisfaction density using GA.

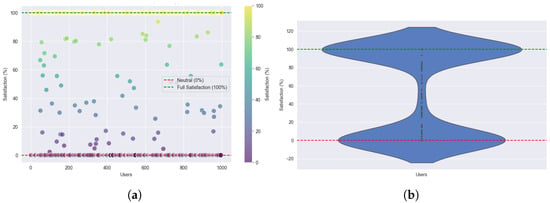
Figure 18. User satisfaction under high load: (a) Individual user satisfaction. (b) User satisfaction density using GA.

These observations highlight the characteristics of GA optimization: it aims for near-optimal solutions through iterative improvement but lacks strong prioritization mechanisms under a heavy load. As a result, while many users maintain high satisfaction, greater disparities emerge compared to more structured methods such as ILP. Still, GA manages to deliver acceptable service to a substantial subset of users despite resource constraints. In contrast, SA consistently achieves higher satisfaction with greater fairness and uniformity. While ILP offers optimal solutions, it may sacrifice equitable distribution. GA shows the least consistent satisfaction profile. These findings underscore the suitability of the SA-based framework for user-centric, delay-sensitive, and high-QoS applications in dynamic, resource-limited LEO satellite environments.

4.7. Overall Comparison Across Scenarios

To consolidate the evaluation, this subsection compares the overall performance of the three assignment strategies under varying traffic loads. The analysis focuses on three key metrics: average satellite utilization, average user satisfaction, and the number of blocked users. Figure 19 shows the average utilization for each method from light to high load conditions. The SA strategy consistently achieves higher utilization than ILP and GA, highlighting its efficiency in resource allocation. Even under high load, SA maintains balanced usage across satellites, demonstrating resilience in managing limited capacity without causing underutilization or excessive congestion.

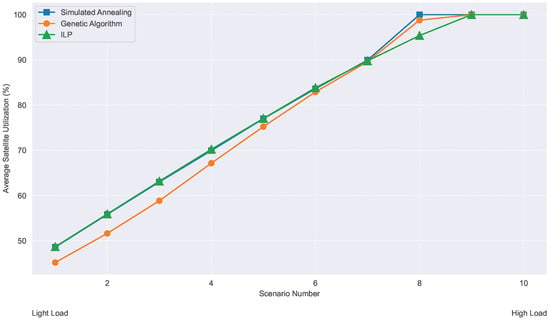
Figure 19. Average satellite utilization under light and high load.

Figure 20 shows that SA achieves higher user satisfaction than GA and performs comparably to ILP under both light and high load conditions.

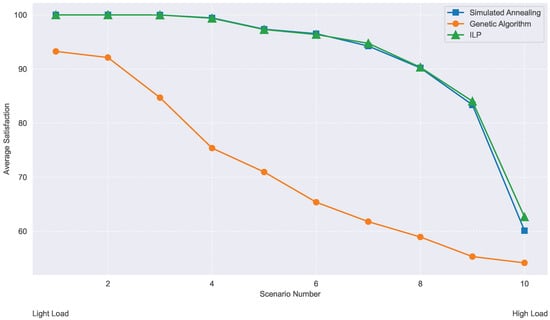
Figure 20. Average user satisfaction under light to high load.

Finally, Figure 21 shows that SA matches ILP in blocking rate while outperforms GA under both load conditions. This highlights SA’s effectiveness in maximizing user admission while managing limited resources.

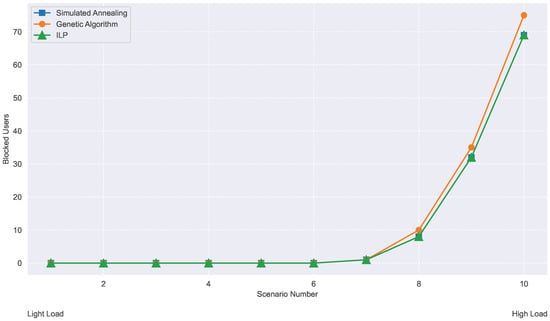
Figure 21. Number of blocked users under light and high loads.

Collectively, these results confirm that the SA framework strikes an effective balance between user satisfaction, resource utilization, and blocking rate, making it well-suited for dynamic and resource-limited LEO satellite environments. While the proposed MCSA demonstrates consistent scalability and adaptability across simulation scenarios, real-world deployment may involve additional considerations such as signaling coordination and on-board processing constraints, which are further outlined in the conclusion.

5. Conclusions

This paper has proposed an adaptive real-time handover framework for LEO satellite networks in dynamic environments like urban canyons. By integrating a real-time scoring engine with a Markov chain-guided simulated annealing algorithm, the framework ensures SLA compliance and efficient resource allocation.

Simulation results demonstrate that the proposed approach outperforms ILP and GA in terms of user satisfaction, handover reliability, scalability, and resource balance, confirming its practicality for large-scale LEO deployments. While performance comparisons were made under identical runtime and parameter budgets, we note that, in line with the No-Free-Lunch theorem, the relative advantage of one heuristic over another may vary under different parameterizations or problem instances. On average, the MCSA framework improves user satisfaction by about 10% and satellite resource utilization by 10–15% compared to GA, enabling support for nearly 50% more users under dense-load conditions without requiring additional capacity.

Future work will focus on real-time deployment, multi-layer NTN architectures integration, and adaptive policies to address diverse mobility and service demands.