Abstract
Most flow metering methods used in industrial applications produce results sensitive to the local velocity profile. In response, manufacturers often implement correction algorithms; however, these are rarely supported by rigorous uncertainty evaluations. This paper presents a Reynolds number-dependent velocity profile correction, applicable under fully developed flow conditions and for the Reynolds-dependent part of the correction in disturbed flows, demonstrated on the example of an ultrasonic clamp-on flow meter. Measurement uncertainties are evaluated and propagated through a regression model using Monte Carlo simulation, in compliance with the Guide to the Expression of Uncertainty in Measurement (GUM). Special care is taken to assess the validity range and impact of assuming fully developed flow conditions at the test rig. A validation case demonstrates the reliability of the correction algorithm and its associated uncertainty within the tested conditions. The proposed approach is applicable to other meter types and can be extended to corrections for specific flow disturbances.
1. Introduction
For most flow metering methods, the measurement result is sensitive to the shape of the local velocity profile. This applies to a broad range of meter types, including electromagnetic, ultrasonic, turbine, and orifice meters. Ultrasonic clamp-on meters can be installed externally on existing pipe configurations without interrupting the ongoing processes, making them an attractive and cost-effective alternative to conventional inline meters. As a trade-off, clamp-on meters are particularly susceptible to the local flow conditions due to the use of diametrical acoustic paths. For example, an asymmetric velocity profile can alter the path-averaged velocity and thereby the measured transit time, which directly affects the indicated flow rate. Non-ideal flow conditions can be accounted for during operation using fluid-mechanical correction factors. Otherwise, measurement errors of up to 15% can occur [1,2,3].
In general, the volumetric flow rate , expressed in units of volume per time, can be calculated as the product of the average flow velocity and the cross-sectional area A. Ultrasonic transit time meters measure the time difference between one or more pairs of transducers proportional to the average flow velocity along the ultrasonic path , see Section 3.2, Equation (10). The volumetric flow rate is then determined as follows:
where is the velocity profile correction factor that accounts for the difference between and . This correction factor reflects the influence of the velocity distribution along the ultrasonic paths, which, in turn, is shaped by the upstream piping geometry, including bends, valves, or other installations. In addition, the velocity profile, and thus , depends on the Reynolds number , a dimensionless parameter proportional to (see Figure 1 and Section 2.1, Equation (4)). As for flow disturbances, Reynolds effects can be accounted for by introducing a Reynolds-dependent correction, e.g., as part of the correction factor .
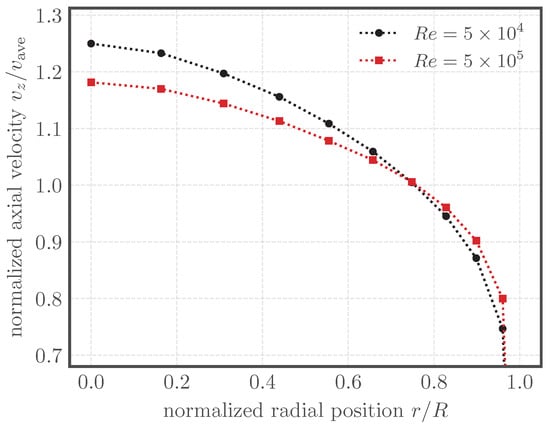
Figure 1.
LDV measurements [4] taken 90 diameters downstream of a Zanker plate [5] showing fully developed profiles at and of the axial velocity averaged over all paths and normalized by the average velocity plotted over the radial position r normalized by the pipe radius R. Due to the different shapes, the ratio of the average path velocity to varies. This Reynolds dependency is accounted for by the correction factor , or, more specifically, , if the separation approach is applied (see Section 2.1).
In metrology, the reliability of measurement results is established through a quantified assessment of the associated uncertainty at corresponding confidence intervals. Unquantified uncertainties limit the traceability of measurement results and reduce their value for process control or further analysis. The widely accepted standard for evaluating uncertainties is the Guide to the Expression of Uncertainty in Measurement (GUM) [6] and its supplements, which provide an internationally recognized framework for uncertainty evaluation. For , as determined by the ultrasonic meter in Equation (1), uncertainty propagation for multiplicative terms yields the combined uncertainty
assuming uncorrelated contributions, in line with the treatment in ISO 24062:2023 [7]. In the equation, relative uncertainties, e.g., , are used to improve readability, a common representation in metrology. For clamp-on measurements, both and can be evaluated in accordance with the guidelines given in ISO 24062:2023 [7]. In contrast, the standard does not provide an explicit derivation or example calculation for the uncertainty contribution of . While ISO 24062 acknowledges the need to determine through experiments or simulations and clearly states that an associated uncertainty evaluation is required, the standard does not prescribe a specific methodology, reflecting that no accepted approach for evaluating is currently available.
Several studies have addressed profile corrections for ultrasonic meters under disturbed conditions [3,8,9,10,11,12,13,14] or Reynolds-dependent effects [15,16,17] using either theoretical, experimental, or simulation-based models. Others combined corrections with some kinds of uncertainty values, but without transparent propagation methods in alignment with the GUM [18,19]. To the authors’ knowledge, no published study has yet presented a fully GUM-compliant uncertainty evaluation specifically for flow profile corrections applied to ultrasonic flow meters. This paper aims to close this gap by developing a correction for the Reynolds-dependent part of the velocity profile based on measured data and its associated uncertainties. The data are processed to isolate Reynolds effects, and an empirical regression model is fitted using nonlinear least squares to describe the correction as a continuous function. Uncertainties in both the measurement values and the corresponding are propagated through the model by means of Monte Carlo simulation. Residuals, i.e., the differences between the measured values and the regression model, are included as an additional uncertainty component and are validated together with the overall model performance. The approach yields a comprehensive, GUM-compliant uncertainty evaluation, applicable to other meter types and to corrections for specific flow disturbances.
Section 2 introduces the methodological concepts and assumptions as well as the limitations that define the scope and applicability of the model. Section 3 explains how is determined and how the measurement data are processed to isolate the Reynolds-dependent part of the correction factor. It also covers the associated measurement uncertainties and the uncertainty in the realization of at the test rig, both of which serve as inputs to the regression analysis. The modeling itself, along with the evaluation of its uncertainty, is detailed in Section 4. Both Section 3 and Section 4 combine methodological descriptions with the presentation of results, reflecting the stepwise workflow in which each methodological stage directly produces the quantitative inputs for the next. Finally, Section 5 provides a validation case, where the Reynolds-dependent correction is applied to clamp-on flow measurements under independent conditions.
2. Methodological Concepts and Model Scope
This section introduces the central idea of separating into a Reynolds-dependent part and a disturbance-related component. It addresses the prerequisite for fully developed flow conditions at the test rig and the need to account for the residual influence of the velocity profile through an associated uncertainty. Furthermore, the section defines the applicable range of Reynolds numbers and discusses limitations related to wall roughness.
2.1. Separation Approach
This work builds on the separation of the correction factor into two multiplicative components according to
where accounts for the variations in a fully developed velocity profile as a function of (see Figure 1), while captures the effects of specific flow disturbances, such as a 90° bend. This separation is motivated by the observation that the influence of flow disturbances can be treated as independent of (see also Johnson et al. [20]). This approximation holds up well at distances where the near-field effects of the disturbance have decayed. As a result, only a generic function and disturbance-specific need to be stored in the device, rather than a separate matrix for each disturbance across the full range. This reduces memory demand and computational load in firmware implementations.
The Reynolds number is a dimensionless parameter defined as follows:
where D is the internal pipe diameter and the kinematic viscosity of the fluid. In fluid dynamics, is used to describe the ratio of inertial to viscous forces that allows for a classification of the flow regime from laminar to turbulent, with laminar flow typically occurring for . It governs the development of the boundary layer and the steepness of velocity gradients near the wall, and thus the overall velocity profile across the pipe and ultrasonic paths. For a constant D and , is directly proportional to the average flow velocity or volumetric flow rate (see Equation (4)).
For an ultrasonic clamp-on meter in reflection mode, the theoretical range of varies from 0.75 for laminar flows to 1 for an infinitely high in a smooth pipe. In practical applications, typically falls between 0.90 and 0.97 in the turbulent regime.
2.2. Assumption of Fully Developed Flow Conditions at the test rig
To construct a Reynolds-dependent correction following the separation approach, measurement data for are required; however, cannot be measured directly. It must be inferred from under the assumption that the flow is fully developed; in other words, that . This premise is critical for the development of the correction algorithm and introduces its own uncertainty.
The clamp-on measurements presented in Section 3 were taken at the Gravimetric Thermal Energy Standard Flow Facility (GraTESt) at PTB Berlin (see Heitmann et al. [21]). To meet the requirement for isolating , the meters were installed at a minimum distance of 52 D downstream of a tube bundle flow conditioner [5]. This configuration actively removed secondary velocity structures, while the straight inlet length ensured the recovery of the axial velocity profile.
Several sources confirm that tube bundle flow conditioners are effective in producing fully developed flow conditions over much shorter distances. For example, ISO 5167-2 [22] specifies that a distance of is sufficient to eliminate swirl and avoid additional measurement uncertainty in flow measurements with orifice meters. Yin et al. [23] present a numerical investigation of a tube bundle flow conditioner installed downstream of a double bend out-of-plane, showing that the flow straightens and approaches a nearly fully developed state approximately 20 D downstream. Based on these references, the assumption of fully developed flow at 52 D downstream of the tube bundle is well supported.
Nonetheless, proving fully developed flow conditions in a test rig is particularly difficult, as it can only be defined by the absence of further profile changes along the pipe axis, which is a slowly converging process. To reflect this limitation, the assumption is associated with a newly proposed uncertainty component denoted as , which can be derived from laser Doppler measurement data. Its calculation is introduced and evaluated in Section 3.4.
2.3. Validity Range
The regression model presented in Section 4 was designed to describe flows in the fully turbulent regime with . Laminar and transitional flows are not covered, as measurement data from these regimes were not investigated. The lower bound was chosen conservatively to avoid the transitional range. Although the theoretical onset of turbulence is often placed at , transition has been observed across a much broader range, extending up to approximately 1 × 104 [24]. Below this range, the model merely extrapolates turbulent behavior into the transitional and laminar regimes, which is not physically correct.
Furthermore, the model is restricted to hydraulically smooth wall conditions. A quantitative criterion for this can be based on the dimensionless roughness height
not exceeding a value of 5. Here, denotes the equivalent sand roughness height, while is the Darcy friction factor (see, e.g., White [25] for a theoretical background). For , walls are considered hydraulically smooth, as the roughness elements remain fully buried within the viscous sub-layer, which extends up to a dimensionless wall distance () of 5. In this regime, the velocity profile—and thus —is not affected by surface roughness.
A common issue in practice is the limited knowledge of the exact roughness height . While in laboratory setups, drawn or polished pipes are typically used with roughness values . Roughness in industrial steel pipes varies with manufacturing processes and may be significantly higher. Standard references such as the Moody diagram recommend a conservative value of for commercial pipes, whereas more recent studies report lower values of for new stainless-steel pipes (see White [25]). In contrast, aged or corroded pipes can exhibit roughness exceeding 1 [26].
Figure 2 shows for between 1 × 105 and 1 × 103. The upper limit corresponds to a DN 50 pipe with , close to the standard Moody value for commercial steel pipes. The plot includes a reference line at , indicating the upper bound of the hydraulically smooth regime. A secondary x-axis shows values for a pipe in DN 100. In that example, the flow remains hydraulically smooth up to for and for . In both the experimental setup for determining in Section 3 (DN 200) and the validation case in Section 5 (DN 100), remains below 5 at the highest , respectively.
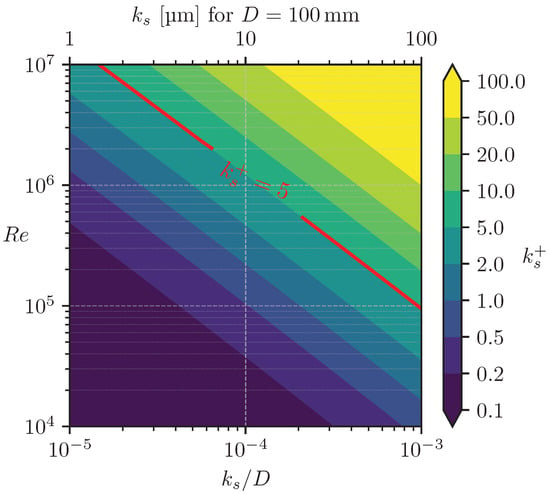
Figure 2.
Validity range of with respect to wall roughness. The plot shows the dimensionless roughness height (Equation (5)) as a function of the equivalent sand roughness and a red line at indicating the upper bound of the hydraulically smooth regime.
3. Determination and Uncertainty of Model Inputs
This section describes the sequence of data processing steps used to determine and assess the associated uncertainty . The sequence begins with the following:
- The experimental determination of the combined correction factor at the test rig;
- The evaluation of the associated measurement uncertainty ;
- The reduction of to a function of the reference volume flow of the test rig by averaging over the angular and axial installation positions, including the associated uncertainty;
- The calculation of the uncertainty due to the assumption that at the test rig;
- The transformation of to by applying the separation approach;
- The calculation of by incorporating the uncertainty due to the assumption that .
In addition, the section addresses the uncertainty in realizing the Reynolds number for the test rig. Together, these quantities form the input for the regression analysis in Section 4. All steps and their interconnections are illustrated in the flow chart in Figure 3.
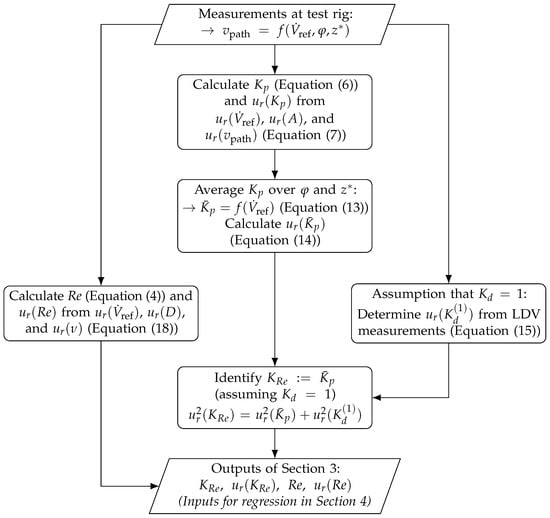
3.1. Experimental Determination of
At GraTESt [21], a total of four dual-channel clamp-on meters (Flexim FLUXUS F721) in a V-configuration were used. This corresponded to eight sensor pairs installed at four different axial locations (), each with two angular orientations (). They were installed on a honed pipe with an internal diameter of (see Figure 4). Measurements were carried out at a water temperature of 20 °C across 12 Reynolds numbers ranging from 2 × 104 to 1.5× 106, corresponding to average flow velocities between −1 and −1. Given an equivalent sand roughness of , this yielded a dimensionless roughness height of (Equation (5)) at the highest , confirming that all measurements fell within the hydraulically smooth regime.
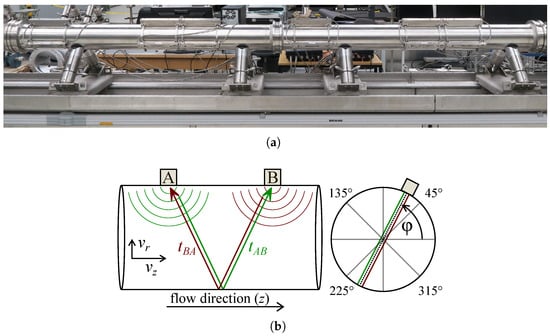
Figure 4.
(a) Clamp-on meters (Flexim FLUXUS F721) installed at GraTESt for the determination of ; (b) schematic of an ultrasonic flow meter in reflection mode. Source: Straka et al. [27].
To determine from the measurement values of , Equation (1) is rearranged and is replaced with the reference volume flow of the test rig at GraTESt, resulting in
All values measured for are shown in Figure 5 (left).
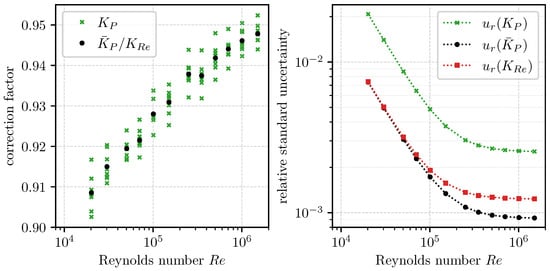
Figure 5.
(Left) Measurement values of and its mean , equivalent to ; (right) relative standard uncertainties for , , and .
3.2. Measurement Uncertainty of
The combined relative uncertainty for is given by the law of uncertainty propagation for the product and ratio of the uncorrelated quantities in Equation (6) as follows:
Here, represents the relative uncertainty of the flow rate realization at GraTESt as described by Mathies [28]. In the laboratory setup, the cross-sectional area A can be determined via the pipe diameter D. Using the specified diameter tolerance and assuming a rectangular distribution, the relative uncertainty in D is estimated by
resulting in for and . Based on the definition , the relative uncertainty in the cross-sectional area A is given by
To calculate the relative uncertainty , must be decomposed into its constituent components according to
See ISO 24062 [7] for further details. In the equation, is the path geometry factor, the measured transit time difference, the transit time at zero flow, and the delay time. Applying uncertainty propagation yields
where the device-specific uncertainties were established during the manufacturer’s calibration procedure. Their values are listed in the uncertainty calculation for presented in Table 1. The standard uncertainty reflects the temporal resolution of the meter. In practice, this resolution is influenced by the effective signal-to-noise ratio (SNR) and the signal-to-clutter-plus-noise ratio (SCNR), which characterizes the separation of the desired correlation peak from spurious contributions, but the specified value already represents a conservative estimate under typical operating conditions. Unlike the uncertainties for , , and , depends on . For a single sensor pair, is specified as . Equation (11) also includes the relative sensitivity coefficients for and given by

Table 1.
Uncertainty calculation for the flow profile correction factor .
All remaining terms have relative sensitivity coefficients equal to 1 and are therefore not explicitly shown. In the investigated range, varied between 2.08 × 10−2 and 2.55 × 10−3 (see Table 1 and Figure 5 (right)). While dominated the combined uncertainty at low values, became the largest contributor at high values. In contrast, and had a negligible impact in the experimental setup at GraTESt, as they were at least one order of magnitude smaller than across the entire flow range.
3.3. Reduction of to a Function of
To reduce the number of independent variables to , values are averaged over the angular () and axial () installation positions according to
In the equation, the arithmetic mean is used because all angular and axial installation positions are of equal relevance. No weighting is justified, as neither measurement accuracy nor physical significance varies systematically across the positions.
In the uncertainty evaluation for , , as defined in Equation (11), is assumed to be a random and uncorrelated contribution for all measurement positions. In contrast, and are treated as systematic. Following the GUM approach for averaging uncorrelated contributions, the corresponding uncertainty component is reduced by the square root of the number of measurements, i.e., divided by , while systematic components remain unaffected. Thus, the uncertainty in is given by
The development of is included in Figure 5 (right).
3.4. Uncertainty Due to the Assumption That
To assess the validity of the assumption that the flow is fully developed and derive an associated uncertainty denoted as , LDV measurements were performed at GraTESt using the setup described by Straka et al. [29]. Velocity profiles were recorded at Re = 5 × 104 and 1 × 106 at five axial positions , covering both upstream and downstream positions around the clamp-on meters. From these, values were derived following the procedure described by Straka et al. [27]. Their values are depicted in Figure 6. Based on the LDV data between 40 D and 85 D, is proposed to be estimated as follows:
where is the average over the angular paths at each and denotes the empirical standard deviation of the path-averaged values. Furthermore, denotes the standard deviation of the angular values at position . The term thus represents the standard error of the mean at . In the equation, the first term captures the variability between axial positions, which may be interpreted as a residual systematic deviation from a fully developed profile. The second term represents the uncertainty in the mean due to random measurement uncertainties or remaining asymmetries. It is included as the standard error of the mean averaged over the axial positions.
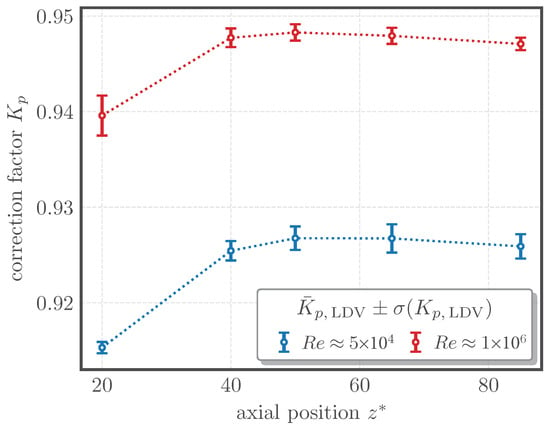
Figure 6.
derived from laser Doppler velocimetry (LDV) measurements, represented by the mean and standard deviation over the measurement paths.
At GraTESt, values of and 6.04 × 10−4 were obtained for Re = 5 × 104 and 1 × 106, respectively. Both values were of similar magnitude. To provide a conservative estimate applicable over the full range, the larger of the two values, , is used in the uncertainty propagation in Section 3.5.
3.5. Transformation from to
In accordance with the separation approach described in Section 2.1, the correction factor is generally obtained by rearranging Equation (3) as . In the present analysis, is directly identified as the averaged profile correction factor according to
Accordingly, is determined by combining with the uncertainty associated with the assumption that (see Section 3.4). Following uncertainty propagation for uncorrelated quantities, the combined relative uncertainty is given by
Values for are included in Figure 5 (right).
3.6. Uncertainty in the Realization of
In the regression analysis, it is not but the Reynolds number that is used as the relevant input parameter. Accordingly, in addition to , the uncertainty in the realization of at the flow facility must be taken into account. This uncertainty is obtained by applying the law of uncertainty propagation to Equation (4), resulting in
In the equation, [28] and (see Section 3.2). This leaves , which is estimated based on the temperature dependence of the kinematic viscosity as follows:
Here, and represent the kinematic viscosity of water and its sensitivity to temperature at 20 °C, whereas is the uncertainty in the realization of temperature at GraTESt according to Heitmann et al. [21].
4. Regression Analysis and Model Uncertainty
This section describes the development of the regression model and the evaluation of its associated uncertainty. At first, a functional form is selected to represent the dependence of on . The model parameters are then identified through a Monte Carlo simulation that propagates the uncertainties of the input data. In addition, the residual standard uncertainty is evaluated from the scatter between measured and fitted values. Both contributions are combined to yield the total uncertainty of .
4.1. Modeling Approach
is modeled as a function of using an inverse power law given by
where B and n are fitting parameters. This functional form was selected empirically, but it is consistent with physical expectations, preserving the asymptotic behavior, where approaches 1 as . As shown in Figure 7 (left), this model is consistent with the measurement data.
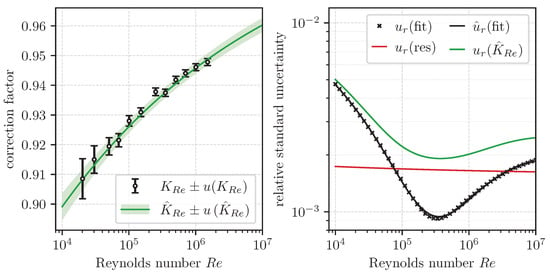
Figure 7.
(Left) Measurement values of and the regression model with corresponding standard uncertainties; (right) contributions and combined relative standard uncertainty for .
4.2. Monte Carlo-Based Estimation of Model Parameters and Uncertainty Propagation
The parameters B and n of the regression model are determined using a Monte Carlo simulation in accordance with GUM Supplement 1 [30]. A total of 2 × 105 simulation runs are performed, a number chosen such that the resulting means and standard deviations of are stabilized, i.e., further increasing the number of runs does not change the results within numerical precision. In each run, a nonlinear regression is carried out using the curve_fit function from the SciPy Python library [31] (version 1.15.2, Python 3.11.12), which minimizes the residual sum of squares between model and perturbed data. Convergence of the regression is monitored during the simulations, and no failed fits occurred. This robustness is ensured by physically motivated initial guesses and the smooth behavior of the measurement data. This procedure yields distributions for B and n, whose sample means define the model parameters for . Their values are listed in Table 2.

Table 2.
Fitting parameters for and .
To quantify the impact of input variability onto the model, an uncertainty component referred to as is evaluated. It arises from the propagation of uncertainty in both and through the regression. The uncertainties of and D, which influence both quantities, are varied jointly to preserve their induced correlation. All other inputs are sampled independently. Each perturbed dataset is independently re-fitted, producing a set of models . These are evaluated at 50 logarithmically spaced values between 1 × 104 and 1 × 107. The standard deviation of the resulting models at each defines .
The development of is depicted in Figure 7 (right). Unlike , which decreases with increasing , exhibits a minimum in the mid-Reynolds range and increases toward both lower and higher values. This behavior is plausible, as the fit is generally more robust in regions with high data density, while uncertainty grows near the edges due to reduced constraints from the input data.
4.3. Analytical Fitting of
Rather than storing discrete uncertainty values and relying on interpolation, a continuous analytical function is used for efficient implementation in the clamp-on meters. The fit function for is given by
This formulation combines a Gaussian term in , which captures the exponential decay and central minimum in , and a power-law term that reflects the increasing trend at higher . The parameters B, k, and determine the amplitude, width, and location of the Gaussian dip, while C and n define the shape of the power-law tail. The parameters are identified through a nonlinear regression analysis using curve_fit [31]. Their values are included in Table 2. As shown in Figure 7 (right), the relative uncertainty is in good agreement with across the entire range.
4.4. Residual Standard Uncertainty
In addition to , a contribution inherent to the regression known as the residual standard uncertainty must be accounted for. It quantifies the remaining variability between the measured values and the model prediction , i.e., the residuals . While accounts for the effect of input uncertainty propagated through the regression model, quantifies how well the model represents the underlying data. It describes the systematic deviations and imperfections of the model that are not explained by propagated input uncertainties. It is defined as follows:
where is the number of used in the regression analysis and the number of parameters in the model. For , Equation (22) yields .
4.5. Combined Model Uncertainty
Since there is no correlation between the individual contributions, the combined relative standard uncertainty of can be calculated as follows:
Within the validity range of , varies between 1.92 × 10−3 and 5.01 × 10−3. Its development over is depicted in Figure 7 (right).
5. Validation Case
To demonstrate the applicability and reliability of the regression model , a validation measurement was carried out at a separate flow test facility not involved in the model development. In this setup, the clamp-on readings were corrected using and compared to the reference flow rate of the test rig. The validation was considered successful if the deviations between the corrected and reference values (including the contribution of ) were correctly distributed within the uncertainty bands of the clamp-on meters according to the respective confidence intervals.
5.1. Experimental Setup
The validation case was carried out at the Long-Term Ultrasonic and Laser Measurement Facility [32] (LULA) at PTB Berlin. At LULA, the flow rate is regulated using an electromagnetic reference meter (KROHNE WATERFLUX 3070), for which the combined relative uncertainty is specified as [4]. A total of four dual-channel clamp-on meters (Flexim FLUXUS F721) were used, corresponding to eight sensor pairs at four axial locations and two angular orientations. In contrast to the setup at GraTESt, they were mounted onto a honed pipe in DN 100 with . In addition to having a reduced pipe diameter, the validation setup also differed in water temperature (30 °C instead of the 20 °C at GraTESt) and in the flow conditioning system, which combined a tube bundle straightener with a Zanker plate [5]. To ensure fully developed flow conditions, the meters were installed at a minimum distance of downstream of this conditioning unit.
Measurements were performed across six values ranging from 2 × 104 to 7 × 105, corresponding to average flow velocities between and . With an equivalent sand roughness of and a dimensionless roughness height of (Equation (5)) at the highest , all measurements fell within the hydraulically smooth regime.
5.2. Measurement Uncertainty
The volumetric flow rate determined by the clamp-on meters at LULA was obtained by substituting the separation approach (Equation (3)) into Equation (1), resulting in
Here, is assumed to be 1 and the Reynolds-dependent correction is established using the regression model described in Section 4. Following standard uncertainty propagation, the combined relative uncertainty in is given by
At LULA, the relative uncertainty in A is determined as using the specified tolerance of in Equation (8). Furthermore, is determined using Equation (23), while is evaluated as described in Section 3.2.
For , LDV data at and from Straka [4] are used, applying the evaluation procedure introduced in Section 3.4. Since only positions are available, the empirical standard deviation does not provide a reliable estimate of the variability. In this case, a rectangular distribution is proposed instead, leading to a conservative uncertainty estimate that does not understate the possible deviation. Such an approach is generally preferred when the number of available samples is too small (i.e., fewer than four) to support a meaningful empirical variance. Equation (15) therefore becomes
All uncertainties are listed in Table 3. This includes the relative expanded uncertainty
where k denotes the coverage factor. A value of is commonly used as an approximation, corresponding to a confidence level of approximately 95% under the assumption of a normal distribution. The variation of the individual uncertainty components as a function of is also shown in Figure 8 (left). Both the figure and Table 3 illustrate that the combined uncertainty is primarily driven by and , whereas the contributions from and are negligible. In the present setup, remains the largest contribution across all values, yet may become dominant in configurations where multiple sensor pairs are used, while is reduced by averaging (see Section 6.1).

Table 3.
Uncertainty calculation for the volume flow rate in the validation case. Shading indicates grouping: light-green rows correspond to the individual contributions to , while light-violet rows correspond to the contributions entering .
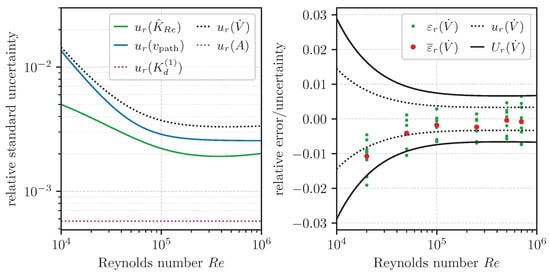
Figure 8.
(Left) Contributions and standard measurement uncertainty of in the validation case; (right) relative error between and , as well as its mean value at each . Standard and expanded uncertainty bands of are shown with and , respectively. Out of the 48 validation measurements, % fall within the standard uncertainty band () and % within the expanded uncertainty band ().
5.3. Comparison with Reference Flow Rate
To evaluate the Reynolds-dependent correction, the relative error between and the reference flow rate at LULA is calculated as follows:
Its variation across the six values is depicted in Figure 8 (right), together with the uncertainty bands corresponding to and . At the lowest , the average deviation of the corrected values from amounts to roughly 1%, indicating a comparatively large systematic error in that region (see Section 6.1). For the remaining , the correction performs consistently well. Overall, 26 out of 48 clamp-on measurements ( %) fall within the standard uncertainty band of , while 41 values ( %) fall within the band defined by . As a reference, a normal distribution with sufficiently high sampling suggests a coverage of approximately 68% for and 95% for . Given the limited sample size, the observed coverage can be considered broadly consistent with theoretical expectations, with the systematic deviation at the lowest explaining the shortfall.
6. Discussion
The results presented in this work provide a consistent basis for evaluating the Reynolds-dependent correction algorithm and its associated uncertainty . This section discusses key aspects for interpreting the model: its performance under independent validation conditions, the assumption of fully developed flow at the test rig, and its validity range with respect to the Reynolds number and wall roughness. Finally, the transferability of the approach to other meter types and to disturbed flow conditions is discussed.
6.1. Validation
To test the model’s reliability, a validation case was performed on a different test rig with a different nominal diameter, as mounting the meters onto different pipes and the local inlet conditions at the installation position are considered to be the most influential factors in practical use. Furthermore, a slightly increased water temperature was used. Together, these differences ensured that the validation was not merely a repetition of the initial setup, but a meaningful test of the model’s transferability under varied conditions.
After applying the correction, the clamp-on measurements agreed well with the reference values within the predicted uncertainty bounds with the exception of the lowest . This comparatively large deviation at is most likely related to the limitations of the clamp-on measurements at such low velocities. In this regime, the devices operate close to their specified range, where the uncertainty in provided by the manufacturer is assumed to include a systematic component that is not fully independent across repeated measurements. This explains the consistent offset of the results at the lowest and may also have influenced the fitted parameters n and B derived from the measurement data at GraTESt in Section 3, where was also used as the lowest .
In the validation, the uncertainty of the path velocity exceeded due to the use of a single sensor pair. However, in practical applications, is typically reduced through averaging over two or four sensor pairs of multi-channel meters with different circumferential or axial positions. Apart from the lower velocity range of the meter, where is dominant, this can result in becoming the largest contributor to the overall flow rate uncertainty, which highlights the importance of extending the existing ISO 24062 guidelines to uncertainties for flow corrections.
6.2. Fully Developed Flow Assumption
In this study, identifying directly with the measured values of was based on the assumption of a fully developed velocity profile at the measurement locations. Due to the use of a tube bundle flow conditioner and a minimum straight inlet length of , this assumption was well supported. Nonetheless, the effect was quantified by the newly introduced uncertainty component , derived from LDV measurements.
Proving that a flow is fully developed is particularly difficult in turbulent regimes, where the velocity distribution cannot be described by an analytical solution. Instead, the condition is typically defined by the absence of further profile changes along the pipe axis. Accordingly, the approach used here assumes the profile to be fully developed if remains effectively constant over increasing axial distances, i.e., within a quantifiable uncertainty. In this case, is assumed to be valid, and equal to .
In the uncertainty evaluation, the first term in was used to capture axial variations in , reflecting potential deviations from a fully developed state. Ideally, converges asymptotically to a constant value; however, such behavior was not clearly observed. In addition to actual flow development effects, this could be attributed to random uncertainties in the LDV data. Since these contributions cannot be separated in the current approach, the uncertainty may be conservatively overestimated. The same holds for the second term in , which accounts for remaining asymmetries in the flow. In contrast, systematic LDV biases (e.g., from probe alignment) are assumed to affect all positions equally and are thus irrelevant for assessing the axial flow development.
Both in the determination of and in the validation case, was found to be a minor contributor to the combined uncertainty. Thus, while the inclusion of the random LDV uncertainty cannot be ruled out, the resulting overestimation is acceptable, as it ensures a conservative treatment in compliance with the GUM, without noticeably increasing the total uncertainty of . The negligible impact of in the total uncertainties further suggests that could be neglected in the determination of in other test rigs, provided fully developed flow conditions can be confidently assumed due to the use of flow conditioners and a sufficient inlet length.
In cases where deviations from a fully developed profile are more significant, the proposed methodology remains valid, but the associated uncertainty would increase accordingly and propagate into . For this reason, determining close to fully developed conditions is strongly recommended, while determinations under clearly disturbed conditions (e.g., in close proximity to bends) are not meaningful, as the separation between and would no longer hold.
6.3. Validity Range with Respect to
The correction model developed in this work was designed to describe turbulent flows with , covering the domain typically encountered in field applications of clamp-on flow measurements. Within the turbulent regime, the behavior of could be captured with a comparatively simple functional approach. An expansion into the transitional or laminar regime, on the other hand, would require more complex modeling and fine-grained characterization of the transition behavior. This would imply experiments with smaller pipe diameters or fluids with lower viscosities.
In contrast, the model was designed to converge toward 1 as increases, making it suitable for extrapolation beyond the fitted range. As for the lower bounds, however, the associated fit uncertainty was found to increase near the edge of the data range due to the absence of supporting measurements. Reducing this uncertainty would require additional measurements at a higher using higher pipe diameters to avoid cavitation.
6.4. Validity Range with Respect to Wall Roughness
In this study, was limited to hydraulically smooth pipe flows characterized by a dimensionless roughness height of . This ensured that the near-wall velocity profile—and thus the Reynolds correction—was not influenced by surface roughness. Within this range, the model applies to stainless-steel pipes and many commercially available pipes manufactured with modern techniques across practically the entire relevant range. However, the threshold does not cover high and small pipe diameters when conservative roughness values such as are assumed.
Recent studies suggest that velocity profiles may not be strongly affected in the mildly rough regime up to , depending on the specific roughness geometry. To extend the operational range of beyond the smooth regime, future work may therefore introduce an additional uncertainty contribution, accounting for the systematic deviation caused by moderate wall roughness. This will require an experimental or numerical validation, or suitable analytical models that quantify the influence on the axial velocity profiles.
In practical applications, operators should verify that the pipe roughness remains within the hydraulically smooth range before applying the model. For higher roughness levels, i.e., in the upper transitional or fully rough regime, correction algorithms may be developed that include as an input parameter. This would imply that as well as the geometric characteristics of the roughness can be estimated with sufficient accuracy, which is usually not the case. Furthermore, the practical application of any roughness-based correction is complicated by the fact that wall roughness not only affects , but poses additional challenges, especially for clamp-on ultrasonic flow meters. For instance, if the surface roughness approaches or exceeds the acoustic wavelength (e.g., ), it may scatter the sound field and degrade the signal quality.
6.5. Transferability to Other Meter Types
The validation results show that the correction developed in this work can be reliably applied using clamp-on meters operating in reflection mode. For multi-beam ultrasonic meters, the individual path velocities are typically combined internally using a predefined weighting scheme based on the beam geometry. The framework remains applicable in this case, since the resulting effective path velocity and its associated uncertainty can be treated in the same way as a single diametrical path.
For other flow meter types that are sensitive to the local flow conditions, the uncertainty framework and regression approach developed in this study may be used analogously. This applies to electromagnetic, orifice, turbine, or other mechanical meters. In these cases, is not linked to , but must instead be established through dedicated measurements comparing the device-indicated flow rate with a traceable reference flow rate in a test rig. The corresponding meter outputs, e.g., the differential pressure signal of an orifice meter or other device-specific constants, must be coupled with appropriate uncertainties in accordance with the GUM. Once these measurement data and uncertainty evaluations are available, the same regression analysis and uncertainty propagation procedure as presented in this work may be applied.
6.6. Extension to Disturbed Flows Conditions
In field applications, flow conditions are typically not fully developed. Instead, flow meters are exposed to disturbed velocity profiles caused by upstream bends or other installations. For such cases, future research should address the development of correction algorithms for specific disturbances along with corresponding uncertainty estimates. Following the separation approach, the total correction under disturbed conditions could then combine and , along with their respective uncertainties, and . In this regard, the methodology established in this work for evaluating provides a suitable foundation for assessing , particularly the inherent uncertainty contributions associated with the model itself. In contrast to , evaluating would also require a characterization of the operational uncertainties regarding, e.g., the meter’s angular alignment, its axial position relative to the disturbance, and the influence of disturbances upstream of the disturbance itself. As one of the most common installations with practical relevance, a single 90° bend would be a recommended first candidate for developing and combining it with in future works.
7. Conclusions
This study presents a framework for correcting Reynolds-dependent velocity profile effects in ultrasonic clamp-on flow measurements combined with a GUM-compliant uncertainty evaluation. A regression model for in the turbulent regime was derived from experimental data, with uncertainties propagated by Monte Carlo simulation and complemented by a residual component. Both and were approximated by analytical functions, allowing efficient implementation in the measurement devices. Validation on an independent test rig confirmed that the corrected clamp-on results agreed with the reference values within the predicted uncertainty bounds. The uncertainty analysis further showed that, while dominates at low values, both and are of similar magnitude at high values when using a single sensor pair, with becoming the dominant contribution when multiple sensor pairs are employed. In addition, the newly introduced uncertainty contribution , accounting for the assumption of fully developed flow, was investigated and found to be negligible under laboratory conditions, where flow conditioners and sufficient inlet lengths are used. While developed for clamp-on ultrasonic meters in reflection mode, the methodology is transferable to other meter types sensitive to local flow conditions, provided device-specific values of and their uncertainties can be determined. From a standards perspective, the method addresses a critical gap in ISO 24062 [7], which currently lacks provisions for velocity profile corrections and their uncertainties. To close this gap, the methodology to determine and may be incorporated in a future revision of the standard. Future work should extend the framework to disturbed flow conditions by deriving correction factors for specific installations (e.g., bends or valves) and evaluating their uncertainties using the same Monte Carlo methodology, enabling a unified and traceable uncertainty evaluation for field applications.
Author Contributions
Conceptualization, M.S., C.H., C.K., B.F. and T.E.; methodology, M.S., C.H., C.K., B.F. and T.E.; software, M.S.; validation, M.S. and C.K.; formal analysis, M.S., C.H. and C.K.; investigation, M.S., C.H., C.K., B.F. and T.E.; data curation, M.S., C.K. and T.E.; writing—original draft preparation, M.S.; writing—review and editing, M.S., C.H., C.K., B.F. and T.E.; visualization, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The measurement data used in this study were obtained through research collaboration and cannot be shared publicly or upon request due to contractual restrictions.
Acknowledgments
The measurements used in this study were performed as part of a joint research cooperation between Physikalisch-Technische Bundesanstalt and Emerson|Flexim Flexible Industriemesstechnik GmbH.
Conflicts of Interest
Authors Christian Höhne and Bernhard Funck were employed by the Emerson|Flexim Flexible Industriemesstechnik GmbH. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DN | Diameter Nominal |
| GraTESt | Gravimetric Thermal Energy Standard Flow Facility |
| GUM | Guide to the Expression of Uncertainty in Measurement |
| ISO | International Organization for Standardization |
| LDV | Laser Doppler Velocimetry |
| LULA | Long-Term Ultrasonic and Laser Measurement Facility |
| PTB | Physikalisch-Technische Bundesanstalt |
References
- Weissenbrunner, A.; Fiebach, A.; Schmelter, S.; Bär, M.; Thamsen, P.; Lederer, T. Simulation-based determination of systematic errors of flow meters due to uncertain inflow conditions. Flow Meas. Instrum. 2016, 52, 25–39. [Google Scholar] [CrossRef]
- Mattingly, G.E.; Yeh, T.T. Effects of Pipe Elbows and Tube Bundles on Selected Types of Flowmeters. Flow Meas. Instrum. 1991, 2, 4–13. [Google Scholar] [CrossRef]
- Synowiec, P.; Andruszkiewicz, A.; Wędrychowicz, W.; Piechota, P.; Wróblewska, E. Influence of Flow Disturbances behind the 90 Bend on the Indications of the Ultrasonic Flow Meter with Clamp-On Sensors on Pipelines. Sensors 2021, 21, 868. [Google Scholar] [CrossRef] [PubMed]
- Straka, M. Vergleich Realer und Synthetisch Generierter Strömungszustände in Rohrleitungen Mittels Numerischer und Laseroptischer Verfahren. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2021. [Google Scholar] [CrossRef]
- ISO 5167-1:2003; Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 1: General Principles and Requirements. International Organization for Standardization: Geneva, Switzerland, 2003.
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008. [Google Scholar]
- ISO 24062; Measurement of Fluid Flow in Closed Conduits—Clamp-on Ultrasonic Transit-Time Meters for Liquids and Gases. International Organization for Standardization: Geneva, Switzerland, 2023.
- Papathanasiou, P.; Kissling, B.; Berberig, O.; Kumar, V.; Rohner, A.; Bezděk, M. Flow disturbance compensation calculated with flow simulations for ultrasonic clamp-on flowmeters with optimized path arrangement. Flow Meas. Instrum. 2022, 85, 102167. [Google Scholar] [CrossRef]
- Hakansson, E.; Delsing, J. Effects of Flow Disturbance on an Ultrasonic Gas Flowmeter. Flow Meas. Instrum. 1992, 3, 227–233. [Google Scholar] [CrossRef]
- Heritage, J.E. The Performance of Transit Time Ultrasonic Flowmeters Under Good and Disturbed Flow Conditions. Flow Meas. Instrum. 1989, 1, 24–30. [Google Scholar] [CrossRef]
- Martins, R.S.; Ramos, R. Bend Installation Effects on the Correction Factor of Single Path Ultrasonic Flow Meters. In Proceedings of the XXXII Iberian Latin American Congress on Computational Methods in Engineering, Ouro Preto, Brazil, 13–16 November 2011. [Google Scholar]
- Masasi, B.; Frazier, R.S.; Taghvaeian, S. Review and Operational Guidelines for Portable Ultrasonic Flowmeters; Fact Sheet Bae-1535; Oklahoma State University Extension: Stillwater, OK, USA, 2017. [Google Scholar]
- Yang, T.; Leggoe, J.; McEwan, D. Use of Flow Measurement Devices in Restricted Environments. In Proceedings of the CEED Seminar Proceedings, Perth, Australia, 17 September 2019; The University of Western Australia: Perth, Australia, 2019. [Google Scholar]
- Zhao, H.; Peng, L.; Stephane, S.A.; Ishikawa, H.; Shimizu, K.; Takamoto, M. CFD Aided Investigation of Multipath Ultrasonic Gas Flow Meter Performance Under Complex Flow Profile. IEEE Sens. J. 2014, 14, 897–907. [Google Scholar] [CrossRef]
- Cranfield University. Guidelines for the Use of Ultrasonic Non-Invasive Metering Techniques; Technical Report, Report for NMSPU Flow Programme Project KT12; Cranfield University: Cranfield, UK, 2002. [Google Scholar]
- NEL—National Engineering Laboratory. Project FEUS05 Final Report on Clamp-on Transit Time Ultrasonic Flowmeter Performance; Final Report DTI Reference: GBBK/C/0; National Engineering Laboratory: East Kilbride, UK, 2005. [Google Scholar]
- Zhang, H.; Guo, C.; Lin, J. Effects of Velocity Profiles on Measuring Accuracy of Transit-Time Ultrasonic Flowmeter. Appl. Sci. 2019, 9, 1648. [Google Scholar] [CrossRef]
- Jung, J.C.; Seong, P.H. Estimation of the Flow Profile Correction Factor of a Transit-Time Ultrasonic Flow Meter for the Feedwater Flow Measurement in a Nuclear Power Plant. IEEE Trans. Nucl. Sci. 2005, 52, 714–718. [Google Scholar] [CrossRef]
- Shi, H.; Kang, X.; He, S.; Meng, T. Study on the Influences of Multiple Parameters With Uncertainty in the Clamp-On Ultrasonic Flowmeter. IEEE Access 2020, 8, 183787–183798. [Google Scholar] [CrossRef]
- Johnson, A.L.; Benham, B.L.; Eisenhauer, D.E.; Hotchkiss, R.H. Ultrasonic Water Measurement in Irrigation Pipelines with Disturbed Flow. Trans. ASAE 2001, 44, 899–910. [Google Scholar] [CrossRef][Green Version]
- Heitmann, F.; Leonhardt, J.; Juling, M.; Furuichi, N. Validation of the gravimetric Thermal Energy standard flow facility after extensive modernisation. Meas. Sens. 2024, 38, 101550. [Google Scholar] [CrossRef]
- ISO 5167-2:2003; Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 2: Orifice Plates. International Organization for Standardization: Geneva, Switzerland, 2003.
- Yin, G.; Ong, M.C.; Zhang, P. Numerical investigations of pipe flow downstream a flow conditioner with bundle of tubes. Eng. Appl. Comput. Fluid Mech. 2023, 17, e2154850. [Google Scholar] [CrossRef]
- Tam, L.M.; Ghajar, A.J. Effect of inlet geometry and heating on the fully developed friction factor in the transition region of a horizontal tube. Exp. Therm. Fluid Sci. 1997, 15, 52–64. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 7th ed.; McGraw-Hill Education: Columbus, OH, USA, 2011. [Google Scholar]
- Idelchik, I.E. Handbook of Hydraulic Resistance, 3rd ed.; Begell House: Danbury, CT, USA, 2005. [Google Scholar]
- Straka, M.; Koglin, C.; Eichler, T. Segmental orifice plates and the emulation of the 90∘-bend. Tm-Tech. Mess. 2019, 87, 18–31. [Google Scholar] [CrossRef]
- Mathies, N. Messunsicherheit Einer Gravimetrischen Kalt- und Warmwasser-Normalmessanlage Für große Volumenströme. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2005. [Google Scholar]
- Straka, M.; Fiebach, A.; Koglin, C.; Eichler, T. Hybrid simulation of a segmental orifice plate. Flow Meas. Instrum. 2018, 60, 124–133. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Straka, M.; Weissenbrunner, A.; Koglin, C.; Höhne, C.; Schmelter, S. Simulation Uncertainty for a Virtual Ultrasonic Flow Meter. Metrology 2022, 2, 335–359. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).