Abstract
For fighting the COVID-19 pandemic, countries used control measures of different severity, from “relaxed” to lockdown. Drastic lockdown measures are considered more effective but also have a negative impact on the economy. When comparing the financial value of lost lives to the losses of an economic disaster, the better option seems to be lockdown measures. We developed a new parameter, the effectiveness of control measures, calculated from the 2nd time derivative of daily case data, for 92 countries, states and provinces. We compared this parameter, and also the mortality during and after the effective phase, for countries with and without lockdowns measures by means of the Mann–Whitney test. We did not find any statistically significant difference in the effectiveness between countries with and without lockdowns (p > 0.76). There was also no significant difference in mortality during the effective phase (p > 0.1); however, a significant difference after the effective phase, with higher mortality for lockdown countries, was identified. The effectiveness correlated well with a parameter derived from the reproductive number (R2 = 0.9480). The average duration of the effective phase was 17.3 ± 10.5 days. The results indicated that lockdown measures are not necessarily superior to relaxed measures, which in turn are not necessarily a recipe for failure. Relaxed measures are, however, more economy-friendly.
1. Introduction
In December 2019, China detected a cluster of pneumonia cases in the city of Wuhan. In January 2020, this disease (COVID-19) was attributed to the discovery of a novel coronavirus, named SARS-CoV-2. Since then, COVID-19 spread rapidly to 120 countries [1,2,3,4] before the World Health Organization (WHO) declared a pandemic on 11 March 2020 [5]. In the media briefing on the same day, the WHO Director-General summed up the challenges and problems associated with controlling the pandemic [5]:
- −
- Several countries have demonstrated that this virus can be suppressed and controlled.
- −
- The challenge for many countries…is not whether they can do the same—it’s whether they will.
- −
- We know that these measures are taking a heavy toll on societies and economies…
- −
- All countries must strike a fine balance between protecting health, minimizing economic and social disruption and respecting human rights.”
This “fine balance” was addressed by each country in different ways, by introducing various control measures. While many countries imposed nation-wide lockdowns, such as France, Italy, Spain, Austria and Norway, Sweden adopted a “relaxed” approach, by “largely using voluntary measures” [6]. Anders Tegnell, the current State Epidemiologist of Sweden, commented that “Lockdown, closing borders—nothing has a historical scientific basis” [6].
Even though historical evidence for the effectiveness of lockdown measures seems to be missing, these measures were implemented for preventing a shortage of hospital beds and medical equipment (e.g., respirators), as well as for reducing the death toll.
Even more so, the “fine balance” [5] between saving lives and saving the economy was debated [7]. Holden and Preston [7] compared the financial value lost to fatalities (assuming a fatality rate of 1% and using the Australian value of a statistical life), resulting in losses of A$ 1.1 trillion, to the economic value lost from a lockdown, estimated at A$ 180 billion, and concluded that these dollar figures make “the case for shutdown clear” and “the shutdown wins”.
The nature of the COVID-19 pandemic offers the opportunity of comparing different countries in terms of the effectiveness of their control measures. However, how can we measure their effectiveness?
The problem was attempted qualitatively by using the decline of the instantaneous or effective reproduction number (Reff) [8,9,10,11,12] and the drop of the infected patient’s ratio [13]. Similarly, Haug et al. [14] evaluated and ranked the effectiveness of government interventions based on the amount of Reff decrease, i.e., ΔReff.
The drawback of estimating Reff hinges on the accuracy of the reported number of confirmed cases and on the accurate estimates of the serial interval distribution [15]. The reported number of confirmed cases is affected by various degrees of underreporting [16,17]. The average (or median) of the serial interval varies between different sources, from 3.95 days [18] to 7.5 [19] days. Moreover, Reff is determined with different equations and methods [20,21,22], which do not necessarily deliver the same results [23].
Alfano and Ercolano [24] investigated the “difference between the cases of today and those of yesterday” and the “absolute value of cases found yesterday” from 202 countries and claimed “that lockdown is effective in reducing the number of new cases in the countries that implement it, compared with those countries that do not”.
Pincombe et al. [25] defined their effectiveness measure as “larger decreases in mobility” and “smaller COVID-19 case and death growth rates” but did not combine these variables in a single effectiveness parameter.
Chen et al. [26] attempted the assessment of “effects of containment and closure policies” by cross-correlating the Oxford Stringency Index [27] and the “number of confirmed cases during the early period of outbreaks”.
The effectiveness of individual control measures such as personal protective equipment (PPE; e.g., masks) were addressed by Leech et al. [28], by relating the degree of wearing masks to incidence cases. Their results indicated that wearing masks in public reduces Reff by 25.8%, but without any evidence that compulsory mask-wearing decreases the transmission. Moosa [29] investigated the social distancing, which proves effective. However, it appeared difficult to separate the effect of imposed control measures from the one of voluntary measures. Prakash et al. [30] modeled the impact of social distancing and found that the introduction of strict lockdown policies improves the containment of the pandemic. Further modelling studies on social distancing revealed that early and late interventions delay and flatten the epidemic curve, respectively [31], and that the prevention of within-household transmission is a critical factor for flattening the curve [32].
Talic et al. [33] conducted a systematic review on the effectiveness of public health measures on the COVID-19 pandemic and noticed a reduction in incidence associated with hand hygiene, wearing masks and social distancing. However, the authors were not able to assess the effect of lockdowns.
Based on the doubtful reliability of Reff and different methods of assessing the effectiveness of control measures, it is paramount to find a method for calculating the effectiveness that is independent of the number of cases and unaffected by systematic errors.
The aim of this research is to develop a definition and a method for measuring the effectiveness of control measures of different countries as a new epidemiological parameter, as well as to provide or refute the evidence for lockdown measures being effective.
2. Materials and Methods
2.1. Rationale of the Method
Our method uses the black box approach, a standard method in systems theory, which abstracts a complex system in terms of an input and an output, and hypothesises a causal relationship between the input and the output, whilst considering the inner structure of the box irrelevant to the approach, as “only the behavior of the system will be accounted for” [34]. The input and the output in our method are the control measures and their effectiveness, respectively. In epidemiology and public health, “black box epidemiology” is a standard term, referring to “methods and inference to arrive at conclusions about cause–effect relations between risk factors and disease outcomes without necessarily understanding or attempting to explain detailed causal mechanisms or the pathogenesis of the specific disease that is being studied” [35]. In this study, we applied the same principle to the relation between control measures and disease outcomes. There has been some philosophical controversy around “black box epidemiology” [36,37], with arguments such as “empty search for associations, unguided by underlying theory” versus providing “identified useful interventions and that the absence of a known causal mechanism has no bearing on the validity of the study results” [38]. On top of this, Greenland et al. [37] defend “black box epidemiology” as a “valuable source of seemingly unrelated facts that provide empiric tests of theories”.
If the number of infected people grows naturally, exponentially or sub-exponentially [39], then the slope of the daily case numbers becomes steeper with time. If this development is interrupted by effective control measures, then the slope flattens. The more effective the measures, the quicker the slope flattens, such that the slope eventually becomes negative, resulting in a deceleration and a decline of the daily case numbers.
This decline is not only induced by control measures (which include vaccinations if available), but also, in absence of control measures, the herd immunity and self-elimination if the mortality is 100%. This decline is also what policymakers are interested in, as the best and immediate measure of the effectiveness of their control policies, publicised through radio and television reports, informing the public by how much the data drop from day to day.
The higher the daily case numbers, the steeper their slopes. It is, therefore, evident that any effectiveness index should be independent of “numbers” (daily case numbers in this context). Our proposed method and the derivation of the effectiveness hinge on normalising the time derivatives of daily case numbers, such that the effectiveness is independent of scaling factors. If two countries share the same geometrical identity of daily cases that differ only by their scaling factors, then the effectiveness of their control measures is identical. The “force” required for interrupting the natural growth and for bending the slope is supposed to be generated by control measures, at least in the early stages of an epidemic. As this “force” is applied daily over a certain period, it is more appropriate to refer to the “force rate” (force per unit time). It is shown subsequently that the outcome of this force rate is directly related to the effectiveness of control measures.
The term “effectiveness” used in this study stems from the two different types of intervention studies, where “efficacy can be defined as the performance of an intervention under ideal and controlled circumstances, whereas effectiveness refers to its performance under ‘real-world’ conditions” [40,41].
As explained above, the causal relationship between the input (control measures) and the output (their effectiveness) is only a hypothesis within the black box approach. Thus, the cardinal hypothesis of our study is that lockdown measures are more efficient than non-lockdown ones. This hypothesis addresses the knowledge gap and the contribution to the literature, even if it seems to be common sense, as the “scientific basis” of the effectiveness of a lockdown is missing [6]. To test this hypothesis, according to Thom [42], “… the only conceivable way of unveiling a black box, is to play with it”. This means that we investigated different countries and control measures, starting with dividing them into two cohorts and comparing their effectiveness in terms of significant differences. If there were significant differences, then more groups could be considered. We classified the two cohorts by the severity of the control measures, specifically lockdown and no lockdown countries, where the line drawn between these two cohorts hinged on the definition of a lockdown. For the latter, we extracted the minimum requirement or least common characteristics of a lockdown, common to all countries that qualified for a lockdown.
2.2. Effectiveness Parameters, Mathematical Derivation and Terminology
Most commonly, confirmed cases are reported and visualised as cumulative cases, CC, which approximately follow an S-shaped curve between two constant values, 0 and the maximum number of cases Cmax.
The speed of the increase in cases, velocity v, corresponds to the daily case count (unit: cases per day, c/d). It has to be noted that the (numerical) integral of v does not result in CC, but rather in CI, as CC is a summation. Thus, , where t is the time in days. This implies that if v is exponential, CI is exponential too, but CC is not. Note that v is always positive.
The acceleration of the disease spreading, a, equals the (numerical) time derivative of v, namely a = dv/dt (unit: c/d2). The acceleration is positive and negative (= deceleration), if the velocity v increases and decreases, respectively.
In mechanical terms, the “force” mentioned above equals the acceleration of an object times its mass, whereas the “force rate” equals the jerk times the mass of the object.
The jerk (or jolt), j, of the spreading disease is the (numerical) time derivative of a, namely j = da/dt (unit: c/d3). The jerk j is positive or negative, if the acceleration increases or decreases, respectively. The major decrease of the acceleration (i.e., the major transition from acceleration to deceleration) is denoted by the effective phase or period, TE (measured in days). During TE, j is negative on average.
As will be shown later, the higher Cmax, the larger the absolute jerk, |j|. This relationship prevents the direct comparison of the j-data of different countries. Therefore, for comparative reasons, j has to be normalised to v. This normalisation process has three advantages, i.e., comparability across different Cmax values, independence of the actual case numbers and their associated systematic errors (such as under-reporting) and the definition of an effectiveness parameter, E, where E = −j/v (unit: d−2).
2.2.1. Mathematical Derivation of Effectiveness Parameters
A simple and suitable model for exemplifying and understanding the dynamics of the effectiveness E is by applying a Gaussian function (bell curve) to the v-data:
where b is a multiplier (proportional to Cmax), t is the time (in days), m is the day where v reaches its maximum, and s represents the width of the bell curve. The Gaussian function is symmetrical about m. Note that the standard structure of a Gaussian involves a multiplier of two in the denominator of the exponent, which was omitted here for simplification purposes.
In addition, note that the Gaussian function is only one out of other suitable models and will by no means be used as a fit function applied to actual daily cases data. It simply serves to understand the dynamics and principles of the effectiveness.
When simplifying Equation (1) and setting m to 0, t = 0 occurs at the velocity peak, and the time has a negative sign before the v-peak:
The acceleration is then written as:
and the jerk is described as:
The two turning points (Figure 1), where the acceleration is at the maximum and starts to decrease and the deceleration is at its minimum value and starts to increase, are at j = 0. The time of the two turning points, tE1 and tE2, marks the boundaries of the effective phase. As the bell curve is symmetrical, tE1 + tE2 = 0, if m = 0.
Equating Equation (4) to zero and solving for t yields:
Thus,
The magnitude of acceleration and deceleration at ±tE is written as:
which also corresponds to the half impulse of the jerk j over the effective phase.
For obtaining average jerk over the half-impulse (the same as average jerk over the full-impulse ) of the effective phase, we had to divide aE by tE, yielding:
Peak jerk, jmin, and peak velocity, vmax, occur at t = 0. Setting t to zero in Equations (4) and (2) yields:
and
As seen from Equations (2)–(4) and (7)–(10), all parameters are dependent on the number of cases, as these equations share the same multiplier b, which is identical to vmax.
As such, to render these parameters independent of the number of cases, the parameters have to be normalised to vmax or to the average v over the effective phase, .
To calculate , we took the integral of v from tE1 to tE2 and divided by 2tE:
where erf denotes the error function.
The effectiveness is the mirrored jerk, normalised to the velocity. The smaller (more negative) the jerk, the greater the effectiveness. After the normalisation of the jerk, we obtained the following effectiveness parameters, namely:
- −
- the effectiveness E in general:
- −
- the peak effectiveness, Emax:
- −
- the average effectiveness, :
Note that defined as –/ is a weighted average, in contrast to an unweighted defined by the average of the ratio of to . The weighting factor thereby is v, via = Σ(E∙v)/Σ(v) = Σ(j)/Σ(v) = –/ as per Equation (14).
The ratio ρ of average effectiveness to duration of effective phase TE is written as:
This ratio combines the opposite trends of E and TE in a single parameter.
Equations (12)–(15) are functions of s but no longer functions of b and thus independent of the case data v. More precise, Equations (12)–(15) are functions of s−x (where x = 1, 2 and 3), which indicates that the narrower (more leptokurtic) the v-peak, the more effective the control measures. This applies to two cardinal parameters, namely and ρ. A third cardinal parameter, TE, is a function of s+1 according to Equation (6) in a sense that the shorter the effective phase, the more effective are the control measures. “Real-world” data are required for evaluating the three cardinal parameters, applied to daily case data (calculated from cumulative data) of different countries.
Figure 1 shows all parameters, required for determining the effectiveness, in relation to each other, namely v, a, j, TE, and Emax.
2.2.2. Relationship between Average Effectiveness, , and the Instantaneous Effective Reproduction Number Reff
For deriving Reff, we took the logarithm of velocity v and used Equation (2) to obtain:
where log denotes the natural logarithm. The time derivative of this function is the logarithmic growth rate K, written as:
Note that the multiplier b drops out, which makes the gradient independent of the actual number of daily cases v, as already seen in Equations (12)–(14). This fact proves that Reff can be very well calculated from underestimated data, which stands in contrast to the criticism by Leung et al. [15].
By using the exponential method of Diekmann et al. [22], Reff was finally calculated as:
where SI is the serial interval.
As 0 ≤ Reff << ∞ and as the transition from epidemic to endemic occurs at Reff = 1, taking the logarithm of Equation (18) puts this transition at log(Reff) = 0:
The time derivative of this function is expressed as:
which is expectedly a constant, since Equation (19) is a linear function. This means that, in a Gaussian function model, the rate of log(Reff) decreasing with time is constant. However, Equation (20) is dependent of s2. The larger the value of s, the wider the Gaussian curve, and the smaller this gradient in Equation (20). This principle establishes the relationship between Reff, or more precise, the derivative of log(Reff), with the effectiveness E of preventive control measures, which is also a function of s−2, according to Equation (14). Thus, the steeper the gradient of log(Reff), i.e., –2SI s−2, the more effective the control measures.
Normalising Equation (20) to SI, if the average or median SI is a COVID-19-associated constant, delivers the effectiveness ER calculated from Reff, expressed as:
ER stands in sharp contrast to the mere (absolute) decrease [14] or decline [8,9,10,11,12] of Reff, as ER corresponds to the decrease of log(Reff) per unit time, across TE.
From Equations (14) and (21), ER is expressed as:
This constant applies to Gaussian models only.
2.2.3. Data Processing of Real-World Data
The processing procedure started with daily cumulative case data, CC, commonly reported on websites as further specified below. The daily case data, v, were determined from ΔCC. Due to the noisy nature of the original v-data, they were pre-filtered by subjecting them to a double-running average filter (1st-order Savitzky–Golay filter) with a window width of 3 data. The major data fit for identifying the trend was performed with a running quadratic filter (2nd-order Savitzky–Golay filter) over a window of 13 data. This filter method, specifically a window width of 13 data, was obtained from a convergence test. In principle, the absolute peak data (minimum and maximum) of a and j became smaller and may finally asymptote, as the window width widened (e.g., from 5 to 23 data). At smaller windows, the magnitude of the peak data was greater for two reasons, i.e., the slope of the filter data was steeper and the local noise (data fluctuations) was more pronounced. Consequently, the data fluctuations were assessed by means of a randomness index (RI; RI-p-ap method [43]; 0 = perfectly correlated, 0.5 = perfectly random; 1 = perfectly anticorrelated). The smaller the RI, the less the data fluctuate. The RI-data of a and j asymptoted at an average window width of 13 (11–15) data. Using the quadratic filter without the preceding double average filters would require a wider window than 13 data to achieve the same RI effect but resulted in smaller peak data.
The resulting dataset of the filtered v-data served for two purposes:
- −
- Each filtered v-datum corresponds to the midpoint of a quadratic fit curve over 13 pre-filtered v-data. The residuals between the filtered v-data and the original v-data were used to calculate the confidence interval of each filtered v-datum. The residual standard deviation of each filtered v-datum was divided by √13 to obtain the standard error, which was multiplied by the t-distribution of degrees of freedom of 10 and α = 0.05 to obtain the 95% confidence interval for each filtered v-datum.
- −
- The filtered v-data including their 95% confidence interval data were numerically differentiated twice by calculating the slope over 3 data points to obtain a and j.
Finally, E was computed from –j/v.
The effective phase TE was defined as the time between an amax and an amin, where amax was positive and amin was negative (Figure 1), and
where |Δa| was at its maximum across the entire dataset. amax and amin were determined visually, according to the aforementioned guidelines.
Δa = amin − amax.
The impulse S of the jerk over the effective phase was written as:
Sj = Δa.
The duration of the effective phase, TE, was determined from its boundaries tE1 and tE2, where tE corresponded to the intersections of the j-data and the zero line (intersection of a straight line between two consecutive data points, one positive and one negative), one intersection at amax and one at amin. Note that TE is usually non-integer.
TE = Δt = tE2 − tE1,
was calculated from averaging the v-data over TE.
The parameters obtained from Equations (23)–(27) were determined from the filtered v-data and their confidence bounds (lower and upper). Note that after differentiating v with time, once and twice, the resulting confidence bounds for the parameters obtained from Equations (23)–(27) were not necessarily lower and upper anymore, as their value depended on the instantaneous slope of the v-curve and that of the a-curve.
The profile or shape of the velocity curve v was assessed theoretically and practically. It is evident that real-life velocity data (daily cases data, v) did not necessarily follow a Gaussian function.
When modifying Equation (2) to
where h modifies the shape, then we obtained a Gaussian function if h = 2. If h → 1, the function became more triangular. If h > 2, then the curve became more trapezoidal and finally rectangular at h >> 2; both shapes were characterised by a distinct plateau. The v-data simulated from Equation (28) served for classifying TE and data in relation to the Gaussian function (h = 2).
Practically, different shapes were determined from the deviation from the initial theoretical Equation (2), where all TE and data followed a Gaussian function. As such, the s-parameter was determined for TE and from Equations (5) and (14), respectively:
If the TE and data followed a Gaussian function, then sE = sT, and the ratio ς = sE/sT must be unity. The ratio ς is defined as:
The ratio ς, when expressed as logς, determines the shape of the velocity profile, where logς > 0 is more triangular-shaped, logς < 0 is more trapezoidal-shaped, and logς = 0 is bell-shaped (Gaussian function).
For constructing an isoline with a fixed ς-value, is calcuated from ς as a function of TE:
The principle of the average effectiveness and the effective phase TE is shown in Figure 1, calculated from the simulated daily case numbers (velocity v) and their consecutive time derivatives, acceleration a, and jerk j.
The average effectiveness derived from Reff, i.e., , was calculated as:
where ΔlogReff denotes the decrease of logReff during the effective phase.
was correlated to and to the shape factor logς. From the three values of the coefficient of determination (R2) of multiple and single regressions, the combined influence was calculated from the sum of the R2 of the single regressions minus the R2 of the multiple regression. The individual influences (semi-partial correlations) of and logς were calculated from the single regression R2 minus the combined influence. The influences were expressed as a percentage, resulting from 100R2.
This correlation exercise served to prove practically that was directly related to , a proof that was already established theoretically in Equation (22) for a Gaussian v-profile and for cross-validating the two different methods. The drawback of the 2nd method, namely calculating the effectiveness () from Reff, is, however, that the start and the end of the effective phase have to be predetermined from the first method, which are the positive and negative peak data of the acceleration a (Figure 1). Taking the steepest gradient of log(Reff) or the gradient at Reff = 1 results only in a local maximum or value of ER, respectively, instead of an average across the effective phase. Using the amount of Reff-decrease, i.e., ΔReff as a measure [8,9,10,11,14] of the quality or efficiency of a control measure is concerning, as two countries with the same ΔReff but achieved over different times clearly showed that the steeper the gradient of the Reff-curve, the more efficient the control measure. This fact is reflected in Equation (33), with the time window in the denominator.
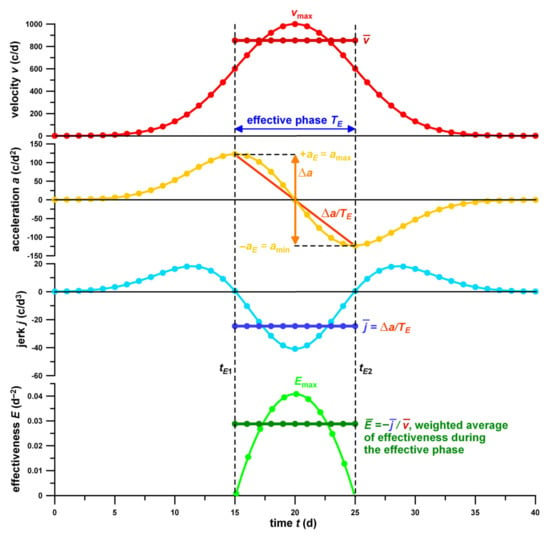
Figure 1.
Explanation of the derivation of the effectiveness parameters. Daily case data (velocity v; following a hypothetical Gaussian function of v = 1000 exp[−(t − 20)2/72]) against time t ( = average velocity of the effective phase TE; vmax = peak velocity); acceleration a, first time derivative of the daily case data (amax = +aE = maximum acceleration; amin = −aE = minimum; Δa = amin − amax; Δa/TE = acceleration gradient across the effective phase); jerk j, second time derivative of the daily case data ( = average jerk of the effective phase); and effectiveness E of control measures against time ( = average effectiveness of the effective phase); tE1,2 = start and end of the effective phase.
2.3. Data Sets of Real-World Data
We collected publicly available data of cumulative and daily cases [1,2,3,4] reported for the countries, states and provinces listed in Table 1. We analysed the daily case data, calculated from the cumulative data of 92 countries, states and provinces using the method described above. The countries, states and provinces were selected based on the following inclusion criteria: TE ending the latest on 15 May 2020 and CC ≥ 250 at this date. We took the cumulative case data and the cumulative death data from several websites that provide databases for different countries, states and provinces [1,2,3,4].
2.4. Classification of Intervention Measures
There are several webpages available [1,44,45,46,47,48], which provide (at least partially) information on lockdowns and restrictions related to the COVID-19 pandemic. We used the information and associated references found on these webpages for assigning countries, states and provinces to two groups—lockdown and no lockdown—according to the definition below and to our best of our knowledge, belief and understanding, when compiling all the information found on the Internet. We excluded the following countries from this classification: Russia, as there was no nationwide lockdown but only in some cities and regions; USA, which was treated by states; and China, which was treated by provinces.
Defining a “lockdown” for decision making is a subjective process, more exclusive rather than inclusive, mostly by judging what it is not. Nevertheless, we identified measures that were common to most countries that implemented severe measures; and we used these measures to classify a lockdown country under the following definition:
- (a)
- A nationwide (state-wide/territory-wide) compulsory stay-home order for 24 h per day and at least for 14 days;
- (b)
- Enforced by law, police and by penalties in case of infringement;
- (c)
- With very few exceptions that allow people to leave their home (e.g., essential work and study; shopping for essential goods; medical care; exercise).
It is evident that this compulsory stay-home order further, but not necessarily entirely, implies the following: the closure of schools and universities, non-essential businesses, and places for public gathering such as restaurants and entertainment facilities; prohibition of visiting of friends and relatives (indoor gatherings) and outdoor gatherings; abiding social distancing rules and mask orders. It is also evident that this compulsory stay-home order and its implications have the highest impact on the economics of a country.
What a “lockdown” by our definition is not infer the following: any of the implications, single or combined, which arise from a compulsory stay-home order, in the absence of the cardinal compulsory stay-home order; voluntary stay-home orders, where people are advised or directed to stay home (e.g., in Florida, people “shall stay home” or “shall limit their movements” [49] instead of must); age-dependent compulsory stay-home orders (e.g., elderly citizens only); curfews for less than 24 h such as during night time (e.g., Serbia); compulsory stay-home orders of less than 14 days (e.g., Israel); movement control orders only (e.g., Malaysia); fines for breaching the physical distancing rule, in the absence of a compulsory lockdown (e.g., The Netherlands).
For a comparison of terminology, Desvars-Larrive et al. [50] used their term “national lockdown” (their Level 1, theme 8, Level 2 category 5) under a category of travel restriction (Level 1, theme 8), whereas we included in our lockdown definition further measures automatically enforced during a lockdown such as travel restrictions in general (Level 1, theme 8), as well as social distancing measures (Level 1, theme 7; [50]).
The Oxford Stringency Index [27] lists eight Indicators under the Category C “Containment and Closure”, namely C1 School closing, C2 Workplace closing, C3 Cancel public events, C4 Restrictions on gathering size, C5 Close public transport, C6 Stay at home requirements, C7 Restrictions on internal movement and C8 Restrictions on international travel. Our lockdown definition corresponds to the Oxford Stringency Index level C6-2 (stay at home requirements which require not leaving the house with exceptions for daily exercise, grocery shopping and “essential” trips). This definition has implications on other categories to a certain extent, e.g., on workplace closing or at least partial workplace closing if essential work cannot be conducted from home. Therefore, our definition of a lockdown is aligned to the Oxford Stringency Index [27] categories C1–C7.
2.5. Statistics
From the daily case data, the following parameters were calculated, by using the method described above, i.e., v (filtered), a, j, TE, , ρ and ς. Except for ρ and ς, for all the other parameters, the upper and lower confidence interval bounds were determined. As TE, and ρ data were not normally distributed, we used the Mann–Whitney U-test (MWU-test) for comparing these parameters for countries with and without a lockdown. The threshold for a significant difference was α = 0.05. The effect size r was calculated from the smaller U: r = 1 − 2U/(n1 × n2), where n1 and n2 are the numbers of data of each of the 2 groups. The effect sizes r were interpreted according to McGrath and Meyer [51]. The effectiveness was visualised as a map in Matlab (Release 2018b, The MathWorks, Natick, MA, USA) for European countries by colour-coding the parameters TE, , ρ and ς.
The mortality was determined from the number of deaths in a population normalised to the size of the population of countries/states/provinces listed in Table 1 at a specific point in time during the COVID-19 pandemic (data at the beginning, middle and end of the effective phase as of 26/06/2020). We compared the mortality of countries with and without a lockdown with the MWU-test. For calculating the mortality, we collected the publicly available data of cumulative and daily deaths [1,2,3,4] reported for the countries, states and provinces listed in Table 1.
2.6. Validation
For validating our approach, we investigated the influences of external factors for which a hypothetical outcome could be estimated. These external factors were as following: population size [52], land area ([53]; not total area, i.e., not land + water area), population density (population per unit land area), gross domestic product (GDP) [54]; and small islands. We evaluated these external factors in terms of TE, and ρ. For the GDP analysis, only 82 out of the 92 countries states and provinces were included due to missing GDP data of dependencies and Chinese provinces. The influence was tested first with a trend analysis from a power law regression, its R2 value (as a percentage: R2% = R2 × 100 × sgnR, where sgn denotes the sign function, to identify positive and negative correlations) and its p-value (α = 0.1). R2% explains at which percentage the effectiveness of control measures can be explained from an external factor. For example, we can assume theoretically that the greater the population, the less efficient the same control measures, comparatively applied to a smaller population. If the trend was significant (p < 0.1), then a threshold value (e.g., of the population) was determined, which separates two groups (below and above the threshold) and at which the medians of both groups are significantly different (MWU-test; p < 0.05).
We hypothesised that countries with greater and denser populations, larger areas and higher country GDP are more difficult to control (interventions are less efficient; for GDP because of both population and education), whereas small islands are easier to control (interventions are more efficient).
For assessing the individual and combined influences of the population size and the country GDP on the effectiveness , we analysed multiple and single regressions: population size + GDP vs. , population size vs. , and GDP vs. . All regressions had to be significant (α = 0.1). From the three R2 values of multiple and single regressions, the combined influence, which has to be positive, was calculated from the sum of the R2 of the single regressions minus the R2 of the multiple regression. The individual influences (semi-partial correlations) of the population size and the country GDP were calculated from the single regression R2 minus the combined influence.

Table 1.
Countries and effectiveness parameters for countries, states and provinces of which the effective phase ended the latest on 15 May 2020. LOCK: lockdown measures (Y = yes, N = no; X: lockdown only in some cities, or a specific country replaced by individual states or provinces (USA and CHN)); TE, effective phase; CI, 95% confidence interval; E, effectiveness; ρ = E/TE; ς, shape parameter of the velocity profile); 3-letter country codes according to ISO 3166-1 Alpha-3; Chinese provinces 2-letter codes: ISO 3166-2:CN; 2-letter code of the states of the USA: ISO 3166-2:US; KOS, Kosovo; Reff, effective reproduction number.
Table 1.
Countries and effectiveness parameters for countries, states and provinces of which the effective phase ended the latest on 15 May 2020. LOCK: lockdown measures (Y = yes, N = no; X: lockdown only in some cities, or a specific country replaced by individual states or provinces (USA and CHN)); TE, effective phase; CI, 95% confidence interval; E, effectiveness; ρ = E/TE; ς, shape parameter of the velocity profile); 3-letter country codes according to ISO 3166-1 Alpha-3; Chinese provinces 2-letter codes: ISO 3166-2:CN; 2-letter code of the states of the USA: ISO 3166-2:US; KOS, Kosovo; Reff, effective reproduction number.
| Country | ISO Code | LOCK | TE (d) | TE, Lower CI | TE, Upper CI | Average E (10−3 d−2) | E, Lower CI | E, Upper CI | ρ (10−3 d−3) | log ς | Average ER (10−3) from Reff |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Alaska | AK | N | 19.6 | 19.8 | 20.8 | 11.49 | 14.09 | 11.23 | 0.587 | −0.096 | 14.23 |
| Albania | ALB | Y | 36.6 | 35.9 | 36.9 | 8.19 | 10.02 | 8.02 | 0.224 | −0.293 | 11.94 |
| Andorra | AND | N | 6.9 | 6.3 | 7.7 | 28.63 | 40.99 | 21.39 | 4.168 | 0.161 | 34.08 |
| Australia | AUS | Y | 12 | 11.9 | 13.7 | 18.81 | 20.49 | 15.2 | 1.562 | 0.008 | 26.21 |
| Austria | AUT | Y | 9.8 | 10.3 | 9.8 | 22.06 | 21.6 | 21.33 | 2.254 | 0.064 | 29.16 |
| Belgium | BEL | Y | 35.2 | 33.9 | 36 | 5.67 | 6.01 | 5.78 | 0.161 | −0.197 | 10.04 |
| Bosnia and Herzegovina | BIH | N | 37 | 36 | 38.2 | 5.6 | 7.28 | 5.02 | 0.151 | −0.216 | 6.22 |
| Bulgaria | BGR | Y | 7.1 | 5.9 | 7.3 | 24.74 | 32.76 | 22.98 | 3.499 | 0.18 | 28.63 |
| Canada | CAN | N | 37.2 | 37.5 | 37.2 | 3.67 | 3.85 | 3.55 | 0.099 | −0.127 | 4.65 |
| China | CHN | X | 10.1 | 11.1 | 9.8 | 18.93 | 17.24 | 19.93 | 1.865 | 0.081 | 23.87 |
| Colorado | CO | N | 8 | 6.9 | 8.9 | 20.59 | 25.76 | 19.91 | 2.581 | 0.168 | 24.05 |
| Connecticut | CT | N | 20.3 | 19.8 | 20.3 | 8.91 | 12.57 | 8.11 | 0.439 | −0.056 | 11.06 |
| Croatia | HRV | N | 13 | 12.3 | 13.3 | 14.05 | 16.05 | 13.39 | 1.082 | 0.039 | 26.59 |
| Cyprus | CYP | N | 19.8 | 18.2 | 20.7 | 13.63 | 16.75 | 12.33 | 0.688 | −0.138 | 20.26 |
| Czech Republic | CZE | Y | 20 | 16.7 | 20.2 | 8.95 | 10.63 | 9.6 | 0.447 | −0.051 | 13.46 |
| Estonia | EST | N | 15.2 | 14.5 | 15.5 | 19.38 | 25.08 | 16.34 | 1.278 | −0.098 | 27.38 |
| Finland | FIN | N | 5.3 | 5.3 | 5.5 | 26.88 | 36.14 | 19.77 | 5.029 | 0.284 | 29.65 |
| Florida | FL | N | 25.1 | 25.4 | 24.8 | 5.93 | 6.65 | 6.16 | 0.236 | −0.059 | 7.89 |
| France | FRA | Y | 18.3 | 17.4 | 18.5 | 9.2 | 11.06 | 8.56 | 0.503 | −0.018 | 11.49 |
| Georgia | GEO | N | 22.6 | 21.8 | 23.1 | 12.39 | 15.66 | 11.57 | 0.547 | −0.175 | 16.59 |
| Germany | DEU | N | 17.5 | 18.5 | 17.1 | 9.39 | 9.57 | 9.39 | 0.536 | −0.004 | 13.07 |
| Greece | GRC | Y | 21.8 | 23.5 | 20 | 10.08 | 18.67 | 10 | 0.463 | −0.113 | 17.1 |
| Guangdong | GD | N | 9.3 | 8.4 | 10.1 | 27.88 | 31.67 | 24.79 | 2.996 | 0.035 | 39.75 |
| Guernsey | GGY | Y | 9.3 | 10.2 | 9.2 | 28.13 | 29.27 | 26.42 | 3.023 | 0.033 | 37.51 |
| Hawaii | HI | Y | 9.3 | 9.2 | 9.5 | 19.76 | 23.98 | 17.05 | 2.126 | 0.11 | 23.59 |
| Henan | HA | N | 13.3 | 12.5 | 13.6 | 20.14 | 21.85 | 19.52 | 1.51 | −0.051 | 30.08 |
| Hong Kong | HKG | N | 8.7 | 9.3 | 8.5 | 21.1 | 20.6 | 22.4 | 2.424 | 0.125 | 24.63 |
| Hubei | HB | Y | 9 | 7.6 | 9.1 | 23.22 | 27.06 | 22.18 | 2.577 | 0.089 | 30.35 |
| Hunan | HN | N | 13.9 | 13.3 | 14.8 | 17.65 | 20.08 | 15.98 | 1.266 | −0.041 | 25.45 |
| Hungary | HUN | N | 7.3 | 6.6 | 7.6 | 33.71 | 40.85 | 30.72 | 4.627 | 0.1 | 44.63 |
| Iceland | ISL | N | 21.4 | 19.7 | 21.5 | 11.92 | 13.15 | 12.41 | 0.557 | −0.142 | 20.49 |
| Idaho | ID | N | 7.9 | 7.5 | 8 | 42.29 | 46.75 | 39.51 | 5.375 | 0.017 | 59.97 |
| Iowa | IA | N | 8.9 | 8 | 12.3 | 17.08 | 23.86 | 12.06 | 1.921 | 0.161 | 20.12 |
| Iran | IRN | N | 10.3 | 9 | 11.5 | 15.82 | 19.19 | 14.26 | 1.529 | 0.112 | 20.05 |
| Ireland | IRL | Y | 6.8 | 5 | 7.9 | 22.03 | 37.93 | 17.55 | 3.249 | 0.224 | 24.7 |
| Isle of Man | IMN | Y | 15.8 | 14.5 | 16.5 | 17.23 | 27.31 | 15.6 | 1.087 | −0.092 | 22.5 |
| Israel | ISR | N | 14.7 | 13.4 | 15.3 | 14.96 | 16.5 | 15 | 1.021 | −0.027 | 22.2 |
| Italy | ITA | Y | 15.2 | 15.2 | 14.8 | 7.97 | 7.8 | 8.28 | 0.526 | 0.095 | 10.48 |
| Jamaica | JAM | N | 18.1 | 17.4 | 19.1 | 16.83 | 24.08 | 13.37 | 0.929 | −0.145 | 28.85 |
| Japan | JAP | N | 15.9 | 15.5 | 16 | 10.74 | 10.6 | 10.97 | 0.676 | 0.01 | 13.72 |
| Jersey | JEY | Y | 10.5 | 13.7 | 9.5 | 20.93 | 29.55 | 19.4 | 1.988 | 0.044 | 27.56 |
| Jordan | JOR | Y | 6.3 | 5 | 6.9 | 33.98 | 52.26 | 30.62 | 5.374 | 0.16 | 39.81 |
| Kansas | KS | N | 21.9 | 21.9 | 21.3 | 8.59 | 11.48 | 7.41 | 0.393 | −0.081 | 13.19 |
| Kosovo | KOS | N | 19.8 | 18.3 | 21 | 13.55 | 19.34 | 12.82 | 0.683 | −0.137 | 21.13 |
| Latvia | LVA | Y | 8.4 | 8.8 | 8.5 | 18.32 | 22.71 | 17.21 | 2.174 | 0.169 | 33.21 |
| Lebanon | LBN | Y | 7.2 | 5.7 | 8.9 | 27.46 | 49.3 | 21.48 | 3.825 | 0.151 | 39.68 |
| Lithuania | LTU | Y | 32.9 | 31.5 | 34.7 | 9.25 | 11.49 | 8.96 | 0.281 | −0.274 | 23.69 |
| Louisiana | LA | Y | 8.3 | 6.6 | 9.2 | 31.36 | 47.2 | 27.4 | 3.775 | 0.059 | 42.69 |
| Luxembourg | LUX | N | 19 | 19.9 | 17.8 | 11.66 | 14.08 | 11.87 | 0.613 | −0.086 | 17.12 |
| Malaysia | MYS | N | 34 | 33 | 34.6 | 6.82 | 7.58 | 6.47 | 0.2 | −0.222 | 13.92 |
| Malta | MLT | Y | 7.6 | 6.7 | 9.7 | 37.16 | 62.48 | 24.99 | 4.879 | 0.06 | 46.91 |
| Massachusetts | MA | Y | 8.2 | 7.5 | 8.9 | 19.49 | 21.03 | 18.06 | 2.367 | 0.166 | 22.42 |
| Mauritius | MUS | Y | 7.5 | 5.5 | 7.7 | 37.05 | 67.36 | 32.62 | 4.95 | 0.068 | 50.61 |
| Michigan | MI | Y | 9.5 | 8.8 | 10.3 | 18.2 | 20.64 | 16.25 | 1.909 | 0.117 | 23.74 |
| Montana | MT | Y | 17 | 16.4 | 18 | 15.14 | 16.73 | 13.23 | 0.892 | −0.093 | 22.55 |
| Montenegro | MNE | N | 6.4 | 5 | 7.3 | 52.98 | 76.69 | 42.65 | 8.282 | 0.058 | 72.22 |
| Morocco | MAR | N | 29.7 | 27.7 | 31.2 | 7.03 | 8.99 | 6.98 | 0.237 | −0.17 | 8.92 |
| Netherlands | NLD | N | 26.9 | 26.6 | 28.2 | 5.96 | 6.56 | 6.03 | 0.222 | −0.091 | 7.53 |
| New Hampshire | NH | Y | 37.2 | 36.2 | 37.5 | 4.61 | 4.64 | 4.88 | 0.124 | −0.176 | 5.24 |
| New Jersey | NJ | Y | 27 | 27.4 | 26.7 | 5.13 | 5.36 | 4.96 | 0.19 | −0.06 | 6.7 |
| New York | NY | Y | 38.6 | 38.7 | 38.2 | 4.6 | 4.88 | 4.34 | 0.119 | −0.191 | 9 |
| New Zealand | NZL | Y | 15.9 | 15.1 | 16.6 | 18.01 | 19.77 | 17.19 | 1.132 | −0.103 | 29.3 |
| North Macedonia | MKD | N | 7 | 5.7 | 8.5 | 32.64 | 53.3 | 24.06 | 4.68 | 0.126 | 39.74 |
| Norway | NOR | Y | 15.5 | 15.5 | 15.5 | 14.51 | 15.51 | 13.79 | 0.935 | −0.045 | 19.92 |
| Oregon | OR | Y | 49.7 | 48.6 | 49.8 | 3.71 | 4.44 | 3.22 | 0.075 | −0.255 | 5.22 |
| Pennsylvania | PA | Y | 9.2 | 8.7 | 12.1 | 14.71 | 18.04 | 10.95 | 1.591 | 0.176 | 19.29 |
| Portugal | POR | N | 20.5 | 18.4 | 20.8 | 9.19 | 11.02 | 9.19 | 0.449 | −0.067 | 12.7 |
| Reunion | REU | N | 7.4 | 7.1 | 7.5 | 27.28 | 32.45 | 24.44 | 3.681 | 0.138 | 33.45 |
| Rhode Island | RI | N | 21.2 | 20.3 | 21.7 | 7.57 | 8.42 | 7.18 | 0.357 | −0.04 | 11.58 |
| Romania | ROU | Y | 45.8 | 47.2 | 46.1 | 3.14 | 3.29 | 3.21 | 0.069 | −0.183 | 5.68 |
| Russia | RUS | X | 13.5 | 12.6 | 14.2 | 6.63 | 7.41 | 6.37 | 0.489 | 0.184 | 7.74 |
| San Marino | SMR | Y | 23.8 | 24.1 | 23.3 | 12.57 | 20.91 | 9.8 | 0.528 | −0.2 | 17.21 |
| Serbia | SRB | N | 6.9 | 6 | 7.6 | 25.09 | 29.94 | 22.69 | 3.639 | 0.188 | 29.1 |
| Singapore | SGP | Y | 8.4 | 7.7 | 9 | 24.35 | 29.81 | 22.35 | 2.913 | 0.111 | 30.15 |
| Slovakia | SVK | N | 7.6 | 6.3 | 8.5 | 32.39 | 59.38 | 26.73 | 4.262 | 0.09 | 39.19 |
| Slovenia | SVN | N | 9.2 | 8.8 | 9.6 | 18.49 | 20.65 | 17.03 | 2.015 | 0.13 | 22.05 |
| South Korea | KOR | N | 8.3 | 7.2 | 9 | 37.58 | 44.25 | 36.57 | 4.514 | 0.018 | 51.06 |
| Spain | ESP | Y | 15.3 | 17.1 | 14.5 | 10.15 | 9.59 | 11.19 | 0.662 | 0.037 | 12.86 |
| Sweden | SWE | N | 32 | 33.2 | 33.8 | 4.55 | 5.72 | 3.67 | 0.142 | −0.108 | 5.02 |
| Switzerland | CHE | N | 22 | 22.2 | 21.5 | 8.61 | 9.4 | 8.06 | 0.392 | −0.084 | 6.08 |
| Taiwan | TWN | N | 11.2 | 10.6 | 12.3 | 20.78 | 24.84 | 18.04 | 1.853 | 0.018 | 29.87 |
| Thailand | THA | N | 15.5 | 13.8 | 16.1 | 14.87 | 19.61 | 14.29 | 0.961 | −0.049 | 22.3 |
| Tunisia | TUN | N | 26.4 | 25.7 | 27 | 10.91 | 14.25 | 9.5 | 0.413 | −0.215 | 15.12 |
| Turkey | TYR | N | 16.3 | 16.1 | 17.3 | 8.27 | 8.82 | 7.72 | 0.508 | 0.055 | 10.35 |
| United Kingdom | GBR | Y | 41.8 | 42.8 | 41.8 | 3.07 | 2.94 | 3.32 | 0.073 | −0.138 | 4.5 |
| United States | USA | X | 37.9 | 39.2 | 37.5 | 2.78 | 2.66 | 2.96 | 0.073 | −0.074 | 3.68 |
| Uruguay | URY | N | 27.5 | 26.5 | 29 | 11.87 | 17.27 | 9.93 | 0.432 | −0.249 | 24.1 |
| Uzbekistan | UZB | N | 7.3 | 5.6 | 7.2 | 30.46 | 48.27 | 30.1 | 4.146 | 0.118 | 36.64 |
| Vermont | VT | N | 8.5 | 8.4 | 8.7 | 24.63 | 27.65 | 24.24 | 2.892 | 0.1 | 29.57 |
| Vietnam | VNM | N | 14.4 | 13.9 | 14.8 | 15.51 | 19.92 | 12.83 | 1.076 | −0.028 | 20.59 |
| Washington | WA | N | 16.9 | 15.7 | 17.5 | 9.38 | 10.35 | 9.35 | 0.555 | 0.012 | 13.15 |
| Zhejiang | ZJ | N | 8.8 | 8.6 | 8.9 | 35.46 | 36.22 | 34.49 | 4.049 | 0.009 | 47.49 |
3. Results
3.1. Practical Explanation of Effectiveness Parameters
Very efficient preventive measures implemented are associated with a short TE and a great and ρ. Table 1 shows the data of countries and states of which the effective phases ended before 16 May 2020. From this table, the average duration of the effective phase TE was 17.3 ± 10.5 d (5.3–49.7; range: 44.4 d). The average effectiveness was 17.0 × 10−3 ± 10.3 × 10−3 d−2 (2.8 × 10−3 – 53.0 × 10−3; range: 50.2 × 10−3 d−2). The average of the ratio ρ was 1.73 × 10−3 ± 1.70 × 10−3 d−3 (0.07 × 10−3 – 8.28 × 10−3; range: 8.21 × 10−3 d−3).
The effectiveness parameters were exemplified by four countries in Figure 2.
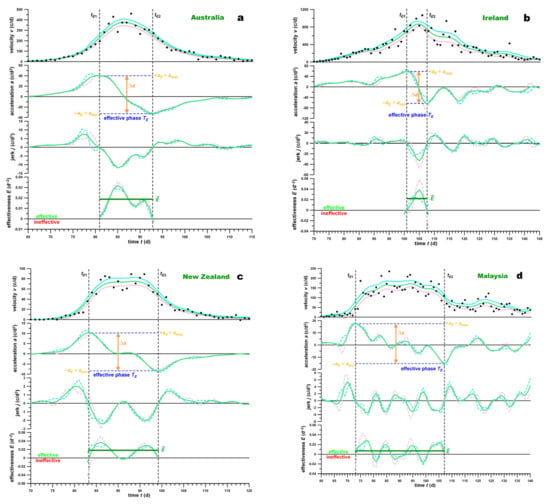
Figure 2.
Velocity, acceleration, jerk and effectiveness of the spreading virus against time (day 1 = 01/01/2020) for 4 different velocity profiles: (a) Gaussian (Australia, logς = +0.01, medium effective, ρ = 1.56 × 10−3); (b) triangular (Ireland, logς = +0.22, very effective, ρ = 3.25 × 10−3); (c) short trapezoidal (New Zealand, logς = −0.10, medium effective, ρ = 1.13 × 10−3); (d) long trapezoidal (Malaysia, logς = −0.22, marginally effective, ρ = 0.20 × 10−3). The green curve represents filtered velocity data and their time derivatives; the light blue and pink curves denote upper and lower confidence intervals (note that after differentiation, the upper and lower boundaries can switch their positions); tE1,2, start and end of the effective phase; a, acceleration.
Australia followed a (slightly asymmetrical) Gaussian velocity profile (logς = +0.01, close to 0) of the medium effectiveness (18.8 × 10−3 d−2, close to the overall country average), a medium duration of the effective phase of 12.0 d (still shorter than the overall country average) and ρ of 1.56 × 10−3 d−3 (close to the overall country average).
Ireland exhibited a triangular velocity profile (logς = +0.22) of the medium-to-high effectiveness (22.0 × 10−3 d−2), a short duration of the effective phase of 6.8 d and a high ρ of 3.25 × 10−3 (twice as high as Australia).
New Zealand was characterised by a short trapezoidal velocity profile (logς = −0.10) of the medium effectiveness (18.0 × 10−3 d−2, the same as Australia, close to the overall country average), a medium duration of 15.9 d (close to the overall country average) and a smaller ρ of 1.13 × 10−3.
Malaysia was affected by a long trapezoidal velocity profile (logς = −0.22) of very low effectiveness (6.8 × 10−3 d−2), a long duration of 34.0 d (twice the overall country average) and a marginally effective ρ of 0.20 × 10−3.
In general, long trapezoidal plateaus were subjected to fluctuations, which rendered the plateau alternating effective and ineffective, yet on average (marginally) effective. In the short trapezoidal plateau of New Zealand (Figure 2c), the plateau was almost flat, which made the effectiveness profile double-humped, with zero effectiveness between the two humps.
3.2. Interrelationship of Effectiveness Parameters
Figure 3 shows the relationship between and TE, with respect to the hypothetical data of a Gaussian function (separating triangular and trapezoidal v-profiles). The point map and its power-law fit function (R2 = 0.8337) deviated from and crossed over the hypothetical Gaussian function data. The data can be divided into three areas: velocity data profiles ranging between Gaussian and triangular with high effectiveness (green area); profiles ranging from triangular over Gaussian to trapezoidal with the medium effectiveness (yellow area); and profiles ranging from Gaussian to trapezoidal with the low effectiveness (pink area). Figure 3 shows that there were no marginally effective triangular velocity profiles and no highly effective trapezoidal profiles. Figure 4 shows , TE, ρ and logς colour-coded on the country map of Europe. Finland had the shortest effective phase (5.3 d), and Romania had the longest effective phase (45.8 d). The least and most effective countries () were Great Britain (3.1 × 10−3) and Montenegro (53.0 × 10−3), respectively (Figure 4).
is directly related to , i.e., the effectiveness calculated from Reff, as shown in Figure 5a. The slope of the regression line is 1.2656 and is not 1.41 according to Equation (22), which is applicable to Gaussian functions only. The intercept of the regression function is very close to 0. In Figure 5b, the regression slope of vs. is plotted against the averages of logς, showing that the slope decreases as logς increases. The intercept of the regression function is 1.4003, which corresponds to the slope predicted at logς = 0 and is close to the predicted multiplier of 1.41 according to Equation (22). Figure 5 proves that and are comparable and complementary measures.
The magnitude of is 94.80% explained from (100R2; Figure 5a) and 22.61% from logς. The multiple regression dependency of on and logς was 96.19%. The dependency of on and logς of 3.81% remained unexplained. The individual influences (semi-partial correlations) of and logς on were 73.58% and 1.39%, respectively, and the combined influence of and logς on was 21.11%. The semi-partial correlations revealed that any influence of logς on happened only in combination with . The reason for this could be explained from the fact that logς was 43.41% influenced by and even 44.66% by of <0.03. More efficient countries tended to have a triangular v-profile, whereas less efficient countries were characterised by a more trapezoidal v-profile.
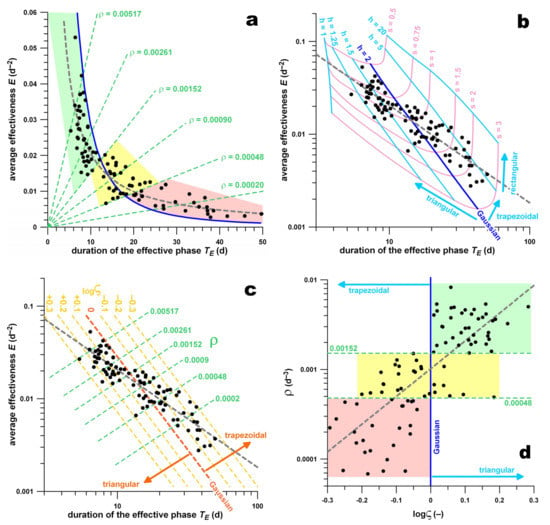
Figure 3.
(a) Average effectiveness () against the duration of the effective phase (TE). The blue curve represents a Gaussian function; the green area indicates the velocity profiles between triangular and Gaussian; the yellow area represents the velocity profile transition from triangular across Gaussian to trapezoidal; the pink area represents the velocity profiles between Gaussian and trapezoidal; the dark-green dashed lines denote isolines of the /TE ratio (ρ); the dashed grey curve represents the power function fit of all data; note that the data located on the blue curve (Gaussian function) are not necessarily Gaussian but can be pseudo-Gaussian, as a transition from triangular to trapezoid velocity profile (as shown in (b)) can be a very short trapezoid plateau (shorter than the one of New Zealand shown in Figure 2b). (b) Average effectiveness ( ) against the duration of the effective phase (TE) on a double-logarithmic graph. The pink lines are isolines of the shape parameter s, associated with the width of the velocity profile (the smaller s, the greater the effectiveness); The light-blue lines are isolines of shape parameter h, associated with the shape of the velocity profile, indicating the transition from a triangular velocity profile over Gaussian and trapezoidal to an extreme and hypothetical rectangular profile. (c) Average effectiveness ( ) against the duration of the effective phase (TE) on a double-logarithmic graph. Parameter ρ is the ratio of to TE, (the greater ρ, the greater the effectiveness); parameter ρ is another parameter associated with the shape of the velocity profile, which indicates the transition from a triangular velocity profile over Gaussian to a trapezoidal profile. (d) ρ against logς on a single-logarithmic graph. The green, yellow and pink areas correspond to the areas of the same colours shown in (a).
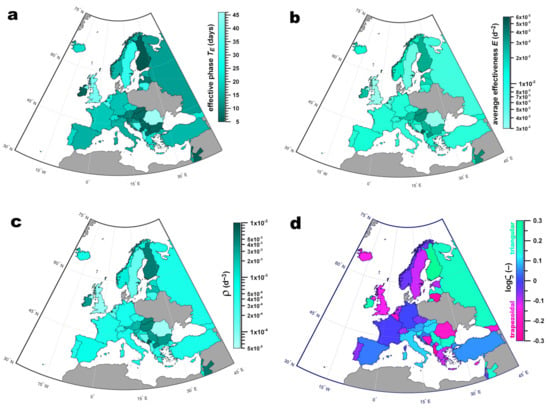
Figure 4.
Maps of Europe, showing the effectiveness of control measures of each country, for countries whose effective phase TE ended the latest on 15 May 2020; upper row: (a): duration of effective phase TE; (b) average effectiveness ; (c) ρ ( /TE ratio); (d) logς (shape parameter: blue: Gaussian velocity profile, green: triangular velocity profile, red: trapezoidal velocity profile); for subfigures (a–c): the darker the more effective.
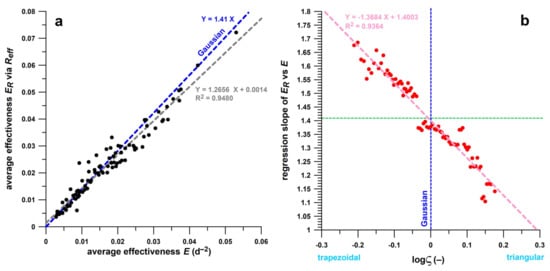
Figure 5.
Average effectiveness calculated from the effective reproductive number Reff against the average effectiveness (a) and the slope of the regression of vs. (b). In (a), the dashed grey line represents the linear fit function of the regression, whereas the dashed blue line represents the function expected from a Gaussian model; in (b), to assess the dependency of the regression slope on the shape parameter logς, the data of , and logς were sorted with respect to logς; and the averages of logς and the regression slope of vs. were calculated across a running window of 15 data; the dashed green line indicates the slope value expected from a Gaussian model; the dashed blue line represents Gaussian model data at logς = 0.
3.3. Timeline Graphs of the Effectiveness
Figure 6 shows the timeline of the effectiveness. The first cluster was China and its provinces, followed by South Korea about a month later. Eight days after Korea left the effective phase, Malaysia started with her effective phase, followed by Uruguay, Iceland, Italy, Thailand and Switzerland. The first countries that left the effective phase were as following: Lebanon; followed by Jordan, Massachusetts and Taiwan on the same day; followed by Andorra. The five most effective countries and states with the greatest were Montenegro, Idaho, South Korea, Malta and Mauritius.
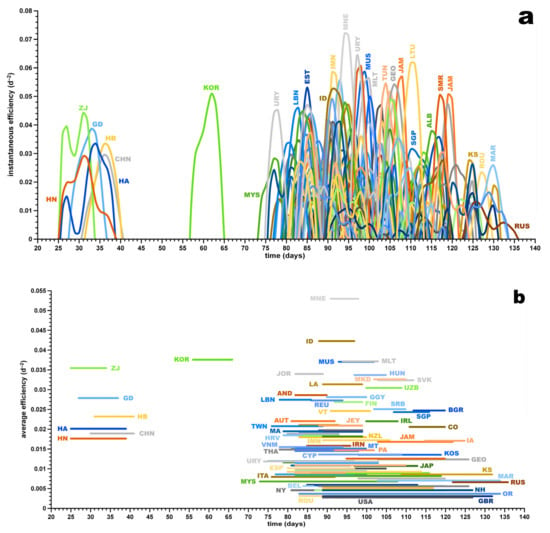
Figure 6.
Instantaneous effectiveness E (a) and average effectiveness (b) against time in days (day 1 = 01/01/2020) for countries, states and provinces of which the effective phase ended the latest on 15 May 2020 (day 136). Three-letter country codes according to ISO 3166-1 Alpha-3; Chinese provinces 2-letter codes: ISO 3166-2:CN; 2-letter code of the states of the USA: ISO 3166-2:US; KOS, Kosovo; note that countries can exhibit multiple effectiveness peaks, as seen in (a) for Uruguay and some Chinese provinces and in Figure 2.
3.4. Comparison of the Effectiveness of Control Measures
In 37 countries, lockdown measures were implemented as defined in the Methods section. Fifty-two countries were classified as no-lockdown. Although the medians followed the expected trend, i.e., lockdown measures seemed slightly more effective with a shorter effective phase, the medians were statistically identical (p > 0.76; Table 2). The effect sizes were “very small” for all three parameters. The box–whisker plots of the three effectiveness parameters are shown in Figure 7a–c. These results showed clearly that drastic lockdown measures were not more efficient than less severe control measures. Our hypothesis could therefore not be confirmed.

Table 2.
Medians and significance testing (Mann–Whitney U-test (MWU-test)) of the effectiveness parameters, comparing countries/states/provinces with a lockdown to without a lockdown listed in Table 1. Effect size r interpretation was according to McGrath and Meyer [51]. IQR, interquartile range; TE, duration of effective phase; , effectiveness; ρ = /TE.
Table 2.
Medians and significance testing (Mann–Whitney U-test (MWU-test)) of the effectiveness parameters, comparing countries/states/provinces with a lockdown to without a lockdown listed in Table 1. Effect size r interpretation was according to McGrath and Meyer [51]. IQR, interquartile range; TE, duration of effective phase; , effectiveness; ρ = /TE.
| Statistical Parameters | TE (d) | ρ (d−3 10−3) | |
|---|---|---|---|
| Median (IQR) no lockdown (n = 52) | 15.32 (12.61) | 14.9 (15.4) | 0.99 (2.47) |
| Median (IQR) lockdown (n = 37) | 15.16 (15.39) | 17.2 (13.1) | 1.13 (2.13) |
| MWU p-value (α = 0.05) | 0.8415 | 0.7642 | 0.7642 |
| U | 986 | 999 | 998 |
| Effect size r | 0.0249 | 0.0385 | 0.0374 |
| r interpretation | very small (r < 0.1) | very small (r < 0.1) | very small (r < 0.1) |
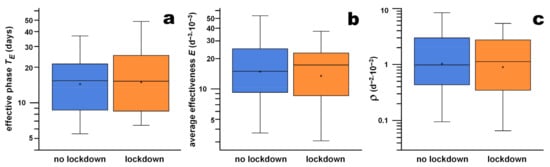
Figure 7.
Comparison of countries with and without lockdown measures for TE (a), (b) and ρ (c) by means of box–whisker plots.
3.5. Mortality Rate
Comparing the mortality of lockdown and no lockdown countries at the beginning, middle and end of the effective phase did not reveal any significant difference (Table 3). The only significant difference was found when comparing the mortality data of 26/06/2020 with a medium effect size and a higher mortality for countries with lockdowns (Table 3). To investigate this result further, we divided the mortality data in the middle of the effective phase in two groups (greater than 50 deaths per one million population, n = 67, median = 614.5, interquartile range (IQR) = 525.2; and smaller than 50 deaths per one million population, n = 19, median = 32.3, IQR = 78.3). The associated mortality data of 26/06/2020 were significantly different between and directly correlated with these two groups (MWU-test, p < 0.0001, U = 25, r = 0.9607, large effect size). This result indicated that the lockdown countries in the higher mortality group (as of middle of effective phase) were not able to flatten the mortality curve better than the non-lockdown countries despite lockdown measures. The significantly higher mortality rate of lockdown countries as of 26/06/2020 was explained simply from the fact that more countries with lockdowns had a higher mortality since the effective phase than countries without lockdowns.

Table 3.
Mortality (no. of deaths per million population), medians and significance testing (MWU-test) comparing countries/states/provinces with lockdowns to those without lockdowns; and with mortality in the middle of the effective phase of greater and smaller 50 deaths per million population; the interpretation of the effect size r was according to McGrath and Meyer [51]).
3.6. Influences of the Population Size, the Land Area, the Population Density and the GDP on TE, and ρ
Significant influences were calculated from the R2 value and indicated as a percentage (R2% = R2×100×sgn(R), where sgn denotes the sign function).
None of the four country parameters had a significant influence on the duration of the effective phase TE.
None of the three effectiveness parameters was significantly (p ≈ 0.5) influenced by the population density. This result, although surprising, is reasonably explained from the significant influences of the population size and the land area, both of which had the same negative trend and influence on the effectiveness and ρ.
The greater the population, the smaller the effectiveness and ρ. This effect on and ρ can be explained from the population size in –7.38% (p = 0.0088) and –4.44% (p = 0.0438), respectively. The threshold for a significant difference of and ρ was found at a population size of 10 million. The medians of below and above 10 million inhabitants were 18.1 × 10−3 d−2 and 9.7 × 10−3 d−2, respectively, and significantly different (p = 0.0041; U = 649; r = 0.356; medium effect size). The medians of ρ below and above 10 million inhabitants were 1.59 × 10−3 d−3 and 0.53 × 10−3 d−3, respectively, and significantly different (p = 0.0076; U = 674; r = 0.331; medium effect size).
The larger the land area, the smaller the effectiveness and ρ. This effect on and ρ can be explained from the land area in −8.87% (p = 0.0039) and −5.94% (p = 0.0192), respectively. The threshold for a significant difference of and ρ was found at a land area of 115,000 km2. The medians of below and above 115,000 km2 were 18.5 × 10−3 d−2 and 11.9 × 10−3 d−2, respectively, and significantly different (p = 0.0093; U = 721; r = 0.316; medium effect size). The medians of ρ below and above 115,000 km2 were 1.85 × 10−3 d−3 and 0.68 × 10−3 d−3, respectively, and significantly different (p = 0.0293; U = 774; r = 0.265; medium effect size).
The smaller the population size and the land area, the more effective the control measures. This result is supported by comparing TE, and ρ of eight small islands (Singapore, Hong Kong, Mauritius, Reunion, Guernsey, Jersey, Isle of Man and Malta) to the data of the remaining 84 countries and states. TE, and ρ of both cohorts were significantly different as following: TE: 8.5 d (islands) vs. 15.7 d (rest), p = 0.0203, U = 168, r = 0.500 (large effect size); : 25.8∙× 10−3 d−2 (islands) vs. 14.3∙× 10−3 d−2 (rest), p = 0.0028, U = 120, r = 0.643 (large effect size); ρ: 3.97 × 10−3 d−3 (islands) vs. 0.91 × 10−3 d−3 (rest), p = 0.0054, U = 135, r = 0.598 (large effect size). Islands had the advantage of natural boundaries which further improved the controllability.
The greater the country GDP, the smaller the effectiveness and ρ. This effect on and ρ can be explained from the country GDP in −15.11% (p = 0.0003) and −7.94% (p = 0.0103), respectively. The threshold for a significant difference of and ρ was found at a country GDP of 600,000 USD million. The medians of below and above 600,000 USD million (country GDP) were 15.5 × 10−3 d−2 and 8.3 × 10−3 d−2, respectively, and significantly different (p = 0.0006; U = 287; r = 0.520; large effect size). The medians of ρ below and above 600,000 USD million (country GDP) were 1.08 × 10−3 d−3 and 0.50 × 10−3 d−3, respectively, and significantly different (p = 0.0048; U = 341; r = 0.430; large effect size).
The per-capita GDP had no significant influence on the three effectiveness parameters. This result mirrored the missing effect of the population density, because the ratio of variables with the same trend led to near-constant data with an R2 of close to zero and p-values greater than 0.1. Nevertheless, this result questions the significant influence of the country GDP on the effectiveness. Correlating the country GDP and the population size of the countries and states listed in Table 1 with a power-law regression results in a positive trend with an R2 value of 0.7076. It is therefore possible that the influence of the county GDP was only an indirect one and the direct influence comes from the population size, as already explained above. To obtain clarity on this despite the missing influence from the per-capita GDP (country GDP normalised to the population size), we investigated the individual and combined influences of both the country GDP and the population size on the effectiveness . The individual influences (semi-partial correlations) of the population size and the country GDP on were 0.6% and 7.6%, respectively, and their combined influence on was 7.6%. These data explained that the population influence occurred only combined with GDP, whereas the GDP influence had two components, individual and combined, both of which were at 7.6%. Although the total influence on was only 15.7%, the country GDP was the dominating and primary factor, whereas the population size had only an indirect influence.
Our hypotheses that countries with a greater population, a larger area and a higher country GDP are more difficult to control and the interventions are less efficient were confirmed. However, the hypothesis that countries with a greater population density are more difficult to control was not confirmed, as the population density did not influence .
4. Discussion
The objective of our study was to develop a method for measuring the effectiveness of control measures on decreasing the transmission of the SARS-Cov-2.
The most striking result of our study was that no significant difference in terms of the effectiveness of control measures could be found between countries (and states / provinces) with and without lockdown measures. This result has serious implications for the management of control measures.
First, our study provides the necessary support for Anders Tegnell’s comment that a “lockdown” has no “historical scientific basis” (for being efficient), even if our data are from the present.
Second, the “fine balance” [5] (between saving lives and saving the economy) is not immediately valid anymore, as the allegedly efficient lockdown is supposed to save lives, but also—as a side effect—brings the economy down. Countries with lockdowns are as efficient as countries without lockdowns on average (based on the comparisons of the medians). There was also no evidence that lockdown measures manage the mortality (deaths per population) better than measures without lockdowns. Our hypothesis could therefore not be confirmed. Control measures do indeed reduce the acceleration, i.e., the first time derivative of the daily case data, but there is no causal relationship between the severity of control measures and their effectiveness.
The statements “the case for shutdown clear” and “the shutdown wins” [7] are therefore no longer valid either, as the losses from COVID-19 casualties per population depend on the mortality during the effective phase rather than on lockdown measures themselves, and the burden of the economic downturn after lockdown still affects these countries. It must be emphasised, however, that these conclusions are valid across a range of countries in terms of average or median data, whereas individual countries will respond differently to lockdown or no lockdown, in terms of effectiveness.
If lockdown measures are not more effective than measures without lockdowns, what are the drivers of effectiveness in the absence of lockdown measures, which help keep the economy alive?
According to MacIntyre [55], “In the absence of a vaccine, control of COVID-19 relies on four main strategies.” These strategies are as following: (1) identification of new cases and isolating them; (2) contacts tracking and quarantining; (3) personal protection; and (4) travel restrictions. Strategy (3) refers to “social distancing, ranging from spatial separation of 1–2 m to banning of mass gatherings and imposing lockdowns” [55]. Some typical lockdown measures are part of strategy (3) only, as one extreme of a wide range of measures (i.e., all strategies). The minimum requirement of strategy (3) was addressed by Chu et al. [56], who found in a meta-analysis review of physical distancing face masks and eye-protection that “no intervention, even when properly used, was associated with complete protection from infection”. These findings [56] seem to support many countries’ decisions for advising or compulsorily requiring wearing face masks in public such as Canada, South Korea, the Czech Republic and Austria.
According to Haug et al. [14], the most significantly effective interventions with an effectiveness score greater than 50% (0% and 100% account for least and most effective, respectively) are as following: small gathering cancellation (83%); closure of educational institutions (73%); border restriction (56%); mass gathering cancellation (53%); increased availability of PPE (such as masks; 51%). All these five interventions can be implemented without the typical lockdown measures. Shopping, for example, can be maintained by restricting the number of customers on the shop floor and by wearing masks under a compulsory outdoor and indoor mask order. Food business can be kept alive by implementing online order and click-and-collect policies, instead of closing the industry entirely.
These five interventions are probably the main reason for the missing significant difference between lockdown and no-lockdown, as they are applicable to both categories, independent of the degree of enforcement. That the mere availability of PPE constitutes an efficient measure [14], in the absence of any enforced mask order, is a striking example.
Why do countries respond differently to strategies and measures for controlling COVID-19? Why do some countries suffer from long plateaus of daily case data despite control measures and even lockdown measures?
The effectiveness of physical distancing and wearing PPE depends on the compliance of the citizens. Being compliant with control measures, however, is not just an expression of personal protection, but even more so “shifts the focus … to altruism, actively involves every citizen, and is a symbol of social solidarity in the global response to the pandemic” [57]. Compliance is mainly driven by the “duty to obey authorities and personal morality” rather than by “perceived risk of legal sanctions and perceived risk of the virus” [58]. A lockdown is nothing but enforces compliance, specifically by rules, law, police and fines, which in turn risks “increasing non-compliance (or so-called lockdown fatigue)” [59]. A study [58] that investigated the compliance of Australian citizens during the (first) lockdown revealed that the participants’ non-compliance was approximately 50% for each of the following reasons: “socialised in person with friends/relatives” they did not live with and “left the house without a really good reason”. This striking behaviour of non-compliance with strict lockdown rules and measures resulted in a medium effectiveness of control measures, close to the averages of the data shown in Table 1.
Another important driver of compliance, often overlooked and underestimated, is “that persuasion and education encourage normative compliance with rules and laws, because they promote a sense that people should comply with laws because it is the right thing to do” [60]. Proper education is facilitated by leadership by example, exhibited by leading politicians and scientists on the mass media and in public [61], e.g., by wearing masks, demonstrating good physical distancing practice, information session led by epidemiologists, etc. Leaders should refrain from conveying anecdotic evidence, such as which medication or personal measures could protect from attracting COVID-19. According to Haug et al. [14], educating and actively communicating with the public has an effectiveness score of 48%.
A further unexpected, if not counterintuitive, driver of the compliance seems to be the country GDP with a 15% influence on the effectiveness . Does this mean that the control measures of “richer” countries are less effective? And if so, why? There is statistical evidence that better education has a positive influence on the GDP [62]. However, we are dealing with the country GDP here, which is influenced by the population size. When investigating the individual and combined influences of the world data of the education index [63] and the population size [52] on the country GDP [54], then there is no combined influence on the GDP (which is expected as they are not supposed to influence each other: education index vs. population size, power law regression, R2 = 0.0109, p = 0.1654). The individual influence of the population size on the GDP is approximately three times greater than the one of the educational index (power law regression: R2 = 0.6066 and 0.1892, respectively; p < 0.0001). This result supports that countries with a higher GDP are more educated on average. We therefore hypothesised that a better education leads to less acceptance of and compliance with government rules related to control measures. This hypothesis is supported by the results of Hall et al. [64], who found the correlations between education and protest attitudes and concluded that “education increases opposition to government repression”. Lockdowns are evidently not related to political repression; nevertheless, political repressions and medical control measures during epidemics/pandemics have one thing in common: controlling citizens. However, the result that control measures of “richer” countries are less effective and stands in sharp contrast to the conclusions of Pincombe et al. [25], namely that “containment and closure policies were more effective in high-income countries” (the GNI / gross national income [65] is related to the GDP [54] at R2 = 0.99). Pincombe et al. [25], however, defined their effectiveness measure in a different way we did, namely from “larger decreases in mobility” and ”smaller COVID-19 case and death growth rates”.
Finally, the “fine balance” [5] between saving lives and saving the economy as an alternative and opposed strategy is affected by a component, with all too often forgotten: saving the economy does save lives—not immediately during a pandemic, but in the short-to-medium run. There is well-documented statistical evidence that economic recessions result in substantial rise in the following: (1) “economic suicides” [66,67], mainly because of job losses, debts and foreclosures; (2) myocardial infarction [68]; and (3) stroke [69].
It has been postulated that traffic data can provide insight into the effectiveness of control measures, e.g., “traffic data can show the effects that lockdown measures have had across the world”; “Can traffic be a measure of the degree to which a confinement strategy has been implemented”; and “If the answer is yes, traffic data could close the loop for policy makers, allowing them to track the effects of policy decisions and adjust if necessary” [70]. The effect of control measures on mobility levels is only one effect of control measures. For example, traffic data do not reflect the degree to which other control measures are observed, such as distancing and wearing masks. Furthermore, traffic data do not necessarily reflect the severity of control measures, as mobility levels depend very much on compliance as other measures do (e.g., distancing). Policymakers, such as governments issuing lockdown policies, measure their success from daily incidence data, as we saw and heard on the mass media during the last months, as traffic data did not tell us how many infected people were recorded within one day. However, disconnected from the daily case data, mobility levels provide the qualitative information of relaxed and voluntary control measures, as seen in Stockholm’s mobility data [71]: although Sweden followed a relaxed approach, relying largely on voluntary measures [6], traffic levels decreased in Stockholm in March and April 2020.
A favourable approach to both controlling a virus outbreak and saving the economy of a country would involve the following: (1) an early start with control measures, even before case zero; (2) improvement of compliance by the thorough education, information and explanation of the restrictions and appealing to the solidarity and morality of the people; (3) and adopting economy-friendly but outbreak-preventive control measures in the absence of lockdown rules.
It will take time and further research to align the hitherto contrary priorities—saving lives and preserving the economy—and provide a comprehensive and holistic strategy based on lessons learnt from the COVID-19 crisis. Considering that we have to deal with such a pandemic for the first time after 100 years, the inexperience of fighting this battle contributes decisively to the varying effectiveness of control measures.
5. Conclusions
In this study, we provided three new epidemiological parameters, related to the effectiveness of controlling a highly contagious disease, as well as a method for calculating these parameters. These data were determined for 92 different countries, states and provinces. Comparing the effectiveness data of countries with and without lockdowns revealed that there was no statistically significant difference in the effectiveness between lockdown and “relaxed” measures. Furthermore, there was also no statistically significant difference in the mortality during the effective phase between lockdown and “relaxed” measures. These results did not provide any evidence that, on average, lockdown measures are more efficient and that the number of casualties per population is less.
The implications of this study are that there is neither guarantee for lockdown measures being successful nor certainty that relaxed measures lead to failure. The advantage of relaxed control measures is that they are economy-friendly and prevent associated effects on mental health such as “lockdown fatigue” and increased mortality from suicides, myocardial infarction and stroke. Instead of (late) lockdown measures, any control measure should start very early, accompanied by improving the compliance of citizens through thorough education in epidemiologically necessary changes (i.e., behavioural and others) and appealing to the solidarity and morality of people.
Author Contributions
All authors contributed equally to the conceptualization, methodology, validation, investigation, formal analysis, resources, writing—original draft preparation, writing—review and editing, visualization and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from any qualified researcher to the corresponding author.
Acknowledgments
The authors would like to thank the two anonymous reviewers for their valuable and detailed comments and suggestions that helped us improve the quality of our paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- COVID-19 Pandemic by Country and Territory. Available online: https://en.wikipedia.org/wiki/COVID-19_pandemic_by_country_and_territory (accessed on 1 June 2020).
- Our World in Data. Available online: https://ourworldindata.org/grapher/total-cases-covid-19 (accessed on 1 June 2020).
- The COVID Tracking Project. Available online: https://covidtracking.com/data/download (accessed on 1 June 2020).
- Worldometer. Available online: https://www.worldometers.info/coronavirus/#countries (accessed on 1 June 2020).
- WHO. WHO Director-General’s Opening Remarks at the Media Briefing on COVID-19. 11 March 2020. World Health Organisation, Geneva, Switzerland. Available online: https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19-11-march-2020 (accessed on 1 July 2020).
- Paterlini, M. Q&A: Sweden’s coronavirus strategist. Nature 2002, 580, 574. [Google Scholar]
- Holden, R.; Preston, B. The Costs of the Shutdown Are Overestimated—They’re Outweighed by Its $1 Trillion Benefit. Conversation. 2020. Available online: https://theconversation.com/the-costs-of-the-shutdown-are-overestimated-theyre-outweighed-by-its-1-trillion-benefit-138303 (accessed on 26 May 2020).
- Fang, Y.; Nie, Y.; Penny, M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions: A data-driven analysis. J. Med. Virol. 2020, 92, 645–659. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Zhao, S.; Li, H.; Song, Y.; Wang, L.; Wang, M.H.; Peng, Z.; Li, H.; He, D. Real-time estimation of the reproduction number of the novel coronavirus disease (COVID-19) in China in 2020 based on incidence data. Ann. Transl. Med. 2020, 8, 689. [Google Scholar] [CrossRef] [PubMed]
- Kucharski, A.J.; Klepac, P.; Conlan, A.J.K.; Kissler, S.M.; Tang, M.L.; Fry, H.; Gog, J.R.; Edmunds, W.J. Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 1151–1160. [Google Scholar] [CrossRef]
- Tang, B.; Xia, F.; Tang, S.; Bragazzi, N.L.; Li, Q.; Sun, X.; Liang, L.; Xiao, Y.; Wu, J. The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemics in the final phase of the current outbreak in China. Int. J. Infect. Dis. 2020, 95, 288–293. [Google Scholar] [CrossRef]
- Liu, S.; Ermolieva, T.; Cao, G.; Chen, G.; Zheng, X. Analyzing the effectiveness of COVID-19 lockdown policies using the time-dependent reproduction number and the regression discontinuity framework: Comparison between countries. Eng. Proc. 2021, 5, 8. [Google Scholar] [CrossRef]
- Amer, F.; Hammoud, S.; Farran, B.; Boncz, I.; Endrei, D. Assessment of Countries’ Preparedness and Lockdown Effectiveness in Confronting COVID-19. Disaster Med. Pub. Health Prep. 2020, 15, e15–e22. [Google Scholar] [CrossRef]
- Haug, N.; Geyrhofer, L.; Londei, A.; Dervic, E.; Desvars-Larrive, A.; Loreto, V.; Pinior, B.; Thurner, S.; Klimek, P. Ranking the effectiveness of worldwide COVID-19 government interventions. Nat. Hum. Behav. 2020, 4, 1303–1312. [Google Scholar] [CrossRef] [PubMed]
- Leung, K.; Wu, J.T.; Liu, D.; Leung, G.M. First-wave COVID-19 transmissibility and severity in China outside Hubei after control measures, and second-wave scenario planning: A modelling impact assessment. Lancet 2020, 395, 1382–1393. [Google Scholar] [CrossRef]
- Jagodnik, K.M.; Ray, F.; Giorgi, F.M.; Lachmann, A. Correcting under-reported COVID-19 case numbers: Estimating the true scale of the pandemic. medRXiv 2020, 2020, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Maciejewski, M. Fixing Covid-19 Case Number and Death Toll Underreporting. 2020. Available online: https://towardsdatascience.com/fixing-covid-19-case-number-and-death-toll-underreporting-bd9422c88cc4 (accessed on 15 November 2021).
- Ganyani, T.; Kremer, C.; Chen, D.; Torneri, A.; Faes, C.; Wallinga, J.; Hens, N. Estimating the generation interval for coronavirus disease (COVID-19) based on symptom onset data. Eurosurveillance 2020, 25, 2000257. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Yeging, T.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Lipsitch, M.; Cohen, T.; Cooper, B.; Robins, J.M.; Ma, S.; James, L.; Gopalakrishna, G.; Chew, S.K.; Tan, C.C.; Samore, M.H.; et al. Transmission dynamics and control of severe acute respiratory syndrome. Science 2003, 300, 1966–1970. [Google Scholar] [CrossRef] [Green Version]
- Cori, A.; Ferguson, N.M.; Fraser, C.; Cauchemez, S. A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Breban, R.; Vardavas, R.; Blower, S. Theory versus Data: How to Calculate R0? PLoS ONE 2007, 2, e282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alfano, V.; Ercolano, S. The Efficacy of Lockdown Against COVID-19: A Cross-Country Panel Analysis. Appl. Health Econ. Health Policy 2020, 18, 509–517. [Google Scholar] [CrossRef]
- Pincombe, M.; Reese, V.; Dolan, C.B. The effectiveness of national-level containment and closure policies across income levels during the COVID-19 pandemic: An analysis of 113 countries. Health Policy Plan. 2021, 3, 1152–1162. [Google Scholar] [CrossRef]
- Chen, S.X.; Lam, B.C.P.; Liu, J.H.; Choi, H.-S.; Kashima, E.; Bernardo, A.B.I. Effects of containment and closure policies on controlling the COVID-19 pandemic in East Asia. Asian J. Soc. Psych. 2021, 24, 42–47. [Google Scholar] [CrossRef]
- Hale, T.; Angrist, N.; Cameron-Blake, E.; Hallas, L.; Kira, B.; Majumdar, S.; Petherick, A.; Phillips, T.; Tatlow, H.; Webster, S. Oxford COVID-19 Government Response Tracker; Blavatnik School of Government, University of Oxford: Oxford, UK, 2020. [Google Scholar]
- Leech, G.; Rogers-Smith, C.; Sandrick, J.B.; Snodin, B.; Zinkov, R.; Rader, B.; Brownstein, J.S.; Gal, Y.; Bhatt, S.; Sharma, M.; et al. Mass mask-wearing notably reduces COVID-19 transmission. medRXiv 2021, 2021, 1–37. [Google Scholar] [CrossRef]
- Moosa, I.A. The effectiveness of social distancing in containing Covid-19. Appl. Econ. 2020, 52, 6292–6305. [Google Scholar] [CrossRef]
- Prakash, N.; Srivastava, B.; Singh, S.; Sharma, S.; Jain, S. Effectiveness of social distancing interventions in containing COVID-19 incidence: International evidence using Kalman filter. Econ. Hum. Biol. 2022, 44, 101091. [Google Scholar] [CrossRef] [PubMed]
- Matrajt, L.; Leung, T. Evaluating the effectiveness of social distancing interventions to delay or flatten the epidemic curve of coronavirus disease. Emerg. Infect. Dis. 2020, 26, 1740–1748. [Google Scholar] [CrossRef]
- Nande, A.; Adlam, B.; Sheen, J.; Levy, M.Z.; Hill, A.L. Dynamics of COVID-19 under social distancing measures are driven by transmission network structure. PLoS Comput. Biol. 2021, 17, e1008684. [Google Scholar] [CrossRef] [PubMed]
- Talic, S.; Shah, S.; Wild, H. Effectiveness of public health measures in reducing the incidence of covid-19, SARS-CoV-2 transmission, and covid-19 mortality: Systematic review and meta-analysis. BMJ 2021, 375, e068302. [Google Scholar] [CrossRef]
- Bunge, M. A general black-box theory. Philos. Sci. 1963, 30, 346–358. [Google Scholar] [CrossRef]
- Last, J.M. A Dictionary of Public Health; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Weed, D.L. Beyond black box epidemiology. Am. J. Public Health 1998, 88, 12–14. [Google Scholar] [CrossRef]
- Greenland, S.; Gago-Dominguez, M.; Castelao, J.E. The value of risk-factor (“black-box”) epidemiology. Epidemiology 2004, 15, 529–535. [Google Scholar] [CrossRef]
- Savitz, D.A. In defense of black box epidemiology. Epidemiology 1994, 5, 550–552. [Google Scholar]
- Viboud, C.; Simonsen, L.; Chowell, G. A generalized-growth model to characterize the early ascending phase of infectious disease outbreaks. Epidemics 2016, 15, 27–37. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Revicki, D.A.; Frank, L. Pharmacoeconomic evaluation in the real world. Effectiveness versus efficacy studies. Pharmacoeconomics 1999, 15, 423–434. [Google Scholar] [CrossRef]
- Singal, A.G.; Higgins, P.D.R.; Waljee, A.K. A Primer on Effectiveness and Efficacy Trials. Clin. Translat. Gastroenterol. 2014, 5, e45. [Google Scholar] [CrossRef]
- Thom, R. Mathematical Models of Morphogenesis; Ellis Horwood: Chichester, UK, 1983. [Google Scholar]
- Fuss, F.K.; Weizman, Y.; Tan, A.M. The non-linear relationship between randomness and scaling properties such as fractal dimensions and Hurst exponent in distributed signals. Comm. Nonlin. Sci. Num. Simul. 2021, 96, 105683. [Google Scholar] [CrossRef]
- Lockdown. Available online: https://en.wikipedia.org/wiki/Lockdown (accessed on 2 June 2020).
- COVID-19 Pandemic Lockdowns. Available online: https://en.wikipedia.org/wiki/COVID-19_pandemic_lockdowns (accessed on 2 June 2020).
- COVID-19 Pandemic Curfews. Available online: https://en.wikipedia.org/wiki/Template:COVID-19_pandemic_curfews (accessed on 3 June 2020).
- ACAPS. Available online: Acaps.org/covid19-government-measures-dataset (accessed on 3 June 2020).
- Covid-19 Intervention Measures. Available online: https://github.com/amel-github/covid19-interventionmeasures (accessed on 3 June 2020).
- State of Florida, Office of the Governor, Executive Order Number 20/91, April 1, 2020. Available online: https://web.archive.org/web/20200402024354/https://s33330.pcdn.co/wp-content/uploads/2020/04/EO-20-91.pdf (accessed on 15 November 2021).
- Desvars-Larrive, A.; Dervis, E.; Haug, N.; Niederkrotenthaler, T.; Chen, J.; Di Natale, A.; Gliga, D.S.; Roux, A.; Sorger, J.; Chakraborty, A.; et al. A structured open dataset of government interventions in response to COVID-19. Sci. Data 2020, 7, 1–9. [Google Scholar] [CrossRef]
- McGrath, R.E.; Meyer, G.J. When effect sizes disagree: The case of r and d. Psychol. Meth. 2006, 11, 386–401. [Google Scholar] [CrossRef] [Green Version]
- List of Countries and Dependencies by Population. Available online: https://en.wikipedia.org/wiki/List_of_countries_and_dependencies_by_population (accessed on 15 November 2021).
- List of Countries and Dependencies by Area. Available online: https://en.wikipedia.org/wiki/List_of_countries_and_dependencies_by_area (accessed on 15 November 2021).
- Comparison Between U.S. States and Sovereign States by GDP. Available online: https://en.wikipedia.org/wiki/Comparison_between_U.S._states_and_sovereign_states_by_GDP (accessed on 15 November 2021).
- MacIntyre, C.R. Case Isolation, Contact Tracing, and Physical Distancing are Pillars of COVID-19 Pandemic Control, not Optional Choices. Lancet Infect. Dis. 2020, 20, 1105–1106. Available online: https://www.thelancet.com/action/showPdf?pii=S1473-3099%2820%2930512-0 (accessed on 15 November 2021). [CrossRef]
- Chu, D.K.; Akl, E.A.; Duda, S.; Solo, K.; Yaacoub, S.; Schünemann, H.J. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet 2020, 395, 1973–1987. [Google Scholar] [CrossRef]
- Cheng, K.K.; Lam, T.H.; Leung, C.C. Wearing face masks in the community during the COVID-19 pandemic: Altruism and solidarity. Lancet 2020. Available online: https://www.thelancet.com/action/showPdf?pii=S0140-6736%2820%2930918-1 (accessed on 15 November 2021).
- Murphy, K.; Williamson, H.; Sargeant, E.; McCarthy, M. Why people comply with COVID-19 social distancing restrictions: Self-interest or duty? Aust. N. Z. J. Criminol. 2020, 53, 477–496. [Google Scholar] [CrossRef]
- Drake, T.M.; Docherty, A.B.; Weiser, T.G.; Yule, S.; Sheikh, A.; Harrison, E.M. The effects of physical distancing on population mobility during the COVID-19 pandemic in the UK. Lancet 2020. Available online: https://www.thelancet.com/action/showPdf?pii=S2589-7500%2820%2930134-5 (accessed on 15 November 2021).
- Murphy, K. Enforcing tax compliance: To punish or persuade? Econ. Anal. Policy 2008, 38, 113–135. [Google Scholar] [CrossRef] [Green Version]
- The Guardian. Leading by Example: World Leaders Wearing Face Masks—In Pictures. 2020. Available online: https://www.theguardian.com/world/gallery/2020/may/28/world-leaders-wearing-face-masks-in-pictures-coronavirus (accessed on 15 November 2021).
- OECD (Organisation for Economic Co-operation and Development). How Does Education Affect the Economy? In Education at a Glance 2012: Highlights; OECD Publishing: Paris, France, 2012; Available online: https://www.oecd-ilibrary.org/docserver/eag_highlights-2012-15-en.pdf?expires=1612740761&id=id&accname=guest&checksum=B2D7E60CC4F69EA6A7DF26ACB7618750 (accessed on 15 November 2021). [CrossRef]
- Education Index. Available online: https://en.wikipedia.org/wiki/Education_Index (accessed on 15 November 2021).
- Hall, R.L.; Rodeghier, M.; Useem, B. Effects of Education on Attitude to Protest. Am. Soc. Rev. 1986, 51, 564–573. [Google Scholar] [CrossRef]
- GNI. Atlas Method. Available online: https://data.worldbank.org/indicator/NY.GNP.ATLS.CD (accessed on 15 November 2021).
- Reeves, A.; McKee, M.; Stuckler, D. Economic suicides in the Great Recession in Europe and North America. Br. J. Psychiatry 2014, 205, 246–247. [Google Scholar] [CrossRef] [Green Version]
- Oyesanya, M.; Lopez-Morinigo, J.; Dutta, R. Systematic review of suicide in economic recession. World J. Psychiatry 2015, 5, 243–254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torbica, A.; Maggioni, A.P.; Ghislandi, S. The economic crisis and acute myocardial infarction: New evidence using hospital-level data. PLoS ONE 2015, 10, e0142810. [Google Scholar] [CrossRef]
- Falconi, A.; Gemmill, A.; Karasek, D.; Goodman, J.; Anderson, B.; Lee, M.; Bellows, B.; Catalano, R. Stroke-Attributable Death Among Older Persons During the Great Recession. Econ. Hum. Biol. 2016, 21, 56–63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mescheder, D. Can Traffic Data Help Us Find a Way Out of the Lockdown? Available online: https://www.tomtom.com/blog/moving-world/covid-19-traffic-mobility/ (accessed on 15 November 2021).
- Clarke, S. The Traffic Data That Shows the Road Into—And out of—Covid-19 lockdown. Available online: https://www.theguardian.com/world/ng-interactive/2020/apr/27/the-traffic-data-that-shows-the-road-into-and-out-of-covid-19-lockdown (accessed on 15 November 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).