Abstract
Strategic fleet renewal represents a fundamental challenge for small and medium-sized enterprises (SMEs) and public entities seeking to align their operational objectives with sustainable mobility practices. This paper proposes a hybrid decision support model based on fuzzy logic, combining the Fuzzy Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method with the Fleet Renewal Priority Index (FRPI). The model evaluates and prioritizes different vehicle alternatives based on multiple economic, environmental, and operational criteria, including total cost of operation, CO2 emissions, maintenance, autonomy, infrastructure compatibility, and energy independence. The criteria are evaluated by linguistic judgments converted into triangular fuzzy numbers (TFN), allowing uncertainty and subjectivity to be addressed. A simulated case study illustrates the application of the model, identifying the vehicles most aligned with a sustainability and efficiency strategy, as well as those that present a greater urgency for replacement. The results demonstrate the potential of the approach to support rational, transparent and sustainable decisions in fleet modernization.
1. Introduction
Sustainable mobility is a crucial component in the transition to clean energy globally. It impacts public policy, logistics, and business strategy. The transport industry accounts for approximately 14% of greenhouse emissions globally through road transport [1,2]. As a result, replacing fleet cars is necessary since it enables substituting regular cars for cleaner alternatives, such as electric or EVs, and plug-in hybrids or PHEVs. Both technologies can significantly reduce emissions directly since they emit less carbon than cars that rely on fossil fuels [3,4]. Additionally, installing renewable energy-powered charging stations, particularly solar power, can enhance environmental benefits through the decline in using regular electricity grids and fossil fuels when using EVs [5,6]. This combination of renewable energy and electric cars effectively reduces carbon emissions for transport and encourages more environmentally friendly travel practices [7].
However, the decision to renew a fleet is not trivial [8]. In addition to the direct costs associated with vehicle acquisition and operation, managers face a complex set of factors to consider, from vehicle autonomy and infrastructure requirements to the availability of tax incentives and specific environmental regulations [9]. In the case of small and medium-sized enterprises (SMEs) and local public entities, these decisions are particularly sensitive, since financial and technical resources are limited and decisions need to be justified regarding economic, operational, and environmental viability [10,11].
The literature on fleet management has grown in recent decades, emphasizing approaches focused on route optimization, life cycle cost (LCC) analysis, and maintenance planning [12,13,14]. However, many of these studies assume ideal conditions [12,15], with accurate and fully quantifiable information, which rarely corresponds to the reality of decision makers [16]. Furthermore, few studies simultaneously integrate the three critical dimensions—economic, environmental, and strategic—that shape decision-making on fleet renewal in organizational contexts [17].
Several authors have proposed decision support models based on multicriteria techniques (MCDM) [18,19], which allow the integration of multiple factors, assigning them relative weights according to the preferences of decision makers [20,21,22,23]. This situation can be helpful in fleet management analysis. Among others, fuzzy techniques have been proven to manage uncertainty, ambiguity, and subjectivity, which mainly characterize linguistic evaluation criteria, e.g., “low cost”, “high autonomy”, and “moderate environmental impact” [24,25,26,27].
The Fuzzy TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) method [22] has been widely used to rank alternatives based on their proximity to the ideal solution and distance from the undesirable solution, considering imprecise data represented by triangular fuzzy numbers (TFNs) [28]. This method has proven applications in several areas [29,30,31,32] such as supplier selection, environmental performance assessment, and risk analysis [33,34,35], but its direct application to sustainable fleet management remains limited.
Most existing work on electric vehicles focuses on technical aspects (such as battery capacity and autonomy), consumer acceptance studies, or public policy analyses [36,37]. However, there is a lack of studies that offer concrete tools for organizational decision-makers facing strategic choices under multiple criteria and high uncertainty, particularly for SMEs or municipalities with their fleet [38,39]. This gap is even more evident when it comes to evaluating not only the technical attributes of vehicles, but also their alignment with organizations’ strategic and environmental objectives.
This paper proposes a fuzzy-based decision support model for strategically managing sustainable fleets. This model allows for evaluating different vehicle technologies based on six criteria distributed across three dimensions (economic, environmental, and operational). In addition to the proximity index to the ideal technological solution for vehicles resulting from Fuzzy TOPSIS, the Fleet Renewal Priority Index (FRPI) is introduced, a new indicator that considers vehicle age, maintenance cost, and environmental performance, allowing the identification of current vehicles in a given fleet that require the greatest urgency for replacement. This dual approach not only supports the selection of future technologies but also fills a methodological gap by introducing a practical and interpretable index—the FRPI—designed to prioritize fleet vehicle replacement when traditional methods such as LCC or Condition-Based Maintenance (CBM) are impractical due to data or resource limitations.
The model is applied in a simulated case study representative of an SME with a mixed fleet, enabling the validation of its contribution to sustained decisions aligned with sustainability and efficiency objectives. The work differs from the existing literature by uniting, in a single model, the prioritization of substitutions and the selection of technological alternatives, integrating technical, operational, and strategic factors in a practical and replicable approach.
The remainder of this paper is organized as follows: Section 2 presents the multi-criteria decision support model, outlining the integration of Fuzzy TOPSIS and the Fleet Renewal Priority Index (FRPI). Section 3 details the evaluation of technological alternatives using Fuzzy TOPSIS. Section 4 applies the FRPI to assess the replacement priority of existing fleet vehicles. Section 5 discusses the strategic implications of the results and provides practical recommendations. Finally, Section 6 concludes the paper and highlights its main contributions and limitations.
2. Multicriteria Decision Support Model
2.1. General Structure of the Model
This study proposes a decision support model to assist small and medium-sized enterprises (SMEs) and public entities in selecting and prioritizing vehicle alternatives for fleet renewal. The model was developed to deal with the subjective and uncertain nature of assessments carried out by decision-makers, incorporating multiple economic, environmental, and operational criteria.
The developed model (Figure 1) combines two main components: the evaluation of vehicle technological alternatives based on the Fuzzy TOPSIS method and the calculation of an auxiliary priority index (FRPI) to support the renewal of the existing fleet. The goal is to provide a complete decision-making tool for fleet managers who face multiple decision criteria in a context of uncertainty.
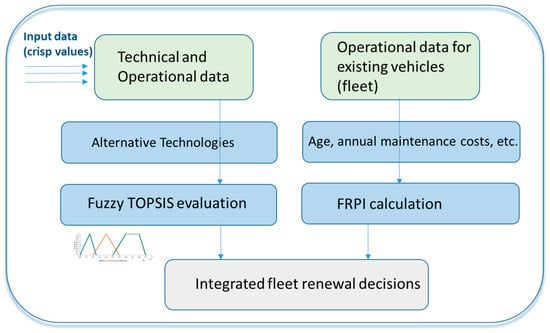
Figure 1.
Multicriteria decision support model.
The proposed model aims to support strategic fleet renewal decisions by combining two complementary approaches:
- ▪
- Multicriteria evaluation of vehicle technological alternatives, based on the Fuzzy TOPSIS method (Technique for Order Preference by Similarity to Ideal Solution), allows for comparing different replacement options according to multiple criteria. Fuzzy methods can transform linguistic evaluations into quantifiable values in the form of fuzzy numbers, representing the uncertainty and ambiguity inherent in human preferences. The Fuzzy TOPSIS method ranks alternatives based on their relative distance to the ideal (most desirable) and anti-ideal (least desirable) solutions.
- ▪
- Calculate the FRPI (Fleet Renewal Priority Index), which prioritizes current fleet vehicles that must be replaced, based on real data such as age, maintenance, and environmental impact.
The model was developed to deal with the subjective and uncertain nature of assessments carried out by decision-makers, incorporating multiple economic, environmental, and operational criteria.
The Fuzzy TOPSIS method supports evaluating external acquisition options, whereas the FRPI index prioritizes existing fleet replacements. This articulation promotes an integrated approach that transcends simple technical and economic considerations of vehicles by offering a structured decision solution with flexibility for diverse organizational contexts, mainly SMEs and public entities.
2.2. Fuzzy TOPSIS Steps
The Fuzzy TOPSIS method is an extension of the classic TOPSIS method that incorporates the uncertainty and subjectivity of human evaluations. Its application in this model aims to compare different technological vehicle alternatives based on multiple criteria, expressed in linguistic terms.
The process consists of the following steps:
In this model (Table 1), the method is used to compare different vehicle technology alternatives based on multiple criteria expressed in linguistic terms. Each alternative is evaluated according to the defined criteria, and these evaluations are converted into triangular fuzzy numbers (TFNs) (1) and organized in a fuzzy decision matrix (2). The fuzzy matrix is normalized to allow comparability between criteria. In the case of maximization criteria (such as energy independence or ease of loading), the values are normalized about the highest observed value. For criteria to be minimized (such as costs and emissions), a proportional inversion is applied. This step corresponds to expression (3). After normalization, each fuzzy value is multiplied by the corresponding criterion weight through scalar-fuzzy multiplication, generating the weighted fuzzy matrix that reflects the relative importance of each criterion in the decision (4). Then, two reference solutions are determined: the Fuzzy Positive Ideal Solution (FPIS), composed of the best TFN values in all criteria, and the Fuzzy Negative Ideal Solution (FNIS), composed of the worst ones. For each alternative, its fuzzy distance to the ideal solution (5) and the anti-ideal solution (6) is then calculated, using the Euclidean distance between TFNs. Finally, the degree of relative proximity of each alternative (7) to the ideal solution is calculated, allowing its ordering. The closer this value is to 1, the more appropriate the alternative is for the decision. Table 1 summarizes the process mathematically.

Table 1.
Fuzzy TOPSIS method: Equations Summary *.
Table 1.
Fuzzy TOPSIS method: Equations Summary *.
| No. | Step | Expression |
|---|---|---|
| (1) | Triangular Fuzzy Number (TFN) | ) |
| (2) | Fuzzy Decision Matrix | |
| (3) | Normalization for Benefit Criteria | |
| (4) | Weighted Fuzzy Matrix | |
| (5) | Distance to Ideal Solution (FPIS) | |
| (6) | Distance to Negative-Ideal Solution (FNIS) | |
| (7) | Relative Closeness Coefficient |
* l, m, u: lower limit, modal value, and upper limit of a TFN; normalized fuzzy value of ; wj: weight assigned to criterion j; weighted fuzzy value of alternative i for criterion j; ideal and anti-ideal fuzzy values for criterion j; distance from alternative i to the ideal and anti-ideal solutions; Ci: relative closeness coefficient of alternative i.
To justify the selection of Fuzzy TOPSIS in this study, a brief comparison with alternative MCDM methods is presented below.
While MCDM offers a wide array of techniques [37]—hierarchical methods, such as Fuzzy AHP and Fuzzy ANP [40], compromise ranking methods, such as VIKOR [41], and outranking approaches, such as ELECTRE and PROMETHEE [42]—Fuzzy TOPSIS was chosen because it practically aligned with the capacities and needs of the organization for decision-making. From a computational standpoint, Fuzzy TOPSIS is easier and conceptually much more straightforward than Fuzzy AHP, which requires thorough pairwise comparisons and consistency checking [43]. This makes it especially suitable for SME and public entities with limited analytical resources, while still producing a clear, standardized ranking of alternatives based on proximity to ideal and anti-ideal solutions.
A further advantage arises with Fuzzy TOPSIS in the evaluation of automotive technologies, as these involve criteria that are often not strictly numeric; these include perceived environmental impact, expectations of autonomy, or operational risk. The method formalizes qualitative judgments using fuzzy triangular membership functions to form a coherent decision matrix [44,45,46]. This type of liberty lends further sophistication in simulating decision contexts and accounting for economic, environmental, and operational aspects within one evaluation framework. By contrast, compromise-based methods like VIKOR prioritize balancing conflicting objectives but yield results that can be less transparent and more sensitive to weight adjustments [41,47]. ELECTRE, on the other hand, handles discordant and incomparable alternatives using outranking thresholds, but requires careful tuning of concordance–discordance parameters and results in partial orderings which may complicate operational interpretation [48].
While these methods offer analytical depth, their relative complexity and reduced interpretability led us to choose Fuzzy TOPSIS as the most effective balance of robustness and ease-of-use, particularly in sustainability-oriented decision-making environments with limited expertise.
Although some of the alternative MCDM methods discussed do not natively operate under fuzzy logic, they are commonly compared in the literature with fuzzy extensions, and their methodological characteristics offer valuable points of contrast when evaluating decision-making suitability under uncertainty.
2.3. Fleet Renewal Priority Index
An organizational fleet management decision involves the analysis of future technological alternatives and determining which vehicles should be replaced as a matter of urgency, all while simultaneously considering operational, economic, and environmental factors. While there are standard methods, such as Life Cycle Cost (LCC) or predictive maintenance methods (Condition-Based Maintenance), many require detailed data, long histories, or onboard sensors, limiting their applicability to SMEs or public entities with limited resources.
Moreover, Life Cycle Sustainability Assessment (LCSA) approaches are also confronted with significant methodological challenges [49]. In a systematic review of the automotive industry, inconsistencies in the choice of functional units, system boundaries, and indicators are highlighted that affect the balanced integration of the three pillars of sustainability: economic, environmental, and social. This lack of harmonization leads to the impossibility of utilizing models like LCC or LCSA in strategic-level asset replacement management.
On the other hand, traditional fleet renewal models based on economic metrics, such as the EUAC (Uniform Annual Equivalent Cost), are often used to identify the optimal timing for vehicle or equipment replacement based on minimizing the equivalent annual cost. Studies such as those by Almobarek et al. [50] and Kauffmann et al. [51] demonstrate their usefulness in asset management but also reveal a significant limitation: their exclusive focus on the financial dimension, without integrating environmental impact or operational functional wear and tear.
In this context, the Fleet Renewal Priority Index (FRPI) is proposed as a complementary and accessible approach that allows for the simultaneous incorporation of three critical dimensions—vehicle age, annual maintenance cost, and average CO2 emissions—in a continuous, weighted, and interpretable manner. FRPI aims to support strategic vehicle replacement decisions based on readily available data, adapting to the reality of organizations with technical and financial constraints, and thus complementing more complex models such as Fuzzy TOPSIS, which focus on future technology selection.
A fleet management research background is used as a basis for choosing the criteria included in the FRPI. These indicators are widely recognized as relevant to supporting strategic operational efficiency, cost-effectiveness, or environmental responsibility decisions. Combined, they attempt to provide as much vehicle condition and renewal requirement assessment as feasible without resorting to an advanced system or some sensor-based data. Together, they provide for a realistic priority model that often suffers from practical constraints and objectives of many organizations.
The vehicle age is a main determinant of fleet assets’ functional and financial performance [3,52]. Operating and maintenance costs increase with age, whereas vehicle reliability and fuel efficiency tend to decline. Boudart and Figliozzi [53] found that older buses suffer much higher operating and maintenance costs for each mile, thus highlighting the urgency for timely replacement to minimize lifecycle costs. Conversely, pollution emissions tend to increase with older vehicles, with the degradation of the engines over time [54]. These lines of reasoning justify considering the age in the FRPI model.
The annual maintenance cost criterion captures the financial burden of operating aging or underperforming vehicles. Maintenance costs are a significant component of the total cost of ownership and are often used as a proxy for mechanical degradation. According to the recent research carried out by Crespo del Castillo and Parlikad [55], combining the two approaches—predictive and preventive maintenance—can optimize asset management and at the same time lessen unforeseen expenses. Without advanced monitoring systems, annual cost summaries are the basis for deciding which equipment to replace first. This is especially relevant for SMEs and public entities that lack the infrastructure to implement condition-based maintenance systems.
The CO2 emissions criterion reflects growing concerns over environmental performance and regulatory compliance. Integrating emissions into strategic fleet decisions aligns with sustainability goals and regulatory standards. Studies by Castillo and Álvarez [56] and Corazza et al. [54] encourage incorporating emissions models to track and manage environmental impact. These models support emission reduction strategies and are widely used in fleet sustainability planning. Although this paper does not rely on sophisticated simulation tools, emission bands allow for realistic approximations of vehicle environmental performance. Moreover, while the FRPI framework has not yet undergone formal expert panel validation, its structure was reviewed informally with fleet managers from both private and public organizations. Their feedback confirmed the practical relevance and interpretability of the three criteria used, supporting the real-world applicability of the proposed index.
The FRPI is an auxiliary indicator that supports vehicle replacement decisions in organizational fleets. Its function systematically identifies vehicles requiring the most urgent replacement based on multiple performance factors. Instead of a linear weighted average, this model uses continuous penalty functions that are better suited to capturing non-linear variations and cumulative effects over time.
The FRPI value (Table 2) is obtained by the weighted combination of three penalizing functions, as shown in the general expression (8). The index considers three fundamental dimensions: vehicle age, annual maintenance cost, and average carbon dioxide (CO2) emissions. Each of these variables is converted to a scale between 0 and 1 through a specific function, which simulates the increasing impact of ageing, economic inefficiency, and environmental impact. The penalty associated with vehicle age is modelled by an increasing exponential function (9), reflecting that older vehicles represent increased operational risks and costs. The annual maintenance cost is treated by a limited linear function (10), which reaches a maximum from a reference value. CO2 emissions are treated similarly, increasing linear penalties from a minimum emissions level (11). The weights assigned to each criterion may be changed according to the organization’s priorities. The result enables the classification of fleet vehicles according to the priority of their replacement, thus providing structured support for decision-making.

Table 2.
FRPI calculation: penalty functions and structure.
Table 2.
FRPI calculation: penalty functions and structure.
| No. | Step | Expression |
|---|---|---|
| (8) | General | |
| (9) | Vehicle age penalty function | |
| (10) | Maintenance cost penalty function | |
| (11) | CO2 emissions penalty function |
Ak: Age of vehicle k (years);: annual maintenance cost of vehicle (Euros);: average CO2 emissions of vehicle (g/km);enalizing function for criterion j and vehicle k;: weight assigned to criterion j.
The penalty functions used in the FRPI calculation were defined based on realistic assumptions and adjusted to fleet management practices. For the age of the vehicle, an increasing exponential function with a rate of 0.15 was adopted to reflect a progressive penalty from 10 years onwards, saturating close to the maximum value in vehicles over 15 years old. The annual maintenance cost was treated as a limited linear function, with a reference value of €2000, which is considered the reasonable upper threshold for light vehicles in a business context. In terms of CO2 emissions, the starting penalty point is set at 100 g/km, which is in line with current standards of ecological efficiency and rises to a maximum of 300 g/km, thus including most traditional cars. The bands are adjustable according to the strategic or regulatory objectives of the company. In relation to carbon dioxide emissions, the initial threshold for penalties is established at 100 g per kilometre, which aligns with prevailing ecological efficiency standards, and escalates to a ceiling of 300 g per kilometre, thereby encompassing most conventional automobiles. These parameters are subject to modification.
In summary, while alternative indicators exist that individually assess costs, emissions, or operational performance, the FRPI stands out for integrating these dimensions in an aggregated manner, with adjustable penalty functions, allowing for clear, transparent, and adaptable prioritization of replacements to each organization’s strategic priorities. This approach makes the FRPI particularly useful for resource-constrained contexts, such as SMEs, and represents an innovative contribution to supporting sustainable fleet renewal decisions.
3. Multi-Criteria Evaluation of Technological Alternatives (Fuzzy TOPSIS)
3.1. Technological Alternatives
Five typical technological alternatives for vehicles for organizational fleets were considered (Table 3). These alternatives reflect the technological diversity currently available on the market and allow us to evaluate solutions with different levels of sustainability, cost, and technological maturity. The comparison between technologies with different sustainability profiles, life cycle costs, levels of external energy dependence, and operational requirements may be particularly relevant for strategic decisions in SMEs or public entities.

Table 3.
Technological vehicle alternatives.
3.2. Evaluation Criteria
The evaluation of technological alternatives was based on multidimensional criteria, defined from a literature review [57] and consultation with fleet management and sustainability experts. The choice of criteria accounts for economic, environmental, and operational aspects to see a balanced view between total cost, environmental impact, and logistical feasibility. Table 4 lists the four criteria used, with the type of data (quantitative or qualitative) for each, as well as their preferred orientations (maximize or minimize).

Table 4.
Evaluation criteria.
Criterion C1 (TCO) represents the total cost of ownership over 10 years, including acquisition, energy consumption, maintenance, and depreciation. Criterion C2 assesses the direct environmental impact of alternatives. Criterion C3 measures the relative energy autonomy of the solution—for example, electric vehicles charged using renewable energies such as photovoltaics obtain higher values. Criterion C4, of a qualitative nature, reflects the ease of implementation and operation of the charging infrastructure in organizational contexts.
3.3. Input Data and Language Conversion
The technological alternatives were evaluated based on quantitative and qualitative data that reflect realistic operating conditions in a business context. The values correspond to usage estimates over a 10-year cycle, considering an average distance of 100 km per day. The data for criterion C1 (TCO—Total Cost of Ownership) were adapted from a previous study [10], which considered acquisition, loading, maintenance, depreciation, and infrastructure installation costs.
Table 5 presents the quantitative values used for the three objective criteria (C1, C2, and C3) and the qualitative value attributed to the subjective criterion C4 (ease of loading). Experts evaluated this last criterion based on the availability of infrastructure, ease of installation, and operational compatibility using a five-level linguistic scale.

Table 5.
Quantitative and qualitative input data.
To apply the Fuzzy TOPSIS method, the quantitative values of criteria C1, C2, and C3 were converted into linguistic terms, using ranges defined based on market standards and organizational practices. Table 6 presents the corresponding values in linguistic terms for all criteria. This step allows the data to be standardized, facilitating representation by triangular fuzzy numbers (TFNs) in the next step.

Table 6.
Linguistic representation of evaluation criteria.
The linguistic classifications presented in Table 6 result from the comparative analysis of the values attributed to each alternative based on four multidimensional criteria. In criterion C1—Total Cost of Ownership (TCO), BEV (A1), and BEV + PV (A2) vehicles were classified as “Very Low” due to their reduced operating costs, low maintenance charges, and, in the case of A2, the virtual elimination of energy costs through solar charging. The C2—CO2 Emissions criterion directly reflects the local emissions of each technology; 100% electric vehicles (A1 and A2) have zero emissions and were therefore classified as “Very Low”, plug-in hybrids were classified (A3) as “Media”, and combustion vehicles (A4 and A5) as “High” and “Very High”, respectively, due to their high environmental impact. In criterion C3—Energy Independence, BEV + PV (A2) obtained the “Very High” classification for guaranteeing energy autonomy through local renewable sources, while BEV (A1) depends on the electricity grid and was classified as “Medium”; conventional vehicles (A4 and A5) show a high dependence on fossil fuels and were, therefore, classified as “Low” or “Very Low”. Finally, criterion C4—Charging Infrastructure Ease, of a qualitative nature, assessed the ease of implementing the charging infrastructure in the organizational context. The BEV + PV (A2) received the highest rating (“Very High”) due to the integration of the solar charging. At the same time, the other electric and hybrid vehicles were evaluated based on availability and ease of installation, receiving ratings of “High” (A1 and A4), “Medium” (A3), and “High” (A5) based on the experts’ assessment.
3.4. Fuzzy Decision Matrix
To apply the Fuzzy TOPSIS method, the linguistic terms assigned to the evaluation criteria were converted into TFN. This conversion allows us to represent the uncertainty and subjectivity inherent in qualitative assessments mathematically. Each linguistic term corresponds to a TFN of the form where l is the lower limit, m is the most likely value, and u is the upper limit of the evaluation. This study adopted a standardized five linguistic scale (Table 7). These terms are widely used in multicriteria fuzzy decision applications. The terms were applied to construct the fuzzy decision matrix based on the conversion of the values in Table 7. In the practical application of the model to real contexts, it is recommended that these linguistic terms be assigned by specialists with adequate technical and operational knowledge, ensuring coherence with the reality of the organization. Based on this scale, the linguistic terms assigned in Table 6 were converted into the fuzzy decision matrix shown in Table 8. This matrix forms the basis for the next steps of the Fuzzy TOPSIS method.

Table 7.
Linguistic terms and corresponding TFNs.

Table 8.
Fuzzy decision matrix (TFNs).
3.5. Fuzzy Normalization and Weighting
After constructing the fuzzy decision matrix, the fuzzy numbers associated with each alternative and criterion are weighted. According to expression (12) in Table 1 (Normalization for Benefit Criteria), normalization is generally applied to make the values assigned to different criteria comparable. However, in this study, all criteria were previously transformed into triangular fuzzy numbers based on a common linguistic scale. For this reason, the criteria are considered implicitly normalized, allowing weighting to be applied directly.
Fuzzy weighting is performed according to expression (13) in Table 1, multiplying each TFN by the weight assigned to the corresponding criterion. This expression corresponds to the weighted fuzzy decision matrix, where each normalized fuzzy value is multiplied by the corresponding criterion weight.
Expressions (12) and (13) are repeated below for convenience and to improve clarity:
In this study, different weights were assigned to each criterion, reflecting their relative importance in strategic fleet management:
- ▪
- Criterion C1—Total Cost of Ownership (TCO) was assigned a relevant weight of 0.30 due to its direct influence on the economic dimension.
- ▪
- Criterion C2—Carbon Dioxide (CO2) Emissions was assigned a relevant weight of 0.30, due to its immediate influence on ecological dimensions.
- ▪
- Criterion C3—Energy Independence was allocated a diminished weight (0.15), signifying its enduring strategic relevance.
- ▪
- Criterion C4—Ease of Loading received an intermediate weight (0.25) due to its practical relevance in implementing the technology.
This article does not aim to explore specific methods for defining criteria weights, which require distinct methodological frameworks. In practical applications, weights can be assigned by expert judgment [58] or derived through structured fuzzy approaches, including interval-valued hesitant fuzzy information [31], interval intuitionistic trapezoidal fuzzy numbers [58,59], intuitionistic fuzzy sets with scoring functions [60], fuzzy Pythagorean sets [61] or vague sets [62], and hybrid models such as the fuzzy TOPSIS–CRITIC method [63].
Table 9 presents the weighted fuzzy matrix resulting from the multiplication of each TFN of the decision matrix by the weighting attributed to each criterion. Figure 2 illustrates, for example, the TFN assigned to Criterion C3—Energy Independence, as presented in Table 9.

Table 9.
Weighted fuzzy decision matrix.
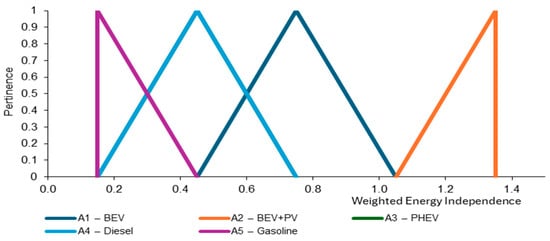
Figure 2.
Weighted TFN for Criterion C3—Energy Independence.
3.6. Ideal and Negative-Ideal Solutions and Fuzzy Distances
As described in Section 2.2, the Fuzzy TOPSIS method allows evaluating alternatives based on distance from two reference solutions: FPIS, which represents the most favourable combination of criteria, and the FNIS, which represents the least desirable combination. Expressions (14)—Fuzzy Positive Ideal Solution—and (15)—Fuzzy Negative Ideal Solution—in Table 1 define the calculation of the partial distances of each alternative to the two solutions, by summing the fuzzy distances for each criterion. For the reader’s convenience and to improve clarity, these expressions are restated below.
Defining the distance metric between two triangular fuzzy numbers (TFNs) is necessary to apply these formulas to the case study. This metric, not included in Table 1, is introduced here as a fundamental tool for computational calculation. Considering two TFNs , and , the fuzzy distance between them is given by (16):
This metric quantifies the dissimilarity between imprecise evaluations, considering all components of the fuzzy number. Even though the triangular fuzzy numbers (TFNs) used follow a regular linguistic scale, the distance calculation remains essential to quantify the relative position of each alternative concerning the ideal and anti-ideal solutions, ensuring meaningful ranking under uncertainty.
Once the total distances of each alternative to the FPIS and FNIS have been calculated, Expression (17) from Table 1 is applied to determine the relative proximity coefficient Ci, which allows the alternatives to be ordered according to their attractiveness. For coherence and to support the interpretation of the results, Expression (17) is reproduced below:
The following section presents the results obtained for , and the final ordering of the evaluated alternatives.
3.7. Fuzzy TOPSIS Results and Alternatives Ranking
Based on the weighted fuzzy matrix presented in Table 9 and using the expressions described in Section 2.2 and Section 3.6, the distances of each technological alternative to the fuzzy positive (FPIS) and fuzzy negative (FNIS) ideal solutions were calculated. The relative proximity coefficient (17) was obtained through these distances, which quantifies the global attractiveness of each alternative in relation to the ideal solution. Table 10 presents the results obtained. Figure 3 graphically illustrates the Relative Closeness Coefficient.

Table 10.
Fuzzy TOPSIS results: distances and relative closeness coefficients.
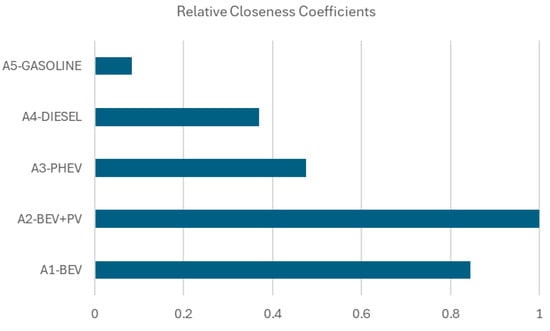
Figure 3.
Relative closeness coefficients.
Alternative A2—Electric Vehicle with Photovoltaic System (BEV + PV) presents the highest value of Ci = 1.0, proving to be the option closest to the ideal solution. This result highlights the positive impact of EV charging from its renewable energy sources. By eliminating electricity costs and reinforcing energy independence, BEV + PV offers both economic (lower TCO) and environmental (zero emissions and clean energy) advantages while benefiting from a high rating for ease of charging. The second position in the ranking belongs to alternative A1—BEV without a solar system, with Ci = 0.845. Despite producing no direct emissions and involving lower maintenance requirements, dependence on the electricity grid for charging may reduce the overall attractiveness of this alternative, particularly in terms of operational costs and energy availability constraints. The third best option is the A3—Plug-in Hybrid Vehicle (PHEV), with a Ci rating of 0.476. Although it provides partial electrical operation and functionality, this alternative’s emissions and ownership costs are considerably greater than those of fully electric vehicles. This alternative, nonetheless, may be viewed as a bridge option for fleets without suitable electric infrastructure or for fleets working in regions with logistic constraints.
On the other hand, the alternatives A4—Diesel and A5—Gasoline recorded the lowest attractiveness values (Ci = 0.369 and Ci = 0.084, respectively). These results reflect unfavourable factors, such as high TCO, higher environmental impact (CO2 emissions), dependence on fossil fuels, and limitations in aligning with sustainability and digitalization strategies.
These results are significant for SMEs and public entities that intend to align their mobility strategy with sustainability, operational efficiency, and digitalization principles. Adopting electric vehicles, especially with photovoltaic solutions, is the most robust option considering a broad set of technical, economic, and environmental criteria. Furthermore, fuzzy methods allow the systematic incorporation of subjective assessments and uncertain factors, contributing to more informed decisions, especially in organizational contexts with limited resources or incomplete information.
The analysis presented in this section provides objective and structured information to support the selection of vehicle technologies best aligned with the energy transition and long-term competitiveness.
4. Fleet Renewal Priority: Application of FRPI
Building on the hybrid approach proposed in Section 2.1, this section focuses on the second component of the model: the use of the Fleet Renewal Priority Index (FRPI) to support operational decisions on which vehicles should be prioritized for replacement in the current fleet. This tool complements the technological analysis of Fuzzy TOPSIS, offering a perspective oriented towards the concrete management of existing assets.
4.1. Fleet Data and Vehicle Characteristics
A standard fleet of five vehicles used by an SME in the technical–operational sector (installations, maintenance, and logistics) was considered for demonstration purposes. The fleet includes gasoline, diesel, and hybrid models, with different levels of wear, operating costs, and environmental impact. Although the TCO calculation used in the Fuzzy TOPSIS analysis assumed a standardized usage of 100 km per day—equivalent to approximately 36,500 km per year—the application of FRPI considers values adapted to the operational reality of each vehicle in the fleet. The variation in kilometres driven annually reflects the functional diversity of vehicles, their specific missions, and the degree of accumulated wear. This approach allows for a more realistic and well-founded assessment of the urgency of replacement, integrating technical and contextual factors specific to each fleet unit. These data reflect the typical diversity of an organizational fleet with vehicles from different technological generations and usage patterns. The corresponding values will be input into the previously defined membership functions to compute the FRPI index based on vehicle age, maintenance cost, and CO2 emissions. Table 11 presents the technical and operational characteristics of the simulated vehicles, which will serve as a basis for calculating the FRPI.

Table 11.
Characteristics of fleet vehicles.
4.2. Definition of Weights by Experts
Similar to the Fuzzy TOPSIS approach, the calculation of the Fleet Renewal Priority Index (FRPI) requires the assignment of weights to the evaluation criteria: vehicle age, annual maintenance cost, and CO2 emissions. These weights represent the relative importance attributed to each factor in prioritizing the replacement of fleet vehicles.
Assigning weights to multicriteria criteria is, by nature, a process sensitive to the context and preferences of decision-makers. Thus, as mentioned in Section 2.2, weights can be defined by fleet management, automotive engineering, and sustainability experts or by formal decision support methods, such as the Analytic Hierarchy Process (AHP) or Delphi consensus techniques.
In the present study, the weights were obtained through consultation with experts with practical experience in small and medium-sized organizational contexts and reflect a balance between technical (depreciation and maintenance costs) and environmental factors.
4.3. FRPI Calculation and Results
Based on the fleet’s operational data (Table 11) and the weights assigned to the criteria (Table 12), the Fleet Renewal Priority Index (FRPI) was calculated for each vehicle. This index combines, in a weighted manner, three membership functions associated with the criteria:

Table 12.
FRPI criteria and assigned weights.
- ▪
- f1(Ak): Vehicle age (increasing exponential function).
- ▪
- f2(Mk): Average annual maintenance cost (linear function up to €2000).
- ▪
- f3(Ek): CO2 emissions (linear function up to 200 g/km).
Functions (19)–(21) were normalized within the [0, 1] interval, allowing their aggregation as defined in Expression (22), which unfolds the formulation introduced in Expression (18). For clarity, Expressions (18) to (21) are presented again below to support the interpretation of the indicators used in the evaluation.
With the weights defined (Table 12), the FRPI calculation is presented below for each vehicle in the fleet (Table 13).

Table 13.
FRPI calculation for each vehicle.
Analysis of the results (Figure 4) shows that the V5—Gasoline vehicle has the highest FRPI value (0.601), which indicates that it should be the first candidate for replacement. This result is justified by its high age (10 years), high maintenance cost, and high level of CO2 emissions. Next comes the V1–diesel vehicle with an FRPI of 0.55 and strong accumulated wear. V4 and V2 vehicles are in intermediate positions, with reasonable levels of maintenance and wear. The V3—PHEV vehicle has the lowest index (0.329), reflecting its good overall performance and low need for replacement in the short term.
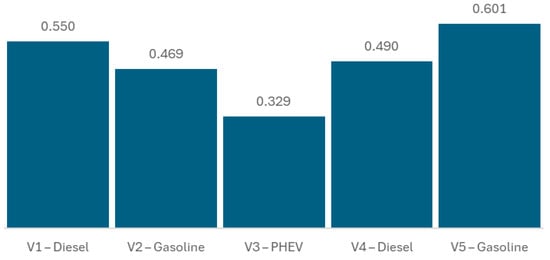
Figure 4.
FRPI Calculation for Each Vehicle.
These results provide decision-makers with a clear replacement hierarchy, guiding investments in fleet renewal based on objective criteria. The combination of FRPI and the analysis of technological alternatives via Fuzzy TOPSIS (Section 3.7) allows for integrated and sustained management of organizational mobility.
5. Discussion—Strategic Integration of Results and Management Recommendations
The results obtained in the previous sections offer an integrated perspective for decision-making in the renewal of organizational fleets, combining two complementary levels of analysis.
The multicriteria evaluation of vehicle technology alternatives, carried out using the Fuzzy TOPSIS method (Section 3), allowed us to identify that the BEV solution with a photovoltaic system (A2) presents the most attractive performance in terms of total cost, environmental impact, and energy autonomy.
The analysis of the renewal priority of the current fleet, carried out using the FRPI index (Section 4), allowed the existing vehicles to be sorted based on objective operational criteria, highlighting the most urgent replacement cases.
This combined approach allows us to answer the following two critical questions for strategic fleet management simultaneously:
- ▪
- “What kind of vehicles should we purchase in the future?”—answered by Fuzzy TOPSIS, which pointed out the viability of BEV + PV (A2).
- ▪
- “Which current vehicles should we replace first?”—answered by FRPI, which indicated V5 (Gasoline) and V1 (diesel) vehicles as a priority due to their high wear and environmental impact.
The progressive replacement of internal combustion vehicles with electric alternatives that guarantee charging with renewable energy is aligned with reducing greenhouse gas emissions, reducing external energy dependence, and meeting environmental and corporate social responsibility goals. At the same time, fleet analysis with the FRPI enables the planning of this transition in a financially balanced manner, thus prioritizing those vehicles that constitute heightened operational risks and costs. The Fleet Renewal Priority Index (FRPI) complements already existing methods such as Life Cycle Cost (LCC) and Condition-Based Maintenance (CBM) by introducing a new lightweight integrated tool designed for contexts with minimal data or resources. In these situations, the more established approaches may not be feasible.
Unlike these heavy procedures that demand detailed historical records of faults or failures, or even advanced online monitoring systems, the FRPI bases its estimation on operational indicators that straightforward observations can readily obtain. This design feature makes it most helpful to those SMEs and public entities desirous of evaluating fleet renewal strategies, given sustainability goals on a tight budget.
Based on this integration, the following practical actions are recommended:
- ▪
- Replace the V5 (Gasoline) vehicle with a BEV + PV, aligning the renewal with the most advantageous alternative identified by TOPSIS.
- ▪
- Plan the replacement of V1 (Diesel) in the medium term, ideally also with an electric solution.
- ▪
- Monitor V2 and V4 vehicles, which have intermediate FRPI, and reassess their operational condition annually.
- ▪
- Keep the V3 (PHEV), currently with good performance and low replacement priority.
Integrate periodic analyses with real data, allowing adjustment of weights, and criteria based on changes in the energy, technological, or regulatory context. This integrated strategy offers SMEs and public entities a practical and well-founded tool to plan fleet renewal in a gradual, sustainable, and financially responsible way.
6. Conclusions
Strategic fleet renewal is a complex challenge that requires the simultaneous consideration of multiple technical, economic, and environmental factors, often assessed under uncertain conditions and lacking accurate information. In this context, this paper proposed a hybrid decision support model that combines the Fuzzy TOPSIS method with a replacement priority index (FRPI), offering an integrated, structured, and accessible approach to support decisions on sustainable mobility in organizations.
The method demonstrated an ability to translate qualitative and subjective judgments into quantifiable criteria, allowing technological alternatives to be compared coherently, even in contexts of incomplete information. By dealing with the natural imprecision of human language, fuzzy methods have proven particularly effective in capturing decision-makers’ preferences regarding criteria such as total cost, emissions, or ease of charging.
Mainly, a contribution of this model is in the practical application: it is computationally light and relies solely on basic operational data while being easy to interpret, features that make it primarily suitable for small and medium-sized enterprises, or some public entities, without advanced software requirements or technically specialized human resources. At the same time, it remains robust enough to support informed strategic decisions. Furthermore, combining the evaluation of external acquisition alternatives and the internal prioritization of replacement needs offers a comprehensive and operationalizable perspective on fleet management. However, its effectiveness as a decision support system depends on the reliability of the input data and the firmness of an organization’s strategic objectives. Although possible based on expert judgment, the definition of the criteria weights remains a sensitive point that can affect the results. Additionally, the simulation used in this study, although representative, does not replace empirical validation in real contexts with historical operational data.
Integrating FRPI with the Fuzzy TOPSIS method avoids redundancies by assigning each tool a distinct but complementary function: replacement prioritization and technology assessment. This separation allows organizations to coherently and practically address both internal fleet renewal needs and the strategic selection of sustainable alternatives.
While the conceptual development of the FRPI is supported by literature and informal interactions with practitioners, there has not been any formal or expert validation of the FRPI. This limitation is, however, acknowledged, and future studies along the same lines must be concerned with structured validation processes for strengthening the connotation and applicability of the model. These include implementation in real operational settings and formal consultation with domain experts.
The proposed model offers a transparent and straightforward tool to support decision-making in organizational environments, steering the way into more sustainable mobility options. Its flexibility and adaptability to differing realities make it an interesting essential method for strategic fleet renewal, thus paving the way for applications and further advanced methodological developments.
Author Contributions
Conceptualization, S.G., D.H.d.l.I., J.L.A. and A.J.L.R.; methodology, S.G., D.H.d.l.I. and J.L.A.; validation, J.L.A. and A.J.L.R.; formal analysis, D.H.d.l.I., J.L.A. and A.J.L.R.; investigation, S.G.; data curation, P.V., E.G. and S.G.; writing—original draft, S.G.; writing—review and editing, S.G.; supervision, D.H.d.l.I. and J.L.A.; project administration, J.L.A., P.V. and E.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
Regarding authors Sónia Gouveia, Daniel H. de la Iglesia, and José Luís Abrantes, this research work is made within the University of Salamanca PhD Programme on Education in the scope of Knowledge Society. The present work is also part of the project “Sustainable Mobility and Strategic Value Creation in SMEs” (PIDI/CISeD/2025/017), developed within the scope of CISeD—Research Centre in Digital Services.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ackrill, R.; Zhang, M. Sustainable Mobility—Editorial Introduction. Sustain. Mobil. 2021, 1, 1–6. [Google Scholar] [CrossRef]
- Longo, M.; Foiadelli, F.; Yaïci, W. Electric Vehicles Integrated with Renewable Energy Sources for Sustainable Mobility. IntechOpen 2018, 10, 203–223. [Google Scholar] [CrossRef]
- Soltanpour, A.; Jazlan, F.; Ghamami, M.; Zockaie, A. Sustainable Fleet Operation Strategies to Minimize the Economic and Societal Emission Costs. In Proceedings of the IEEE Conference on Technologies for Sustainability, Portland, OR, USA, 19–22 April 2023; IEEE: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Abdi, A.; Taghipour, S. An Optimization Model for Fleet Management with Economic and Environmental Considerations, under a Cap-and-Trade Market. J. Clean. Prod. 2018, 204, 130–143. [Google Scholar] [CrossRef]
- Jung, H.; Jang, H.; Han, H.; Cho, K.; Kang, B.; Park, S. Electric Vehicle Charging System to Reduce Carbon Emissions Using Photovoltaic Power Generation and ESS. In Proceedings of the 2022 IEEE 5th Student Conference on Electric Machines and Systems (SCEMS), Busan, Republic of Korea, 24–26 November 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Freire, R.; Delgado, J.; Santos, J.; Almeida, A.T. Integration of Renewable Energy Generation with EV Charging Strategies to Optimize Grid Load Balancing. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Madeira Island, Portugal, 19–22 September 2010; pp. 392–396. [Google Scholar] [CrossRef]
- Holmatov, B.; Hoekstra, A.Y. The Environmental Footprint of Transport by Car Using Renewable Energy. Earth’s Future 2020, 8, e2019EF001428. [Google Scholar] [CrossRef]
- Li, L.; Lo, H.K.; Xiao, F.; Cen, X. Mixed Bus Fleet Management Strategy for Minimizing Overall and Emissions External Costs. Transp. Res. Part D Transp. Environ. 2018, 60, 104–118. [Google Scholar] [CrossRef]
- Abdi, A.; Taghipour, S. Optimal Replacement of a Fleet of Assets with Economic and Environmental Considerations. In Proceedings of the 2018 Annual Reliability and Maintainability Symposium (RAMS), Reno, NV, USA, 22–25 January 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Gouveia, S.; de la Iglesia, D.H.; Abrantes, J.L.; López Rivero, A.J.; Silva, E.; Gouveia, E.; Santos, V. Creating Value Through Strategic Management: Sustainable Mobility for Family-Owned Small- and Medium-Sized Enterprises with Electric Vehicles in the Digital Era. Sustainability 2025, 17, 1785. [Google Scholar] [CrossRef]
- Bae, S.H.; Yoo, C.S.; Sarkis, J. Greening Transportation Fleets. Soc. Sci. Res. Netw. 2008. [Google Scholar] [CrossRef]
- Iwan, S.; Nürnberg, M.; Kijewska, K. Analysis of Fleet Management Systems as Solutions Supporting the Optimization of Urban Freight Transport; Springer: Cham, Switzerland, 2018; pp. 55–69. [Google Scholar] [CrossRef]
- Baldo, L. Condition-based-maintenance for fleet management. Mater. Res. Proc. 2023, 33, 57–60. [Google Scholar] [CrossRef]
- Aiello, G.; Quaranta, S.; Inguanta, R.; Certa, A.; Venticinque, M. A Multi-Criteria Decision-Making Framework for Zero Emission Vehicle Fleet Renewal Considering Lifecycle and Scenario Uncertainty. Energies 2024, 17, 1371. [Google Scholar] [CrossRef]
- Anderson, N.W. Management of Vehicles Based on Operational Environment. U.S. Patent US20060217993A1, 19 August 2008. Available online: https://patents.google.com/patent/US20060217993A1/en (accessed on 1 June 2020).
- Cassady, C.R.; Murdock, W.P.; Nachlas, J.A.; Pohl, E.A. Comprehensive fleet maintenance management. Syst. Man Cybern. 1998, 5, 4665–4669. [Google Scholar] [CrossRef]
- Orošnjak, M.; Jocanović, M.; Gvozdenac-Urošević, B.D.; Šević, D.; Duđak, L.; Karanović, V. Bus Fleet Management—A Systematic Literature Review. Promet-Traffic Transp. 2020, 32, 761–772. [Google Scholar] [CrossRef]
- Brlek, P.; Cvitković, I.; Kolarevic, N.; Stojanovic, K.; Sovreski, Z. Application of fleet management in intelligent transport systems. In Proceedings of the 2022 57th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Ohrid, North Macedonia, 16 June 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Tomita, E. Transportation Fleet Management; Elsevier eBooks: Amsterdam, The Netherlands, 2022; pp. 113–129. [Google Scholar] [CrossRef]
- Alves, M.A.; Guimarães, F.G. Fuzzy Multi-Criteria Decision Making Methods with Uncertainty Scenario; Universidade Federal de Minas Gerais: Belo Horizonte, Brazil, 2018. [Google Scholar] [CrossRef]
- Dursun, M. A new integrated fuzzy MCDM approach and its application to wastewater management. Int. J. Intell. Syst. Appl. Eng. 2018, 6, 19–28. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Multiple Attribute Decision Making; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1981; Volume 186, pp. 58–191. [Google Scholar] [CrossRef]
- Dean, M. Multi-Criteria Analysis; Academic Press: Cambridge, MA, USA, 2020; Volume 6, pp. 165–224. [Google Scholar] [CrossRef]
- Wang, W.; Poh, K.-L. Fuzzy MCDM based on confidence analysis. Fuzzy Econ. Rev. 2003, 8, 25–37. [Google Scholar] [CrossRef]
- Chen, L.; Chen, B. Fuzzy Logic-Based Electric Vehicle Charging Management Considering Charging Urgency. In Proceedings of the IEEE Innovative Smart Grid Technologies-Asia, Chengdu, China, 21–24 May 2019; pp. 3441–3446. [Google Scholar] [CrossRef]
- Coşkun, M.Z.; Karakaya, B. A Case Study: Fuzzy Logic Based Decision-Making System for Electric Vehicle Charging. Int. J. Energy Smart Grid 2024, 9, 42–50. [Google Scholar] [CrossRef]
- Tang, H.; Ahmad, N.S. Fuzzy Logic Approach for Controlling Uncertain and Nonlinear Systems: A Comprehensive Review of Applications and Advances. Syst. Sci. Control Eng. 2024, 12, 2394429. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Krohling, R.A.; Campanharo, V.C. Fuzzy TOPSIS for Group Decision Making: A Case Study for Accidents with Oil Spill in the Sea. Expert Syst. Appl. 2011, 38, 4190–4197. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Gitinavard, H.; Mousavi, S.M.; Siadat, A. An Interval-Valued Hesitant Fuzzy TOPSIS Method to Determine the Criteria Weights; Springer: Berlin/Heidelberg, Germany, 2015; pp. 157–169. [Google Scholar] [CrossRef]
- Siddiqui, R.; Khan, N.; Ahmad, S.; Ahmad, S. A Fuzzy TOPSIS-Based Analysis to Prioritize Enabling Factors for Strategic Information Technology Management. EAI Endorsed Trans. Context-Aware Syst. Appl. 2022, 8, e3. [Google Scholar] [CrossRef]
- Abdelhafeez, A.; Shreyas, J.; Udayaprasad, P.K. A Fuzzy TOPSIS Method for Assessment Blockchain Technology Strategies. Deleted J. 2024, 1, 1–9. [Google Scholar] [CrossRef]
- Chen, C.-T. Extensions of the TOPSIS for Group Decision-Making under Fuzzy Environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Ye, F.; Li, Y. An extended TOPSIS model based on the Possibility theory under fuzzy environment. Knowl. Based Syst. 2014, 67, 263–269. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Saeed, M.; Ali, B.; Abdal, S.; Saqlain, M.; Ahamad, M.I.; Zafar, Z. Generalized Fuzzy TOPSIS to Solve Multi-Criteria Decision-Making Problems. In Proceedings of the International Conference on Emerging Trends in Smart Technologies (ICETST), Karachi, Pakistan, 26–27 March 2020. [Google Scholar]
- Çakır, E.; Demircioğlu, E. Multi-Criteria Evaluation of Battery Electric Vehicles via Circular Intuitionistic Fuzzy PROMETHEE. In Proceedings of the 2024 IEEE 18th International Symposium on Applied Computational Intelligence and Informatics (SACI), Siófok, Hungary, 21–25 May 2024; pp. 151–156. [Google Scholar] [CrossRef]
- Kumar, P.; Channi, H.K.; Kumar, R.; Stević, Ž.; Singh, S.; Bhattacherjee, A.; Bhowmik, A. Optimizing Electric Mobility: A Multi-Criteria Decision-Making Approach for Sustainable Future of Electric Vehicles through Smart Motor Choices. J. Eur. Syst. Autom. 2024, 57, 1825–1845. [Google Scholar] [CrossRef]
- Lindberg, G.; Fridstrøm, L. Policy Strategies for Vehicle Electrification. Research Papers in Economics. Discussion Paper No. 2015-16, International Transport Forum, OECD, Paris, France. 2015. Available online: https://www.itf-oecd.org/sites/default/files/docs/dp201516.pdf (accessed on 2 May 2025).
- Rocha, C.M.M.; Ospino, M.D.; Ramos, I.B.; Guzman, A.M. Enhancing Sustainable Mobility: Multi-Criteria Analysis for Electric Vehicle Integration and Policy Implementation. Int. J. Energy Econ. Policy 2024, 14, 205–218. [Google Scholar] [CrossRef]
- Alshehri, S. Multicriteria decision making (MCDM) methods for ranking estimation techniques in extreme programming. Eng. Technol. Appl. Sci. Res. 2018, 8, 3073–3078. [Google Scholar] [CrossRef]
- Taherdoost, H.; Madanchian, M. An effective compromising ranking technique for decision making. Macro Manag. Public Policies 2023, 5, 27–33. [Google Scholar] [CrossRef]
- Anand, A.; Agarwal, M.; Aggrawal, D. Multiple Criteria Decision-Making Methods; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2022. [Google Scholar] [CrossRef]
- Zulqarnain, M.; Dayan, F. Choose best criteria for decision making via fuzzy TOPSIS method. Math. Comput. Sci. 2017, 2, 113. [Google Scholar] [CrossRef][Green Version]
- Dharmalingam, M.; Mahapatra, G.S.; Georgise, F.B.; Deb, M. Comparative ranking preferences decision analysis through a novel fuzzy TOPSIS technique for vehicle selection. J. Eng. 2024, 2024, 6812801. [Google Scholar] [CrossRef]
- Toklu, M.C. The Technique for Order of Preference by Similarity to Ideal Solution Method in Fuzzy Environment: Fuzzy TOPSIS Method; Advanced multi-criteria decision making for addressing complex sustainability issues; Toklu, M.C., Ed.; IGI Global: Hershey, PA, USA, 2020; pp. 139–168. [Google Scholar] [CrossRef]
- Ceballos, B.; Lamata, M.T.; Pelta, D.A. Fuzzy multicriteria decision-making methods: A comparative analysis. Int. J. Intell. Syst. 2017, 32, 722–738. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.-H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Genç, T. Application of ELECTRE III and PROMETHEE II in evaluating the military tanks. Int. J. Procure. Manag. 2015, 8, 457–475. [Google Scholar] [CrossRef]
- Ostojic, S.; Traverso, M. Application of Life Cycle Sustainability Assessment in the automotive sector—A systematic literature review. Sustain. Prod. Consum. 2024, 47, 105–127. [Google Scholar] [CrossRef]
- Almobarek, M.; El-Sayed, M.; Hassan, M. Fleet replacement analysis by equivalent uniform annual cost method. In Proceedings of the 1st European International Conference on Industrial Engineering and Operations Management, Rome, Italy, 2–5 August 2021; Available online: https://ieomsociety.org/proceedings/2021rome/519.pdf (accessed on 6 June 2025).
- Kauffmann, P.; Howard, E.; Yao, J.; Harbinson, D.; Brooks, N.; Williams, R.; Gurganus, C. Criteria for fleet management: Identification of optimal disposal points with the use of equivalent uniform annual cost. Transp. Res. Rec. 2012, 2292, 171–178. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; He, K.; Zheng, B. Modeling fuel-, vehicle type-, and age-specific CO2 emissions from global on-road vehicles in 1970–2020. Earth Syst. Sci. Data 2024, 16, 4497–4509. [Google Scholar] [CrossRef]
- Boudart, J.; Figliozzi, M.A. Key Variables Affecting Decisions of Bus Replacement Age and Total Costs. Transp. Res. Rec. 2012, 2274, 109–113. [Google Scholar] [CrossRef]
- Corazza, M.V.; Vasari, D.; Petracci, E.; Lizana, P.C.; Pascucci, M. Facilitating Bus Fleets Emissions Assessment. In Proceedings of the International Conference on Environment and Electrical Engineering, Madrid, Spain, 9–12 June 2020. [Google Scholar] [CrossRef]
- Crespo del Castillo, A.; Parlikad, A.K. Dynamic Fleet management: Integrating predictive and preventive maintenance with operation workload balance to minimise cost. Reliab. Eng. Syst. Saf. 2024, 249, 110243. [Google Scholar] [CrossRef]
- Castillo, O.; Álvarez, R. Electrification of Last-Mile Delivery: A Fleet Management Approach with a Sustainability Perspective. Sustainability 2023, 15, 16909. [Google Scholar] [CrossRef]
- Vigneshwaran, A.; Kumar, K.A.N. Electric vehicles and their types. In Artificial Intelligence Applications in Battery Management Systems and Routing Problems in Electric Vehicles; Angalaeswari, S., Deepa, T., Kumar, L., Eds.; IGI Global: Hershey, PA, USA, 2023; pp. 92–108. [Google Scholar] [CrossRef]
- Wang, T.-C.; Lee, H.-D. Developing a fuzzy TOPSIS approach based on subjective weights and objective weights. Expert Syst. Appl. 2009, 36, 8980–8985. [Google Scholar] [CrossRef]
- Liu, G.; Wang, X. Multi-Attribute Decision-Making Method Based on Interval Intuitionistic Trapezoidal Fuzzy Number to Determine the Expert Weight. In Proceedings of the 2022 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), Melbourne, Australia, 17–19 December 2022; pp. 33–39. [Google Scholar] [CrossRef]
- Gupta, P.; Mehlawat, M.K.; Grover, N. A Generalized TOPSIS Method for Intuitionistic Fuzzy Multiple Attribute Group Decision Making Considering Different Scenarios of Attributes Weight Information. Int. J. Fuzzy Syst. 2019, 21, 369–387. [Google Scholar] [CrossRef]
- Du, X.; Lu, K.; Zhou, R.; Lv, Y.; Qiu, S.M. A Weighting Method Based on the Improved Hesitation of Pythagorean Fuzzy Sets. Electronics 2023, 12, 3001. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, W.; Chang, W. An Improved TOPSIS with Weighted Hesitant Vague Information. Chaos Solitons Fractals 2016, 89, 47–53. [Google Scholar] [CrossRef]
- Wang, P.W.; Lin, Y.; Wang, Z. An Integrated Multi-Criteria Group Decision-Making Model Applying Fuzzy TOPSIS-CRITIC Method with Unknown Weight Information. Int. J. Innov. Comput. Inf. Control 2022, 18, 815–836. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).