Abstract
Complex compounds are under close scrutiny by scientists as precursors, which are needed to produce functional materials. When the thermolysis method of double complex salts is used on an industrial scale, the most detailed information on the thermal decomposition, including the kinetics of decomposition, is required. The kinetics of pyrolysis, solid, and gaseous products of [Co(NH3)6][Fe(C2O4)3]∙2H2O (I) and [Co(en)3][Fe(C2O4)3] (II) (en—ethylenediamine) thermolysis were studied in this work. The solid products of thermal decomposition were studied using scanning electron microscopy and elemental analysis, and the specific surface area (8 and 71 m2/g, respectively) was measured. It was determined that a double complex salt (DCS) with a coordinated en has a higher thermal stability than with NH3 due to the chelation effect.
1. Introduction
The number of complex compounds of 3d metals is constantly growing. One of the reasons for this phenomenon is their potential as precursors for the synthesis of functional materials [1]. For example, it is possible to obtain nanoparticle electrodes for aqueous sodium and potassium ion batteries that can withstand at least five thousand deep cycles at high current densities [2]. Thermal decomposition is of interest as one of the methods for obtaining functional materials. Thus, for example, it is possible to obtain thermochromic materials that can withstand repeated heating–cooling cycles with a color effect temperature from 80 °C [3] to 220 °C [4]. Complexes with such complexing metals as cobalt and iron can find wide industrial applications as catalysts for the Fischer–Tropsch process [5], oxidation electrocatalysts [6], oxygen evolution reaction electrocatalysts [7], materials with interesting dielectric properties [8], and for various model catalytic reactions [9]. Therefore, their study requires increased attention.
Dividing the thermal decomposition process into several stages and calculating the characteristics for each of them helps to identify the pyrolysis mechanism at each level.
To control the multi-stage decomposition processes of substances, it is necessary to determine the kinetic parameters (activation energy, pre-exponential factor, and reaction model). This will help to predict the behavior of materials upon heating [10]. This is especially important for the development of controlled synthesis technologies. The use of non-isothermal kinetics, in particular isoconversional approaches and model-fitting methods, is necessary to establish the mechanism and rate of reactions at each stage. These data help to identify the autocatalytic mechanism of the processes. The products accelerate the reaction in these processes. Kinetic parameters also help to optimize the heat treatment conditions, namely the temperature and heating rate. The determination of kinetic parameters helps to optimize thermal treatment processes and significantly increase the efficiency of various technological processes, for example, pyrolysis of biomass and polymers [11,12], extraction of substances [13], hardening of steel [14], and the stability of drugs [15].
The developed model of thermal decomposition can be used in two main directions: firstly, as a model for an already synthesized complex, it is possible to determine the parameters of its thermal decomposition, for example, the heating rate and dwelling time, to obtain the target product with specified properties; and secondly, for the analysis of thermal decomposition models for a number of complexes with different central atoms and ligands, it makes it possible to predict the thermolysis process for new, not yet synthesized complexes with similar ligands. Thus, based on thermal decomposition models, it is possible to select the chemical composition of the complex and its decomposition parameters in order to subsequently obtain functional materials with specified properties, for example, with a certain phase composition.
It is important to study in detail the process of thermal decomposition of DCSs in connection with the probable use of thermolysis products in industry. The most complete picture can be obtained by simultaneously studying the solid and gaseous phases that form during decomposition. Despite the removal of the gas phase during the decomposition process, its presence must be taken into account from the point of view of the environmental impact when scaling up the pyrolysis process in industry. Qualitative analysis of gaseous thermal decomposition products (GTDPs) is possible using mass spectrometry (MS) and/or IR spectrometry (IR) methods.
For example, scientists from the work [16] using the MS method showed that during thermolysis in a He atmosphere of the double complex salts (DCSs) [Pt(NH3)4][VO(H2O)(C2O4)2]·2H2O (A), the following were recorded among the GTDPs: NH3, H2O, CO2, and CO. Despite the identical chemical composition of DCS {[Pt(NH3)4][VO(C2O4)2]}n (B), H2O, N2, CO2, and CO were found among the GTDPs. The solid products for DCSs A and B are identical and consist of PtxV1-x solid solution (>99%) and V2O3 (<1%). The difference in the GTDPs is probably due to the fact that DCS A has an island structure, while DCS B has a polymeric structure. During the decomposition of [Bu4N][VO(C2O4)2], CO2 and CO were also not found, as well as the decomposition products of Bu4N+.
The authors [17] used the gas phase IR analysis method to study the GTDPs of the DCSs [Co(NH3)6][Fe(CN)6] (C) and [Cu(tn)]3[Fe(CN)6]2·8H2O (tn—1,3-diaminopropan) (D) in air and nitrogen. HCN and NH3 are determined among the identical GTDPs in the nitrogen current for these complexes. H2O and tn are also recorded in the GTDPs for D. CO2, N2O, HCN, and NH3. Water is detected for both DCSs during pyrolysis in air. It was determined that the nature of the complexing agents and the structure of the DCS have a significant impact on the chemical nature and temperature range of the release of the GTDP. For example, the release of HCN occurs almost completely in one stage in the temperature range of 200–400 °C for C when calcined in an inert atmosphere, and for D in three stages in the region of 200–600 °C.
The above examples show that determining the nature of the thermal degradation process is a necessary stage in studying the thermal degradation process since even different thermal degradation processes can be observed in DCSs with identical chemical compositions.
Previously, we determined the thermokinetic parameters of decomposition and the physicochemical properties of thermolysis products for DCSs [Co(NH3)6][Fe(CN)6] and [Co(NH3)6]4[Fe(CN)6]3·13H2O [18,19]. The thermolysis of [Co(NH3)6][Fe(CN)6] occurs in two autocatalytic stages with activation energies of ≈130 kJ/mol and ≈350 kJ/mol. In [Co(NH3)6]4[Fe(CN)6]3·13H2O, the first stage occurs in a wide range of Eₐ (100–250 kJ/mol) and the second has reduced values (200–300 kJ/mol) compared to the second stage of [Co(NH3)6][Fe(CN)6] thermolysis.
Thus, the analysis of kinetic parameters is of crucial importance in the prediction and control of chemical processes, ensuring their high efficiency and cost-effectiveness. Further research in this area is the basis for developing more advanced methods for the synthesis and processing of materials.
The substitution of cyano-ligand with oxalate-ligand in the DCS anion reduces the thermal stability of the DCS [20]. This can lead to obtaining a calcination product with a higher specific surface area. This is one of the key characteristics for catalysts.
C2O42− ions are widely used as ligands in complex compounds. These DCSs are then subjected to thermolysis in the process of obtaining functional materials. For example, nanoalloys of the composition Cu–Rh and Zn–Rh were obtained by the thermolysis of systems [(C2O4)(H2O)2Rh−(μ-C2O4)−M(H2O)2−(μ-C2O4)–Rh(H2O)2(C2O4)]·6H2O (M = Cu, Zn) in He and H2 atmospheres already at 300 °C [21].
Combinations of NH3-C2O42− ligands are often used in the synthesis of DCSs since these ligands are removed at relatively low temperatures when heating the DCS. These ligands are also completely removed during thermal decomposition (they do not contaminate the resulting solid phase with pyrolysis products). For example, the complete decomposition of [M1(NH3)6][M2(C2O4)3], (M1, M2 = Co, Rh), and K3[Rh(NH3)6][Rh(C2O4)3]2∙6H2O in hydrogen and helium atmospheres resulting in metals or CoxRh1−x solid solutions is achieved at temperatures of 320–450 °C [22].
The introduction of the chelate en in the cation instead of the monodentate NH3 into the DCS [Co(A)3][Fe(C2O4)3]∙2H2O (A=2NH3, en (ethylenediamine)) was carried out in [23]. It was determined that during heat treatment in argon, in both cases the intermetallic compound CoFe is formed with a very different carbon content—15.8% for the DCS with en and 0.1% for the DCS with NH3, respectively. However, oxide phases are also present in the residue for the complex with NH3. The influence of residual carbon content on specific surface area has not been considered in this work.
Complexes with low thermally stable ligands in the anion and various ligands in the cation have been synthesized in the current study: [Co(NH3)6][Fe(C2O4)3]∙2H2O (I) and [Co(en)3][Fe(C2O4)3] (II).
The physical and chemical properties are discussed in [23,24,25]. The physical and chemical properties are as follows: thermal decomposition of [Co(NH3)6][Fe(C2O4)3]∙xH2O (x = 2.3) and [Co(en)3][Fe(C2O4)3] in various dynamic and stationary conditions with different heating rates, the study of crystal structures, and the investigation of carbon–metal compositions which are obtained by acid treatment of the solid decomposition products of DCSs are considered in [23,24,25].
Thermokinetic studies and analysis of gas products released during thermal degradation have been carried out. The physical and chemical properties of solid thermal decomposition products have been studied in detail. To level out the influence of the oxidizing effect of air and the reduce effect of hydrogen, all work has been carried out in a flow of inert gas, argon.
2. Materials and Methods
2.1. Synthesis
Yellow crystals of [Co(NH3)6][Fe(C2O4)3]·2H2O (I) and [Co(en)3][Fe(C2O4)3] (II) were obtained in a quantitative yield of ~90% by mixing solutions of K3[Fe(C2O4)3]·3H2O and a cationic precursor complex. To synthesize the DCSs, reactive K3[Fe(C2O4)3]·3H2O (synthesized according to [26]), [Co(NH3)6]Cl3 (reagent grade, Vecton, Russia), and [Co(en)3]Cl3·3H2O (synthesized according to [27]) were used.
An elemental analysis of (I), wt.%: C—14.0 ± 0.1, calculated, wt.%: C—13.9.
An elemental analysis of (II), wt.%: C—25.7 ± 0.1, calculated, wt.%: C—25.8.
The results of IR spectrometric, X-ray phase for DCSs (I) and (II) coincide with the data given in [25]. Therefore, these data are not given in this work.
2.2. Equipment
X-ray phase analysis of the initial DCS was made in the 2θ range 5–90° on a Shimadzu XRD 6000 powder diffractometer (Kyoto, Japan, 2008) equipped with a Cu-Kα source (λ = 1.5418 Å) and a graphite monochromator for the diffracted beam. The X-ray phase analysis of the calcination products was recorded on a Rigaku Mini Flex-600 powder diffractometer (Rigaku, Tokyo, Japan) equipped with a tube with a Cu anode, a Ni-Kβ filter, and a D/Tex Ultra multichannel detector in the “scanning” recording mode with a step of 0.01°, an exposure of 300 ms and suppression (discrimination) of fluorescent radiation in the secondary beam (detector option). The qualitative analysis was performed using the powder diffraction database PDF-2 2022 SN:PD2D220425-9587 (ICDD, Newtown Square, PA, USA). Data processing by the full-profile analysis method (Rietveld method) was performed in Smart Lab Studio software v.4.5.286.0 (Rigaku, Japan). The software is supplied with the device.
IR spectra for solid samples were recorded on a Nicolet 6700 FT-IR spectrometer in the 400–4000 cm−1 region, KBr pellets (Thermo Fisher Scientific Inc., Hillsboro, OR, USA, 2010). The porous structure of the samples and value-specific surface areas were studied by the method of low-temperature sorption of nitrogen on a Tristar 3020 instrument (Norcross, GA, USA, 2009). To determine the morphology of the final solid products, micrographs were taken using a scanning digital electron microscope with the SEM LEO-420 software V03.01 (LEO Electron Microscopy Ltd., Cambridge, UK 1995). Elemental analysis was carried out using the analyzer ELTRA-2000 (Alpha Resources, LLC, Stevensville, MI, USA, 2004).
2.3. Simultaneous Thermal Analysis (STA)
2.3.1. STA Measurements for Kinetics Research
A comprehensive thermal analysis, including thermogravimetry (TG) and differential scanning calorimetry (DSC), was conducted using the STA 449 F1 Jupiter micro-thermal analyzer (Zelb Gerbruder-Netzsch strasse, Selb, Germany, 2014). The experiments were carried out in an argon atmosphere with a gas flow rate of 75 mL/min. The samples were heated at rates of 1, 5, 10, 15, and 20 °C/min within a temperature range of 40 to 1000 °C. Sample masses between 10 and 20 mg were placed in Al2O3 crucibles (40 µL) covered with lids featuring a single 0.5 mm hole for the analysis.
2.3.2. Kinetic Analysis
Kinetic parameters were determined using both model-fitting methods and isoconversional approaches. To evaluate the activation energy of the thermolysis process, Friedman’s analysis and the Kissinger–Akahira–Sunose (KAS) method were employed. Model-based methods involve the estimation of kinetic parameters by minimizing the discrepancy between experimental and theoretical values. This minimization was carried out using linear regression techniques. The models analyzed included n-dimensional nucleation following an nth-order reaction (Fn), the Avrami–Erofeev model (An), an nth-order reaction with m-power autocatalysis by the product (Cnm), the extended Prout–Tompkins equation (Bna), and the expanded Sestak–Berggren equation (Sb). The description of the model is given in [20]. Thermolysiskinetic parameters were derived based on various heating rates. The kinetic analysis was performed in accordance with ICTAC recommendations [10,28] using the NETZSCH Kinetics Neo 2.6.6.7 software package. The decomposition curves were divided into several stages according to the differential TG data (Figure S1).
2.3.3. Synchronous Thermal Analysis + IR
Synchronous thermal analysis with IR-spectroscopic analysis of exhaust gases (STA+IR) was performed on an HQT-4 device (Beijing Hengjiu HENVEN Experimental Equipment Co., Ltd., Beijing, China, 2022) in argon flow in open Al2O3 lids. The flow rate was 71 mL/min, sample mass was 15 mg, heating rate was 10 °C/min, and temperature range was 40–900 °C.
The IR spectroscopic analysis of the evolved gases was performed using an SC-8000 device (Beijing Hengjiu Experimental Equipment Co., Ltd., Beijing, China, 2022) in a flow of dried air. The spectra were continuously registered in the 400–4000 cm−1 wavelength and 40–900 °C temperature ranges in 16 scans. The temperature of the Pike chamber and pipeline was 200 °C. Qualitative analysis was performed using HR Nicolet TGA Vapor Phase, HR Aldrich Vapor, and other libraries. A detailed description of the method of identification of gaseous products is given below. Examples of the identification of gaseous products are given in the Supplementary Materials (Figure S2). The temperatures that correspond to the most intense gas emission were selected.
Methodology for the identification of gaseous products by the STA-IR method.
- By operating a synchronous thermal analysis device with IR analysis of the gas phase, thermogravimetric data and an array of IR spectrometric data in .srs format were obtained (see Figure 1). The data array is obtained in the form of a three-dimensional diagram. Coordinates of diagram: time, transmittance, and wavenumber (λ).
 Figure 1. The result of the STA-IR analysis.
Figure 1. The result of the STA-IR analysis. - Thermal analysis data helped determine the temperature in the thermogravimetric curve that corresponds to maximum mass loss. A general IR spectrum is observed at this time in the wavelength range of 400–4000 cm−1.
- We apply the “automatic search by integrated libraries” feature of the Omnic program to this IR spectrum. We configure the autosearch for 50 hypothetical gas products. In our experience, more than this number is often not necessary.
- We manually select gas products based on the following criteria: (1) matching chemical nature (chemical elements that were not part of the original uncalcined compound cannot be released); and (2) experience from literary sources.
- Thus, ~10 of the most likely actually released ones are selected from 50 hypothetical gas products.
- We search libraries for the spectra of these 10 compounds in the gaseous state. It is critical that the compounds be in the gaseous, not condensed, state.
- We select the wavelength values λ with the highest intensity in each of the 10 library spectra. For example, we considered 4 wavelengths (647, 675, 2360, and 3595 cm−1) in the case of CO2.
- We cut out the spectrum in the “time-transmission” coordinates for each of the selected wavelengths in the .srs data array.
- Plot all the obtained spectra on a single graph. The number of spectra on the graph should correspond to the number of wavelengths chosen as characteristic wavelengths. If necessary, the spectra are enlarged; therefore, that they have the same intensity. Here, a multiplication factor is introduced, which is given in a separate table (for example, in this work it is in Table 1). If the curves match, the gaseous product is considered present in the exhaust gases. If they do not match, the product is considered absent.
 Table 1. Parameters of the IR spectroscopic analysis of the evolving gases and multiplication factors.
Table 1. Parameters of the IR spectroscopic analysis of the evolving gases and multiplication factors. - If a gaseous product, according to points 1–9, is present in the gas mixture, then one spectrum with the highest intensity is selected for identification. For example, we considered 2360 cm−1 in the case of CO2. However, it is necessary to analyze all spectra for all products simultaneously. Since if there is an overlap for any characteristic frequencies (for example, a product with a high intensity at closely spaced wavelengths may obscure a product with a lower intensity), these spectra cannot be considered for identification and further processing. For example, if 10 gas products are detected and 4 characteristic wavelengths are selected for each product, then 40 spectra must be considered for overlap simultaneously.
- The most intense spectra for the identified gaseous products (one product is one spectrum) are subjected to mathematical processing and reconstructed into one common summary graph with “temperature–transmission” axes.
A similar approach to the analysis of STA-IR data during the thermolysis of DCSs was first presented in 2017 [19], and the same method was used in a 2025 work [29]. The wavelengths used for the product’s identification are collected in Table 1.
The presence of some more non-identified products may be caused by the overlapping of characteristic bands and their presence at the detectability limit.
When heating a relatively small sample mass of the initial DCS, the amount of the evolving gases is relatively insignificant. Therefore, it is difficult to obtain an intense IR signal of the released gaseous products. The spectrum, which is given in Section 3.2. “Analysis of Gaseous Products of Thermal Decomposition”, are provided with a certain multiplication factor for a more convenient perception of the obtained data. The amount of gases released for these compounds is comparable due to the similar composition and structure. Therefore, the multiplication factors for some gaseous products of thermal decomposition coincide (Table 1).
2.3.4. Static Thermal Analysis
The calcinated of double salt samples were placed in quartz vessels and heated in a Nabertherm RT 50-250/11 programmable tube furnace (Nabertherm GmbH, Lilienthal, Germany, 2013) under argon flow at 950 °C (upon reaching this temperature the mass loss almost ceases); the heating rate was 10 °C/min for 1 h. The products were cooled in an argon atmosphere. The samples were designated I-950 and II-950, respectively.
3. Results and Discussion
3.1. Kinetics
The mismatch of the TG curves is observed during the calcination of I in argon in [23,24,25] and in this investigation (Figure 2).
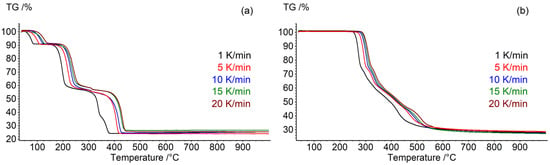
Figure 2.
TG heating curves of samples: (a) (I) and (b) (II) at rates of 1, 5, 10, 15, and 20 K/min in a dynamic argon atmosphere (75 mL/min).
The end of thermal decomposition (the minimum level of the TG curve) occurs at speeds of 5 and 10 °C and at very close temperatures of the order of ~430 °C in this work (STA for calculating the kinetics and for determining the nature of GTDPs were carried out on two different instruments) and in [23,24]. Thermolysis ends at 350 °C in [20], and the authors do not explain the discrepancy between the experimental data from [23,24]. However, the course of the curves in this work and [20] is the same, only the TG curve is significantly narrowed along the temperature axis in article [20]. The explanation of this observation is currently difficult.
Also, “dips” are clearly visible on the TG curves at ~430 °C. This may indicate the use of argon mixed with oxygen in the products [23,24]. The maximally reduced metals are formed during the calcination of DCSs in an argon current up to ~430 °C. The oxidation of metals, the formation of oxides, and the increase in mass along the TG curve begin at higher temperatures.
An opposite situation is observed for DCS II. The TG curve in this study and in [20] have significant similarities both in the course of weight loss and in temperature ranges.
The effect of the ligand of a coordinated ligand of a cation can be considered using the example of the pyrolysis process of [Co(A)6]x[Fe(CN)6]y·nH2O (A=NH3, en/2, 2< n <15), x = y = 1 or x = 4, y = 3 [30]. The STA data show that complexes with the same degree of iron oxidation (the ratio of central atoms Co:Fe = 1:1) have extremely similar TG curves and the temperature at which the TG curve reaches the plateau, respectively. However, point static experiments indicate that the formation of monophase solid compositions of CoxFeyCz for DCSs with NH3 occurs at lower temperatures than for DCSs with en.
The data indicate that DCSs coordinated with en exhibit higher thermal stability compared to DCSs with NH3. This is explained by the fact that en is a chelating ligand.
The results of thermogravimetric analysis (Figure 2) show that each of the samples is characterized by a complex multi-stage thermal decomposition process. The thermolysis process of DCS (II) was conditionally divided into three stages of outgoing DTG data: from 240 to 320 °C is the first stage, from 320 °C to 380 °C is the second stage, and from 380 °C to 600 °C is the third stage. For (I), the thermolysis process was conditionally divided into four stages: the first from 50 to 150 °C, the second from 150 to 280 °C, the third from 280 to 330 °C, and the fourth from 330 to 460 °C.
To determine the kinetic parameters of the thermolysis process of the samples, Friedman’s analysis and the Kissinger–Akahira–Sunose (KAS) isoconversional approaches were used. The values of activation energy (E) and pre-exponential factor (logA) calculated using isoconversional approaches for the thermolysis process of the studied samples are presented in Figures S3–S9. Taking into account the change in kinetic parameters, thermolysis stages (II) are characterized by single-stage processes with increasing degrees of conversion. This distinguishes them from (I), which exhibits a “shoulder” at stages 2, 3, and 4. “Shoulder” indicates a two-stage process. The average values of the kinetic parameters of the thermolysis process of (II) and (I) determined using isoconversional approaches are presented in Table 2 and Table 3.

Table 2.
Kinetic parameters of the thermolysis process of (II) and (I) determined using isoconversion approaches.

Table 3.
Kinetic parameters of the thermolysis process of (I) determined using model methods.
During thermolysis (I), an increase in energy is observed in the initial stages from 65 to 70 kJ/mol, and the energy increases to 200–220 kJ/mol in the later stages. This indicates the complex nature of the processes taking place. The activation energy increases from 188 to 199 kJ/mol and reaches a maximum of 320–330 kJ/mol in the thermolysis of (II). This also indicates a change in the nature of the thermolysis process. However, close values of the activation energy of thermolysis are observed: ~150 kJ/mol at the last stage in the case of (I) and the last stage in the case of (II). This may indicate the same speed and mechanism for obtaining the final product.
A model method was used for a detailed study of individual stages of the thermolysis process of the studied samples. The analyzed models included n-dimensional nucleation following an nth-order reaction (Fn), the Avrami–Erofeev model (An), an nth-order reaction with m-power autocatalysis by the product (Cnm), the extended Prout–Tompkins equation (Bna), and the expanded Sestak–Berggren equation (Sb). These models are most often used to determine the kinetic parameters of chemical reactions, including thermolysis parameters. The models with the best correlation coefficient (R2) values are presented in Table 3 and Table 4.

Table 4.
Kinetic parameters of the thermolysis process of (II) determined using model methods.
The analysis of the kinetic parameters of the thermolysis process of (I) and (II) carried out using model-fitting methods confirms the complex and multi-stage nature of the processes.
The data presented in Table 3 indicate that the Cnm model is optimal for describing all stages of the (I) thermolysis process. This model demonstrates high compliance with the experimental data (the correlation coefficient R2 varies from 0.98990 to 0.99993). The activation energy increases from 67 kJ/mol in the first stage to 216 kJ/mol in the third stage. This indicates a change in the mechanism with increasing temperature. The activation energy decreases to 122.2 kJ/mol at the fourth stage. The pre-exponential factor also increases from 7.2 to 17.7, and the reaction order with a value of 4.3 reaches a maximum in the third stage, and this emphasizes the complexity of the kinetic process. High values of the autocatalytic factor 2.99, can indicate a significant role of autocatalysis.
Table 4 presents the results for (II). The optimal model at the first stage describing the ongoing processes is the Cnm model (R2 = 0.99980), the activation energy is 201.3 kJ/mol and log(A) = 13.3. The process is divided into two stages at the second stage: the first is described by the Sb model (expanded Sestak–Berggren equation) (E = 217.9 kJ/mol); the second is described by the Cnm model (E = 283.2 kJ/mol), the parameter m takes the value 10, this can indicate a strong contribution of autocatalysis. The third stage of thermolysis of (II) is well described using Cnm models and also consists of two stages: the activation energy of the first reaches 315.6 kJ/mol, but decreases in the second stage to 120.6 kJ/mol.
Comparison of the results of the model method with the data of isoconversional approaches (Friedman’s Analysis and KAS model) shows good convergence. The E values are close to the isoconversional values (65–220 kJ/mol) for (I). They were determined using model approaches (67.2–216.2 kJ/mol). The results of the model method (201.3–315.6 kJ/mol) are also consistent with the values determined using isoconversional approaches (188–340 kJ/mol) for (II). The activation energies of both samples at the final stages have similar values—22.2 kJ/mol for (I) and 120.6 kJ/mol for (II). This is consistent with the isoconversional data (~150 kJ/mol) and may indicate the similarity of the mechanism and rate of the final decomposition process.
It is worth noting that all stages and phases of the thermolysis process of (I) and (II) samples are described by autocatalytic models of Cnm and Sb. This indicates a major role of decomposition products in accelerating reactions. The Cnm model consistently describes all stages with a high correlation coefficient (R2 from 0.98990 to 0.99993) for (I) and the autocatalytic factor (m) values reach 2.99. This indicates a strong influence of autocatalysis, especially in the third stage. The autocatalytic model Cnm is also optimal for (II), especially in the second and third stages, where the parameter m reaches a high value and is equal to 10.0. The data indicate a pronounced autocatalytic effect. Thermolysis of (I) and (II) occurs through complex multi-stage processes with pronounced autocatalysis. This confirms the need for precise temperature control for optimal production of the final product under industrial conditions. The obtained data can be used to develop energy-efficient technologies for the synthesis of nanostructured materials using thermolysis.
3.2. Analysis of Gaseous Products of Thermal Decomposition
Figure 3 provides the results of STA with IR analysis of evolving gases. Hence, most intense bands were identified as belonging to the following gaseous products: H2O, CO2, CO, and NH3. The unchanged ligands of the cation (NH3 for (I) and en for (II)) are removed during the heating process. Ammonia released during thermolysis of (II) is a product of the thermal degradation of en. The release of N2O for (I) was recorded for a similar reason: the transformation of NH3. The replacement of the ligand in the cation led to a change in the amount of NH3 released.
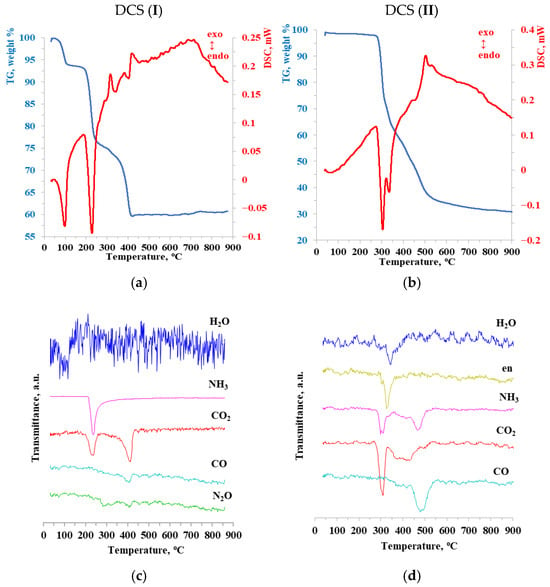
Figure 3.
Synchronous thermal analysis with IR at the end of the gas phase: (a,c) [Co(NH3)6][Fe(C2O4)3]∙2H2O; (b,d)—[Co(en)3][Fe(C2O4)3].
The results of thermogravimetric analysis and IR analysis of the GTDPs are shown in Figure 2. The thermolysis process for DCS (I) can be roughly divided into four stages. These stages can be correlated with the release of the following GTDPs. The first stage (from 50 to 150 °C) is characterized by an endothermic process with a minimum at 100 °C; water removal is also recorded. The second stage (150 to 280 °C) is characterized by an endothermic process with a minimum at 200 °C and the release of the first stage of CO2 and ammonia. The third stage occurs from 280 to 330 °C. An exothermic process is observed with a maximum at 300 °C and traces of N2O are detected. The fourth stage (from 330 to 460 °C) is accompanied by an exothermic process with a maximum at 420 °C and gaseous products include CO, CO2, and N2O.
The process of thermolysis of DCS (II) was roughly divided into three stages. No loss of mass, caloric effects, and, consequently, no release of GTDPs are observed up to a temperature of 240 °C. The first stage of decomposition (heating from 240 to 320 °C) is accompanied by an endoeffect with a minimum at 300 °C; the release of CO2, NH3, and the beginning of the release of en and water are recorded. Simultaneous intensity maxima are observed at ~290 °C for en, CO2, and NH3. The end of the release of NH3 coincides with the beginning of the release of en; therefore, initially, the decomposition of en and the removal of its degradation products occurs, then the removal of en in its unchanged form begins. The second stage of thermal decomposition (from 320 °C to 380 °C) is accompanied by an endoeffect with a minimum at 340 °C; an insignificant portion of NH3 is released among the GTDPs: en, CO2, and the main is water. The third stage (380 °C to 600 °C) is accompanied by an exothermic effect with a maximum at 500 °C. The third stage of the release of ammonia, the main part of CO and a small amount of CO2 are noted among the GTDPs.
Each of the DCS, (I) and (II) samples is characterized by a complex multi-stage process of thermal decomposition. GTDP identification follows a series of clearly defined steps. These steps correlate well with the temperature ranges that were determined using kinetic analysis. The increase in the complexity of the cationic ligand led to a change in the chemical composition of the GTDPs and the temperature range of their release. It should be emphasized that if each peak of GTDP release has one minimum for DCS (I), then almost all peaks, except for the CO peak, have several minima for DCS (II). For example, the GTDP of CO2 and NH3 have three minima in a relatively narrow temperature range of 280–320 °C. This indicates the occurrence of several successive processes accompanied by the release of identical GTDPs.
3.3. Analysis of Solid Products of Thermal Decomposition
The decomposition products of [Co(NH3)6][Fe(C2O4)3]∙2H2O and [Co(en)3][Fe(C2O4)3] at 950 °C were further investigated. Changing the ligand in the cation altered the course of thermal decomposition. The structure (Table 5) and morphology of the resulting solid phase (Figure 4) also changed. An element analysis revealed that increasing the amount of initial carbon content resulted in a significant change in the residual amount of carbon. This explains the difference in specific surface area by almost 10 times. It was previously shown that residual carbon forms the main part of the specific surface area of the solid residue from calcination [30].

Table 5.
Physicochemical properties of pyrolysis products in Ar DCSs (I) and (II) at 950 °C.

Figure 4.
SEM micrographs of calcination products: (a,c,e) [Co(NH3)6][Fe(C2O4)3]∙2H2O; (b,d,f) [Co(en)3][Fe(C2O4)3].
The average pore size of II-950 is two times smaller than that of I-950. This occurred because a relatively large amount of GTDPs of DCSs with the NH3 ligand were released over a relatively narrow temperature range. Moreover, the reducing power of NH3 was low compared to en and its decomposition products, respectively. This also applies to explaining the difference in the nature of the solid products that are formed. II-950 consists entirely of the reduced form of CoFe, while I-950 consists only of half the reduced form of CoFe (Co7Fe3).
The solid products of the thermolysis of two DCSs have a structure of layered plates, often rectangular in shape. As was previously determined by the Scherrer equation, the crystallite size of I-950 is higher than that of II-950. This is confirmed by scanning electron microscopy (SEM) data.
Thus, the generalized scheme of thermal decomposition of DCSs can be represented as follows.
[Co(NH3)6][Fe(C2O4)3]∙2H2O → CoFe2O4 + Co7Fe3 + α-Co + H2O + NH3 + CO + CO2 + N2O
[Co(en)3][Fe(C2O4)3] → CoFe + H2O + en + NH3 + CO + CO2
Stoichiometric coefficients were not determined. This is because the objective of this study was not to quantitatively evaluate the ratio of various solid and gaseous products. It should be noted that the release of water in case (I) occurs due to the removal of coordinated water molecules, while water is a product of the oxidation of coordinated ligands for case (II).
4. Conclusions
Despite the related structure of DCSs [Co(NH3)6][Fe(C2O4)3]∙2H2O (I) and [Co(en)3][Fe(C2O4)3] (II), the processes of their thermal decomposition and the products of their pyrolysis have a large number of differences.
The thermolysis of (I) occurs in four stages in the range from 50 to 460 °C. The process begins with a relatively low activation energy (65–70 kJ/mol) at the initial stages and reaches higher values (up to 220 kJ/mol) at subsequent stages. Additionally, (II) decomposes in three stages at higher temperatures (from 240 to 600 °C). (II) is more thermally stable; the activation energy is already 188–199 kJ/mol at the first stage and the maximum values reach 330 kJ/mol. In addition, both samples are characterized by similar values of kinetic parameters at the final stage. This may indicate similar rates and mechanisms of formation of the final product. Thus, the decomposition of (II) occurs at higher temperatures and is characterized by higher activation energies. This confirms its greater stability compared to (I).
Replacing ammonia in the cationic ligand with en resulted in a 9-fold increase in the specific surface area and a 2-fold decrease in the pore size. The nature of the gaseous products is uniform (H2O, CO2, CO, NH3): unchanged cation ligands and its degradation products. However, the temperature ranges and the number of release stages differ significantly between DCS (I) and (II). This confirms the difference in the mechanisms of pyrolysis. It was determined that DCSs coordinated with en have greater thermal stability than that coordinated with NH3 due to the chelation effect.
The formation of a single-phase decomposition product of wairauite for DCS [Co(en)3][Fe(C2O4)3] makes it possible to consider this salt as a promising precursor for catalysts for the Fischer–Tropsch process.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/thermo5040050/s1, Figure S1: DTG curves of samples (a) [Co(NH3)6][Fe(C2O4)3]∙2H2O and (b) [Co(en)3][Fe(C2O4)3] at rates of 1, 5, 10, 15, and 20 K/min in a dynamic argon atmosphere (75 mL/min); Figure S2: IR spectra of gaseous products at temperatures, that correspond to the most intense gas emissions (a) [Co(NH3)6][Fe(C2O4)3]∙2H2O and (b) [Co(en)3][Fe(C2O4)3]; Figure S3: Dependence of activation energy (a) and pre-exponential factors (b) on conversion for stage 1 of the thermolysis process of [Co(NH3)6][Fe(C2O4)3]∙2H2O; Figure S4: Dependence of activation energy (a) and pre-exponential factors (b) on conversion for stage 2 of the thermolysis process of [Co(NH3)6][Fe(C2O4)3]∙2H2O; Figure S5: Dependence of activation energy (a) and pre-exponential factors (b) on conversion for stage 3 of the thermolysis process of [Co(NH3)6][Fe(C2O4)3]∙2H2O; Figure S6: Dependence of activation energy (a) and pre-exponential factors (b) on conversion for stage 4 of the thermolysis process of [Co(NH3)6][Fe(C2O4)3]∙2H2O; Figure S7: Dependence of activation energy (a) and pre-exponential factors (b) on conversion for stage 1 of the thermolysis process of [Co(en)3][Fe(C2O4)3]; Figure S8: Dependence of activation energy (a) and pre-exponential factors (b) on conversion for stage 2 of the thermolysis process of [Co(en)3][Fe(C2O4)3]; Figure S9: Dependence of activation energy (a) and pre-exponential factors (b) on conversion for stage 3 of the thermolysis process of [Co(en)3][Fe(C2O4)3].
Author Contributions
Conceptualization, A.G. (Alevtina Gosteva), A.G. (Alexander Gerasimov); methodology, A.G. (Alevtina Gosteva), S.L.; validation, S.L., A.G. (Alevtina Gosteva); formal analysis S.L.; investigation, A.G. (Alevtina Gosteva), S.L.; resources, A.G. (Alevtina Gosteva); data curation A.G., S.L.; writing—original draft preparation, A.G. (Alevtina Gosteva), S.L., A.G. (Alexander Gerasimov); writing—review and editing, A.G. (Alevtina Gosteva), S.L., A.G. (Alexander Gerasimov); visualization, S.L.; supervision, A.G. (Alevtina Gosteva), A.G. (Alexander Gerasimov); project administration, A.G. (Alevtina Gosteva), A.G. (Alexander Gerasimov); funding acquisition, A.G. (Alevtina Gosteva). All authors have read and agreed to the published version of the manuscript.
Funding
The work was carried out within the framework of the Russian Science Foundation; Project No. 24-29-20076.
Data Availability Statement
The raw data required to reproduce these findings are available from authors on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DCS | double complex salt |
| STA | synchronous thermal analysis |
| TG | thermogravimetry |
| DSC | differential scanning calorimetry |
| STA+IR | synchronous thermal analysis with IR-spectroscopic analysis of exhaust gases |
| GTDP | gaseous thermal decomposition products |
| XRD | X-ray diffraction |
| SEM | scanning electron microscopy |
| en | ethylenediamine |
| tn | 1,3-diaminopropan |
References
- Rudneva, Y.V.; Korenev, S.V. Dispersed Metal Alloys: Synthesis Methods and Catalytic Properties (Review). Žurnal Neorganičeskoj Himii 2024, 69, 1181–1200. (In Russian) [Google Scholar] [CrossRef]
- Wessells, C.D.; Peddada, S.V.; Huggins, R.A.; Cui, Y. Nickel Hexacyanoferrate Nanoparticle Electrodes For Aqueous Sodium and Potassium Ion Batteries. Nano Lett. 2011, 11, 5421–5425. [Google Scholar] [CrossRef] [PubMed]
- Mezentsev, K.V.; Cherkasova, T.G. Reversible Chrome Thermoindicator. RU Patent No. 2187081 C1, 2002. Available online: https://patents.google.com/patent/RU2187081C1/en (accessed on 10 October 2025).
- Cherkasova, T.G.; Tatarinova, E.S.; Kuznetsova, O.A.; Trjasunov, B.G. Reversible Thermochromic Materials. RU Patent No. 2097714 C1, 1997. Available online: https://patents.google.com/patent/RU2097714C1/en (accessed on 10 October 2025).
- Scherzer, J.; Fort, D. Zeolite-supported metal catalysts for Fischer-Tropsch reactions: I. A new preparation method. J. Catal. 1981, 71, 111–118. [Google Scholar] [CrossRef]
- Khan, R.; Arshad, J.; Khan, S.; Mansoor, M.A.; Ali, S.; Nisar, T.; Wagner, V.; Asghar, M.A.; Haider, A. Surfactant-assisted fabrication of prussian blue analogs as bifunctionalelectrocatalysts for water and hydrazine oxidation. Mol. Catal. 2023, 548, 113415. [Google Scholar] [CrossRef]
- Lin, Y.; Ren, H.; Zhang, S.; Liu, S.; Zhao, T.; Jiang, W.J.; Zhou, W.; Hu, J.S.; Li, Z. Enhancing Interfacial Dynamic Stability Through Accelerated Reconstruction to Inhibit Iron—Loss During Initial Electrochemical Activation. Adv. Energy Mater. 2024, 14, 2302403. [Google Scholar] [CrossRef]
- Liang, C.; Liu, P.; Xu, J.; Wang, H.; Wang, W.; Fang, J.; Wang, Q.; Shen, W.; Zhao, J. A simple method for the synthesis of Fe-Co Prussian Blue analogue with novel morphologies, different structures, and dielectric properties. Synth. React. Inorg. Met-Org. Nano-Met. Chem. 2011, 41, 1108–1113. [Google Scholar] [CrossRef]
- Domonov, D.P.; Pechenyuk, S.I.; Semushina, Y.P.; Yusenko, K.V. Solid-state transformations in inner coordination sphere of [Co(NH3)6][Fe(C2O4)3]∙ 3H2O as a route to access catalytically active Co-Fe materials. Materials 2019, 12, 221. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Mahmood, H.; Moniruzzaman, M.; Yusup, S.; Khan, M.I.; Khan, M.J. Kinetic modeling and optimization of biomass pyrolysis for bio-oil production. Energy Sour. A 2016, 38, 2065–2071. [Google Scholar] [CrossRef]
- Chen, X.; Liu, L.; Zhang, L.; Zhao, Y.; Zhang, Z.; Xie, X.; Qiu, P.; Chen, G.; Pei, J. Thermogravimetric analysis and kinetics of the co-pyrolysis of coal blends with corn stalks. Thermochim. Acta 2018, 659, 59–65. [Google Scholar] [CrossRef]
- Toda, T.A.; Visioli, P.D.C.F.; de Oliveira, A.L.; da Costa Rodrigues, C.E. Conventional and pressurized ethanolic extraction of oil from spent coffee grounds: Kinetics study and evaluation of lipid and defatted solid fractions. J. Supercr. Fluids 2021, 177, 105332. [Google Scholar] [CrossRef]
- Sarkar, R.; Li, Z. Isothermal and non-isothermal crystallization kinetics of mold fluxes used in continuous casting of steel: A review. Metall. Mater. Trans. B 2021, 52, 1357–1378. [Google Scholar] [CrossRef]
- Jelić, D.; Papović, S.; Vraneš, M.; Gadžurić, S.; Berto, S.; Alladio, E.; Gajić, D.; Janković, B. Thermo-analytical and compatibility study with mechanistic explanation of degradation kinetics of ambroxol hydrochloride tablets under non-isothermal conditions. Pharmaceutics 2021, 13, 1910. [Google Scholar] [CrossRef]
- Vorobyeva, S.N.; Rudzis, Z.V.; Sukhikh, T.S.; Filatov, E.Y.; Plusnin, P.E.; Nadolinny, V.A.; Bogomyakov, A.S.; Korenev, S.V. Double complex salts based on tetraamminplatinum (II) and vanadyl (IV) bisoxalate for the preparation of bimetallic Pt–Valloys. N. J. Chem. 2024, 48, 15894–15903. [Google Scholar] [CrossRef]
- Pechenyuk, S.I.; Domonov, D.P.; Shimkin, A.A.; Semushina, Y.P.; Ivanov, Y.V. Thermal behavior of binary complex compoundscontaining the hexacyanoferrate anion. Russ. J. Gen. Chem. 2017, 87, 2212–2223. [Google Scholar] [CrossRef]
- Gosteva, A.N.; Kulikova, M.V.; Ivantsov, M.I.; Grabchak, A.A.; Semushina, Y.P.; Lapuk, S.E.; Gerasimov, A.V.; Tsvetov, N.S. CO2 Hydrogenation over Fe-Co Bimetallic Catalyst Derived from the Thermolysis of [Co(NH3)6][Fe(CN)6]. Catalysts 2023, 13, 1475. [Google Scholar] [CrossRef]
- Gosteva, A.N.; Kulikova, M.V.; Svidersky, S.A.; Grabchak, A.A.; Lapuk, S.E.; Gerasimov, A.V. CO2 hydrogenation reaction on catalysts based on double complex Fe-Co salts. Mendeleev Commun. 2025, in press.
- Filatov, E.Y.; Semushina, Y.P.; Gosteva, A.N. Obtaining and catalytic properties investigation of the products of double-complex salts [Cr(ur)6][M(L)6] thermal oxidation (M= Co, Fe; L= CN−, 1/2C2O42−). J. Therm. Anal. Calorim. 2018, 134, 355–361. [Google Scholar] [CrossRef]
- Garkul, I.A.; Zadesenets, A.V.; Filatov, E.Y.; Baidina, I.A.; Plyusnin, P.E.; Urlukov, A.S.; Potemkin, D.I.; Korenev, S.V. Double oxalates of Rh(III) with Cu(II) and Zn(II)—Effective precursors of nanoalloys for hydrogen production by steam reforming of propane. Int. J. Hydrogen Energy 2024, 82, 611–623. [Google Scholar] [CrossRef]
- Smirnov, P.; Filatov, E.; Kuratieva, N.; Plyusnin, P.; Korenev, S. Crystal Structure and Thermal Properties of Double-Complex Salts [M1(NH3)6][M2(C2O4)3] (M1, M2 = Co, Rh) and K3[Rh(NH3)6][Rh(C2O4)3]2∙6H2O. Int. J. Mol. Sci. 2023, 24, 12279. [Google Scholar] [CrossRef]
- Pechenyuk, S.I.; Semushina, Y.P.; Mikhailova, N.L.; Ivanov, Y.V. Binary complexes [Co(A)6][M(C2O4)3] (A = NH3, 1/2C2H8N2, M = Fe, Cr): Synthesis, properties, and thermal decomposition. Russ. J. Coord. Chem. 2015, 41, 175–181. [Google Scholar] [CrossRef]
- Yusenko, K.V.; Pechenyuk, S.I.; Vikulova, E.S.; Semushina, Y.P.; Baidina, I.A.; Filatov, E.Y. Isostructurality and Thermal Properties in the Series of Double Complex Salts [M1(NH3)6][M2(C2O4)3]·3H2O (M1 = Co, Ir, M2 = Fe, Cr). J. Struct. Chem. 2019, 60, 1062–1071. [Google Scholar] [CrossRef]
- Domonov, D.P.; Pechenyuk, S.I.; Semushina, Y.P.; Kadyrova, G.I. Solid-state transformations by thermal decomposition of [Co(en)3][Fe(C2O4)3] in an inert atmosphere. Thermochim. Acta 2020, 687, 178578. [Google Scholar] [CrossRef]
- Brauer, G. Handbook of Preparative Inorganic Chemistry; Academic Press: New York, NY, USA, 1985; Volume 5, pp. 1744–1762. [Google Scholar]
- Novakovskii, M.S. Laboratory Work on the Chemistry of Complex Compounds; Kommunist: Khar‘kov, Northeastern Ukraine, 1972; p. 66. [Google Scholar]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Pérez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Charkin, D.O.; Gosteva, A.N.; Kireev, V.A.; Banaru, A.M.; Dmitriev, D.N.; Deyneko, D.V.; Tsvetov, N.S.; Tananaev, I.G.; Aksenov, S.M. Double sulfates with 1-methylpiperazinediium and divalent cations: Synthesis, structures, spectroscopic characterization, thermal stability, and topological features of (C5H14N2)[M(H2O)6](SO4)2∙H2O (M = Mg, Mn, Fe, Co, Ni, Zn, and Cd) and (C5H14N2)(SO4)∙H2O. Polyhedron 2025, 117763. [Google Scholar] [CrossRef]
- Pechenyuk, S.I.; Domonov, D.P.; Semushina, Y.P.; Tsvetov, N.S.; Kadyrova, G.I.; Belyaevskii, A.T. Metal-carbon compositions as thermolysis products of complex compounds [Co(A)6]x[Fe(CN)6]y·nH2O (A = NH3, en/2). Thermochim. Acta 2021, 703, 179009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).