Stratification-Induced Porosity Variations in Granular Packings—Part II: A Step Closer to Natural Sediments via DEM
Abstract
1. Introduction
Porosity Predictor of Yu & Standish for Well-Mixed Grain Packings
2. Numerical Simulation
2.1. Methodology
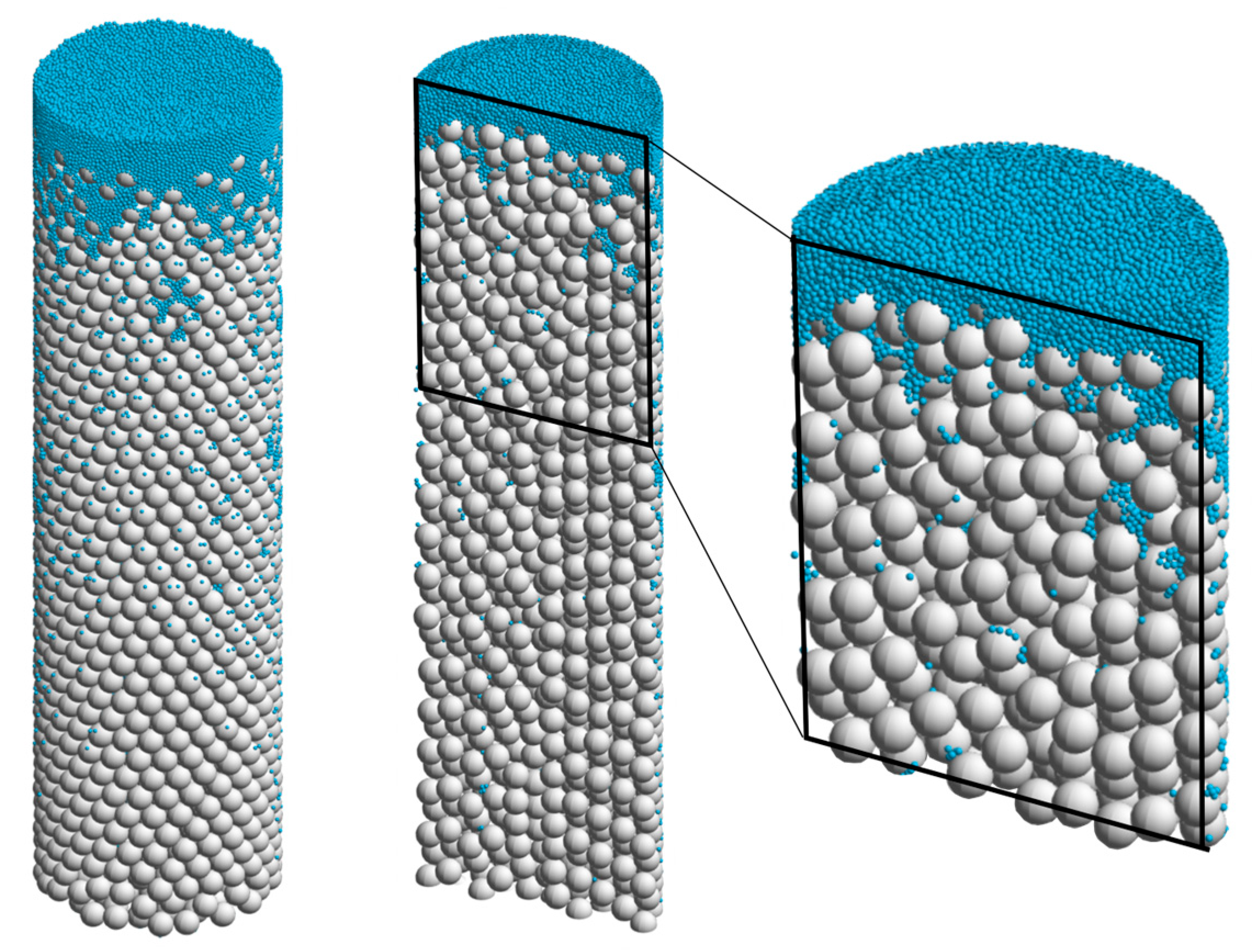
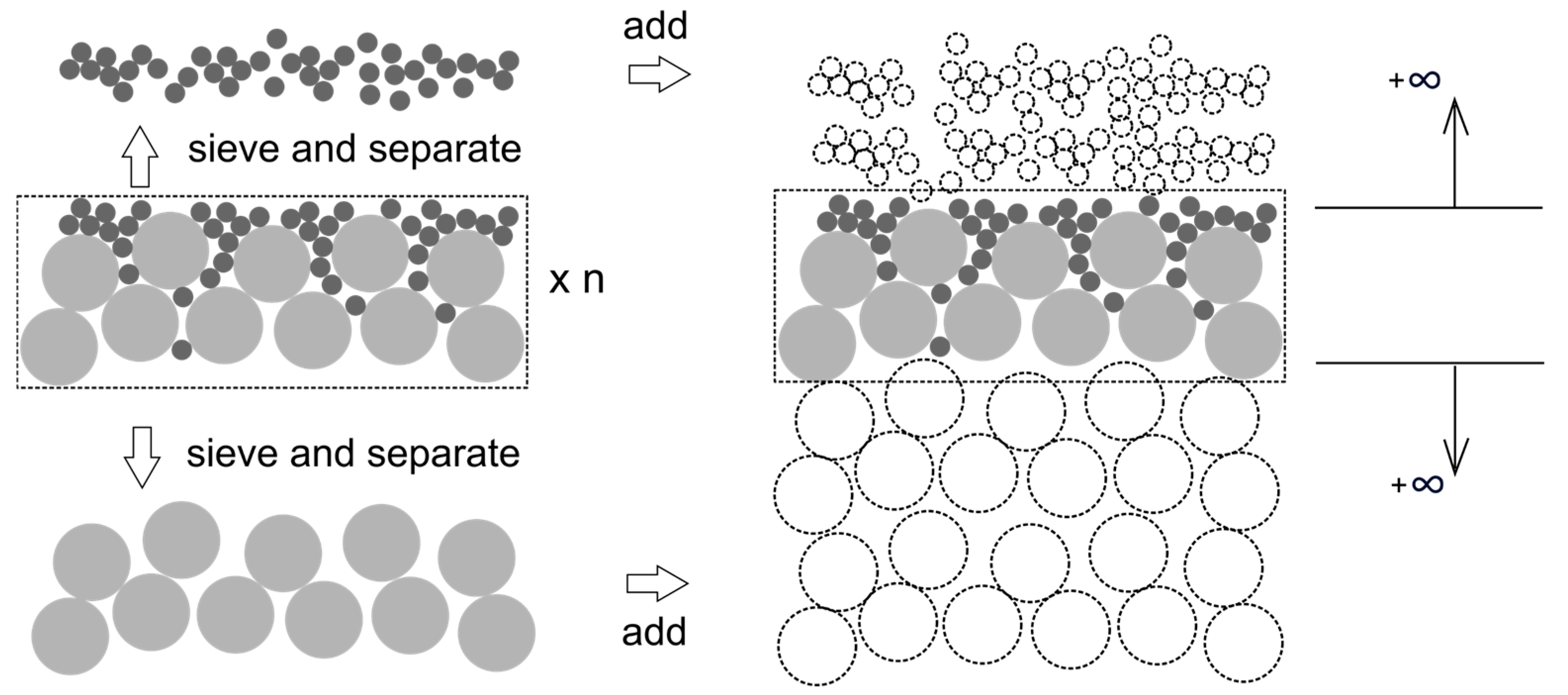
2.1.1. Simulation Setup
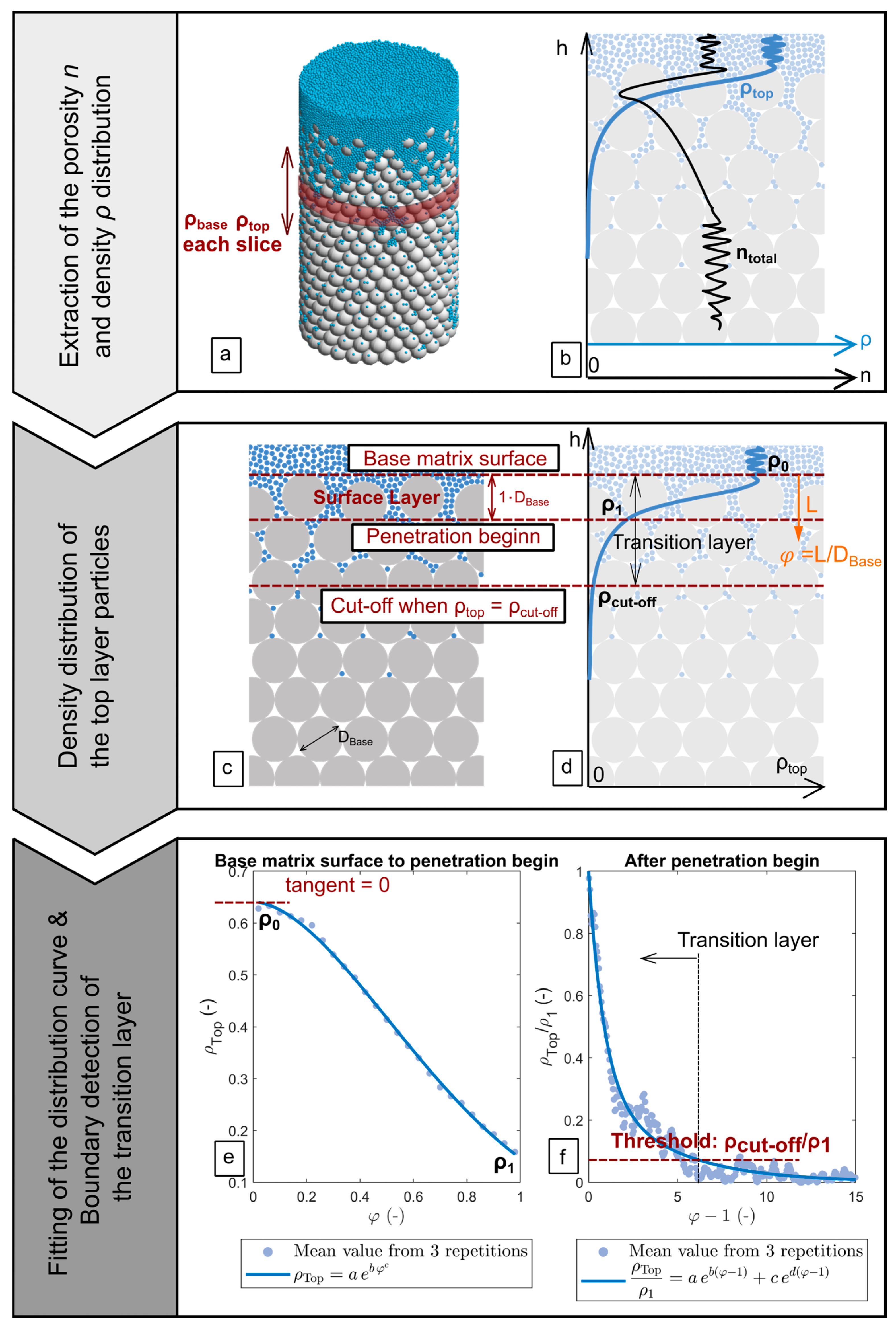
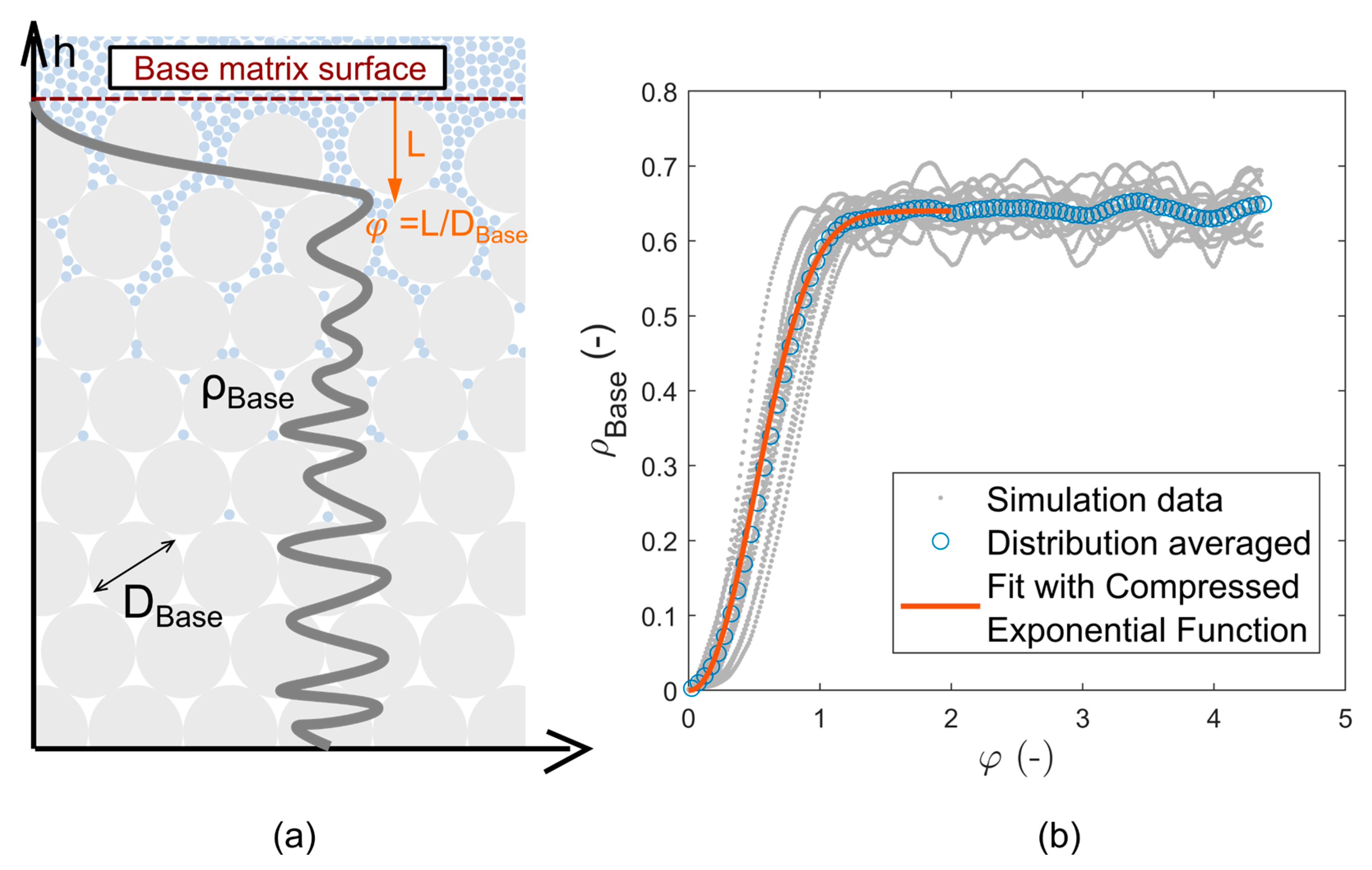
2.1.2. Data Analysis
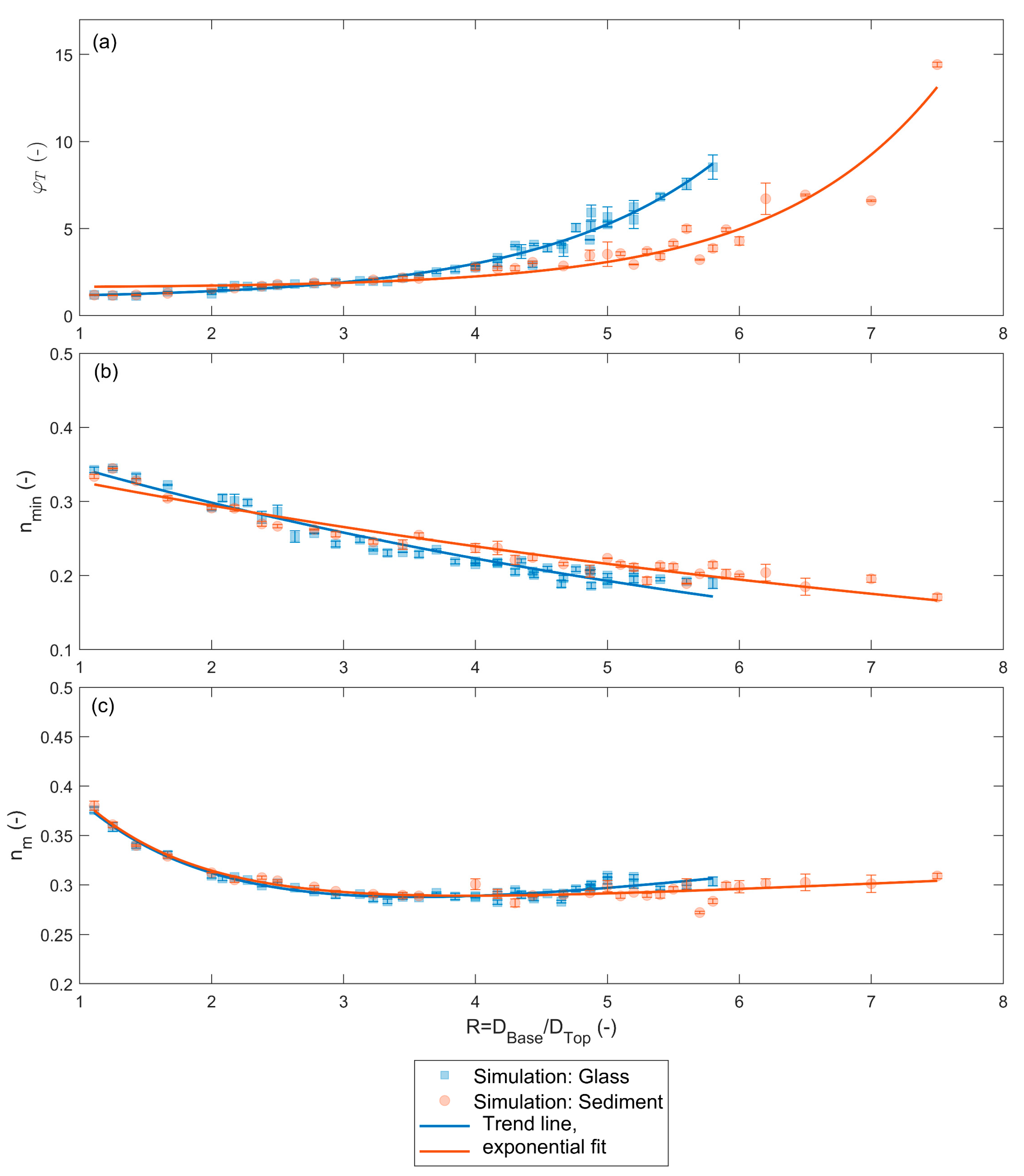
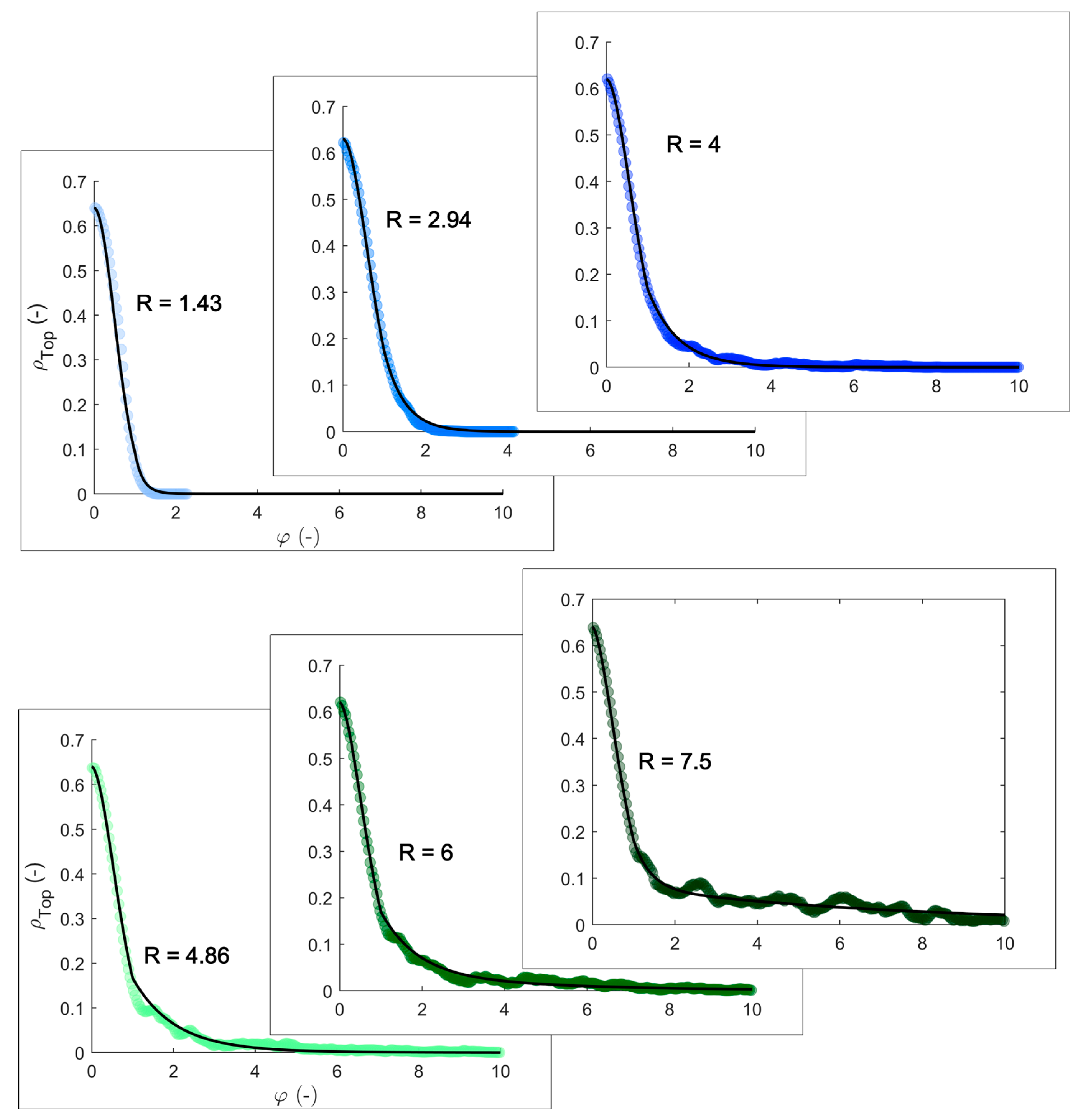
2.2. Results of Numerical Simulations
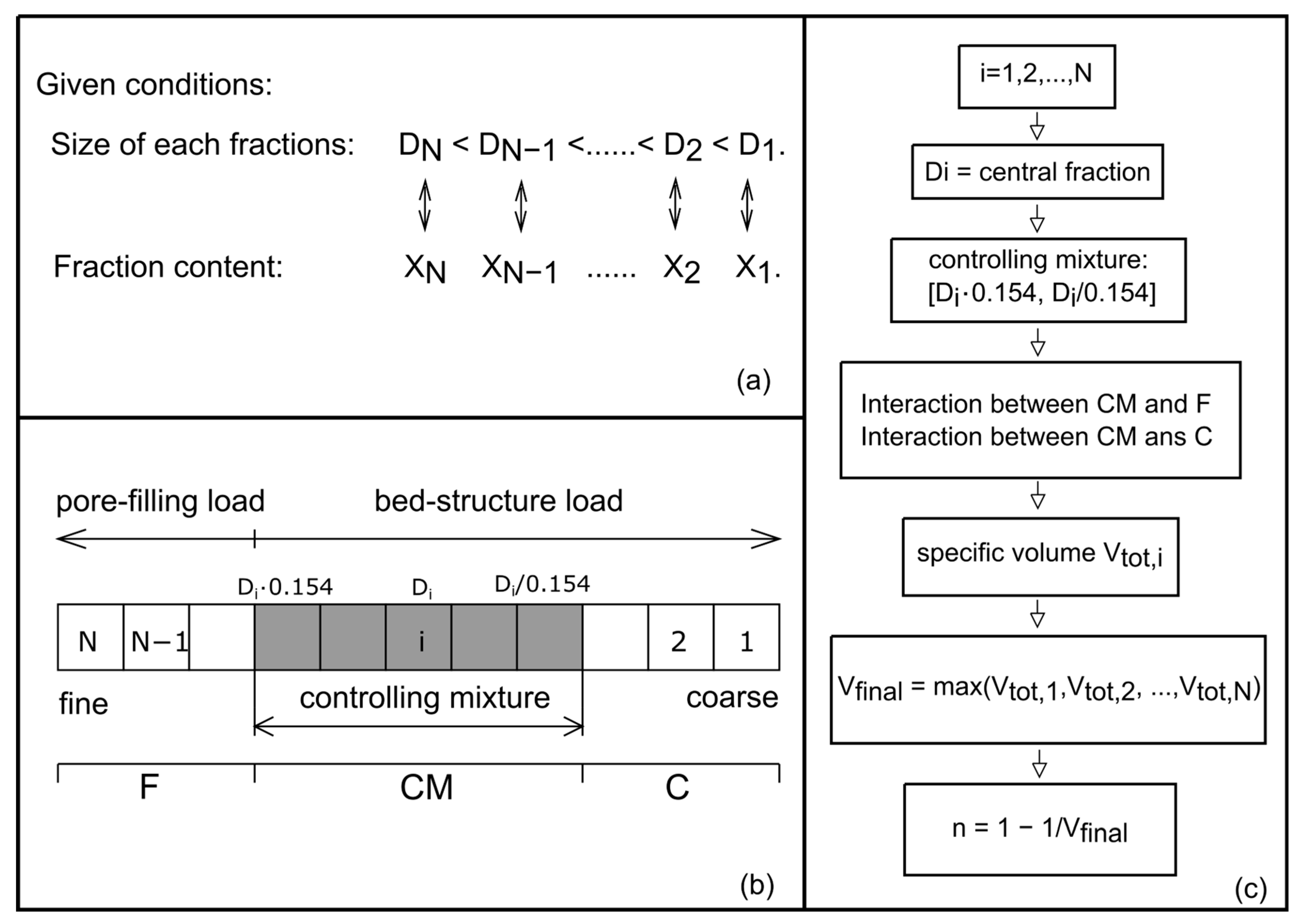
3. An Empirical Porosity Predictor for Layered Sphere Packings
3.1. Methodology
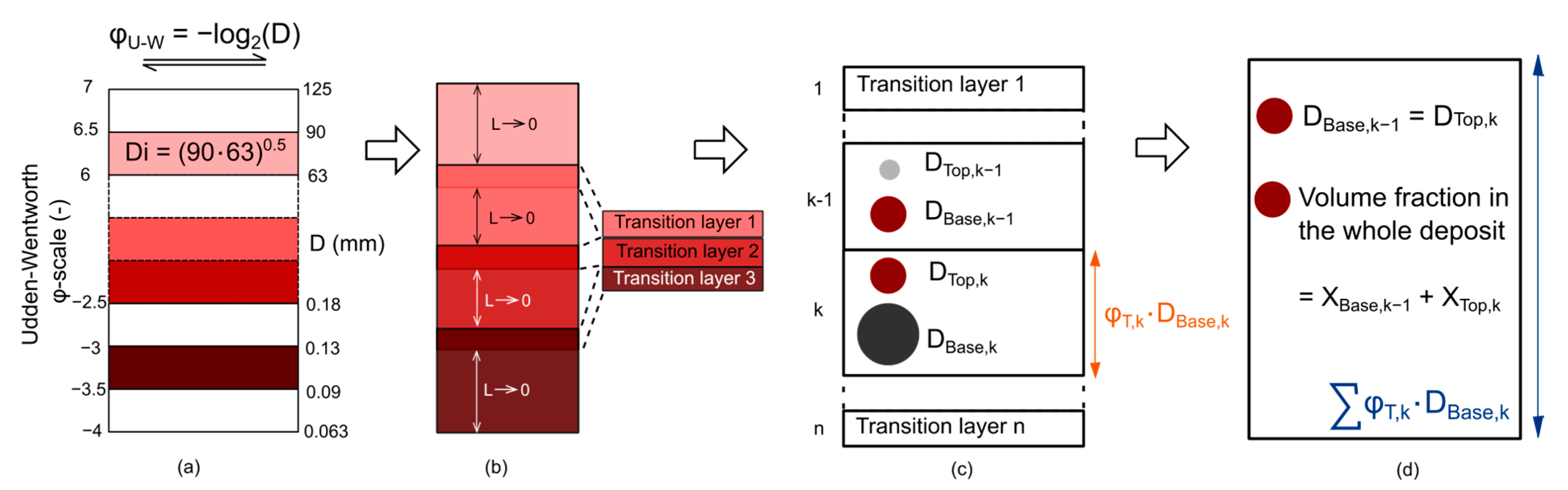
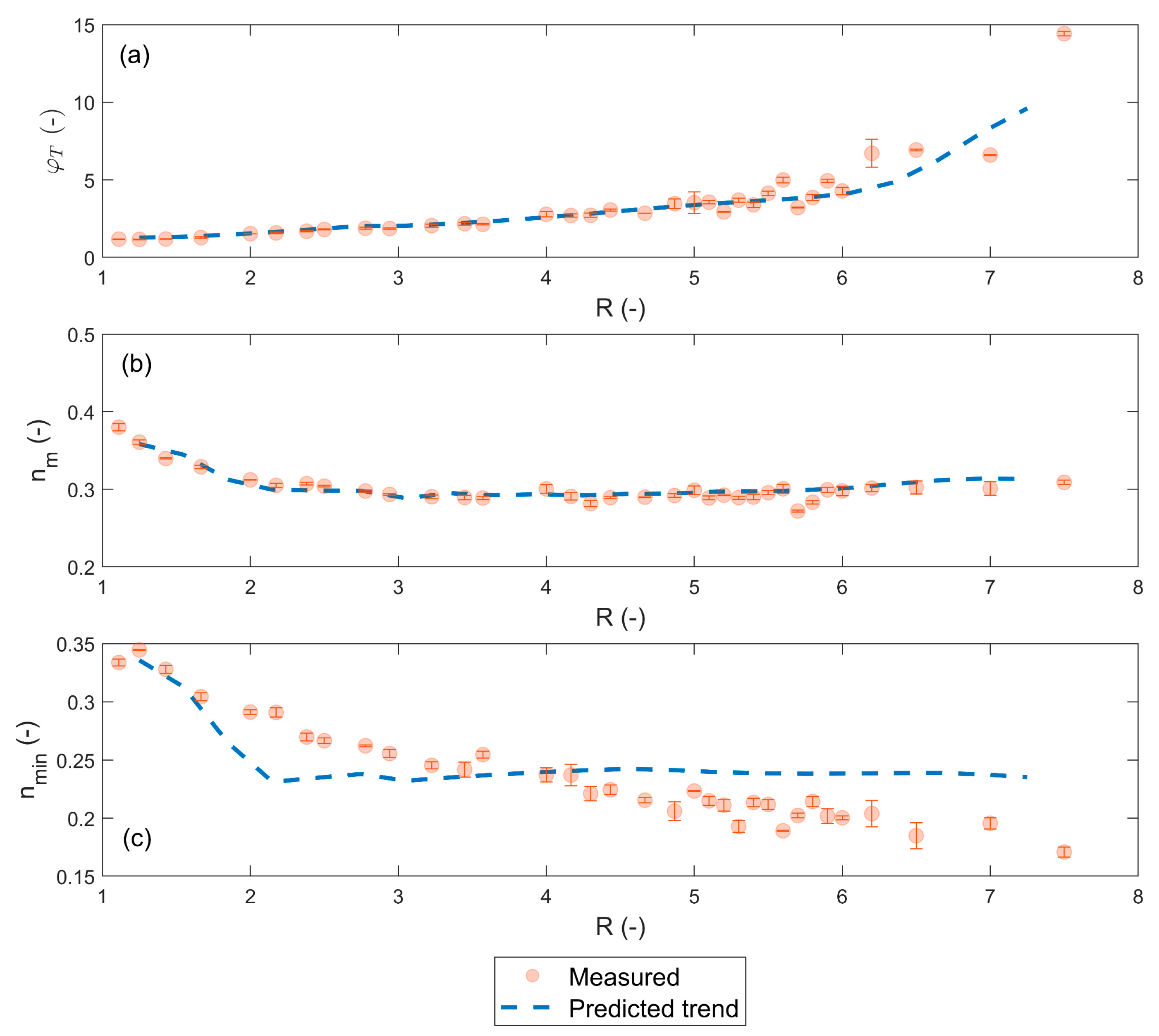
3.1.1. Density Distribution Prediction for Top and Base Layer Particles Based on R
3.1.2. Coupling with Yu & Standish—Predictor
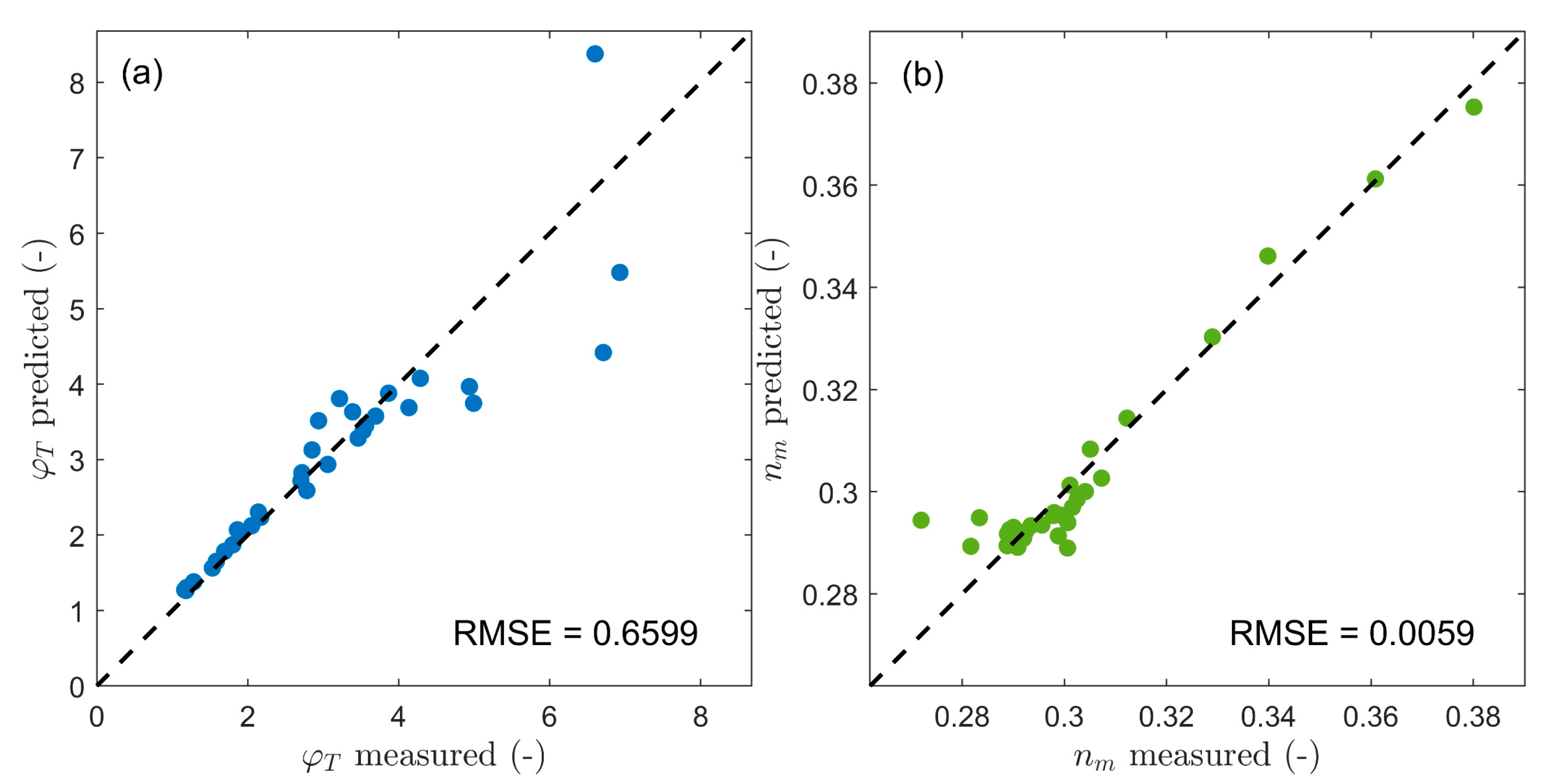
3.2. Results of Empirical Predictor
3.2.1. Performance Check
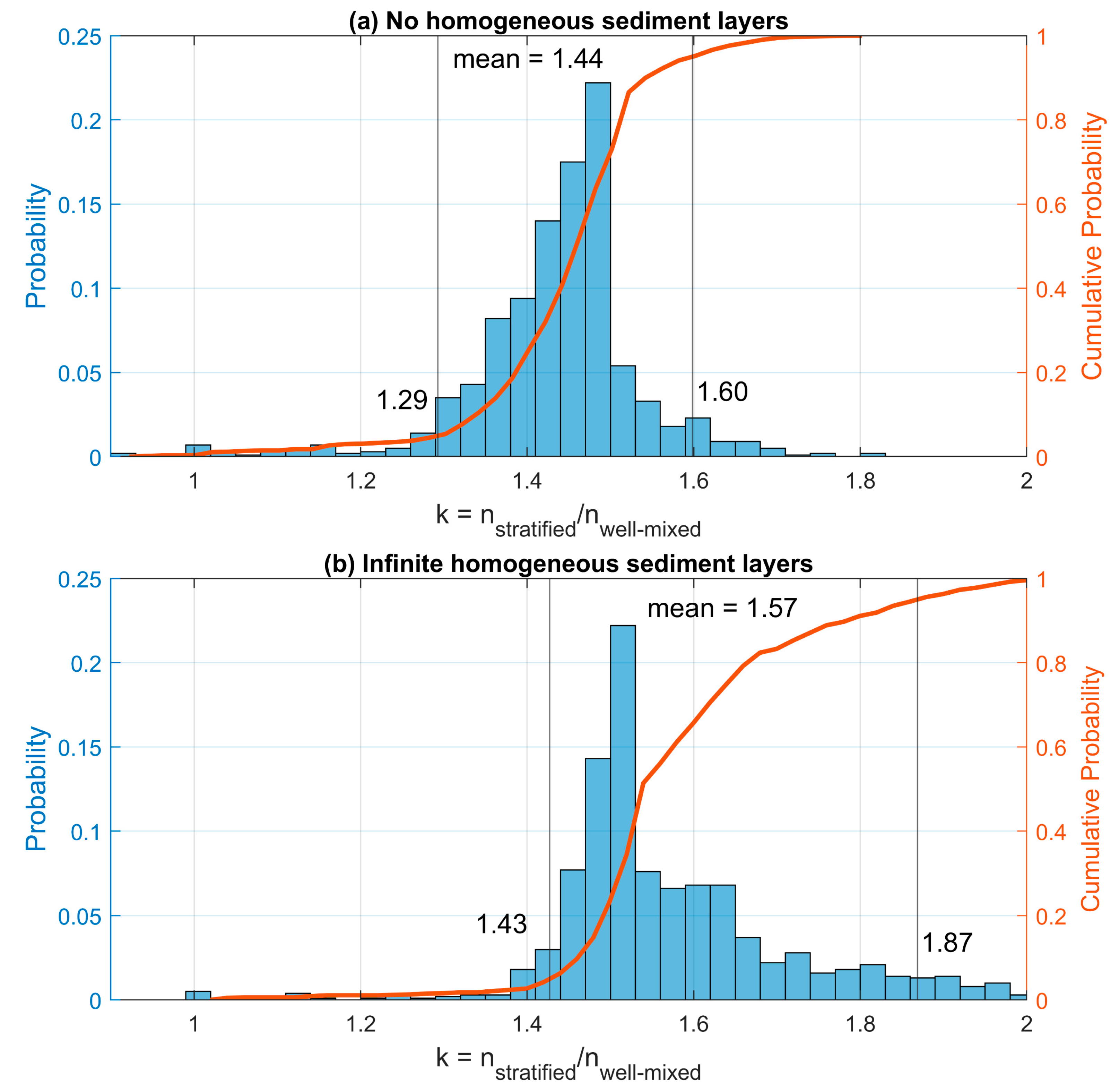
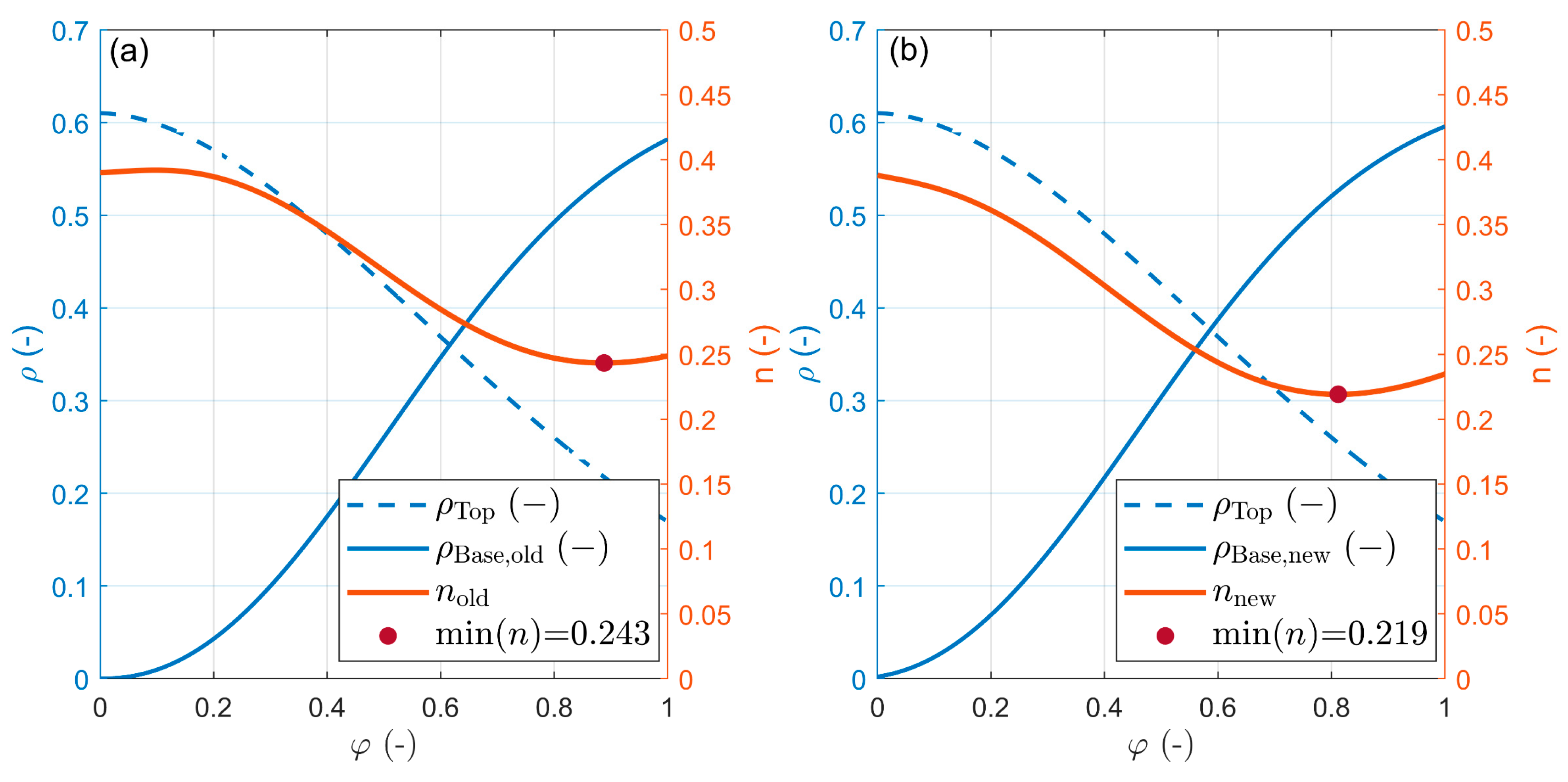
3.2.2. nstratified Versus nwell-mixed
4. Discussion
4.1. Discussion on the Influence of Inter-Particle Friction on the Transition Layer Length
4.2. Discussion on the Empirical Porosity Predictor for Stratified Packings
4.3. Discussion on the Effect of Stratification on Packing Porosity
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DTop and DBase | diameter of the top-layer and base-layer spheres |
| DGrain | diameter of spheres in a measurement container |
| DContainer | diameter of the measurement container |
| n | porosity value measured within a container of finite size |
| n0 | porosity value measured in an infinitely large container |
| nm | the average porosity of the transition layer |
| nmin | the minimum porosity within the transition layer |
| ntotal | porosity value in a slice (1 − ρSolid) |
| nstratified | average porosity of a stratified structure |
| nwell-mixed | porosity of a well-mixed sediment sample |
| ρBase | density of the base-layer particles in a slice |
| ρTop | density of the top-layer particles in a slice |
| ρsolid | density of all particles in a slice (ρBase + ρTop) |
| ρcut-off | density threshold to identify the lower boundary of the transition layer |
| ρ0 | density of top-layer particles at the base matrix surface |
| ρ1 | density of top-layer particles at the penetration begin line |
| R | size ratio between the top-layer and base-layer spheres (DBase/DTop) |
| Rc | critical size ratio between the large and small spheres when percolation of small particles is possible |
| R′ | critical value of R corresponding to the onset of unlimited percolation of top-layer particles |
| LTransition_Layer | length of the transition layer |
| φ | dimensionless penetration depth |
| φT | dimensionless transition layer length (LTransitionLayer/DBase) |
| X | volume fraction of particles with a certain size |
Appendix A
| Simulation with Natural Sediments | |||
|---|---|---|---|
| DBase - Dtop (mm) | R | DBase - Dtop (mm) | R |
| 10-9 | 1.11 | 14-3 | 4.67 |
| 10-8 | 1.25 | 14.6-3 | 4.87 |
| 10-7 | 1.43 | 15-3 | 5.00 |
| 10-6 | 1.67 | 15.3-3 | 5.10 |
| 10-5 | 2.00 | 15.6-3 | 5.20 |
| 10-4.6 | 2.17 | 15.9-3 | 5.30 |
| 10-4.2 | 2.38 | 16.2-3 | 5.40 |
| 10-4 | 2.50 | 16.5-3 | 5.50 |
| 10-3.6 | 2.78 | 16.8-3 | 5.60 |
| 10-3.4 | 2.94 | 17.1-3 | 5.70 |
| 10-3.1 | 3.23 | 17.4-3 | 5.80 |
| 10-2.9 | 3.45 | 17.7-3 | 5.90 |
| 10-2.8 | 3.57 | 18-3/21-3.5 | 6.00 |
| 12-3 | 4.00 | 21.7-3.5 | 6.20 |
| 12.5-3 | 4.17 | 19.5-3/22.75-3.5 | 6.50 |
| 12.9-3 | 4.30 | 21-3/24.5-3.5 | 7.00 |
| 13.3-3 | 4.43 | 26.25-3.5 | 7.50 |
Appendix B
- ρ0 = 1 − n0 (n0 = 0.36–0.4)
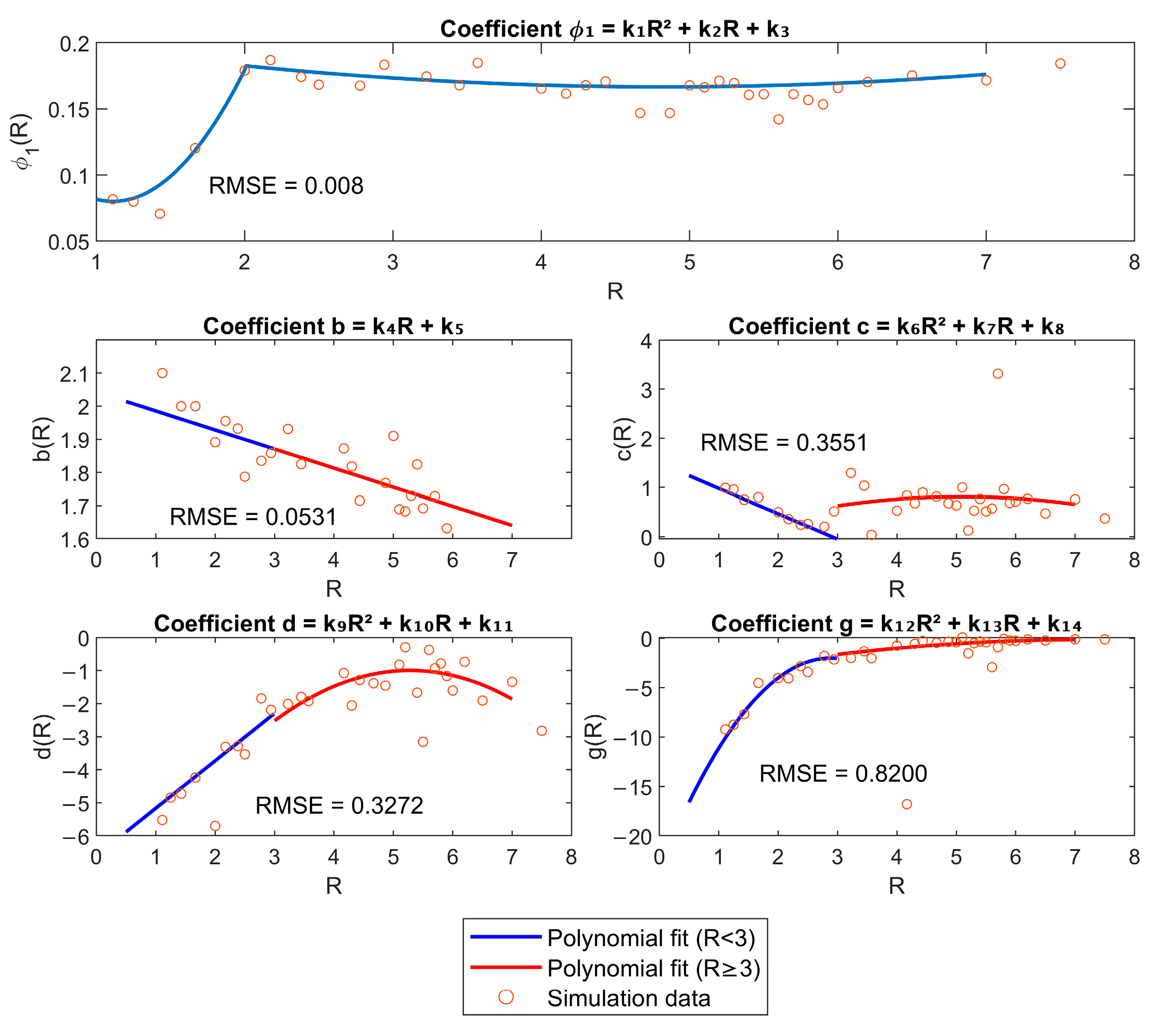
- ρ1 = k1R3 + k2R2 + k3R + k4
- a = log(ρ1/ρ0)
- b = k5R + k6
- c = k7R2 + k8R + k9
- d = k10R2 + k11R + k12
- f = 1 − c
- g = k13R2 + k14R + k15
| Coefficient | R ≤ 2 | 2 < R < 3 | R ≥ 3 |
|---|---|---|---|
| k1 | 0 | 0 | 0 |
| k2 | 0.1258 | 0.0020 | 0.0020 |
| k3 | −0.2797 | −0.0193 | −0.0193 |
| k4 | 0.2355 | 0.2132 | 0.2132 |
| k5 | −0.0575 | −0.0575 | −0.0575 |
| k6 | 2.0429 | 2.0429 | 2.0429 |
| k7 | 0 | 0 | −0.0420 |
| k8 | −0.5149 | −0.5149 | 0.4277 |
| k9 | 1.4955 | 1.4955 | −0.2786 |
| k10 | 0 | 0 | −0.2931 |
| k11 | 1.4343 | 1.4343 | 3.0952 |
| k12 | −6.5978 | −6.5978 | −9.1680 |
| k13 | −2.5594 | −2.5594 | −0.0827 |
| k14 | 14.7797 | 14.7797 | 1.2033 |
| k15 | −23.3567 | −23.3567 | −4.5205 |
References
- Chwang, A.T.; Chan, A.T. Interaction Between Porous Media and Wave Motion. Annu. Rev. Fluid Mech. 1998, 30, 53–84. [Google Scholar] [CrossRef]
- Ting, C.-L.; Lin, M.-C.; Cheng, C.-Y. Porosity effects on non-breaking surface waves over permeable submerged breakwaters. Coast. Eng. 2004, 50, 213–224. [Google Scholar] [CrossRef]
- Frings, R.M.; Kleinhans, M.G.; Vollmer, S. Discriminating between pore-filling load and bed-structure load: A new porosity-based method, exemplified for the river Rhine. Sedimentology 2008, 55, 1571–1593. [Google Scholar] [CrossRef]
- Frings, R.M. Sedimentary Characteristics of the Gravel-Sand Transition in the River Rhine. J. Sediment. Res. 2011, 81, 52–63. [Google Scholar] [CrossRef]
- Vollmer, S.; Kleinhans, M.G. Predicting incipient motion, including the effect of turbulent pressure fluctuations in the bed. Water Resour. Res. 2007, 43, W05410. [Google Scholar] [CrossRef]
- El Kadi Abderrezzak, K.; Die Moran, A.; Tassi, P.; Ata, R.; Hervouet, J.-M. Modelling river bank erosion using a 2D depth-averaged numerical model of flow and non-cohesive, non-uniform sediment transport. Adv. Water Resour. 2016, 93, 75–88. [Google Scholar] [CrossRef]
- Miwa, H.; Parker, G. Effects of sand content on initial gravel motion in gravel-bed rivers. Earth Surf. Process. Landf. 2017, 42, 1355–1364. [Google Scholar] [CrossRef]
- Mulatu, C.A.; Crosato, A.; Moges, M.M.; Langendoen, E.J.; McClain, M. Morphodynamic Trends of the Ribb River, Ethiopia, Prior to Dam Construction. Geosciences 2018, 8, 255. [Google Scholar] [CrossRef]
- Frings, R.M.; Hillebrand, G.; Gehres, N.; Banhold, K.; Schriever, S.; Hoffmann, T. From source to mouth: Basin-scale morphodynamics of the Rhine River. Earth-Sci. Rev. 2019, 196, 102830. [Google Scholar] [CrossRef]
- van Bui, H.; Bui, M.D.; Rutschmann, P. Advanced Numerical Modeling of Sediment Transport in Gravel-Bed Rivers. Water 2019, 11, 550. [Google Scholar] [CrossRef]
- Hatch, C.E.; Fisher, A.T.; Ruehl, C.R.; Stemler, G. Spatial and temporal variations in streambed hydraulic conductivity quantified with time-series thermal methods. J. Hydrol. 2010, 389, 276–288. [Google Scholar] [CrossRef]
- Athy, L.F. Density, Porosity, and Compaction of Sedimentary Rocks. Bulletin 1930, 14, 1–24. [Google Scholar] [CrossRef]
- Vollmer, S.; Ramos, F.d.L.S.; Daebel, H.; Kühn, G. Micro scale exchange processes between surface and subsurface water. J. Hydrol. 2002, 269, 3–10. [Google Scholar] [CrossRef]
- Noack, M.; Ortlepp, J.; Wieprecht, S. An Approach to Simulate Interstitial Habitat Conditions During the Incubation Phase of Gravel-Spawning Fish. River Res. Appl. 2017, 33, 192–201. [Google Scholar] [CrossRef]
- Aitken, M.J. An Introduction to Optical Dating. The Dating of Quaternary Sediments by the Use of Photon-Stimulated Luminescence; Oxford Science Publications; Oxford University Press: Oxford, NY, USA, 1998. [Google Scholar]
- Goff, J.A.; Kraft, B.J.; Mayer, L.A.; Schock, S.G.; Sommerfield, C.K.; Olson, H.C.; Gulick, S.P.; Nordfjord, S. Seabed characterization on the New Jersey middle and outer shelf: Correlatability and spatial variability of seafloor sediment properties. Mar. Geol. 2004, 209, 147–172. [Google Scholar] [CrossRef]
- Boggs, S. Principles of Sedimentology and Stratigraphy, 4th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Al Ibrahim, M.A.; Kerimov, A.; Mukerji, T.; Mavko, G. Particula: A simulator tool for computational rock physics of granular media. Geophysics 2019, 84, F85–F95. [Google Scholar] [CrossRef]
- Cui, Y.; Wooster, J.K.; Baker, P.F.; Dusterhoff, S.R.; Sklar, L.S.; Dietrich, W.E. Theory of Fine Sediment Infiltration into Immobile Gravel Bed. J. Hydraul. Eng. 2008, 134, 1421–1429. [Google Scholar] [CrossRef]
- Dubuis, R.; de Cesare, G. The clogging of riverbeds: A review of the physical processes. Earth-Sci. Rev. 2023, 239, 104374. [Google Scholar] [CrossRef]
- Siriwardene, N.R.; Deletic, A.; Fletcher, T.D. Clogging of stormwater gravel infiltration systems and filters: Insights from a laboratory study. Water Res. 2007, 41, 1433–1440. [Google Scholar] [CrossRef]
- Vani, N.; Escudier, S.; Jeong, D.-H.; Sauret, A. Role of the constriction angle on the clogging by bridging of suspensions of particles. Phys. Rev. Res. 2024, 6, L032060. [Google Scholar] [CrossRef]
- Marin, A.; Lhuissier, H.; Rossi, M.; Kähler, C.J. Clogging in constricted suspension flows. Phys. Rev. E 2018, 97, 21102. [Google Scholar] [CrossRef]
- Yu, A.B.; Standish, N. Estimation of the porosity of particle mixtures by a linear-mixture packing model. Ind. Eng. Chem. Res. 1991, 30, 1372–1385. [Google Scholar] [CrossRef]
- Yu, A.B.; Standish, N. Limitation of proposed mathematical models for the porosity estimation of nonspherical particle mixtures. Ind. Eng. Chem. Res. 1993, 32, 2179–2182. [Google Scholar] [CrossRef]
- Xu, W.; Brüll, C.; Schüttrumpf, H.; Frings, R.M. The effect of imbrication on the porosity value of non-uniform gravel bed: A case study from the Buëch River, France. Granul. Matter 2025, 27, 39. [Google Scholar] [CrossRef]
- Hahn, J.K. Realistic animation of rigid bodies. Comput. Graph. 1988, 22, 299–308. [Google Scholar] [CrossRef]
- Mirtich, B.V. Impulsebased Dynamic Simulation of Rigid Body Systems. Ph.D. Thesis, University of California at Berkeley, Berkeley, CA, USA, 1996. [Google Scholar]
- Gavrea, B.I.; Anitescu, M.; Potra, F.A. Convergence of a Class of Semi-Implicit Time-Stepping Schemes for Nonsmooth Rigid Multibody Dynamics. SIAM J. Optim. 2008, 19, 969–1001. [Google Scholar] [CrossRef][Green Version]
- Ridgway, K.; Tarbuck, K.J. Voidage fluctuations in randomly-packed beds of spheres adjacent to a containing wall. Chem. Eng. Sci. 1968, 23, 1147–1155. [Google Scholar] [CrossRef]
- Güntel, B.; Acar, A. Rockfall Modelling with Remedial Design and Measures along Part of a Mountainous Settlement Area, Southern Turkey. IOP Conf. Ser. Earth Environ. Sci. 2016, 44, 22013. [Google Scholar] [CrossRef]
- Schruff, T. Taking a Closer Look at the Causes and Impacts of Fine Sediment Infiltration into Gravel Beds. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2018. [Google Scholar]
- Frings, R.M.; Schüttrumpf, H.; Vollmer, S. Verification of porosity predictors for fluvial sand-gravel deposits. Water Resour. Res. 2011, 47, W07525. [Google Scholar] [CrossRef]
- Lopes, R.H.C. Kolmogorov-Smirnov Test. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 718–720. [Google Scholar]
- Wooster, J.K.; Dusterhoff, S.R.; Cui, Y.; Sklar, L.S.; Dietrich, W.E.; Malko, M. Sediment supply and relative size distribution effects on fine sediment infiltration into immobile gravels. Water Resour. Res. 2008, 44, W03424. [Google Scholar] [CrossRef]
- Haughey, D.P.; Beveridge, G.S.G. Structural properties of packed beds—A review. Can. J. Chem. Eng. 1969, 47, 130–140. [Google Scholar] [CrossRef]
- Sakthivadivel, R.; Einstein, H.A. Clogging of Porous Column of Spheres by Sediment. J. Hydr. Div. 1970, 96, 461–472. [Google Scholar] [CrossRef]
- Gibson, S.; Heath, R.; Abraham, D.; Schoellhamer, D. Visualization and analysis of temporal trends of sand infiltration into a gravel bed. Water Resour. Res. 2011, 47, W12601. [Google Scholar] [CrossRef]
- Dermisis, D.; Papanicolaou, A.N.T. The effects of protruding rock boulders in regulating sediment intrusion within the hyporheic zone of mountain streams. J. Mt. Sci. 2014, 11, 1466–1477. [Google Scholar] [CrossRef]

| Simulation Parameters | Effect of Surface Friction |
|---|---|
| Buffer length fraction (-) | 0.1 |
| Fixed Delta Time (s) | 0.005 |
| Solver Iteration Count (-) | 60 |
| Sleep Threshold (-) | 0.0005 |
| Shaking Fraction (-) | 0.001 |
| Bounciness (-) | 0.53 [31] |
| Friction coefficient (-) | 0.425 [32] |
| Drop rate (m3/(m2·s)) | 1.8 × 10−4 |
| Density (kg/m3) | 2650 |
| Materials | Natural sediments |
| φ | Absolute Error | ||
|---|---|---|---|
| 1 | 0.269 | 0.298 | 0.029 |
| 2 | 0.450 | 0.466 | 0.016 |
| 3 | 0.513 | 0.524 | 0.011 |
| 4 | 0.545 | 0.553 | 0.008 |
| 5 | 0.564 | 0.570 | 0.006 |
| 6 | 0.577 | 0.582 | 0.005 |
| 7 | 0.586 | 0.590 | 0.005 |
| 8 | 0.592 | 0.596 | 0.004 |
| 9 | 0.598 | 0.601 | 0.004 |
| 10 | 0.602 | 0.605 | 0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Brüll, C. Stratification-Induced Porosity Variations in Granular Packings—Part II: A Step Closer to Natural Sediments via DEM. Geotechnics 2025, 5, 78. https://doi.org/10.3390/geotechnics5040078
Xu W, Brüll C. Stratification-Induced Porosity Variations in Granular Packings—Part II: A Step Closer to Natural Sediments via DEM. Geotechnics. 2025; 5(4):78. https://doi.org/10.3390/geotechnics5040078
Chicago/Turabian StyleXu, Wenjia, and Catrina Brüll. 2025. "Stratification-Induced Porosity Variations in Granular Packings—Part II: A Step Closer to Natural Sediments via DEM" Geotechnics 5, no. 4: 78. https://doi.org/10.3390/geotechnics5040078
APA StyleXu, W., & Brüll, C. (2025). Stratification-Induced Porosity Variations in Granular Packings—Part II: A Step Closer to Natural Sediments via DEM. Geotechnics, 5(4), 78. https://doi.org/10.3390/geotechnics5040078






