Drought Projections in the Northernmost Region of South America Under Different Climate Change Scenarios

Abstract

Climate change research is increasingly important in regions vulnerable to extreme hydrometeorological events like droughts, which pose significant socio-economic and environmental challenges. This study examines future variability of meteorological drought in northernmost South America using the Standardized Precipitation Index (SPI) and precipitation projections from CMIP6 models. We first evaluated model performance by comparing historical simulations with observational data from the Climate Hazards Group InfraRed Precipitation with Station dataset for 1981–2014. Among the models, CNRM-CM6-1-HR was selected for its superior accuracy, demonstrated by the lowest errors and highest correlation with observed data—specifically, a correlation coefficient of 0.60, a normalized root mean square error of 1.08, and a mean absolute error of 61.37 mm/month. Under SSP1-2.6 and SSP5-8.5 scenarios, projections show decreased rainfall during the wet months in the western Perijá mountains, with reductions of 3% to 26% between 2025 and 2100. Conversely, the Sierra Nevada of Santa Marta is expected to see increases of up to 33% under SSP1-2.6. During dry months, northern Colombia and Venezuela—particularly coastal lowlands—are projected to experience rainfall decreases of 10% to 17% under SSP1-2.6 and 13% to 20% under SSP5-8.5. These areas are likely to face severe drought conditions in the mid and late 21st century. These findings are essential for guiding water resource management, enabling adaptive strategies, and informing policies to mitigate drought impacts in the region.

1. Introduction

Droughts are among the most notorious extreme events, characterized by an extended decline in rainfall, which can significantly alter ecosystem functions and substantially impact agricultural output, water supplies, and global and local economies [1]. Moreover, droughts can exacerbate forest fires, increase food prices, and restrict access to drinking water [2]. The intricate and unpredictable characteristics of drought analysis, along with its widespread effects, present difficulties; nevertheless, studies on drought are essential for managing agricultural water, planning water resources, assessing risks associated with natural hazards, and developing adaptation strategies [3,4]. Shortfalls in rainfall during specific periods can reduce the levels of surface and groundwater, significantly impacting the availability of water for various uses, including household, agricultural, industrial, and ecological needs. The global land area impacted by droughts has doubled since 1900, with 40% of the planet currently facing more frequent and intense drought conditions. Droughts are believed to be responsible for approximately 34% of deaths related to disasters. Additionally, projections indicate that by 2035, the average cost associated with droughts is expected to increase by at least 35%, a change driven by the escalating frequency and intensity attributed to climate change [5]. Likewise, a deficiency in soil moisture content has a detrimental impact on crop production [6].

While the concept of drought is generally understood, there is no universally accepted definition of it. Droughts can be broadly categorized into four interrelated types: meteorological, agricultural, hydrological, and socioeconomic droughts [7]. The meteorological drought refers to periods characterized by a deficit in atmospheric water supply, typically marked by reduced precipitation [8]. On the other hand, the hydrological drought is characterized by low water levels in rivers, lakes, groundwater, and reservoirs. Agricultural drought occurs when there is a shortage of soil moisture, leading to diminished crop production [2]. Then, a socioeconomic drought emerges when water resource systems fail to meet the community’s water demands, thereby impacting various socioeconomic activities [1]. The gradual onset of droughts, combined with their extensive impacts, renders drought analysis complex and uncertain. Nonetheless, studies on drought are crucial for agricultural water management, water resource planning, natural hazard risk assessment, and the development of adaptation strategies.

A drought index serves as a crucial tool for monitoring and assessing various types of droughts. Numerous indices have been created and utilized for this aim. This includes the Standardized Precipitation Index (SPI) [7], the Standardized Evapotranspiration and Precipitation Index (SPEI) [8], the Standardized Soil Moisture Index [9], and the Standardized Runoff Index [10]. These Indices are commonly used to assess meteorological, hydrological, and agricultural droughts. However, it is essential to note that these indices only focus on one aspect of drought, as they consider a single variable representing the water supply of a specific component in hydrological processes. Conversely, drought is associated with multiple variables and is caused by water imbalance [11]. The SPI is the most widely used index and is recommended by the World Meteorological Organization for detecting meteorological droughts across different time scales [12]. Although more integrative indices such as the Standardized Precipitation and Evapotranspiration Index, which incorporates additional variables related to evapotranspiration, are available, their application requires reliable temperature and radiation data, which can introduce biases in regions with limited information [13]. For these reasons, and to ensure alignment with previous studies, the SPI was considered the most suitable tool for this work. The SPI is straightforward, efficient, and well-suited for regional drought assessments, making it a valuable tool for monitoring drought, especially in areas with limited data [7].

The ongoing global climate change and the increase in human activities demand a detailed understanding of the spatial and temporal variations in droughts [14]. Climate models have become a fundamental tool for understanding climate behavior and generating projections that are essential for informed decision-making in managing risks associated with extreme events [15]. In this context, the different phases of the Coupled Model Intercomparison Project (CMIP) have played a central role. In particular, the use of CMIP5 and its previous iterations enabled the evaluation of drought frequency and severity, providing a clearer understanding of the influence of greenhouse gases and the potential risks they pose for the future. In 2014, the IPCC launched a new phase aimed at addressing emerging challenges related to climate change [16]. This phase jointly incorporates the Shared Socioeconomic Pathways (SSP) and the Representative Concentration Pathways (RCP), with the objective of generating more accurate climate projections by taking socioeconomic development into account [17,18].

Although there have been significant advancements in the creation and use of Earth System Models (ESMs), along with the production of climate change forecasts on global and regional levels, a notable shortcoming persists: the lack of targeted studies focusing on drought predictions in particularly vulnerable areas, like the far northern part of South America. The Institute of Hydrology, Meteorology, and Environmental Studies (IDEAM, acronym in Spanish) has produced projections for precipitation, temperature, and relative humidity under different climate change scenarios in Colombia [19]. These projections indicate that Colombia may experience significant changes in precipitation patterns but do not consider changes in Venezuela, where climate change-influenced processes may influence rainfall patterns. The projections reveal substantial inconsistencies when analyzed under a single scenario, as they are derived from the average of projections tied to the four Representative Concentration Pathways described in the Fifth Assessment Report of the IPCC. Consequently, this limits the capacity to assess potential future conditions, thereby reducing the effectiveness of proposing various greenhouse gas emission trajectories. It also eliminates a clear threshold of uncertainty that policymakers require for making informed decisions regarding climate change adaptation strategies. However, these projections fail to provide a specific analysis of droughts’ intensity, frequency, or duration, leaving a critical gap in our understanding of this phenomenon in regional contexts.

Climatic phenomena such as the El Niño-Southern Oscillation (ENSO), which alters precipitation patterns, influence rainfall variability in the northernmost part of South America. Among the most severe drought episodes are the 1997–1998 and 2009–2010 events, which stood out for their intensity and duration. From 1997 to 1998, the region experienced a drastic decrease in precipitation, which resulted in severe water shortages and decreased economic activity in several sectors by approximately 20%. Similarly, during the 2009–2010 event, drought conditions intensified in several areas of the region, where river levels in the main river basins dropped by up to 50% of their normal values. These events highlight the area’s vulnerability to prolonged droughts and the potential consequences that may arise. It is believed that these already significant effects may worsen due to climate change. Analyzing drought predictions is essential for making informed decisions and effectively planning agricultural practices. Therefore, this study examines the variability of meteorological drought on 3-month scales using the SPI projected in CMIP6 model precipitation estimates in the northernmost region of South America. We evaluated the estimated precipitation data from 50 CMIP6 models, as well as an ensemble model derivative of all models, to assess their performance in predicting precipitation. Next, we applied the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method to rank the selected CMIP6 based on these performance measures, identifying the most effective model for predicting future changes in precipitation and drought. The study involved the following steps: (i) Assessing the historical CMIP6 model simulations by comparing them with CHIRPS-estimated precipitation data from 1981 to 2014 and (ii) Analyzing the spatiotemporal variability of droughts based on SPI under various climate change scenarios. Our research is the initial investigation into future drought characteristics in the northernmost region of South America utilizing CMIP6 model results. This study aims to comprehensively evaluate and assess occurrences of severe drought, acknowledging the limitations of relying on a single index for deriving actionable insights in decision-making processes. The research presents several novel aspects. While prior studies have predominantly focused on specific regions of South America, this investigation uniquely targets the northernmost area of the continent. In this region, topographic features and natural systems contribute to conditions that can facilitate convective precipitation and moisture transport from the atmosphere, resulting in arid conditions. This specific focus enables a more profound understanding of the dynamics of severe drought within the studied area. Furthermore, the application of a multiple-criteria decision-making method for model ranking, combined with bias correction techniques, enhances our comprehension of severe drought occurrences and their relationship with the increase in climate variability.

2. Materials and Methods

2.1. Study Area

The study domain covers a land area of approximately 314,818 km² (12°43′ N–70°43′ W), with a coastline length of 1303 km along the Caribbean Sea, in the northernmost part of South America. The study area includes the northern regions of Colombia and Venezuela (Figure 1). Prominent mountain systems are found in northern Colombia, such as the Sierra Nevada de Santa Marta and the Serranía del Perijá, with an altitude of 5710 m asl and 3630 m asl, respectively. In addition, La Guajira Peninsula covers an area of 25,000 km². On the other hand, in the northern part of Venezuela, multiple mountain systems are situated where the Coastal Range transitions into the Andean Mountain Range. There is also a peninsula covering an area of 3405 km². The study area has a tropical climate with temperatures ranging from 23 °C to 30 °C. However, there are significant variations in climatic characteristics according to altitude. Rainfall variability in the region is influenced by climatological phenomena such as El Niño-Southern Oscillation causes droughts. Rainfall patterns also depend on the location of the Intertropical Convergence Zone (ITCZ) since its presence generates a decrease in the trade winds and a reversal of the surface current in a west–east direction [20]. The wet season in the region occurs from July to November, with average rainfall between 99 mm and 250 mm. The dry season lasts from December to February, with rainfall ranging from 27 mm to 75 mm.

We divided the study area into four zones based on the topography and economic activities in the region. The GUA zone includes a large plain with mountains in the southwest and southeast. The MAG zone is located west of the study area and is influenced by the leeward wind of the Sierra Nevada de Santa Marta. The CES zone covers the southern part of the area and is bordered to the east by a mountain range separating Colombia and Venezuela. Lastly, the VEN zone encompasses the entire northern territory of Venezuela.

2.2. Precipitation Dataset

The study employed a comprehensive approach using CMIP6 historical simulations of monthly precipitation. (1981–2014) from 50 Earth System Models of the Coupled Model Intercomparison Project (CMIP6 ESMs), which are publicly available on the Copernicus Climate Data Store platform (https://cds.climate.copernicus.eu/ (accessed on 3 September 2024)). The CMIP6 models and their horizontal resolution are presented in

Table 1. List of 50 CMIP6 ESMs utilized for estimating historical precipitation in the northernmost region of South America.

CMIP6 Model	Institute	Country	Horizontal Resolution (°Lat × °Lon)
ACCESS-CM2_	CSIRO-ARCCSS	Australia	1.80° × 1.25°
ACCESS-ESM1-5	CSIRO	Australia	1.87° × 1.25°
AWI-CM-1-1-MR	AWI	Germany	0.93° × 0.93°
AWI-ESM-1-1-LR	AWI	Germany	1.87° × 1.86°
BCC-CSM2-MR	BCC	China	1.12° × 1.12°
BCC-ESM1	BCC	China	2.81° × 2.79°
CAMS-CSM1-0	CAMS	China	1.12° × 1.12°
CanESM5	CCCma	Canada	2.81° × 2.79°
CanESM5-CanOE	CCCma	Canada	2.80°× 2.80°
CESM2	NCAR	USA	1.25° × 0.94°
CESM2-FV2	NCAR	USA	2.50° × 1.89°
CESM2-WACCM	NCAR	USA	1.25° × 0.94°
CESM2-WACCM-FV2	NCAR	USA	2.50° × 1.89°
CMCC-CM2-HR4	CMCC	Italy	1.25° × 0.94°
CMCC-CM2-SR5	CMCC	Italy	1.25° × 0.94°
CMCC-ESM2	CMCC	Italy	1.25° × 0.94°
CNRM-CM6-1	CNRM	France	1.40° × 1.40°
CNRM-CM6-1-HR	CNRM	France	0.50° × 0.50°
CNRM-ESM2-1	CNRM	France	1.40° × 1.40°
E3SM-1-0	E3SM-Project	USA	1.00° × 1.00°
E3SM-1-1	E3SM-Project	USA	1.00° × 1.00°
EC-Earth3-AerChem	EC-Earth Consortium	Europe	0.70° × 0.70°
EC-Earth3-CC	EC-Earth Consortium	Europe	0.70° × 0.70°
EC-Earth3-Veg	EC-Earth Consortium	Europe	0.70° × 0.70°
ESM2-0	GFDL	USA	1.00° × 1.00°
FGOALS-f3-L	CAS	China	1.25° × 1.00°
FGOALS-g3	CAS	China	2.00° × 2.30°
FIO-ESM-2-0	FIO-QLNM	China	1.30° × 0.90°
GFDL-ESM4	NOAA-GFD	USA	1.30° × 1.00°
GISS-E2-1-H	NASA-GISS	USA	2.50° × 2.00°
HadGEM3-GC31-LL	MOHC	United Kingdom	1.87° × 1.25°
HadGEM3-GC31-MM	MOHC	United Kingdom	0.83° × 0.55°
IITM-ESM	CCCR-IITM	India	1.90° × 1.90°
INM-CM4-8	INM	Russia	2.00° × 1.50°
INM-CM5-0	INM	Russia	2.00° × 1.50°
IPSL-CM5A2-INCA	IPSL	France	2.50° × 1.30°
IPSL-CM6A-LR	IPSL	France	2.50° × 1.30°
KACE-1-0-G	NIMS-KMA	Korea	1.88° × 1.25°
MCM-UA-1-0	UA	USA	3.75° × 2.23°
MIROC6	MIROC	Japan	1.40° × 1.40°
MIROC-ES2H	MIROC	Japan	1.10° × 1.10°
MIROC-ES2L	MIROC	Japan	2.80° × 2.80°
MPI-ESM1-2-HR	MPI-M	Germany	0.93° × 0.93°
MPI-ESM1-2-LR	MPI-M	Germany	0.93° × 0.93°
NESM3	NUIST	China	1.87° × 1.86°
NorCPM1	NCC	Norway	2.50° × 1.89°
NorESM2-MM	NCC	Norway	1.25° × 0.94°
SAM0-UNICON	SNU	Korea	1.25° × 0.94°
TaiESM1	AS-RCEC	Taiwan	1.25° × 0.94°
UKESM1-0-LL	UKESM	United Kingdom	1.25° × 1.87°

. The Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) was used as a reference to validate the historical precipitation simulations. CHIRPS is a global precipitation dataset that combines weather station data with satellite data from NASA and NOAA. This dataset is freely accessible on the Climate Hazards Center website (https://www.chc.ucsb.edu/data (accessed on 15 September 2024)), created by the U.S. Geological Survey’s Earth Resources Observation and Science Center and the University of California Santa Barbara Climate Center. The CHIRPS dataset offers daily scale precipitation data at a resolution of 0.05° × 0.05°. We applied the modified Mann–Kendall (MMK) test and Theil-Sen’s estimator to assess trends and magnitudes of monthly precipitation for both historical data and projected scenarios [21].

2.3. Bias-Corrected CMIP6 ESMs

The CMIP6 ESMs have varying resolutions, ranging from 2.81° × 2.79° to 0.50° × 0.50°, which limits their applicability for local or regional scale impact studies. Spatial resampling was applied to refine the CMIP6 ESMs, adjusting their resolution to 0.05° × 0.05° for bias correction [22]. The Climate Data Operators (CDO) software (https://code.mpimet.mpg.de/projects/cdo (accessed on 13 September 2024)) was developed for data analysis and processing. CDO is proper for re-mapping and interpolations. The interpolation techniques utilized in ESMs are inverse distance weighting (IDW), bilinear interpolation, bicubic interpolation, and kriging interpolation. Therefore, this study employed the bilinear interpolation was applied as a resampling technique to adjust the spatial resolution of the CMIP6 data.

We followed these steps to perform bilinear interpolation in CDO. First, we created a description of the target spatial resolution using the CHIRPS database, and then applied the CDO remapbil command to remap each CMIP6 model to this grid. This procedure corresponds to a resampling step rather than a statistical downscaling method, which constitutes an important methodological consideration when interpreting the results and represents a limitation of this study. This study made a bias correction to the historical data and precipitation projections generated by the CMIP6 models. The adjustment data is essential because climate models can have systematic biases when simulating variables such as precipitation, which can affect the accuracy of historical data and projections. The technique we employed for bias correction was Quantile Mapping (QM), a method that adjusts the simulated data distributions to match the values of reference precipitation distributions [23]. Quantile Mapping was applied for historical precipitation estimates in each zone and for each model from 1981 to 2014. Each generated distribution of monthly precipitation values was used to adjust future projections (2025–2100). The adjustment starts with estimating the empirical quantiles from the data distributions of the CMIP6 models and the data estimated by CHIRPS. In this context, the quantiles represent specific values associated with particular percentiles within the corresponding empirical cumulative distributions. The quantiles are calculated by applying the inverse function to the cumulative distributions, which allows the model data to be fitted to the recorded estimates.

2.4. CMIP6 ESMs Performance

A performance evaluation was conducted on 50 CMIP6 models, together with an additional ensemble model, to determine which best reproduced the historical precipitation estimated by CHIRPS in each study area. Both the individual model simulations and the ensemble were evaluated using statistical metrics such as BIAS, Normalized Mean Squared Error (NRMSE), correlation coefficient (r), Nash Sutcliffe coefficient (NSE), and Mean Absolute Error (MAE). BIAS in global climatological models measures the systematic difference between model simulations and observation data, indicating the average deviation of a climatological model from observed climate conditions (Equation (1)) [24]. NRMSE and MAE estimate the difference between simulated and observed values and provide a direct measure of the variance between the data (Equations (2)–(5)). A low NRMSE value suggests high model accuracy, while a high NRMSE value indicates poor prediction [25]. The correlation coefficient r and NSE were used to determine the linear relationship between variables and assess the relationship’s strength in predictive models (Equations (2) and (4)) [26]. To represent future projections, the model that achieved the best score in the Technique for Order Preferences by Similarity to an Ideal Solution (TOPSIS) was used. The GCMs were then ranked from least skilled to most skilled. The TOPSIS method allows for multi-criteria decision-making, providing a transparent and reproducible framework for model selection, consistent with practices adopted in previous studies that have yielded satisfactory results. The best model has also been used to forecast rainfall, soil moisture, and total runoff.

$$\mathrm{B}\mathrm{I}\mathrm{A}\mathrm{S}=\sum _{\mathrm{t}=1}^{\mathrm{n}}{\displaystyle \frac{{\mathrm{\varnothing }}_{\mathrm{S}}-{\mathrm{\varnothing }}_{\mathrm{O}}}{{\mathrm{\varnothing }}_{\mathrm{O}}}}$$

(1)

$$\mathrm{N}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{\sqrt{\sum _{\mathrm{t}=1}^{\mathrm{n}}\frac{{{(\mathrm{\varnothing }}_{\mathrm{S}}-{\mathrm{\varnothing }}_{\mathrm{O}})}^2}{\mathrm{n}}}}{\overline{{\mathrm{\varnothing }}_{\mathrm{O}}}}},$$

(2)

$$\mathrm{r}={\displaystyle \frac{1}{(\mathrm{n}-1)}}\sum _{\mathrm{t}=1}^{\mathrm{n}}\left({\displaystyle \frac{{\mathrm{\varnothing }}_{\mathrm{S}}-\overline{{\mathrm{\varnothing }}_{\mathrm{S}}}}{{\mathsf{\sigma }}_{\mathrm{S}}}}\right)\left({\displaystyle \frac{{\mathrm{\varnothing }}_{\mathrm{O}}-\overline{{\mathrm{\varnothing }}_{\mathrm{O}}}}{{\mathsf{\sigma }}_{\mathrm{O}}}}\right),$$

(3)

$$\mathrm{N}\mathrm{S}\mathrm{E}=1-{\displaystyle \frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{O}}_{\mathrm{i}}-{\mathrm{S}}_{\mathrm{i}}\right)}^2}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{O}}_{\mathrm{i}}-\overline{\mathrm{O}}\right)}^2}},$$

(4)

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{\mathrm{n}}}\mathrm{x}\sum _{\mathrm{i}=1}^{\mathrm{n}}\left|{\mathrm{O}}_{\mathrm{i}}-{\mathrm{S}}_{\mathrm{i}}\right|,$$

(5)

where $\mathrm{S}$ represents the simulated data, O represents the observed data of the climate variable, ${\mathsf{\sigma }}_{\mathrm{S}}$ is the standard deviation of the simulations, ${\mathsf{\sigma }}_{\mathrm{O}}$ is the standard deviation of the observed values, $\mathrm{i}$ refers to the simulated and observed data, and $\mathrm{n}$ is the total number of data points.

After calculating the performance metrics, we conducted a decision matrix transformation that considered both the most desirable and least desirable performance measures. Ideally, we seek larger values for the correlation coefficient and the NSE, while smaller values for BIAS, NRMSE, and MAE are preferred. Subsequently, we established the weights for each measure. We then employed the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) approach to rank the selected CMIP6 ESMs based on these performance measures. TOPSIS is a multiple-criteria decision-making method utilized to rank alternatives according to a defined set of criteria [27]. The implementation of the TOPSIS method encompasses the following steps: (1) The normalized performance measure ${\mathrm{N}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)$ for a set of options $\left(\mathrm{i}\right)$ and their corresponding statistical performance measures $\left(\mathrm{j}\right)$ is calculated according to Equation (6).

$${\mathrm{N}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)={\displaystyle \frac{{\mathrm{x}}_{\mathrm{i}\mathrm{j}}}{\sqrt{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}\mathrm{j}}^2}}}\mathrm{i}=1,\dots ,\mathrm{n}; \mathrm{j}=1,\dots ,\mathrm{m}$$

(6)

(2) We calculated the weighted normalized performance measure, referred to as ${\mathrm{v}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)$. The cumulative weight of all performance measures has been established to Equation (1). Thereafter, we identified the positive ideal solution $(\mathrm{S}+)$ and the negative ideal solution $(\mathrm{S}-)$ following the formulations presented in Equations (7) and (8).

$$\left(\mathrm{S}+\right)=\left\{{\mathrm{v}}_1^{+},\dots ,{\mathrm{v}}_{\mathrm{n}}^{+}\right\}=\left({\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)|\mathrm{j}\in \mathrm{b}\right),\left({\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)|\mathrm{j}\in {\mathrm{b}}^{\mathrm{’}}\right),\mathrm{i}=1,\dots ,\mathrm{n}$$

(7)

$$\left(\mathrm{S}-\right)=\left\{{\mathrm{v}}_1^{-},\dots ,{\mathrm{v}}_{\mathrm{n}}^{-}\right\}=\left({\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)|\mathrm{j}\in \mathrm{b}\right),\left({\mathrm{m}\mathrm{a}\mathrm{x}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)|\mathrm{j}\in {\mathrm{b}}^{\mathrm{’}}\right),\mathrm{i}=1,\dots ,\mathrm{n}$$

(8)

Here, $\mathrm{b}$ and ${\mathrm{b}}^{\mathrm{’}}$ represent the benefit and cost elements, respectively. We then estimated the separation distances from $(\mathrm{S}+)$ and $(\mathrm{S}-)$ using the Euclidean distance equations presented in Equations (9) and (10).

$${\mathrm{d}}_{\mathrm{k}}^{+}=\sqrt{{{\sum }_{\mathrm{j}=1}^{\mathrm{m}}\left[{\mathrm{v}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)-{{\mathrm{v}}_{\mathrm{j}}^{+}}_{\mathrm{j}}\left(\mathrm{x}\right)\right]}^2,\mathrm{i}=1,\dots ,\mathrm{n}}$$

(9)

$${\mathrm{d}}_{\mathrm{k}}^{-}=\sqrt{{\sum }_{\mathrm{j}=1}^{\mathrm{m}}{\left[{\mathrm{v}}_{\mathrm{i}\mathrm{j}}\left(\mathrm{x}\right)-{{\mathrm{v}}_{\mathrm{j}}^{-}}_{\mathrm{j}}\left(\mathrm{x}\right)\right]}^2,\mathrm{i}=1,\dots ,\mathrm{n}}$$

(10)

The closeness measure ${\mathrm{c}}_{\mathrm{k}}^{+}$, derived from the set $(\mathrm{S}+)$, was estimated using Equation (11).

$${\mathrm{c}}_{\mathrm{k}}^{+}={\displaystyle \frac{{\mathrm{d}}_{\mathrm{k}}^{-}}{{\mathrm{d}}_{\mathrm{k}}^{+}+{\mathrm{d}}_{\mathrm{k}}^{-}}},\mathrm{i}=1,\dots ,\mathrm{n}$$

(11)

The alternative with the highest value of ${\mathrm{c}}_{\mathrm{k}}^{+}$ is considered the most preferable, while the alternative with the lowest value of ${\mathrm{c}}_{\mathrm{k}}^{+}$ is viewed as less preferable. In this study, the selected ESMs from the CMIP6 models were treated as alternatives, and statistical performance measures were used as the criteria for evaluation.

2.5. Drought Assessment

Droughts in the study area were assessed under different climate change scenarios, SSP1-2.6 and SSP5-8.5, which represent a range of future greenhouse gas emissions. SSP5-8.5 corresponds to a high-emission scenario with a radiative forcing of 8.5 W/m², while SSP1-2.6 corresponds to a low-emission scenario with a radiative forcing of 2.6 W/m².

The Standardized Precipitation Index (SPI) was employed to evaluate drought conditions in the study area [7]. This index is widely used due to its simplicity and the ability to compare drought conditions across different regions and periods. We calculated the drought indices on a 3-month scale, as the World Meteorological Organization recommended [28,29]. The standard deviation values depict the variability of the variable observed over a specific time frame, such as precipitation. The calculated index can vary based on the resolution of the source data and the intended application, allowing for different durations (e.g., three months) and spatial aggregations.

The calculation of the SPI followed these steps: (1) We determine a historical time series of precipitation from CMIP6 models and fit a probability distribution to the data, according to Equation (12), (2) we used the distribution to estimate the cumulative probability of each precipitation value. Afterward, we converted the cumulative probability to a standard average deviation and calculated from a numerical approximation to the normal cumulative distribution function (CDF), as shown in Equation (13), (3) For the SPI, we transformed the standardized cumulative distribution to a standardized Gamma distribution according to Equation (14).

$$\mathrm{f}\left(\mathrm{x};\mathsf{\alpha },\mathsf{\beta }\right)={\displaystyle \frac{{\mathrm{x}}^{\mathsf{\alpha }-1}{\mathrm{e}}^{-\mathrm{x}/\mathsf{\beta }}}{{\mathsf{\beta }}^{\mathsf{\alpha }}\mathsf{\Gamma }\left(\mathsf{\alpha }\right)}},$$

(12)

$$\mathrm{F}\left(\mathrm{x}\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\mathsf{\alpha }\right)}}{\int }_0^{\mathrm{x}}{\mathrm{t}}^{\mathsf{\alpha }-1}{\mathrm{e}}^{-\mathrm{t}/\mathsf{\beta }}\mathrm{d}\mathrm{t},$$

(13)

$$\mathrm{S}\mathrm{P}\mathrm{I}={\mathrm{ɸ}}^{-1}\mathrm{F}\left(\mathrm{x}\right)$$

(14)

where $\mathrm{x}$ is the accumulated precipitation, $\mathsf{\alpha }$ is the shape parameter, $\mathsf{\beta }$ is the scale parameter, and Γ(α) is the gamma function, and ${\mathrm{ɸ}}^{-1}$ is the inverse function of the CDF of the standard normal distribution. The ranges for drought are as follows: moderate (−1.0 to 1.49), severe (−1.50 to −1.99), and extreme (less than or equal to −2.0). We defined a drought event as significant when the 3-month scale SPI values remained within the established classification ranges for three months or more. This study did not consider SPI values that fell within the classification range for two months or less.

3. Results

3.1. Performance CMIP6 ESMs

Figure 2 shows the statistical evaluation of the CMIP6 models’ performance in determining historical precipitation. The BIAS values ranged from −3.85 to 0.84, showing significant variability in model trends. About 55% of the models had a negative bias, indicating they tend to underestimate precipitation compared to the CHIRPS datasets. The MIROC-ES2H, CanESM5, and KACE-1-0-G models had BIAS values closest to zero. The NRMSE values ranged from 1.08 to 2.17, indicating varying prediction accuracy among the evaluated models. Out of 51 models, 13 had average NRMSE values below 1.4. The lowest NRMSE values were 1.08, 1.13, and 1.13 for the CNRM-CM6-1-HR, CNRM-ESM2-1, and EC-Earth3-AerChem models, respectively. The mean r value for all models was 0.38, ranging from 0.15 to 0.60. The CMIP6 models with the highest positive linear relationship with CHIRPS data were CNRM-CM6-1-HR (0.60), Ensemble 50-CMIP6 (0.57), and CNRM-CM6-1 (0.55). NSE values were ranging from −2.82 to 0.59, indicating that the modeled precipitation time series had a significantly more significant estimation error variance than the CHIRPS dataset’s precipitation values. The NSE values reached their highest at 0.59, 0.52, and 0.47 for CNRM-CM6-1-HR, CNRM-ESM2-1, and EC-Earth3-AerChem, respectively. Furthermore, the MAE spanned from 61.37 to 89.88 mm/month for the CMIP6 models, with the CNRM-CM6-1-HR model demonstrating the lowest MAE at 61.37 mm/month, followed by CNRM-CM6-1 at 63.83 mm/month. These results highlight the significance of acknowledging the variability in climate model performance when formulating precise precipitation projections within specific regional climate contexts, such as northern South America.

These results highlight the significance of acknowledging the variability in climate model performance when formulating precise precipitation projections within specific regional climate contexts, such as northern South America. After considering various statistical metrics, we have chosen the CNRM-CM6-1-HR model for rainfall and drought projections.

Based on the average ranking scores, the models CNRM-CM6-1-HR, CNRM-ESM2-1, and EC-Earth3-AerChem achieved the highest scores, as shown in

Table 2. Average TOPSIS ranking scores of CMIP6 ESMs for reproducing monthly precipitation over the northernmost region of South America.

CMIP6 Model	Average Score	Rank	CMIP6 Model	Average Score	Rank
ACCESS-CM2	0.44	22	FGOALS-g3	0.37	37
ACCESS-ESM1-5	0.39	33	FIO-ESM-2-0	0.37	38
AWI-CM-1-1-MR	0.45	19	GFDL-ESM4	0.41	24
AWI-ESM-1-1-LR	0.33	39	GISS-E2-1-H	0.17	51
BCC-CSM2-MR	0.39	34	HadGEM3-GC31-LL	0.43	23
BCC-ESM1	0.45	20	HadGEM3-GC31-MM	0.48	11
CAMS-CSM1-0	0.47	14	IITM-ESM	0.26	45
CanESM5	0.15	51	INM-CM4-8	0.28	44
CanESM5-CanOE	0.20	47	INM-CM5-0	0.29	43
CESM2	0.46	15	IPSL-CM5A2-INCA	0.18	49
CESM2-FV2	0.32	40	IPSL-CM6A-LR	0.37	36
CESM2-WACCM	0.44	21	KACE-1-0-G	0.51	8
CESM2-WACCM-FV2	0.30	42	MCM-UA-1-0	0.19	48
CMCC-CM2-HR4	0.41	26	MIROC6	0.40	30
CMCC-CM2-SR5	0.40	32	MIROC-ES2H	0.40	31
CMCC-ESM2	0.45	18	MIROC-ES2L	0.17	50
CNRM-CM6-1	0.54	5	MPI-ESM1-2-HR	0.41	27
CNRM-CM6-1-HR	0.64	1	MPI-ESM1-2-LR	0.47	13
CNRM-ESM2-1	0.57	2	NESM3	0.40	29
E3SM-1-0	0.49	10	NorCPM1	0.23	46
E3SM-1-1	0.45	17	NorESM2-MM	0.48	12
EC-Earth3-AerChem	0.57	3	SAM0-UNICON	0.41	25
EC-Earth3-CC	0.54	6	TaiESM1	0.31	41
EC-Earth3-Veg	0.52	7	UKESM1-0-LL	0.46	16
ESM2-0	0.40	28	Ensemble 50-CMIP6	0.55	4
FGOALS-f3-L	0.38	35

. In contrast, the MIROC-ES2L and CanESM5 models received the lowest scores, with values of 0.17 and 0.15, respectively. However, it is crucial to note that approximately 18% of the models scored above 0.50 according to the TOPSIS method, underscoring the need for further evaluation and refinement of these models.

The analysis of different climate models revealed a significant association between spatial resolution and accuracy. Models with finer native-resolution, such as CNRM-CM6-1-HR, performed better in simulating precipitation in the study area. These models could capture spatial and temporal variations more effectively than lower-resolution models, possibly due to a more accurate representation of physical processes and climate parameterizations. However, it is crucial to note that higher spatial resolution guarantees better simulation if other model components, such as parameterizations and input data quality, are equally optimized. After considering various statistical metrics, we have chosen the CNRM-CM6-1-HR model for rainfall and drought projections.

3.2. Performance of CNRM-CM6-1-HR Model in Each Region

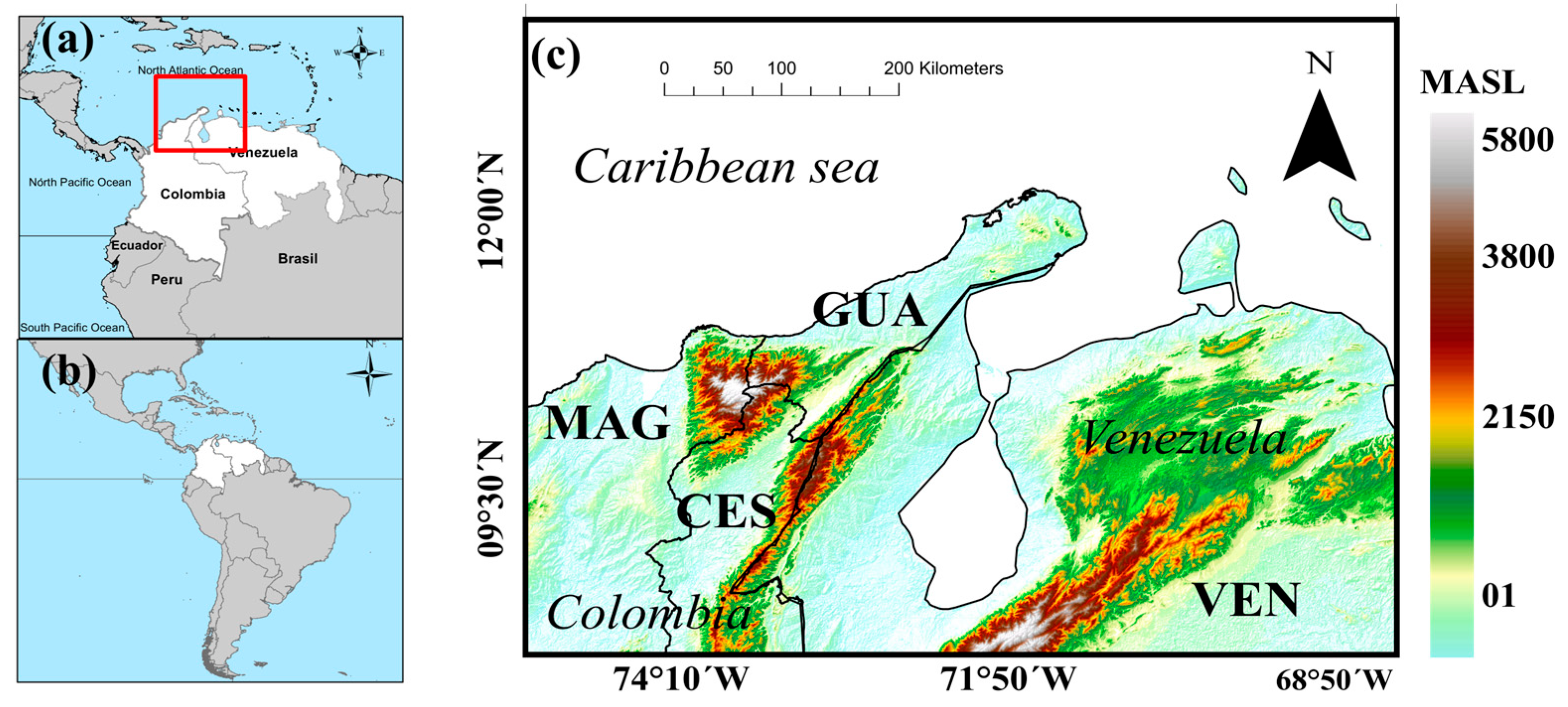
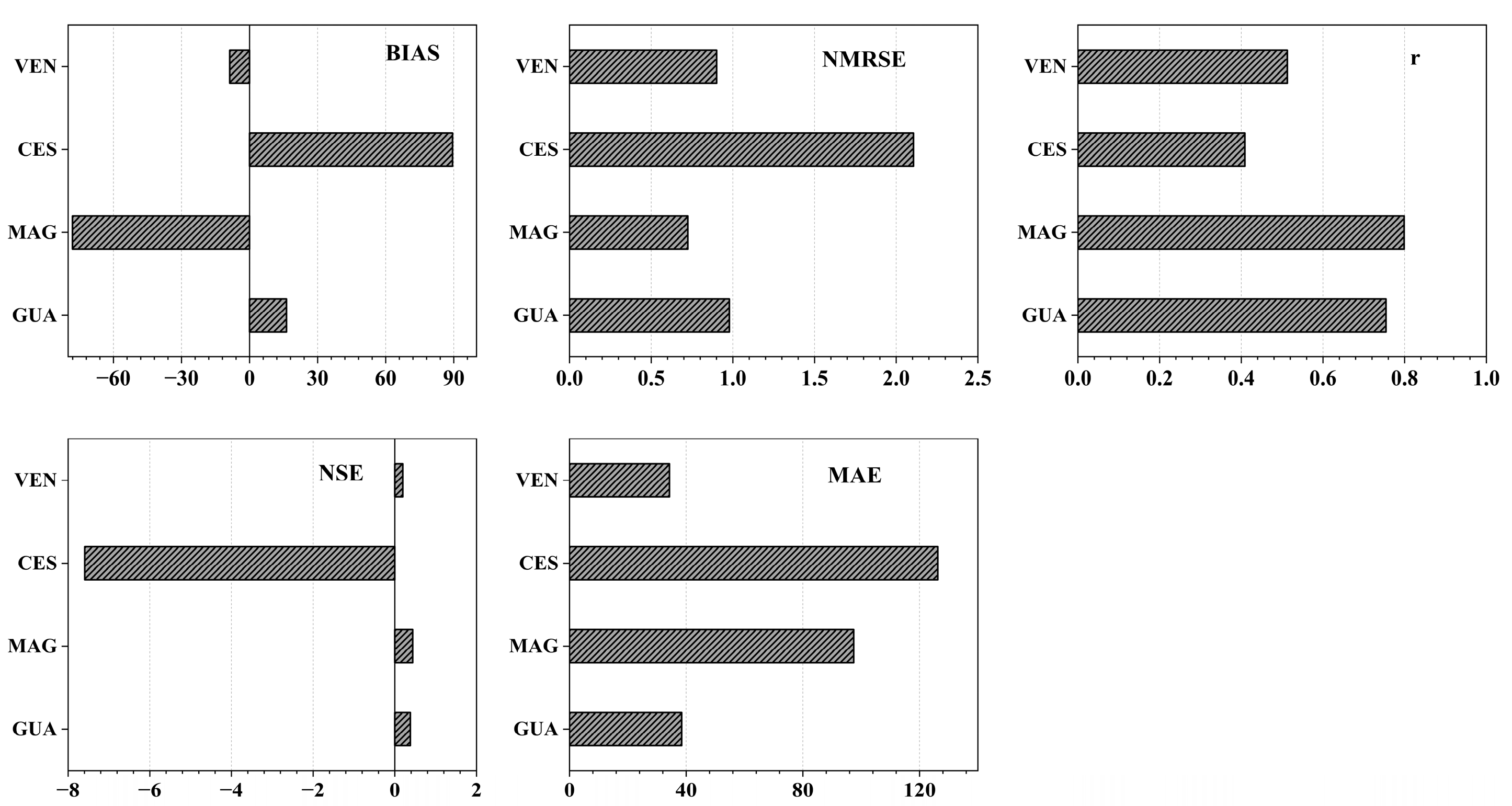
The performance of the corrected CNRM-CM6-1-HR model in estimating monthly rainfall from 1981 to 2014 in four study zones (GUA, MAG, CES, and VEN) is shown in Figure 3. The model had a positive BIAS (16.26) in the GUA zone, indicating a slight overestimation. The NRMSE, r, NSE, and MAE values were 0.98, 0.75, 0.38, and 38.45 mm/month, respectively. The rainfall estimates deviated considerably from the CHIRPS data range, but the two datasets had a strong linear relationship. The model had a significant negative BIAS in the MAG zone, indicating considerable underestimation. The NRMSE was lower at 0.72 compared to the GUA zone and achieved the highest r value of 0.80. The NSE value was 0.44, and the MAE was approximately 97 mm/month. On the other hand, The CES zone showed the lowest performance in all metrics, with NRMSE greater than 2, an r-value of 0.41, and an MAE greater than 120 mm/month. The negative NSE (−7.59) indicates inferior model performance in this zone. The model was slightly underestimated in the VEN zone, with the lowest MAE (64.25 mm/month) compared to the other zones.

3.3. Spatial Patterns of Historical Precipitation

Figure 4 presents the maps of mean monthly precipitation estimated by CHIRPS and the CNRM-CM6-1-HR model for the study area. The CNRM-CM6-1-HR model shows a high level of accuracy in capturing the spatial patterns of precipitation, particularly over flat terrain. In contrast, the model’s performance was lower in high-elevation regions, such as the Sierra Nevada de Santa Marta (470 mm) and the eastern sector of the Perijá mountain range (460 mm). This reduced performance can be attributed to the complex topography of these mountainous areas, where localized factors, such as orographic uplift and microclimatic variability, significantly influence precipitation patterns. Similar limitations have been reported in other studies conducted in regions with pronounced topographic gradients, highlighting the need for caution when interpreting projections in these locations [30]. The CNRM-CM6-1-HR model can reproduce the historical precipitation patterns in all zones except the estimated precipitation east of the Perijá mountain range. It reproduces precipitation in the center of the VEN zone that is not estimated in CHIRPS. In addition, the estimated precipitation in the center of the Sierra Nevada de Santa Marta is more extensive and of higher intensity than the CHIRPS estimates. Percent bias varied between 17% and −17%. The highest overestimation values are estimated in the CES zone, located in the central and eastern areas. In addition, percent bias values reaching −17% are pronounced in the south of the CES zone, indicating underestimation in this site. Also, a band of underestimation values is noticeable across the VEN region. Although the CNRM-CM6-1-HR model shows a remarkable ability to simulate monthly precipitation spatial patterns, it is important to consider area-specific variations in the accuracy of the estimates for a more comprehensive and accurate assessment of its performance.

3.4. Precipitation Projections

Figure 5 shows the monthly precipitation projections under the SSP1-2.6 scenario in the four study zones in South America’s northernmost region. In the MAG zone, higher precipitation is expected from June to November, ranging from 301 mm to 498 mm; the winter period is longer compared to other zones. The GUA and VEN zones are anticipated to have wet periods of up to three months, with October being the wettest month (up to 190 mm). The GUA zone is estimated to have an average monthly rainfall of 8 mm in the first three months of the year, reflecting a 10% reduction compared to historical data. The VEN zone is foreseen to experience precipitation declines of up to 17% in the year’s first quarter. Under the SSP1-2.6 scenario, the wettest month for the CES area will be October (191 mm), while February (12 mm) will be the driest. The wettest months in CES are expected to see precipitation decreases of 3% to 26% compared to historical data. Conversely, the MAG zone is estimated to have the wettest months, with increases of up to 33% (368 mm).

Monthly precipitation projected by the CNRM-CM6-1-HR model for the study zones under the SSP5-8.5 scenario is shown in Figure 6. In this scenario, October is projected to have the highest amount of precipitation, while February and March will be the driest months. In the GUA and VEN zones, there is an expected reduction in precipitation of up to 13% and 20%, respectively, from January to May compared to historical data. Conversely, there will be an increase in precipitation throughout most of the year in the MAG zone. During the wet months, all regions are expected to experience precipitation increases ranging from 24% to 76% compared to historical levels. In comparison to the SPP1-2.6 scenario, the SSP5-8.5 scenario predicts a redistribution of precipitation throughout the year, with reductions between March–April (up to 4 mm/month) and August–September (up to 44 mm/month) that will be spread between November and December.

3.5. Precipitation Trends

Table 3. Monthly precipitation trends in the northernmost region of South America by Theil-Sen’s estimator values. The values included in the tables are statistically significant, as determined by the MMK test. Any values that did not demonstrate a significant trend have been excluded (p-value of 0.05).

	Historical Precipitation				SSP1-2.6 Scenario				SSP5-8.5 Scenario
	GUA	MAG	CES	VEN	GUA	MAG	CES	VEN	GUA	MAG	CES	VEN
January	−0.08	−0.16	−0.12	−0.20	−0.03	-	-	−0.04	-	0.12	-	−0.07
February	-	-	-	-	−0.01	−0.06	−0.03	−0.03	-	0.11	-	−0.07
March	-	-	−0.20	−0.08	−0.01	−0.11	−0.05	-	−0.02	-	−0.04	−0.04
April	-	-	-	-	-	-	-	−0.08	-	0.60	0.12	−0.04
May	-	-	-	-	−0.20	-	-	−0.08	-	0.42	0.12	−0.11
June	−0.37	-	-	-	−0.09	-	-	−0.13	-	0.53	0.21	-
July	-	-	-	-	-	0.26	-	-	−0.26	-	−0.21	-
August	-	-	-	-	−0.29	−0.27	−0.21	−0.19	−0.32	-	−0.25	-
September	−0.29	-	-	−0.31	0.18	0.90	0.41	0.15	−0.47	-	−0.22	−0.24
October	-	-	-	-	0.12	-	0.13	0.25	−0.50	-	-	−0.68
November	-	0.73	0.20	-	−0.20	−0.41	−0.18	-	0.60	2.88	0.93	0.25
December	0.16	1.17	0.60	0.05	−0.04	-	-	−0.07	0.15	0.88	0.33	0.04

shows the monthly precipitation trends for the northernmost region of South America, based on historical data and the SPP1-2.6 and SSP5-8.5 scenarios. Historically, monthly precipitation data for the study area indicate a decrease in January precipitation in the GUA, MAG, CES, and VEN regions, with recorded changes of −0.08, −0.16, −0.12, and −0.20 mm/month, respectively. In contrast, December shows a positive trend, particularly in the MAG zone, which has an increase of 1.17 mm/month. In the SPP1-2.6 scenario, the trends in monthly precipitation vary throughout the year. A decrease in precipitation is projected for the first half of the year, while an increase is anticipated in September (0.15–0.90 mm/month) and October (0.12–0.25 mm/month). The SSP5-8.5 scenario predicts greater increases in precipitation for November and December, particularly in November, with values of 0.60, 2.88, 0.93, and 0.25 for GUA, MAG, CES, and VEN, respectively. Overall, reductions in monthly precipitation are expected throughout the year, especially for GUA and VEN.

Notably, MAG shows a significant positive trend of 0.73 in November based on historical data, which increases to 2.88 under the SSP5-8.5 scenario, indicating a substantial rise in precipitation at this location over time. There is a clear distinction between the SPP1-2.6 and SSP5-8.5 scenarios. For example, in the SSP5-8.5 scenario, April shows a significant positive trend for MAG (0.60), while no significant trend is observed in the SSP1-2.6 scenario. The high-emission scenario often indicates more intense shifts in precipitation, with some months and locations showing significant positive or negative trends. It suggests that under more extreme global warming scenarios, regions may experience more drastic changes in precipitation patterns.

3.6. Projected SPI

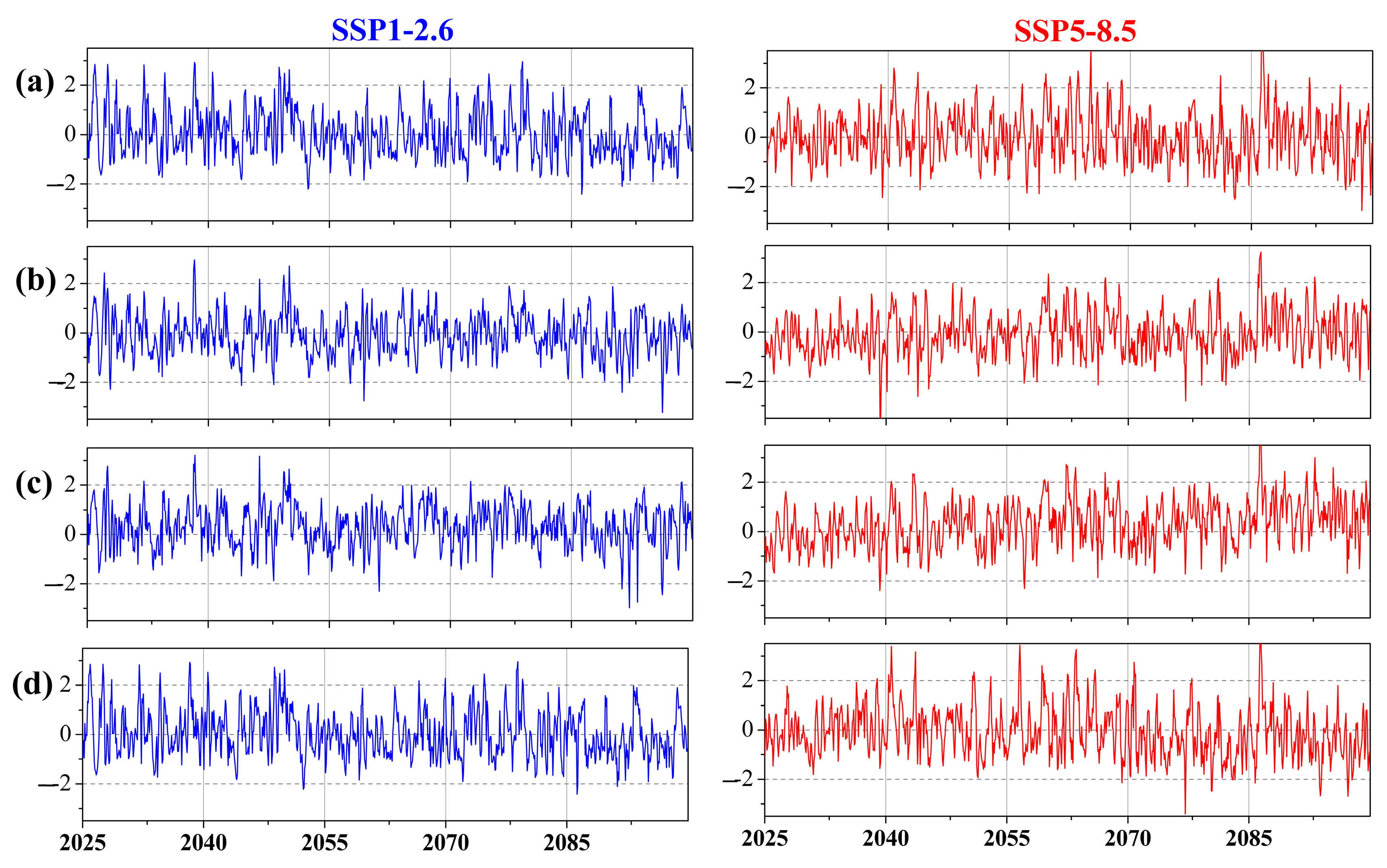
Figure 7 shows the projected SPI variations for the study areas under the two climate scenarios, SSP1-2.6 and SSP5-8.5. These figures illustrate how these indices will change over the projected period from 2025 to 2100, providing a detailed view of drought trends and patterns in each area. Under the SSP1-2.6 scenario, moderate drought events are estimated to be 18, 3, 21, and 18 for the GUA, MAG, CES, and VEN zones. The highest number of these events is expected for the first and last quarters of the year. Additionally, severe droughts are projected mainly in the middle and end of the century in the GUA and VEN zones. However, no extreme droughts with continuous durations of 3 months or more are expected based on this scenario.

Under the SSP5-8.5 scenario, the estimated moderate drought events are 18, 3, 3, 16, and 22 for the GUA, MAG, CES, and VEN zones, respectively. There is no specific pattern predicting the months when these events will occur. On the other hand, the highest number of severe drought events is anticipated in the VEN zone, with 6 events projected in the last two decades of the century, followed by the GUA zone, with 4 events projected in the middle and end of the century.

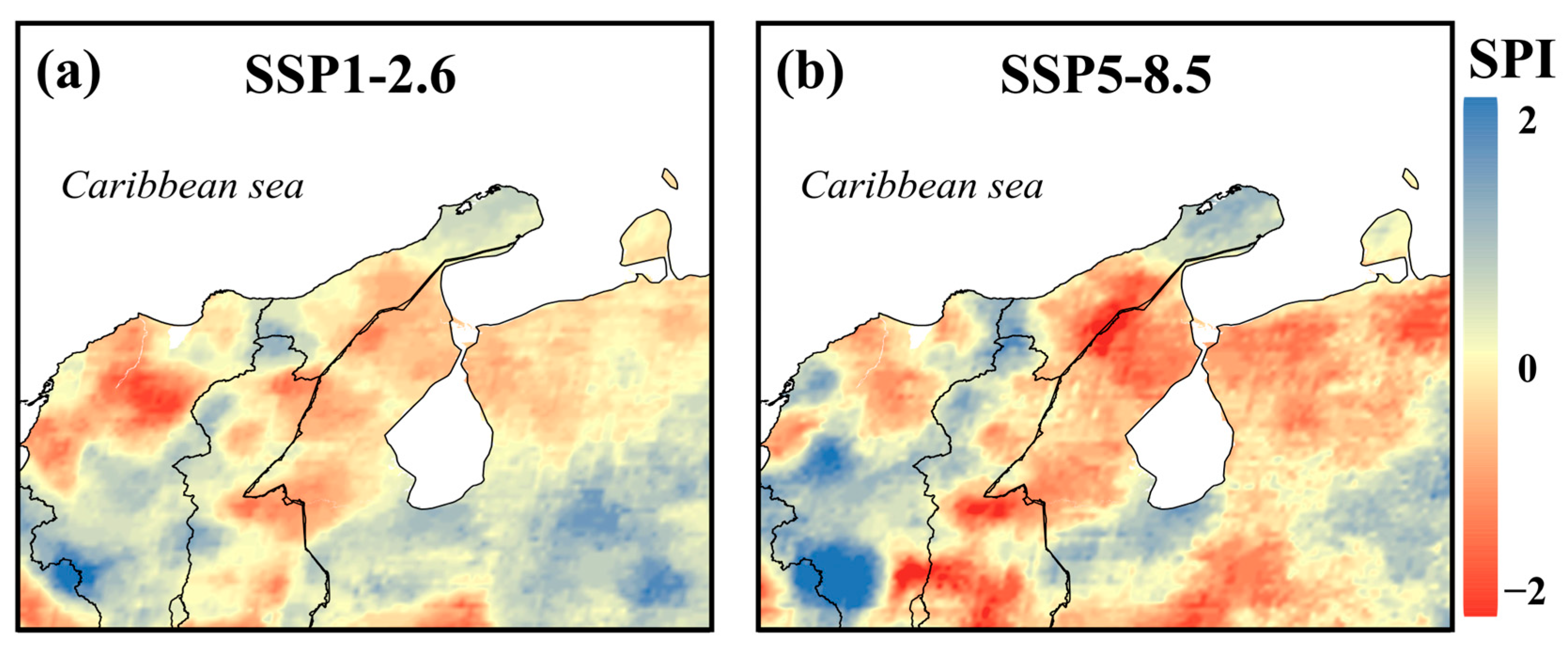
Figure 8 show the spatial distribution of SPI values calculated over 3-month periods under two scenarios, SSP1-2.6 and SSP5-8.5, using the CNRM-CM6-1-HR model for the period 2025–2100. On a 3-month time scale, most regions exhibit a mix of dry and wet patterns. The SPI values indicate higher intensity under the SSP5-8.5 scenario than the SSP1-2.6 scenario. Specifically, under the SSP1-2.6 scenario, moderate to severe drought conditions are expected in the central GUA, eastern CES, and coastal regions of VEN, as well as severe drought conditions in the northern region of MAG. These conditions strongly suggest a likelihood of meteorological droughts and subsequent water resource losses across these areas, underscoring the practical implications of our research. Under the SSP5-8.5 scenario, drought conditions are projected to intensify. Extreme drought conditions are anticipated in the GUA, CES, and VEN zones, with severe drought conditions extending from the coastal areas to the center of the VEN zone.

At 3-month time scales, the percentage of grid points is approximately 20.5%, 32.8%, 40%, and 49.2% for the GUA, MAG, CES, and VEN zones, respectively. Moreover, the percentage of grid points experiencing extreme drought conditions (SPI < 2) is around 3% for SPI-3 in all studied areas under the SSP1-2.6 scenario. On the other hand, under the SSP5-8.5 scenario, the ratio of grid points at 3-month time scales is approximately 38.6%, 33.6%, 45.3%, and 50.2% for the GUA, MAG, CES, and VEN zones, respectively. This analysis suggests an increase in the spatial extent of the dry pattern with a change in scenario. In this scenario, around 22% of the grid points are under an extreme drought state with SPI-3.

4. Discussion

The evaluation of CMIP6 ESMs in predicting historical precipitation revealed significant variability in their performance. BIAS values indicated that approximately 55% of the models underestimated precipitation compared to CHIRPS datasets. The top-performing models were MIROC-ES2H, CNRM-CM6-1-HR, CanESM5, and KACE-1-0-G. The models showed different levels of prediction accuracy, with NRMSE values ranging from 1.08 to 2.17. Notably, CNRM-CM6-1-HR achieved the lowest NRMSE, indicating the highest accuracy among the models tested. Models with finer native-resolutions, like CNRM-CM6-1-HR, demonstrated improved accuracy, highlighting the importance of model quality in regional climate projections. As a result, CNRM-CM6-1-HR was selected for future rainfall and drought forecasting. The CNRM-CM6-1-HR model has demonstrated strong performance in simulating precipitation in tropical climates, thanks to its updated dynamics and physics that effectively represent atmospheric processes [31]. However, there is a systematic underestimation of rainfall in our study area, primarily attributed to the model’s insufficient representation of various processes. Bilinear interpolation can introduce moderate errors that diminish accuracy, particularly when assessing extreme precipitation events and in complex terrains. This method often underestimates variability and contributes to the uncertainty present in downscaled projections. Furthermore, the interpolation process can create artificial correlations by producing smooth transitions that do not accurately represent the true physical conditions [32]. The smoothing effect can enhance apparent spatial coherence, potentially inflating skill metrics such as correlation coefficients. To mitigate these challenges, techniques such as quantile mapping are effective in reducing biases and better preserving the tails of distributions, thereby improving climate impact assessments. While the CNRM-CM6-1-HR model incorporates cumulus convection, ocean-atmosphere interactions, soil moisture, and surface processes, its limited horizontal resolution impacts the analysis of precipitation magnitude and distribution across different zones [33]. Our results indicate that the model underestimates the precipitation in the CES (89 mm/month) and GUA (16 mm/month) zones at the local scale. The CNRM-CM6-1-HR model tends to generate excessively intense precipitation due to overly vigorous modeled convection and inadequate representation of topography in these areas [33]. Furthermore, the CNRM-CM6-1-HR model shows increased uncertainty in forested regions, where convective processes differ significantly from those in coastal areas. De Oliveira et al. [34] evaluated 50 CMIP6 models, noting that the CNRM-CM6-1-HR was not identified as the top performer for subdomains in South America, including the southern Amazon and southeastern Brazil, where the dominant land uses are vegetation and forest areas.

The northernmost region of South America experiences intense precipitation at higher altitudes and topographic zones. In contrast, lower precipitation levels are found at higher latitudes and near coastal areas. The Atlantic Ocean and terrestrial recycling, particularly from the Orinoco and Amazon basins, represent significant sources of moisture for Colombia. These sources play a crucial role in contributing to the region’s precipitation through long-range cross-equatorial flows and the influence of low-level westerly winds and Caribbean jet streams [35]. The ENSO notably impacts Colombia’s precipitation patterns; specifically, El Niño years are typically associated with drier conditions, whereas La Niña years often lead to wetter weather extremes [36]. In the SSP1-2.6 scenario, the study area is projected to experience increased rainfall from June to November and significant decreases in precipitation during the early part of the year. In contrast, the SSP5-8.5 scenario suggests a general redistribution of rainfall, showing increases in wet months and reductions in early months, particularly for coastal regions. The research findings indicate that across all studied regions, there is a consistent and persistent pattern of monthly precipitation under two climate change scenarios (SSP1-2.6 and SSP5-8.5). This finding suggests that current climate patterns are likely to continue, albeit with variations in precipitation intensity. The dry period occurs from December to April, while the wet period is October. This seasonal pattern persists regardless of the climate change scenario, although the intensity of precipitation varies depending on the severity of the projected climate change. The precipitation deficit observed during the year’s initial quarter is attributed to seasonal and regional climatic phenomena. These are expected to persist across different scenarios [37]. In contrast, the amount of rainfall in October is affected by the movement of the intertropical convergence zone [38]. Spatial precipitation projections suggest that certain areas may experience more significant variations. For instance, regions near the Sierra Nevada de Santa Marta may experience a substantial increase in precipitation due to orographic effects and moisture transport from the Caribbean Sea, which is a concerning potential impact of climate change.

Under SSP1-2.6, moderate drought events are forecasted in the northernmost region of South America, with a notable presence in coastal areas. Conversely, SSP5-8.5 predicts more intense drought conditions overall, with the Venezuelan country experiencing the highest frequency of severe droughts and the emergence of extreme droughts. The drought conditions will worsen over time, leading to significant implications for water resources and highlighting the increasing spatial extent of dry patterns, particularly under the SSP5-8.5 scenario. Higher emissions rates will likely lead to drying trends, while lower emissions scenarios may result in wetter conditions. In humid environments, such as the coastal areas of northern South America, these changes might be linked to the weakening of the land-atmosphere coupling [39]. Similar results to our study have also been observed in other tropical regions. Nooni et al. [40] conducted a comprehensive investigation into the future changes in drought events across the African continent, utilizing the CNRM-CM6 model. Their regional trend analysis highlighted significant differences in spatial patterns, with diverse projections of wetter and drier conditions observed in humid and non-humid regions under all SSP scenarios. The key findings suggest that arid regions north of the equator will likely experience moderate drying conditions across all SSP scenarios. The response to meteorological drought will be influenced by large-scale atmospheric circulation patterns and local underlying surfaces across both long- and short-time scales [41]. Some studies underscore the significant spatial variability in drought projections across South America, indicating distinct trends and characteristics associated with drought occurrences. Temporal analyses have revealed notable seasonal shifts, including delayed wet seasons and extended dry spells, which carry substantial implications for water management and agricultural practices [42,43]. Additionally, large-scale climate variability patterns, such as the ENSO, play a critical role in modulating the frequency and intensity of drought events in the region [44]. These teleconnections influence precipitation patterns, thereby affecting both the spatial and temporal dynamics of drought. Ongoing assessments aim to quantify the extent to which these influences affect drought patterns [45]. Projections indicate substantial and consistent runoff and soil moisture decreases are still expected across northern South America [6]. This underscores the critical role of non-precipitation factors in the occurrence of drought. Furthermore, these findings suggest that even with the most favorable scenarios for climate action, mitigation efforts alone may not be sufficient to address the drought responses associated with climate change entirely. As such, it will be essential to implement adaptive measures to enhance resilience in the study area as it faces a drier future. Future research initiatives should integrate multimodel ensembles, employ advanced statistical downscaling techniques, and explore the socioeconomic implications of increased drought risk.

5. Conclusions

The assessment of CMIP6 ESMs for historical precipitation estimation indicated that the CNRM-CM6-1-HR, CNRM-ESM2-1, and EC-Earth3-AerChem models exhibited notable performance, as evidenced by their low NRMSE values of 1.08, 1.13, and 1.13, respectively. Notably, the CNRM-CM6-1-HR model demonstrated outstanding accuracy in historical monthly rainfall simulations, as reflected by its minimal MAE values (61 mm/month), signifying heightened rainfall estimation reliability. This reliability led to the selection of the CNRM-CM6-1-HR model for precipitation and drought projections spanning 2025–2100. Projections indicate anticipated reductions in precipitation levels during the wet seasons under the SSP1-2.6 scenario, with estimated reductions ranging from 3% to 26%. Conversely, an increase in precipitation of up to 33% is projected in the western section of our study area. In the SSP5-8.5 scenario, all regions will experience increased precipitation during the wet months. However, during the dry months, a decrease in precipitation of 10% and 17% is expected in the GUA and VEN areas, respectively. The SSP5-8.5 scenario also projects extreme drought episodes in the GUA and CES zones, with an increasing frequency expected during the mid and late 21st century. Additionally, the analysis indicates that from 2025 to 2100, projected drought conditions under all scenarios show significantly different patterns in northern South America. While the SSP1-2.6 scenario shows moderate to severe droughts in several regions, the SSP5-8.5 scenario indicates a marked intensification, with extreme drought conditions in large areas of the study domain. This study delivers significant insights into drought variability and projections in northern South America, utilizing the CNRM-CM6-1-HR model. The results suggest a heightened frequency of drought events under the SSP5-8.5 scenario, particularly in semi-arid regions such as La Guajira. However, these findings should be approached with caution, as they are derived from a single model and represent only one possible trajectory for future climate conditions. Future research should enhance this work by integrating multi-model ensembles, employing advanced statistical downscaling techniques, and examining the socioeconomic implications of increased drought risk to provide a more comprehensive understanding of the impacts of regional climate change.