Abstract
This paper introduces a dynamic consensus-based economic dispatch (ED) algorithm utilizing the Alternating Direction Method of Multipliers (ADMM) to optimize real-time pricing and generation/demand decisions within a decentralized energy management framework. The increasing complexity of modern energy markets, driven by the proliferation of Distributed Energy Resources (DER) and variable demands from hybrid electric vehicles, necessitates a departure from traditional centralized dispatch methods. This research proposes a novel ADMM-based solution tailored for non-responsive and responsive demand units that integrates demand response mechanisms to adaptively manage real-time fluctuations while enhancing security and privacy through distributed data management. The testing of the algorithm on the IEEE 39 bus system under various load conditions over 24 h demonstrated the algorithm’s effectiveness in handling traditional and renewable energy sources, particularly highlighting the economic benefits of shifting controllable loads to periods of low-cost renewable availability. The findings underscore the algorithm’s potential to reduce energy costs, enhance energy efficiency, and offer a scalable solution across diverse grid systems, contributing significantly to advancing global energy policy and sustainable management practices.
1. Introduction
Conventional power generation predominantly relies on fossil fuels, thereby exacerbating environmental degradation through increased greenhouse gas emissions. Due to the increasing commitment of international societies to a low-carbon economy and exceptional technological advancement, the steady growth of distributed energy resources (DER) is questioning the relative benefit of large-scale traditional electricity generation, which is supposed to pile up high economies of scale. This indicates that alternative energy sources such as photovoltaic and wind power are imperative despite their inherent intermittency [1]. In systems with high PV penetration, surplus energy is generated during sunny periods, while deficits occur at other times. The energy output is highly fluctuating even within its available period. The proliferation of intermittent renewable energy sources alongside the introduction of electric vehicles presents significant challenges in managing and controlling the power grid. Furthermore, as the electricity sector witnesses a surge in active participants, there emerges a pressing need for a more efficient system that can benefit both the supply and demand sides. The intricate energy landscape impacts both technical operations and economic considerations, underscoring the importance of Optimal Energy Management (OEM) for efficient resource allocation. In response to these multifaceted challenges, the development and implementation of SMART grid technology represent an inevitable and transformative evolution.
ED is a crucial aspect of demand-side management, which deals with the allocation of resources in a power system. In this process, every generator unit determines its optimal strategy to maintain power balance within the network [2]. The traditional electricity market is vertically integrated: the utility has to supply all the load demand whenever it occurs, and in response to providing demand, the utility charges the consumers. Ensuring a precise balance between supply and demand in real-time is essential for enhancing the reliability of the electricity system. Various factors contribute to the complexity of this task, including transmission and distribution line failures, abrupt changes in generation and load patterns, and unexpected outages of generation units, which can swiftly alter both supply and demand levels. To enhance the reliability of the supply system, significant investments in additional infrastructure are required, representing a substantial capital incentive. Consequently, the costs associated with ensuring reliability are inevitably transferred to consumers, resulting in higher consumer expenses. Therefore, electric utilities and power network companies have been forced to restructure their operation from a vertically integrated classical model to an open market system. Within an open market system, electricity consumers are more responsive to market dynamics, and correspondingly, the market adapts to consumer behaviors. Therefore, the incorporation of Demand Response (DR) in economic dispatch would be an appropriate approach for optimal energy management.
DR plays a crucial role in optimal energy management by enabling the voluntary reduction or shifting in electric energy usage in response to monetary incentives or changes in energy prices over time. Beyond merely shifting load from peak to off-peak periods, DR enhances both customer benefits and grid efficiency. Integrating DR with economic dispatch offers a solution that aligns the interests of both suppliers and consumers, ultimately maximizing energy efficiency. Addressing the Social Welfare Maximization problem allows for the formulation and solving of real-time pricing mechanisms, ensuring that both suppliers and consumers reap maximum benefits from electricity transactions. In [3], factors that highly impact the future power grids have been defined: policies from the governmental and federal level, efficiency needed for the consumers and consumers’ utility, and the most intelligent technologies of computer software and hardware. Allowing the integration of renewable energy resources, active customer participation to enable better energy conservation, secure communication to protect from cyber-attacks, and the optimization of the energy-supplying strategy and energy flow to lower and reduce losses are the basic requirements of future smart power grids. In [4], the authors have proposed different approaches to controllable load management in smart grids. Traditional load control approaches such as controllable end users’ appliances, battery storage, vehicle-to-grid and grid-to-vehicle, and heat storage are reviewed. Furthermore, virtual power plants, load aggregators, and microgrids are presented as effective ways of broad controllable load management. Effective management of controllable loads provides a flexible solution to integrating highly intermittent renewable sources in grids.
The literature contains significant research on different aspects of economic dispatch. In [5], a multi-agent-based distributed sub-gradient algorithm has been used to coordinate among multiple microgrids to balance active power. Supply and demand are kept balanced by adjusting the utilization level of renewable generations based on local frequency, i.e., frequency is considered the controlled parameter in coordination. A two-level Incremental cost consensus (ICC) algorithm is proposed in [6]. At the lower level, the average consensus algorithm is run, and the average mismatch in each node is found. The ICC is run at the higher level of the consensus network. The operation is based on a distributed algorithm, more than one consensus algorithm is run, and the dynamic behavior of demand is not accounted for. In [7], an ADMM algorithm and model predictive control are used in a decentralized micro-grid to schedule and control the distributed energy resources in real-time. The central coordinator collects information from all the agents to find the optimal decision variables and sends it back to each agent. A central leader’s involvement in communicating directly with all units for the operation may be vulnerable to single-point failure and might have data privacy concerns. In [8], an accelerated distributed gradient-based algorithm for economic dispatch is proposed, but an extra momentum term is added to ensure power balance by communicating with all the agents. Multi-parameter matrix perturbation theory and graph theory have been proposed in [9] to find the economic dispatch solution in a distributed manner, in which mismatch energy is used as feedback in the control logic. This research takes conventional generation units, and the generation ramp rate limit is not considered.
The literature contains a plethora of research, including responsive demand in economic dispatch. In [10], the Social Welfare Maximization problem in the smart grid was solved using Lagrangian and projected gradient methods. The supply and demand mismatch in a distributed way was derived using the Multi-Agent System (MAS) framework. In [11], the author has presented the distributed algorithm for the optimal scheduling of resources, where the social welfare problem is formulated and solved. A gradient algorithm is used to jointly compute utility and customer equilibrium points. However, communication at each iteration is all-to-all. At the beginning of the day, the utility companies and customers compute their prices, consumption, and battery charging schedules for each period in advance. In [12], an incremental welfare consensus algorithm for energy management is presented. The author addresses both the generation and demand sides simultaneously for a single period, aiming to optimize benefits for all participants. An additional observer has been introduced to approximate the generation and load mismatch. In [13], social welfare optimization employs dual decomposition methods to achieve a distributed solution for optimal energy generation and demand. However, this algorithm does not ensure power balance. In [14], the VCG mechanism is proposed for demand-side management. Each user provides their demand information to the energy provider, who then computes optimal energy consumption levels and costs. The optimization problem maximizes user utility while minimizing energy costs. However, information must be collected from all participating units.
The conventional power grid employs a centralized communication structure where a central coordinator collects data from various units and forwards them to a central data operation center. This system simplifies data management but is vulnerable to failures due to its dependency on a central coordinator for data gathering, processing, decision-making, and distribution. Sharing decision variables and cost parameters for optimization raises concerns about fair market implementation. Many popular algorithms based on the ADMM have been extensively used to provide distributed solutions for energy resource allocation in power systems. These algorithms solve distributed economic dispatch problems with a coordinator acting as a leader of the network, and the leader addresses the mismatched power. Many researchers have proposed solutions to eliminate the need for coordinators [5,6,15], though none of them fully addresses the real-time demand fluctuations without some system adjustment. Another aspect is that utilities in traditional power grids typically overlook demand response when scheduling energy resources, primarily focusing on meeting consumer demand irrespective of energy prices. Ensuring reliable operation of the energy system necessitates a real-time balance between supply and demand. However, factors such as sudden changes in supply and demand, forced outages of generation units, and disruptions in transmission and distribution infrastructure contribute to imbalances. These unforeseen conditions underscore the critical importance of real-time demand-supply balancing for effective energy management. Enhancing supply reliability up to the limit of handling any contingencies requires substantial investment in robust infrastructure, leading to increased consumer costs. Therefore, there is a pressing need for electric utilities and power network companies to restructure their operations to incorporate responsive demand along with the status of generating units while preserving the privacy of each participant. Different approaches discussed in the literature, such as Lagrangian and gradient methods, dual decomposition, the VCG mechanism, etc., either require extensive communication and data sharing among all units or do not adequately address real-time imbalances and demand fluctuations. This paper presents an algorithm incorporating dynamic consensus-based ADMM to provide a more practical, reliable, and efficient solution for distributed economic dispatch integrating demand response to ensure the real-time balance between supply and demand. The ADMM is more robust—it can handle data more accurately even when there is communication delay or partial data loss and scalable—the size of the problem does not grow with the network size as the problem is broken down into smaller subproblems and computation can be conducted in a parallel sequential fashion. The main contributions of this paper are as follows:
- Design of distributed economic dispatch algorithm incorporating demand response in time-variant demands. The generation limit and ramp rate limit of the generating unit and power consumption limit of the responsive demand units are considered;
- Finding optimal generation, optimal demand, and real-time pricing of electrical energy and maximizing social welfare;
- Analyzing the effect of renewable sources in real-time pricing and social welfare maximization.
- The proposed algorithm prioritizes privacy by exclusively sharing the energy mismatch with neighboring agents, safeguarding the privacy of each individual. Furthermore, it ensures robustness and scalability, making it a reliable and adaptable solution.
The remainder of this paper is organized as follows: Section 2 provides an overview of graph theory, the dynamic consensus algorithm, the Karush–Kuhn–Tucker (KKT) conditions, and the ADMM. Section 3 details the problem formulation of economic dispatch with different approaches. Section 4 presents the result, and Section 5 concludes the paper.
2. Preliminaries
2.1. Graph Theory
Electric grid networks can be treated as graphs, and graph theory principles can be used to analyze them. A graph, G, can be denoted by a pair of sets (V, E), where a set of vertices, V, indicates the number of nodes in the graph, and a set of edges, E, denotes the line joining the two nodes i and j. N represents the number of nodes V, and or is the degree of the nodes, which means the number of nodes in the neighbor. In [16], it states that the Laplacian matrix of the graph serves as the foundation for the distributed consensus dynamics. Laplacian matrix, L, of the graph G is given as
where D is the diagonal degree matrix, and A is the adjacency matrix. A graph with N nodes has an adjacency matrix of size N∗N. The Laplacian consensus dynamics can be represented in differential equation form as
The dynamics of each agent can be expressed as
The above dynamic shows that each agent only interacts with its neighboring agents to update its value, forming a completely distributed approach. For an undirected Graph G, if the Laplacian is a symmetric positive-semi definite matrix, then all its eigenvalues are positive and real, which means the dynamics are stable and converge to a steady state.
2.2. Dynamic Consensus Algorithm
Each agent of the network has an initial value and the initial vector value . In this paper, we consider that each agent only communicates with their neighbors, so using the distributed linear iteration, we can calculate the average value [17] as
where and is the weight on at node i, and denotes the set of all neighbors of agent i. Setting for , this iteration can be written as
The Equation (5) indicates that for all k. With proper selection of weight matrix A, any initial value makes converge to the average vector.
where “1” represents a vector consisting of N-elements, all set to one.
The coefficient matrix A, i.e., the adjacency matrix is based only on the incident node and is computed by the Metropolis algorithm [16] as follows:
In order to achieve consensus for a dynamically changing signal, some adjustments are necessary. If y represents the signal and indicates the difference between two consecutive time steps, the following modification (8) can track the dynamically varying signal towards the common consensus value.
where is the bias and each agent possesses its unique bias, such that the modification remains distributive in nature.
2.3. KKT Conditions
A set is convex if for any two points , and for any , the point is also in S. Mathematically, this is represented as [18]:
A function f is convex over a convex domain if it satisfies the inequality:
A typical constrained optimization problem can be stated as [19]:
The Lagrange function for this problem is given by:
Considering that represents a local solution to the optimization problem, the following conditions are essential for optimality [19]:
- (i)
- Stationary: The gradient of the Lagrange function with respect to x must be zero:
- (ii)
- Primal Feasibility: The solution must satisfy the constraints:
- (iii)
- Dual Feasibility: The Lagrange multipliers for inequality constraints must be non-negative:
- (iv)
- Complementary Slackness: For each inequality constraint, either the constraint is active or the corresponding Lagrange multiplier is zero:
In some cases (such as when the objective and constraint functions are convex), the KKT conditions are also sufficient for optimality, meaning that a solution meeting these conditions is optimal.
2.4. ADMM
A typical constrained optimization problem can be written as,
The equivalent Lagrange relaxed function is:
where is the Lagrangian multiplier.
A penalty term is added to the objective function in order to increase the convergence speed to form the augmented Lagrangian function [18].
where is the penalty parameter. In scaled form, the Equation (12) can be written as
where is the scaled dual variable or scaled Lagrange multiplier. Equation (13) is convergent without strict convexity. The ADMM introduces decomposability into the augmented Lagrangian without the need to assume strict convexity for the function. In ADMM, primal iterates are updated sequentially, and a global dual updater collects all the information to adjust the dual variable by pulling all decision variables to their optimum points. The scaled problem (13) can be simplified and expressed in a compact form as follows:
If we are concerned with control theory, the penalty parameter is equivalent to the proportional gain that determines the convergence speed. Additionally, the scaled Lagrange multiplier, u, is equivalent to an integrator as it integrates the error until the desired error is obtained.
3. Problem Formulation
Economic dispatch is the resource allocation in power system in which the generation units are scheduled in such a way that the combined generated power balances the load demand in the network at a marginal cost.
3.1. Centralized Economic Dispatch with Demand Response
When integrating demand response into economic dispatch, both power generation units and demand-side units share responsibility for managing demand. They work together to reach an optimal operating point where economic efficiency is maximized for both. To achieve this, demand units need to be flexible and able to adjust their power consumption based on electricity prices and system conditions. This requires demand units to be uninterruptible and controllable.
Utility functions for demand units represent the level of consumer satisfaction relative to their power usage and are used as decision variables in the economic dispatch process.
For economic dispatch, conventional generating units are typically modeled with a quadratic cost function. The cost equation for the generating unit is given as:
where , , denote the predetermined coefficients assigned to the generating units, and represents the generation at the bus.
Let us say the cost of producing each megawatt-hour (MWh) of energy by generating sources is denoted as dollars per MWh. If represents the set of all generation and consumption, then the welfare on the generation side is calculated as the net profit.
Each customer acts independently according to their preferences. As a result, varied consumption patterns can be modeled using utility functions, which quantify a customer’s welfare or satisfaction as a function of energy usage. To define appropriate utility functions for the consumer, three key properties must be met [12].
- (i)
- The marginal utility should be positive, indicating that as consumption increases, the utility also rises.
- (ii)
- As power consumption increases, the level of satisfaction should eventually reach a point of saturation.
- (iii)
- If there is no consumption, the utility for the consumer should be zero.
To meet these requirements a typical example of a utility function that meets these criteria is the quadratic utility function. Thus, the utility function for the i-th consumer can be expressed as [20].
The term indicates the demand at the bus, and parameters and are predetermined and serve to distinguish between different consumers. The utility function for varying values of the utility coefficient is illustrated in Figure 1.
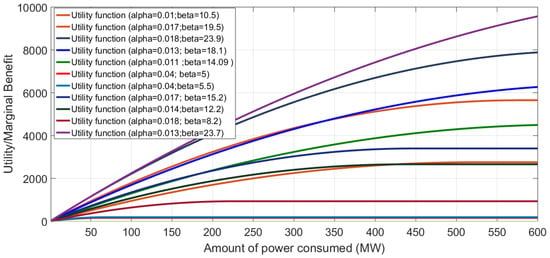
Figure 1.
Utility function for controllable load in IEEE 39 bus system.
The welfare on the demand side is the utility of demand minus the cost of energy.
To determine the economic dispatch with demand response, the combined social welfare problem is formulated and optimized to find the optimal distribution of generation and demand units. Consider each agent as a node in the power system. The Social Welfare Maximization (SWM) problem, which needs to be optimized, can be described as follows:
The limits for generation are and , representing the minimum and maximum capacity for each generator. Similarly, the demand limits are and , which are the minimum and maximum capacity for each demand unit. Given that maintaining power balance across the entire network is crucial in a power system, Equation (19b) serves as the global constraint. Equations (19c) and (19e) set the limits for generation and demand, while Equation (19d) defines the ramp rate limit, functioning as local constraints within the optimization process. In this optimization, represents the set of power generation values, and represents the set of demand values for all buses. These sets serve as the decision variables for the optimization process.
Equation (19) can be expressed in an augmented Lagrangian form with scaling, using the Alternating Direction Method of Multipliers (ADMM), as follows [21]:
where u is the dual variable; is the penalty parameter, is the Euclidean norm and is the energy price = u.
The power mismatch of each agent N can be defined as
Therefore, Equations (20) and (21)can be re-written as
Equation (24) represents a centralized optimization strategy, where the scaled Lagrange multiplier is computed centrally and disseminated to individual agents for localized decision-making. This approach aims to achieve fully distributed decision variables without necessitating the exchange of private data, thereby eliminating the need for all-to-all communication.
3.2. Decentralized Economic Dispatch with Demand Response
In a distributed approach, one can employ a dynamic power mismatch algorithm, which focuses on the power mismatch of individual nodes as a primary consideration. Figure 2 illustrates the flow of information within a distributed platform. The mathematical analysis of this approach is presented below.
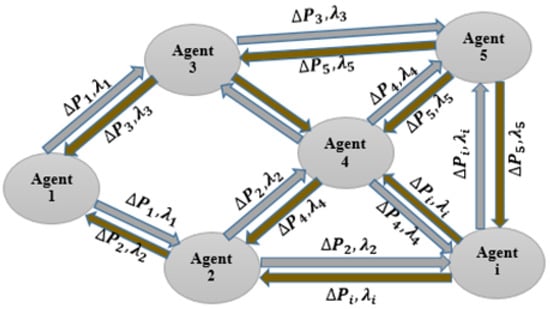
Figure 2.
Information flow in Distributed Platform.
If N represents the total number of agents or units in the system, the mean generating power difference in two successive iterative values can be expressed as:
and for demand units,
From Equations (23) and (24)
Equation (25) provides the average power mismatch for each agent or unit in a fully distributed manner, utilizing and as elements of the weight matrix acquired through Metropolis weight methods. By integrating this average power mismatch, the dual variable of the algorithm can be derived in a decentralized fashion.
Dual variable is the scaled variable of the market price , expressed as
The optimal generated power can be determined through KKT conditions, we need to differentiate Equation (24) with respect to that gives:
There are two distinct cases for the optimal power consumption for each demand unit.
- Case I:
- In this case, the optimal power consumption for the demand unit is given by
- Case II:
- For this case, the optimal power consumption for the demand unit is given by
The decentralized economic dispatch with demand response algorithm’s general process is outlined in Algorithm 1.
| Algorithm 1 Simplified Economic Dispatch with Demand Response |
Execute for all agents: • Update using Equation (31) • Update using Equations (33) or (34) • Update using Equation (27) • Update scaled dual variable using Equation (28) • Update price updater using Equation (29) end for |
4. Results
The results and analysis of the proposed Algorithm 1 are discussed in three different cases:
- →
- In Section 4.2, the case where the proposed algorithm does not incorporate demand response is explained.
- →
- In Section 4.3, the case where the proposed algorithm is utilized to its full capability, considering demand response is presented.
- →
- Lastly, in Section 4.4, the effect of renewable energy in the proposed algorithm is examined.
4.1. Simulation Setup for the Algorithm Test
The algorithm was executed within the MATLAB R2020a environment to assess the effectiveness of the proposed algorithm on the IEEE 39 test bus system, which contains 10 generating units and 21 demand units. The coefficient used to randomize the load demands of the standard IEEE 39 bus system over 24 periods for each hour is given in Table A1. The IEEE 39 bus system is shown in Figure 3. Although the cost parameters in each generation unit remain consistent with the data available in Matpower, adjustments have been made to these cost coefficients to vary the incremental cost among generators. The minimum and maximum generation limits are determined as specified, and the ramp rate limit (both up and down) is set at 30% of their respective maximum generation capacity for each unit.
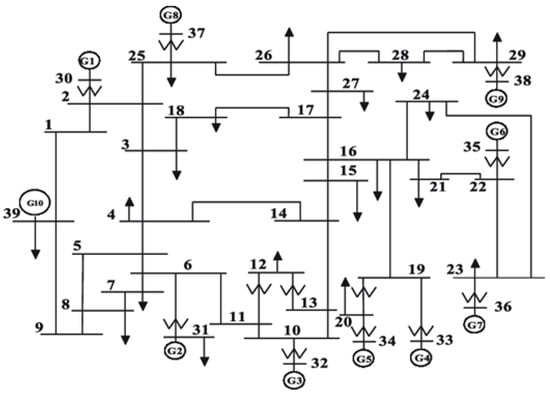
Figure 3.
Single line diagram of IEEE 39 bus test system.
In the scenario where the proposed algorithm is tested with demand response, the simulation setup is adjusted accordingly. The demand units are classified into two categories: controllable and uncontrollable time-variant demand. Among the 21 demand units, 10 are designated as uncontrollable demand, while the remaining 11 are categorized as controllable demand units. Uncontrollable loads are treated as time-variant loads, fluctuating on an hourly basis, resulting in 24 steps in the time-variant uncontrollable load demand units. The cost coefficients, generator limits, and initial values of power demand at each bus were set according to the specifications outlined in MATPOWER [22]. Parameters for the demand utility function (, ) were derived through approximation, leveraging the characteristics of the utility function, as described in Section 3.1. These parameters were intentionally varied from each other to reflect the differentiation in demand units based on their values.
The utility coefficients of the 11 controllable demand units connected to the load bus, which ranges from bus 1 to bus 20, are fictitiously generated to test the proposed economic dispatch algorithm with demand response. Based on these coefficients, each demand’s utility or marginal benefit, correlated with their power consumption levels, is illustrated in Figure 1. The corresponding values of these coefficients are indicated in Figure 1. For controllable loads, the consumption level is constrained within a specified range. The lower limit is 90% below, and the upper limit is set at 90% above the given demand in the IEEE39 test bus system. The rest of the demand units connected to the buses from bus 21 to bus 39 are considered uncontrollable.
4.2. Result and Discussion of the Proposed Algorithm with No Demand Response
The distributed economic dispatch problem formulation without demand response using the ADMM approach is clearly stated in [23]. The simulation outcomes depicting the load distribution throughout a 24-h period are illustrated in Figure 4, Figure 5, Figure 6 and Figure 7. Each unit’s load demand has been pre-scheduled for specific periods, and the utility’s obligation is to meet all demanded loads at the most economically advantageous market rate available at any given period. In Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20, presenting in Section 4.2 to Section 4.4, the blue numbers on the x-axis represent the time in hours, while the black numbers indicate the number of iterations.
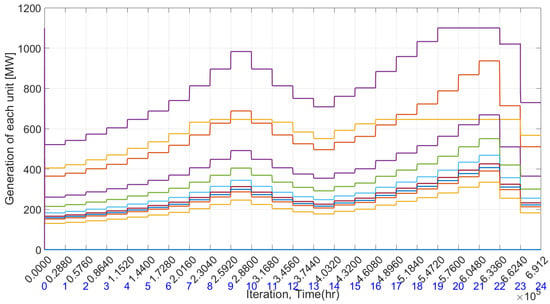
Figure 4.
Optimal generation level for each generating unit in the absence of demand response.
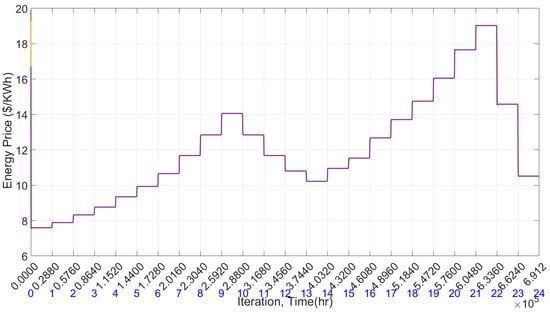
Figure 5.
Energy price in the absence of demand response.
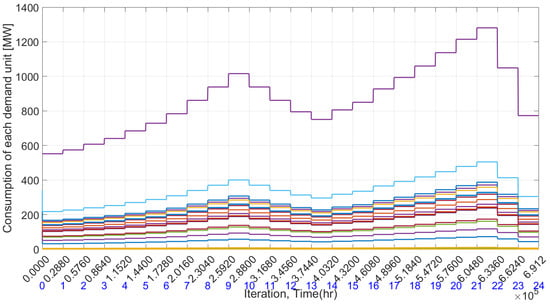
Figure 6.
Consumption of each demand in the absence of demand response.
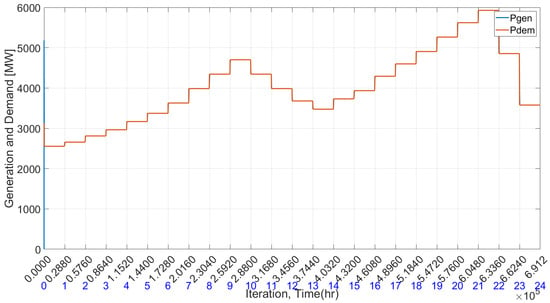
Figure 7.
Sum of total energy generation and total demand in the absence of demand response.
Figure 4 illustrates the optimal generation of each generating unit, with different colored lines representing each unit. The corresponding optimal market energy prices are shown in Figure 5. This price reflects the common consent energy price. Each generating unit adjusts its output to generate power optimally based on this consensus price, ensuring that the total generation matches the demand precisely. The power demand of each load unit over a 24-h period is presented in Figure 6. An increase in demand correlates with a higher market price, while a decrease in demand leads to a lower consensus price, in line with the supply-demand curve. Furthermore, Figure 7 illustrates the total generation and demand, which are perfectly balanced, resulting in zero energy mismatch upon convergence. Two peaks in demand are notable: one at the 9th time period and another at the 21st time period. The utility successfully meets all demands, irrespective of energy prices, which fluctuate between 2455 MW and 5926 MW. The total energy consumption over the day amounts to 96383 Megawatt-hours, with a corresponding cost of $1,219,256. The average cost per Megawatt-hour stands at approximately $12.65.
4.3. Result and Discussion of Proposed Algorithm with Demand Response
The results for this case are depicted in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. Figure 8 presents the optimal generation levels for each conventional generating unit in each time period, with maximum generation occurring during periods of peak demand and minimum generation during times of low energy demand. In Figure 9, the hourly variation of uncontrollable load across 24 time periods is illustrated, with peak consumption observed in the 21st period and a secondary peak in the 9th period, while consumption is minimal during the start of the day.
Figure 10 represents the market energy prices for all participating agents in $/MWh. The algorithm is designed to establish a common optimal value for each participating agent, leading to the convergence of market prices to a consensus value for a specific load demand period and transitioning to the next common value for different loads. With every change in load, convergence to an optimal common value ensures the algorithm’s effectiveness for dynamic loads. Figure 11 illustrates the optimal demand for all controllable loads per time slot. The graph clearly demonstrates that the consumption of controllable units varies significantly based on energy prices—they consume more power when prices are low and less when prices increase. For instance, energy prices are at their minimum during the first period, coinciding with the highest consumption of controllable demand units. Conversely, energy prices reach their maximum in the 21st time period, with corresponding minimal consumption of controllable demand units. This highlights the effectiveness of demand response in conjunction with economic dispatch.
Figure 13 depicts the total generation and total demand in each time frame, showcasing a near-perfect match between generation and demand, resulting in minimal mismatch among units, as displayed in Figure 14. Additionally, Figure 12 illustrates the power consumption of individual demand units across all time periods. A noticeable trend emerges where uncontrollable and controllable demand units exhibit contrasting energy consumption patterns—consumption of controllable units decreases when uncontrollable load increases, and vice versa. This underscores the efficacy of the proposed economic dispatch algorithm, which not only optimizes generation scheduling but also significantly contributes to demand-side management. The demand curve in Figure 13 reveals that power consumption levels are confined between 3460 MW and 4859 MW.
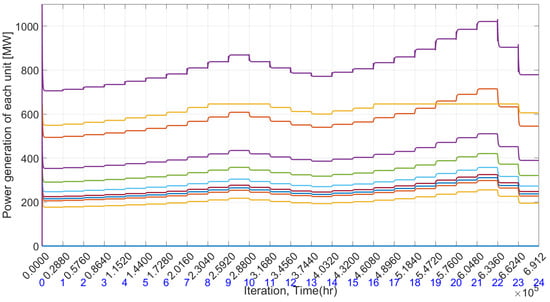
Figure 8.
Optimal generation level for each generating unit.
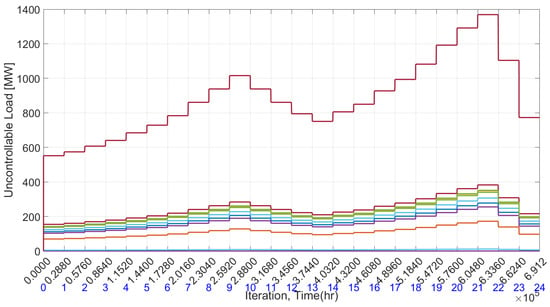
Figure 9.
Time-variant uncontrollable load demand.
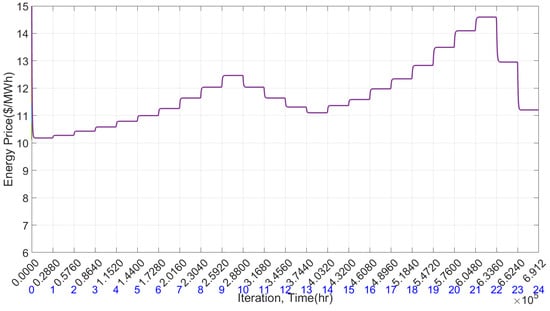
Figure 10.
Energy price .
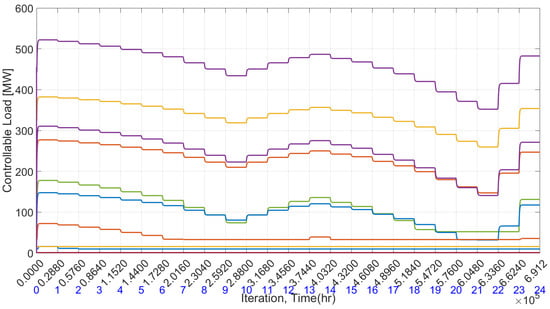
Figure 11.
Optimal demand of each demand unit.
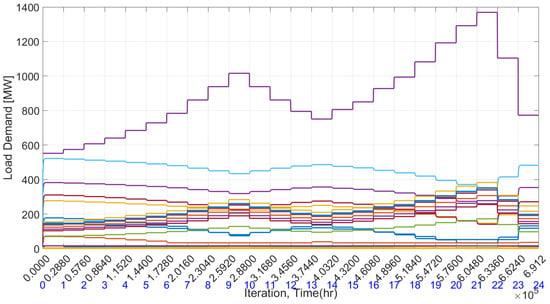
Figure 12.
Combined plot of each controllable and uncontrollable load.
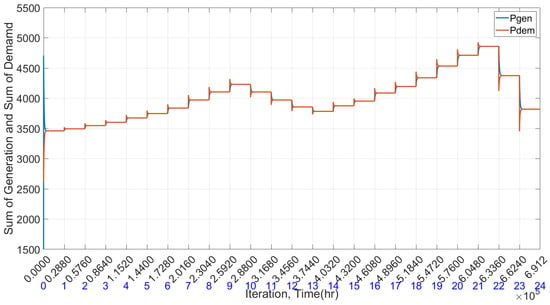
Figure 13.
Sum of total energy generation and total demand.
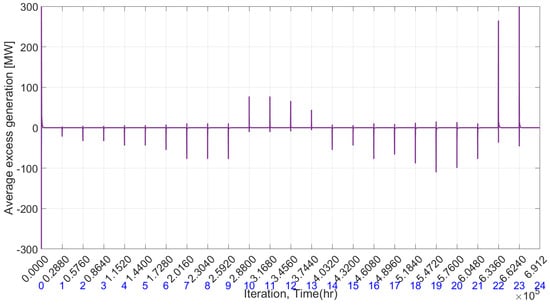
Figure 14.
Mismatch of generation and demand.
The total energy cost for the consumed quantity amounts to $1,147,345, with a cumulative energy usage of 96,134 megawatt-hours over the course of one day, incorporating demand response measures. When compared to Economic Dispatch without Demand Response, the utilization of Demand Response resulted in approximately $71,911 less cost for 249 megawatt-hours less energy. The average electricity cost per megawatt-hour in this scenario is approximately $11.93, compared to $12.65 in the previous case without Demand Response.
4.4. Result and Discussion on Effect of Renewable Generation in Proposed Algorithm with Demand Response
The simulation setup is exactly the same as that outlined in Section 4.1, except for the incorporation of additional renewable energy resources in this section, specifically photovoltaic (PV) generation. Six identical PV energy generation setups are randomly integrated into the system, spanning buses from bus 1 to bus 6. Irradiance and temperature data for these six locations over a single day are sourced from the National Renewable Energy Laboratory (NREL), and recorded every 10 min throughout the day. A 2-square-kilometer area is considered for PV energy generation. The efficiency of the solar panels is standardized at 20% for each station throughout the simulation period.
The time-varying uncontrollable load is the same as analyzed in Section 4.1 and is depicted in Figure 9. The remaining results, which were influenced by renewable energy, are displayed in the figure from Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20. Figure 15 showcases the optimized power generation of each conventional unit throughout the time periods, and Figure 16 displays the power generation from photovoltaic units based on given irradiance and temperature in corresponding periods. Both sources work in tandem to satisfy the required power demand.
Figure 17 displays the market energy price in $/MWh for all system agents. As demand fluctuates, prices adjust accordingly, lowering with reduced demand and rising with increased demand. The integration of renewable sources decreases the need for conventional generation, reducing overall energy costs due to their lower prices.
Figure 18 illustrates the optimal demand of all controllable loads for each time slot. The graph illustrates how power consumption by controllable demand units changes with energy prices: consumption rises when prices are low and falls when prices increase. When renewable energy is fully available, energy prices are lowest, leading to peak consumption. Conversely, energy prices peak at the 21st time period, aligning with the lowest consumption of controllable demand units. Overall, consumption levels move inversely with energy prices. The proposed algorithm facilitates the shifting of peak demand from the 21st slot to other periods when the electric grid receives maximum power from PV generation. This indicates that the concept of demand response, coupled with renewable generation such as PV, effectively flattens the demand curve in conjunction with economic dispatch.
Figure 19 depicts the combined total generation and total demand for each time interval. It is noticeable that generation and demand align perfectly, resulting in an average mismatch approaching zero for each unit, as depicted in Figure 20.
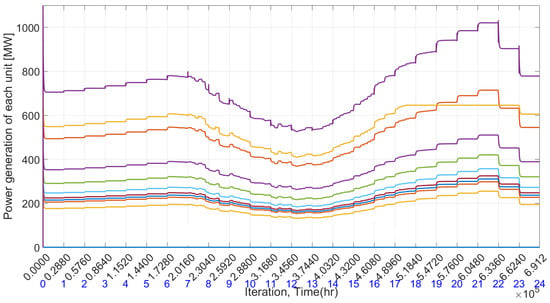
Figure 15.
Optimal generation level for each generating unit in presence of renewable energy.
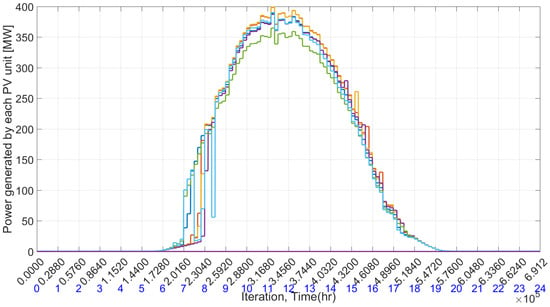
Figure 16.
Power generated by each PV units.
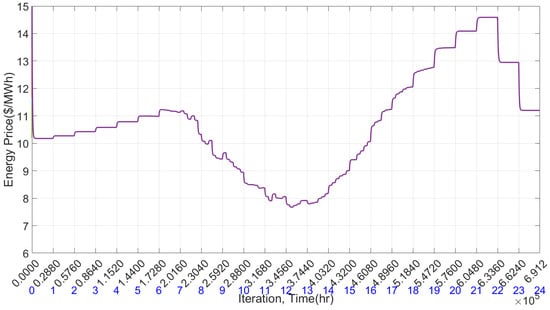
Figure 17.
Energy price in presence of the renewable energy.
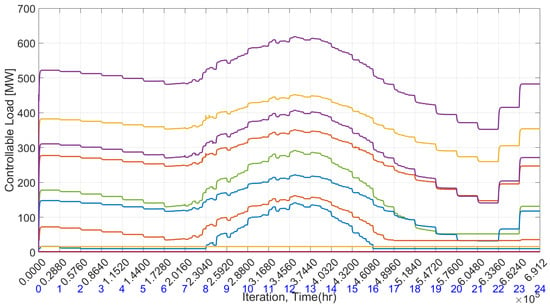
Figure 18.
Optimal demand of each demand unit in presence of the renewable energy.
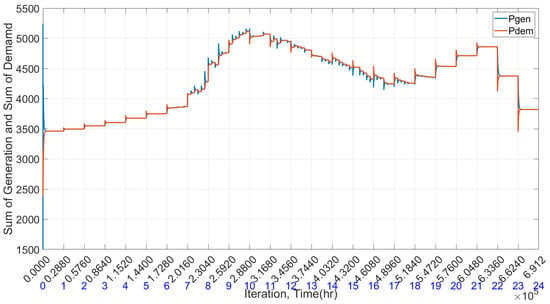
Figure 19.
Sum of total energy generation and total demand in the presence of renewable energy.
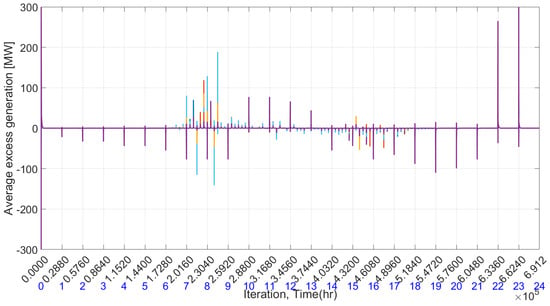
Figure 20.
Mismatch of generation and demand in the presence of renewable energy.
By integrating photovoltaic generation, the total energy usage over a single day, incorporating demand response measures, amounts to approximately 103,482 megawatt-hours, with a total cost of $1,189,187.7 for this energy consumption. With renewable energy and Demand Response considered, approximately 2205.71 megawatt-hours more energy is utilized compared to scenarios with only Demand Response under Economic Dispatch. However, the overall energy cost in this scenario is $41,842 higher than it would be without photovoltaic generation.
When both photovoltaic generation and demand response are integrated, the average cost per megawatt-hour of energy consumed stands at $11.492, compared to $11.93 with no renewable generation and only demand response measures.
With demand response in place, power consumption remains within the range of 3460 MW to 4859 MW. In contrast, without demand response, the variance in power consumption is significant, ranging from a low of 2455 MW to a maximum of around 5926 MW. It can be inferred that by effectively incorporating demand response measures into the power system, fluctuations in demand can be significantly reduced. This reduction in demand variability not only decreases the required plant installation capacity but also enhances plant factor, thereby improving overall profitability.
5. Conclusions
This paper proposes a novel, fully distributed economic dispatch algorithm based on the ADMM, eliminating the need for a central coordinator to compute global decision variables and incorporating demand response for optimal demand-side management. The approach formulates the social welfare maximization problem to determine the optimal generation of power units and the optimal demand for controllable loads. Each agent only shares their average energy mismatch with their neighbors as a control variable during the welfare maximization process. A dynamic consensus protocol is employed to establish a common optimal market price. Based on this price, each generating unit produces its optimal output, and each controllable load consumes its optimal amount of energy. This ensures the privacy of each agent throughout the economic dispatch process.
Theoretically, it is evident that market prices directly influence controllable loads, which adjust their consumption accordingly. The proposed algorithm was tested on the standard IEEE 39 bus test system, with simulation results showing its effectiveness in achieving real-time economic dispatch for generation units, optimal demand for controllable loads, and optimal energy pricing. Comparisons between economic dispatch with and without demand response revealed that, without demand response, generation units operate based on incremental generation costs to meet all required loads. With demand response, however, controllable loads adjust their consumption based on energy prices, consuming more energy when prices are low and less when prices are high. This helps to flatten the energy demand curve and improves demand-side management. Furthermore, the impact of renewable resources on demand-responsive economic dispatch was analyzed. The results demonstrated that peak load demand shifts to periods when renewable generation is at its maximum. Thus, the proposed economic dispatch algorithm significantly enhances demand-side management, optimizing generation and energy consumption while ensuring the data privacy of each participating agent. The aggregation demonstrated here does not capture detailed load flow analysis. It has been assumed that the system’s transmission infrastructure can successfully deliver designated power demand from the source to the demand unit, meeting all power flow constraints of the power system. The distributed economic dispatch that incorporates demand response is discussed in this paper, in which the the generation limit and generation ramp rate limit are considered. The future work is to perform the security-constrained economic dispatch (SCED) with demand response to ensure both economic efficiency and system reliability under normal system operations and different types of contingencies such as an outage of generation, outage of transmission lines, maintaining transmission limits, voltage limits, and stability constraints.
Author Contributions
Conceptualization, B.D. and N.R.K.; methodology, B.D.; software, B.D.; validation, B.D., K.P. and N.R.K.; formal analysis, B.D., K.P. and N.R.K.; investigation, B.D., K.P. and N.R.K.; writing—original draft preparation, B.D. and K.P.; writing—review and editing, B.D., K.P. and N.R.K.; supervision, N.R.K.; project administration, B.D. and N.R.K.; funding acquisition, B.D., K.P. and N.R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Considered Hourly power distribution factor from the indicated power of IEEE standard bus system.
Table A1.
Considered Hourly power distribution factor from the indicated power of IEEE standard bus system.
| Time (Hr) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Factor | 0.50 | 0.52 | 0.55 | 0.58 | 0.62 | 0.66 | 0.71 | 0.78 | 0.85 | 0.92 | 0.85 | 0.78 |
| Time (Hr) | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Factor | 0.72 | 0.68 | 0.73 | 0.77 | 0.84 | 0.90 | 0.98 | 1.08 | 1.17 | 1.24 | 1.00 | 0.70 |
References
- Kabindra, P.; Li, W.; Sonee, S.; Zhang, Y.; Zhao, H.; Umar, S. Autonomous transient power management strategy based on improved droop control for DC microgrid. Electr. Eng. 2022, 104, 4321–4334. [Google Scholar]
- Wood, A.J.; Wollenberg, B.F.; ShebleB, G.B. Power Generation, Operation, and Control, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Arnold, G.; Batten, D.; Bose, A.; Hauser, C.; Whitehead, D.; Zweigle, G.; Gomez-Exposito, A.; Abur, A.; delaVillajaen, A.; Gomez-Quiles, C. Smart grid: The electric energy system of the future. Proc. IEEE 2011, 99, 1–11. [Google Scholar]
- Shen, J.; Jiang, C.; Li, B. Controllable Load Management Approaches in Smart Grids. Energies 2015, 8, 11187–11202. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Liu, W.; Wang, X. Distributed Subgradient-Based Coordination of Multiple Renewable Generators in a Microgrid. IEEE Trans. Power Syst. 2014, 29, 23–33. [Google Scholar] [CrossRef]
- Zhang, Z.; Ying, X.; Chow, M.Y. Decentralizing the economic dispatch problem using a two-level incremental cost consensus algorithm in a smart grid environment. In Proceedings of the IEEE North American Power Symposium (NAPS), Boston, MA, USA, 4–6 August 2011; pp. 1–7. [Google Scholar]
- Wang, T.; O’Neill, D.; Kamath, H. Dynamic Control and Optimization of Distributed Energy Resources in a Micro-grid. IEEE Trans. Smart Grid 2015, 29, 2884–2894. [Google Scholar] [CrossRef]
- Guo, F.; Li, G.; Wen, C.; Wang, L. An Accelerated Distributed Gradient-Based Algorithm for Constrained Optimization With Application to Economic Dispatch in a Large-Scale Power System. IEEE Trans. Smart Grid 2021, 51, 2041–2053. [Google Scholar] [CrossRef]
- Wang, R.; Li, Q.; Zhang, B.; Wang, L. Distributed Consensus Based Algorithm for Economic Dispatch in a Microgrid. IEEE Trans. Smart Grid 2019, 10, 3630–3640. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, Y.; Liu, W.; Zang, C. Optimal Demand Response Based on Utility Maximization in Power Networks. IEEE Trans. Ind. Inform. 2015, 11, 717–727. [Google Scholar] [CrossRef]
- Li, N.; Chen, L.; Liu, W.; Zang, C. Distributed Online Optimal Energy Management for Smart Grids; Engineering & Applied Science Division, California Institute of Technology: Pasadena, CA, USA, 2011. [Google Scholar]
- Rahbari-Asr, N.; Ojha, U.; Zhang, Z.; Chow, M.Y. Incremental Welfare Consensus Algorithm for Cooperative Distributed Generation/Demand Response in Smart Grid. IEEE Trans. Smart Grid 2014, 5, 2836–2845. [Google Scholar] [CrossRef]
- Samadi, P.; Mohsenian-Rad, H.; Schober, R.; Vincent, W.S. Optimal Real-Time Pricing Algorithm Based on Utility Maximization for Smart Grid. In Proceedings of the First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 415–420. [Google Scholar]
- Samadi, P.; Mohsenian-rad, H.; Schober, R.; Vincent, W.S. Advanced Demand Side Management for the Future Smart Grid Using Mechanism Design. IEEE Trans. Smart Grid 2012, 3, 1170–1180. [Google Scholar] [CrossRef]
- Hug, G.; Kar, S.; Schober, R. Consensus + Innovations Approach for Distributed Multiagent Coordination in a Microgrid. IEEE Trans. Smart Grid 2015, 5, 1893–1903. [Google Scholar] [CrossRef]
- Demetri, P.S.; Reza, O.; Richard, M.M. Dynamic consensus for mobile network. In Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 3–8 July 2005. [Google Scholar]
- Hug, G.; Kar, S.; Schober, R. Fast linear iterations for distributed averaging. Syst. Control Lett. 2004, 53, 65–78. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization, 1st ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Nocedal, J.; Wright, S.J. Wright. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Nguyan, D.H.; Narikiyo, T.; Kawanishi, M. Optimal Demand Response and Real-time Pricing by a Sequential Distributed Consensus-Based ADMM Approach. IEEE Trans. Smart Grid 2018, 9, 4964–4974. [Google Scholar] [CrossRef]
- Stephen, B.; Neal, P.; Eric, C.; Borja, P.; Jonathan, E. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2010, 3, 1–122. [Google Scholar]
- Ray, D.Z.; Carlos, E.M.; Robert, J.T. MATPOWER: Steady-State Operations, Planning and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2010, 26, 12–19. [Google Scholar]
- Dhamala, B.; Karki, N.R.; Mishra, A. Economic Dispatch in Electric Grid Considering Demand Response using Dynamic Consensus-Based ADMM approach. In Proceedings of the 11th IOE Graduate Conference, Pokhara, Nepal, 10–11 March 2022; pp. 36–43. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).