Hardware-in-the-Loop Emulation of a SEPIC Multiplier Converter in a Photovoltaic System
Abstract
1. Introduction
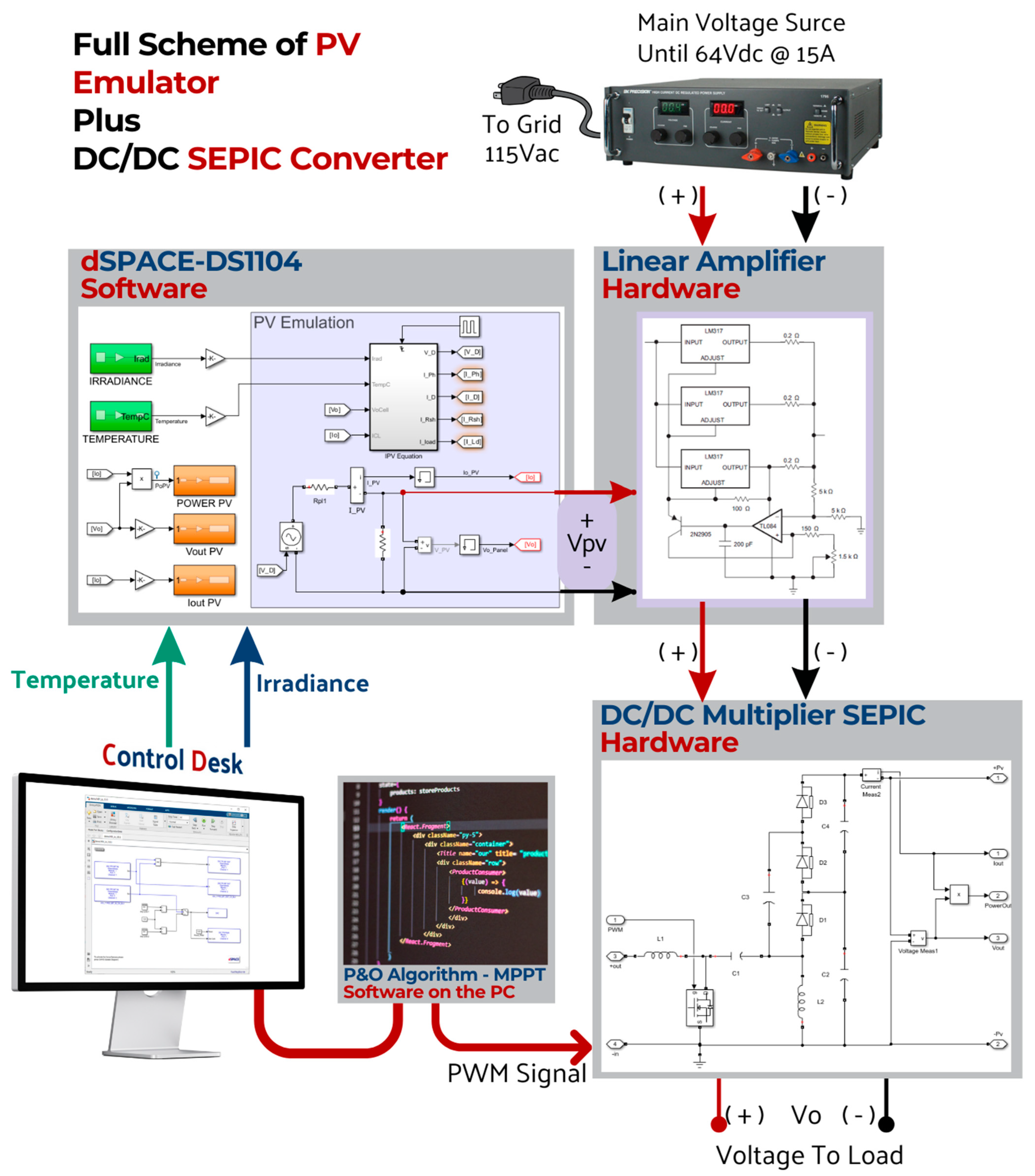
2. Emulating a Photovoltaic Panel-Based Source
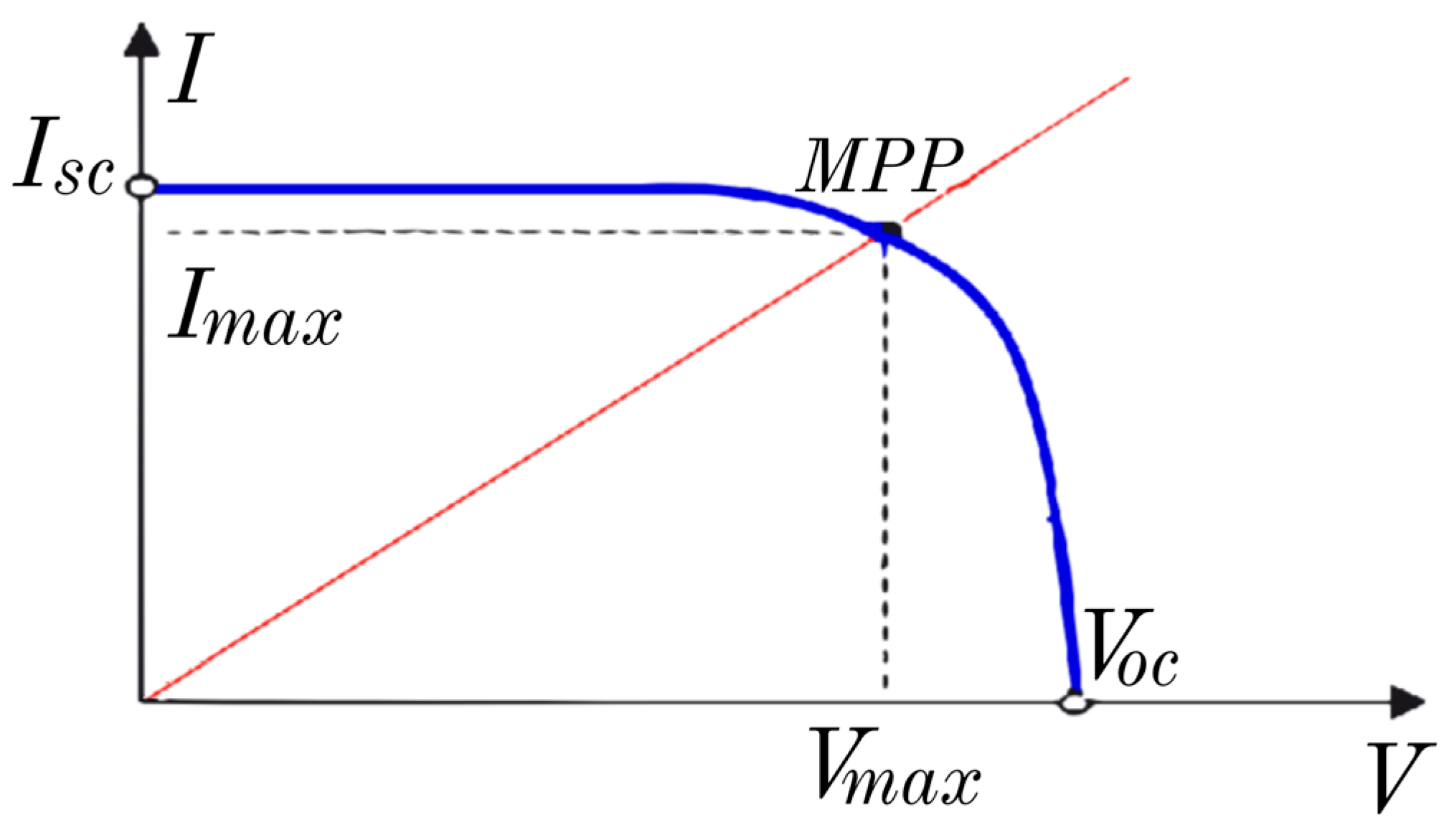
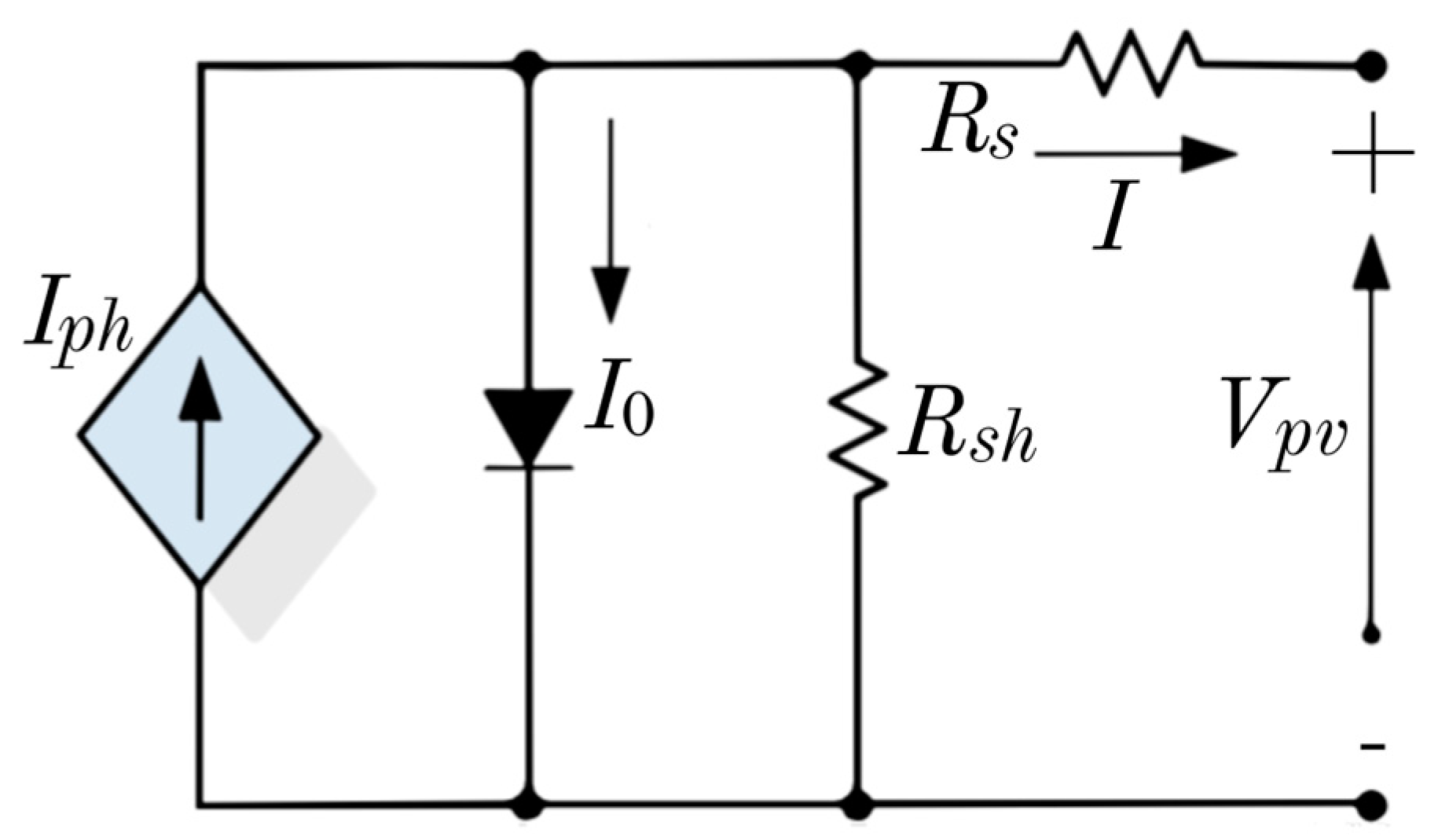
2.1. Modeling and Characteristics
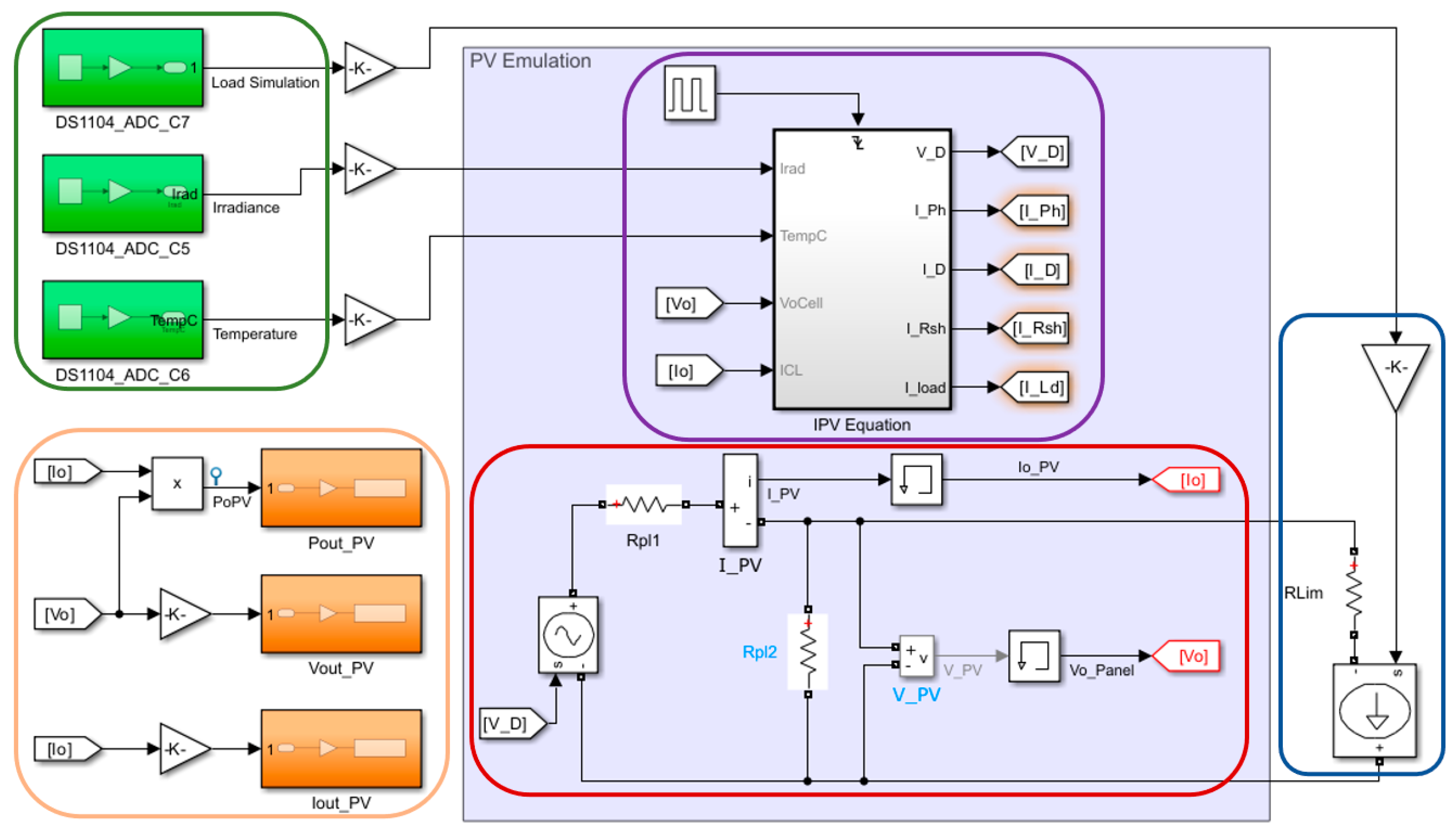
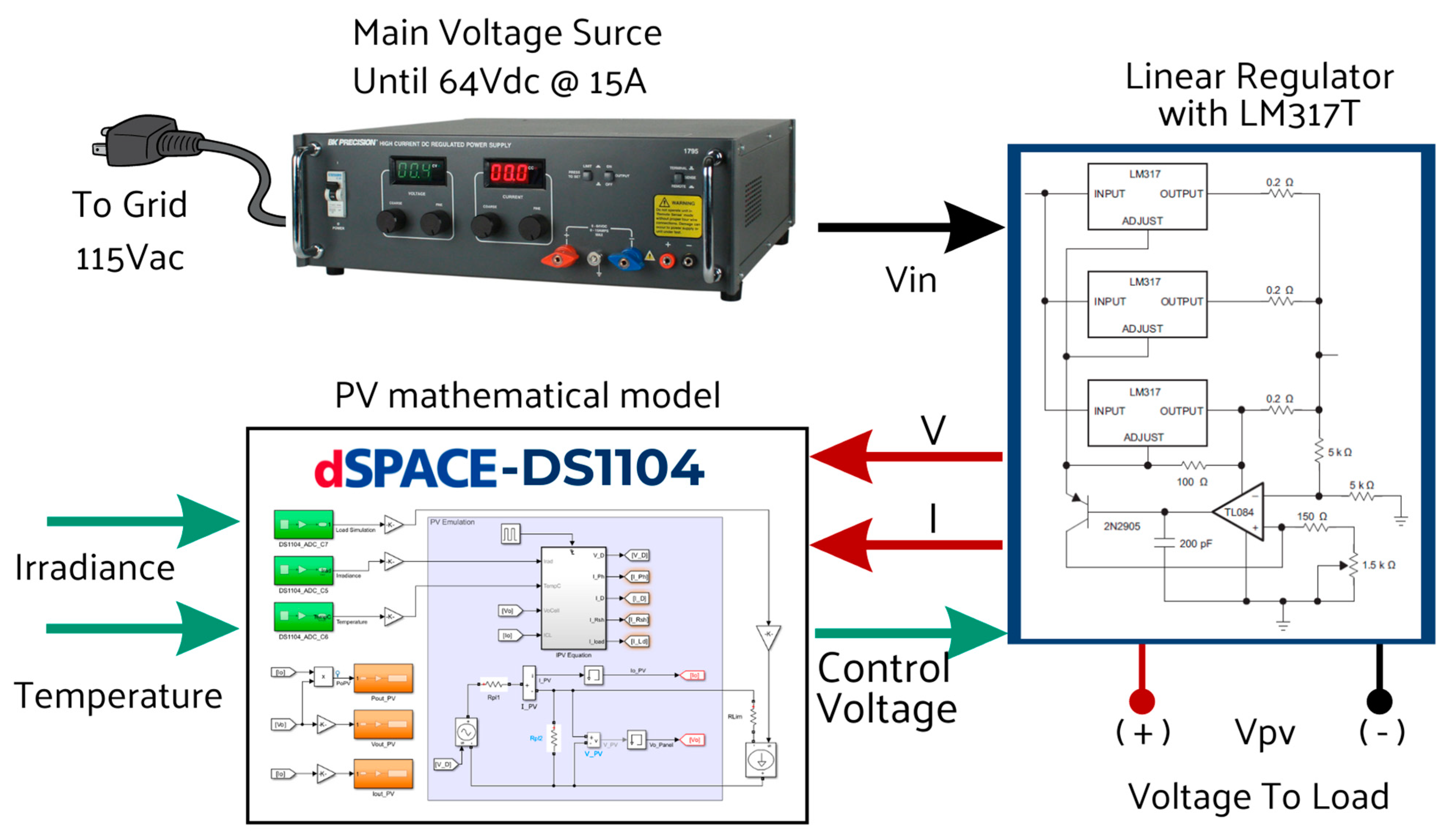
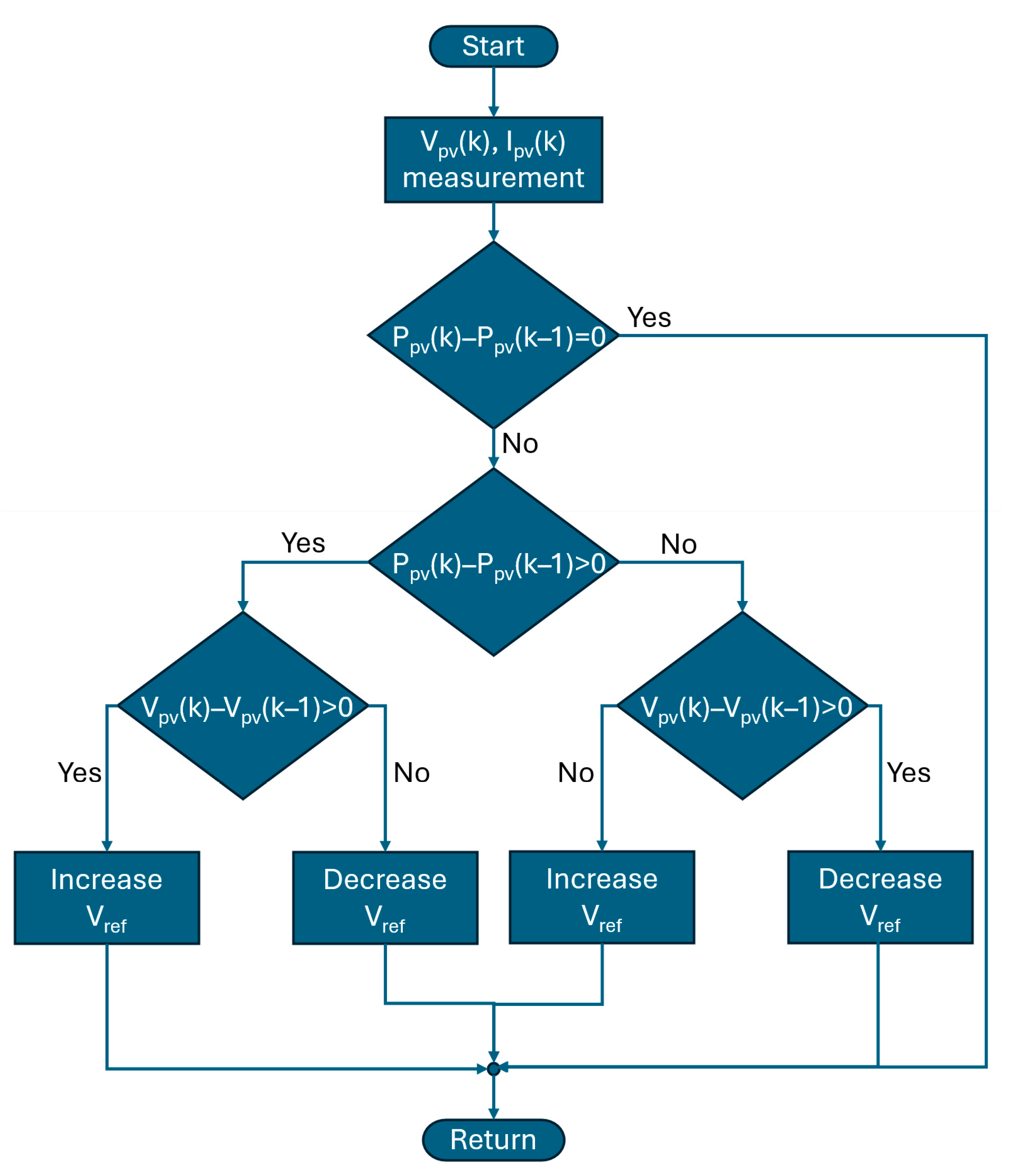
2.2. PV Simulation
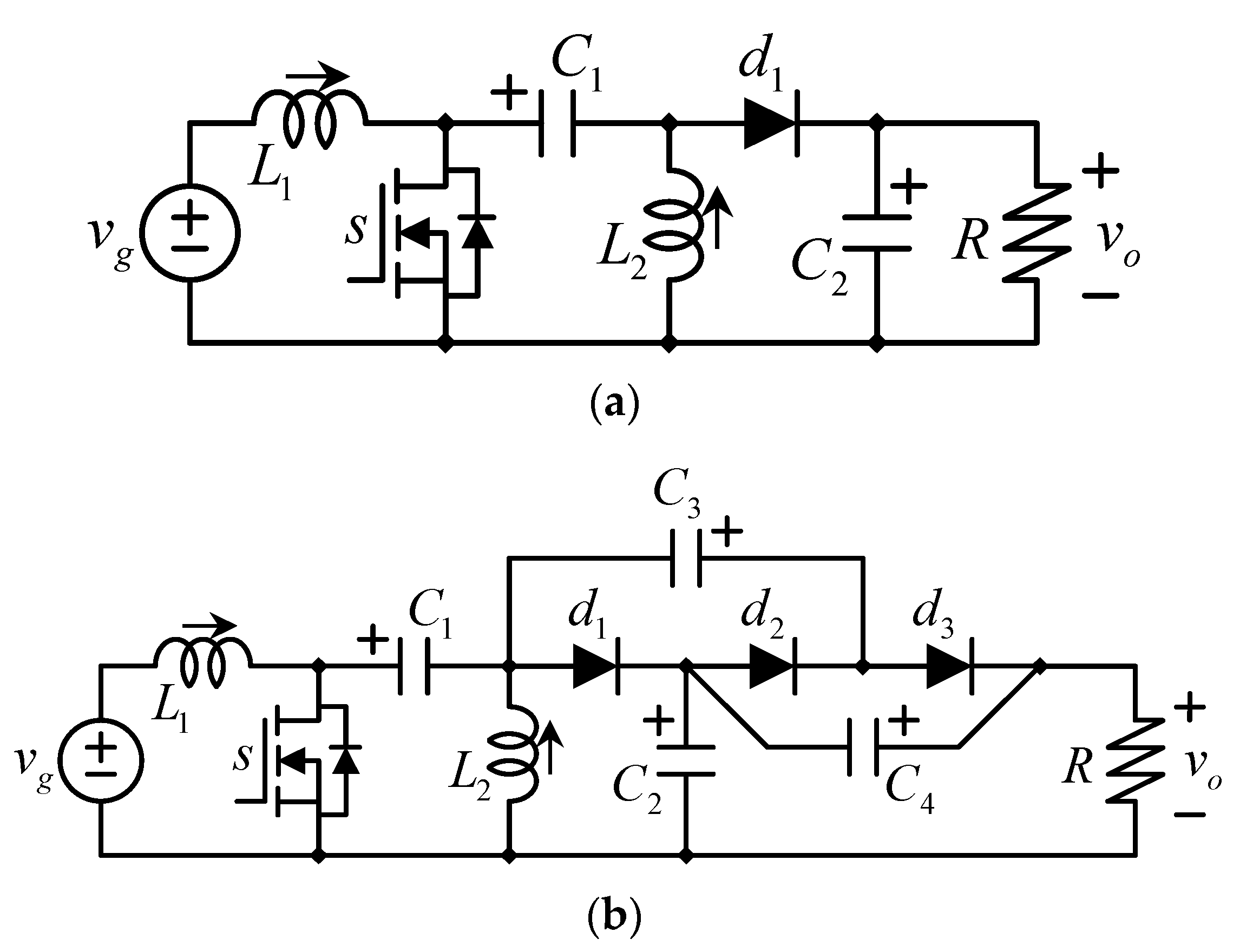
3. Multiplier SEPIC Converter
- (i)
- (ii)
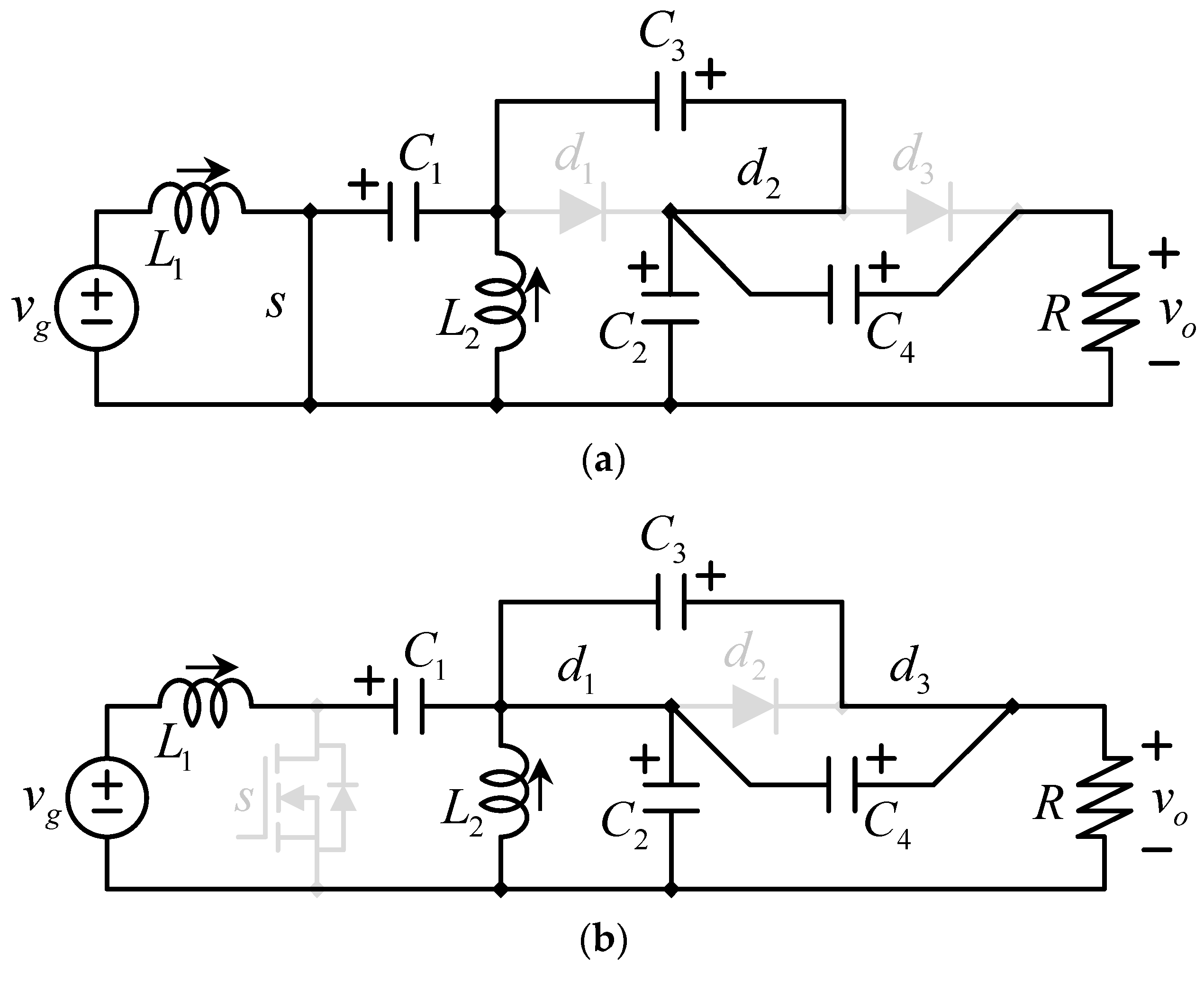
- When the switch opens (see Figure 8b), it allows L1’s current to infuse C1 with a positive voltage (in alignment with the designated signs) since they are connected in series, and the current gets through the positive voltage sign of C1.
- (iii)
- The switching action of the transistor is periodic; it inevitably closes again, but this time the capacitor C1 already has some charge; it gets in parallel connection with the inductor L2, facilitating C1 in endowing L2 with a positive flow of current.
- (iv)
- Upon the transistor’s subsequent opening, L2’s current moves through d1, enriching C2 with a positive charge.
- (v)
- With the transistor open and L2’s current passing through d1, as seen in Figure 8b, the negative terminals of C3 and C4 are conjoined at the same potential, subsequently allowing C3 to engage d3 to positively charge C4.
- (vi)
- With the transistor’s closure, C1 aligns in a series setup with C2, as shown in Figure 8a, which then permits the charging of C3 through the engagement of d2.
Multiplier SEPIC Simulation and Hardware Test
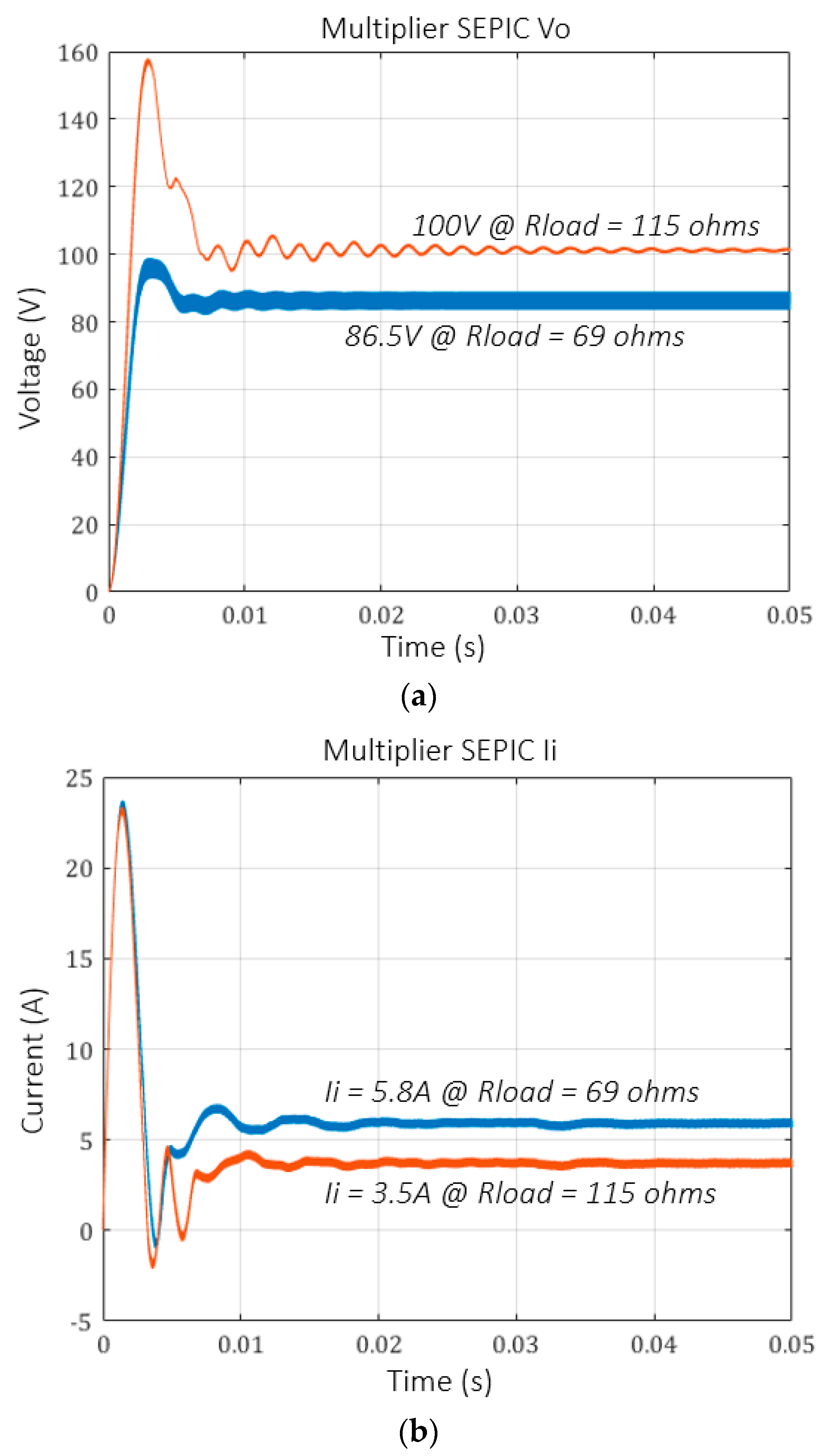
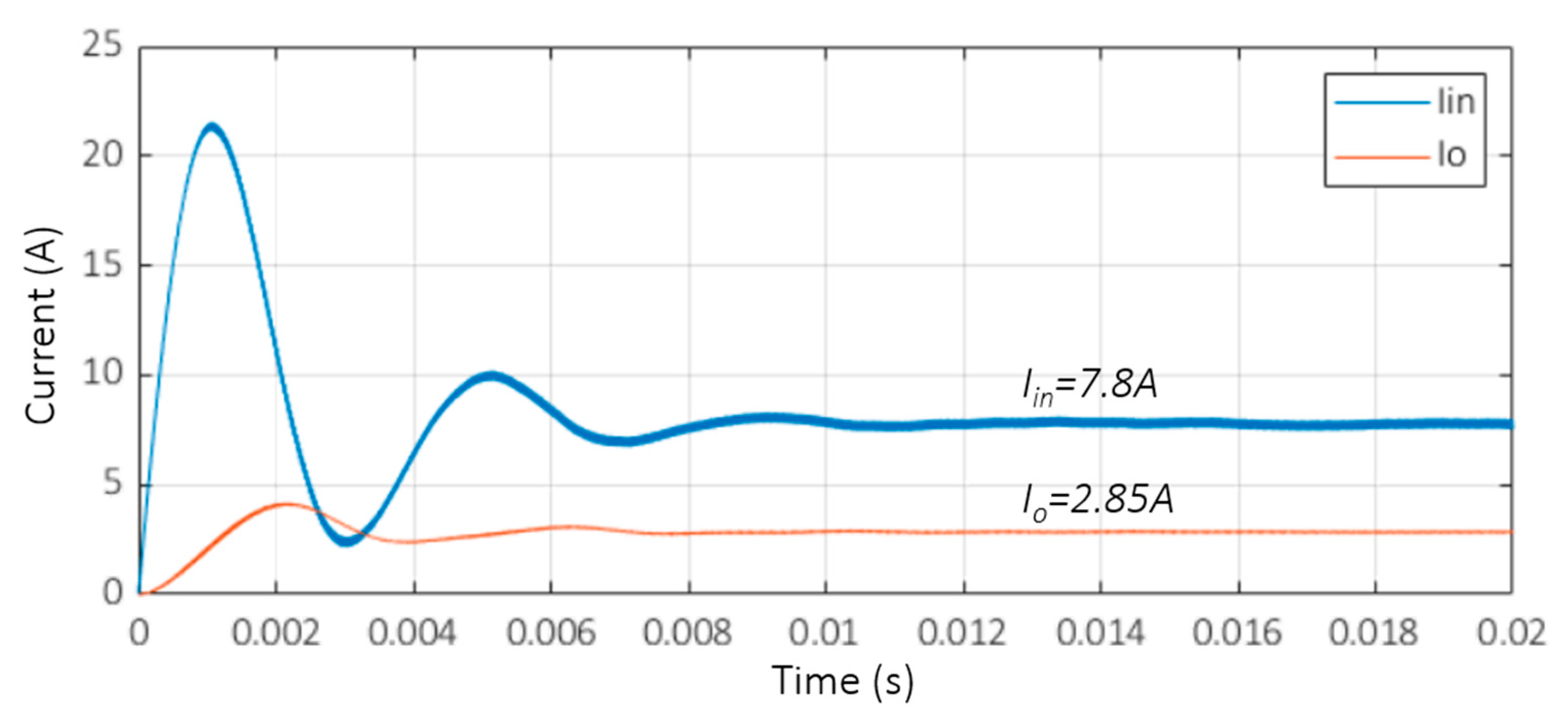
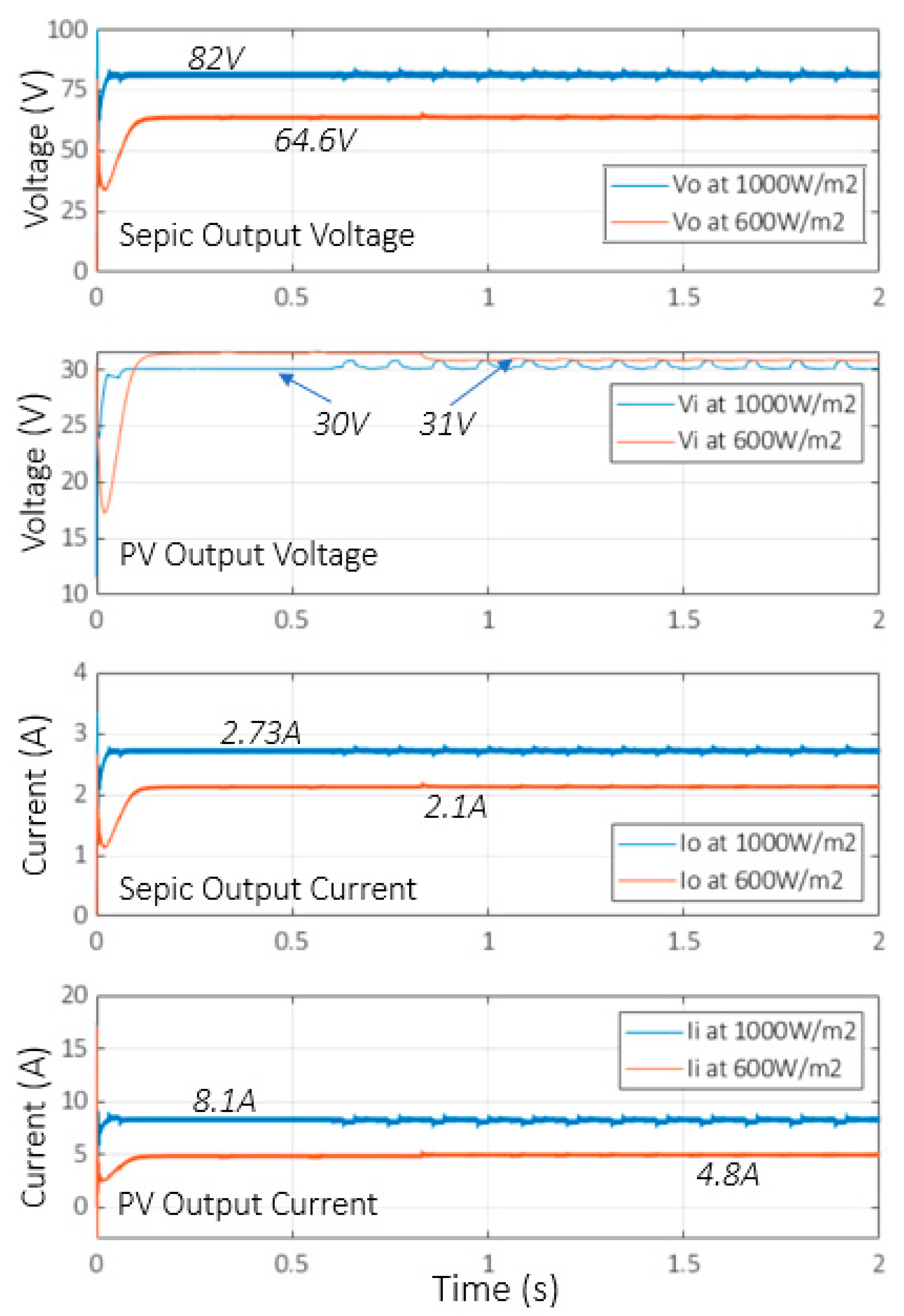
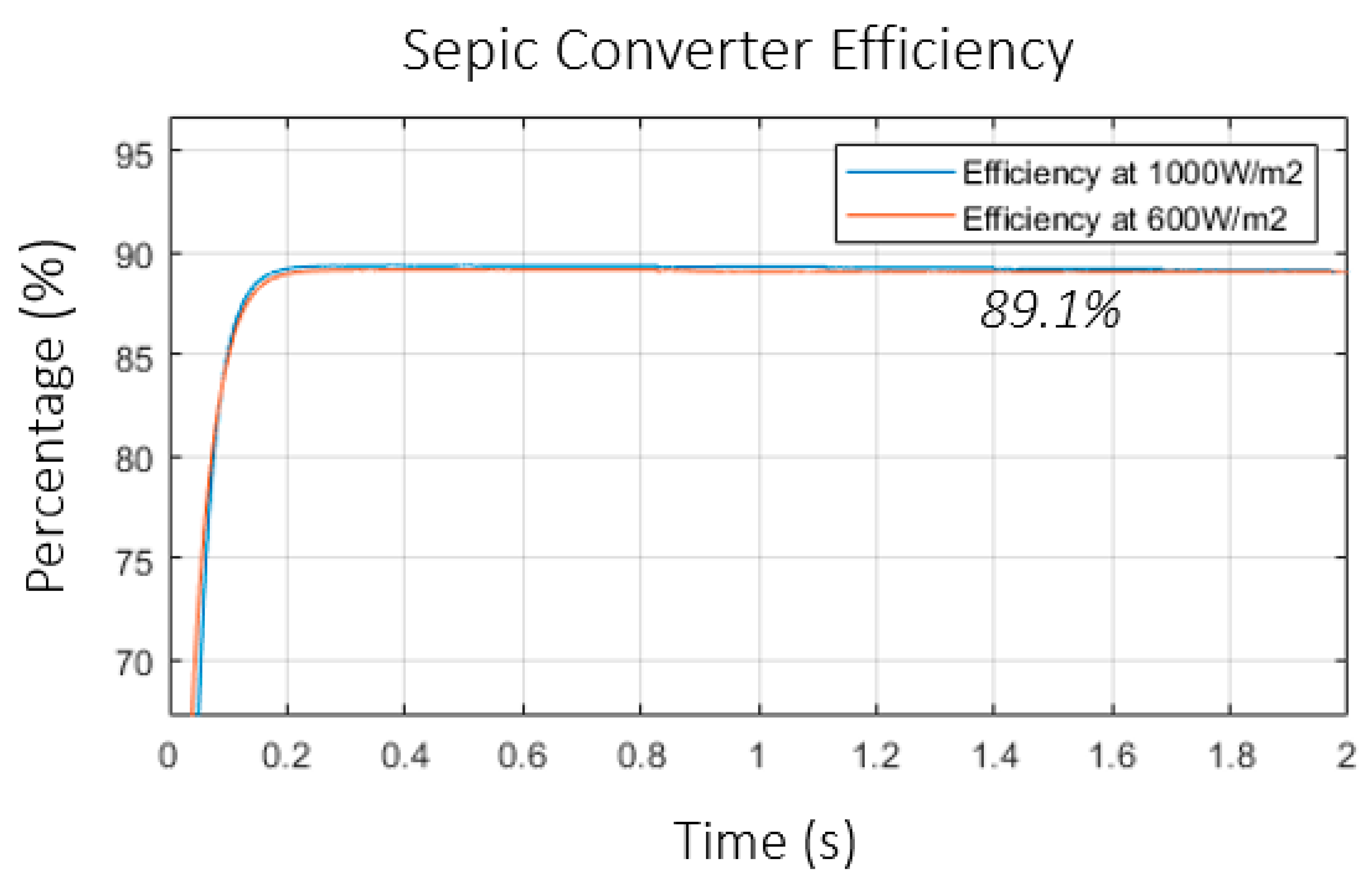
4. Simulation Results for the PV + Multiplier SEPIC
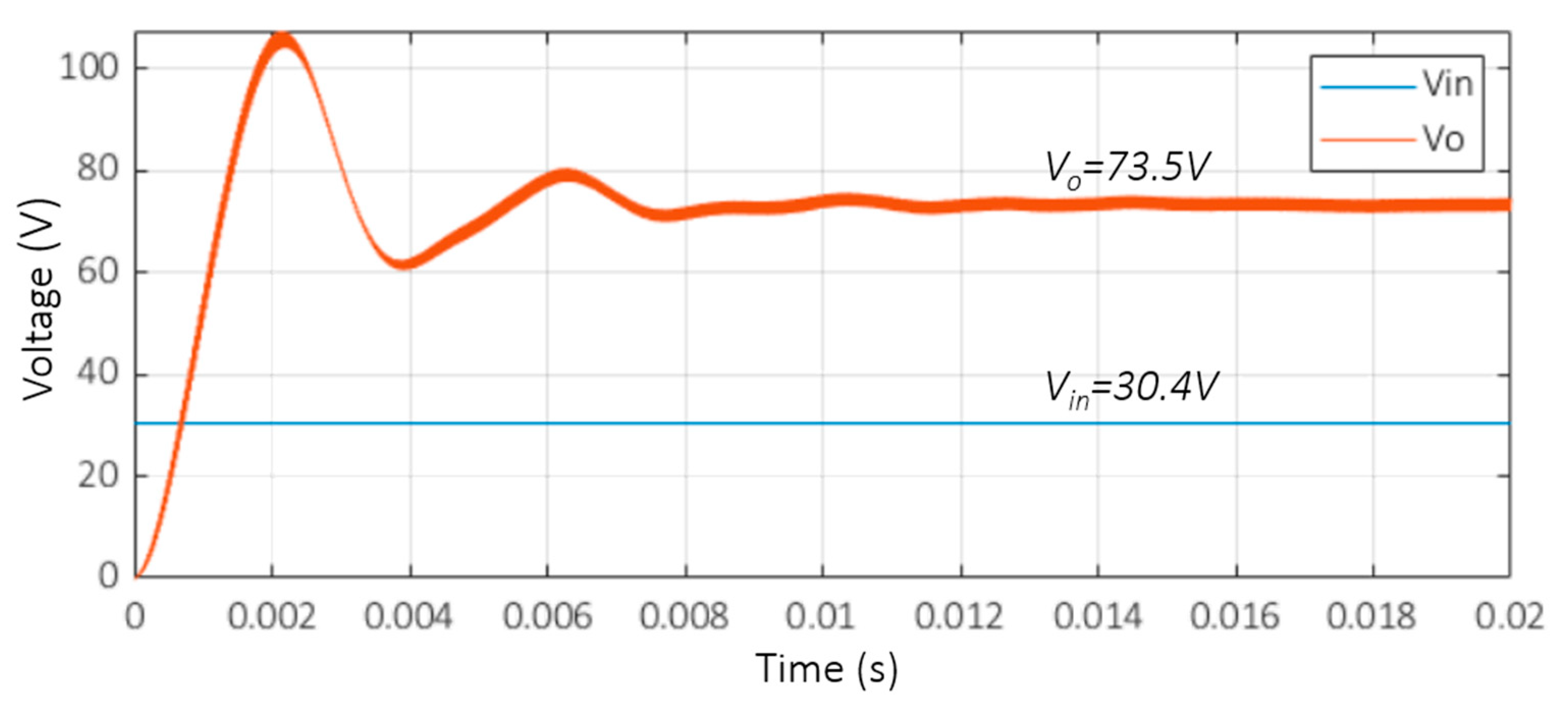
5. Hardware Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Subbulakshmy, R.; Palanisamy, R.; Alshahrani, S.; Saleel, C.A. Implementation of Non-Isolated High Gain Interleaved DC-DC Converter for Fuel Cell Electric Vehicle Using ANN-Based MPPT Controller. Sustainability 2024, 16, 1335. [Google Scholar] [CrossRef]
- Khan, M.R.; Haider, Z.M.; Malik, F.H.; Almasoudi, F.M.; Alatawi, K.S.S.; Bhutta, M.S. A Comprehensive Review of Microgrid Energy Management Strategies Considering Electric Vehicles, Energy Storage Systems, and AI Techniques. Processes 2024, 12, 270. [Google Scholar] [CrossRef]
- Daccò, E.; Falabretti, D.; Ilea, V.; Merlo, M.; Nebuloni, R.; Spiller, M. Decentralised Voltage Regulation through Optimal Reactive Power Flow in Distribution Networks with Dispersed Generation. Electricity 2024, 5, 134–153. [Google Scholar] [CrossRef]
- Bordbari, M.J.; Nasiri, F. Networked Microgrids: A Review on Configuration, Operation, and Control Strategies. Energies 2024, 17, 715. [Google Scholar] [CrossRef]
- Min, C.; Kim, H. A Practical Framework for Developing Net-Zero Electricity Mix Scenarios: A Case Study of South Korea. Energies 2024, 17, 926. [Google Scholar] [CrossRef]
- Gayathri, R.; Chang, J.-Y.; Tsai, C.-C.; Hsu, T.-W. Wave Energy Conversion through Oscillating Water Columns: A Review. J. Mar. Sci. Eng. 2024, 12, 342. [Google Scholar] [CrossRef]
- Mihalič, F.; Truntič, M.; Hren, A. Hardware-in-the-Loop Simulations: A Historical Overview of Engineering Challenges. Electronics 2022, 11, 2462. [Google Scholar] [CrossRef]
- Yousefzadeh, M.; Hedayati Kia, S.; Hoseintabar Marzebali, M.; Arab Khaburi, D.; Razik, H. Power-Hardware-in-the-Loop for Stator Windings Asymmetry Fault Analysis in Direct-Drive PMSG-Based Wind Turbines. Energies 2022, 15, 6896. [Google Scholar] [CrossRef]
- Hermassi, M.; Krim, S.; Kraiem, Y.; Hajjaji, M.A.; Alshammari, B.M.; Alsaif, H.; Alshammari, A.S.; Guesmi, T. Design of Vector Control Strategies Based on Fuzzy Gain Scheduling PID Controllers for a Grid-Connected Wind Energy Conversion System: Hardware FPGA-in-the-Loop Verification. Electronics 2023, 12, 1419. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Modeling and Control Simulation of Power Converters in Automotive Applications. Appl. Sci. 2024, 14, 1227. [Google Scholar] [CrossRef]
- Lamo, P.; de Castro, A.; Sanchez, A.; Ruiz, G.A.; Azcondo, F.J.; Pigazo, A. Hardware-in-the-Loop and Digital Control Techniques Applied to Single-Phase PFC Converters. Electronics 2021, 10, 1563. [Google Scholar] [CrossRef]
- Estrada, L.; Vázquez, N.; Vaquero, J.; de Castro, Á.; Arau, J. Real-Time Hardware in the Loop Simulation Methodology for Power Converters Using LabVIEW FPGA. Energies 2020, 13, 373. [Google Scholar] [CrossRef]
- Sanchez, A.; Todorovich, E.; De Castro, A. Exploring the Limits of Floating-Point Resolution for Hardware-In-the-Loop Implemented with FPGAs. Electronics 2018, 7, 219. [Google Scholar] [CrossRef]
- De Souza, I.D.T.; Silva, S.N.; Teles, R.M.; Fernandes, M.A.C. Platform for Real-Time Simulation of Dynamic Systems and Hardware-in-the-Loop for Control Algorithms. Sensors 2014, 14, 19176–19199. [Google Scholar] [CrossRef] [PubMed]
- Regatron Programmable Power Supplies. Available online: https://www.regatron.com/programmable-power-supplies/en/#hardware-in-the-loop (accessed on 16 June 2024).
- Chroma Solar Array Simulator Model 62000H-S Series. Available online: https://www.chromaate.com/en/product/solar_array_simulator_62000h_s_series_205 (accessed on 16 June 2024).
- Martínez, J.R.; Rengifo, H.R.; Córdoba, J.S.; Palacios, J.; Posada, J. Design and Implementation of a Multiplier SEPIC Converter to Emulate a Photovoltaic System Using Power HIL. In Proceedings of the 2019 FISE-IEEE/CIGRE Conference—Living the energy Transition (FISE/CIGRE), Medellin, Colombia, 4–6 December 2019; pp. 1–7. [Google Scholar]
- Olayiwola, T.N.; Hyun, S.-H.; Choi, S.-J. Photovoltaic Modeling: A Comprehensive Analysis of the I–V Characteristic Curve. Sustainability 2024, 16, 432. [Google Scholar] [CrossRef]
- Pan, W.; Zhang, Y.; Jin, W.; Liang, Z.; Wang, M.; Li, Q. Photovoltaic-Based Residential Direct-Current Microgrid and Its Comprehensive Performance Evaluation. Appl. Sci. 2023, 13, 12890. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, Photovoltaics and Wind; Wiley: New York, NY, USA, 1991; pp. 762–772. [Google Scholar]
- Rashid, M.H. Power Electronics: Circuits, Devices, and Applications, 3rd ed.; Pearson Education: Hoboken, NJ, USA, 2009; pp. 289–292. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Robbins, W.P. Power Electronics in Converters, Applications, and Design, 3rd ed.; Whiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 3rd ed.; Springer: New York, NY, USA, 2020. [Google Scholar]
- Valdez-Resendiz, J.E.; Mayo-Maldonado, J.C.; Alejo-Reyes, A.; Rosas-Caro, J.C. Double-Dual DC-DC Conversion: A Survey of Contributions, Generalization, and Systematic Generation of New Topologies. IEEE Access 2023, 11, 38913–38928. [Google Scholar] [CrossRef]
- Rosas-Caro, J.C.; Mayo-Maldonado, J.C.; Valdez-Resendiz, J.E.; Alejo-Reyes, A.; Beltran-Carbajal, F.; López-Santos, O. An Overview of Non-Isolated Hybrid Switched-Capacitor Step-Up DC–DC Converters. Appl. Sci. 2022, 12, 8554. [Google Scholar] [CrossRef]
- Rosas-Caro, J.C.; Mayo-Maldonado, J.C.; Valdez-Resendiz, J.E.; Salas-Cabrera, R.; Gonzalez-Rodriguez, A.; Salas-Cabrera, E.N.; Cisneros-Villegas, H.; Gonzalez-Hernandez, J.G. Multiplier SEPIC converter. In Proceedings of the CONIELECOMP 2011, 21st International Conference on Electrical Communications and Computers, Cholula, Puebla, Mexico, 28 February–2 March 2011; pp. 232–238. [Google Scholar]
- Rosas-Caro, J.C.; Sanchez, V.M.; Vazquez-Bautista, R.F.; Morales-Mendoza, L.J.; Mayo-Maldonado, J.C.; Garcia-Vite, P.M.; Barbosa, R. A novel DC-DC multilevel SEPIC converter for PEMFC systems. Int. J. Hydrogren Energy 2016, 41, 23401–23408. [Google Scholar] [CrossRef]







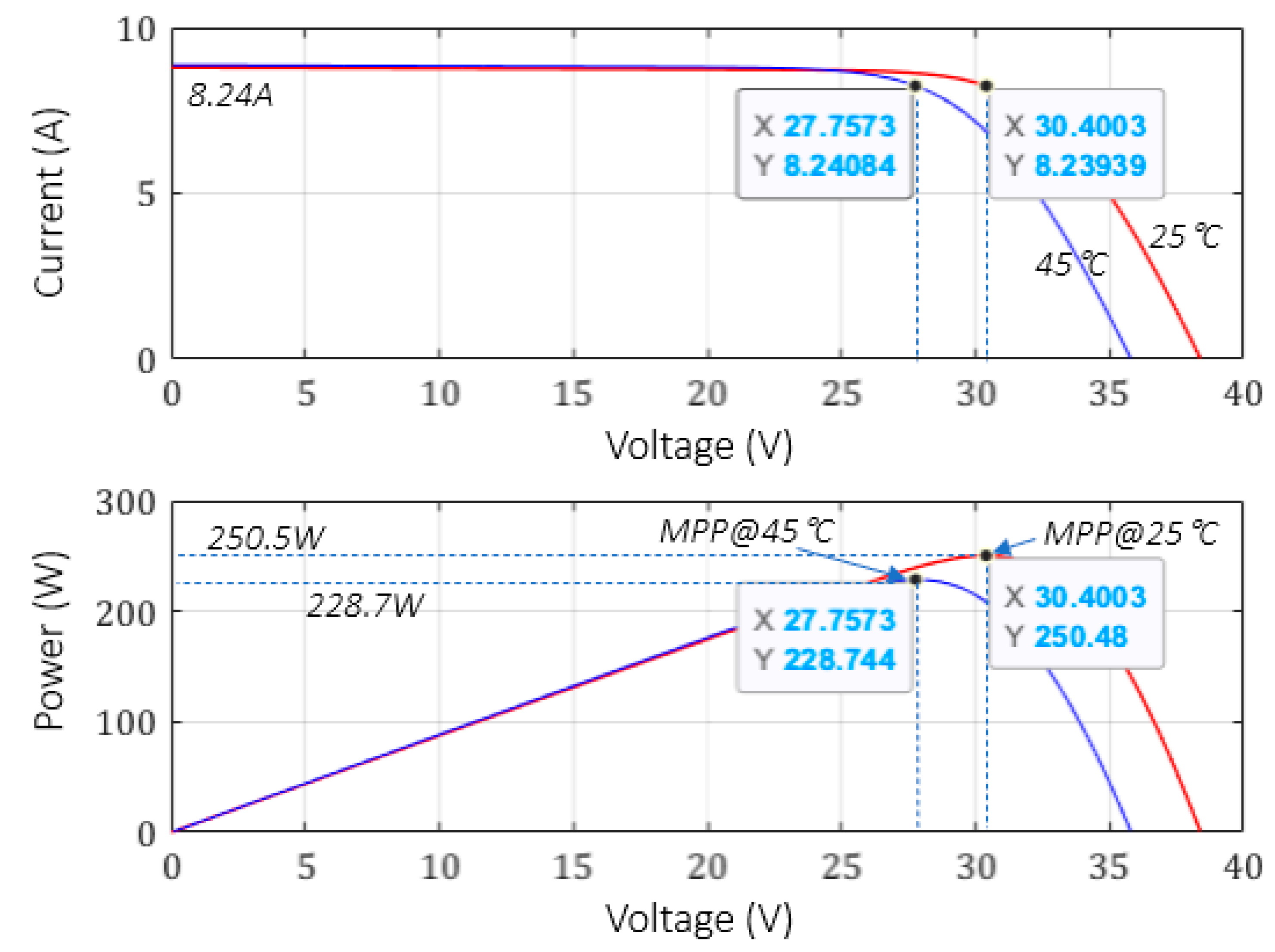

| Electrical Characteristics | Symbol | Manufacturer’s Value | Simulation Result | %Error |
|---|---|---|---|---|
| Voltage at Pmax | Vmpp | 29.8 V | 30.4 V | 2.01% |
| Current at Pmax | Impp | 8.39 A | 8.25 A | 1.67% |
| Short-circuit current | Isc | 8.92 A | 8.80 A | 1.36% |
| Open-circuit voltage | Voc | 37.6 V | 38.4 V | 2.13% |
| Theoretical Component | Selected Component |
|---|---|
| Four 420 uH inductors for a current of 9 A | |
| One 60 uF film capacitor (C4ATDBW5600A30J), 250 V, ESR = 3.9 mOhms | |
| Semiconductors | MOSFET mode IRFP250N with a max current equal to 30 A and a maximum power dissipation of 214 W at 175 °C, Ron = 1 × 10−5 Ω |
| Diode 30CPF10: 30 A, 1000 V max |
| Voltage at the input | 30.4 V | Power at the output | 250 W |
| Voltage at the output | 80.3 V | ||
| Current at the input | 8.25 A | Current at the output | 3.11 A |
| Maximum duty ration | 45% | Load resistor | 25.8 Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Posada Contreras, J.; Rosas-Caro, J.C. Hardware-in-the-Loop Emulation of a SEPIC Multiplier Converter in a Photovoltaic System. Electricity 2024, 5, 426-448. https://doi.org/10.3390/electricity5030022
Posada Contreras J, Rosas-Caro JC. Hardware-in-the-Loop Emulation of a SEPIC Multiplier Converter in a Photovoltaic System. Electricity. 2024; 5(3):426-448. https://doi.org/10.3390/electricity5030022
Chicago/Turabian StylePosada Contreras, Johnny, and Julio C. Rosas-Caro. 2024. "Hardware-in-the-Loop Emulation of a SEPIC Multiplier Converter in a Photovoltaic System" Electricity 5, no. 3: 426-448. https://doi.org/10.3390/electricity5030022
APA StylePosada Contreras, J., & Rosas-Caro, J. C. (2024). Hardware-in-the-Loop Emulation of a SEPIC Multiplier Converter in a Photovoltaic System. Electricity, 5(3), 426-448. https://doi.org/10.3390/electricity5030022








