A Fuzzy Programming Approach for a Multi-Objective Design of a Sustainable Closed-Loop Supply Chain Network in the Case of End-of-Life Medical Textiles ^†

Abstract

The reverse logistics of medical textiles has become a major concern in Morocco today, compelling authorities and professionals to develop a sustainable reverse logistics model. This study proposes a model for designing a sustainable closed-loop supply chain network in a fuzzy environment, using the medical textile life cycle as a case study. The model aims to generate economic gains, increase corporate social responsibility through job creation, and mitigate risks associated with the transportation of end-of-life products. In addition, the uncertainty of the model parameters is considered. The multi-objective model, formulated as a mixed-integer linear program, was solved using an exact approach, enabling strategic and tactical decision-making. Furthermore, the results demonstrate that accounting uncertainty can significantly impact strategic and tactical decisions in network design.

1. Introduction

The reverse logistics of health textiles (HTs), as a potential source of contamination, increasingly affects the quality of life of citizens [1]. Therefore, authorities and professionals are compelled to establish a sustainable reverse logistics model.

This paper aims to design a sustainable closed-loop supply chain network (SCLSCN) that integrates all stakeholders involved in the healthcare textile life_cycle, from manufacturing to product end-of-life. Indeed, the literature has proven the positive impact of sustainable logistics network design on the ecosystem of several sectors [2,3,4,5,6,7,8]. Nevertheless, the design of supply chain networks often faces challenges related to parameter uncertainty, a critical issue highlighted by M. B. and F. Goodarzian [9].

Several studies have focused on the design of the textile supply chain [10,11]. Hashim et al. [12] examined the critical supply chain risks associated with sustainable development goals in the Pakistani textile industry. However, this study provides a broad perspective on supply chain risks. Another study was conducted by Hu et al. [13], where they proposed a new sustainable model for managing the fashion supply chain, aiming to reduce waste. Nonetheless, the study did not address the specific risk posed by certain textiles after use. Taslimi et al. [14] introduced a periodic, load-dependent, capacitated vehicle routing problem to minimize risks in medical waste collection, but the study was limited to the operational level of the supply chain and did not consider environmental uncertainties.

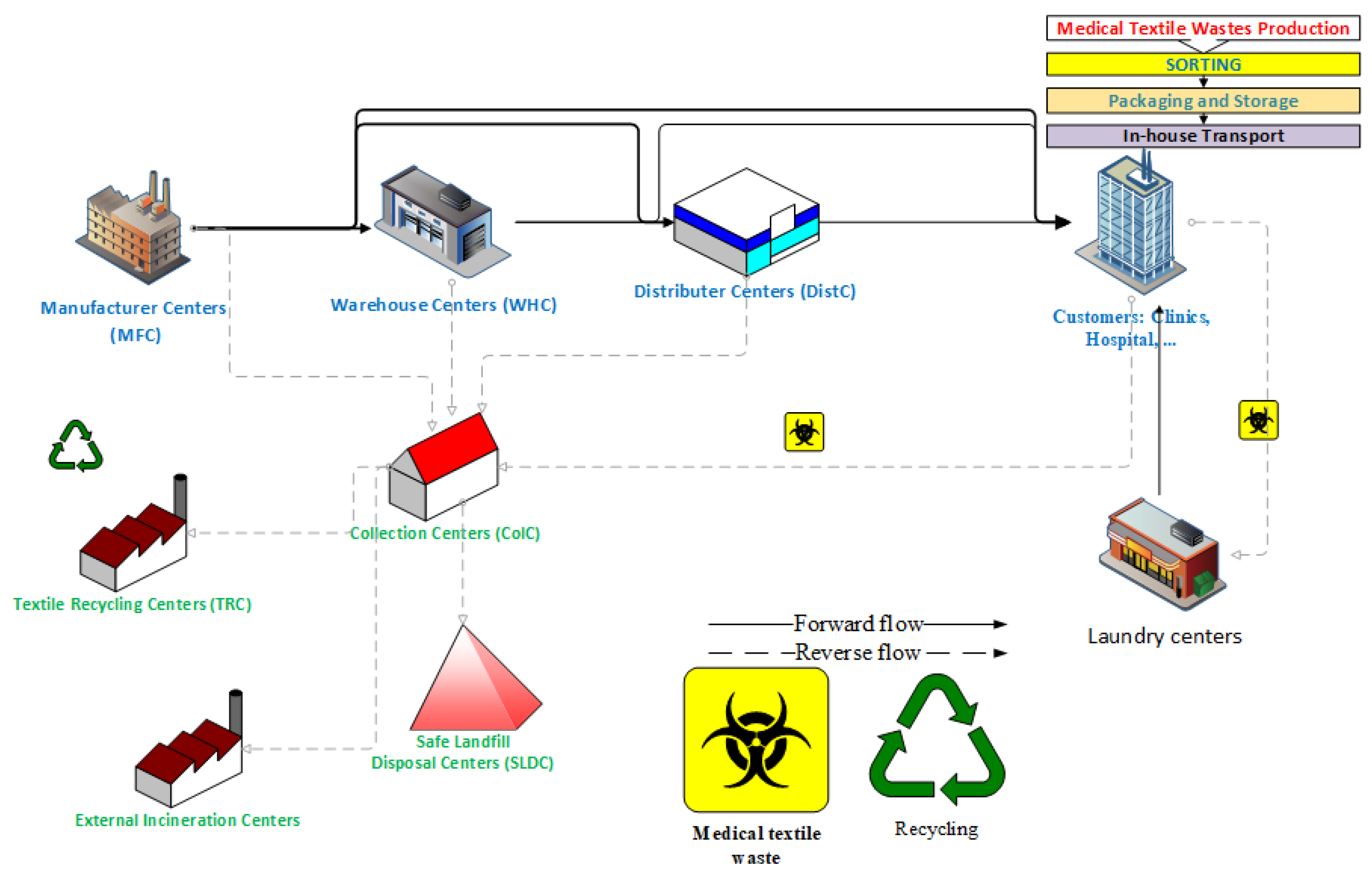
In our proposed network, shown in Figure 1, we adopt a semi-centralized collection for recyclable healthcare textiles, where the collection responsibilities are shared between the care units and the collection centers. This proposal aligns with previous studies that demonstrated the feasibility of semi-centralized collection of textiles and recyclables [15].

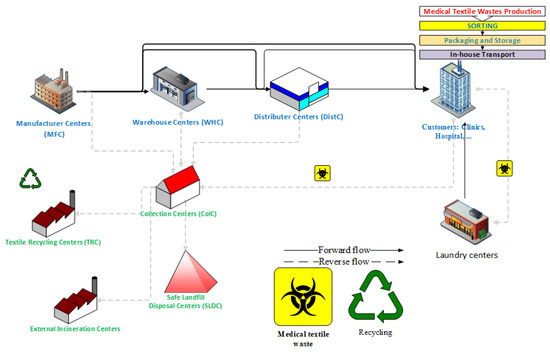
Figure 1. The proposed SCLSCN scheme to manage end-of-life medical textiles.

None of the above studies addressed the specific case of sustainable design for the medical textile supply chain. Therefore, the main contributions of this paper, which distinguish it from related studies, are as follows:

• A sustainable closed loop supply chain network integrating inventory constraints and location allocation decisions.
• A novel environmental objective function to minimize the risk coming from the transport of used healthcare textiles (Hazmat items).
• A multi-objective model designed to maximize revenue and job creation and minimize transportation risks.
• A three-phase fuzzy mathematical programming approach to optimize the proposed model.

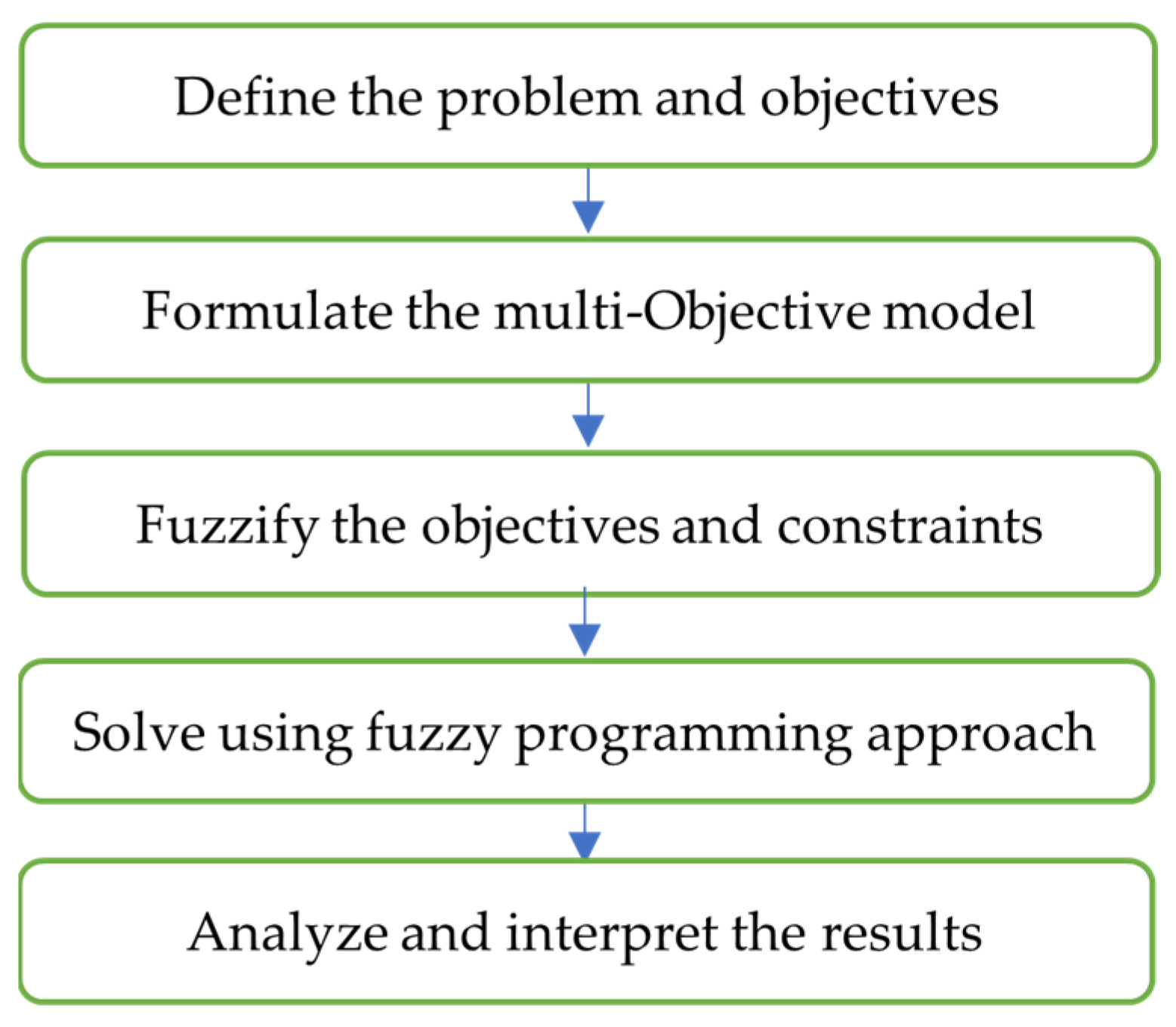
The basic methodology shown in Figure 2 seeks a trade-off between the main objectives related to the supply of end-of-life medical textiles. First, we will present our mathematical model. Then, we will solve the model using crisp numbers. Finally, we will provide conclusions and recommendations for future research.

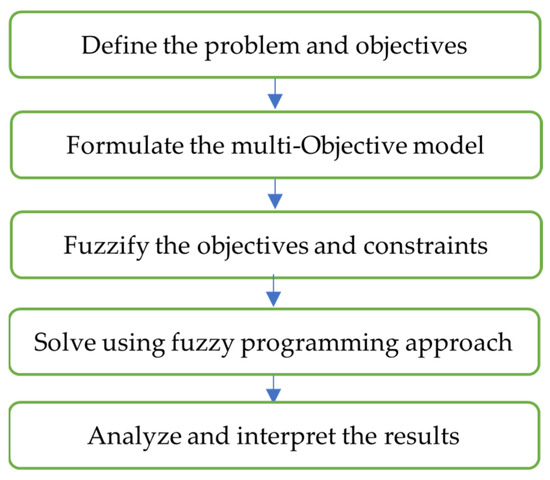
Figure 2. Flowchart of the methodology.

2. Material and Methods

2.1. Mathematical Formulation

We define the mathematical formulation of our multi-objective, mixed-integer linear programming (MOMILP) model, which aims to minimize costs, risks, and maximize job opportunities while accounting for the unique aspects of the proposed model. The mathematical formulation is based on the model presented by Ahlaqqach et al. in [5].

We consider three objective functions: profit, risk and job creation.

Profit (W₁) is defined as the total sales minus total cost, including fixed opening center cost, job creation cost, purchased cost, return product from customer cost, facilities operating cost, non-used facility capacity cost, non-utilized collectors capacity cost, shortage cost, and transportation Cost.

The risk function (W₂) accounts for contamination risks from accidents on routes used by vehicles transporting medical textiles.

$$\begin{array}{c}{\mathit{W}}_{\mathbf{2}}={\displaystyle \sum _{\mathit{c}\in \mathit{C}}}{\displaystyle \sum _{\mathit{l}\in \mathit{L}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{c}\mathit{l}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{c}\mathit{l}}+{\displaystyle \sum _{\mathit{l}\in \mathit{L}}}{\displaystyle \sum _{\mathit{s}\in \mathit{S}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{l}\mathit{s}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{l}\mathit{s}}+{\displaystyle \sum _{\mathit{l}\in \mathit{L}}}{\displaystyle \sum _{\mathit{e}\in \mathit{E}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{l}\mathit{e}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{l}\mathit{e}}\\ +{\displaystyle \sum _{\mathit{l}\in \mathit{L}}}{\displaystyle \sum _{\mathit{r}\in \mathit{R}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{l}\mathit{r}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{l}\mathit{r}}+{\displaystyle \sum _{\mathit{c}\in \mathit{C}}}{\displaystyle \sum _{\mathit{n}\in \mathit{N}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{c}\mathit{n}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{c}\mathit{n}},\end{array}$$

(1)

where

• R_ijpt: Contamination risk on road (i, j) for medical textiles p at time t;
• L_ij: Binary variable equals ‘1’ if links is established between facilities ‘i’ and ‘j’;
• C: Set of customers indexed by ‘c’;
• L: Set of collector’s centers indexed by ‘l’;
• S: Set of Safe landfill disposal centers indexed by ‘s’;
• R: Set of textile Recycling centers indexed by ‘r’;
• E: Set of External incinerator centers indexed by ‘e’;
• N: Set of Laundry centers indexed by ‘e’.

The third objective aims to maximize job opportunities.

$${\mathit{W}}_3={\sum }_{\mathit{a}\in \mathit{A}}{\mathit{J}\mathit{a}}_{\mathit{a}} \mathit{\ast } {\mathit{L}}_{\mathit{a}},$$

(2)

where

• J_a: Number of jobs create with center a, a∈A, with A represent all types of facility;
• L_i: binary variable equals ‘1’ if location ‘i’ is open and ‘0’ otherwise.

Our multi-objective function is expressed as a scalar function:

$$\mathit{\alpha } \mathit{\ast } \mathit{W}1-\mathit{\beta } \mathit{\ast } \mathit{W}2+\mathit{\delta } \mathit{\ast } \mathit{W}3,$$

(3)

where α, β, and δ are, respectively, the weight of profit, risk, and job creation objectives. Instead of using the absolutes values of W₁, W₂, and W₃, respectively, we normalize them, so they become comparable. We use normalization in Bronfman et al. [1], where Y_i and, U_i are the normalized objective function in case of minimization and maximization, respectively. W_imax, W_imin, and W_i represent the maximum possible, minimum possible, and actual value of each objective before normalization.

$${\mathit{Y}}_{\mathit{i}}=\left[{\displaystyle \frac{{\mathit{W}}_{\mathit{i}}-{\mathit{W}}_{\mathit{i}\mathit{m}\mathit{i}\mathit{n}}}{{\mathit{W}}_{\mathit{i}\mathit{m}\mathit{a}\mathit{x}}-{\mathit{W}}_{\mathit{i}\mathit{m}\mathit{i}\mathit{n}}}}\right]{\& \mathit{U}}_{\mathit{i}}=\left[{\displaystyle \frac{{\mathit{W}}_{\mathit{i}\mathit{m}\mathit{a}\mathit{x}}-{\mathit{W}}_{\mathit{i}}}{{\mathit{W}}_{\mathit{i}\mathit{m}\mathit{a}\mathit{x}}-{\mathit{W}}_{\mathit{i}\mathit{m}\mathit{i}\mathit{n}}}}\right],$$

(4)

2.2. Fuzzifying the Model

We validate our model using Optimization Studio, Version IDE 22.1, IBM Corporation, Armonk, NY, USA. The results obtained are relevant, they respect all constraints, and the experiments enabled us to fine-tune the trade-off between the objectives of our model. However, the resolution of the first model supposes that all parameters are deterministic. In practice, we encounter fuzzy values associated with the risk and capacity parameters of each center, which are involved in both objective functions and constraints. Thus, the fuzzy, multi-objective, mixed-integer linear programming (FMOMILP) model with fuzzy risk may be formulated as follows:

$$\begin{array}{c}{\mathit{W}}_2={\displaystyle \sum _{\mathit{c}\in \mathit{C}}}{\displaystyle \sum _{\mathit{l}\in \mathit{L}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{c}\mathit{l}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{c}\mathit{l}}+{\displaystyle \sum _{\mathit{l}\in \mathit{L}}}{\displaystyle \sum _{\mathit{s}\in \mathit{S}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{l}\mathit{s}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{l}\mathit{s}}+{\displaystyle \sum _{\mathit{l}\in \mathit{L}}}{\displaystyle \sum _{\mathit{e}\in \mathit{E}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{l}\mathit{e}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{l}\mathit{e}}\\ \hspace{1em}+{\displaystyle \sum _{\mathit{l}\in \mathit{L}}}{\displaystyle \sum _{\mathit{r}\in \mathit{R}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{R}}_{\mathit{l}\mathit{r}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{l}\mathit{r}}+{\displaystyle \sum _{\mathit{c}\in \mathit{C}}}{\displaystyle \sum _{\mathit{n}\in \mathit{N}}}{\displaystyle \sum _{\mathit{p}\in \mathit{P}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\tilde{\mathit{R}}}_{\mathit{c}\mathit{n}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{c}\mathit{n}}, \end{array}$$

(5)

$${\displaystyle \sum _{\mathit{a}\in \mathit{A}}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}}{\mathit{Q}}_{\mathit{a}\mathit{i}\mathit{p}\mathit{t}}\le {\tilde{\mathit{C}}}_{\mathit{i}\mathit{p}\mathit{t}} \mathit{\ast } {\mathit{L}}_{\mathit{i}},$$

(6)

where ${\tilde{R}}_{cnpt}$ and ${\tilde{C}}_{ipt}$ represent the fuzzy set of the risk objective function values and the capacity of each center, respectively. The fuzzy parameters are expressed by a triangular distribution of parameters: the most probable, the most optimistic, and the most pessimistic value.

To solve this model, we used a three-phase fuzzy mathematical programming approach, transforming the model into a deterministic equivalent.

In the first two phases, we used the weighted average method proposed by Lai and Hwang [16] to convert the FMOMILP model into an equivalent auxiliary crisp MOMILP model. Several studies have sought to determine the best way to convert FMOMILP to MOMILP. In our study, we opted for the approach by Lai and Hwang [16], due to its suitability for our case [17]. This method provides more flexibility for decision-makers to achieve a fuzzy solution according to their preferences [18]. Therefore, the Positive Ideal Solutions (PIS) and Negative Ideal Solutions (NIS) of all crisp objective functions were calculated as follows:

$$\begin{gathered} {\mathit{Z}}_1^{\mathit{P}\mathit{I}\mathit{S}}=\mathit{M}\mathit{a}\mathit{x} \mathit{W}1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{Z}}_1^{\mathit{N}\mathit{I}\mathit{S}}=\mathit{M}\mathit{i}\mathit{n} \mathit{W}1 \\ {\mathit{Z}}_2^{\mathit{P}\mathit{I}\mathit{S}}=\mathit{M}\mathit{i}\mathit{n} {\mathit{W}2}^{\mathit{m}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{Z}}_2^{\mathit{N}\mathit{I}\mathit{S}}=\mathit{M}\mathit{a}\mathit{x} {\mathit{W}2}^{\mathit{m}} \\ {\mathit{Z}}_3^{\mathit{P}\mathit{I}\mathit{S}}=\mathit{M}\mathit{a}\mathit{x} \left({\mathit{W}2}^{\mathit{m}}-{\mathit{W}2}^{\mathit{o}}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{Z}}_3^{\mathit{N}\mathit{I}\mathit{S}}=\mathit{M}\mathit{i}\mathit{n} \left({\mathit{W}2}^{\mathit{m}}-{\mathit{W}2}^{\mathit{o}}\right) \\ {\mathit{Z}}_4^{\mathit{P}\mathit{I}\mathit{S}}=\mathit{M}\mathit{i}\mathit{n} \left({\mathit{W}2}^{\mathit{p}}-{\mathit{W}2}^{\mathit{m}}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{Z}}_4^{\mathit{N}\mathit{I}\mathit{S}}=\mathit{M}\mathit{a}\mathit{x} \left({\mathit{W}2}^{\mathit{p}}-{\mathit{W}2}^{\mathit{m}}\right) \\ {\mathit{Z}}_5^{\mathit{P}\mathit{I}\mathit{S}}=\mathit{M}\mathit{a}\mathit{x} \mathit{W}3\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathit{Z}}_5^{\mathit{N}\mathit{I}\mathit{S}}=\mathit{M}\mathit{i}\mathit{n} \mathit{W}3 \end{gathered}$$

(7)

Here, W2^m, W2^o, and W2^p (the most probable, the most optimistic, and the most pessimistic value) are the three corner points that geometrically define the fuzzy objective W2. The related linear membership functions of these objective functions are given by:

$$\begin{gathered} {\mathit{\mu }}_{\mathit{z}\mathit{i}}=\left\{\begin{array}{c}1 \mathit{I}\mathit{f} {\mathit{Z}}_{\mathit{i}}<{\mathit{Z}}_{\mathit{i}}^{\mathit{P}\mathit{I}\mathit{S}}\\ {\displaystyle \frac{{\mathit{Z}}_{\mathit{i}}^{\mathit{N}\mathit{I}\mathit{S}}-{\mathit{Z}}_{\mathit{i}}}{{\mathit{Z}}_{\mathit{i}}^{\mathit{N}\mathit{I}\mathit{S}}-{\mathit{Z}}_{\mathit{i}}^{\mathit{P}\mathit{I}\mathit{S}}}} \mathit{I}\mathit{f} {\mathit{Z}}_{\mathit{i}}^{\mathit{P}\mathit{I}\mathit{S}}\le {\mathit{Z}}_{\mathit{i}}\le {\mathit{Z}}_{\mathit{i}}^{\mathit{N}\mathit{I}\mathit{S}} \\ 0 \mathit{I}\mathit{f} {\mathit{Z}}_{\mathit{i}}>{\mathit{Z}}_{\mathit{i}}^{\mathit{N}\mathit{I}\mathit{S}}\end{array}\right.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathit{f}\mathit{o}\mathit{r} \mathit{i}=1,2,4 \\ {\mathit{\mu }}_{\mathit{z}\mathit{j}}=\left\{\begin{array}{c}1 \mathit{I}\mathit{f} {\mathit{Z}}_{\mathit{j}}>{\mathit{Z}}_{\mathit{j}}^{\mathit{P}\mathit{I}\mathit{S}}\\ {\displaystyle \frac{{\mathit{Z}}_{\mathit{j}}-{\mathit{Z}}_{\mathit{j}}^{\mathit{N}\mathit{I}\mathit{S}}}{{\mathit{Z}}_{\mathit{j}}^{\mathit{P}\mathit{I}\mathit{S}}-{\mathit{Z}}_{\mathit{j}}^{\mathit{N}\mathit{I}\mathit{S}}}} \mathit{I}\mathit{f} {\mathit{Z}}_{\mathit{j}}^{\mathit{N}\mathit{I}\mathit{S}}\le {\mathit{Z}}_{\mathit{j}}\le {\mathit{Z}}_{\mathit{j}}^{\mathit{P}\mathit{I}\mathit{S}} \\ 0 \mathit{I}\mathit{f} {\mathit{Z}}_{\mathit{j}}<{\mathit{Z}}_{\mathit{j}}^{\mathit{N}\mathit{I}\mathit{S}}\end{array}\right.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathit{f}\mathit{o}\mathit{r} \mathit{j}=3,5 \end{gathered}$$

(8)

In the third phase, we applied the fuzzy goal programming techniques from various approaches, including Zimmermann [19,20], Li, Zhang, and Li (LZL) [20], Werners [21], Selim and Ozkarahan (SO) [22], and the Torabi and Hassini (TH) approach [23], to solve the MOMILP model effectively.

3. Results and Discussion

The first set of experiments aimed to normalize our objective function using an exact approach. The results showed good performance for small instances.

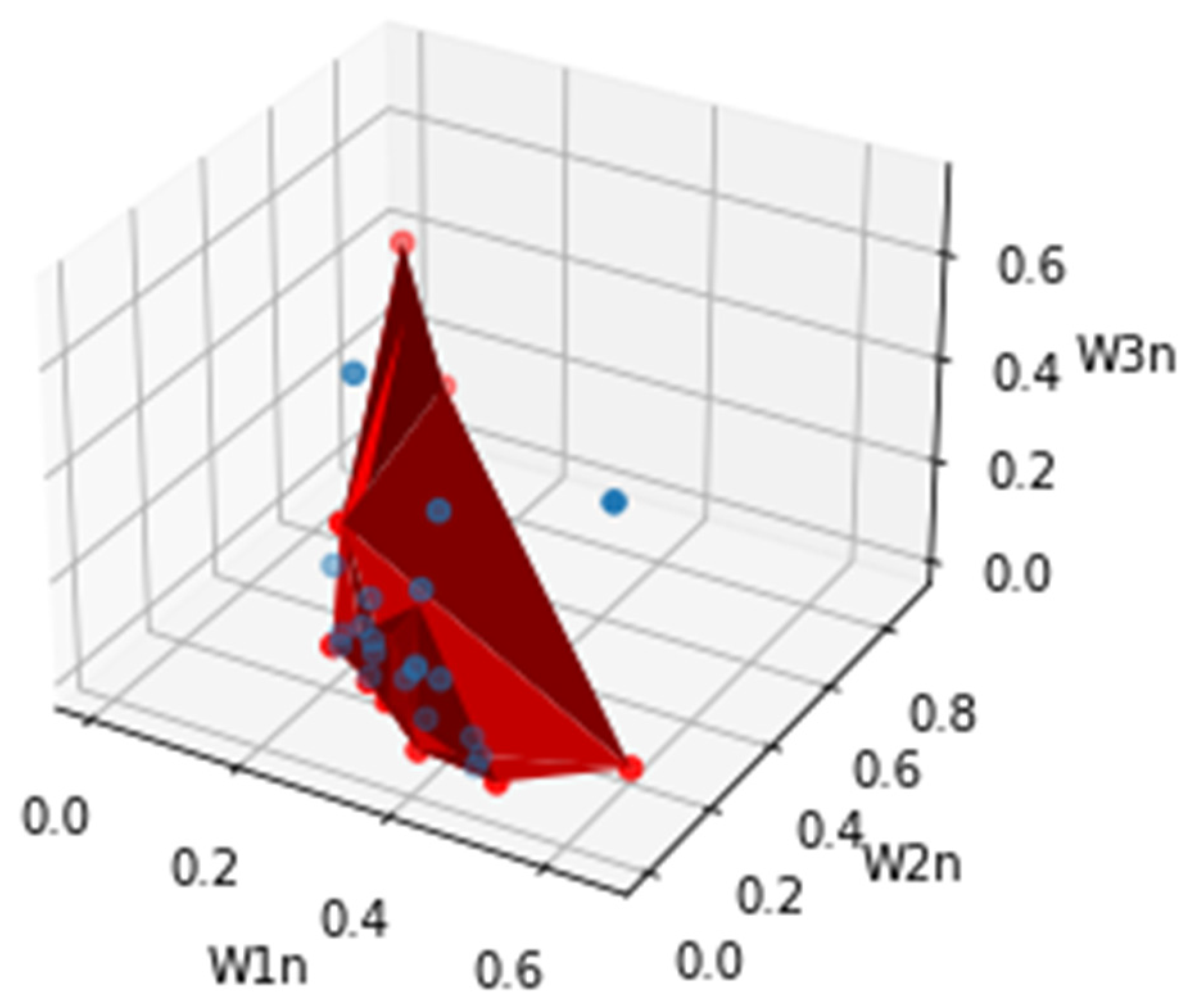
The second experiment allowed us to verify the feasibility of a trade-off between the studied objectives, highlighting the need for uncertainty integration in the design process. The three-dimensional Pareto front in Figure 3 provides a red region, which represents a trade-off among the three objectives. The blue points represent the dominated solutions, which will be avoided; certainly, they give preferential treatment to some objectives to the detriment of others.

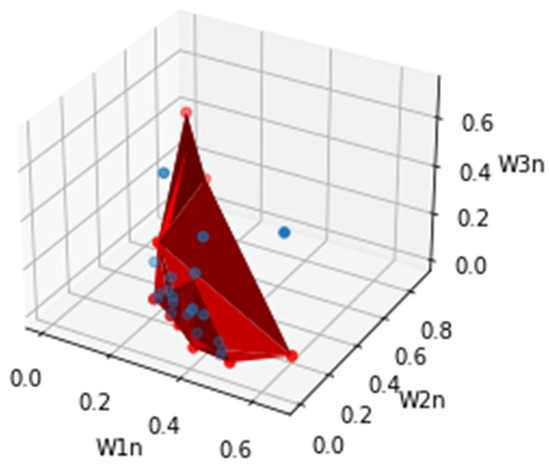
Figure 3. 3D Pareto front of normalized objectives.

The third experiment highlighted the significant differences between deterministic models and those incorporating uncertainty, emphasizing the importance of integrating uncertainty into the design of sustainable closed-loop supply chain networks (SCLSCNs).

To address this challenge, a three-phase fuzzy mathematical programming was applied to solve our model and obtain optimum objectives. The results from this experiment, presented in Table 1, include the total satisfaction degree (TSD), membership function (MF), and objective function (OF) for each fuzzy goal programming approach tested. Based on these results, it can be concluded that the TH approach is the most appropriate method for the FMOMILP model of SCLSCN.

Table 1. Satisfaction degree of objective functions.

Zimmermann max–min Approach
MF 1	MF Value	OF 2	OF Value	TSD 3
μz1	0.496	Z1	3.5 × 106	2.518
μz2	0.506	Z2	1221
μz3	0.552	Z3	521
μz4	0.439	Z4	402
μz5	0.525	Z5	1233
LZL Approach
MF	MF Value	OF	OF Value	TSD
μz1	0.777	Z1	6.08 × 106	3.362
μz2	1.000	Z2	1831
μz3	0.566	Z3	512
μz4	0.440	Z4	403
μz5	0.580	Z5	1165
TH Approach
MF	MF Value	OF	OF Value	TSD
μz1	0.943	Z1	7.63 × 106	3.664
μz2	1.000	Z2	1831
μz3	0.521	Z3	542
μz4	0.531	Z4	456
μz5	0.670	Z5	1057
Selim and Özkarahan Approach
MF	MF Value	OF	OF Value	TSD
μz1	0.433	Z1	2.9 × 106	3.001
μz2	1.000	Z2	1831
μz3	0.527	Z3	538
μz4	0.483	Z4	429
μz5	0.557	Z5	1194
Werners Approach
MF	MF Value	OF	OF Value	TSD
μz1	0.433	Z1	2.9 × 106	3.001
μz2	1.000	Z2	1831
μz3	0.527	Z3	538
μz4	0.483	Z4	429
μz5	0.557	Z5	1194

¹ MF: The related linear membership function; ² OF: the crisp objective function; ³ TSD: total satisfaction degree.

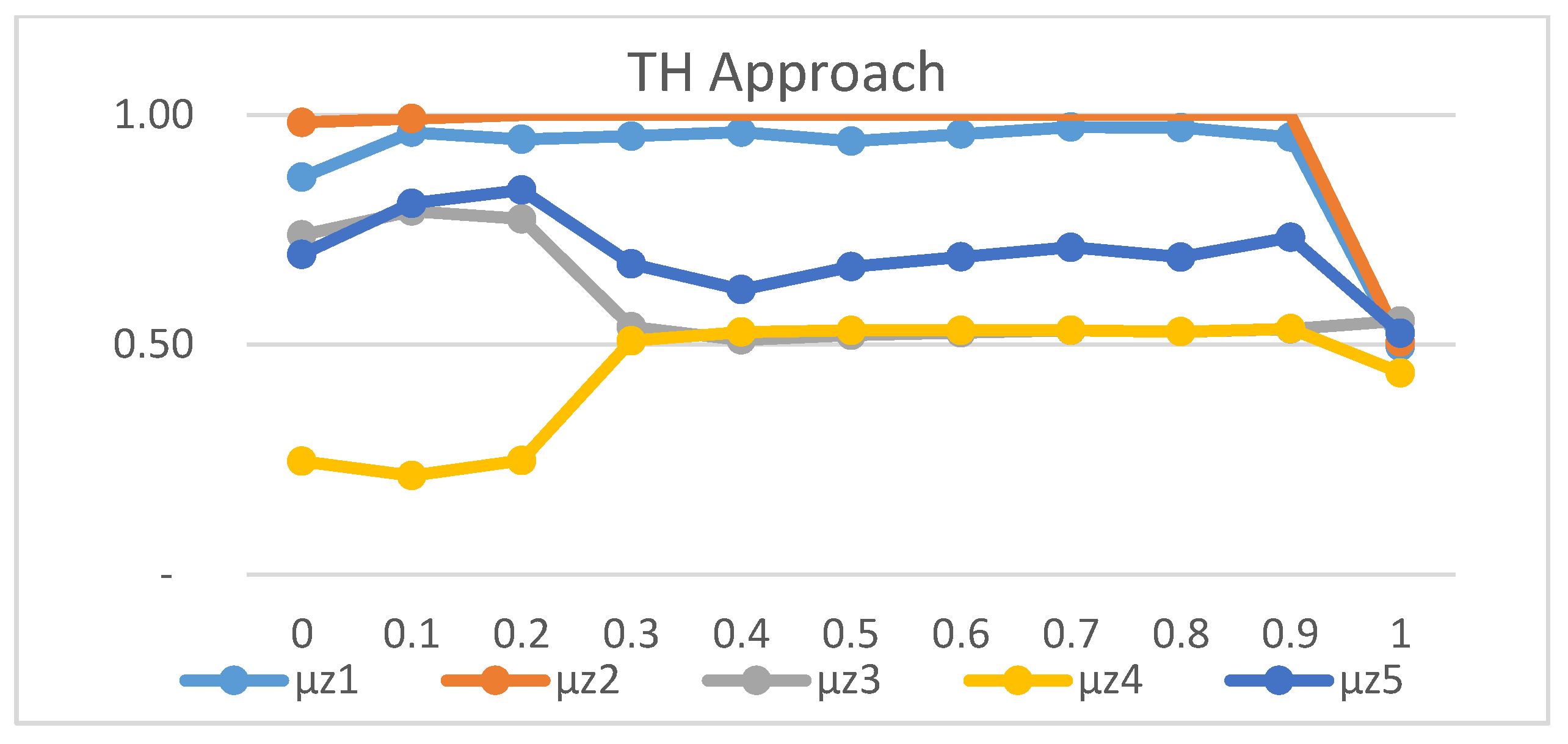
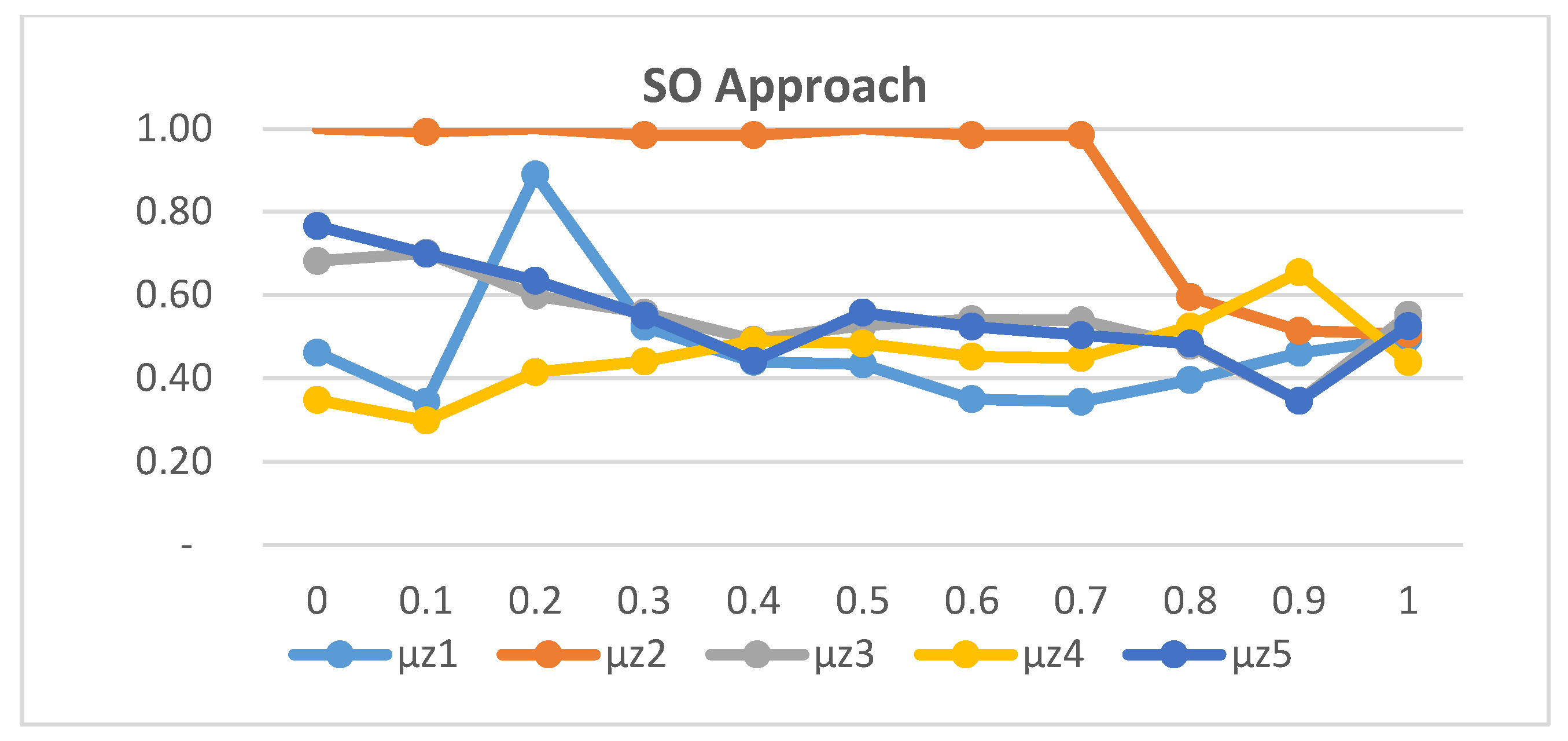
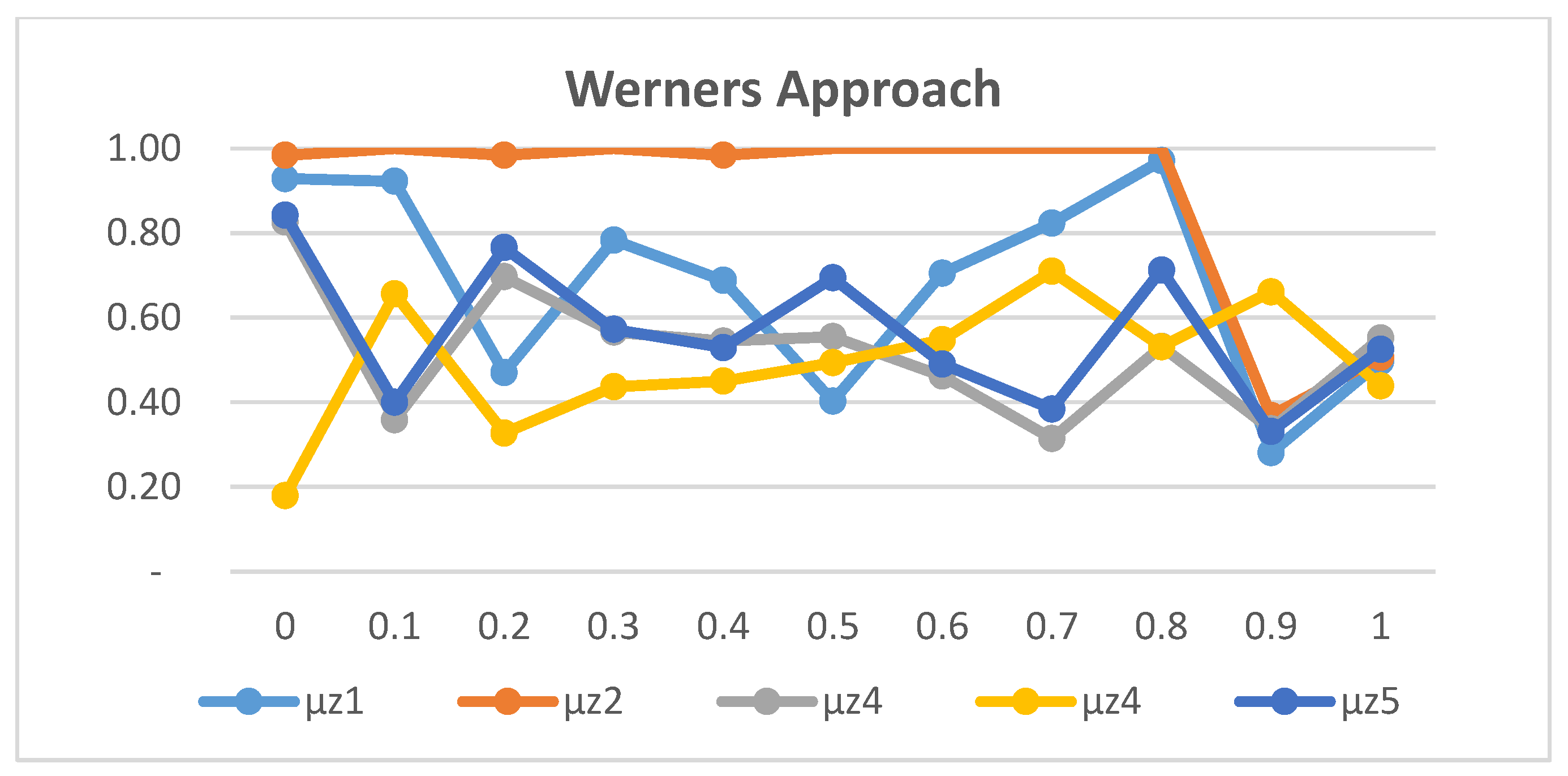
The second experiment, which focused on sensitivity analysis for the compensation coefficient γ demonstrated, as shown in Figure 4, Figure 5 and Figure 6, that the TH approach is relatively insensitive to changes in γ value. In contrast, the SO and Werners methods produced unbalanced solutions, while the TH approach maintained stable values for γ between 0.3 and 0.9.

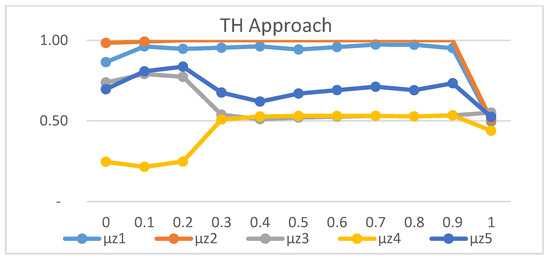
Figure 4. Sensibility analysis of γ value for the TH approach.

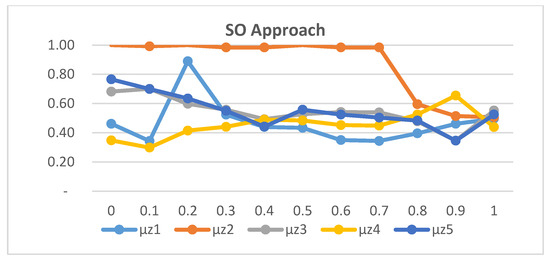
Figure 5. Sensibility analysis of γ value for the SO approach.

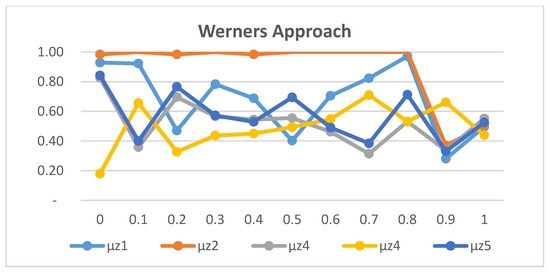
Figure 6. Sensibility analysis of γ value for the Werners approach.

The third experiment helped us to examine the impact of uncertainty on SCLSCND. We noticed that the SCLSCN proposed by the first experimentation (deterministic parameters) differed from the model that considered uncertainty. Since the external data (demand, capacity of public platforms) as well as the internal data (production capacity …) are often uncertain, accounting for these uncertainties is crucial for designing effective and robust logistic networks. This demonstrates the necessity of integrating uncertainty into the design process to ensure reliable decision-making.

4. Conclusions

To the best of our knowledge, this paper is one of the first to apply supply chain network design practices and tools to the reverse flows of medical textiles. It provides new insights into reverse logistics for used medical textile waste under uncertainty by proposing a multi-objective mathematical model with a three-phase fuzzy mathematical programming as an approach to cope with uncertainties.

This study developed a closed-loop supply chain network model to cope with conflicting sustainable development objectives. The hazardous nature of the healthcare textile has led us to integrate the risks associated with the transport of these materials. The social responsibility of the fabrics company is considered in sustainable closed-loop supply chain network designs with the integration of job opportunity created in the objective function. To encourage the company to adopt our approach, we have integrated the profit aspect to show the possibility of coexistence between these conflicting objectives. This model aims to generate economic gains, increase corporate social responsibility in terms of job creation, and reduce the risk associated with the transportation of used products. In addition, the uncertainty of the model parameters is considered. The multi-objective model expressed as a mixed-integer linear program was solved by an exact approach; this resolution allowed us to make strategic and tactical decisions. Furthermore, the result showed that considering uncertainty can significantly change the strategic and tactical decision making for the network design.

In this study, we focused on small instances to validate the model. Future work will concentrate on developing an efficient metaheuristic algorithm to address larger, more complex instances, enabling scalable and robust decision-making in real-world applications.