Study on the Influence of Preload in a Rubber Vibration Isolator on Its Buffering Performance ^†

Abstract

In this paper, by studying the basic principle of buffering, it was analyzed that damping and natural frequency have a great influence on the buffering effect. In order to obtain the influence of rubber preload on structural damping and natural frequency, a series of impact tests were carried out. The test data show that when the diameter of the smooth rod is increased by 0.2 mm, the buffering rate in a horizontal direction is reduced from 96.59% to 81.74%. The buffer ratio in the other direction is reduced from 97.37% to 85.81%. When the length is increased by 0.2 mm, the vertical buffer ratio is increased from 85.52% to 93.26%.

1. Introduction

With the development of weapon equipment that operates at high speed and with a large number of levels, precision electronic equipment has higher and higher accuracy requirements, and the instantaneous impact directly harms the normal use of equipment, so it is necessary to use vibration isolators for shock resistance design.

2. Development of Research Questions

According to the method of obtaining the shock stiffness, combined with hysteresis loop theory and experimental research, De Gao [1] derived the eight-parameter polynomial F-S expression, which can describe the shock response. Hong Gang Li [2] selected ABAQUS finite element analysis software to carry out the CAE design of the rubber vibration isolator and carried out test verification. With the aim of using it in the harsh space environment, Zhang Zhi [3] studied a double-layer vibration damping and isolation system, and analyzed the factors affecting the impact resistance of a rubber shock absorber.

3. Methodology

Buffering means that the vibration isolator converts the kinetic energy into potential energy and stores it, and the other part of the energy is dissipated by damping, thus slowing down the impact. When a body m is acted upon by a force F in a momentary Δt time interval, the velocity of the body changes ΔV and the energy dissipates Q, which is expressed as follows [4]:

$$m\Delta V+Q={\displaystyle {\int }_0^{\Lambda t}F(t)dt}$$

(1)

Impact is a transient process. When it occurs, the kinetic energy transfer time between systems is very short, the impact function is non-periodic, its spectrum is continuous, and the motion generated by the system under impact excitation is transient. Its motion state is related to the impact duration and the inherent characteristics of the system.

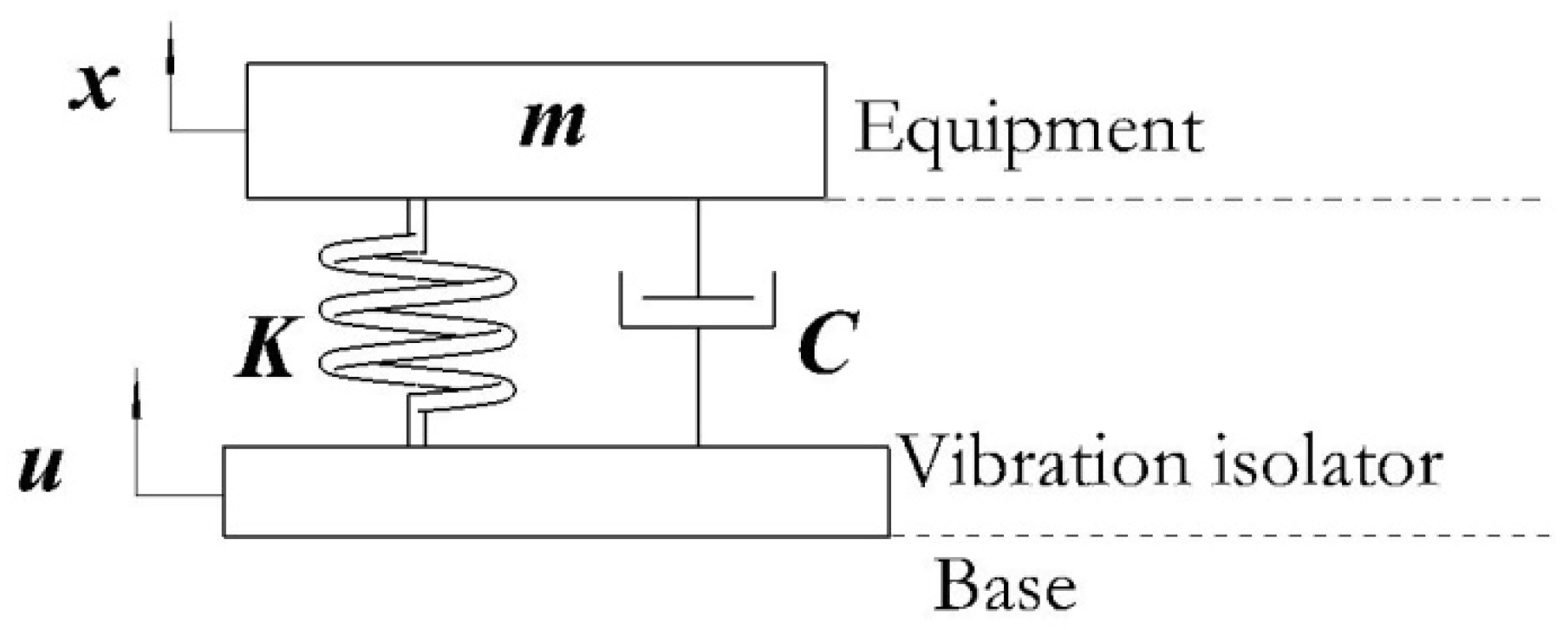
A vibration isolator can be simplified into a viscous damping buffer system, as shown in Figure 1.

If the buffer system is regarded as a linear spring with viscous damping, then:

$$\{\begin{array}{l}mx+F(\delta ,\ddot{\delta })=0\\ F(\delta ,\ddot{\delta })=k\delta +c\dot{\delta }\end{array}$$

(2)

In the formula, δ is the compression of the vibration isolator and F is the force generated by the isolator.

When the system is excited by a velocity step, the equation of motion and the initial state of the system can be expressed as follows:

$$\{\begin{array}{l}\ddot{\delta }+2\xi \omega \dot{\delta }+{\omega }^2\delta =0\\ \delta (0)=0,\dot{\delta }(0)=-{\dot{u}}_m\end{array}$$

(3)

In the formula, the natural frequency $\omega =\sqrt{{\displaystyle \frac{k}{m}}}$, and the relative damping coefficient $\xi ={\displaystyle \frac{c}{2m\omega }}$.

From Formula (3), it can be solved as follows:

$$\delta =-{\displaystyle \frac{{\dot{u}}_m}{\omega \sqrt{1-{\xi }^2}}}{e}^{-\xi \omega t}\sin \sqrt{1-{\xi }^2}\omega t$$

(4)

In the formula, ${\dot{u}}_m$ is the peak value of the speed step, which denotes an external impact.

Let $\dot{\delta }=0$, where the maximum compressed response ${\delta }_m={\displaystyle \frac{{\delta }_m\omega }{{\dot{u}}_m}}=e^{-\xi \omega t_1}$,

$$\omega t_1={\displaystyle \frac{1}{\sqrt{1-{\xi }^2}}}t{g}^{-1}{\displaystyle \frac{\sqrt{1-{\xi }^2}}{\xi }}$$

(5)

On account of $\ddot{x}=\ddot{\delta }$, the maximum absolute acceleration ${\ddot{x}}_m$ can be derived from the formula in which $\delta$ passes through.

$$\{\begin{array}{l}{\displaystyle \frac{{\ddot{x}}_m}{{\dot{u}}_m\omega }}=e^{-\xi \omega t_2}\\ \omega t_2={\displaystyle \frac{1}{\sqrt{1-{\xi }^2}}}t{g}^{-1}{\displaystyle \frac{(4{\xi }^2-1)\sqrt{1-{\xi }^2}}{\xi (4{\xi }^2-3)}}\\ {\displaystyle \frac{{\ddot{x}}_m}{{\dot{u}}_m\omega }}=2\xi ,0.5\le \xi <1\end{array}$$

(6)

According to Equation (6),when $\xi <0.5$, then ${\displaystyle \frac{{\ddot{x}}_m}{{\dot{u}}_m\omega }}<1$. This shows that the existence of damping reduces the maximum acceleration and improves the buffering effect; when $\xi >0.5$, then ${\displaystyle \frac{{\ddot{x}}_m}{{\dot{u}}_m\omega }}>1$. This shows that the existence of damping increases the maximum acceleration and reduces the buffering effect, so it is necessary to choose the appropriate parameters of damping. The buffering effect is also related to the natural frequency $\omega$ of the vibration isolator. When $\omega$ is too small, it will cause ${\delta }_m$ to increase, which may exceed the allowable displacement of the vibration isolator and cause collision. When $\omega$ is too large, it will make the ΔV change amplitude of the linear spring smaller, where the energy storage effect is weak and the vibration isolation effect is reduced. Therefore, the appropriate parameters of damping and natural frequency are selected after comprehensive consideration.

4. Results and Analysis

The damping of the rubber vibration isolator is not only related to the damping parameters of rubber itself, but is also related to structural damping. The preload of rubber affects the natural frequency of the vibration isolator, and also changes the size of the structural damping. Therefore, after determining the hardness of rubber, the structural damping and natural frequency can be adjusted by changing the axial or radial preload of rubber pads and metal parts.

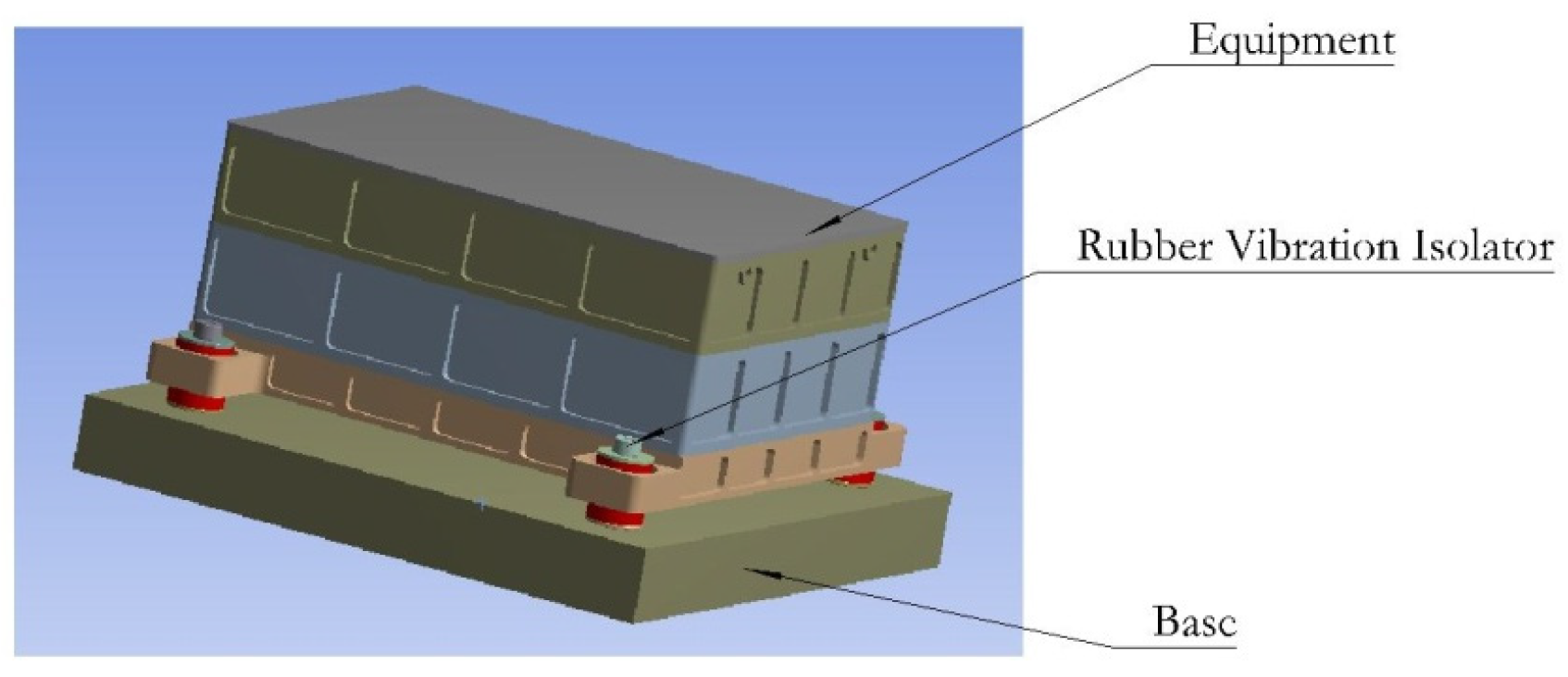
The vibration isolation system consists of a vibration isolator, substrate and equipment, as shown in Figure 2. A rubber vibration isolator is installed at the base of the equipment. The vibration isolator consists of two T-shaped rubber pads, a screw and two gaskets, among which the screw consists of a smooth rod part, a threaded part and a screw head. The natural frequency of the side can be adjusted by changing the diameter of the rod part and the amount of lateral preload when the rubber hardness is unchanged. By changing the length of the rod part and changing the amount of axial preload, the natural frequency of the axial can be adjusted.

According to the control variable method, a series of screws of different specifications are designed and tested on the impact test bench with the same impact response test spectrum, in the range of 100 Hz to 2000 Hz. It consists of a diagonal line with a slope of +12 dB/Oct in the range of 2000 Hz to 4000 Hz, and the acceleration is 2700 g. A control sensor is installed on the substrate and a measurement sensor on the device lug attachment near the vibration isolator, as shown in Figure 3.

The initial diameter of the screw rod is denoted as d₀ and the initial length as l₀. The horizontal impact response value caused by the change in the diameter of the rod is shown in

Table 1. Statistical table of horizontal impact test results.

The Change in Diameter of the Rod	Maximum Horizontal Impact Response	Maximum an Horizontal Impact Response
d0	92 g	71 g
d0 + Δ0.1	225 g	297 g
d0 + Δ0.2	493 g	383 g

, and the vertical impact response value caused by the change in the length of the rod is shown in

Table 2. Statistical table of vertical impact test results.

The Change in the Length of the Rod	Maximum Vertical Impact Response
l0	391 g
l0 + Δ0.1	327 g
l0 + Δ0.2	182 g

.

According to the data in the tables, the larger the diameter of the smooth rod and the higher the preload, the higher the impact response value of the two horizontal directions and the worse the buffering effect. When the diameter increased by 0.2 mm, the impact response value of the horizontal direction increased from 92 g to 493 g, the buffering rate decreased from 96.59% to 81.74%, and the impact response value of the other horizontal direction increased from 71 g to 383 g. The buffer ratio reduced from 97.37% to 85.81%. The longer the length of the smooth rod, the smaller the preload, the smaller the impact response value of the two horizontal directions, and the better the buffering effect. The length increased by 0.2 mm, the vertical impact response value decreased from 391 g to 182 g, and the buffering rate increased from 85.52% to 93.26%.

5. Discussion and Conclusions

In this paper, the basic principle of buffering is studied, the vibration isolator is simplified into a buffering system with viscous damping, and the parameters affecting the maximum acceleration are derived, among which damping and natural frequency have a greater impact on the buffering effect. The influence of rubber preload on structural damping and natural frequency is studied, and a series of impact tests are conducted. The test data show that the diameter of the smooth rod is increased by 0.2 mm. The buffer ratio in one horizontal direction is reduced from 96.59% to 81.74%, and the buffer ratio in the other direction is reduced from 97.37% to 85.81%. When the length is increased by 0.2 mm, the vertical buffer ratio is increased from 85.52% to 93.26%.