Driving Strategy Optimization in Experimental Electric Vehicles: A Study on Optimization Algorithms ^†

Abstract

In this paper, the driving strategy simulations for a single-seat, lightweight, energy-efficient experimental electric vehicle are introduced. The vehicle’s operation is simulated using a developed measurement-based vehicle model in the simulation environment. The optimization was performed for the UniTrack platform at the ZalaZone proving ground using the algorithms Particle Swarm Optimization (PSO) and Genetic Algorithm (GA), with different optimization settings corresponding to varying iterations and initial population/swarm sizes. A 2.95% difference was observed between the least effective and the best PSO results, where both the number of iterations and swarm size were doubled. This demonstrates the effectiveness of PSO in solving the presented driving strategy problem, even when using fewer iterations and a smaller swarm size.

1. Introduction

Energy efficiency is a commonly discussed topic in various fields, including transportation. It has a dual effect by reducing both environmental impacts and costs, making it highly beneficial in transportation. While energy efficiency is important for all vehicles, the reduction of environmental impact is often associated with electric vehicles (EVs) today. The introduction of battery-electric vehicles (BEVs) on the road has contributed to improved air quality and reduced fossil fuel consumption. However, the global environmental impact of BEVs is heavily dependent on the power mix. Utilizing renewable energy sources can significantly reduce emissions during both operation and vehicle production [1]. Transitioning to EVs has a positive long-term impact according to calculations made in [2]. The expansion of electric cars will increase electricity demand, leading to higher carbon emissions, but transport emissions will significantly drop, resulting in a 12% annual reduction in CO₂ levels in the United Kingdom. Energy efficiency can be improved by using lightweight materials in vehicle manufacturing. The lightweighting strategy adopted in the automotive industry is growing due to the basic principles of the circular economy and is believed to effectively reduce the environmental impacts of modern mobility and transportation [3]. Based on these findings, the role of lightweight electric vehicles is important in the future of cleaner transportation. In this paper, a single-seat electric vehicle used for experimental research is investigated, which is built for the Shell Eco-marathon (SEM), the largest energy efficiency challenge in the world (Figure 1), where the goal is to finish the race using the least amount of fuel. Besides vehicle design aspects such as aerodynamics, suspension, powertrain, and power electronics, vehicle operation and the driving strategy applied are key to achieving ultimate energy efficiency. In this study, the same driving strategy optimization problem was solved using the Particle Swarm Optimization (PSO) algorithm and the Genetic Algorithm (GA), and their effectiveness was compared across different optimization settings. The research addresses a gap in the comparison of algorithm performance in the context of electric vehicle driving strategy optimization.

Figure 1. SZEmission, the energy-efficient Urban Concept (UC) vehicle dedicated to the Shell Eco-marathon.

2. Vehicle Modeling and Driving Strategy Optimization

Appropriate vehicle modeling is necessary for determining the driving strategy for eco-driving. Since the energy consumption is calculated following SEM regulations, battery modeling can be neglected, and the vehicle resistance and powertrain are the sole elements to be considered from the vehicle side. A grey-box type model with a measurement basis was presented in [4], which also provided an overview of the fundamentals of applied vehicle modeling. The traction force, cumulative road resistance forces, and slope force from the track are used by the mathematical vehicle model based on longitudinal dynamics to calculate the velocity of the vehicle. The powertrain model is utilized to compute energy consumption.

Similar approaches can be found in the literature, where both GA and PSO algorithms are employed to solve the optimization problems. Optimization was carried out using GA in [5,6] to solve driving strategy problems for SEM-related experimental vehicles. The rule-based strategy was optimized by PSO for a plug-in hybrid (PHEV) electric vehicle in [7]. The driving strategy of a light-duty, high-efficiency fuel cell vehicle was carried out using PSO in [8].

The cost function of optimization is discussed in detail in [9], where the optimization vector is the torque reference value (z) to the corresponding vehicle position on the track. The torque reference is also the input of the vehicle model; this can also be deemed as the throttle position of the vehicle. The formulation of the cost function is described in Equation (1).

$$\mathrm{M}\mathrm{inimize} \mathrm{Energy} \mathrm{Consumption} \mathrm{subject} \mathrm{to}:\left\{ \begin{array}{c}{\mathrm{s}}_{\max }-2\le {\int }_0^{\mathrm{T}}\mathrm{v}\left(\mathrm{t}\right) \mathrm{dt} \le {\mathrm{s}}_{\max }\\ \mathrm{T}\le { \mathrm{T}}_{\max }\\ \mathrm{v}\left(0\right)=0 \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{v}\left(\mathrm{T}\right)\le 8\end{array}\right.$$

(1)

The vehicle needs to complete the track distance (${\mathrm{s}}_{\max }$) within a tolerance of 2 m while keeping vehicle speed ($\mathrm{v}$) below 8 km/h. These soft boundaries prevent penalizing near-completed tries of the optimization. The track distance is segmented into parts according to track length, as described in Equation (2). The interval of 10 m was chosen for practical reasons, defined in Equation (3). The optimization vector, z, needs to be found for the corresponding $\mathrm{s}$ vector within the given upper and lower bounds, as formulated in Equation (4).

$$\mathrm{n}={\displaystyle \frac{{\mathrm{s}}_{\max }}{10}}+1$$

(2)

$$\mathrm{s}=\left({\mathrm{s}}_0,{\mathrm{s}}_1\dots {\mathrm{s}}_{\mathrm{n}-1}\right) {\mathrm{s}}_{\mathrm{i}}=\mathrm{i}\cdot 10 \left(\mathrm{i}=0 \dots \mathrm{n}-1\right)$$

(3)

$$\begin{gathered} \mathrm{z}=\left({\mathrm{z}}_0,{\mathrm{z}}_1,\dots {\mathrm{z}}_{\mathrm{n}-1}\right) \\ 0\le {\mathrm{z}}_{\mathrm{i}}\ge 39.08 \end{gathered}$$

(4)

During the study, the driving strategy for the UniTrack at the ZalaZone proving ground was considered as the racetrack. The track is dedicated to research and development tasks and is suitable for testing energy-efficient vehicle operations. The track is 577 m in length and needs to be completed in under 100 s to simulate SEM conditions.

3. Applied Optimization Algorithms

For this study, two widely used, population-based, iterative search algorithms were tested. The PSO and GA share common traits by using fitness evaluation of the cost function, selection mechanism, and convergence criteria. The essence of GA is based on competition among individuals and beneficial inheritance, following the principle of “survival of the fittest”. Compared to GA, PSO is based on the social behavior of particles in a search space (defined by upper and lower boundaries) and uses a collaborative strategy with a cooperative population, where members of the population work together to optimize performance. PSO involves individuals sharing their best solutions and combining the previous best results of the group to discover new, potentially better solutions [10]. In both cases, built-in MATLAB algorithms were utilized. According to the algorithms, velocity and position updates are carried out for the particles according to Equations (5) and (6), respectively [11].

$$v_i\left(t+1\right)=\mathsf{\omega }\cdot v_i\left(t\right)+c_1\cdot r_1\cdot \left(p_i-x_i\left(t\right)\right)+c_2\cdot r_2\cdot \left(g-x_i\left(t\right)\right)$$

(5)

In the PSO algorithm, $v_i\left(t+1\right)$ represents the new velocity of particle $i$ at time $t+1.$ The term $\omega$ is known as the inertia weight, which controls the influence of the previous velocity on the current one. The current velocity of particle $i$ at time $t$is denoted by $v_i\left(t\right)$. The cognitive and social coefficients are represented by $c_1$ and $c_2$, respectively, indicating the degree of confidence in each particle’s best solution. The random numbers $r_1$ and $r_2$ are generated using the Mersenne Twister generator with seed 0 during optimization. The best personal position of particle $i$ is indicated by $p_i$, while $g$ denotes the global best position of the entire swarm. Finally, $x_i\left(t\right)$ represents the current position of particle $i$ at time $t$ [11,12].

$$x_i\left(t+1\right)=x_i\left(t\right)+v_i\left(t+1\right)$$

(6)

The position update equation indicates that the new position $x_i\left(t+1\right)$ of particle $i$ at time $t+1$ is determined by adding the new velocity, $v_i\left(t+1\right)$, to the current position, $x_i\left(t\right)$. The new velocity $v_i\left(t+1\right)$ is influenced by the previous velocity, the best-known position of its own, and the entire swarm [12]. Based on their attributes, these algorithms are well-suited for solving the driving strategy optimization problem mentioned earlier.

4. Optimization Results

Since the vehicle model is implemented and simulated in the simulation environment, it is practical to utilize built-in optimization algorithms, which were covered earlier, that evaluate the objective function by running the model at each iteration. The objective function for the optimization is the vehicle’s energy consumption over a full lap. The main goal of the optimization process is to minimize this objective function. In our previous works related to driving strategy optimization, GA was exclusively employed, because those studies primarily focused on the modeling and problem definition rather than the optimization solver itself. In this study, we apply the PSO algorithm to the same problem as GA, considering that the collaborative strategy of PSO may help to achieve a better result. During the evaluation, a total of eight optimization attempts were conducted. The generation or iteration limits and the number of initial populations or swarm sizes were varied. In the case of PSO, both the self-adjustment and social-adjustment coefficients were set to 1.49, while for GA, the crossover fraction was set to 0.8 and the mutation rate to 0.01.

The primary objective was to determine the significance of these optimization parameters on the optimization outcomes. In this current optimization problem, 57 optimization variables are defined, so the selected population/swarm sizes are set to ten or twenty times this value. To ensure the optimization runs within a practical time frame, the generation/iteration limits were set to 50 and 100. In Figure 2, the optimization attempts are grouped according to these parameters, showing the iteration process of PSO and GA, respectively.

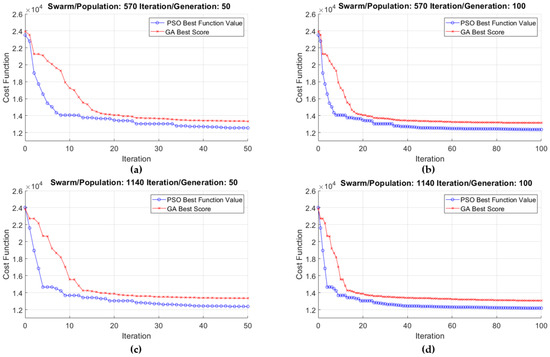
Figure 2. Optimization results, Particle Swarm Optimization (PSO) algorithm marked with blue, Genetic Algorithm (GA) marked with red: (a) Swarm/Population size of 570 with the Iteration/Generation limit of 50; (b) Swarm/Population size of 570 with the Iteration/Generation limit of 100; (c) Swarm/Population size of 1140 with the Iteration/Generation limit of 50; (d) Swarm/Population size of 1140 with the Iteration/Generation limit of 100.

The optimization metrics are collected in Table 1, where all eight attempts are shown with their respective parameter sets. The differences between the attempts and the results of the best attempt (Attempt 8) are also displayed. From the data in Table 1, it is evident that none of the GA optimization attempts achieved a better score than even the least effective PSO attempt.

Table 1. Comparison of optimization attempts.

Metrics	Attempt 1	Attempt 2	Attempt 3	Attempt 4	Attempt 5	Attempt 6	Attempt 7	Attempt 8
Algorithm	GA	GA	GA	GA	PSO	PSO	PSO	PSO
Generation/Iteration	50	50	100	100	50	50	100	100
Population/Swarm	570	1140	570	1140	570	1140	570	1140
Best Score [J]	13,326.60	13,332.32	13,133.88	13,050.42	12,549.60	12,375.29	12,355.95	12,179.32
Difference	8.61%	8.65%	7.27%	6.67%	2.95%	1.58%	1.43%	-

5. Conclusions

In this study, the driving strategy optimization problem was defined for the UniTrack at the ZalaZone proving ground, following Shell Eco-marathon regulations. The optimization utilized a vehicle model relying on measurement-based data to evaluate the cost function, which aimed to minimize the electric energy consumption of the vehicle while completing the track. The main objective was to investigate two different optimization algorithms—Genetic Algorithm (GA) and Particle Swarm Optimization (PSO)—with varying parameter sets to understand the relevance of these parameters to the optimization results. A total of eight optimization attempts were made with different sizes of generation/iteration and population/swarm. The results demonstrate the effectiveness of PSO compared to GA in all attempts. It was found that it is sufficient for the size of the initial populations or swarms to be ten times the number of variables in both GA and PSO cases. It is noteworthy that, despite the best result requiring four times more calculation time, the difference between the least effective and best PSO results is only 2.95%, primarily due to the favorable weight coefficients. The speed profiles of the attempts, showcasing the best and least effective results, are presented in Figure 3. There is an 8.61% difference in energy consumption between these attempts with the same simulation model. To improve efficiency and decrease running times, it could be interesting to explore more specialized PSO algorithm versions in future research.

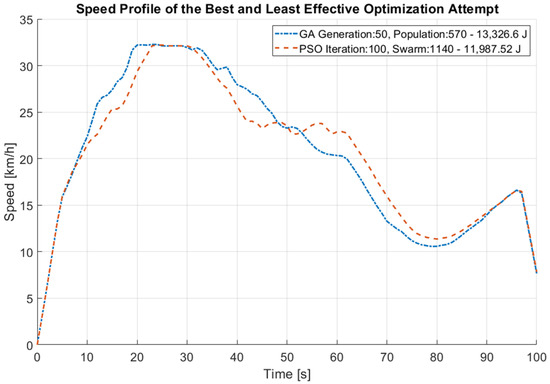
Figure 3. Speed profile of the best and least effective optimization attempt; Attempt 1—13.326.6 J; Attempt 8—12.179.32 J energy consumption.