TwinOptPRO—Digital Platform for Online Pump Scheduling Optimization ^†

Abstract

Climate change is leading to a general shortage of raw water availability combined with more pronounced seasonality and dry phases. The goal of the collaborative research project TwinOptPRO is to contribute to EU-wide climate neutrality in 2050 by the minimization of energy supply for water treatment and pumps in drinking water distribution systems. For that purpose, a digital platform that combines different forecasting models with simulation and optimization modules was developed. The aim is to ensure secure and compliant supply to customers in the future while maximizing the use of renewable energy and minimizing costs.

1. Introduction

Climate change poses enormous challenges for drinking water utilities in Germany and around the world. For example, there is generally less raw water available, and seasonal fluctuations and dry periods are more pronounced. In addition, the goal of climate neutrality defined in the Paris Agreement [1] requires drastic energy savings in all sectors. To prepare the water supply for these challenges, the participants in the TwinOptPRO joint collaborative research project, which is funded by the German Ministry for Education and Research BMBF, are developing a digital platform that companies can use to optimize their drinking water treatment and storage tank management. The platform combines various forecasting models with simulation and optimization modules.

The basic idea, to decouple the water production and transport from the consumption over time by utilizing the storage volume of the reservoirs, is not new. However, besides the uncertainties of the demand, the availability of spring water is also considered by hydrological modeling. Another challenge for efficient pump scheduling is the commonly highly fluctuating spot market prices for electricity that are mostly driven by the availability of renewable energy. For an unknown water demand, data-driven forecasting models are trained using historical data from the control system. One of the most important challenges is the development of a state machine that integrates the different models and data from numerous sources into one central platform and allows the automatized communication between the components.

The objective of the optimization module is to determine a timetable for the next 24 h for which the energy costs are minimized. The decision variables are the individual pump speeds and control valve settings. The optimization is restricted by numerous constraints. As a top priority, the reliability of supply at any time and any place with qualitatively perfect drinking water must be secured. Therefore, the minimum (min.) and maximum (max.) water levels in the tanks must be complied with. In the case of the pilot system of the project, hard groundwater is mixed with soft spring water. The resulting hardness of the water must comply with a given target hardness.

For a solution, the problem is formulated as a mathematical bi-level optimization problem. The decision variables of the upper level are the lumped pump flows delivered by the different pumping stations. The objective function contains the electricity cost, and the constraints include the min. and max. tank water levels and the continuity equation expressed by the tank differential equations. The lower levels of the optimization refer to the pumping stations and deliver the combinations of pumps or, respectively, pump speeds for which the pumps can deliver the desired flow of the upper level with minimum electrical energy consumption.

In the first part of this paper, the main idea and theoretical background are presented. In the second part, the application to a real-world urban water distribution system is demonstrated.

2. Materials and Methods

2.1. System Description

In the project, two use cases are considered: a medium sized urban water supply system and the parts of a regional water supply system. This paper refers only to the former. The drinking water network supplies roughly 30,000 inhabitants and an extensive commercial area. The water supplied to the customers consists of mixed water from two groundwater wells as well as spring water from an adjacent mountain range. The groundwater is pumped into two storage tanks in which it is mixed with the spring water. One important constraint is to maintain a constant water hardness of 8.5 °dH (about 1.52 mmol/L CaCO₃). Therefore, the groundwater must be softened using membrane technology before it is mixed with spring water. The mixing ratio is determined by the availability of spring water and the target water hardness. In recent years, the volatility of the spring water discharge has increased while the total amount of available spring water has been constantly decreasing. For the optimization, the availability is estimated by prognosis models for the short term (24 h) as well as long term (years); the mixing conditions must be considered as additional constraints, which presents a particular challenge compared to conventional procedures.

2.2. Digital Platform and Dashboards

The data platform is employed for both demand forecasting and operational optimization. In both cases, multiple process steps (e.g., data preprocessing, calculation, and storage) are necessary, resulting in the creation of data processing pipelines. Since various services communicate with each other and low latency is required, the center of the data platform consists of the streaming database Kafka. Within the streaming platform, data are exchanged asynchronously through a publisher–subscriber model, making it considerably faster compared to a traditional database. To present results to operators, user centric dashboards were developed. For example, demand forecasts for specific zones for the next 24 h, including the uncertainty, are visualized for operators and updated every hour.

2.3. Hydrological Model for Forecasting Short-Term and Long-Term Spring Water Availability

The springs utilized for water supply are sourced from a catchment area of 2.5 km², resulting in rapid responses to rainfall. To achieve forecast lead times exceeding 24 h, a combination of the ICON-EU weather forecast model and a hydrological model is employed. The hydrological transfer function is modeled using two competing approaches: the SuperflexPY framework [2] and an artificial intelligence strategy. A major constraint is the effect of the conveyance infrastructure, which limits flow to 60 m³/h, consequently restricting analysis to only the lower segments of the hydrograph for accurate fitting.

2.4. Water Demand Forecasting Models

The water demand is forecasted with state-of-the-art DeepAR models [3], a specific artificial neural network architecture based on the popular long short-term memory network (LSTM) [4]. DeepAR provides probabilistic results and can incorporate both numerical and categorical data. In this project, we calculate 24h demand forecasts in a sequence-to-sequence mode, based on hourly data and with an optimized number of input time steps for each local model. The input data are past demand data, weather data, derived weather features, and datetime/calendar features (weekday, day of year, etc.). For more details, please refer to our submission to this year’s Battle of Water Demand Forecasting (BWDF) at the WDSA/CCWI Joint Conference 2024, in which we demonstrate and explain the approach in more detail and provide code in an associated repository.

2.5. Pump Scheduling Optimization and Digital Twin

The mathematical model of the pump scheduling problem is formulated as a bi-level optimization problem. The objective function of the upper level is the pumping cost; the decision variables are the pumping flows. As constraints, the water level in the storage tanks and the mixing ratio between groundwater and spring water must be considered. The lower level includes the minimization of the required electrical power for the transport of the given flow defined by the upper level. The decision variables of the pumping station optimization depend on the type of pumps. For variable speed pumps, the optimal combination of pump speeds is calculated; for simple pumps, the combination of pump states, on/off, is utilized. Further, combinations are possible in which only one pump has a frequency controller and the other pumps run on a fixed pump curve. The dependence of the frictional head loss along the transport pipes is taken into account by hydraulic models. In terms of computational costs, it has been shown to be advantageous not to use the hydraulic model directly but to use it to train a neural network offline and use it as a surrogate model in the online case. For an online application, the optimization model is connected to the central platform and its Kafka database. From there, the demand prognosis of the different supply zones, the current state of the system, and the cost of electricity for the next 24 h are available.

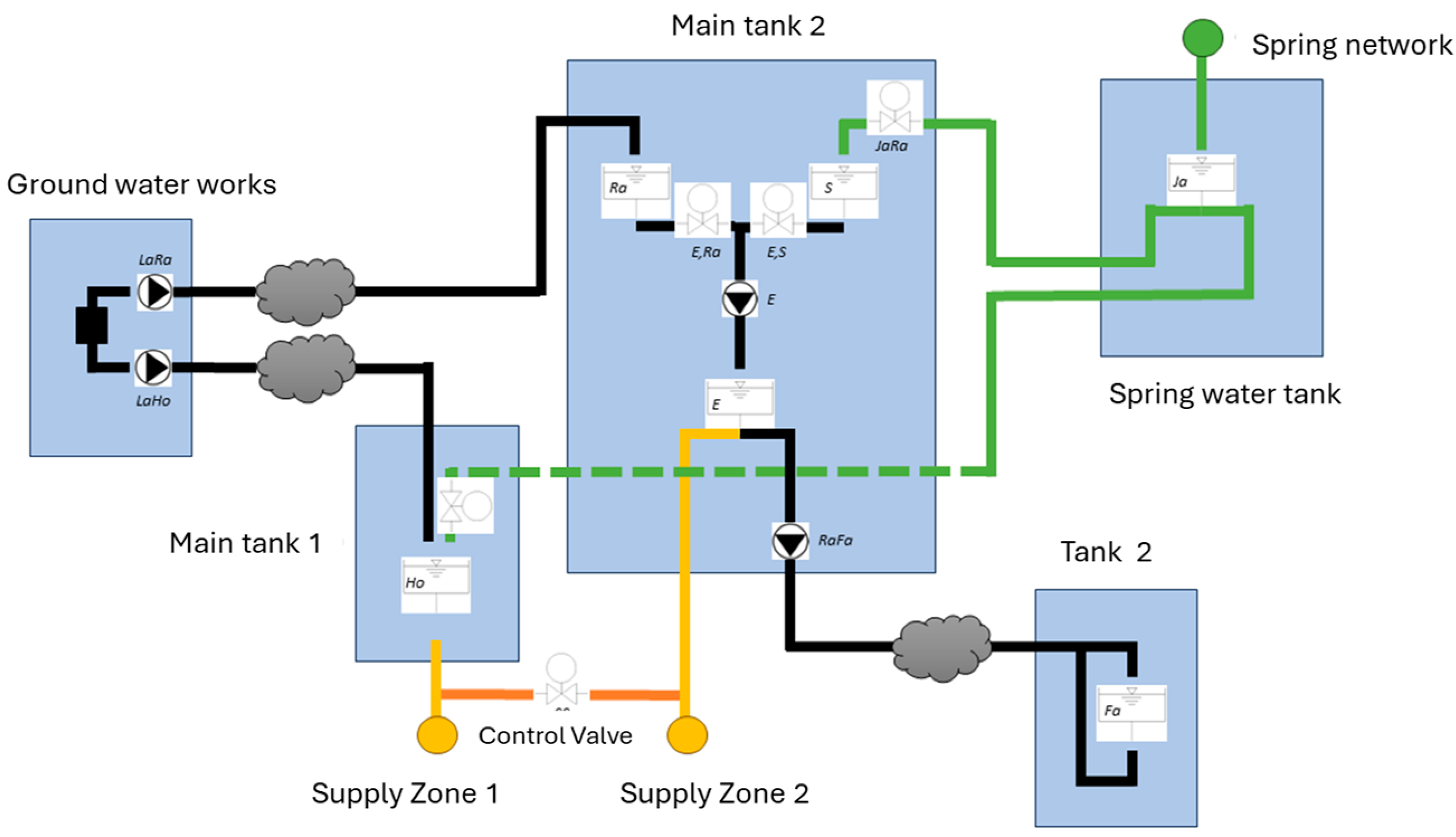
A simplified view of the optimization model consisting of the two boundary nodes, i.e., groundwater works (left) and spring water input node (right); two main storage tanks where the water is mixed; three pumping stations; and the two main demand zones is shown in Figure 1. The cloud symbols indicate the parts of the hydraulic model that were replaced by neural networks.

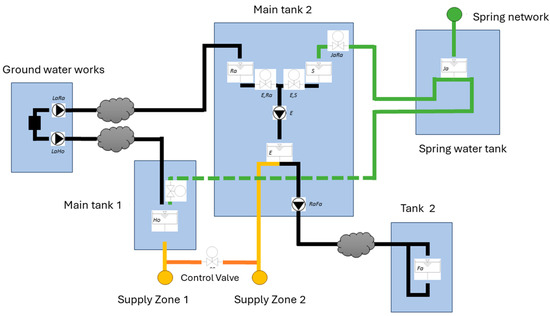
Figure 1. Simplified schematic view of the optimization model.

In the online application, the results of the optimizer are transferred via the platform to a digital twin of the complete water distribution system for validation of the optimization results by means of a 24 h look-ahead extended period simulation.

3. Results

The project is not yet finished. However, the first test calculations show possible cost savings of around 20% (30%, if no mixing constraints are considered).

4. Discussion and Conclusions

Digitalization offers a wide range of improvements in the management of drinking water networks. In this research project, it was specifically shown that digital data in combination with mathematical models and algorithms enable cost savings, greenhouse gas reductions, and the stabilization of the electrical grid. The project has also shown that the integration of multiple software components and stakeholders is still a challenge.