Imaging Incoherent Target Using Hadamard Basis Patterns ^†

Abstract

In this paper, we present a correlation-based imaging technique in a single-pixel imaging scheme using Hadamard basis illumination. The Hadamard basis, which has the characteristics of a two-bit value {−1, 1} and sparsity in its transformed domain, has been used in the illumination patterns and successfully utilized for imaging the incoherent target. It gives image reconstruction even in low-light conditions. Such deterministic patterns also help to solve the problem of large numbers of measurements in single-pixel imaging, and hence simplify the experimental implementation. Furthermore, to compare the quality of imaging with Hadamard basis patterns, we also compare imaging with Fourier basis patterns and simulation results of both methods, namely Hadamard and Fourier basis, are presented.

1. Introduction

The correlation-based imaging technique is an unconventional approach where an object is reconstructed as the distribution of correlations of the light field to image the desired target [1]. Single-pixel imaging, part of the unconventional techniques, is a novel imaging scheme where an object can be imaged by a single-pixel detector without having any spatial resolution. Pixelated detectors are mostly expensive and not capable of detecting signals on the spectrum, such as x-ray and infrared. Moreover, a low-cost imaging system can be designed with a single-pixel detector that can operate at other wavelength regions, even in low-light conditions, and techniques such as ghost imaging, and non-line of sight (NLOS) imaging have greatly benefited from single-pixel detection [2].

Ghost imaging (GI) provides object information from correlation-based measurements between two light beams. One light beam that interacts with the object to be imaged is collected by a bucket detector having no spatial resolution. Another beam is collected with a spatially resolved detector, such as a charged coupled device (CCD), which samples the light that has never interacted with the object by an array of pixels. The GI was first demonstrated using the correlation of quantum entangled photons generated by spontaneous parametric downconversion. It was later demonstrated that GI can be performed with a classical incoherent (pseudothermal) light source in the same way as quantum entangled photons. Computational ghost imaging is very similar to single-pixel imaging, where an object is illuminated with digitally structured light patterns, and corresponding to each light pattern, the single-pixel detector records light signals [3]. The illumination light patterns are projected onto the object by a spatial light modulator (SLM) or digital micro-mirror device (DMD). The light patterns can be random or can be deterministic illumination patterns that can reduce the measurement number and acquisition time in a single-pixel imaging scheme. The Hadamard patterns are such patterns; they are made of orthogonal basis vectors. The Hadamard matrix has the characteristics of a 2-bit binary value {−1, 1} and sparsity in its transformed domain. In Hadamard single-pixel imaging (HSI), Hadamard matrices form illumination patterns to reconstruct the image of an object [4]. Fourier single-pixel imaging (FSI) is also another robust imaging technique based on a deterministic model that uses Fourier basis patterns [5].

In this work, we present a single-pixel correlation imaging technique using Hadamard illumination to image an incoherent target object. Such deterministic illuminations help in reducing the number of measurements and acquisition time. Object retrieval in the FSI with the four phase shifts requires 4 × M × M number of measurements, which can be reduced to the 2 × M × M number of measurements for the imaging with the Hadamard pattern by a differential measurement approach. M × M is the size of the image that has to be reconstructed. Hadamard basis patterns are binary (black and white), which makes HSI naturally suitable for single-pixel imaging systems. HSI is more noise-robust compared to FSI [2]. In order to qualitatively compare imaging with Hadamard and the Fourier basis patterns, we present simulation results for both cases. This reconstruction highlights that the Hadamard illumination patterns can be an alternative to FSI depending on the nature of requirements.

2. Theory

In the HSI scheme, the Hadamard transform (H{ }) of an object A(x, y) is expressed as [6]

$$H\left\{A\left(x,y\right)\right\}={\sum }_{x=0}^{L-1}{\sum }_{y=0}^{L-1}A(x,y){(-1)}^{w(x,y,u,v)}$$

(1)

where x,y are coordinates in spatial domain and u,v are coordinates in Hadamard domain. L is the order of the Hadamard matrix and L is number of rows and columns of the image.

$$w(x,y,u,v)={\sum }_{i=0}^{n-1}{[g}_i\left(u\right)x_i+g_i\left(v\right)y_i]$$

(2)

$$\begin{gathered} g_0\left(u\right)=u_{n-1} \\ {g}_1\left(u\right)=u_{n-1}+u_{n-2} \\ {g}_2\left(u\right)=u_{n-2}+u_{n-3} \\ ..... \\ {g}_{n-1}\left(u\right)=u_1+u_o \end{gathered}$$

(3)

where n = log₂N and u_i, v_i, x_i, y_i are the binary representations of u, v, x, and y, respectively.

Hadamard basis pattern P_H(x, y) is presented as follows

$$P_H\left(x,y\right)=\frac{1}{2}[1+H^{-1}\left\{{\delta }_H\left(u,v\right)\right\}]$$

(4)

$${\delta }_H\left(u,v\right)=\left\{\begin{array}{c}1,if u=u_0 and v=v_0\\ 0,otherwise\end{array}\right.$$

where $H^{-1}$ represents inverse Hadamard transform and ${\delta }_H\left(u,v\right)$ is the delta function.

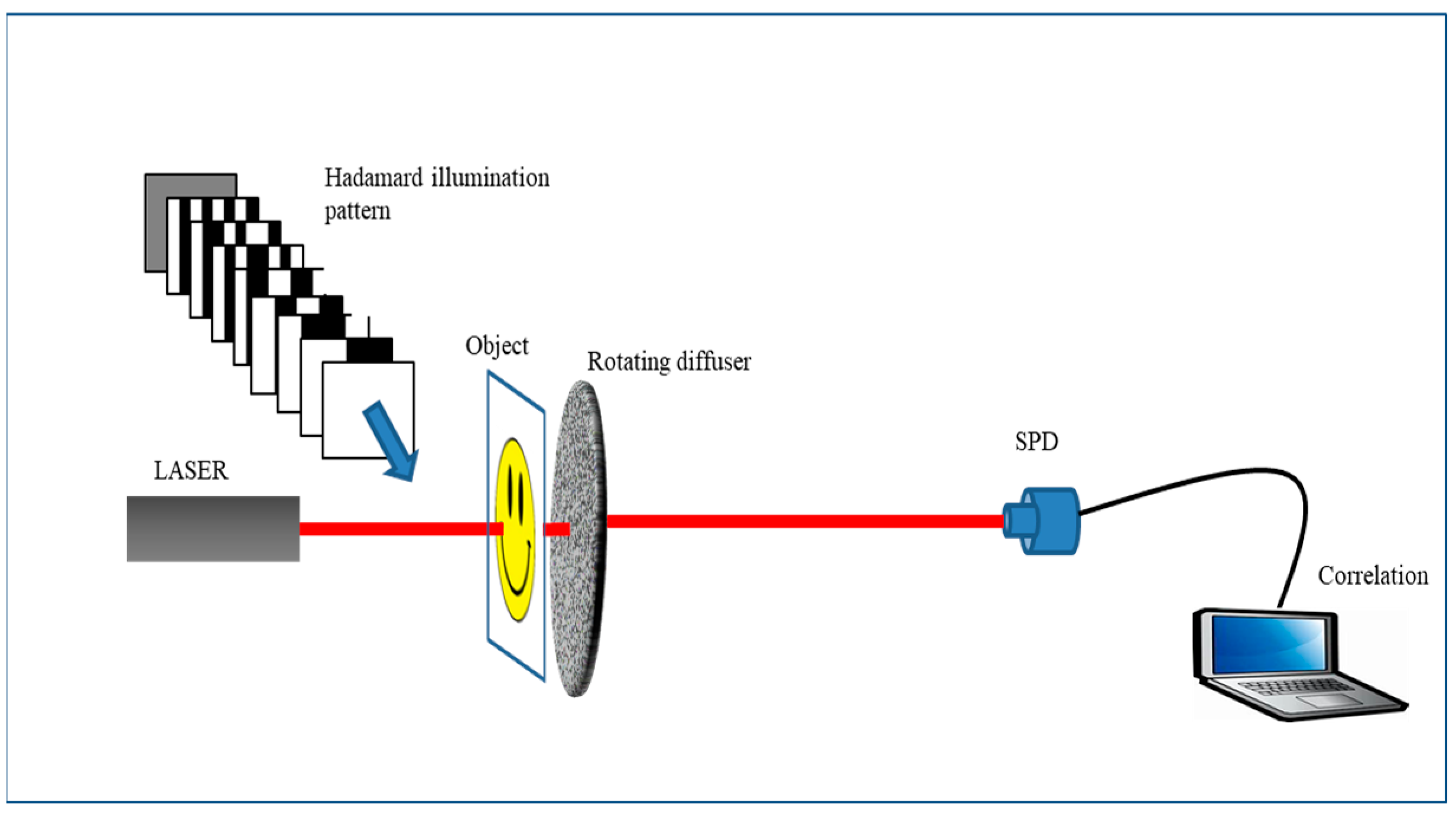
In order to consider the imaging of an incoherent target, we consider an object obscured by a rotating diffuser, as shown in Figure 1. The incoherent target is realized by a sequence of a random scatterer, which corresponds to each step of the rotating diffuser. A step of the diffuser is considered to introduce an independent and a uniformly distributed phase on the interval (−π,π). An object is illuminated by the Hadamard patterns $P_H\left(x,y\right)$, and a single-pixel detector (SPD) measures the responses corresponding to each pattern. Similarly, inverse Hadamard patterns, i.e., $1-P_H\left(x,y\right)$, are also projected in sequence onto the object, and the same process is followed to record the responses at the SPD. $D_{+}$ and $D_{-}$ are the SPD responses corresponding to the patterns $P_H\left(x,y\right)$ and $1-P_H\left(x,y\right)$. Then, the Hadamard coefficient is derived from the two responses, i.e., $D_{+}$ and $D_{-}$, by this differential measurement formula.

$$H\left(u,v\right)=D_{+}-D_{-}$$

(5)

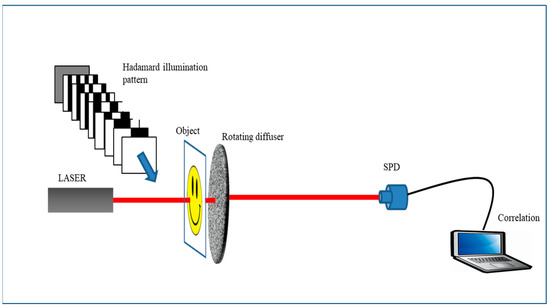
Figure 1. Schematic diagram of Hadamard single-pixel imaging of incoherent target object.

The object is reconstructed by taking the inverse Hadamard transformation of $H\left(u,v\right)$. A schematic diagram of the Hadamard illumination with the SPD is shown in Figure 1, where an object is placed behind a rotating diffuser. Hadamard patterns and inverse Hadamard patterns illuminate the object, as shown in Figure 1. SPD collects signals corresponding to each pattern. After correlation of these patterns, objects are reconstructed.

3. Results and Discussion

We have shown here image reconstruction for an incoherent object “1” using both HSI and FSI in Figure 2. Simulation results using MATLAB are presented below. To image the incoherent target of size 256 × 256, 2 × 256 × 256, the number of Hadamard patterns, including Hadamard patterns ($P_H\left(x,y\right)$) and inverse Hadamard patterns (${1-P}_H\left(x,y\right)$), are projected onto the object. Hadamard patterns are formed according to equation number four. Similarly, Fourier-structured light is projected onto the object of size 256 × 256. To reconstruct the object, a total 4 × 256 × 256 number of Fourier patterns is needed to illuminate the object to apply four phase shifts in the FSI scheme.

Figure 2. Reconstruction of an incoherent object using (a) HSI (b) FSI.

4. Conclusions

In summary, a correlation-based single-pixel imaging technique using Hadamard illumination is presented. The Hadamard patterns are formed with an orthogonal basis vector consisting of two binary values, +1 and −1. Such a deterministic pattern improves the single-pixel imaging scheme by solving the problem of having a large number of measurements. We have successfully used Hadamard basis illumination to image an incoherent target hidden behind the diffuser. A differential measurement of Hadamard coefficient reduces noise, and it is easier than phase shifting in the case of the Fourier basis pattern. Furthermore, to compare reconstruction qualities, we have also shown simulation results using the Fourier basis pattern.