Hydrodynamic and Thermal Energy Characteristics of a Gravitational Water Vortex ^†

Abstract

In the present study, a numerical analysis has been conducted to investigate the hydrodynamic and thermal energy transfer capacity of a vortex formed under the effect of gravity. For this purpose, the study uses a gravitational water vortex heat exchanger (GWVHE), which includes baffles around a cylindrical basin in which a water vortex is formed under the effect of gravity. The results have been examined for different inlet boundary conditions based on flow and temperature to determine the strength of vortex formation and comparative energy transfer rate for both fluid domains. A strong vortex is formed in the basin at a height to diameter ratio between 0.41 and 0.54 with a minimum inlet mass flow rate of 0.005 kg/s, which effectively increases the energy exchange potential due to the centrifugal effect. The reasonable energy agreement has been obtained for the minimum flow rates of both fluid domains; however, the thermal energy losses are increased with the increase in the inlet mass rate of the hot domain, due to the reduction in the time of contact. The existence of an acceptable energy balance and strong vortex formation at a minimum flow rate sparks the need for a new configuration to enhance the thermal performance of GWVHE.

1. Introduction

Heat exchangers (HEs) are the devices that are used in the heat transfer process without physically mixing the fluid streams. The classification of HEs is usually based on the flow arrangement or the design configuration. Parallel flow, counter flow, and cross flow HEs are the examples of flow arrangement-based HEs, whereas compact types, shell and tube HEs are classified according to their design configuration [1]. The direction of two fluid streams and the structural configuration of HEs are very important features when improving the heat exchange process. Active and passive approaches are used to reduce the thermal losses, as well as to improve the heat transfer performance in various thermal systems [2].

Another important flow configuration in HEs is a vortex flow. The fluid circulates around a central axis in a vortex flow, forming either a forced vortex or a free vortex. The free vortex is generated naturally, whereas the forced vortex is formed because of solid body rotation. The free vortex can be artificially created if a viscous fluid flows through a hole at the bottom of a tank under the force of gravity [3,4]. The present study at first determines the strength of a strong vortex under the effect of gravity called a gravitational vortex and then investigates its thermal energy exchange capacity using a GWVHE [5]. A new design of GVHE with baffles on the outer side of the cylinder and a height to diameter ratio of 0.54 has been employed to numerically investigate the energy balance by varying the inlet conditions.

2. Mathematical Modeling and Governing Equation

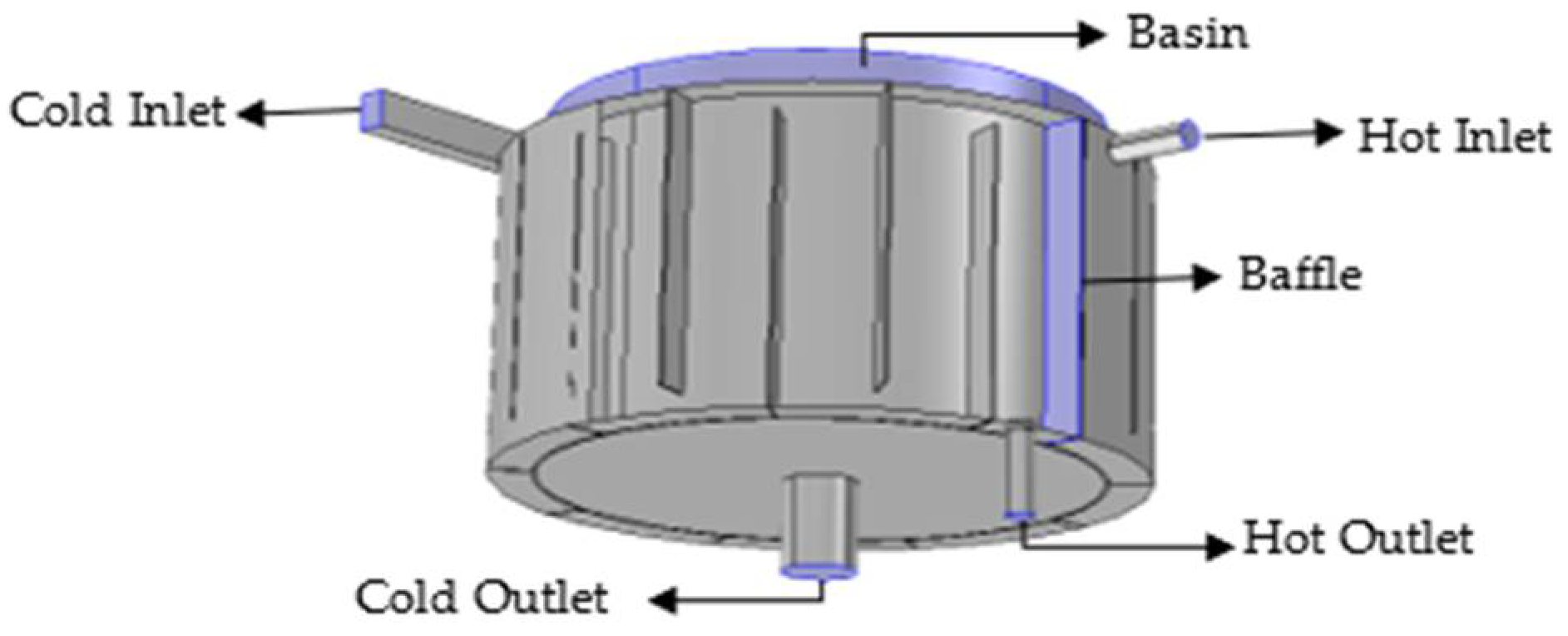
The 3D computational model of GWVHE used in the present study is shown in Figure 1. The height and diameter of the basin are 380 mm and 700 mm, respectively. There are two fluid domains separated by a solid domain. In both fluid domains, the fluid is water. The outer cylinder with baffles contains hot water, while the central basin cylinder has cold water. The solid domain is assumed to be made of steel. To effectively induce the gravitational effect, the top interface of the basin cylinder remains open to the atmosphere. Steady state heat transfer analysis of the GWVHE is performed using COMSOL-Multiphysics (V 6.0) and a user control mesh is applied on each domain to discretize the geometric model.

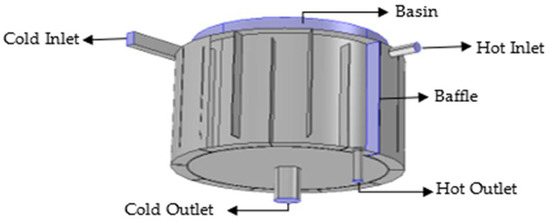
Figure 1. The 3D computational model of GWVHE.

2.1. Fluid Flow Modeling

A high Reynolds number fluid is required for the vortex formation and this is why a turbulent flow is considered in both domains. For the investigation of fluid characteristics, the turbulent k-ε model is applied on both fluid domains, along with conservation equations related to mass and momentum. The governing equations for the turbulent k-ε model are given as follows [2]:

$$\nabla ·\left[\left(\mu +\frac{{\mu }_T}{{\sigma }_k}\right)\nabla k\right]+{\rho }_l{\mu }_l·\nabla k=\frac{1}{2}{\mu }_T{\left(\nabla {\mu }_l+{\left(\nabla {\mu }_l\right)}^T\right)}^2-{\rho }_l\epsilon +S_k$$

(1)

$$\nabla ·\left[\left(\mu +\frac{{\mu }_T}{{\sigma }_{\epsilon }}\right)\nabla \epsilon \right]+{\rho }_l{\mu }_l·\nabla \epsilon =\frac{1}{2}{C}_{\epsilon 1}\frac{\epsilon }{k}{\mu }_T{\left(\nabla {\mu }_l+{\left(\nabla {\mu }_l\right)}^T\right)}^2-{\rho }_l{C}_{\epsilon 2}\frac{{\epsilon }^2}{k}+\frac{\epsilon }{k}{C}_{\epsilon }{S}_k$$

(2)

The values for the constants are taken as σ_k = 1.0, σ_ɛ = 1.3, C_ɛ1 = 1.44, C_ɛ2 = 1.92 and C_μ = 0.09.

2.2. Heat Transfer Modeling

The energy equations for fluid and solid domains are given as the following equations, respectively [2].

$$\rho C_{pf}\left(V_r\frac{\partial T_f}{\partial r}+\frac{V_{\theta }}{r}\frac{\partial T_f}{\partial \theta }+V_z\frac{\partial T_f}{\partial z}\right)=k_f\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T_f}{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^2{T}_f}{\partial {\theta }^2}+\frac{{\partial }^2{T}_f}{\partial z^2}\right)$$

(3)

$$k_s\left(\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T_s}{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^2{T}_s}{\partial {\theta }^2}+\frac{{\partial }^2{T}_s}{\partial z^2}\right)=0$$

(4)

where T_f, K_f, and C_pf denote the temperature, thermal conductivity, and specific heat, respectively.

3. Results and Discussion

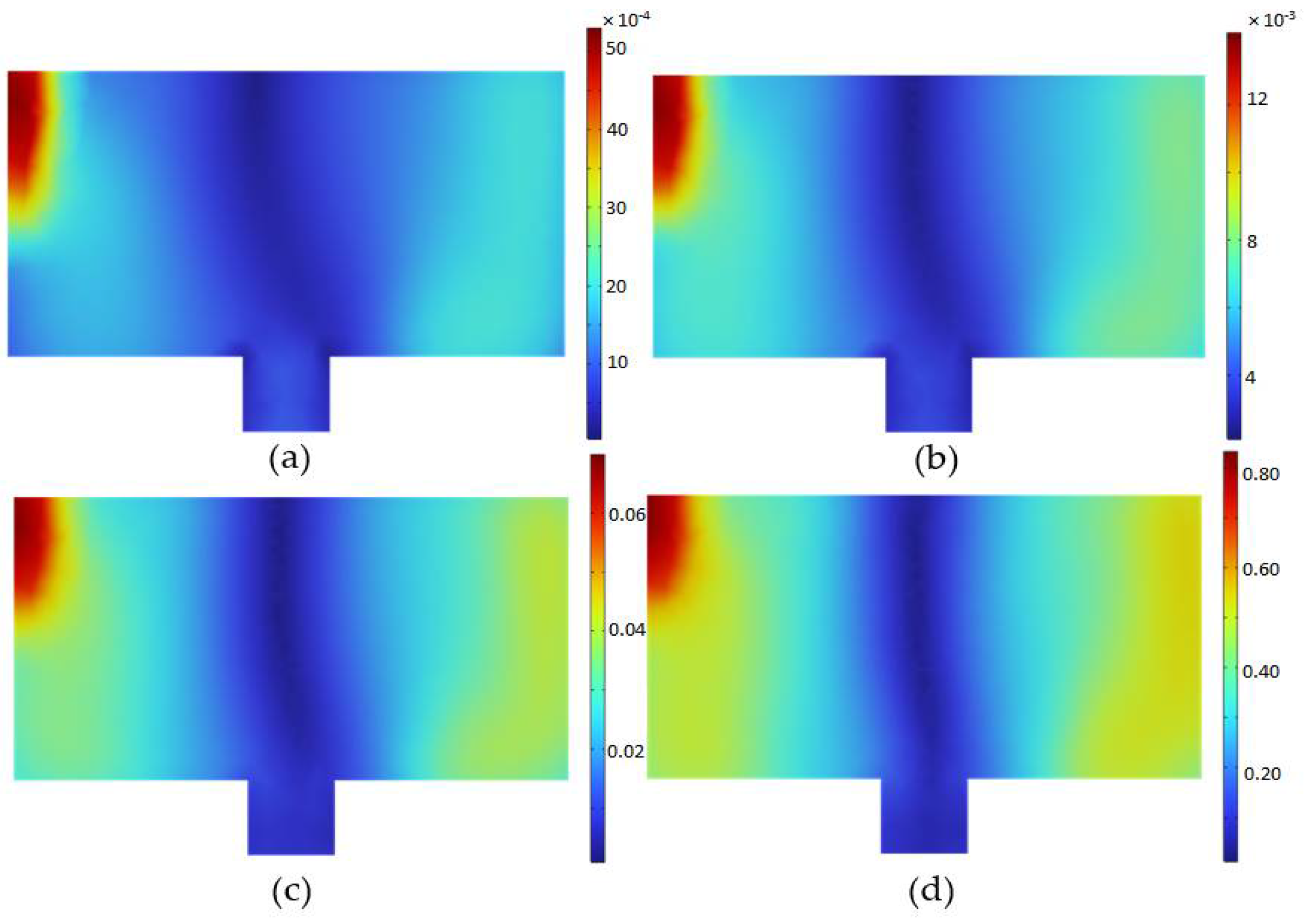
Figure 2a–d show the velocity distributions in the form of contours that make the air core at the mid-section from top to bottom, indicating the formation of a strong vortex. The strong vortex formation in the basin is achieved at all inlet mass flow rates of the cold domain from 0.005 to 0.5 kg/s and also the ratio of height to diameter is calculated, ranging from 0.41 to 0.54 for the strong vortex formation. The strength of the gravitational vortex enhances the heat transfer effect due to the centrifugal phenomena.

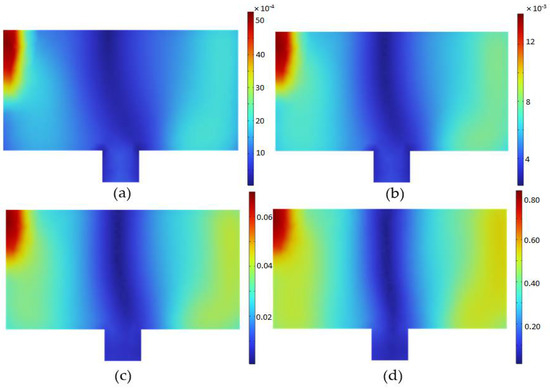
Figure 2. Formation of velocity vortex air core in the center of basin at ${\stackrel{·}{m}}_{\mathrm{h}}$ = 2.29 kg/s, (a) ${\stackrel{·}{m}}_{\mathrm{c}}$ = 0.005 kg/s, (b) ${\stackrel{·}{m}}_{\mathrm{c}}$ = 0.01 kg/s, (c) ${\stackrel{·}{m}}_{\mathrm{c}}$ = 0.05 kg/s, (d) ${\stackrel{·}{m}}_{\mathrm{c}}$ = 0.5 kg/s.

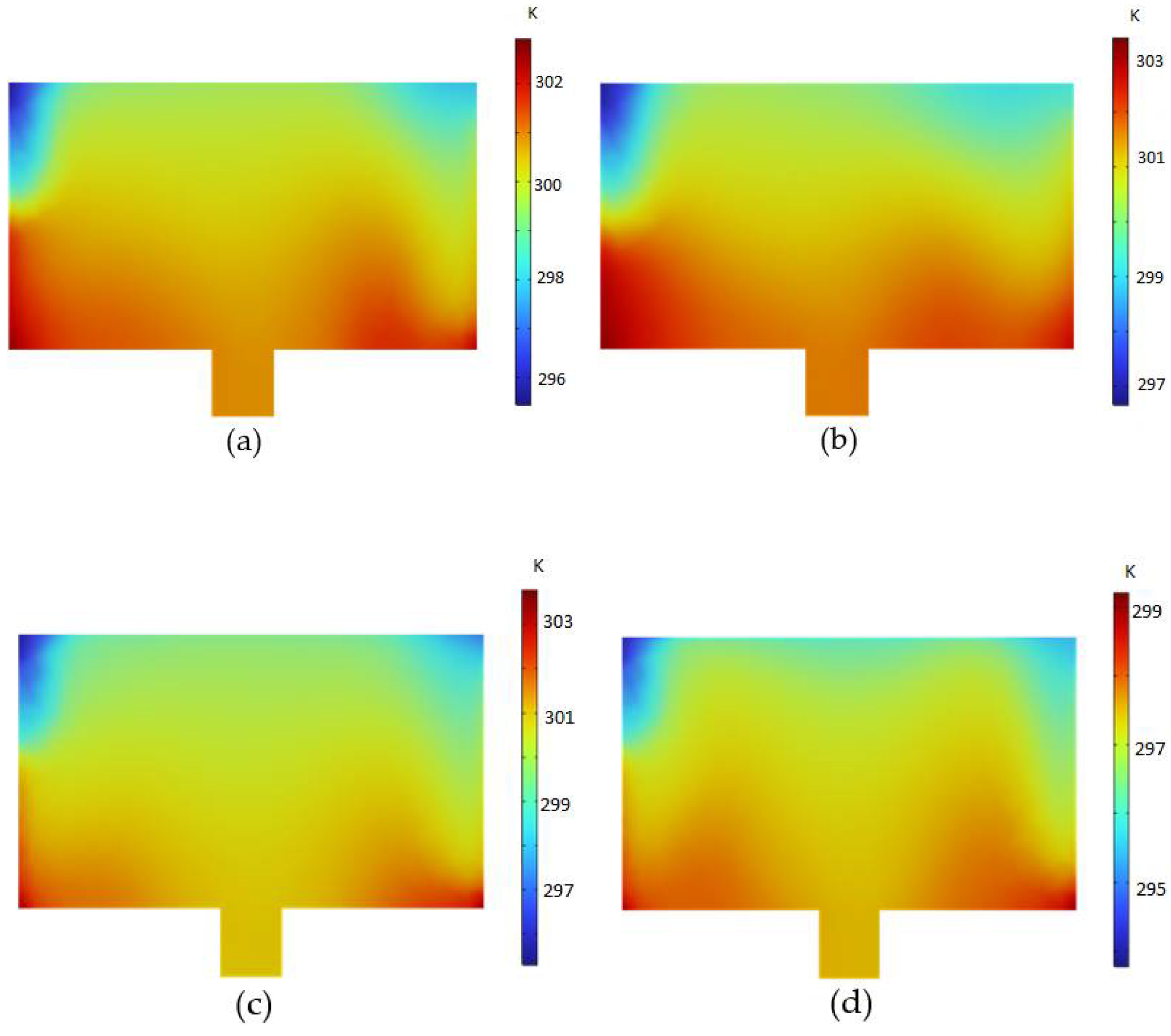
Figure 3a–d show the temperature distributions of the cold fluid domain at constant inlet mass flow of the hot domain, which represent the temperature gradient at the mid-section of the basin. It is observed from the simulation analysis that the highest temperature gradient is obtained at the lowest inlet mass flow rate of 0.005 kg/s. This shows that the time of contact between both fluids is very important to exchange energy.

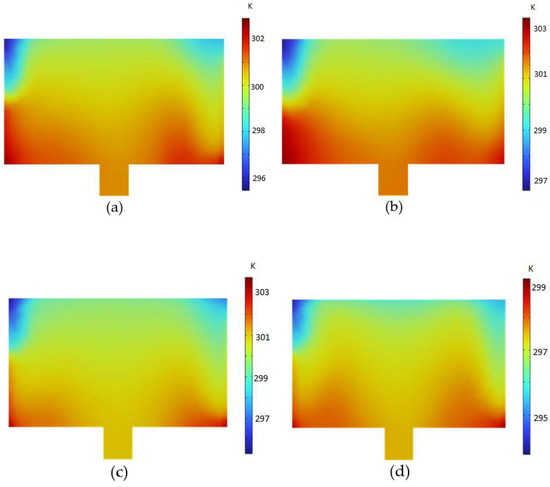
Figure 3. Temperature gradient in the center of basin at ${\stackrel{·}{m}}_{\mathrm{h}}$ = 2.29 kg/s, (a) ${\stackrel{·}{m}}_{\mathrm{c}}$ = 0.005 kg/s, (b) ${\stackrel{·}{m}}_{\mathrm{c}}$ = 0.01 kg/s, (c) ${\stackrel{·}{m}}_{\mathrm{c}}$ = 0.05 kg/s, (d) ${\stackrel{·}{m}}_{\mathrm{c}}$ = 0.5 kg/s.

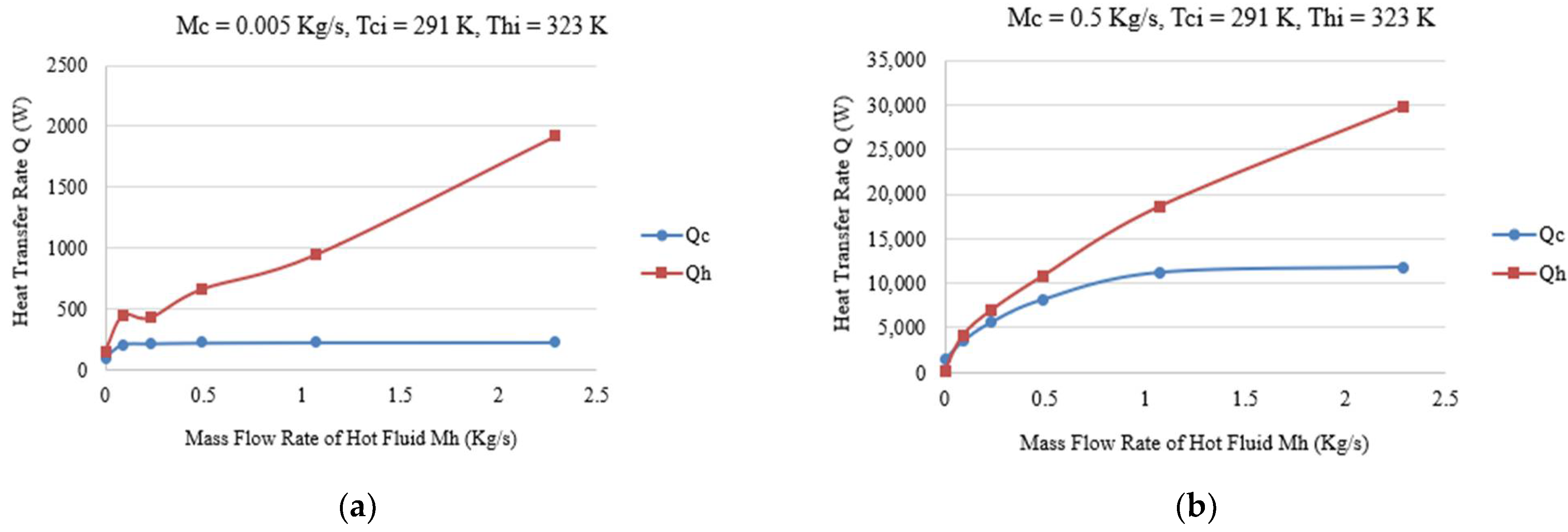
Figure 4a,b show the energy balance comparison of both fluid streams with (0.005 kg/s to 0.5 kg/s) the inlet mass flow rate of the cold domain. However, the inlet mass flow of the hot domain varies from 0.002 kg/s to 2.29 kg/s. It can be observed that at the smaller flow rates of both domains, the thermal losses are less but as the hot side inlet mass flow rate increases, the energy losses to the environment are increased.

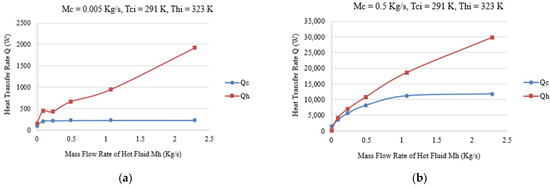
Figure 4. Energy balance comparision with different mass flow rates.

Therefore, the hot inlet mass flow rate is critical to investigate the rate of heat transfer. For the energy balance calculation, the general relationship for heat transfer rate is used for both domains.

4. Conclusions

In the present study, a simulation analysis has been performed for the investigation of GWVHE with vortex flow-based configuration. Different flow and temperature conditions are analyzed, and the computational results reveal that the purposeful configuration can be used to enhance the thermal performance of GWVHE, due to strong vortex formation at the minimum mass flow rate.