Confinement Specific Design of SOI Rib Waveguides with Submicron Dimensions and Single-Mode Operation ^†

Abstract

The full-vectorial finite difference method with perfectly matched layer boundaries is used to identify the single-mode operation region of submicron rib waveguides fabricated using silicon-on-insulator material system. Achieving high-mode power confinement factors is emphasized while maintaining the single-mode operation. As opposed to the case of large cross-section rib waveguides, theoretical single-mode conditions have been demonstrated to hold for sub-micron waveguides with accuracy approaching 100%. Both the deeply and the shallowly etched rib waveguides are considered and the single-mode condition for the entire sub-micrometer range is presented while adhering to design specific-mode confinement requirements.

1. Introduction

The first step in designing many of the photonic devices incorporating waveguides is to design a waveguiding structure that supports the fundamental mode only, i.e., the waveguide should be a single-mode one [1,2,3,4]. For the desired performance, in addition to the single-mode requirement, most of the devices require the power confined by the waveguide to have a benchmark value [5]. For large dimensions (height and width of the order of 5 µm) in the SOI rib waveguides, the single-mode condition (SMC) is analytically shown to hold [6], as follows:

$$\frac{W}{H}\le \alpha +\frac{r}{\sqrt{1-r^2}};$$

(1)

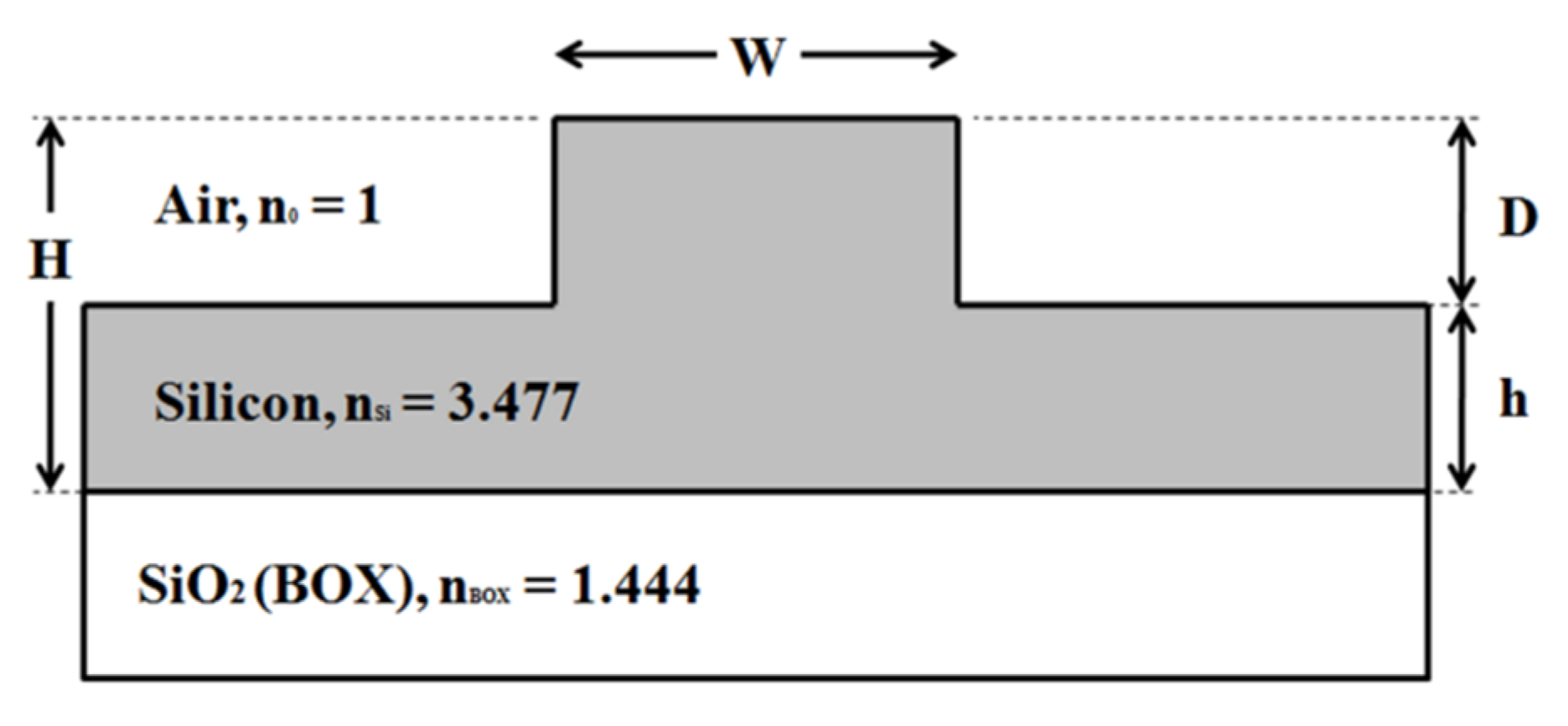
where W, H, and r are the rib width, height, and slab height to rib height ratio (r = h/H), respectively, as shown in Figure 1.

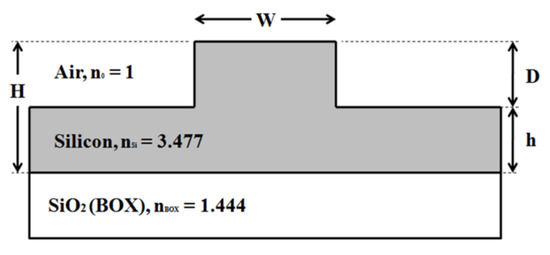
Figure 1. A typical rib waveguide structure (n₀, n_Si and n_BOX are real refractive indices of corresponding layers).

Various works [7,8] supported the same relationship as of (1) with α = 0.3, with the exception of Pogossian [9] who reported the same value of α to be zero. This change is very significant, suggesting at least 30% variation between the two formulae. Apart from several other studies on the design of a large single mode, the work of Lousteau et al. [10], based on rigorous finite-difference (FD) and beam propagation methods (BPM), suggested that no equation or dimensional conditions can be suggested for the design of large single-mode rib waveguides. These results meant that it was impossible to know the dimensional range of a larger rib waveguide beforehand, either analytically or intuitively, where it would support only the fundamental mode, thereby rendering device optimization impossible. However, with the ever-pursued quest of reducing the dimensional features of photonic devices for better utilization of wafer real estate, waveguide devices with a cross-sectional size below a micrometer were demonstrated. This opens up a new arena of waveguide devices working in the subwavelength regime. This work demonstrates that it is possible to give a couple of conditions which, if fulfilled, guarantees the single-mode operation of submicron waveguides confining an acceptable amount of mode power.

2. Methodology

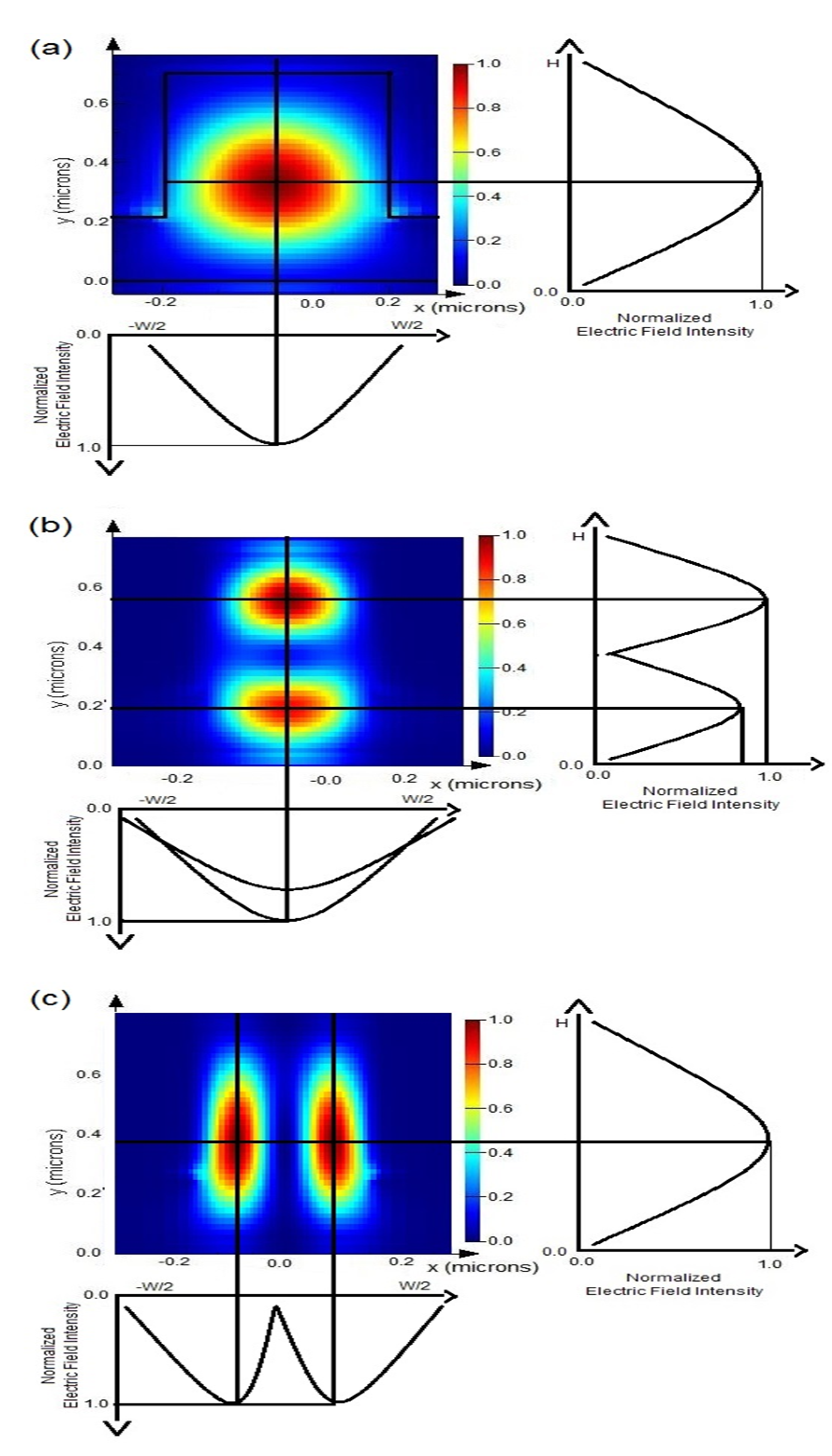
An industry standard simulation tool based on the finite-difference frequency domain method employing perfectly matched layers (PMLs) was used to calculate the complex propagation constant of the waveguide structures under study. Using an advanced scripting environment of the simulation tool, a routine was developed which analyzes the optical mode profile supported by the sub-micrometer-sized rib structure, as shown in Figure 1. The analysis was carried out at the center of the rib in both vertical and horizontal directions, as shown in Figure 2. A single-mode waveguide would only support the fundamental mode profile for either a TE mode or a TM mode or both, depending on the exact waveguide dimensions. Apart from separating single-mode and multi-mode (MM) dimensions, the routine also stored the fraction of power confined under the rib and the nature of the mode (quasi-TE or quasi-TM) for each of the single-mode waveguides. The dimensions were chosen in this way so as to cover every possible combination in which a practical sub-micrometer waveguide could be fabricated. The simulation window size was optimized so that the results converge and the memory and computational requirements remain under acceptable limits. For all waveguide structures, the wavelength of the operation was 1550 nm.

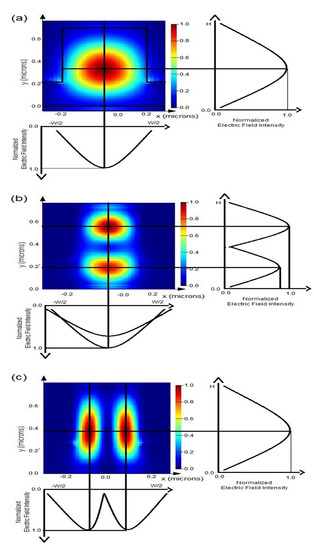
Figure 2. Mode field profile under the rib and its respective intensity variation with respect to the vertical (right hand side to the mode profile) and horizontal (below the mode profile) directions through the mode peaks: (a) fundamental mode (b) first-order vertical mode; (c) first-order horizontal mode. A single-mode waveguide would only support the fundamental mode profile. Reprinted by permission from American Scientific Publishers: J. Nanoelectron. Optoelectron. [5], Copyright 2017.

3. Results and Discussion

The results obtained in this work are compared with other works [11,12] to validate the procedure conducted to obtain the results. The general agreement in the results validate the procedure used in this work [5].

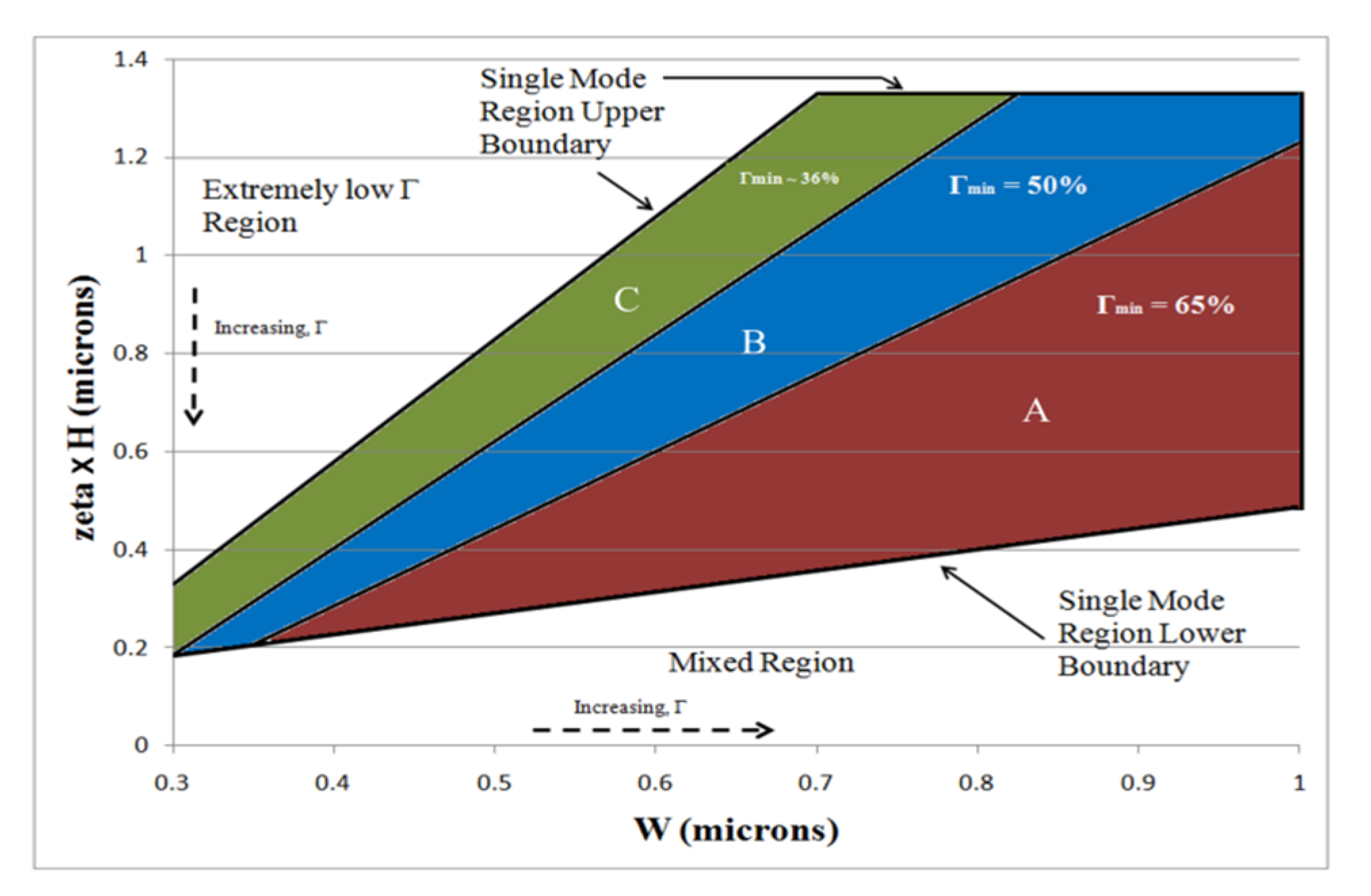
The main result of analysis is presented in Figure 3. All the submicron dimensions supporting only the single-mode are plotted with a unique set of axes (ζH vs. ‘W’). Other works [6,7,9] have used a standard set of axes (W/H vs. h/H) to express their results which is thought to give a boundary between the single-mode and multi-mode waveguide operations. This approach, however, did not include any account of the optical mode confinement factor and, moreover, was later shown to be invalid for large rib waveguides [10]. In this work, the parameter ζ is defined as

$$\mathsf{\zeta }=\frac{r}{\sqrt{1-r^2}},$$

(2)

where ‘r’ is the normalized rib height (h/H). The shaded portions in Figure 3 (marked as ‘A’, ‘B’, and ‘C’) represent the single-mode regions with a particular level of minimum optical mode confinement factor (Γ_min).

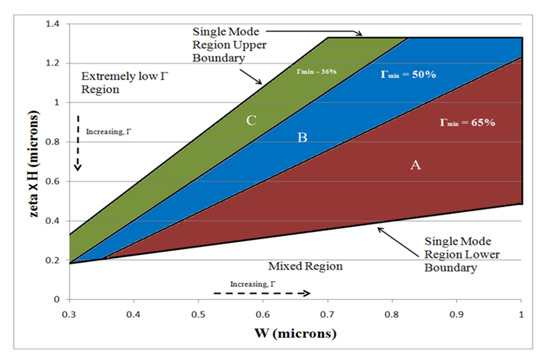
Figure 3. Plot of ζH vs. waveguide width where the shaded areas contain 100% single modes, with respective confinement factors. The broken arrows show the directions in which Γ increases. Reprinted by permission from American Scientific Publishers: J. Nanoelectron. Optoelectron. [5], Copyright 2017.

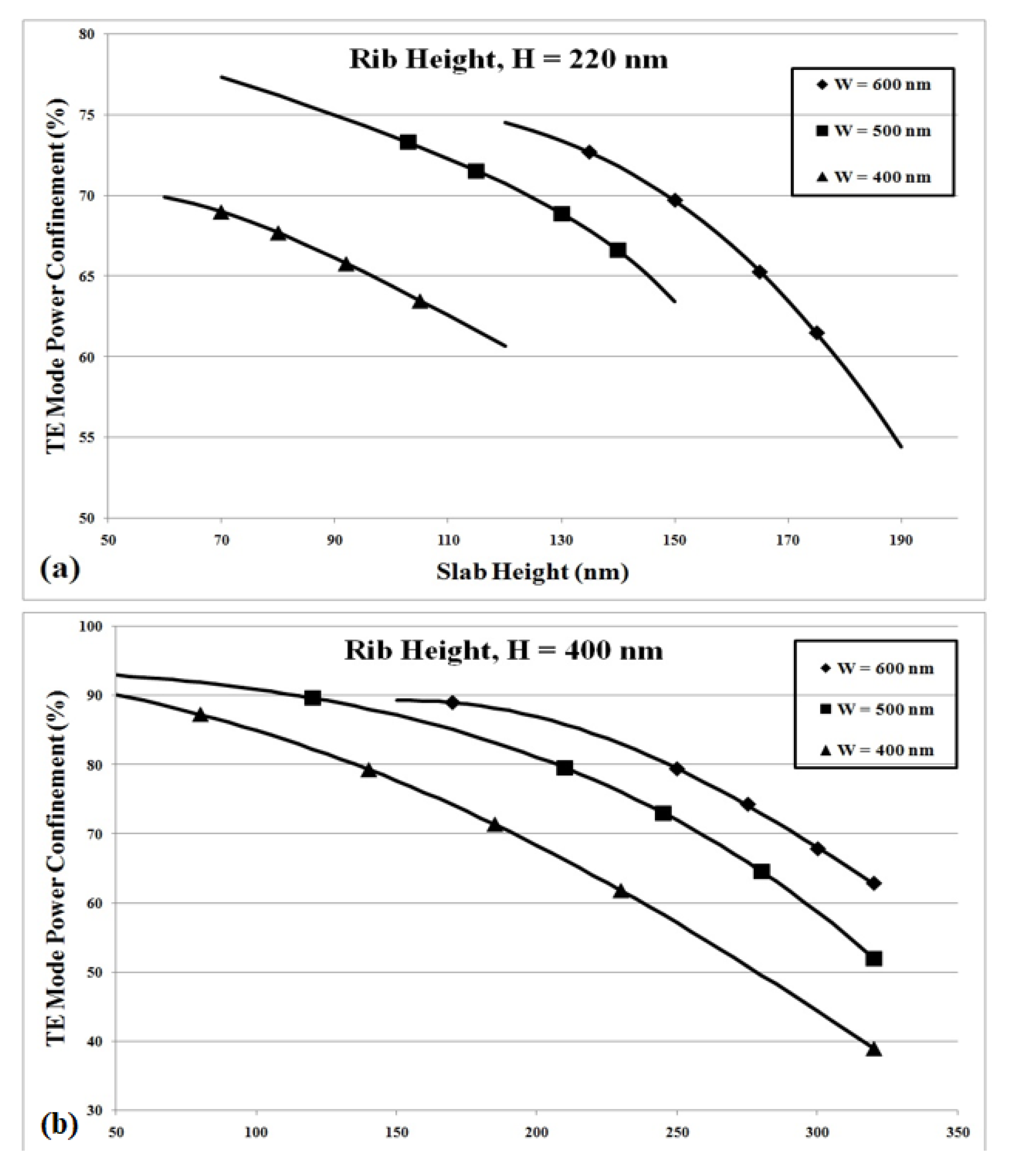
Any point in a particular region of Figure 3 represents a design which confines at least the percentage (given by Γ_min) of the total power propagated in the mode volume. It is clear from the figure that as rib width increases and the slab height (h) decreases (manifests by the decreasing values of ζH product), the confinement factor would increase. This is true as an increasing etch depth (i.e., decreasing ‘h’) “squeezes” the lower portion of the fundamental mode into the rib region by providing an interface to reflect the lower edges of the rib. For this to happen, the rib width should be appropriately large; otherwise, the mode would start to leak out of the silicon region. For a fix slab height, the confinement factor also increases significantly with increasing widths and heights of the rib. Figure 4a shows the transverse electric (TE) mode confinement factor of the most commonly used rib height of 220 nm, while Figure 4b shows the same for 400 nm against the slab height. Here, the rib width is used as a parameter. It is evident from the figures that the slab height affects the mode confinement more drastically when the rib height is smaller; hence, the stringent process control is required for the fabrication of smaller devices. Secondly, the maximum amount of mode power confined by a particular structure is inversely proportional to the rib height. At the same time, to increase the device integration density and the operation speeds of active photonic devices, smaller dimensions are required [5]. Figure 4 shows that achieving this is possible if a waveguide is designed with the careful selection of the rib width and slab height.

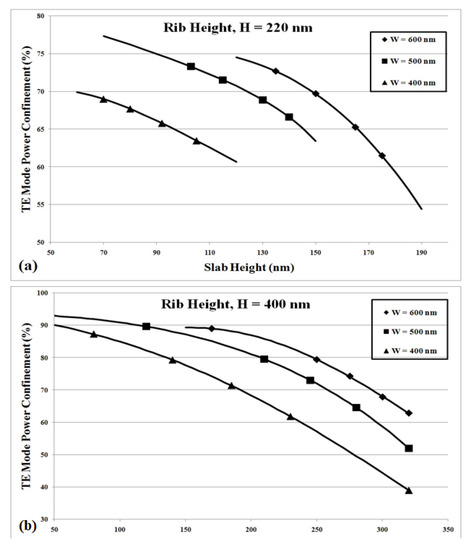
Figure 4. TE-mode confinement factor versus slab height for various rib widths: (a) H = 220 nm and (b) H = 400 nm.

Due to its widespread use, the TE confinement factor relationship with slab height is provided as H = 220 nm for different rib widths in Table 1.

Table 1. Relationships of TE confinement factor with respect to waveguide dimensions for the curves shown in Figure 4.

H = 220 nm
W = 600 nm	${\Gamma }_{TE}=\frac{67.8-0.257h}{1-5.521\times {10}^{-3}+11.03\times {10}^{-6}{h}^2}$
W = 500 nm	${\Gamma }_{TE}=\frac{85.04-0.472h}{1-4.258\times {10}^{-3}-6.08\times {10}^{-6}{h}^2}$
W = 400 nm	${\Gamma }_{TE}=\frac{55.42+1.09h}{1+6.988\times {10}^{-3}+84.62\times {10}^{-6}{h}^2}$
H = 400 nm
W = 600 nm	${\Gamma }_{TE}=\frac{74.82-0.1h}{1-3.269\times {10}^{-3}+7.10\times {10}^{-6}{h}^2}$
W = 500 nm	${\Gamma }_{TE}=\frac{93.76-0.22h}{1-2.287\times {10}^{-3}+1.74\times {10}^{-6}{h}^2}$
W = 400 nm	${\Gamma }_{TE}=\frac{93.53-0.202h}{1-1.621\times {10}^{-3}+2.58\times {10}^{-6}{h}^2}$

4. Conclusions

The analysis and design of submicron rib waveguides, keeping an account for the mode confinement factor, is carried out in this work. Confinement trends have also been provided in mathematical form for the most commonly used rib height, enabling confinement estimates and the optimization of devices requiring single-mode operation with high confinement factors.