Joint User Scheduling and Beamforming Design in Simultaneously Transmitting and Reflecting Reconfigurable-Intelligent-Surface-Assisted Device-to-Device Communications ^†

Abstract

Future wireless networks require efficient device-to-device (D2D) communication to meet the demands of increasing connectivity; however, practical challenges such as limited coverage and severe interference persist. This paper addresses these issues by employing simultaneously transmitting and reflecting reconfigurable intelligent surfaces (STAR-RISs) equipped with low-resolution phase shifters, thereby enabling full-space coverage while conforming to hardware constraints. To further improve system performance, we propose an irregular STAR-RIS configuration, in which only a subset of elements is activated to enhance spatial diversity without increasing power consumption. Additionally, we introduce a group scheduling strategy that assigns users to different time slots, effectively mitigating interference and improving the overall sum rate. To solve the resulting high-dimensional and non-convex optimization problem, we develop a cross-entropy optimization framework that jointly optimizes element selection, amplitude and phase configurations, and user scheduling. Simulation results demonstrate that the proposed design significantly outperforms existing benchmarks in terms of both the sum rate and scalability, thus providing a practical and efficient solution for STAR-RIS-assisted D2D communication systems.

1. Introduction

Device-to-device (D2D) communication is regarded as a promising technology for future wireless networks; yet, it faces significant challenges such as a limited transmission range, signal blockage, and interference. Reconfigurable intelligent surfaces (RISs) have emerged as a potential solution by dynamically controlling signal reflections to enhance coverage and communication quality [1]. However, conventional RIS-assisted D2D systems typically assume an impractically high phase-shifter resolution and often fail to provide full-space coverage.

To address these limitations, we propose a novel D2D communication system that utilizes simultaneous transmitting and reflecting RISs (STAR-RISs) [2,3], equipped with cost-effective, low-resolution phase shifters. Moreover, we introduce an irregular STAR-RIS configuration, where only a subset of RIS elements is selectively activated, thereby enhancing spatial diversity and system performance [4]. To further suppress multi-user interference and enhance spectral efficiency, we incorporate a scheduling-based user grouping strategy.

To jointly optimize the key design variables—including element selection, transmission and reflection amplitudes, discrete phase shifts, and user grouping—we develop a unified cross-entropy optimization (CEO) framework [5]. Simulation results show that the CEO-based approach significantly outperforms conventional benchmarks in terms of sum rate. The integration of scheduling-based user grouping provides further improvements, especially in high-user-density scenarios, while the adoption of irregular STAR-RIS configurations delivers additional gains.

2. System Model and Problem Formulation

2.1. System Model

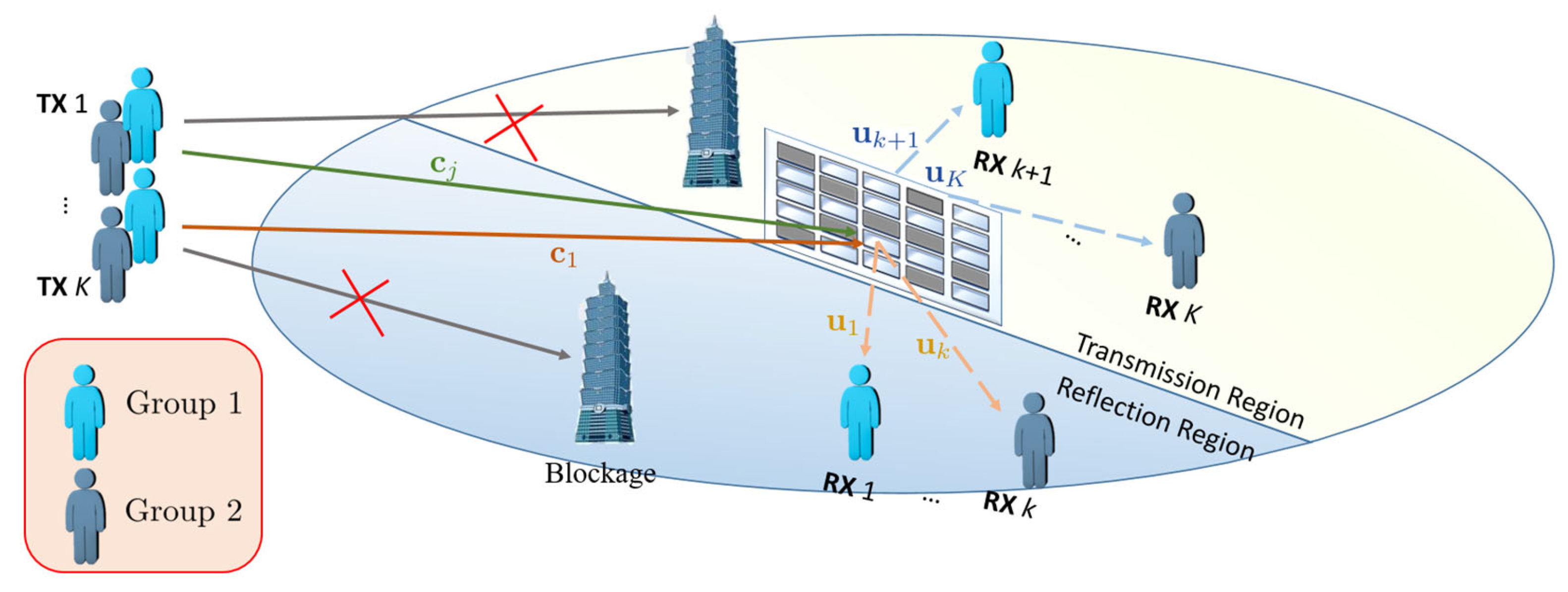
As illustrated in Figure 1, we examine a network consisting of $K$ single-antenna D2D transmitter–receiver pairs that simultaneously operate over a shared frequency band. To support this communication, a STAR-RIS with $N$ elements is deployed, implementing coupled and discrete phase shifts. Each element of the STAR-RIS is characterized by a complex transmission coefficient $t_n{e}^{\mathrm{j}{\vartheta }_n}$ and a reflection coefficient $r_n{e}^{\mathrm{j}{\theta }_n}$, where the amplitude terms $t_n, r_n\in \left[0,1\right]$, and the phase shifts ${\vartheta }_n$ and ${\theta }_n$ belong to a discrete set ${\mathbb{F}}_{\lambda }=\{\alpha | \alpha =1,2,\dots ,2^{\lambda }\}$. Here, $\lambda$ represents the phase resolution, and the phase quantization step is defined as $\mathsf{\Delta }=2\pi /2^{\lambda }$.

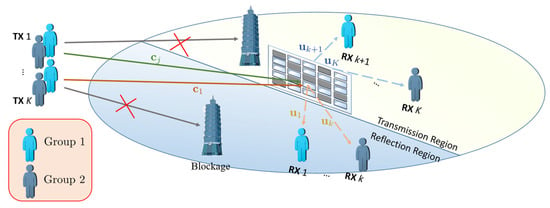
Figure 1. A D2D communication system assisted by a scheduling STAR-RIS supports K simultaneously operating D2D transmitter–receiver pairs with single antennae, utilizing the same frequency band.

The operation of the STAR-RIS is subject to two key constraints. First, energy conservation requires that the total energy of the transmitted and reflected signals at each element equals the incident signal energy, leading to the constraint $t_n^2+r_n^2=1, \forall n\in \left\{1,\dots ,N\right\}$. Second, due to the passive and lossless nature of the STAR-RIS elements, a coupled phase-shift constraint must be satisfied, ensuring that the phase difference between transmission and reflection satisfies $\left|{\vartheta }_n-{\theta }_n\right|\in \left\{\pi /2,-\pi /2\right\}, \forall n$. Consequently, the transmission and reflection coefficient vectors of the STAR-RIS are expressed as $v_t={\left\{t_n{e}^{\mathrm{j}{\vartheta }_n}\right\}}_{n=1}^N$ and $v_r={\left\{r_n{e}^{\mathrm{j}{\theta }_n}\right\}}_{n=1}^N$, respectively.

The channel between the $j$-th transmitter and the STAR RIS is denoted as $c_j\in {ℂ}^{N\times 1}$, while the channel from the STAR-RIS to the $k$-th receiver is represented as $u_k\in {ℂ}^{N\times 1}.$ Since receivers may be positioned on either the transmission or reflection side of the STAR-RIS, we define two sets: ${\mathbb{U}}_r$ for receivers on the reflection side, and ${\mathbb{U}}_t$ for those on the transmission side. Assuming the direct links between transmitters and receivers are blocked, the effective channel from the $j$-th transmitter to the $k$-th receiver is given as follows:

$$h_{k,j}\triangleq \{\begin{array}{c}{u}_k^{\mathsf{{\rm T}}}\mathrm{diag}\left(v_t\right)c_j=a_{k,j}^{\mathsf{{\rm T}}}{v}_t, \mathrm{if} k\in {\mathbb{U}}_t, \\ u_k^{\mathsf{{\rm T}}}\mathrm{diag}\left(v_r\right)c_j=a_{k,j}^{\mathsf{{\rm T}}}{v}_t, \mathrm{if} k\in {\mathbb{U}}_r,\end{array}$$

(1)

where $a_{\mathit{k},\mathit{j}}=\mathrm{diag}\left(c_j\right)u_k$.

As the number of users increases while the number of STAR-RIS elements remains fixed, the system’s degrees of freedom become insufficient, leading to rising interference. To address this issue, we introduce user scheduling and grouping to enhance system flexibility. Specifically, a time-division multiple access (TDMA) scheme is adopted, where $K$ users are divided into $G$ groups. Assuming the scheduling time for the $G$ groups is divided into $T_1,T_2,\dots , T_G$, each time slot $T_g$ corresponds to the communication of users in group $g$. Under this framework, the received signal $y_k$ of the k-th user is expressed as follows:

$$y_k=h_{k,k}{x}_k+{\displaystyle \sum }_{j\ne k}^K{h}_{k,j}{x}_j+{\eta }_k$$

(2)

where $x_k\in ℂ$ is the transmitted symbol for receiver k with an average power of $\mathbb{E}\left[{\left|x_k\right|}^2\right]={\rho }_k$, and ${\mathsf{\eta }}_k~\mathcal{C}\mathcal{N}\left(0,{\sigma }^2\right)$ represents additive white Gaussian noise. The user index set of group $g$ is defined as follows:

$${\mathbb{G}}_g=\left\{k | z_{gk}=1, \forall k\in \left\{1,2,\dots ,K\right\}\right\}$$

(3)

The matrix $Z\in {\left\{0,1\right\}}^{\mathit{K}\times \mathit{G}}$ represents the user grouping status, where each element $z_{gk}$ indicates whether user $k$ belongs to group $g$:

$$z_{gk}=\{\begin{array}{c}1, \mathrm{if} \mathrm{user} k \mathrm{belongs} \mathrm{to} \mathrm{group} g,\\ 0, \mathrm{otherwise}. \end{array}$$

(4)

To ensure each user is assigned to only one group, $Z$ must satisfy the following:

$${\displaystyle \sum }_{g=1}^G{z}_{gk}=1, k\in \left\{1,2,\dots ,K\right\}.$$

(5)

Recent advances in irregular RIS technology have demonstrated their potential to enhance system performance and energy efficiency. By selectively activating only a subset of RIS elements, this approach provides additional spatial diversity and more degrees of freedom for passive beamforming without increasing power consumption. Accordingly, the effective channel gain is updated as follows:

$$h_{k,j}\triangleq \{\begin{array}{c}{u}_k^{\mathsf{{\rm T}}}\mathrm{diag}\left(v_t\circ s\right)c_j=a_{k,j}^{\mathsf{{\rm T}}}\left(v_t\circ s\right), \mathrm{if} k\in {\mathbb{U}}_t \\ u_k^{\mathsf{{\rm T}}}\mathrm{diag}\left(v_r\circ s\right)c_j=a_{k,j}^{\mathsf{{\rm T}}}\left(v_r\circ s\right), \mathrm{if} k\in {\mathbb{U}}_r\end{array}$$

(6)

Here, $s={\left[s_1, \dots ,s_N\right]}^{\mathsf{{\rm T}}}$ is a binary selection vector, where $s_n{s}_n=1$ indicates that the $n$-th STAR-RIS element is active, while $s_n{s}_n=0$ signifies deactivation. Consequently, the sum-rate expression is formulated as follows:

$$f\left(v_t, v_r,{\rm Z},s\right)={\displaystyle \sum }_{g=1}^G{\displaystyle \sum }_{k=1}^K\left\{k\in {\mathbb{G}}_g\right\}{\log }_2\left(1+{\displaystyle \frac{{\left|h_{k,k}\right|}^2{\rho }_k}{{{\displaystyle \sum }}_{j=1, j\ne k,j\in {\mathbb{G}}_g}^K{\left|h_{k,j}\right|}^2{\rho }_j+{\sigma }_k^2}}\right)$$

(7)

2.2. Problem Formulation

The objective of this work is to maximize the sum rate by jointly optimizing the STAR-RIS coefficients. The optimization problem can be formulated as follows:

$$\underset{v_t, v_r,{\rm Z},s}{\mathrm{maximize}} f\left(v_t, v_r,{\rm Z},s\right)$$

(8a)

$$\mathrm{subject} \mathrm{to} t_n^2+r_n^2=1, t_n, r_n\in \left[0,1\right], \forall n,$$

(8b)

$$\left|{\vartheta }_n-{\theta }_n\right|={\displaystyle \frac{\pi }{2}} or-{\displaystyle \frac{\pi }{2}}, {\vartheta }_n, {\theta }_n\in {\mathbb{F}}_{\lambda \ge 2},\forall n,$$

(8c)

$$z_{k,g}\in \left\{0,1\right\}, \forall k,g,$$

(8d)

$${\displaystyle \sum }_{g=1}^G{z}_{k,g}=1, \forall k,$$

(8e)

$$\Vert s{\Vert }_0=N_s.$$

(8f)

Here, $N_s$ is the number of selected STAR-RIS elements. Notably, owing to the coupled phase-shift constraint, the minimum achievable phase resolution is $\mathsf{\lambda }\ge 2$.

Remark 1 (Mode-switching STAR-RIS). 

Unlike the considered STAR-RIS with coupled and discrete phase shifts, which enables elements to simultaneously reflect and transmit signals, Ref. [2] introduces a mode-switching protocol, where each element operates in either reflection or transmission mode in each time slot. For D2D systems using the MS-based STAR-RIS, the sum-rate maximization problem in (8) can be reformulated as follows:

$$\underset{v_t, v_r,{\rm Z}}{\mathrm{maximize}} f\left(v_t, v_r,{\rm Z}\right)$$

(9a)

$$\mathrm{subject} \mathrm{to} t_n^2+r_n^2=1, t_n, r_n\in \left[0,1\right], \forall n,$$

(9b)

$${\vartheta }_n, {\theta }_n\in {\mathbb{F}}_{\lambda },\forall n,$$

(9c)

$$z_{k,g}\in \left\{0,1\right\}, \forall k,g,$$

(9d)

$${\displaystyle \sum }_{g=1}^G{z}_{k,g}=1, \forall k,$$

(9e)

3. Method

3.1. CEO Framework

The CEO method [5] is a powerful, unsupervised stochastic approach for solving complex deterministic optimization problems. It generates random candidate solutions from a parameterized probability distribution and iteratively updates the distribution parameters to focus on regions of high-quality solutions, without requiring prior knowledge of the global optimum.

The CEO-based framework operates through four key steps in each iteration to maximize an objective function $f\left({\mathit{{\rm Y}}}^{\left(i\right)}\right)$ in each iteration $i$, where $f\left({\mathit{{\rm Y}}}^{\left(i\right)}\right)$ represents a feasible solution generated in the $i$-th iteration:

• Sampling: Generate $L$ candidate solutions ${\left\{{{\rm Y}}_{\mathcal{l}}^{\left(i\right)}\right\}}_{\mathcal{l}=1}^L$ from the distribution $\mathcal{P}\left(·;{\pi }^{\left(i-1\right)}\right)$, where ${\pi }^{\left(i-1\right)}$ is the current parameter;
• Selection: Evaluate all samples using the objective function ${\left\{f\left({{\rm Y}}_{\mathcal{l}}^{\left(i\right)}\right)\right\}}_{\mathcal{l}=1}^L$, rank them, and select the top $L^{e\mathrm{lite}}\triangleq \lceil \varsigma L\rceil$ elite samples (with $\varsigma \in \left(0,1\right)$) to form the elite set ${\mathcal{E}}^{\left(i\right)}$;
• Updating: Update the distribution parameters $\pi$ by minimizing the cross-entropy between the current distribution and the one inferred from the elite samples. This is achieved by solving [5]:

  $${\pi }^{\star }=\underset{\pi }{\mathrm{argmax}}{\displaystyle \frac{1}{L}}{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{f\left({{\rm Y}}_{\mathcal{l}}^{\left(\mathbf{i}\right)}\in {\mathcal{E}}^{\left(\mathbf{i}\right)}\right)\right\}}\ln \mathcal{P}\left({{\rm Y}}_{\mathcal{l}}^{\left(\mathbf{i}\right)};\pi \right);$$

  (10)
• Smoothing: To ensure stability and prevent premature convergence, the updated parameters are smoothed using smoothing factor ($\varpi$) as follows:

  $${\pi }^{\left(\mathbf{i}\right)}=\varpi \times {\pi }^{\star }+\left(1-\mathit{\varpi }\right)\times {\pi }^{\left(\mathit{i}-1\right)}.$$

  (11)

3.2. Sampling Distribution Design

Applying the CEO framework to the considered STAR-RIS-assisted D2D optimization requires constructing a sampling distribution capable of jointly generating feasible candidates for all variables of interest. In each iteration, four types of variables are sampled: the reflection phase vector, phase-shift difference vector, reflection amplitude vector, and STAR-RIS element selection vector. Each type is sampled as follows:

3.2.1. Sampling Reflection Phase-Shift Vector $\mathit{\theta }$

Each element ${\theta }_n$ in the phase-shift vector $\mathit{\theta }={\left\{{\theta }_n\right\}}_{n=1}^N$ is constrained to the discrete set ${\mathbb{F}}_{\lambda }$. We sample each ${\theta }_n$ independently from a categorical distribution over $\left|{\mathbb{F}}_{\lambda }\right|$ elements, with associated probability vector ${\left\{p_{n\alpha }\right\}}_{\alpha =1}^{\left|{\mathbb{F}}_{\lambda }\right|}$ where $p_{n\alpha }=\mathrm{Pr}\left\{{{\rm I}}_n\left(\theta \right)=\alpha \mathsf{\Delta }\right\}$. These probabilities form a matrix $P=\left|{\mathit{p}}_{\mathit{n}\mathit{\alpha }}\right|\in {ℝ}^{\mathit{N}\times \left|{\mathbb{F}}_{\lambda }\right|}$, where each row sums to $1:{{\displaystyle \sum }}_{\alpha =1}^{\left|{\mathbb{F}}_{\lambda }\right|}{p}_{n\alpha }=1$. The resulting sampling distribution for $\mathit{\theta }$ parameterized by $P$ is as follows:

$$\mathcal{P}\left(\mathit{\theta };{\rm P}\right)\triangleq {\displaystyle \prod }_{n=1}^N{\displaystyle \sum }_{\alpha =1}^{\left|{\mathbb{F}}_{\lambda }\right|}{p}_{n\alpha }{1}_{\left\{{{\rm I}}_n\left(\mathit{\theta }\right)=\alpha \mathsf{\Delta }\right\}.}$$

(12)

Since we are considering a coupled-mode protocol, the phase difference between the transmission and reflection ends is used as a substitute to ensure that the results satisfy the coupled phase-shift constraint.

3.2.2. Sampling Phase-Shift Difference Vector $\mathit{\phi }$

Since ${\phi }_n\in \left\{{\displaystyle \frac{\pi }{2}},-{\displaystyle \frac{\pi }{2}}\right\}$, we define a binary phase-shift difference vector $\mathit{\phi }={\left\{{\phi }_n\right\}}_{n=1}^N$, and then modeling each ${\phi }_n$ as a Bernoulli random variable: $\mathrm{Pr}\left\{{{\rm I}}_n\left(\mathit{\phi }\right)={\displaystyle \frac{\pi }{2}}\right\}=q_n$, $\mathrm{Pr}\left\{{{\rm I}}_n\left(\mathit{\phi }\right)=-{\displaystyle \frac{\pi }{2}}\right\}=1-q_n$. The sampling distribution for $\mathit{\phi }$, parameterized by $\mathbf{q}={\left\{q_n\right\}}_{n=1}^N$, is given by the following equation. This guarantees the construction of a valid transmission phase vector $\mathit{\vartheta }=\mathit{\theta }+\mathit{\phi }$.

$$\mathcal{P}\left(\mathit{\phi };q\right)\triangleq {\displaystyle \prod }_{n=1}^N{q_n}^{{\displaystyle \frac{1+\frac{2}{\pi }{{\rm I}}_n\left(\mathit{\phi }\right)}{2}}}{\left(1-q_n\right)}^{{\displaystyle \frac{1-\frac{2}{\pi }{{\rm I}}_n\left(\mathit{\phi }\right)}{2}}}.$$

(13)

3.2.3. Sampling Reflection Amplitude Vector r 

Unlike the discrete-valued phase components, the reflection amplitude vector $\mathit{r}={\left\{r_n\right\}}_{n=1}^N$ consists of continuous values. We sample $\mathit{r}$ from a multivariate Gaussian distribution with independent components:

$$\mathcal{N}\left(r;\mu ,\mathbf{\varrho }\right)={\displaystyle \prod }_{n=1}^N{\displaystyle \frac{1}{\sqrt{2\pi }{\varrho }_n}}{e}^{-{\displaystyle \frac{{\left(r_n-{\mu }_n\right)}^2}{2{\varrho }_n^2}}}$$

(14)

Here, $\mathit{\mu }={\left\{{\mu }_n\right\}}_{n=1}^N$ and $\mathit{\varrho }={\left\{{\varrho }_n\right\}}_{n=1}^N$ denote the mean and standard deviation vectors. To ensure valid transmission amplitudes, we compute $t_n=\sqrt{1-r_n}$. To guarantee that all generated samples have valid corresponding transmission amplitudes within the range $\left[0,1\right]$, we either reject and resample or replace it with a valid random value.

3.2.4. Sampling STAR-RIS Selection Vector $s$

Each element of the binary selection vector $\mathit{s}={\left\{s_n\right\}}_{n=1}^N$ determines whether the n-th element is active. We model $s_n$ as an independent Bernoulli variable with probability $\mathrm{Pr}\left\{{{\rm I}}_n\left(\mathit{s}\right)=1\right\}=b_n$, $\mathrm{Pr}\left\{{{\rm I}}_n\left(\mathit{s}\right)=0\right\}=1-b_n$. The sampling distribution for $\mathit{s},$ parameterized by $\mathit{b}={\left\{b_n\right\}}_{n=1}^N$ is described as follows:

$$\mathcal{P}\left(s;b\right)\triangleq {\displaystyle \prod }_{n=1}^N{b}_n^{{{\rm I}}_n\left(s\right)}{\left(1-b_n\right)}^{1-{{\rm I}}_n\left(s\right)}.$$

(15)

3.2.5. Sampling Grouping Matrix $Z$

Similar to the phase difference modeling, each entry in the scheduling group matrix $\mathit{Z}$ is binary, satisfying $z_{gk}\in \left\{0, 1\right\}$. Hence, we adopt a Bernoulli distribution to construct its sampling distribution. Since the grouping variables $z_{gk}$ are assumed to be independent, the overall sampling distribution is factorized across all users and groups. Specifically, $\mathrm{Pr}\left\{{{\rm I}}_{gk}\left(\mathit{Z}\right)=1\right\}=w_{gk}$, $\mathrm{Pr}\left\{{{\rm I}}_{gk}\left(\mathit{Z}\right)=0\right\}=1-w_{gk}$, where $w_{gk}$ denotes the probability that user k is assigned to group $g$. These probabilities form the group assignment probability matrix $\mathit{W}=\left[{\mathit{w}}_{\mathit{g}\mathit{k}}\right]\in {ℝ}^{\mathit{G}\times \mathit{K}}$. Thus, the sampling distribution of $\mathit{Z}$ is given as follows:

$$\mathcal{P}\left(Z;W\right)\triangleq {\displaystyle \prod }_{k=1}^K{\displaystyle \sum }_{g=1}^G{w}_{gk}^{I_{gk}\left(Z\right)}{\left(1-w_{gk}\right)}^{1-I_{gk}\left(Z\right)}.$$

(16)

3.3. Updating Formulae

To address Problem (8), we define a joint sampling distribution over all decision variables:

$$\mathcal{P}\left({\rm Y};\pi \right)\triangleq \mathcal{P}\left(\mathit{\theta };P\right)\times \mathcal{P}\left(\mathit{\phi };q\right)\times \mathcal{P}\left(s;b\right)\times \mathcal{P}\left(Z;W\right)\times \mathcal{P}\left(\mathit{Z};W\right)\times \mathcal{N}\left(r;\mu ,\mathbf{\varrho }\right) ,$$

(17)

where $\mathit{{\rm Y}}=\left\{\mathit{\theta },\mathit{\phi },\mathit{s},\mathit{Z},\mathit{r}\right\}$ and $\mathit{\pi }$ collects all meta-parameters. A mapping function $\mathcal{M}\left(·\right)$ is used to transform each sample $\mathit{{\rm Y}}$ into a feasible solution $\mathit{\psi }= \mathcal{M}\left(\mathit{{\rm Y}}\right)=\left\{\mathit{\theta },\mathit{\phi },\mathit{s},\mathit{Z},\mathit{r},\mathit{t}\right\}$ for Problem (8), where $\mathit{\vartheta }=\mathit{\theta }+\mathit{\phi }$ and $t_n=\sqrt{1-r_n^2}$.

At the $i$-th iteration, we generate $L$ samples ${\left\{{\mathit{{\rm Y}}}_{\mathcal{l}}^{\left(i\right)}\right\}}_{\mathcal{l}=1}^L$, evaluate their objective values, and select the top $L^{\mathrm{elite}}$ samples to form the elite set ${\mathcal{E}}^{\left(i\right)}$. The objective is to minimize the cross-entropy between the current distribution and the elite distribution:

$$\underset{\pi }{\mathrm{maximize} } {\displaystyle \frac{1}{L}}{\displaystyle \sum }_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}\in \mathcal{E}\right\}}\ln \mathcal{P}\left({{\rm Y}}_{\mathcal{l}}^{\left(i\right)};\pi \right)$$

(18a)

$$\mathrm{subject} \mathrm{to} {\displaystyle \sum }_{\alpha =1}^{\left|{\mathbb{F}}_{\lambda }\right|}{p}_{n\alpha }=1, \mathrm{for} n=1,\dots ,N,$$

(18b)

Using the method of Lagrange multipliers, the optimal update formulae for the parameters are derived as follows:

$$p_{n\alpha }={\displaystyle \frac{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}{1}_{\left\{{{\rm I}}_n\left({\mathit{\theta }}_{\mathcal{l}}^{\left(\mathit{i}\right)}\right)=\alpha \mathsf{\Delta }\right\}}}{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}}}.$$

(19a)

$$q_n={\displaystyle \frac{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}\left[\frac{2}{\pi }{{\rm I}}_n\left({\phi }_{\mathcal{l}}^{\left(\mathit{i}\right)}\right)+1\right]}{2{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}}},$$

(19b)

$$b_n={\displaystyle \frac{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}{{\rm I}}_n\left(s_{\mathcal{l}}^{\left(\mathit{i}\right)}\right)}{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}}},$$

(19c)

$$w_{gk}={\displaystyle \frac{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}{{\rm I}}_{gk}\left(Z_{\mathcal{l}}^{\left(\mathit{i}\right)}\right)}{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}}},$$

(19d)

$${\mu }_n={\displaystyle \frac{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}{{\rm I}}_n\left(r_{\mathcal{l}}^{\left(\mathit{i}\right)}\right)}{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}}},$$

(19e)

$${\varrho }_n=\sqrt{{\displaystyle \frac{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}{\left[{{\rm I}}_n\left(r_{\mathcal{l}}^{\left(\mathit{i}\right)}\right)-{\mu }_n\right]}^2}{{{\displaystyle \sum }}_{\mathcal{l}=1}^L{1}_{\left\{{{\rm Y}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\in {\mathcal{E}}^{\left(\mathit{i}\right)}\right\}}}}.}$$

(19f)

3.4. Algorithm Details, Complexity, and Parameter Selection

Algorithm 1 addresses Problem (8) as follows: It first initializes the tilting parameters (line 2) with a uniform or constant value: $p_{n\alpha }^{\left(i\right)}={\displaystyle \frac{1}{\left|{\mathbb{F}}_{\lambda }\right|}}$, $q_n^{\left(i\right)}={\displaystyle \frac{1}{2}}$, $b_n^{\left(i\right)}={\displaystyle \frac{1}{2}}, w_{gk}^{\left(i\right)}={\displaystyle \frac{1}{2}},$ ${\mu }_n^{\left(i\right)}={\displaystyle \frac{1}{2}}$, and ${\varrho }_n^{\left(i\right)}=1$. Samples are generated and evaluated (lines 7–11), where the binary sequence $s^{\left(i\right)}$ must satisfy the constraint $\Vert {\mathit{s}}^{\left(i\right)}{\Vert }_0=N_s$ to select exactly $N_s$ STAR-RIS elements. Since random sampling may not always meet this constraint, the restricted search operator [6] adjusts the samples accordingly. The top-performing samples form the elite set (line 12), which guides the update of tilting parameters (line 13). Smoothing is applied (line 14) to enhance convergence stability and avoid local optima. Finally, the best solution is recorded to ensure non-decreasing objective values across iterations (lines 15–18).

Algorithm 1: CEO for Solving Problem (8)
	Input: Sample size L, elite ratio ς, and smoothing parameter ϖ
1	i ← 0
2	Initialize $P^{\left(i\right)}$, $q^{\left(i\right)}$,${\mu }^{\left(i\right)}$,${\mathbf{\varrho }}^{\left(i\right)}$, $b^{\left(i\right)}$, $W^{\left(i\right)}$
3	Lelite ← ceil(ς L)
4	fbest ← −∞
5	$\mathit{{\rm Y}}$best ← ∅
6	while i ≤ imax do
7	for ℓ = 1 to L do
8	Generate ${\mathit{{\rm Y}}}_{\mathcal{l}}^{\left(\mathit{i}\right)}$ = {${\mathit{\theta }}_{\mathcal{l}}^{\left(\mathit{i}\right)}$, ${\mathit{\phi }}_{\mathcal{l}}^{\left(\mathit{i}\right)}$, $r_{\mathcal{l}}^{\left(\mathit{i}\right)}$, $s_{\mathcal{l}}^{\left(\mathit{i}\right)}$, $Z_{\mathcal{l}}^{\left(\mathit{i}\right)}$}
9	${\mathit{\psi }}_{\mathcal{l}}^{\left(\mathit{i}\right)}= \mathcal{M}\left({\mathit{{\rm Y}}}_{\mathcal{l}}^{\left(\mathit{i}\right)}\right)$←{${\mathit{\theta }}_{\mathcal{l}}^{\left(\mathit{i}\right)}$, ${\mathit{\phi }}_{\mathcal{l}}^{\left(\mathit{i}\right)}$, $r_{\mathcal{l}}^{\left(\mathit{i}\right)}$,$t_{\mathcal{l}}^{\left(\mathit{i}\right)},$ $s_{\mathcal{l}}^{\left(\mathit{i}\right)}$, $Z_{\mathcal{l}}^{\left(\mathit{i}\right)}$}
10	Evaluate f(${\mathit{\psi }}_{\mathcal{l}}^{\left(\mathit{i}\right)}$) using (7)
11	end
12	${\mathcal{E}}^{\left(\mathit{i}\right)}$ = ${\left\{{\mathit{{\rm Y}}}_{\left[\mathcal{l}\right]}^{\left(\mathit{i}\right)}\right\}}_{\mathcal{l}=1}^{L^{\mathrm{elite}}}$ ← Sort(${\left\{f\left({\mathit{\psi }}_{\mathcal{l}}^{\left(\mathit{i}\right)}\right)\right\}}_{\mathcal{l}=1}^{\mathrm{L}}$, descending)
13	Update $P^{\left(i\right)}$, $q^{\left(i\right)}$,${\mu }^{\left(i\right)}$,${\varrho }^{\left(i\right)}$, $b^{\left(i\right)}$, $W^{\left(i\right)}$ using (19)
14	Smooth $P^{\left(i\right)}$, $q^{\left(i\right)}$,${\mu }^{\left(i\right)}$,${\varrho }^{\left(i\right)}$, $b^{\left(i\right)}$, $W^{\left(i\right)}$ using (11)
15	if f(${\mathit{\psi }}_{\left[1\right]}^{\left(\mathit{i}\right)}$) > fbest then
16	fbest ←f(${\mathit{\psi }}_{\left[1\right]}^{\left(\mathit{i}\right)}$)
17	$\mathit{{\rm Y}}$best ←${\mathit{{\rm Y}}}_{\left[1\right]}^{\left(\mathit{i}\right)}$
18	end
19	i ← i + 1
20	end
	Output: $\mathit{{\rm Y}}$best

Remark 2. 

Equation (9) requires sampling four types of variables for the MS-based STAR-RIS in each iteration: the reflection phase-shift vector $\mathit{\theta }$, the transmission phase-shift vector $\mathit{\vartheta }$, the grouping matrix Z, and the reflection amplitude vector r. Since MS-based STAR-RIS does not impose coupled-phase constraints, we independently generate $\mathit{\theta }$ and $\mathit{\vartheta }$ using the sampling distribution derived from Equation (11), but with different probability matrices. Moreover, since each MS-based STAR-RIS element operates in either reflection or transmission mode, the reflection amplitude is modeled as a binary variable. Specifically, the reflection amplitude for the n-th element is modeled as an independent Bernoulli random variable with distribution: $\mathrm{Pr}\left\{I_n\left(\mathit{r}\right)=1\right\}=d_n$, $\mathrm{Pr}\left\{I_n\left(\mathit{r}\right)=0\right\}=1-d_n$, similar to the formulation in Equation (15). Consequently, the sampling distribution for the reflection amplitude vector r, parameterized by $\mathit{d}={\left\{d_n\right\}}_{n=1}^N$, is given by the following: $\mathcal{P}\left(\mathit{r};\mathit{d}\right)\triangleq {{\displaystyle \prod }}_{n=1}^N{d}_n^{{{\rm I}}_n\left(r\right)}{\left(1-d_n\right)}^{1-{{\rm I}}_n\left(r\right)}.$ A feasible transmission amplitude vector $t_n=\sqrt{1-r_n^2}$. Therefore, the overall joint sampling distribution for Equation (9) is expressed as $\mathcal{P}\left(\mathit{{\rm Y}};\mathit{\pi }\right)\triangleq \mathcal{P}\left(\mathit{\theta };\mathit{P}\right)\times \mathcal{P}\left(\mathit{\phi };{\mathit{P}}^{\prime }\right)\times \mathcal{P}\left(\mathit{Z};\mathit{W}\right)\times \mathcal{P}\left(\mathit{r};\mathit{d}\right)$, where $\mathit{{\rm Y}}$ collects all the design variables, and $\mathit{\pi }$ represents the set of all associated sampling parameters.

Remark 3. 

The computational complexity is analyzed in terms of the number of complex multiplications. The main cost per iteration arises from computing the sum rate (Equation (7)). To enhance efficiency, we precompute ${\mathit{a}}_{k,j}\triangleq \mathrm{diag}\left({\mathit{g}}_j\right){\mathit{u}}_k$ in the preprocessing stage using N complex multiplications per pair $k=1,\dots ,K$ and $j=1,\dots ,K$, totaling $K^{2}N$ operations. For sum-rate evaluation, ${\left|{\hslash }_{k,k}\right|}^2$ requires $\left(N+1\right)$ multiplications. ${\displaystyle \sum }_{j\ne k}{\left|{\hslash }_{k,j}\right|}^2$ requires $\left(N+1\right)\left(K-1\right)$ multiplications. Thus, the total for one user is $\left(N+1\right)K$, and, for all users, $\left(N+1\right)K^2$. For $L$ candidate solutions across ${\mathcal{i}}_{max}$ iterations, the total complexity is $K^{2}N+\left(N+1\right)K^{2}L{\mathcal{i}}_{max}$.

Remark 4. 

To determine the parameters employed in the proposed CEO-based algorithm, we draw on insights from Equation [5], which offers empirically validated parameter recommendations. Following these suggestions, a reasonable initial setting for the algorithm parameters is as follows: $L=\zeta ·\chi$ with $1<\zeta <10$, $\varsigma \in \left[0.01, 0.1\right]$, and $\varpi \in \left[0.6, 1\right]$, where $\chi$ is the total number of variables (equal to the number of STAR-RIS elements $N$ in our case). In our implementation, we use $\zeta =0.4, \varsigma =0.1$, and $\varpi =0.6$. The maximum iteration count ${\mathcal{i}}_{max}$ is selected based on empirical results.

4. Result and Discussion

The simulation environment is configured to closely replicate the setup described in Ref. [7]. The STAR-RIS is placed at the Cartesian coordinate origin $\left(0,0,0\right)$. Transmitters are uniformly distributed within the region $\left[5 \mathrm{m}, 45 \mathrm{m}\right]\times \left[-45 \mathrm{m}, -5 \mathrm{m}\right]$. Receivers on the reflection side are uniformly located within $\left[5 \mathrm{m}, 45 \mathrm{m}\right]\times \left[5 \mathrm{m}, 45 \mathrm{m}\right]$, while those on the transmission side are positioned within $\left[5 \mathrm{m}, -45 \mathrm{m}\right]\times \left[5 \mathrm{m}, -45 \mathrm{m}\right].$ The vertical coordinate of all users is fixed at $\mathcal{z}=-20 \mathrm{m}$. The channels between the $j$-th transmitter and the STAR-RIS, and from the STAR-RIS to the $k$-th receiver, are characterized as Rician fading channels with both line-of-sight (LoS) and non-line-of-sight (NLoS) components:

$$c_j={\mathcal{L}}_{1,j}\left(\sqrt{{\displaystyle \frac{\tau }{1+\tau }}}{c}_j^{LoS}+\sqrt{{\displaystyle \frac{\tau }{1+\tau }}}{\mathrm{c}}_j^{NLoS}\right),$$

(20a)

$$u_k={\mathcal{L}}_{2,k}\left(\sqrt{{\displaystyle \frac{\tau }{1+\tau }}}{u}_k^{LoS}+\sqrt{{\displaystyle \frac{\tau }{1+\tau }}}{u}_k^{NLoS}\right),$$

(20b)

where $\tau =10$ denotes the Rician factor. The LoS components are denoted by ${\mathit{c}}_j^{\mathrm{LoS}}$ and ${\mathit{u}}_k^{\mathrm{LoS}}$, and NLoS components by ${\mathit{c}}_j^{\mathrm{NLoS}}$ and ${\mathit{u}}_k^{\mathrm{NLoS}}$. Path loss is modeled with an exponent of $2.2$, assuming a reference path loss of 30 dB at a distance of 1 m. The system operates with a bandwidth of 10 MHz, and the noise power spectral density is set to $170$ dBm/Hz.

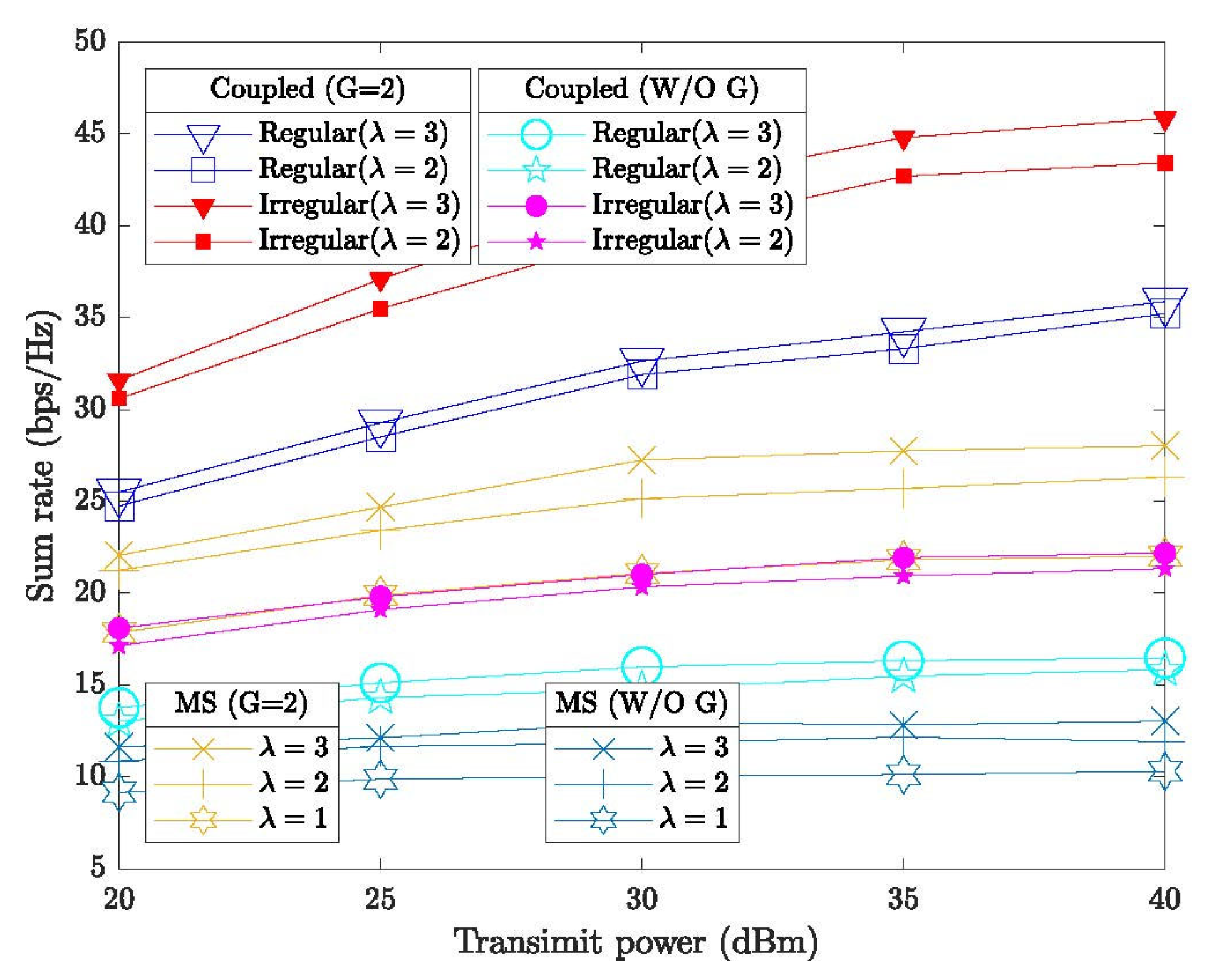
Figure 2 illustrates the sum rate as a function of transmission power for a fixed number of users $K=12$. Several observations can be made. First, the CEO-designed coupled STAR-RIS outperforms MS STAR-RIS, as each element in the coupled mode can simultaneously enable transmission and reflection, thereby improving resource utilization and significantly enhancing the sum rate. Second, for the MS STAR-RIS, a higher phase resolution $\left(\lambda =2 or 3\right)$ yields notably better performance compared with $\lambda =1$, owing to greater phase flexibility. Moreover, the CEO-designed coupled irregular STAR-RIS with $\lambda =1$ achieves higher sum rates than the coupled regular STAR-RIS with $\lambda =1$, demonstrating that irregular element distribution provides greater spatial diversity, mitigates signal fading, and improves performance even with lower-resolution phase shifters, thus reducing power consumption. Finally, employing user grouping with time-division transmission effectively reduces interference and allows the CEO algorithm to dynamically optimize the STAR-RIS phase shifts according to the active users in each timeslot, thereby further enhancing system performance and confirming the effectiveness of TDMA strategies.

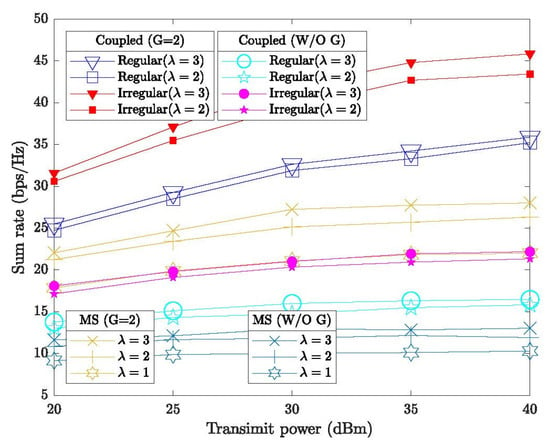
Figure 2. Average sum rate versus transmit power for standard and irregular STAR-RIS-assisted D2D systems with K = 12.

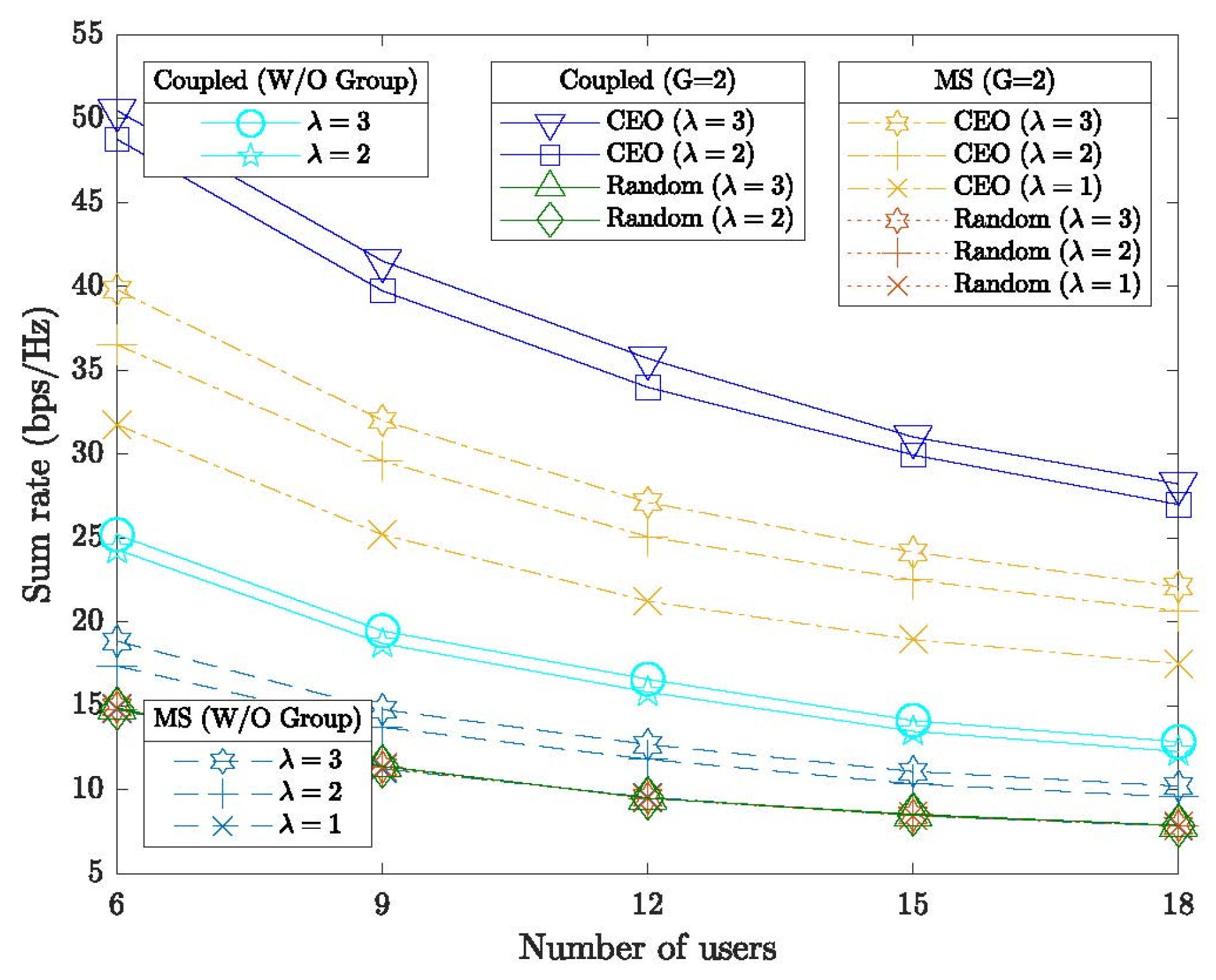
Figure 3 illustrates the impact of varying the number of user pairs on the sum rate in a STAR-RIS-assisted D2D system under a fixed transmission power of $40 \mathrm{dBm}$, with K ranging from $6$ to $18$. As K increases, all schemes exhibit a decreasing sum rate due to intensified multi-user interference. The CEO-designed coupled STAR-RIS consistently outperforms the MS STAR-RIS, which is attributed to its ability to simultaneously transmit and reflect signals, thereby enabling more efficient resource utilization. The introduction of a user grouping strategy further enhances performance—particularly when the total number of users is moderate—by effectively reducing intra-group interference. As the number of users continues to grow, interference becomes more severe, but user grouping helps mitigate its adverse effects. Moreover, without CEO-based optimization for user grouping, both coupled and MS STAR-RIS systems experience significant performance degradation, underscoring the importance of coordinated scheduling and the effectiveness of the CEO algorithm in jointly optimizing system parameters.

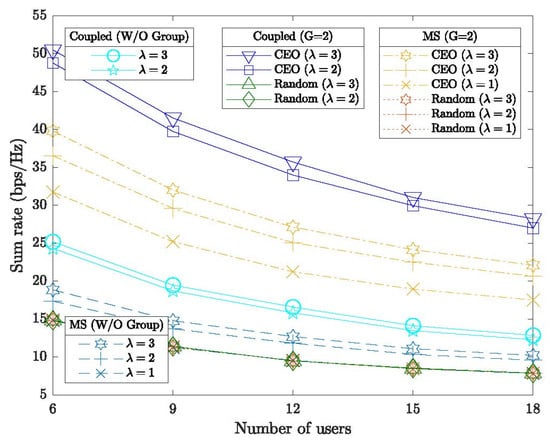
Figure 3. Average sum rate versus the number of users in coupled and MS STAR-RIS-assisted D2D systems.

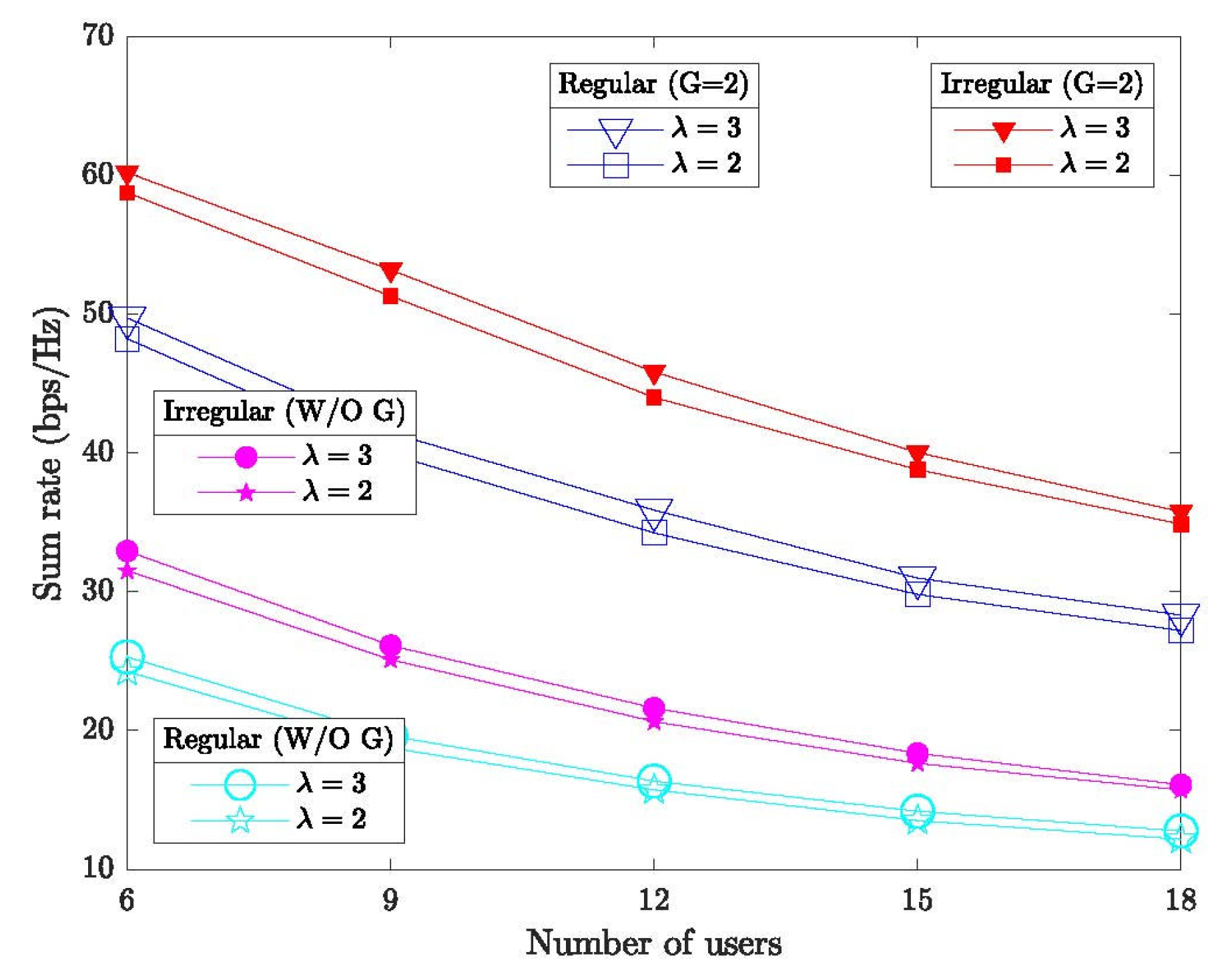
Figure 4 further compares the performance of regular and irregular STAR-RIS configurations, with and without user grouping, under a fixed transmission power of 40 dBm. Both schemes employ $8\times$8 active elements, while the irregular STAR-RIS selects from a pool of $10\times 10$ elements. The number of user pairs, K, varies from $6$ to $18$. As expected, the regular STAR-RIS without grouping achieves the lowest performance, followed by the irregular STAR-RIS without grouping. Introducing the scheduling mechanism and applying CEO-based joint optimization significantly enhances performance in both cases. In particular, as K increases, grouping users into two sets effectively mitigates multi-user interference, demonstrating that the proposed scheduling strategy improves transmission performance for both regular and irregular STAR-RIS systems.

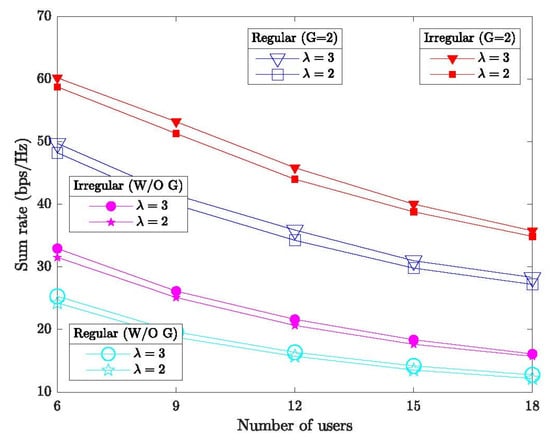
Figure 4. Average sum rate versus the number of users in standard and irregular STAR-RIS-assisted D2D systems.

5. Conclusions

We investigated a STAR-RIS-assisted MU-MISO wireless communication system incorporating user grouping and scheduling to mitigate interference and enhance performance. In MU-MISO systems, simultaneous resource sharing often leads to significant multi-user interference. To address this issue, we adopted a TDMA-based group scheduling strategy that divides users into time slots and optimizes resource allocation within each group. By leveraging a CEO framework, we jointly optimize the grouping strategy and STAR-RIS parameters to suppress intra-group interference and maximize the sum rate. Simulation results demonstrate that, compared to conventional non-scheduling designs, the proposed CEO-based grouping mechanism significantly improves system performance—particularly in high-user-density scenarios—by enabling more effective beam control through STAR-RIS.