Integer-PSO-Optimized Checkerboard Dual-Band Terahertz Metamaterial Absorber for Biomedical Sensing Applications ^†

Abstract

This paper presents a checkerboard-patterned terahertz (THz) metamaterial absorber engineered for wide-band, dual-band absorption. The absorber consists of a gold metal layer patterned on a polyimide substrate, forming a unit cell structure with dimensions of 85 µm × 85 µm. At the core of the design is a square metal patch of 67 µm × 67 µm, which is divided into a 5 × 5 grid of 25 smaller cells. An integer-coded Particle Swarm Optimization (PSO) algorithm is employed to generate the pattern, where an input value of ‘1’ retains the metal in a cell, and a ‘0’ results in the removal of metal from that cell, resulting in a digitally optimized checkerboard pattern. The substrate height is also optimized and fixed at 7 µm to enhance resonance characteristics. The PSO algorithm is run for 50 iterations, with the fitness function defined as the number of frequency points at which the absorption exceeds 90%. The finalized design achieves two distinct absorption peaks with high efficiency: 99.53% at 3.434 THz, with a 90% absorption bandwidth of 212 GHz; and 99.35% at 3.823 THz, with a bandwidth of 177 GHz. While the absorption performance is already significant, it can be further improved by increasing the number of PSO iterations, albeit at the cost of higher computational complexity. The proposed absorber demonstrates strong potential for biomedical sensing, as validated through its ability to differentiate between cancerous and non-cancerous breast and blood cells. This work paves the way for fully automated, algorithm-driven metamaterial design strategies in the THz regime, particularly for applications in non-invasive biomedical diagnostics.

1. Introduction

Terahertz (THz) radiation, positioned between microwave and infrared wavelengths, exhibits unique characteristics that make it valuable for biomedical sensing, spectroscopy, and security screening. A metamaterial absorber is defined as an engineered material that effectively absorbs incident electromagnetic radiation [1]. A special category of these structures are the THz metamaterial absorbers (TMAs) that can absorb THz radiation. The absorption peaks of TMAs can be tailored by the modifying material properties or altering the unit cell design, enabling precise control over the absorption spectrum. This versatility and tunability positions TMAs as a critical element in the advancement of THz technologies and applications. Researchers have developed multi-band, broad-band, and tunable TMAs, often employing traditional design approaches involving modifications to the unit cell [2,3,4]. For example, ref. [5] details a quad-band absorber design employing four resonators of distinct sizes. Similarly, ref. [6] utilized dipolar resonances to construct a quad-band absorber. THz metamaterial absorbers can also be utilized to sense changes in refractive index [7,8]. The conventional design methodology necessitates alterations to the unit cell to achieve the desired absorption characteristics, a process that can be time-consuming and labor-intensive. An alternative approach involves automating the design process using optimization algorithms. Many researchers have used this approach to design unique TMAs. A swastika-shaped design has been optimized using the firefly algorithm to achieve dual-band characteristics [9]. Deep learning was employed in [10] to optimize the TMA to achieve wide-band absorption characteristics. A Taguchi deep neural network was employed to optimize a graphene-based TMA to achieve wide-band characteristics [11]. A machine learning framework was developed to design a multi-band absorber in the THz range [12]. Another deep learning approach to designing a multi-band TMA has been presented in [13]. While reducing manual effort, these approaches still require considerable effort and time to design the initial unit cell, which is followed by parameter optimization to achieve the desired characteristics. Furthermore, this approach can be restrictive, limiting the degree of structural freedom. An alternative is to design the structure entirely using optimization algorithms. Although computationally intensive, this approach offers greater structural freedom and can facilitate achieving the desired absorption characteristics. For detection applications, absorbers with a high Figure of Merit (FoM) are desirable [12,13,14,15].

This work introduces a novel terahertz (THz) metamaterial absorber meticulously designed for efficient, dual-band absorption. The absorber incorporates a digitally optimized checkerboard pattern, created using a Particle Swarm Optimization (PSO) algorithm, to achieve high absorption peaks at 3.434 THz and 3.823 THz. This design, consisting of a gold layer on a polyimide substrate, demonstrates significant potential for biomedical sensing, specifically for distinguishing between cancerous and non-cancerous blood and breast cancer cells. This manuscript is organized into four sections. Section 2 details the design methodology and unit cell structure. Section 3 presents the simulation results and discusses the sensing capability of the design. Section 4 presents the conclusions and outlines the scope for future work.

2. Design Methodology and Unit Cell Structure

The design and optimization of the terahertz metamaterial absorber unit cell were carried out through a co-simulation framework integrating Ansys HFSS with Python 3.11, where the PyAEDT library enabled automated communication between the two platforms. To achieve optimal performance, a PSO algorithm, implemented using the PySwarm library in Python, was employed. In each iteration, the PSO algorithm updated the design parameters of candidate solutions, which were then applied to the HFSS model through PyAEDT. HFSS subsequently simulated the modified unit cell and generated the corresponding absorption spectrum, which was returned to Python for fitness evaluation. The fitness function was defined as the number of frequencies exhibiting absorption greater than 95%, serving as the optimization target. The design space consisted of 27 variables, where 25 binary variables defined a checkerboard distribution of metal patches on the central square (parameter a), with ‘1’ indicating the presence of a metal patch and ‘0’ its absence; while the remaining two continuous variables controlled the overall square dimension (a) and substrate height (h). This automated co-simulation process enabled systematic exploration of the design space, allowing the PSO algorithm to iteratively refine the geometry until the desired broad-band, near-perfect absorption characteristics were obtained. The steps involved in the design methodology are shown in Figure 1.

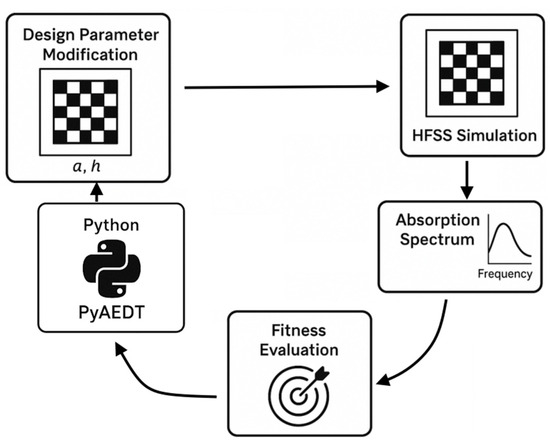
Figure 1. The design methodology.

The fitness function of the PSO simulates a periodic structure within HFSS based on input numerical data. Initially, it prepares the input array, extracts key dimensions and parameters, and creates a “dielectric” box in HFSS. A checkered pattern of gold patches is then generated, defined by a binary sequence within the input array, establishing a repeating motif of gold elements atop a dielectric base. Subsequently, the design is mirrored along the x axis and the y axis to complete the structure. This ensures that the structure is symmetrical. The structure is then simulated in HFSS, and the resulting reflection coefficient data is extracted, processed in Python to calculate absorption values, and optionally saved to a CSV file. The algorithm returns the number of frequencies exceeding a specified absorption threshold. PSO then uses the fitness values to improve the design over subsequent iterations. The pseudo-code for the algorithm is shown in Algorithm 1 below:

Algorithm 1. To calculate the fitness

INPUT: An (Array of Numbers), pl (Boolean) OUTPUT: Result (Number or String) BEGIN // 1. Data Preparation An_flat = Flatten(An) // Convert An to a 1D array // 2. Extract Parameters N = Length(An_flat) − 2 Un = Slice(An_flat, 0, N) h = An_flat[N] // Integer − Height a = An_flat[N + 1] // Integer − Dimension (Width, etc.) // 3. Create ‘dielectric’ box in HFSS CALL CreateHFSSBox(origin = [0, 0, b], sizes = [u, u, h], name = “dielectric”, material = polyimide) // 4. Calculate Simulation Parameters Nx = IntegerSqrt(Length(Un)) Ny = Nx ax = a/(2 ∗ Nx) ay = a/(2 ∗ Ny) // 5. Create Checkered Pattern in HFSS count = 0 FOR i = 0 TO Ny − 1 DO FOR j = 0 TO Nx − 1 DO IF Un[count] == 1 THEN start = [(u − a)/2 + j ∗ ax, (u − a)/2 + i ∗ ay, h + b] CALL CreateHFSSBox(origin = start, sizes = [ax, ay, t], name = “top”, material = “gold”) count = count + 1 ENDIF ENDFOR ENDFOR // 6. Mirror ‘top’ boxes in HFSS CALL MirrorObjects(“top”, origin = [u/2, 0, b + h], vector = [u/2, 0, 0]) CALL MirrorObjects(“top”, origin = [0, u/2, b + h], vector = [0, u/2, 0]) // 7. Run HFSS Analysis CALL RunHFSSAnalysis() // 8. Extract Data for Plotting plot_data = CALL GetHFSSPlotData() // 9. Create HFSS Report report = CALL CreateHFSSReport(plot_data [1]) // 10. Extract Solution Data solution = CALL GetSolutionData(report) // 11. Export Solution to CSV (with Error Handling) TRY CALL ExportSolutionToCSV(solution, “data.csv”, separator = “;”) EXCEPT CALL DeleteHFSSObjects([“dielectric”] + CALL GetHFSSObjectNames(“top”)) RETURN 0 // Indicate Failure ENDTRY // 12. Process Data df = CALL ReadCSV(“data.csv”, separator = “;”) x = CALL GetColumnValues(df, 0) y = CALL GetColumnValues(df, 1) y = 10**(y/20) y = 1 − (y**2) indices = CALL FindIndices(y, >0.95)  CALL DeleteHFSSObjects([“dielectric”] + CALL GetHFSSObjectNames(“top”)) RETURN Length(indices) END ALGORITHM

Figure 2 illustrates the unit cell design of the terahertz metamaterial absorber that was obtained using the PSO. The absorber utilizes gold for both the top and bottom layers, chosen for its high conductivity (4.10 × 10⁷ S/m). Polyimide is used as the substrate, having a dielectric constant of 3 and a loss tangent of 0.06. Through PSO, the dielectric spacer height, denoted as h, was determined to be 6 μm, and the central square dimension, a, was found to be 67 μm. The unit cell’s overall dimension is u = 85 μm. The bottom gold layer, b, was taken to be 2 μm thick to effectively block electromagnetic wave transmission, and the thickness of the top gold layer was taken to be t = 0.4 μm. The simulations were performed using the Ansys HFSS, and master–slave boundary conditions were used to obtain the absorption spectrum. The PSO algorithm was run for 50 iterations. The parameters of the PSO algorithm are as follows: number of particles, 4; dimensions, 27; inertia weight, 0.9; cognitive parameter, 0.5; social parameter, 0.3.

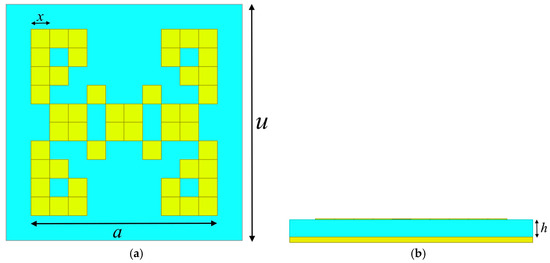
Figure 2. Unit cell of the PSO optimized structure: (a) top view; (b) side view.

3. Results and Sensing Performance

The unit cell was simulated using the Ansys HFSS software. The absorption (A) is measured using the reflection coefficient (s₁₁) and the transmission coefficient (s₁₂) using Equation (1):

$$A = 1-{\left|s_{11}\right|}^2{-\left|s_{12}\right|}^2$$

(1)

The thickness of the bottom ground plane is more than the skin depth of gold, and it prevents the transmission of electromagnetic waves. Thus, the transmission coefficient is almost negligible. The absorption spectrum of the checkered patterned absorber is shown in Figure 3. Also shown in the figure are its absorption spectra at different polarization and incidence angles. The designs offer two distinct absorption peaks with high efficiency: 99.53% at 3.434 THz, with a 90% absorption bandwidth of 212 GHz; and 99.35% at 3.823 THz, with a bandwidth of 177 GHz.

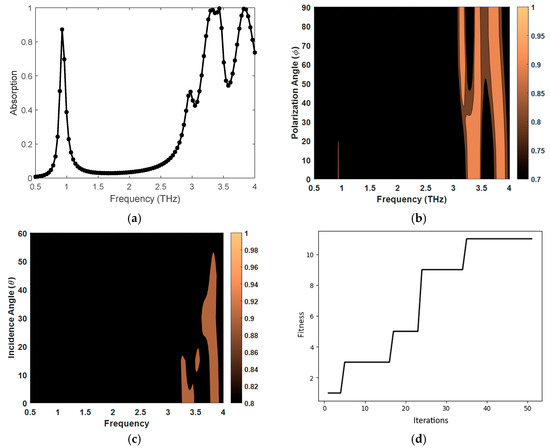
Figure 3. The absorption spectrum of the checkered pattern design at (a) normal incidence and a polarization angle of 0°, (b) at other polarization angles, and (c) at other incidence angles. (d) Convergence curve of the PSO.

The absorption spectra of the design varies slightly with the polarization angle. However, with the incidence angle, the shift is more pronounced. The absorption spectrum also varies with the changes in the refractive index of the surrounding medium. This shift in the absorption spectrum is due to changes in the impedance matching, which can be exploited to detect different biological samples [10]. It is known that cancerous and non-cancerous tissues have different refractive indices. Cancerous breast cells have a refractive index of 1.399, while non-cancerous breast cells have a refractive index of 1.385 [10]. Similarly, cancerous blood cells have a refractive index of 1.39, while non-cancerous blood cells have a refractive index of 1.376 [10]. The absorption spectra of the proposed design, when surrounded by these different biological tissues, is shown in Figure 4.

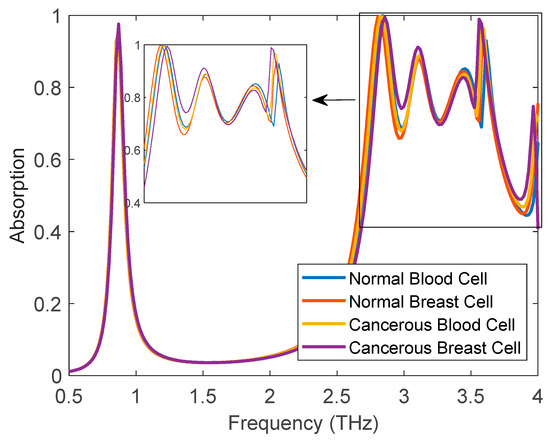
Figure 4. Absorption spectra for different biomedical samples.

From Figure 4, it can clearly be observed that different biomedical tissues have noticeably different absorption spectra. These shifts in the absorption spectra can be used to detect the biomedical samples accurately.

4. Conclusions

This work presents the successful design of a dual-band terahertz metamaterial absorber with wide-band characteristics in both absorption bands. The methodology utilizes an algorithm-driven approach, specifically through the use of a PSO algorithm to generate a checkerboard pattern. The resulting absorber achieves remarkable absorption rates at two distinct frequencies, demonstrating the power of automated design strategies for achieving targeted performance characteristics. Furthermore, the demonstrated ability to differentiate between cancerous and non-cancerous cells validates the potential of this design for advanced biomedical sensing applications. This research not only advances the field of terahertz metamaterial design but also establishes a pathway toward fully automated, algorithm-driven strategies, promising greater efficiency and customization in the development of innovative THz devices for non-invasive diagnostics.