Selection of Optimum Parameters for an Additively Manufactured Wall of SS316L Using PROMETHEE II ^†

Abstract

In this work, the GMAW-based wire arc additive manufacturing technique was used to additively manufacture a wall of SS316L. Consequently, the PROMETHEE II MCDM was used to optimize the process variables in the WAAM of SS316L. The input parameters used were travel speed (TS), feed speed (FS), and voltage (V), and the output parameters were set as depth of penetration (DOP), bead width (BW), and bead height (BH). Bead-on-plate trials were conducted using the response surface analysis-based BBD technique. The PROMETHEE II method and the MEREC weighting approach successfully found the optimal process variables for the WAAM of SS316L. PROMETHEE II analysis revealed the optimal parameter settings to be a WFS of 11 m/min, a TS of 450 mm/min, and a voltage of 27 V. The results highlight the effectiveness of PROMETHEE II in ranking and selecting the most suitable process parameters for SS316L deposition, offering valuable insights for improving the quality and efficiency of WAAM-based stainless steel manufacturing.

1. Introduction

Additive manufacturing (AM) creates products by layering one layer of material on top of another layer. It is becoming popular. The fabrication cost is reduced by up to 50% by using the AM technology compared to the conventional method [1]. It is therefore seen as an economical, realistic, creative, and reliable production method [2]. The main advantage of the AM process is that it reduces production time and material waste [3]. The direct fabrication of finished parts has been made possible in recent years by developments in AM technologies. Because of its many advantages, its application is expanding across a range of industries, including automotive, electronics, medicine, defense, and aerospace [4]. Metal AM is broadly categorized into three groups. Sheet lamination, direct energy deposition (DED), and powder bed fusion. WAAM is a DED process in which wire is used as a raw material [5]. Regardless of the usual GMAW method, WAAM-based technology with a GMAW source is used due to its low equipment cost, favorable mechanical properties, and high deposition rate [6]. A depositing speed in the order of 7.9 kg/h could be achieved with the GMAW-based WAAM approach. However, although it limits the surface quality and dimensional precision, a high metal deposition rate can lead to the production of enormous quantities of components [7]. A rapid rate of deposition, high temperature, and excessive energy input cause distortion and stresses. To obtain advantageous process characteristics, the process parameters such as TS, WFS, arc voltage, and path design should be investigated [8]. The TS plays an exceptional role in deciding the heat input per unit length and the cooling rate. A higher TS generally produces narrower beads and lower heat input, which can affect layer bonding. Conversely, lower TS leads to tremendous heat accumulation, causing distortion or dimensional inaccuracy. WFS controls the material deposition rate and, in conjunction with TS, impacts the bead geometry and wall thickness. An optimal WFS ensures a stable melt pool and compatible layer formation, while too high or too low WFS develops porosity, incomplete fusion, or irregular bead geometry. Arc voltage determines the arc length, distribution of heat, and melt pool dynamics. Higher voltages have a tendency to produce a wider and shallower weld pool, affecting layer overlap and quality of surface, whereas lower voltages result in deeper penetration but risk undercutting or a lack of fusion [9]. SS316L is the material of choice for fields such as nuclear reactors, petrochemical facilities, cars, biomedical equipment, and maritime and offshore applications because of its exceptional joining ability, excellent strength and exceptional ductility, strong biocompatibility, and low cost [10].

Le et al. [11] investigated the use of WAAM to optimize the process parameters of SS316L. They used gray relational analysis (GRA) and TOPSIS methods to examine voltage, FS, and TS. They measured output in the form of weld bead width, height, penetration, and dilution. They identified that the voltage has the greatest effect on BW and DOP, whereas the TS has the most significant effect on BW and BH. They found the optimal parameters to be as follows: voltage = 22 V; I = 110 A; and v = 0.3 m/min. Vora et al. [12] optimized the WAAM of SS309L. They adopted the BBD approach to perform trials of bead-on-plate input parameters of TS, V, and gas mixture ratio (GMR). They used a multi-objective Passing Vehicle Search (PVS) method to find the optimum parameters, which resulted as being TS at 20 mm/s, GMR 3, and a voltage of 22 V. Yu and Jhong [13] optimized the surface roughness of ER70S-6 steel components during WAAM. They validated the optimal setting by fabricating the wall structure. They found an optimal parameter set (20 cm/min, 130 A, 19 V). Vora et al. [14] built a wall using metal-cored wire of 2.25 Cr-1.0 Mo Steel. The input parameters were taken as WFS, TS, and voltage. These parameters were set by using TLBO. In the constrained range of inputs, the single-objective optimization outcome showed the highest BH of 7.81 mm and the lowest BW of 4.73 mm. Kesarwani and Yuvaraj [15] employed the Taguchi technique to reduce porosity and surface roughness. They found the optimal settings of the parameters to be 115 A for IER5, 90 A for IER4, and 6 mm/s for TS. Chaudhary et al. [16] performed a study optimizing the process parameters for the WAAM of SS316L. They adopted the Heat Transfer Search (HTS) technique to achieve the optimum combinations of input parameters. The results showed the optimum parameters as being WFS at 5.50 m/min, a TS of 141 mm/min, and a voltage of 19 V. Sargar et al. [17] compared the performance of CO2- and fiber laser-based machining. They adopted RSM-based BBD technique for their experimental plan. They developed an ANN model for predicting output at 98% accuracy and found that the CO2 laser performed better than the fiber laser. Ambore et al. [18] performed the dry turning of high-hardness materials using an RSM-based CCD design. A new ANN model based on real-time tool acceleration was suggested by them to assess tool wear. The R-squared value of the model was 0.93, which proved that reliability of the model in prediction. In their review, Gaikwad et al. [19] reported the effect of powder parameters, suitable process parameters, and different machine learning algorithms on powder-based AM. Gaikwad et al. [20] investigated the parametric effect on surface integrity during the EDM of NiTi60. Their results revealed that current is significant for MRR, voltage and current influence SR, and for WLT, voltage is a significant factor.

Jadhav et al. [21] developed a wall of SS316L using WAAM based on cold metal transfer (CMT). In the initial phase, the Box–Behnken experimental design was adopted to experiment with single-layer bead trials in flat and overhead positions using a variety of process parameters (i.e., WFR, TS, and wave amplitude). ANOVA was used with the bead cross-section readings to examine the impact of specific process parameters on the bead geometry. The wave amplitude has the greatest impact on BW among all process parameters for single-layer beads, whereas TS has the greatest impact on BH. Mamedeepaka et al. [22] studied the surface roughness and bead properties of WAAM, including height-to-width ratio and percentage dilution. Both the NSGA-II and the RSM-based desirability approach were used in multi-objective optimization. A fuzzy decision method was used to calculate the ideal parameters for NSGA-II, and the results were confirmed experimentally. When it came to response prediction, the NSGA-II method outperformed the conventional RSM-DA model. Findings in the literature highlighted that although WAAM of SS316L has gained significant attention due to its versatility and efficient material use, optimal parameter selection for wall structures remains a significant challenge. The parameter optimization has been mostly approached through trial-and-error or single-objective techniques, overlooking the complex multi-criteria nature of WAAM. While decision-making tools like PROMETHEE II offer a systematic approach to multi-criteria decision analysis, their application in the context of WAAM process parameter optimization is scarce. Furthermore, the integration of experimental validation with PROMETHEE II rankings was lacking in the literature. This highlighted a clear research gap in applying PROMETHEE II for systematically identifying the optimal process parameters for SS316L thin-wall structures, ensuring a balance between quality and efficiency.

2. Experimental Setup and Plan

The experimental setup of the present study is shown in Figure 1. The KEMPPI PRO MIG-530 (Kemppi, Chennai, India) was used as the power source for experiments. It features Wise root for root welding, as well as multiple processes like MIG, 1-MIG, pulsed MIG, MMA, and TIG. A metallic wire of SS316L was used as a spool to fabricate the multilayer structure with a diameter of 1.2 mm. The shielding gas used to construct this multilayer structured wall had a composition of 98% argon (Ar) and 2% oxygen. During the experimentation, the substrate plate of SS316L was mounted on the platform, and a torch was used to deposit the material onto the substrate, layer by layer. The input parameters considered for the present work were TS, WFR, and voltage. The levels of the process parameters were selected based on a literature review and preliminary study trials to find the parameter window. Initially, the 15 bead-on-plate (BOP) trials were performed using an RSM-based BBD design, as shown in Table 1. The BOP welds are shown in Figure 2. The output of BOP was measured in terms of BW, DOP, and BH as shown in Figure 3 and is presented in Table 2. The optimum process parameters were obtained using an MCDM PROMETHEE II method. The weights of the criteria were evaluated using the MCDM technique known as the “Method based on the Removal Effects of Criteria” (MEREC). The steps of the MEREC and PROMETHEE II methods are presented in sections B and C, respectively. The chemical composition for SS316L in wt% is Cr 16.08, Ni 10.42, Mo 2.28, Mn 1.17, Si 0.68, C 0.01, P 0.014, S 0.009, N 0.09, and Fe balance.

Figure 1. The experimental setup for WAAM.

Table 1. Process parameters and levels.

Level	A	B	C
	Torch Travel Speed (TS)	Voltage (V)	Wire Feed Speed (WFS)
1	400	25	9
2	450	26	10
3	500	27	11

Figure 2. Bead-on-plate trials.

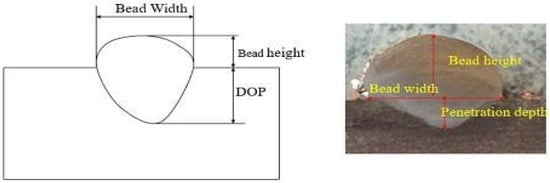
Figure 3. Schematic of the output variable measured.

Table 2. Experimental plan using BBD and measured output.

WFS (m/min)	Travel Speed (mm/min)	Voltage (V)	Bead Width (mm)	DOP (mm)	Bead Height (mm)
11	450	27	8.174	5.478	4.27
9	400	26	7.686	1.871	3.981
10	450	26	7.022	1.608	3.917
11	500	26	6.681	0.147	4.227
11	450	25	7.613	0.148	4.108
11	400	26	9.109	2.55	3.861
10	500	25	8.154	1.89	3.725
9	450	25	7.98	1.976	3.257
9	500	25	7.263	1.679	3.65
9	450	27	8.548	1.964	3.357
10	450	26	7.697	1.424	3.657
10	450	26	7.35	1.636	4.12
10	450	26	7.192	1.484	4.589
10	400	25	7.144	1.388	4.005
10	500	27	8.344	1.826	3.694

2.1. MEREC Steps

Step 1: The elemental data of the normalized matrix are denoted by $n_{ij}^x$. For the normalization of benefit and cost criteria, the equations below can be used:

For Beneficial:

$$n_{ij}^x={\displaystyle \frac{{\mathrm{m}\mathrm{i}\mathrm{n}(X}_{ij})}{X_{ij}}}$$

(1)

For non-Beneficial:

$$n_{ij}^x={\displaystyle \frac{X_{ij}}{{\mathrm{m}\mathrm{a}\mathrm{x}(X}_{ij})}}$$

(2)

Step 2: Find out the overall performance of the alternative.

$$S_i=\mathit{ln}\left(1+\left({\displaystyle \frac{1}{m}}\right)\ast {\Sigma }_j\left|\mathit{ln}\left(n_{\left\{X_{ij}\right\}}^{\ast }\right)\right|\right)$$

(3)

Step 3: Calculate the performance of alternatives by eliminating each criterion.

$$S_{\left\{ij\right\}}^{\mathrm{’}}=\mathit{ln}\left(1+\left({\displaystyle \frac{1}{m}}\right)\ast {\Sigma }_{\left\{k\ne j\right\}\left|\mathit{ln}\left(n_{\left\{X_{ij}\right\}}^{\ast }\right)\right|}\right)$$

(4)

Step 4: Compute the summation of absolute deviation.

$$E_j={\Sigma }_i\left|S_{\left\{ij\right\}}^{\mathrm{’}}-S_i\right|$$

(5)

Step 5: Determine the final weight of the criteria.

$$w_j={\displaystyle \frac{E_j}{{\Sigma }_k}}{E}_k$$

(6)

2.2. PROMETHEE II Steps

The preference ranking organization method for enrichment evaluation (PROMETHEE) is an MCDM method used to provide the rank ordering of the decision options. It was produced by Brans and Vincke in 1985 [23]. There are two methods, PROMETHEE I and PROMETHEE II. PROMETHEE I gives the partial ordering of the decisive alternative. PROMETHEE II gives the full ranking of the alternatives. PROMETHEE II handles both qualitative and quantitative criteria constructively without the need for ratio-scale judgments. It has flexibility for customized preference functions for each criterion, enabling more successful modeling of real-world decision behaviors. PROMETHEE II delivers a complete ranking of alternatives using net flow scores. PROMETHEE II uses direct weight assignment and avoids complex comparison matrices, unlike AHP. This research used PROMETHEE II to obtain the full ranking among alternatives. The procedure steps are performed as outlined below.

Step 1: Normalize the decision matrix.

For the beneficiary criteria,

$$R_{ij}=\left({\displaystyle \frac{X_{ij}-\min \left(X_{ij}\right)}{\max \left(X_{ij}\right)-\min \left(X_{ij}\right)}}\right) \left(i=1,2,\dots ,n;j=1,2,\dots ,m\right)$$

(7)

where $X_{ij}$ is the measure of the performance of the ith alternative concerning the jth criterion.

For non-beneficial criteria, Equation (1) can be rewritten as follows:

$$R_{ij}=\left({\displaystyle \frac{\max \left(X_{ij}\right)-X_{ij}}{\max \left(X_{ij}\right)-\min \left(X_{ij}\right)}}\right)$$

(8)

Step 2: Determine how this choice differs from the others in terms of evaluation. This stage entails calculating the pairwise differences in criterion values between several alternatives.

Step 3: Calculate the preference function, $P\left(i,i^{\prime }\right)$.

There are six major categories of generalized preference functions. However, to use these preference functions, certain preferred factors, like the preference and indifference thresholds, must be defined. However, in real-time applications, the decision maker may find it challenging to identify the parameters involved and to indicate which kind of preference function is appropriate for each criterion. Here, the following streamlined preference function is used to get around this issue:

For the preference function,

$$P\left(i,i^{\prime }\right)=0 if R\left(i,j\right)\le R\left(i^{\prime },j\right)$$

(9)

$$P\left(i,i^{\prime }\right)=\left(R\left(i,j\right)-R\left(i^{\prime },j\right)\right) if R\left(i,j\right)>R\left(i^{\prime },j\right)$$

(10)

Step 4: Compute the aggregated preference function while accounting for the weights of the criterion.

Aggregated equation:

$$\pi \left(i,i^{\prime }\right)=\left({\displaystyle \frac{{\sum }_{j=1}^m{w}_j\times P_j\left(i,i^{\prime }\right)}{{\sum }_{j=1}^m{w}_j}}\right)$$

(11)

Here, $w_j$ is the weight of the jth criterion.

Leaving flow:

$${\varphi }^{+}\left(i\right)={\displaystyle \frac{1}{n-1}}\sum _{i^{\prime }=1,i^{\prime }\ne i}^n\pi \left(i,i^{\prime }\right)$$

(12)

Entering flow:

$${\varphi }^{-}\left(i\right)={\displaystyle \frac{1}{n-1}}\sum _{i^{\prime }=1,i^{\prime }\ne i}^n\pi \left(i^{\prime },i\right)$$

(13)

Every option in this case encounters a (n − 1) other options. How much one alternative dominates the others is expressed by the leaving flow, and how much one alternative is dominated by the others is indicated by the incoming flow. Although it loses a lot of information about preference relations, the PROMETHEE II approach can provide the full pre-order by employing a net flow.

Step 6: Determine each alternative’s net outranking flow.

$$\varphi \left(i\right)={\varphi }^{+}\left(i\right)-{\varphi }^{-}\left(i\right)$$

(14)

Step 7: Based on the values of $\varphi \left(i\right)$, rate each of the alternatives that were taken into consideration. The better the alternative, the greater the value of $\varphi \left(i\right)$. Therefore, the option with the largest $\varphi \left(i\right)$ value is the best one.

With discrete options, PROMETHEE is an interactive technique that handles both qualitative and quantitative criteria. This approach calculates a preference function for each criterion by comparing the alternatives in a pairwise fashion. A preference index for alternative i over i′ is calculated using this preference function. The metric used to support the idea that option i is preferred over i′ is the preference index. Because assessment standards have a trade-off relationship, the PROMETHEE approach can categorize alternatives that are hard to compare as they present as non-comparable alternatives.

3. Results and Discussion

Criteria weight calculation using MEREC:

The weightage was given using the MCDM technique MEREC [24]. This approach uses variations in each alternative’s performance for each criterion to calculate the weights. A higher weight is assigned to the criterion with the most variations.

Normalization is performed by using Equations (1) and (2). The normalized decision matrix is presented in Table 3. After obtaining the normalized equation, calculate the overall performance of the alternative by using Equation (3). Calculate the performance of alternatives by removing each criterion $X_{ij}$ using Equation (4) and compute the summation of absolute deviation using Equation (5) and is shown in Table 4. The final weights that we obtained using Equation (6) are 0.88065 for DOP, 0.06049 for BH, and 0.05886 for BW.

Table 3. Normalized data and overall performance.

Sn. No.	Normalized Data			${\mathit{S}}_{\mathit{i}}$
	DOP	BH	BW
1	0.0268	0.7628	0.8974	0.846894
2	0.0786	0.8181	0.8438	0.678775
3	0.0914	0.8315	0.7709	0.665613
4	1.0000	0.7705	0.7335	0.174144
5	0.9932	0.7928	0.8358	0.130535
6	0.0576	0.8436	1.0000	0.697062
7	0.0778	0.8744	0.8952	0.659058
8	0.0744	1.0000	0.8761	0.647229
9	0.0876	0.8923	0.7973	0.655084
10	0.0748	0.9702	0.9384	0.639415
11	0.1032	0.8906	0.8450	0.616097
12	0.0899	0.7905	0.8069	0.669398
13	0.0991	0.7097	0.7895	0.67485
14	0.1059	0.8132	0.7843	0.640961
15	0.0805	0.8817	0.9160	0.64764
max	5.4780	4.5890	9.1090
min	0.1470	3.2570	6.6810

Table 4. Performance of alternatives.

	${\mathit{S}}_{\mathit{i}\mathit{j}}^{\mathit{’}}$			${\mathit{E}}_{\mathit{j}}$
	Beneficial	Beneficial	Non-Beneficial	Beneficial	Beneficial	Non-Beneficial
Ex No.	DOP	BH	BW	DOP	BH	BW
1	0.1190	0.8074	0.8313	0.7279	0.0395	0.0156
2	0.1165	0.6442	0.6496	0.5623	0.0345	0.0291
3	0.1382	0.6335	0.6200	0.5274	0.0321	0.0456
4	0.1741	0.0983	0.0833	0.0000	0.0758	0.0908
5	0.1286	0.0602	0.0766	0.0020	0.0703	0.0539
6	0.0552	0.6684	0.6971	0.6419	0.0286	0.0000
7	0.0785	0.6356	0.6398	0.5806	0.0234	0.0193
8	0.0432	0.6472	0.6239	0.6041	0.0000	0.0234
9	0.1075	0.6352	0.6151	0.5476	0.0199	0.0400
10	0.0308	0.6341	0.6282	0.6086	0.0053	0.0112
11	0.0905	0.5950	0.5853	0.5256	0.0211	0.0308
12	0.1396	0.6285	0.6321	0.5297	0.0409	0.0373
13	0.1765	0.6149	0.6339	0.4983	0.0600	0.0409
14	0.1397	0.6040	0.5974	0.5013	0.0370	0.0436
15	0.0688	0.6254	0.6322	0.5789	0.0222	0.0154
	Sum			7.4361	0.5107	0.4970

Ranking evaluation using PROMETHEE II:

In this case, we have found the decision matrix by using the L15 method and is presented in Table 5. Furthermore, the decision matrix is normalized by using Equations (7) and (8). When the criteria are beneficial, then Equation (7) is used. For non-beneficial criteria, Equation (8) is used. In this study, BH and DOP are beneficial, and BW is a non-beneficial criterion.

Table 5. Decision matrix.

Weights	0.881	0.060	0.059	Normalized Data
Experiment	DOP	Bead Height	Bead Width	DOP	Bead Height	Bead Width
1	5.478	4.270	8.174	1.000	0.761	0.385
2	1.871	3.981	7.686	0.323	0.544	0.586
3	1.608	3.917	7.022	0.274	0.495	0.860
4	0.147	4.227	6.681	0.000	0.728	1.000
5	0.148	4.108	7.613	0.000	0.639	0.616
6	2.550	3.861	9.109	0.451	0.453	0.000
7	1.890	3.725	8.154	0.327	0.351	0.393
8	1.976	3.257	7.980	0.343	0.000	0.465
9	1.679	3.650	7.263	0.287	0.295	0.760
10	1.964	3.357	8.548	0.341	0.075	0.231
11	1.424	3.657	7.697	0.240	0.300	0.582
12	1.636	4.120	7.350	0.279	0.648	0.724
13	1.484	4.589	7.192	0.251	1.000	0.790
14	1.388	4.005	7.144	0.233	0.562	0.809
15	1.826	3.694	8.344	0.315	0.328	0.315
${\mathrm{m}\mathrm{i}\mathrm{n}(X}_{ij})$	0.147	3.257	6.681
${\mathrm{m}\mathrm{a}\mathrm{x}(X}_{ij})$	5.478	4.589	9.109

After finding the normalized matrix, preference functions are found by using Equations (9) and (10), as shown in Table 6.

Table 6. Preference function.

Experiment	DOP	Bead Height	Bead Width
D(E1–E1)	0.000	0.000	0.000
D(E1–E2)	0.677	0.217	−0.201
D(E1–E3)	0.726	0.265	−0.474
. . . .	. . . .	. . . .	. . . .
D(E15–E14)	0.082	−0.233	−0.494
D(E15–E15)	0.000	0.000	0.000

After finding the preference functions, aggregated functions are found by using Equation (11), as shown in Table 7.

Table 7. Aggregated functions.

Weights	0.881	0.060	0.059	n ∑ wjpj j = 1
D(E1–E1)	0.000	0.000	0.000	0.000
D(E1–E2)	0.596	0.013	0.000	0.609
D(E1–E3)	0.639	0.016	0.000	0.655
. . . .	. . . .	. . . .	. . . .	. . . .
D(E15–E14)	0.072	0.000	0.000	0.072
D(E15–E15)	0.000	0.000	0.000	0.000

After obtaining the aggregated function, the leaving flow and entering flow are calculated by using Equations (12) and (13), and the same is presented in Table 8. After obtaining the leaving and entering flow, the final outranking flow is to be calculated by using Equation (14), and the final ranking is decided based on the results of the outranking flow, as shown in Table 8. As we can see, the first experiment has the first rank, which means that it is the most feasible.

Table 8. Leaving and entering flow.

Experiment	Leaving Flow	Entering Flow	Rank
1	0.672	0.015	1
2	0.081	0.064	3
3	0.067	0.082	7
4	0.045	0.295	14
5	0.021	0.301	15
6	0.172	0.078	2
7	0.073	0.077	4
8	0.083	0.090	5
9	0.062	0.084	11
10	0.078	0.097	9
11	0.040	0.118	13
12	0.068	0.077	7
13	0.082	0.091	6
14	0.055	0.108	12
15	0.065	0.086	10

The multilayer wall was developed using optimal settings achieved using PROMETHEE II, as shown in Figure 4.

Figure 4. Additively manufactured wall of SS316L.

4. Conclusions

The present study investigated the influence of key process variables—welding speed, wire feed rate, and voltage—during the development of a wall of SS316L using WAAM. A total of 15 bead-on-plate experimental trials were performed using an RSM-based BBD technique. The MEREC weighting method was employed to determine the relative importance of these criteria. The MCDM technique, PROMETHEE II, was adopted to find the optimal parameter settings for the output BW, BH, and DOP. Based on experimental and statistical analysis, the following conclusions are drawn:

• The MEREC technique gave the weights of the criteria as 0.88065 for DOP, 0.06049 for BH, and 0.05886 for BW;
• PROMETHEE II analysis revealed the optimal parameter settings to be WFS of 11 m/min, TS of 450 mm/min, and voltage of 27 V.
• The multi-layered wall was successfully fabricated using optimized parameters obtained using PROMITHEE II;
• The optimized parameter settings successfully developed a wall of SS316L using WAAM.