Dimensional Precision of Plastic Gear Tooth Profiles Produced by 3D Printing ^†

Abstract

Plastic spur gears have gained significant attention in the last couple of decades in all industries where rotational motion is involved. Plastic gears have the advantages of light weight, shock absorption, low operation noise levels, and functioning without lubrication. However, the manufacturing precision of gears and gear tooth profiles has a significant effect on the lifetime of the gears. The aim of this study was to investigate the effect of 3D printing (Fused Deposition Modeling) parameters on the precision of the tooth profile. To study the effect of layer thickness, printing speed, and infill parameters, the Box–Behnken experimental design was utilized. The results show that the mean profile deviation was 0.067 ± 0.02 mm, and the printing speed had a statistically significant effect on the precision of the tooth profile. Plastic 3D printing provides more design freedom; therefore, it is a promising technology for low production volumes and special geometry gear manufacturing.

1. Introduction

One of the most important and reliable ways to transmit rotary motion is to use spur gears. Sliding between the contact areas of spur gear teeth is less prominent than in the case of belts or chain drives, thus it is more reliable [1]. Consequently, spur gears are utilized in every industry, from automotive and medical to the aerospace industry. The magnitude of the spur gear market size illustrates, probably better than anything, the ubiquitous use of this special component: the market size was USD 150 million in 2023, and it is estimated to reach USD 218 million by 2030 [2].

While spur gears can be manufactured with various tooth profiles, the involute tooth profile became almost exclusively used due to ease of fabrication and its tolerance to deviations in axis distance. The production of metal spur gears requires specific tools and machinery, and thus it is rather expensive [3]. Metal gears have the advantage of high efficiency and the capability to transmit high torque; however, they are noisy, require lubrication during operation, and are heavy. Some of these disadvantages can be avoided by replacing metal gears with plastic gears in several low or medium-torque applications. Nowadays, plastic gears can be found in a variety of fields, including the automotive, medical, HVAC, and food industries [4]. Plastic spur gears have several advantages, such as low production cost, low mass, quiet operation, shock dissipation, and operation without the use of lubrication [5].

Plastic gears can be produced by gear cutting, although these manufacturing processes are expensive, and they are only used in special cases. In general, plastic gears are produced by injection molding. This process also requires a high upfront cost of investment; however, this is balanced out by high production volume and short cycle times. With the rapid development of plastic processing techniques, it is estimated that with batch sizes under 1000 pieces, it is more beneficial to fabricate plastic spur gears with additive manufacturing, such as Material Extrusion (MEX), 3D printing with the Fused Deposition Modeling (FDM) technique, than with injection molding [6]. The MEX FDM method involves the melting of a plastic filament and the production of the desired geometry layer by layer.

MEX FDM 3D printing has several parameters that influence the dimensional accuracy of the produced parts. Dimensional accuracy is one of the most important features when it comes to spur gears to produce a constant gear ratio during operation. This means that both the dimensional accuracy and tooth profile accuracy are required. Several scientific publications deal with the effect of MEX FDM 3D printing process parameters on the dimensional accuracy of parts of varying geometries [7,8]. While all process parameters influence the dimensional accuracy of the printed parts to some degree, printing temperature, printing speed, layer thickness, number of contours, and infill density are the major contributors. We have previously investigated the effect of layer thickness, printing speed, and infill printing parameters on the dimensional, form, and orientation deviations of spur gears prepared by 3D MEX FDM printing. In the case of spur gears, the surface roughness and dimensional accuracy are key, but so is the loading capacity, which is directly related to the infill parameter. Our results showed that only the infill density had a statistically significant effect on the perpendicularity of the bore relative to the front surface of the gears [9].

Tooth profiles can be measured by using GOM systems [10], 3D scanners [11], line spectral confocal methods [12], or coordinate measuring machines [13]. While several studies deal with the dimensional accuracy of printed spur gears, there is a lack of investigation into tooth profile accuracy. The tooth profile geometry is the most basic gear parameter that influences the gear ratio. This work aims to investigate the effects of layer thickness, printing speed, and infill density on the tooth profile accuracy of spur gears with the aid of Box–Behnken experimental design. Furthermore, we developed a methodology that allows for the examination of an involute tooth profile.

2. Experimental Procedure

2.1. Materials

The gears were printed from a polylactic acid (PLA) filament (Sunlu PLA Black 1510101A, Zhuhai Sunlu Industrial Co., Ltd., Zhuhai, Guangdong, China) with a diameter of 1.75 mm.

2.2. Three-Dimensional Modeling

The 3D model of the gear was created in CATIA V5R17 (Dassault Systèmes SE, Vélizy-Villacoublay, France) in the Generative Shape Design and Part Design workbenches. The 3D model was based on a commercially available steel spur gear (Model no. PM 30021, SATI S.p.A, Bologna, Italy) that had z = 21 teeth and a module of m = 3 mm. The parametric equation system used to generate the involute tooth profile was the one that applies when gearing is performed with a rack cutter, as follows:

$$\left\{\begin{array}{c}\mathrm{x}\left(\mathrm{\phi }\right) = {\mathrm{R}}_{\mathrm{d}}·\cos \left(\mathrm{\phi }\right)- {\mathrm{R}}_{\mathrm{d}}·\mathrm{\phi }·\cos \left(\mathrm{\alpha }\right)·\cos (\mathrm{\alpha } + \mathrm{\phi })\\ \mathrm{y}\left(\mathrm{\phi }\right) ={ \mathrm{R}}_{\mathrm{d}}·\sin (\mathrm{\phi }) +{ \mathrm{R}}_{\mathrm{d}}·\mathrm{\phi }·\cos \left(\mathrm{\alpha }\right)·\sin (\mathrm{\alpha } + \mathrm{\phi })\\ \mathrm{z}\left(\mathrm{\phi }\right) = 0\end{array},\right.$$

(1)

where the pitch circle radius, R_d = 31.5 mm, and the pressure angle of the standard rack, α = 20°, and φ is the parameter. The involute was generated once, then multiplied with mirror and pattern functions.

2.3. Experimental Design

The 3-factor Box–Behnken design (BBD) was generated in MiniTab 16 (Minitab, LLC, State College, PA, USA). The selected parameters were the layer thickness, printing speed, and infill density. Scouting experiments were performed to determine the limiting values for each parameter. Table 1 shows the values for the three levels in each case. The design was created with 3 center points.

Table 1. Box–Behnken experimental design parameters and levels.

Printing Parameter	Low (−1)	Middle (0)	High (+1)
Layer thickness (mm)	0.1	0.15	0.2
Printing speed (mm/s)	40	80	120
Infill density	10%	30%	50%

2.4. Three-Dimensional Printing

The printing was performed with an Artillery Sidewinder X2 3D printer (Shenzhen Yuntu Chuangzhi Technology Co., Ltd., Shenzhen, China). The G-code used by the printer was generated in the PrusaSlicer 2.6 software (Prusa Research, Prague, Czechia) based on its 0.2 mm SPEED Prusa preset, and only the parameters listed in Table 1 were adjusted. The operating temperatures of the nozzle and the table were set at 210 °C and 60 °C, respectively. The gears were printed with a honeycomb (hexagonal) infill pattern and had a thickness of 10 mm. The 15 printed gears were given an ID between G01-15, based on their position in the BBD.

2.5. Coordinate Metrology

The alignment of the gear was realized with the help of a vice and three 8 mm pins. The pins were inserted between the teeth and the jaws of the vice, ensuring consistent rotation. A vice-stop and a gauge block serving as a spacer were used to determine the linear position parallel to the vice jaws.

Coordinate measurement was carried out using a Hexagon TIGO SF coordinate measuring machine (CMM, Hexagon AB, Stockholm, Sweden). The CMM had an associated maximum permissible measuring error E_0,MPE = 2.6 + L/300 μm, and probing error P_FTU = 2.6 μm in the 18–22 °C temperature range, where L is the measured distance in mm. The setup involved a HH-MI-M manual indexing probe head and an HP-TM-MF touch trigger probe equipped with a 40 mm long steel stylus with a spherical ruby tip of 2 mm diameter. The measurements were carried out at 18 ± 0.5 °C.

The software associated with the CMM was Hexagon PC-DMIS 2019. Since the gear module was not included in the software package, the involute profiles were measured with individual vector points. In the case of the steel gear, 5 points were taken on each tooth face, on both sides of 10 teeth. In the case of the 3D-printed gears, 9 points were taken on each tooth surface in the middle plane of the gear (i.e., in 5 mm depth from the frontal surface).

3. Results and Discussion

3.1. Data Fitting

Figure 1a shows the frontal view of the gear and the involute tooth profile. The circles marked in the drawing belong to the addendum (D_a, 69 mm), dedendum (D_d, 56 mm), and bore (D_b, 15 mm). The CMM measurements were performed on two left (1L, 3L) and two right side tooth profiles (1R, 2R).

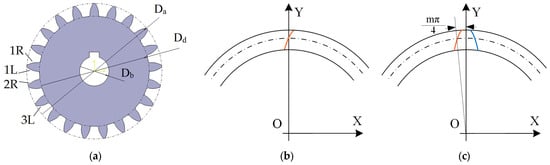
Figure 1. (a) Frontal view of the 3D model of the gear in CATIA V5. The studied profiles are denoted as 1R, 1L, 2R, and 3L. Tooth profiles in various stages during modeling; (b) Theoretical tooth profile generated with the parametric equations; (c) Left-side profile rotated to its intended position (orange) and the right-side profile created by mirroring (blue).

The values of the running φ parameter were chosen in a way that the involute was situated between the base circle and the addendum circle (Figure 1b). A rotation by the circular pitch/4 (${\displaystyle \frac{\mathrm{m}\mathrm{\pi }}{4}}$) around the OZ axis was performed to place the involute profile where eventually the tooth surface would be on the 3D model, and the Y axis would serve as an axis of symmetry (Figure 1c).

The mathematical description of the rotation can be performed with coordinate transformation, by using transformation matrices. The T₁ matrix in Equation (2) provides rotation around the OZ axis with an angle equal to ${\displaystyle \frac{\mathrm{m}\mathrm{\pi }}{4}}$, where m is the module in mm. The left tooth profile is given in terms of φ, as follows:

$${\mathrm{P}}_{\mathrm{L}}={\mathrm{T}}_1\mathrm{P}=\left[\begin{array}{cccc}\cos \left({\displaystyle \frac{\mathrm{m}\mathrm{\pi }}{4}}\right)& \sin \left({\displaystyle \frac{\mathrm{m}\mathrm{\pi }}{4}}\right)& 0& 0\\ -\sin \left({\displaystyle \frac{\mathrm{m}\mathrm{\pi }}{4}}\right)& \cos \left({\displaystyle \frac{\mathrm{m}\mathrm{\pi }}{4}}\right)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}\mathrm{x}\left(\mathrm{\phi }\right)\\ \mathrm{y}\left(\mathrm{\phi }\right)\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_{\mathrm{L}}\left(\mathrm{\phi }\right)\\ {\mathrm{y}}_{\mathrm{L}}\left(\mathrm{\phi }\right)\\ 0\\ 1\end{array}\right],$$

(2)

where x(φ) and y(φ) are given in Equation (1), and φ is in the range of −0.364–0.237 rad. The right profile is acquired by mirroring the left profile across the OY axis (Figure 1c). This was achieved by rotating the left profile by 180° around the OY axis, as follows:

$${\mathrm{P}}_{\mathrm{R}}={\mathrm{T}}_2{\mathrm{P}}_{\mathrm{L}}=\left[\begin{array}{cccc}\cos \left(\mathrm{\pi }\right)& 0& \sin \left(\mathrm{\pi }\right)& 0\\ 0& 1& 0& 0\\ -\sin \left(\mathrm{\pi }\right)& 0& \cos \left(\mathrm{\pi }\right)& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\mathrm{x}}_{\mathrm{L}}\left(\mathrm{\phi }\right)\\ {\mathrm{y}}_{\mathrm{L}}\left(\mathrm{\phi }\right)\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c}{\mathrm{x}}_{\mathrm{R}}\left(\mathrm{\phi }\right)\\ {\mathrm{y}}_{\mathrm{R}}\left(\mathrm{\phi }\right)\\ 0\\ 1\end{array}\right] ,$$

(3)

The evaluation consisted of enveloping the measured data points with two involutes. The normal distance between the two curves is the total profile deviation, as defined in the ISO 1328-1 standard [14]. In the first step the radial distance between a measured point on the tooth, ${\mathrm{M}}_{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{Mi}},{\mathrm{y}}_{\mathrm{Mi}}\right)$ and the center point $\mathrm{C}\left({\mathrm{x}}_{\mathrm{C}},{\mathrm{y}}_{\mathrm{C}}\right)$ is calculated. At this M_iC radius a point is acquired on the generated involute, denoted by the letter E. With these three points the ${\mathrm{r}}_{\mathrm{CM}}$ and ${\mathrm{r}}_{\mathrm{CE}}$ vectors are defined, and the angle between the two vectors is then calculated using their dot product, as follows:

$${\mathrm{\xi }}_{\mathrm{i}}={\cos }^{-1}\left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{CM}\mathrm{i}}·{\mathrm{r}}_{\mathrm{CE}}}{{\mathrm{r}}_{\mathrm{CM}\mathrm{i}}{\mathrm{r}}_{\mathrm{CE}}}}\right),$$

(4)

These steps were repeated for all the measured points, and then the lowest and the highest ξ_i angles were used to rotate the involute, yielding the deviation zone for the respective profile (Figure 2a). The total profile deviation is the normal distance between the two involutes, and these values were used as the response of the experimental design, as specified in ISO 1328-1.

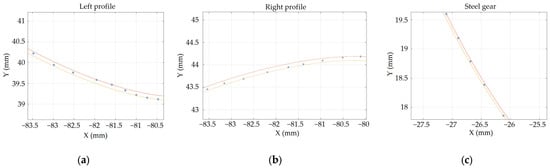
Figure 2. Definition of the total profile deviation zone according to ISO 1328-1 in the case of (a) 1L; (b) 1R of the plastic gears, and (c) the steel gear. The deviation is calculated as the normal distance between the yellow and red bounding involutes.

3.2. Evaluation of the Steel Gear

The measurement on the steel gear was limited to the middle part of the tooth face, since its teeth had tip and root relief. A point set taken on one of the tooth faces can be seen in Figure 2c. The average total profile deviation at the right profiles was 0.032 ± 0.012 mm, while at the left profiles it was 0.039 ± 0.011 mm. The first observation is that the mean deviation values differed on the right and left sides of the teeth, and on eight out of the ten teeth, the deviation of the left profile was larger. There was no reason to believe that the profile deviation population did not follow a normal distribution, so Student’s t-test was used to determine the significance of this difference. The t-test resulted in a p-value of 0.201, suggesting that the difference is not statistically significant. The deviation being larger on the left side of the teeth could be observed regardless of the position of the studied tooth, which indicates that the profile error was not caused by the rotational or positional deviations relative to the reference frame during measurement.

3.3. Evaluation of the 3D-Printed Gears

The printing conditions, as given by the Box–Behnken design, and the measurement results for each gear are presented in Table 2. There were three center points included in the design, and so the table contains the combination of factors of 0.15 mm layer thickness, 80 mm/s printing speed, and 30% infill density three times (no. 3, 9, and 12).

Table 2. Printing conditions of the 15 produced gears.

ID	Layer Thickness (mm)	Printing Speed (mm/s)	Infill	ID	Layer Thickness (mm)	Printing Speed (mm/s)	Infill
G01	0.15	120	50%	G09	0.15	80	30%
G02	0.1	120	30%	G10	0.2	120	30%
G03	0.15	80	30%	G11	0.15	120	10%
G04	0.2	80	10%	G12	0.15	80	30%
G05	0.1	80	10%	G13	0.15	40	10%
G06	0.2	80	50%	G14	0.2	40	30%
G07	0.15	40	50%	G15	0.1	40	30%
G08	0.1	80	50%	-	-	-	-

Printing repeatability can be studied by examining the center points. Table 3 summarizes the profile deviation results for G03, G09, and G12 center points.

Table 3. Average profile deviation values for the three (0, 0, 0) gears at four different tooth faces.

	1R	2R	1L	3L
Mean (mm)	0.0702	0.0818	0.0944	0.0562
Stdev (mm)	0.0075	0.0117	0.0075	0.0121

The standard deviations are similar to the 0.011 (left side) and 0.012 mm (right side) observed in the case of the steel gear. The difference between the means is larger than their standard deviation, and it is between 0.01 and 0.04 mm. For example, the deviation from 2L to 1L increases by 0.038 mm, which is a 68% increase. On the other hand, the difference between 1R and 2R is 0.011 mm, a 16% increase. This suggests that there is a lot of variability in the performance of the printer, not only in repeatedly producing a given geometry at the same spot on the bed (deviation within a group), but also in creating the same geometry at different parts of the bed (difference in the means). The difference turned out to be statistically significant with p = 0.008 (adj. R-sq. = 66%), but Tukey’s method for multiple comparisons revealed that the difference is only significant between 1L and 3L. Looking only at the mean deviation does not provide the full picture. In contrast to the steel gear, where the measured involute profile showed a certain degree of rotation (Figure 2c), in the case of the printed gears, the profile deviation originates from the waviness of the tooth surface, as indicated by the points in Figure 2a,b.

The effects of the printing parameters on the profile deviation were examined on 4 teeth. These are summarized in Table 4.

Table 4. ANOVA results for the four tooth profiles individually and combined.

	1R	2R	1L	3L	Combined
R-squared (%)	90.29	84.14	92.59	66.71	50.94
R-sq. adj. (%)	72.80	55.59	79.25	6.80	42.10
p < 0.05	L, S*S, L*I	S*S	S, S*S	-	S (0.001), S*S (0.000), L*I (0.005)
p < 0.15	S*I	L, L*I	L, I, L*I	L*L	-

The 3L group featured the poorest fit, with an adjusted R-squared of 6.8%, and none of the printing parameters showed a significant effect on the total profile deviation. Looking at the 1R, 2R, and 1L groups, both the L and L*I show up in all three groups when p < 0.15, although p < 0.05 only in the case of 1R. There is an increase in deviation when transitioning from 0.15 to 0.2 mm by 5–9 μm, and the deviation is roughly the same at 0.1 mm and 0.15 mm. At 0.1 mm layer thickness, the deviation decreases from 0.09 to 0.1 to 0.04–0.07 mm as the infill increases from 10% to 50%.

The S*S quadratic term was found to be significant in all three cases, indicating a curvature in the response. Regarding the S, the deviation increases from 0.045 to 0.08 mm on average when the speed goes from 40 to 80 mm/min, and drops between 80 and 120 mm/min; however, these values range from 0.002 to 0.019 mm. In general, it is expected that at higher speeds (and higher accelerations), the position control of the servo motors is less accurate. Depending on the frequency characteristics of the printer, it is possible that at a certain speed (in this case, 80 mm/min), the amplitude of the oscillations is higher than either at 40 mm/min or 120 mm/min, causing a larger profile deviation.

The combined data was also examined. For each gear, four profile deviation values (1R, 2R, 1L, 3L) were considered. Even though the data sets were not proper replicates, as at least one parameter, the position on the printing bed was different, the combined analysis still carries the benefit of a four times larger data set, compared to any of the single profile analyses. At the same time, different teeth having different positions on the printing bed is an inherent property of the manufacturing process when printing with a Cartesian 3D printer equipped with a fixed printing bed. For this reason, the model should be created in a way that can be applied to all profiles, not just a single one.

The average total profile deviation for the combined data set was 0.067 ± 0.02 mm, which is roughly twice as much as in the case of the steel gear produced by gear hobbing. As a basis of comparison, tolerances from the ISO 1328-1 standard were considered. According to the standard, the metal gear belongs to IT10 (44 µm for the given diameter and module) precision class, and the 3D-printed gear falls into the IT12 (89 µm) precision class. The decreased precision of plastic gears compared to the metal gear indicates that 3D-printed gears are more suitable for applications where high precision is not required, such as window-moving mechanisms in the automotive industry, power tools, etc.

The normal probability plot can be seen in Figure 3a. Since p = 0.663 > 0.05, we cannot reject the H₀, which states that the data follow a normal distribution. The data points, marked with red dots, cluster around the blue reference line, which is also an indication of normal distribution.

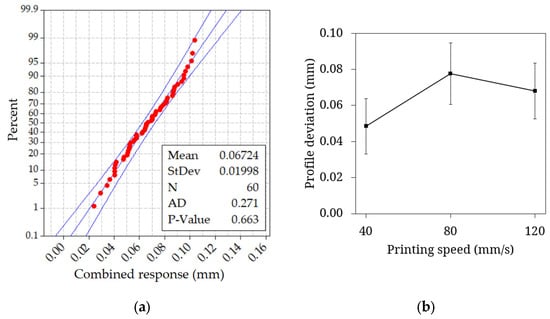
Figure 3. Combined data: (a) normal probability plot; (b) main effect plot of S.

ANOVA showed that S, S*S, and L*I have a p-value < 0.05 (Table 4). As with the 1L profile, changing the printing speed from 40 to 80 mm/s caused an increase in profile deviation from 0.048 to 0.077 mm, but further increasing it to 120 mm/s resulted in a drop to 0.068 mm (Figure 3b). The model carries a coefficient of determination (R-squared) of 50.94%, meaning that ~50% of the observed variation in the profile deviation can be explained by the influence of the studied printing parameters. This indicates that there may be factors of high importance that were not included in the study. One of these can be the position of the teeth, and earlier we saw that the deviation can change in terms of position.

4. Conclusions

In summary, the effect of layer thickness, printing speed, and infill density as 3D printing parameters on tooth profile accuracy of spur gears was studied. We have developed a method to quantify the profile deviation by using bounding involutes. The statistical analysis suggests that only printing speed has a significant effect on the involute tooth profile accuracy. It should be noted that printing speed influences the residence time of the filament, which in turn influences the rheological properties of the molten filament, which could result in printing defects. We benchmarked our results against a commercial metal gear and found that the profile deviation was approximately two times higher, 0.067 ± 0.02 mm, for the 3D-printed gears. This finding suggests that, although 3D printing is an accessible alternative for gear production, it cannot replace traditional gear-cutting technologies when high accuracy is needed. However, 3D printing is a promising and fast-developing technology for producing functional machine elements.