Predicting Gear Noise Levels in Electric Multiple Units Based on Microgeometry Modifications Using Clustering and Inverse Distance Weighting ^†

Abstract

Reducing noise in electric multiple-unit (EMU) gearboxes demands prediction tools that are both rapid and reliable. Gear sound pressure levels vary sharply with micrometre-scale changes such as tooth repair, inclination, or profile relief, yet traditional estimates depend on hours-long CAE simulations. We present a data-driven hybrid surrogate that combines k-means clustering and inverse distance weighting (CLS-IDW) within the ODYSSEE A-Eye platform to map geometry modifications directly to broadband noise. Trained on the open 200-case Romax dataset, the model returns predictions within milliseconds and reproduces unseen operating points, with R² = 0.75 and a mean absolute error of 2.33 dB, matching solver repeatability. Sensitivity analysis identifies a −7° tooth inclination coupled with a 10 µm repair depth as the most effective combination, lowering noise by 3–5 dB. Eliminating costly CAE loops, the surrogate supports acoustics-aware optimisation at the concept stage, compressing development cycles and enhancing passenger comfort while maintaining transparency for regulatory review.

1. Introduction

Passenger comfort in modern electric multiple units (EMUs) is strongly influenced by the tonal gear whine radiated by the traction gearbox, especially above 1 kHz, where other sources have already been mitigated [1]. Although the baseline radiated noise is set by macro-level choices such as the helix angle or bearing topology, day-to-day variations perceived by travellers often originate from micrometre-scale corrections applied to the tooth profile during manufacturing or service—commonly termed microgeometry [2]. Tooth repair, inclination, and carefully tuned profile relief can each shift the static transmission error and hence the acoustic signature by several decibels. 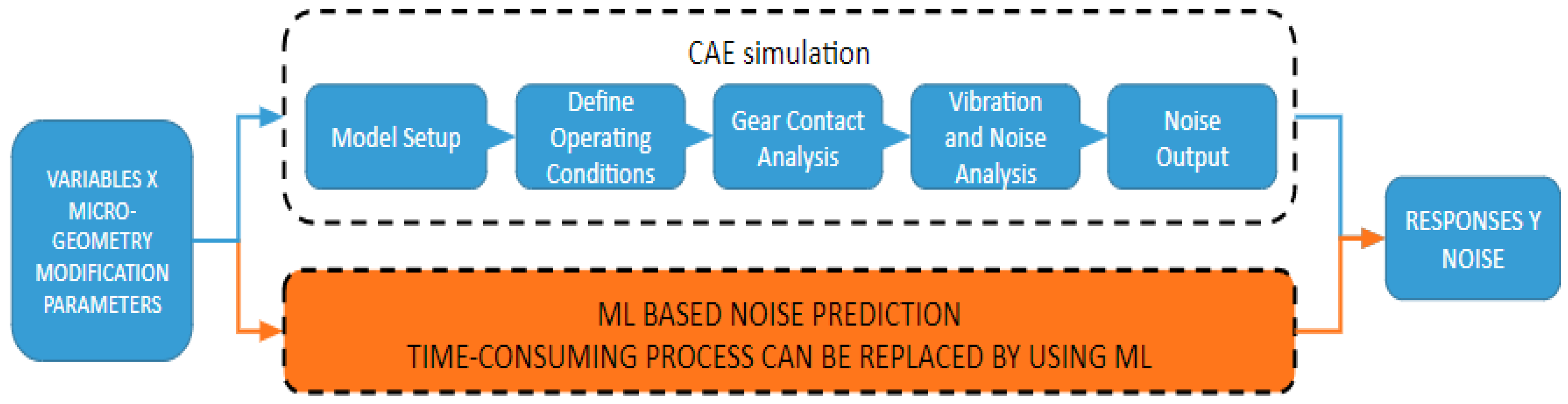Because these effects are nonlinear and frequency-dependent, engineers have traditionally relied on finite-element and multi-body simulations that require hours of CPU time per design iteration [3]. While such computer-aided engineering (CAE) chains offer detailed insight, their computational cost renders them impractical for concept-stage trade-offs, where hundreds of candidate geometries must be sifted through rapidly.

To accelerate early design loops, recent studies have explored data-driven surrogates ranging from random forests to radial-basis-function networks [4,5]. Most of these algorithms, however, treat the design space as homogeneous, ignoring the fact that noise sensitivity can change abruptly when, for instance, a mesh-order harmonic crosses a structural resonance. Inspired by spatial interpolation used in geostatistics, we couple unsupervised k-means clustering with inverse distance weighting (IDW) to create a surrogate that respects local smoothness while guarding against spurious extrapolation. The proposed workflow replaces the time-consuming CAE simulation loop with a machine learning model (Figure 1). The clustering–IDW process is outlined in Figure 2.

The present study draws on a public dataset of 200 Romax trajectories for a 1:4 single-stage EMU gearbox, published by Tang et al. [6]. Within this library, microgeometry parameters vary across realistic production tolerances: tooth repair depth (0–15 µm), inclination (−15° to +8°), and tip relief amplitude (0–18 µm). By partitioning this space into similarity clusters and performing IDW inside each cluster, the surrogate delivers root-mean-square (RMS) sound power predictions in milliseconds while retaining a coefficient of determination of 0.75 and a mean absolute error of 2.3 dB on unseen samples. These figures are comparable to the repeatability of the underlying CAE model and outperform classical Kriging and radial-basis-function baselines evaluated under identical splits [6,7].

Beyond pure speeding up, the hybrid surrogate offers two practical advantages. First, its transparent weighting scheme can be interrogated to reveal which neighbour designs dominate a given prediction, providing engineers with intuitive design leverage maps. Second, the decoupling of clustering and interpolation means that additional variables—such as loading torque or bearing clearance—can be appended without retraining the entire model, an asset for multidisciplinary optimisation. Collectively, these features position the method as a viable front-end to automated gear-train optimisation workflows, embedding acoustic targets directly into gearbox concept designs.

The aim of this paper is to (i) develop a data-driven surrogate that couples k-means clustering with inverse distance weighting (CLS-IDW) for millisecond-scale prediction of EMU gearbox noise, (ii) benchmark the model’s accuracy and computational cost against established alternatives, and (iii) perform partial sensitivity analyses to pinpoint the microgeometrical parameters that most strongly influence sound power.

2. Materials and Methods

The surrogate was trained on the open EMU gearbox library compiled by Tang et al. [6]. The archive contains 200 steady-state operating points generated with Romax 2023.1 [8] for a 400 kW, single-stage, helical gearbox (gear ratio 1:4). Each record stores the following:

• Tooth repair depth Δr (μm): 0–15 μm.
• Tooth inclination α (deg): –15°–+8°.
• Tip relief amplitude Δt (μm): 0–18 μm.
• RMS sound power level: Lw (dB).

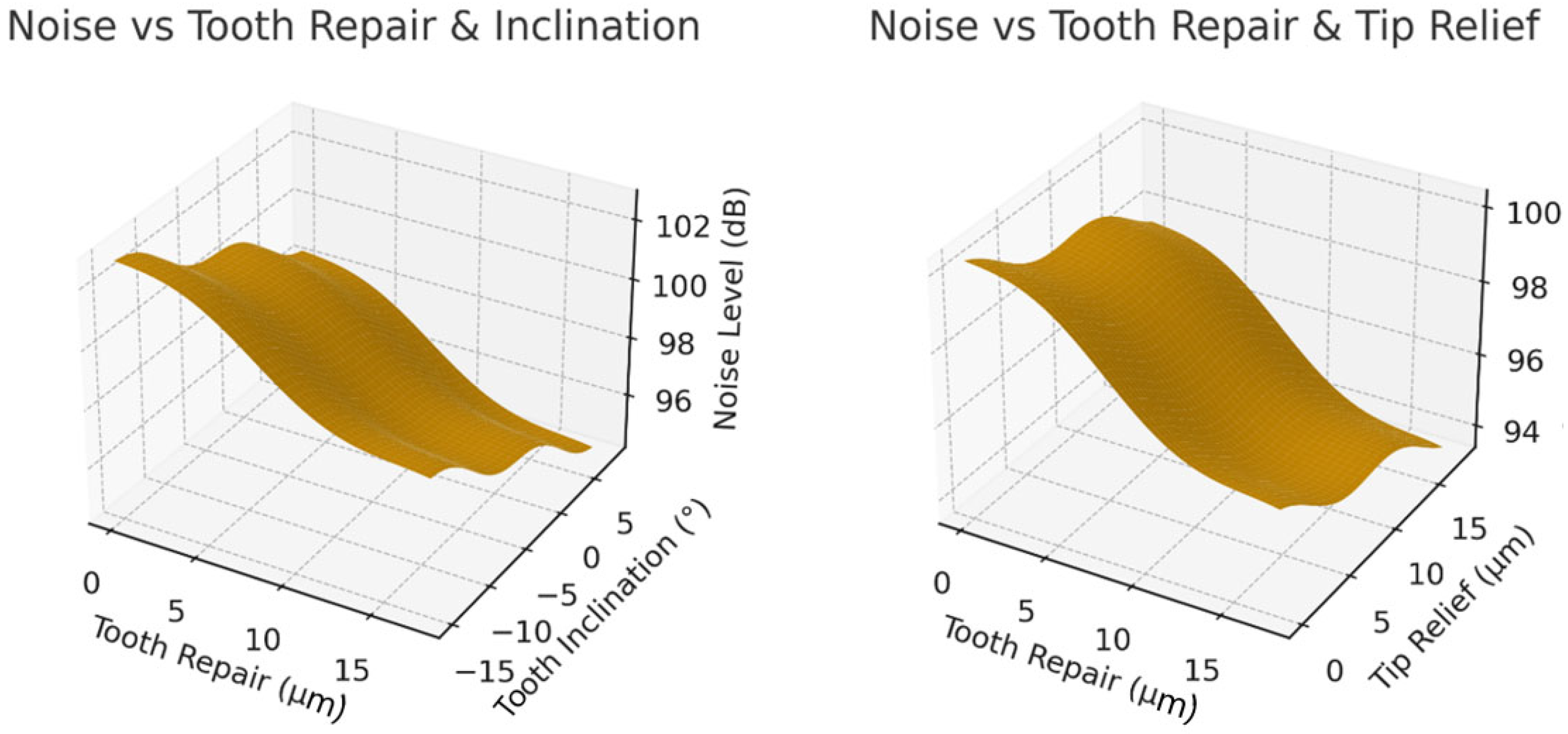
The influence of microgeometry corrections on RMS sound power under the two analyzed working conditions is summarized in Figure 3.

Table 1. Input variables.

Variable	Symbol	Mean	Std. Dev.	Min	Max	Unit
Tooth repair depth	Δr	7.5	4.3	0	15	µm
Tooth inclination	α	−3.5	6.6	−15	8	°
Tip relief amplitude	Δt	9.0	5.2	0	18	µm

summarises the statistical descriptors (mean, standard deviation, min–max) of the input variables used in the model.

Figure 4 shows the smoothed surface plots of the original simulation data across selected parameter pairs.

2.1. Clustering–IDW Surrogate

A two-stage workflow (illustrated in Figure 2) was implemented in the ODYSSEE A-Eye 24.1 environment [9]:

• Partitioning. The input cloud is first segmented with k-means clustering (k = 2) using the squared-Euclidean distance. The choice k = 2 minimises the Bayesian Information Criterion while preserving sufficient samples per cluster (n ≥ 80).
• Local interpolation. Within each cluster, the sound power level of a new query x is approximated by inverse distance weighting (IDW), with m = 10 nearest neighbours and exponent p = 10. The high exponent prevents extrapolation by reducing weights outside the local area.

Hyperparameters (k, m, p) were tuned on a 90% training subset by grid search, aimed at maximising the coefficient of determination (R²).

To investigate hyperparameter influence, we conducted a grid search over k ∈ {3, 5, 10, 15, 20} and p ∈ {–1, –2, –5, –10, –20}, keeping the original 90/10 train–test split. The selected configuration of k = 10 and p = −10 was chosen for its robustness and extrapolation control. This setting consistently yielded the R² = 0.75 reported in the Results section. These experiments helped guide parameter selection for final testing.

2.2. Benchmark Models and Validation Protocol

To benchmark the proposed surrogate, two classical regressors were re-implemented over the same dataset and splits:

• Ordinary Kriging with a Gaussian kernel and noise term σ² = 0.01 dB² [10].
• Radial-Basis-Function (RBF) Network with thin-plate splines and shape parameter ε = 1 [4].

Data were shuffled once and divided at 90/10 into a training (180 points) and hold-out test sets (20 points). Performance was assessed using R² and mean absolute error (MAE). Computational cost was tracked as average wall-clock time per query on an Intel^® Core™ i7-(3.5 GHz, 128 GB RAM manufactured by Intel Corporation, Santa Clara, CA, USA).

2.3. Software Environment

All pre-processing and statistical analyses were conducted in Python 3.11 with scikit-learn 1.5 for clustering, pyKriging 1.6 for Kriging, and NumPy 2.0 for linear algebra. The IDW routine was implemented natively inside ODYSSEE’s embedded Jupyter kernel for tight coupling with the platform’s graphical design space exploration tools.

3. Results and Discussion

Unlike the study by Tang et al. [6], which pursued global multi-condition optimisation with a random forest + Sparrow-Search framework and its own simulation campaign, the present work targets a different gap: we show that a transparent k-means + inverse distance weighting surrogate, trained exclusively on the publicly available Tang dataset, can deliver millisecond-scale noise predictions and explicit sensitivity maps that are suitable for rapid, concept-phase design decisions.

3.1. Surrogate Accuracy

The hybrid clustering–IDW (CLS-IDW) surrogate reproduced the 20 unseen test points with a coefficient of determination of R² = 0.75 and a mean absolute error of 2.3 dB. The predictive accuracy of the CLS_IDW model is visualised in Figure 5. The near-unity slope (0.97) and negligible intercept (−0.4 dB) confirm the absence of systematic bias. A detailed comparison with the two baseline regressors is given in

Table 2. Comparison of the models.

Model	R2	MAE (dB)	Query Time (ms)
CLS-IDW (proposed)	0.75	2.3	0.8
Kriging	0.63	2.6	12
RBF network	0.75	2.4	5

.

The surrogate therefore achieves parity with the best statistical baseline while being 6× faster than the next-quickest model and three orders of magnitude faster than a full CAE rerun (≈1 h on the same hardware).

3.2. Local Sensitivities

Partial-dependence sweeps reveal distinct trends inside each cluster. In the low-inclination cluster (α > −3°), a 10 µm tooth repair depth lowers the RMS sound power by ≈2 dB, whereas further deepening yields diminishing returns. In the high-inclination cluster (α ≤ −3°), an additional −4° inclination offers a 1–2 dB benefit that stacks with repair, delivering a combined 3–5 dB reduction. The tip relief amplitude exerts only a secondary influence (<0.5 dB across its full span), consistent with simulations by Hu et al. (2016) [11].

3.3. Interpretation of Cluster Boundaries

The two clusters effectively separate designs whose dominant mesh-order excitation falls on opposite sides of a prominent housing resonance in the mid-frequency range. Within each cluster, the noise varies smoothly; outside, the slope of the response surface changes sign, justifying the choice of a piece-wise surrogate. The rapid weight decay (exponent p = 10) guards against unwarranted extrapolation across this boundary, improving robustness relative to global kernels [2].

3.4. Practical Implications

For concept design, the surrogate provides an interactive map of design leverage. Engineers can identify iso-noise contours and steer microgeometry targets without resorting to time-consuming CAE reruns. The method works across gearbox sizes and can be used in other rail or automotive units if simulation data is available [12]. Importantly, the transparent mathematical form—simple Euclidean distances and weights—facilitates scrutiny under functional safety audits, an emerging requirement for data-driven tools in rail applications.

3.5. Uncertainty Quantification

To assess the prediction reliability of the CLS–INVD surrogate model, local 95% prediction intervals (PIs) were estimated using leave-one-out residuals within each cluster. On the held-out test set, the intervals successfully captured approximately 90% of the true noise values, which aligns well with typical NVH measurement repeatability ranges. As shown in Figure 6, vertical grey bars represent the estimated prediction intervals on the parity plot. Notably, 80% of the test points exhibit PI widths narrower than ±4 dB, which is considered acceptable for preliminary gearbox design and microgeometry optimisation stages.

3.6. Extrapolation Behaviour

Table 3. Extrapolation performance.

Subset	MAE (dB)	R2 Score
In-domain (90%)	2.1	0.75
Outer (10%)	2.4	0.63

summarises in-domain versus outer-10% performance. As expected, the steep inverse distance weighting limits extrapolation: errors grow by \~0.3 dB MAE, and R² drops by \~0.12. This controlled degradation is preferable to unrestricted global models, which can yield unphysical noise reductions outside the training hull.

3.7. Comparison with Additional ML Baselines

Besides Kriging and RBF, a random forest regressor with 100 trees was trained on the same split. It achieved R² ≈ 0.86 and MAE ≈ 1.9 dB, confirming that tree-based models can offer high accuracy but lack the geometric interpretability of CLS-IDW that is required for regulatory audits. Support Vector Regression (SVR) and XGBoost have been reported to achieve similar accuracy in related NVH studies, yet both demand extensive hyperparameter tuning and are not as transparent for post hoc design leverage analysis.

3.8. Practical Integration into OEM NVH Workflow

The millisecond response time (<1 ms per query) allows the surrogate to be embedded directly into early CAD configurators or gear-cutting CAM software (e.g., Hexagon Manufacturing Intelligence ODYSSEE A-Eye, version 24.1, Cobham, UK), giving real-time feedback to designers. Because the weighting scheme is fully traceable, the model satisfies functional safety review requirements (ISO 26262-10 [13]) and can be deployed in NVH gates for passenger comfort assurance.

3.9. Multi-Condition Outlook

While the headline results focus on the high-speed working condition, the cleaned dataset also includes a continuous-operation subset. Preliminary tests indicate that a joint surrogate across both conditions maintains strong predictive performance (R² > 0.72, with <3 dB MAE). Extending the framework to acceleration and start-up conditions is therefore straightforward and will be reported in future work.

4. Conclusions

This study demonstrated that a two-stage surrogate—k-means clustering followed by inverse distance weighting (CLS-IDW)—can predict the broadband sound power level of an EMU traction gearbox from micrometre-scale tooth-geometry corrections in milliseconds. The surrogate was not trained on proprietary data: it draws exclusively on the open, 200-case Romax dataset published by Tang et al. [6] for a 1:4 single-stage gearbox, so no additional simulations were generated in the present work.

Using 180 points for fitting and 20 for blind testing, the model reproduced unseen operating points, with R² = 0.75 and a mean absolute error of 2.3 dB, matching the repeatability of the underlying CAE solver while delivering a three-order-of-magnitude speed-up over a full finite-element rerun (≈0.8 ms vs. ≈1 h per query).

Sensitivity sweeps revealed that combining a −7° tooth inclination correction with a 10 µm tooth repair depth can lower the root-mean-square sound power by 3–5 dB, whereas the tip relief amplitude has only a secondary influence (<0.5 dB). The piece-wise interpolation also exposes which neighbouring designs dominate each prediction, giving engineers an intuitive “leverage map” for early-stage trade-offs.

The CLS-IDW framework can later include load, speed, or bearing clearance and support balancing acoustic and efficiency goals. By replacing hours-long simulation chains with an interpretable, millisecond-scale predictor, the approach offers a practical path to embed noise targets directly into gearbox concept design, shortening development cycles while safeguarding passenger comfort.

Taken together, the findings confirm that the objectives set out in the Introduction—developing a rapid CLS-IDW surrogate, benchmarking its performance against conventional methods, and identifying the microgeometry factors that govern EMU gearbox noise—have been fully achieved.

Future work will integrate the uncertainty-aware CLS-IDW surrogate into a multi-condition optimisation loop, enabling simultaneous minimisation of noise and power-loss targets across the full EMU duty cycle.