Investigation of Triple-Microcantilever Sensor for Ultra-Low Mass-Sensing Applications ^†

Abstract

This paper discusses a new method and sensor for the detection of ultra-low masses, such as those of viruses and biomarkers. The sensor contains three microcantilevers with a common substrate that vibrates. The detection method processes phase-shifted signals from Wheatstone bridges from connected piezoresistors formed on the vibrating microcantilevers and passive resistors on the rigid substrate. Each microcantilever has a gold pad that can be either active or passive. When a mass is detected, the shape of the amplitude–frequency response changes. The proposed method has high mass sensitivity and can respond up to one minute, which is an important challenge for nanocantilever sensors.

1. Introduction

Microcantilevers with sharp tips have been used in atomic force microscopy for topographic imaging of non-conducting surfaces for over 40 years [1,2]. Single smooth microcantilevers respond to the absorption of molecules and microorganisms by bending and changing their natural frequency [3,4]. Due to their high sensitivity and fast response, they have found wide application in biochemistry, medicine, and physics [5]. The use of two single microcantilevers was intended to improve the sensor performance by introducing a second reference sensor that could be used to measure the natural frequency deviation of the active sensor [6]. Another variation of these sensors is microcantilever arrays, in which the number of cantilevers can vary from 4 to 32 [7]. Microcantilever sensor arrays have diverse applications such as artificial noses [8], analyte detection [9], and DNA hybridization [10].

The authors of this paper have extensive experience in the investigation of dual-microcantilever sensors for the detection of viruses in gas. A common feature in the working principle is that the microcantilevers are attached to a common rigid substrate, which vibrates in a frequency range including the eigenfrequencies of the microcantilevers. The eigenfrequencies of the microcantilevers in the nominal state are shifted by a small value so that the two amplitude–frequency characteristics intersect. When mass is added to the surface of one of the microcantilevers, the intersection of the amplitude–frequency characteristics shifts, and this is an indication of a change in the mass of that beam [11,12,13].

Triple-microcantilever sensors have a more complex design than dual-microcantilever sensors but offer some new capabilities in terms of increased active surface for real-time detection of pathogens, result fidelity, strongly reduced false detection, sensor reliability, and ease of use. The triple-microcantilever coupled sensor system discussed in [14] shows that the mass is comparable to that of a single resonator, and in comparison, to single cantilevers. The system offers significantly improved signal compensation, reduced time for detection of an event, and an opportunity to decode the cantilever where the analyte was captured on the surface, thus providing new options for multi-analyte detection.

The aim of this paper is to investigate the ultra-low mass detection capabilities of a sensor composed of three microcantilevers with a common vibrating rigid substrate. The two offsets of the intercepts in the amplitude–frequency characteristics are the signal of the presence of mass added to a particular microcantilever.

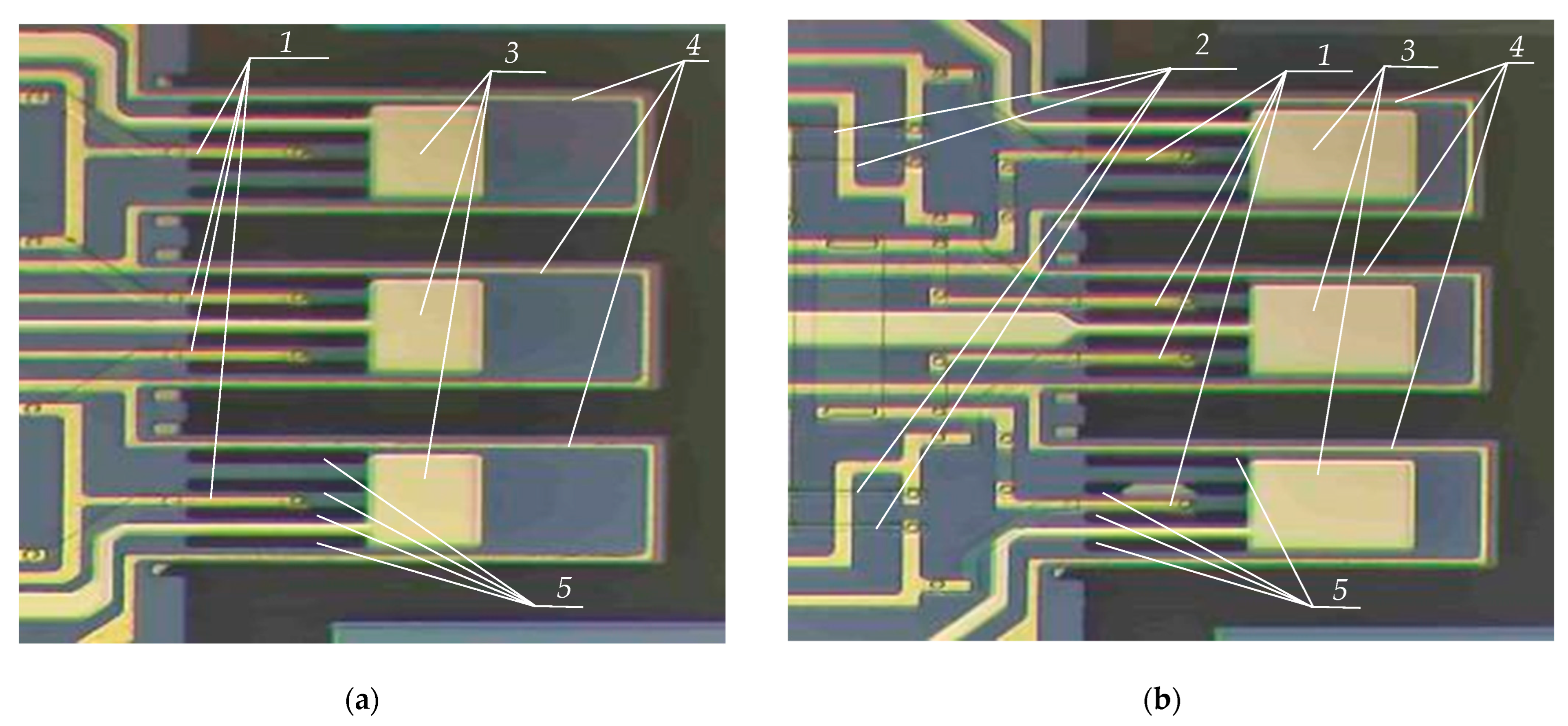
2. Design Concepts and Features of the Investigated Tri-Microcantilever Sensors

The three-cantilever piezoresistor sensors investigated here were designed and fabricated at AMG Technology, Bulgaria, as part of a joint project with a team from the Technical University of Sofia.

During the research, two basic designs of three-cantilever sensors were selected (Figure 1). The first type, shown in Figure 1a, is characterized by containing four active piezoresistors. The second type of sensor (Figure 1b) contains four passive resistors in addition to the four active piezoresistors.

In Figure 1, the common elements can be distinguished, which, in addition to the mentioned piezoresistors and resistors, also contain gold functionalization pads and heaters. The golden pads are formed on each cantilever, allowing each of them to be activated and become sensitive to the detected mass, and the others to serve as a reference. On each of the three cantilevers, there is formed an outer rectangular current frame called a heater. All the heaters are connected in series with intermediate terminals for each cantilever. The heaters have a multifunctional purpose. One of these purposes is to change the frequency of the cantilevers by heating and/or by Lorentz forces [12].

In addition, the terminals of the heater provide the possibility that selected sections of the current loop, located between the respective terminals, can be shunted with a parallel resistance of low value. This is a new functionality specific to these sensors. There are also four rectangular holes in the fixed end of the microcantilevers. These holes are used for additional mechanical tuning of the natural frequency.

An important feature in these sensors is related to the different schemes of connecting the piezoresistors in a bridge. One embodiment of a bridging scheme of a differential connection of two piezoresistors on microcantilevers and two passive resistors in a single bridge, B1, is shown schematically in Figure 2a.

Therein, piezoresistor 4′₁ with one resistor 4₀ having a constant value forms the voltage divider 9₁, and the piezoresistor and 4₂ with another resistor 4₀ having a constant value forms the voltage divider 9₂. Thus, each of the output signals V₁₁ and V₁₂ of the voltage dividers 9₁ and 9₂ depends on the amplitude (A₁ or A₂) and phase (ϕ₁ or ϕ₂) of an oscillation of a single microcantilever (3₁ or 3₂) and, therefore, has a sinusoidal shape similar to the mechanical oscillation of the cantilever.

Another amplifying version of the connection 5′₁ of the same resistors 4i of the bridging scheme is shown schematically in Figure 2b. Specific to this variant of the bridging circuit is that, all conditions and effects being equal, the sinusoidal signal V’₁₁(ϕ₁) is inverted (180° out of phase) with respect to the signal V₁₁(ϕ₁) from the first variant of the coupling. Similarly, there are two coupling variants of the second bridge 5₂. For both of these bridge circuit variants, under the same conditions and effects, each of the sinusoidal signals V₂₂(ϕ₃) and V’₂₂(ϕ₃) is mutually inverted (offset 180° in phase).

The general appearance of this variant of the three-cantilever sensor is shown in Figure 3, with a total of four piezoresistors, one each on the reference cantilevers C₁ and C₃ and two on the working microcantilever C₂. In this case, in addition to the four piezoresistors on the microcantilevers, four passive resistors of constant value are also used, located on the non-deformable substrate.

These totals of eight piezoresistors and passive resistors are connected in two bridges, as was discussed above. Crucially, the two dividers involving the C₂ piezoresistors generate identical signals when the oscillation modes of the cantilever are on the bend. This allows independent comparison of the instantaneous values of their signals with the signals from the piezoresistors on the C₁ and C₃ consoles. Thus, the change in the parameters of the C₂ cantilever is registered simultaneously in both bridges “Bridge #1” and “Bridge #2”.

An amplifying embodiment of the wiring diagram in full bridge 5₁, when only four piezoresistors arranged on three micro-consoles are included in bridge 9₁, is shown in Figure 4a. Accordingly, the signal V₁ from the voltage divider 9₁ depends on the amplitudes A₁ and A₂ and the phases ϕ₁ and ϕ₂ of forced oscillation of the micro-consoles 3₁ and 3₂, and the signal V₂ from the voltage divider 9₂ depends on the amplitudes A₂ and A₃ and the phases ϕ₂ and ϕ₃ of forced oscillation of the microcantilevers 3₂ and 3₃.

A differential wiring diagram of this other variant of sensor 1 in a full 5′₁ bridge is shown in Figure 4b. Accordingly, the signal V₁ from the voltage divider 9₁ depends on the amplitudes A₁ and A₂ and the phases ϕ₁ and ϕ₂ of the forced oscillation of the micro-consoles 3₁ and 3₂, and the signal V’₂ from the voltage divider 9′₂ depends on the amplitudes A₂ and A₃ and the phases ϕ₂ and ϕ₃ of the forced oscillation of the micro-consoles 3₂ and 3₃. In contrast to the previous case, the signal V’₂ is inverted 180° with respect to the coupling from the bridge 5₁.

The specific condition is that the resonant frequencies of the microcantilevers change monotonically with their position in the array. In this case, the condition

f₁ < f₂ < f₃

(1)

A key feature of sensors of this type is the arrangement of the micro-cantilevers in a row of monotonically increasing resonant frequency, with alternating reference (at odd positions) and active (at even positions).

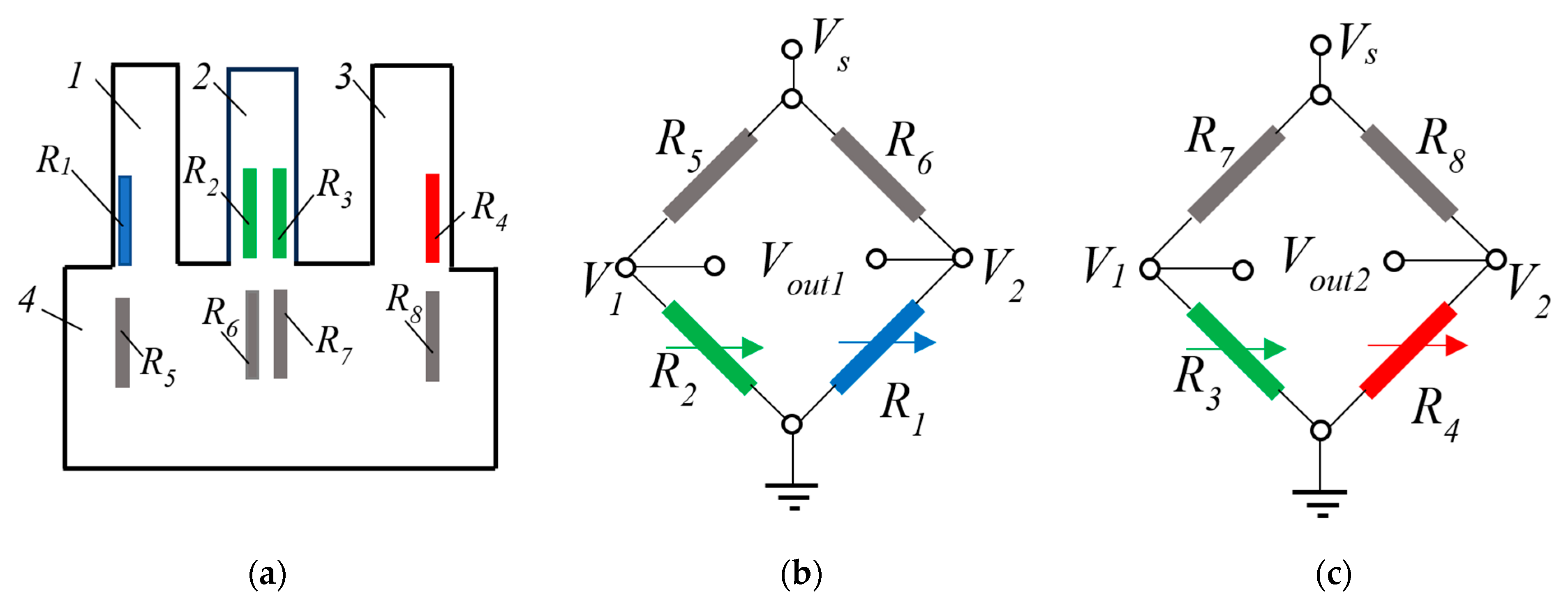
3. Compilation of an Electromechanical Model of the Triple-Microcantilever Sensor

For the sensor with four piezoresistors, the location of the resistors on the corresponding microcantilevers is shown in Figure 5a. Figure 5b shows the corresponding Wheatstone bridge in which the piezoresistors are connected in agreement with the logic outlined in the previous section.

Similarly, for the sensor with four piezoresistors and four resistors, the location of the resistors on the respective microcantilevers and the four resistors on the substrate is shown in Figure 6a. Figure 6b shows the first Wheatstone bridge with the piezoresistors R₁ and R₂ and the resistors R₅ and R₆ connected. The second Wheatstone bridge, consisting of the piezoresistors R₃ and R₄ and the resistors R₇ and R₈, is shown in Figure 6c.

The output voltage $V_{out}$ of the Wheatstone bridge with the four piezoresistors (Figure 5b) can be calculated according to the formula

$$V_{out}=V_1-V_2=\left[{\displaystyle \frac{R_2}{R_1+R_2}}-{\displaystyle \frac{R_4}{R_4+R_3}}\right]V_s={\displaystyle \frac{R_1{R}_4-R_2{R}_3}{(R_1+R_2)(R_4+R_3)}}{V}_s$$

(2)

where $V_1$ and $V_2$ are the voltage of the first and second dividers of the Wheatstone bridge, and $V_s$ is the supplying voltage.

Similarly, the output voltage $V_{out1}$ of the first Wheatstone bridge with four piezoresistors and four resistors (Figure 6b) can be determined by

$$V_{out1}={\displaystyle \frac{R_2{R}_6-R_1{R}_5}{\left(R_2+R_5\right)\left(R_6+R_1\right)}}{V}_s={\displaystyle \frac{R_5\left(R_2-R_1\right)}{\left(R_2+R_5\right)\left(R_6+R_1\right)}}{V}_s$$

(3)

And the output voltage $V_{out2}$ of the second Wheatstone bridge (Figure 6c) is

$$V_{out2}={\displaystyle \frac{R_3{R}_8-R_4{R}_7}{\left(R_3+R_7\right)\left(R_8+R_4\right)}}{V}_s={\displaystyle \frac{R_7\left(R_3-R_4\right)}{\left(R_3+R_7\right)\left(R_8+R_4\right)}}{V}_s$$

(4)

The simplification in (3) is valid if $R_5+R_6$.and in (4) if $R_7+R_8$.

It is assumed that the common substrate of the microcantilevers vibrates by a harmonic function $y_1$ of the form

$$y_1=asin\omega t$$

(5)

where $a$ is the amplitude of the actuation function, $\omega$ is the circular frequency, and $t$ is the time.

Considering a lumpen dynamical model [13,15] of every cantilever, the vibrations can be expressed by the solution of an ordinary differential equation in the form

$$y_i=B_{i}sin\left(\omega t+{\psi }_i\right)$$

(6)

where $y_i$ is the free motion, and the amplitude $B_i$ of the forced oscillations of the i-th cantilever is

$$B_i={\displaystyle \frac{a{\omega }^2}{\sqrt{{\left({\omega }^2-{\varpi }_i^2\right)}^2-4{\beta }_i^2{\omega }^2}}}$$

(7)

The phase of the vibrations of the i-th cantilever is

$${\psi }_i=\mathit{arctan}{\displaystyle \frac{2\omega {\beta }_i}{{\omega }^2-{\varpi }_i^2}}$$

(8)

where ${\varpi }_i$ is the natural (resonant) circular frequency of the i-th cantilever and ${\beta }_i$ is the damping factor of the i-th cantilever.

As is known [16,17], the resistance of a piezoresistor is given by the relation

$$R_j=R_0+∆R_j$$

(9)

where the variable part $∆R_j$ of the piezoresistor in the solution (6) can be considered proportional to the displacement of the free end of the cantilever on which it is formed, i.e.,

$$∆R_j=k_r{B}_i\sin \left(\omega t+{\psi }_i\right)$$

(10)

where $k_r$ is the piezoresistivity coefficient.

Using these formulae, a pre-selection of the parameters and the parameters of the microcantilevers was performed.

4. Experimental Results

Prototypes of microcantilevers with a length in the range of 250–350 µm, a width in the range of 80–120 µm, and a thickness in the range of 2.5–6.0 µm were fabricated. These microcantilevers are of relatively “large size” with respect to modern trends of similar sensors where nano-cantilevers are applied [18,19,20,21]. To investigate the amplitude–frequency responses of the triple-microcantilever sensor, a dedicated experimental setup was built, as shown in Figure 7. A peculiarity of the system is that the eigenfrequencies of the microcantilevers are in the range of 60 to 120 kHz. This necessitated the use of a data acquisition system with a sampling rate of 2 MS/s. For this purpose, a National Instruments PXI system was used. A Digilent sine signal generator was used to generate a high-frequency sine signal for a piezoelectric actuator, used to excite mechanical vibrations at the common substrate of the three microcantilevers. A LabVIEW program was used to process the signals [11]. The experimental setup is capable of measuring frequencies up to 300 kHz with a resolution of 0.01 Hz, which was quite sufficient for the requirements of the proposed method.

Figure 8 presents initial test results from the triple-cantilever sensor with four piezoresistors and four resistors. In Figure 8a, the result of the full bridge of the three cantilevers is shown. Figure 8b depicts the first and second peaks of the amplitude–frequency response and Figure 8c shows the first and third peaks.

5. Conclusions

A new method and sensor containing three microcantilevers on a common rigid substrate was developed for sensing the availability of ultra-low mass analytes, like viruses, pathogens, bio-markers, and trace gases that are bound on the cantilever surface. To achieve detection selectivity, at least one cantilever is provided with a specifically coated pattern. Respectively, the surface of one or three cantilevers is functionalized to bind the same or different targeted analyte(s). Thus, two approaches—with a single active and two reference cantilevers or with three active ones—are formulated. For each of these approaches, two different full Wheatstone bridge configurations have been prototyped. Accordingly, the sensors were fabricated and tested in two of their varieties.

“Large size” microcantilevers significantly (up to ×10⁴) increased the active area; these devices ensure real-time detection (i.e., time between detected events ≤1 min) of an analyte’s availability in gases.

Analogue electrical signals from piezoresistors with identical parameters located on adjacent cantilevers provide various options for their controllable mixing. Particularly, any two of said analogue signals can be either amplified or compensated, meaning parameter drift can be eliminated.

Capturing an ultra-small mass analyte causes a relative eigenfrequency change in a microcantilever by a factor of Δf/f ≈ 10⁻⁶. Despite the ultra-small frequency shift, due to the above-mentioned drift compensation, the new method provides reliable detection of an analyte capturing an event on a specifically functionalized cantilever.

Due to electrically recurrently connected piezoresistors in full bridge configurations, the cantilever that was binding an analyte can be recognized, and initial signal compensation can be recovered, meaning the next event can be detected. Thus, besides the availability of an analyte, its concentration can be assessed, too.