Abstract
This study developed a QSPR model to predict the n-octanol/water partition coefficient (log Kow) of 56 pesticides. Molecular descriptors were calculated using Dragon software. A genetic algorithm and variable subset selection identified key descriptors. The model, built by multiple linear regression, showed strong performance (R2 = 0.9322, Q2LOO = 0.9089, Q2ext = 0.9277). The dataset was split using the Kennard-Stone algorithm to ensure representative sampling. Internal and external validations confirmed robustness and predictive power. This model offers a reliable tool for estimating log Kow, supporting environmental risk assessment and the evaluation of pesticide behavior and toxicity.
1. Introduction
Pesticides are unique among chemicals because they are intentionally introduced into the environment to manage pests and protect crops and industrial goods. However, their effects are not limited to target species; they also impact non-target organisms and ecosystems. Frequent use can reduce biodiversity [1]. Many pesticides are persistent, remaining in soil or leaching into water bodies, which leads to widespread contamination. Due to their chemical nature, they can bioaccumulate in living organisms and affect human health through food chains. The environmental risks of intensive pesticide use are well documented and significant [2].
Quantitative structure–activity relationships (QSARs) offer a way to predict chemical toxicity based on molecular structure, even before synthesis. These models are especially useful when experimental data are scarce [1,2]. QSPR/QSAR methods rely on the idea that molecular properties are linked to specific structural features, called descriptors [3]. These computational tools can forecast chemical behavior, identify key structural elements, and reduce the need for experimental testing, making them cost- and time-effective in areas like drug development [4].
Physicochemical properties—such as vapor pressure, solubility, and partition coefficients—are central to understanding how organic compounds behave in the environment [5]. Among these, the n-octanol/water partition coefficient (Kow) is crucial. A high log Kow suggests a higher potential for bioaccumulation in organisms. This parameter is also used to infer systemic action and environmental fate of compounds [6]. In QSAR models, log Kow is often employed as a descriptor of toxicity [7,8,9]. The partition coefficient is defined as the ratio of equilibrium concentrations of a substance in a biphasic system like octanol and water [10], with octanol mimicking biological lipids [11].
This study aimed to develop QSAR models for predicting the acute toxicity of pesticides and to construct a statistical model for estimating their log Kow. Using multiple linear regression (MLR), the model identifies which molecular descriptors significantly influence variation in log Kow across the pesticide dataset.
2. Materials and Method
2.1. Experimental Data
This study used a dataset of 56 pesticides obtained from the published work of Patil [12]. The partition coefficient values were converted to log Kow to minimize data variability. The dataset was split into two subsets: 42 compounds for training and 14 for external validation.
2.2. Descriptors Generation
The molecular structures of all compounds were built using HyperChem (version 6.02) [13] and initially optimized via the MM+ force field with the Polak–Ribiere algorithm. Final geometries corresponding to the lowest energy conformers were obtained using the semi-empirical PM3 method at the restricted Hartree–Fock level, without configuration interaction, applying a gradient norm threshold of 0.001 kcal·Å−1·mol−1. These optimized structures were used to calculate 1664 molecular descriptors with Dragon software (version 5.4) [14]. Additionally, quantum chemical descriptors—including HOMO, LUMO, the HOMO–LUMO gap (ΔHL), and ionization potential-were computed using the PM3 method in HyperChem and considered during descriptor selection for model development.
3. Results and Discussion
The dataset of 56 compounds was partitioned into two subsets using the Kennard–Stone algorithm implemented in CADEX: a calibration set of 42 compounds and a validation set of 14, as shown in Table 1. The objective was to select a reduced set of descriptors that best account for the variation in the dependent variable (log Kow). Descriptor selection was performed using genetic algorithms provided in the Mobydigs software (version 1.1) [15].

Table 1.
The data set and the corresponding observed and predicted values of log (Kow) by MLR for the training and test sets.
The application of the GA–VSS led to several effective models for predicting the Kow of pesticide chemicals based on various sets of molecular descriptors. The best model, derived from the 56 pesticide compounds, demonstrated high predictive accuracy and was established using the following regression equation:
log Kow = 1.63 + 0.301 × Polarizability − 0.798 × O-058 − 0.230 × nHAcc − 4.55 × E1u
Equation (1) incorporates four distinct categories of molecular descriptors, summarized in Table 2. The model’s performance was assessed using predictive metrics such as Q2LOO and Q2LMO, along with the coefficient of determination (R2) to evaluate the goodness of fit. Additionally, the standard deviation of prediction error (SDEP) and the standard deviation of calculation error (SDEC) within the applicability domain are reported.

Table 2.
Description of the selected descriptors by GA.
As shown in Table 3, the fitting and validation metrics are consistently high, confirming the model’s strong predictive performance. The selected descriptors effectively capture the variation in the partition coefficient. The R2 value reflects a well-fitted model, and the small difference between R2 and Q2LOO indicates strong internal robustness, further supported by a high Fisher statistic. The close values of SDEC and SDEP suggest that the model’s predictive ability is consistent with its fitting accuracy. External validation results, including Q2ext and SDEPext, demonstrate the model’s reliability in predicting data not used during its training phase.

Table 3.
Results and statistical parameters of GA-MLR.
The R2 value reflects the model’s fitting quality, while the small difference between R2 and Q2LOO indicates strong robustness, reinforced by a high Fisher statistic. The similarity between SDEC and SDEP suggests that the model’s predictive accuracy is consistent with its calibration performance. External validation metrics, including Q2ext and SDEPext, confirm the model’s reliability in predicting the behavior of compounds outside the training set.
The symmetrical distribution of errors around the zero line indicates that the model does not exhibit systematic bias. Figure 1 presents the Q2 and R2 coefficients, comparing the real model (black dot) with the randomized models (red circles). The Q2 values of the randomized models are consistently below 20, and in many cases negative, confirming that the developed model is based on real structure–property relationships rather than random chance.
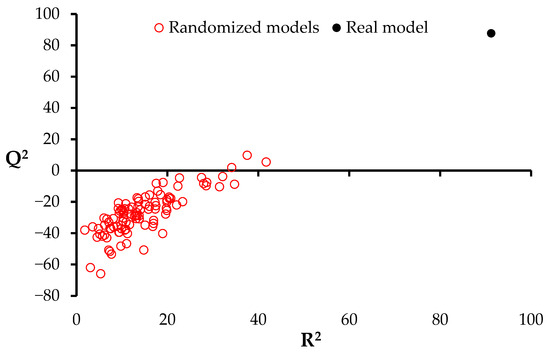
Figure 1.
Randomization test.
4. Conclusions
In this study, the QSPR approach was employed to correlate the log Kow values of 56 pesticides with theoretical molecular descriptors selected using a genetic algorithm. Multiple linear regression was applied to identify linear relationships between the descriptors (independent variables) and log Kow (dependent variable). The resulting model demonstrated optimal performance in terms of goodness of fit, internal and external validation, and predictive accuracy.
Author Contributions
Conceptualization, Y.D.; methodology, Y.D. and M.F.; software, Y.D.; validation, Y.D., M.F. and A.D.; formal analysis, M.F.; investigation Y.D., M.F. and A.D.; resources, Y.D.; data curation, Y.D., M.F. and A.D.; writing—original draft preparation, I.B. and S.Y.; writing—review and editing, R.M., S.N. and A.S.; visualization, Y.D.; supervision, Y.D.; project administration, Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors gratefully acknowledge the Environmental Research Center in Annaba, Algeria, for their support and valuable contributions to this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bradbury, S.P. Predicting modes of toxic action from chemical structure: An overview. SAR QSAR Environ. Res. 1994, 2, 89–104. [Google Scholar] [CrossRef] [PubMed]
- Bearden, A.P.; Schultz, T.W. Structure-Activity Relationships for Pimephales and Tetrahymena: A Mechanism of Action Approach. Environ. Toxicol. Chem. 1997, 16, 1311–1317. [Google Scholar] [CrossRef]
- Liu, H.X.; Hu, R.J.; Zhang, R.S.; Yao, X.J.; Liu, M.C.; Hu, Z.D.; Fan, B.T. The prediction of human oral absorption for diffusion rate-limited drugs based on heuristic method and support vector machine. J. Comput. Aided Mol. Des. 2005, 19, 33–46. [Google Scholar] [CrossRef] [PubMed]
- Si, H.; Yuan, S.; Zhang, K.; Fu, A.; Duan, Y.-B.; Hu, Z. Quantitative structure–activity relationship study on EC50 of anti-HIV drugs. Chemometr. Intell. Lab. Syst. 2008, 90, 15–24. [Google Scholar] [CrossRef]
- Xu, H.Y.; Zhang, J.Y.; Zou, J.W.; Chen, X.S. QSPR models for the physicochemical properties of halogenated methyl-phenyl ethers. J. Mol. Graph. Model. 2008, 26, 1076–1081. [Google Scholar] [CrossRef] [PubMed]
- Wania, F.; Mackay, D. The evolution of mass balance models of persistent organic pollutant fate in the environment. Environ. Pollut. 1999, 100, 223–240. [Google Scholar] [CrossRef] [PubMed]
- Fisher, S.W.; Lydy, M.J.; Barger, J.; Landrum, P.F. Quantitative structure–activity relationships for predicting sediment-sorbed chlorobenzene bioavailability to Chironomus decorus larvae. Environ. Toxicol. Chem. 1993, 12, 1307–1318. [Google Scholar] [CrossRef]
- Van Leeuwen, C.J.; Vanderzandt, P.T.; Aldenberg, T.; Verhaar, H.J.M.; Hermens, J.L.M. The application of QSARs, extrapolation and equilibrium partitioning in aquatic effects assessment for narcotic pollutants. Sci. Total Environ. 1991, 109, 681–690. [Google Scholar] [CrossRef] [PubMed]
- Niculescu, S.P.; Kaiser, K.L.E.; Schüürmann, G. Influence of Data Preprocessing and Kernel Selection on Probabilistic Neural Network Modeling of the Acute Toxicity of Chemicals to the Fathead Minnow and Vibrio fischeri Bacteria. Water Qual. Res. J. Can. 1998, 33, 153–166. [Google Scholar] [CrossRef]
- Wong, S.L. Algal assay evaluation of trace contaminants in surface water using the nonionic surfactant Triton X-100. Aquat. Toxicol. 1985, 6, 115–131. [Google Scholar] [CrossRef]
- Chessells, M.; Hawker, D.W.; Connell, D.W. Critical evaluation of the measurement of the 1-octanol/water partition coefficient of hydrophobic compounds. Chemosphere 1991, 22, 1175–1190. [Google Scholar] [CrossRef]
- Patil, G.S. Prediction of aqueous solubility and octanol–water partition coefficient for pesticides based on their molecular structure. J. Hazard Mater. 1994, 36, 34–43. [Google Scholar] [CrossRef]
- HyperchemTM. Release 6.02 for Windows. Molecular Modeling System. 2000. Available online: http://www.hypercubeusa.com/ (accessed on 12 October 2025).
- Talete srl, Dragon Software, Version 5.4. 2005. Available online: www.talete.mi.it (accessed on 14 October 2025).
- Todeschini, R.; Ballabio, D.; Consonni, V.; Mauri, A.; Pavan, M. MOBYDIGS—Version 1.1—Copyright (c) 2004–2009; TALETE srl: Milano, Italy, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).