Linear Canonical Transform Approach to the Characteristic Function of Real Random Variables

Abstract

The present research demonstrates the utility of the linear canonical transform (LCT) in constructing the characteristic function of real random variables. We refer to this construction as the linear canonical characteristic function (LCCF). The proposed LCCF aims to address the limitations of the classical characteristic function in both theoretical and applied aspects. Using this approach, we investigate its properties, such as Hermitian symmetry, continuity, convolution, and derivatives, which are generalized forms of the classical characteristic function in the literature. Finally, we implement the obtained results by calculating several probability density functions in the LCCF domains.

1. Introduction

Over the past few decades, the linear canonical transform (LCT) has attracted considerable research interest. The LCT may be interpreted as a natural expansion of the classical Fourier transform (FT) and the fractional Fourier transform (FrFT) [1,2], which implies that the LCT is more flexible and superior to the FT and the FrFT. The LCT has received a lot of attention and has become a hot topic due to its usefulness in various disciplines; see, e.g., [3,4,5,6]. In the past ten years, detailed studies on essential properties related to the LCT, such as shifting, modulation, derivatives, Parseval’s relation, inequalities, convolution, and correlation theorems, have been presented in [7,8,9,10].

As is well known, in probability theory, there is a close relationship between the classical characteristic function (CF) and the Fourier transform (FT), where the CF may be considered as the FT of its probability density function. These facts have inspired a promising research direction, and a number of papers have since appeared that contain generalizations and extensions of the characteristic function in various transformations. For instance, the authors of [11,12] have proposed the fractional characteristic function of any random variable, which is a non-trivial generalization of the characteristic function using the Mittag-Leffler transform [13]. Several important properties of this extended characteristic function have been demonstrated in detail. In [14], the authors have discussed the characteristic function in the setting of Clifford algebra using the one-dimensional Clifford Fourier transform. The works of the authors in [15,16,17] have explored the characteristic function in quaternion algebra using the quaternion Fourier transform and quaternion fractional Fourier transform. Recently, the authors of [18,19] have studied the utility of the quaternion linear canonical transform (QLCT) in probability modeling. They also introduced the quaternion characteristic function in the framework of the QLCT. Despite these significant advancements, further exploration is still needed to extend the classical characteristic function in the context of the LCT, which we call the linear canonical characteristic function (LCCF).

In the present work, we first introduce the definition of the LCCF. The direct connection between the LCCF and the classical characteristic function is also presented. Various properties of the LCCF are demonstrated. We make a fascinating connection between the moments and the LCCF. Based on this relation, we obtain a new definition of variance in the context of the LCCF. Finally, some simple examples of the LCCF are also presented to illustrate the obtained theoretical results.

The structure of our paper is as follows. In Section 2, we introduce the basic concept of the LCT and summarize its basic properties, which will be useful for this research. In Section 3, we focus on the construction of the LCCF and derive some of its key properties. In Section 4, an interesting relationship between the moments and the LCCF is investigated in detail. In Section 5, we provide some illustrative examples of the LCCF for well-known probability density functions. Lastly, a simple conclusion is given in Section 6.

2. Linear Canonical Transform and Properties

First, we intend to recall the basic concept of the LCT and then summarize some of its basic properties, which are crucial for the main results of this research.

Definition 1.

Let $B=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\in {\mathbb{R}}^{2\times 2}$ denote the matrix parameter for which $\det \left(B\right)=ad-bc=1$. The LCT of a signal $f\in L^1\left(\mathbb{R}\right)$ is defined by

$$\begin{array}{c}\hfill L_B\left\{f\right\}\left(\omega \right)={\int }_{\mathbb{R}}f\left(x\right)K_B(\omega ,x)dx,b\ne 0\end{array}$$

(1)

where

$$K_B(\omega ,x)={\displaystyle \frac{1}{\sqrt{2i\pi b}}}{e}^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)},$$

(2)

is the kernel function of the LCT.

The original signal f above can be restored using the inversion formula for the LCT as follows:

Definition 2.

Let $f\in L^1\left(\mathbb{R}\right)$, such that $L_B\left\{f\right\}\in L^1\left(\mathbb{R}\right)$. The inversion of the LCT is described through

$$\begin{array}{cc}\hfill f\left(x\right)& ={\displaystyle \frac{1}{\sqrt{2i\pi b}}}{\int }_{\mathbb{R}}{L}_B\left\{f\right\}\left(\omega \right)\overline{K_B(\omega ,x)}d\omega \hfill \\ \hfill & ={\displaystyle \frac{1}{\sqrt{2i\pi b}}}{\int }_{\mathbb{R}}{L}_B\left\{f\right\}\left(\omega \right)e^{\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}d\omega ,\hfill \end{array}$$

(3)

where $\overline{K_B(\omega ,x)}$ represents the complex conjugate of $K_B(\omega ,x)$.

The following lemma collects the elementary properties of the LCT defined above. For more comprehensive information, readers are encouraged to refer to [3,4,5,7,9,10,20].

Lemma 1.

We have the following properties:

1.

Linearity

Let f,g in $L^1\left(\mathbb{R}\right)$ and let $k_1$, $k_1$ be real constants. Then

$$\begin{array}{c}\hfill L_B\{k_{1}f+k_{2}g\}\left(\omega \right)=k_1{L}_B\left\{f\right\}\left(\omega \right)+k_2{L}_B\left\{g\right\}\left(\omega \right).\end{array}$$

(4)

2.

Shifting

Let $f\in L^1\left(\mathbb{R}\right)$, and the shifted operator is defined by ${\tau }_{k}f\left(x\right)=f(x-k)$. Then, we have

$$\begin{array}{cc}\hfill L_B\left\{{\tau }_{k}f\right\}\left(\omega \right)& =L_B\left\{f(x-k)\right\}\left(\omega \right)\hfill \\ \hfill & =e^{-\frac{1}{2}aic{k}^2+ick\omega }{L}_B\left\{f\right\}(\omega -ak).\hfill \end{array}$$

(5)

3.

Modulation

For any function $f\in L^1\left(\mathbb{R}\right)$ with ${\omega }_0\in \mathbb{R}$. If ${\mathbb{M}}_{{\omega }_0}f\left(x\right)=e^{i{\omega }_{0}x}f\left(x\right)$, one gets

$$\begin{array}{cc}\hfill L_B\left\{{\mathbb{M}}_{{\omega }_0}f\right\}\left(\omega \right)& =L_B\left\{e^{i{\omega }_{0}x}f\left(x\right)\right\}\left(\omega \right)\hfill \\ \hfill & =e^{-\frac{1}{2}bd{\omega }_0^2+id\omega {\omega }_0}{L}_B\left\{f\right\}(\omega -b{\omega }_0).\hfill \end{array}$$

(6)

By exploiting Equation (1) above, the LCT definition can be reduced to that of the Fourier transform, that is,

$$\begin{array}{c}\hfill L_B\left\{f\right\}\left(\omega \right)={\displaystyle \frac{1}{\sqrt{2i\pi b}}}{e}^{-i\frac{d}{2b}{\omega }^2}\mathcal{F}\left\{\tilde{f}\right\}\left({\displaystyle \frac{\omega }{b}}\right),\tilde{f}\left(x\right)=f\left(x\right)e^{-i\frac{a}{2b}{x}^2}.\end{array}$$

(7)

This equation is equivalent to

$$\begin{array}{c}\hfill \mathcal{F}\left\{\tilde{f}\right\}\left({\displaystyle \frac{\omega }{b}}\right)=\sqrt{2i\pi b}{e}^{i\frac{d}{2b}{\omega }^2}{L}_B\left\{f\right\}\left(\omega \right),\end{array}$$

(8)

where $\mathcal{F}\left\{f\right\}$ stands for the Fourier transform of the signal $f\in L^1\left(\mathbb{R}\right)$ given by [21,22]

$$\begin{array}{c}\hfill \mathcal{F}\left\{f\right\}\left(\omega \right)={\int }_{\mathbb{R}}f\left(x\right)e^{i\omega x}dx.\end{array}$$

(9)

3. Characteristic Function in LCT

Recently, the authors of [11,12,23] have proposed the fractional characteristic function, which is a natural generalization of the classical characteristic function using a fractional calculus approach. This part will construct the characteristic function in the context of the LCT and investigate its crucial properties.

For a real random variable X with probability density function (pdf) $f_X\left(x\right)$, the (classical) characteristic function of X is defined by

$$\begin{array}{c}\hfill {\phi }_X\left\{f\right\}\left(t\right)={\mathbb{E}}_f\left[e^{itX}\right]={\int }_{\mathbb{R}}{e}^{itx}{f}_X\left(x\right)dx,\end{array}$$

(10)

and the characteristic function of $-X$ is

$$\begin{array}{c}\hfill {\phi }_{-X}\left\{f\right\}\left(t\right)={\mathbb{E}}_f\left[e^{-itX}\right]={\int }_{\mathbb{R}}{e}^{-itx}{f}_X\left(x\right)dx.\end{array}$$

(11)

Equation (10) may be represented as

$$\begin{array}{c}\hfill {\phi }_X\left\{f\right\}\left(t\right)={\int }_{\mathbb{R}}\left({\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(itx\right)}^k}{k!}}\right)f_X\left(x\right)dx={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(it\right)}^k}{k!}}{\mathbb{E}}_f\left[X^k\right],\end{array}$$

(12)

where ${\mathbb{E}}_f\left[X^k\right]$ is the $kth$ moment. Equation (10) shows that the characteristic function is constructed using the kernel of the Fourier transform (FT). Based on this idea, we extend the characteristic function using the LCT kernel, which is called the linear canonical characteristic function (LCCF). The LCCF is obtained by replacing the FT kernel with the LCT kernel in Equation (10). To this end, we start with the following definition:

Definition 3.

Let $X\in \mathbb{R}$ be a real random variable whose probability density function is $f_X$. The LCCF, denoted by ${\phi }_X^B:\mathbb{R}\to \mathbb{C}$, is defined by

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& ={\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]\hfill \\ \hfill & ={\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)dx,\hfill \end{array}$$

(13)

provided the integral exists and is finite.

We may express Equation (13) in the following form:

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& =e^{-i\frac{d}{2b}{\omega }^2}{\int }_{\mathbb{R}}\left({\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(i\frac{\omega }{b}x\right)}^k}{k!}}\right)e^{-i\frac{a}{2b}{x}^2}{f}_X\left(x\right)dx.\hfill \\ \hfill & =e^{-i\frac{d}{2b}{\omega }^2}{\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(i\frac{\omega }{b}\right)}^k}{k!}}{\int }_{\mathbb{R}}{x}^k{e}^{-i\frac{a}{2b}{x}^2}{f}_X\left(x\right)dx.\hfill \\ \hfill & =e^{-i\frac{d}{2b}{\omega }^2}{\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(i\frac{\omega }{b}\right)}^k}{k!}}{\mathbb{E}}_f\left[X^k{e}^{-i\frac{a}{2b}{X}^2}\right].\hfill \end{array}$$

(14)

Now, if we assume that

$$\begin{array}{c}\hfill {\int }_{\mathbb{R}}{\tilde{f}}_X\left(x\right)dx={\int }_{\mathbb{R}}{e}^{-i\frac{a}{2b}{x}^2}{f}_X\left(x\right)dx=1,\end{array}$$

(15)

then Equation (14) may be expressed as

$$\begin{array}{c}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)=e^{-i\frac{d}{2b}{\omega }^2}{\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(i\frac{\omega }{b}\right)}^k}{k!}}{\mathbb{E}}_{\tilde{f}}\left[X^k\right],\end{array}$$

(16)

for which

$$\begin{array}{c}\hfill {\tilde{f}}_X\left(x\right)=e^{-i\frac{a}{2b}{x}^2}{f}_X\left(x\right).\end{array}$$

(17)

It can easily be seen that when we take $B=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$, Equation (16) changes to Equation (12). The relation of the LCCF with the classical characteristic function is given by

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& =e^{-i\frac{d}{2b}{\omega }^2}{\int }_{\mathbb{R}}{f}_X\left(x\right)e^{-i\frac{a}{2b}{x}^2}{e}^{i\frac{\omega }{b}x}dx\hfill \\ \hfill & =e^{-i\frac{d}{2b}{\omega }^2}{\phi }_X\left\{\tilde{f}\right\}\left({\displaystyle \frac{\omega }{b}}\right).\hfill \end{array}$$

(18)

In particular, we have

$$\begin{array}{cc}\hfill {\phi }_{-X}^B\left\{f\right\}\left(\omega \right)& =e^{-i\frac{d}{2b}{\omega }^2}{\int }_{\mathbb{R}}{f}_X\left(x\right)e^{-i\frac{a}{2b}{x}^2}{e}^{-i\frac{\omega }{b}x}dx\hfill \\ \hfill & =e^{-i\frac{d}{2b}{\omega }^2}{\phi }_X\left\{\tilde{f}\right\}\left({\displaystyle \frac{-\omega }{b}}\right).\hfill \end{array}$$

(19)

We collected some of the basic properties of the LCCF in the following lemma:

Lemma 2.

Let X be a real random variable. We have the following properties:

• $|{\phi }_X^B\left\{f\right\}\left(\omega \right)|\le 1$
• ${\phi }_X^{B^{\prime }}\left\{f\right\}\left(0\right)=1$, where $B^{\prime }=\left[\begin{array}{cc}0& b\\ c& d\end{array}\right]$, $bc=-1$.
• ${\phi }_{-X}^B\left\{f\right\}\left(\omega \right)={\phi }_X^B\left\{f\right\}(-\omega ),\forall \omega \in \mathbb{R}$.

Proof. 

We just derived part 3, and the others are similar. With the help of Relation (13), we immediately get

$$\begin{array}{cc}\hfill {\phi }_{-X}^B\left\{f\right\}\left(\omega \right)& ={\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{(-X)}^2-\frac{2}{b}(-X)\omega +\frac{d}{b}{\omega }^2\right)}\right]\hfill \\ \hfill & ={\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a}{b}{(-x)}^2-\frac{2}{b}(-x)\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)dx\hfill \\ \hfill & ={\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a}{b}{x}^2+{\displaystyle \frac{2}{b}}x\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)dx\hfill \\ \hfill & ={\phi }_X^B\left\{f\right\}(-\omega ).\hfill \end{array}$$

(20)

□

In particular, when $B=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$, Expression (20) becomes ${\phi }_{-X}^B\left\{f\right\}\left(\omega \right)=\overline{{\phi }_X^B\left\{f\right\}\left(\omega \right)}$.

Another property of the LCCF is given by

$$\begin{array}{c}\hfill {\phi }_X^{\check{B}}\left\{f\right\}\left(\omega \right)=\overline{{\phi }_X^B\left\{f\right\}\left(\omega \right)}.\end{array}$$

(21)

To verify (21), we see that

$$\begin{array}{cc}\hfill \overline{{\phi }_X^B\left\{f\right\}\left(\omega \right)}& =\overline{{\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)dx}\hfill \\ \hfill & ={\int }_{\mathbb{R}}{e}^{\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)dx\hfill \\ \hfill & ={\phi }_X^{\check{B}}\left(\omega \right).\hfill \end{array}$$

Also, it is quite simple to check that

$$\begin{array}{c}\hfill \overline{{\phi }_X^B\left\{f\right\}(-\omega )}={\phi }_X^{\check{B}}\left\{f\right\}(-\omega ).\end{array}$$

(22)

Here, $\check{B}=\left[\begin{array}{cc}a& -b\\ c& d\end{array}\right]$. By virtue of Relations (18) and (22), one has

$$\Re \left({\phi }_X\left\{f\right\}\left(\omega \right)\right)={\displaystyle \frac{{\phi }_X^B\left\{f\right\}\left(\omega \right)+{\phi }_X^{\check{B}}\left\{f\right\}\left(\omega \right)}{2}},$$

(23)

and

$$\Im \left({\phi }_X\left\{f\right\}\left(\omega \right)\right)={\displaystyle \frac{{\phi }_X^B\left\{f\right\}\left(\omega \right)-{\phi }_X^{\check{B}}\left\{f\right\}\left(\omega \right)}{2i}}.$$

(24)

Furthermore, according to (3), the probability density function $f_X\left(x\right)$ in terms of the LCCF is given by

$$f_X\left(x\right)={\displaystyle \frac{1}{2\pi b}}{\int }_{\mathbb{R}}{e}^{\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}{\phi }_X^B\left\{f\right\}\left(\omega \right)d\omega .$$

(25)

The other properties of the LCCF are collected in the following theorems. These properties are an extended version of the classical characteristic function [24].

Theorem 1.

Let X be a random variable. Let ${\phi }_X^B\left\{f\right\}$ denote the LCCF of the function f, then

$$\begin{array}{c}\hfill {\phi }_{\alpha +\beta X}^B\left\{f\right\}\left(\omega \right)=e^{-i\frac{a}{2b}{\alpha }^2}{e}^{i\frac{1}{b}\alpha \omega }{\phi }_X^{\overline{B}}\left\{h\right\}\left(\beta \omega \right),\end{array}$$

(26)

where α and β are constants. In this case, $\overline{B}=\left[\begin{array}{cc}a{\beta }^2& b\\ c& {\displaystyle \frac{d}{{\beta }^2}}\end{array}\right]$ and $h\left(x\right)=f_X\left(x\right)e^{-i\frac{a}{b}\alpha \beta x}$.

Proof. 

It follows from Equation (13) that

$$\begin{array}{cc}\hfill {\phi }_{\alpha +\beta X}^B\left\{f\right\}\left(\omega \right)& ={\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a}{b}{(\alpha +\beta x)}^2-\frac{2}{b}(\alpha +\beta x)\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)dx\hfill \\ \hfill & ={\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a}{b}({\alpha }^2+2\alpha \beta x+{\beta }^2{x}^2)-\frac{2}{b}(\alpha +\beta x)\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)dx\hfill \\ \hfill & =e^{-i\frac{a}{2b}{\alpha }^2}{e}^{i\frac{1}{b}\alpha \omega }{\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a}{b}{\left(\beta x\right)}^2-\frac{2}{b}\beta x\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)e^{-i\frac{a}{b}\alpha \beta x}dx.\hfill \end{array}$$

The above expression may be rewritten in the form

$$\begin{array}{cc}\hfill {\phi }_{\alpha +\beta X}^B\left\{f\right\}\left(\omega \right)& =e^{-i\frac{a}{2b}{\alpha }^2}{e}^{i\frac{1}{b}\alpha \omega }{\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a{\beta }^2}{b}{x}^2-\frac{2}{b}\beta x\omega +\frac{d/{\beta }^2}{b}{\left(\beta \omega \right)}^2\right)}{f}_X\left(x\right)e^{-i\frac{a}{b}\alpha \beta x}dx\hfill \\ \hfill & =e^{-i\frac{a}{2b}{\alpha }^2}{e}^{i\frac{1}{b}\alpha \omega }{\phi }_X^{\overline{B}}\left\{h\right\}\left(\beta \omega \right),\hfill \end{array}$$

which finishes the proof. □

Remark 1.

Taking the matrix $B=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$ in Theorem 1, we obtain

$$\begin{array}{c}\hfill {\phi }_{\alpha +\beta X}^B\left\{f\right\}\left(\omega \right)=e^{i\alpha \omega }{\phi }_X^B\left\{f\right\}\left(\beta \omega \right),\end{array}$$

(27)

which is the basic property of the characteristic function.

Theorem 2.

Let X be a real random variable. Then ${\phi }_X^B\left\{f\right\}$ is uniformly continuous on $\mathbb{R}$.

Proof. 

It follows from Equation (13) that

$$\begin{array}{cc}\hfill & |{\phi }_X^B\left\{f\right\}(\omega +h)-{\phi }_X^B\left\{f\right\}\left(\omega \right)|\hfill \\ \hfill & =|{\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X(\omega +h)+\frac{d}{b}{(\omega +h)}^2\right)}\right]-{\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]|\hfill \\ \hfill & =|{\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X(\omega +h)+\frac{d}{b}({\omega }^2+2\omega h+h^2)\right)}\right]-{\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]|.\hfill \end{array}$$

(28)

The above identity may be expressed as

$$\begin{array}{cc}\hfill |{\phi }_X^B\left\{f\right\}& (\omega +h)-{\phi }_X^B\left\{f\right\}\left(\omega \right)|\hfill \\ \hfill & =|e^{-\frac{i}{2}\left(\frac{d}{b}(2\omega h+h^2-\frac{2}{b}xh\right)}{\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]-{\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]|\hfill \\ \hfill & =\left|\left(e^{-\frac{i}{2}\left(\frac{d}{b}(2\omega h+h^2-\frac{2}{b}xh\right)}-1\right){\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]\right|.\hfill \end{array}$$

(29)

Equation (29) yields

$$\begin{array}{c}\hfill |{\phi }_X^B\left\{f\right\}(\omega +h)-{\phi }_X^B\left\{f\right\}\left(\omega \right)|\le 2{\mathbb{E}}_f\left[\left|e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right|\right].\end{array}$$

According to the dominated convergence theorem (DCT) and Equation (29), we infer that

$$\begin{array}{c}\hfill |{\phi }_X^B\left\{f\right\}(\omega +h)-{\phi }_X^B\left\{f\right\}\left(\omega \right)|\Rightarrow 0,\end{array}$$

(30)

when $h\to 0$. This shows that ${\phi }_X^B\left\{f\right\}\left(\omega \right)$ is continuous on $\mathbb{R}$. □

The following result explains that the LCCF of the convolution of two probability density functions is equal to the simple product of their respective LCCFs with the chirp signal.

Theorem 3.

Suppose that $f_X$ and $f_Y$ are probability density functions of independent random variables X and Y. Then, we have

$$\begin{array}{c}\hfill {\phi }_X^B\left\{f_X{\ast }_l{f}_Y\right\}\left(\omega \right)=e^{\frac{id}{2b}{\omega }^2}{\phi }_X^B\left\{f\right\}\left(\omega \right){\phi }_Y^B\left\{f\right\}\left(\omega \right),\end{array}$$

(31)

where the convolution of two probability density functions of $f_X$ and $f_Y$ is defined by

$$\begin{array}{c}\hfill \left(f_X{\ast }_l{f}_Y\right)\left(z\right)={\int }_{\mathbb{R}}{f}_X\left(x\right)f_Y(z-x)e^{-i\frac{a}{2b}x(x-z)}dx.\end{array}$$

(32)

Proof. 

By Equations (13) and (31), the left-hand side of (31) is equivalent to

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f_X{\ast }_l{f}_Y\right\}\left(\omega \right)& ={\int }_{\mathbb{R}}(f_X\ast f_Y)\left(z\right)e^{-\frac{i}{2}\left(\frac{a}{b}{z}^2-\frac{2}{b}z\omega +\frac{d}{b}{\omega }^2\right)}dz\hfill \\ \hfill & ={\int }_{\mathbb{R}}\left[{\int }_{\mathbb{R}}{f}_X\left(x\right)f_Y(z-x)e^{-i\frac{a}{2b}x(x-z)}dx\right]e^{-\frac{i}{2}\left(\frac{a}{b}{z}^2-\frac{2}{b}z\omega +\frac{d}{b}{\omega }^2\right)}dz.\hfill \end{array}$$

(33)

Changing variables $y=z-x$ in the above equation yields

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f_X{\ast }_l{f}_Y\right\}\left(\omega \right)& ={\int }_{\mathbb{R}}{\int }_{\mathbb{R}}{f}_X\left(x\right)f_Y\left(y\right)e^{i\frac{a}{2b}xy}{e}^{-\frac{i}{2}\left(\frac{a}{b}{(y+x)}^2-\frac{2}{b}(y+x)\omega +\frac{d}{b}{\omega }^2\right)}dxdy\hfill \\ \hfill & ={\int }_{\mathbb{R}}{f}_X\left(x\right)\left({\int }_{\mathbb{R}}{f}_Y\left(y\right)e^{-i\frac{a}{2b}{y}^2}{e}^{\frac{i}{b}y\omega }{e}^{-\frac{id}{2b}{\omega }^2}dy\right)e^{-i\frac{a}{2b}{x}^2}{e}^{\frac{i}{b}x\omega }dx\hfill \\ \hfill & ={\int }_{\mathbb{R}}{f}_X\left(x\right)e^{-i\frac{a}{2b}{x}^2}{e}^{i\frac{x\omega }{b}}dx{\int }_{\mathbb{R}}{f}_Y\left(y\right)e^{-\frac{i}{2}\left(\frac{a}{b}{y}^2-\frac{2}{b}y\omega +\frac{d}{b}{\omega }^2\right)}dy.\hfill \end{array}$$

(34)

We arrive at

$$\begin{array}{cc}\hfill e^{-\frac{id}{2b}{\omega }^2}{\phi }_X^B\left\{f_X{\ast }_l{f}_Y\right\}\left(\omega \right)& ={\phi }_Y^B\left\{f\right\}\left(\omega \right){\int }_{\mathbb{R}}{f}_X\left(x\right)e^{-i\frac{a}{2b}{x}^2}{e}^{i\frac{x\omega }{b}}{e}^{-\frac{id}{2b}{\omega }^2}dx\hfill \\ \hfill & ={\phi }_X^B\left\{f\right\}\left(\omega \right){\phi }_Y^B\left\{f\right\}\left(\omega \right).\hfill \end{array}$$

The proof is complete. □

4. Moments, Variance, and Their Relationship to LCCF

As is well known, moments and variances of a random variable are closely related to characteristic functions, where they can be obtained from the derivatives of the characteristic functions. In this part, we shall discuss these important facts in relation to the proposed LCCF. The main result of this section is a fundamental relation between the nth derivative of the LCCF calculated at zero and the nth moment. In this regard, we first recall the nth moment of a real random variable X as

$${\mathbb{E}}_f\left[X^n\right]=m_n={\int }_{\mathbb{R}}{x}^n{f}_X\left(x\right)dx,n=1,2,3,\cdots ,$$

(35)

provided the integral exists. Based on Equation (35), we define the nth moment related to the LCCF as

$${\mathbb{E}}_f\left[X^n{e}^{-i\frac{a}{2b}{X}^2}\right]={\int }_{\mathbb{R}}{x}^n{f}_X\left(x\right)e^{-\frac{ia}{2b}{x}^2}dx,n=1,2,3,\cdots .$$

(36)

Equation (36) may be expressed in the following form:

$${\mathbb{E}}_f\left[X^n{e}^{-i\frac{a}{2b}{X}^2}\right]={\int }_{\mathbb{R}}{x}^n{\tilde{f}}_X\left(x\right)dx={\mathbb{E}}_{\tilde{f}}\left[X^n\right],$$

(37)

in which ${\tilde{f}}_X$ is described by Equation (17). In particular, when $n=2$, we may utilize the following result to calculate (36) through the LCCF:

Theorem 4.

Let X be a real random variable and let ${\phi }_X^B\left\{f\right\}$ be the LCCF of X. Then there exists the second continuous derivative for the LCCF, which is described by

$$\begin{array}{c}\hfill {\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}={\displaystyle \frac{-i}{b}}{\int }_{\mathbb{R}}{f}_X\left(x\right)\left(d+{\displaystyle \frac{i}{b}}{(d\omega -x)}^2\right)e^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}dx.\end{array}$$

(38)

Furthermore,

$$\begin{array}{c}\hfill {\mathbb{E}}_f\left[X^2{e}^{-i\frac{a}{2b}{X}^2}\right]=idb{\int }_{\mathbb{R}}{f}_X\left(x\right)e^{\frac{ia}{2b}{x}^2}dx-b^2{\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}.\end{array}$$

(39)

Proof. 

From Equation (13), it follows that

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& ={\int }_{\mathbb{R}}{e}^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}{f}_X\left(x\right)dx\hfill \end{array}$$

(40)

This equation yields

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}& ={\displaystyle \frac{-i}{b}}{\int }_{\mathbb{R}}{f}_X\left(x\right)(d\omega -x)e^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}dx.\hfill \end{array}$$

(41)

Therefore,

$$\begin{array}{c}\hfill {\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}{|}_{\omega =0}={\displaystyle \frac{-i}{b}}{\int }_{\mathbb{R}}(-x)f_X\left(x\right)e^{-\frac{ia}{2b}{x}^2}dx={\displaystyle \frac{i}{b}}{\int }_{\mathbb{R}}x{f}_X\left(x\right)e^{-\frac{ia}{2b}{x}^2}dx.\end{array}$$

(42)

This implies that

$$\begin{array}{c}\hfill {\mathbb{E}}_f\left[X{e}^{-\frac{ia}{2b}{X}^2}\right]=-ib{\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}{|}_{\omega =0},\end{array}$$

(43)

which is the first moment of a real random variable, X, related to the LCCF.

Further computations will lead to

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}\hfill \\ \hfill & ={\displaystyle \frac{d}{d\omega }}\left({\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}\right)\hfill \\ \hfill & ={\displaystyle \frac{-i}{b}}{\int }_{\mathbb{R}}{f}_X\left(x\right){\displaystyle \frac{d}{d\omega }}\left[(d\omega -x)e^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}\right]dx\hfill \\ \hfill & ={\displaystyle \frac{-i}{b}}[{\int }_{\mathbb{R}}{f}_X\left(x\right)\left(d{e}^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}\right)dx\hfill \\ \hfill & +{\int }_{\mathbb{R}}{f}_X\left(x\right)\left(d\omega -x)(-i{\displaystyle \frac{x}{b}}+i{\displaystyle \frac{d\omega }{b}})e^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}\right)dx]\hfill \\ \hfill & ={\displaystyle \frac{-i}{b}}\left[{\int }_{\mathbb{R}}{f}_X\left(x\right)\left(d{e}^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}+{\displaystyle \frac{i}{b}}(d\omega -x)(-x+d\omega )e^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}\right)dx\right]\hfill \\ \hfill & ={\displaystyle \frac{-i}{b}}{\int }_{\mathbb{R}}{f}_X\left(x\right)\left(d+{\displaystyle \frac{i}{b}}{(d\omega -x)}^2\right)e^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}dx,\hfill \end{array}$$

(44)

which gives (38). Thus, we get

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}& ={\displaystyle \frac{i}{b}}{\int }_{\mathbb{R}}{f}_X\left(x\right)\left(d+{\displaystyle \frac{i}{b}}{x}^2\right)e^{-\frac{ia}{2b}{x}^2}dx\hfill \\ \hfill & ={\displaystyle \frac{id}{b}}{\int }_{\mathbb{R}}{f}_X\left(x\right)e^{-\frac{ia}{2b}{x}^2}dx-{\displaystyle \frac{1}{b^2}}{\int }_{\mathbb{R}}{x}^2{f}_X\left(x\right)e^{-\frac{ia}{2b}{x}^2}dx.\hfill \end{array}$$

(45)

Equation (45) is simplified into

$$\begin{array}{c}\hfill {\int }_{\mathbb{R}}{x}^2{f}_X\left(x\right)e^{-\frac{ia}{2b}{x}^2}dx=idb{\int }_{\mathbb{R}}{f}_X\left(x\right)e^{-\frac{ia}{2b}{x}^2}dx-b^2{\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}.\end{array}$$

(46)

This equation is equivalent to

$$\begin{array}{c}\hfill {\mathbb{E}}_f\left[X^2{e}^{-i\frac{a}{2b}{X}^2}\right]=idb{\int }_{\mathbb{R}}{f}_X\left(x\right)e^{-\frac{ia}{2b}{x}^2}dx-b^2{\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0},\end{array}$$

which finishes the proof. □

Remark 2.

By putting the matrix $B=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$ in Equation (39), we immediately obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}=i^2{\mathbb{E}}_f\left[X^2\right].\end{array}$$

(47)

By Equation (36), the variance of the random variable X is therefore defined as

$$\begin{array}{c}\hfill Va{r}_f\left(X^2{e}^{-i\frac{a}{2b}{X}^2}\right)={\sigma }_f^2={\mathbb{E}}_f\left[X^2{e}^{-i\frac{a}{2b}{X}^2}\right]-{\mathbb{E}}_f^2\left[X^2{e}^{-i\frac{a}{2b}{X}^2}\right].\end{array}$$

(48)

If Equation (15) is satisfied, Equation (48) produces

$$\begin{array}{c}\hfill Va{r}_{\tilde{f}}\left(X\right)={\sigma }_{\tilde{f}}^2=E_{\tilde{f}}\left[X^2\right]-E_{\tilde{f}}^2\left[X\right].\end{array}$$

(49)

From Equations (39) and (43), we get the variance in terms of the LCCF as

$$\begin{array}{cc}\hfill {\sigma }_{\tilde{f}}^2& =idb-b^2{\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}-{\left(ib{\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}{|}_{\omega =0}\right)}^2\hfill \\ \hfill & =idb-b^2{\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}+b^2{\left({\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}{|}_{\omega =0}\right)}^2.\hfill \end{array}$$

(50)

If we choose $A=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$, then Equation (50) becomes

$$\begin{array}{c}\hfill {\sigma }_f^2=-{\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}+{\left({\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}{|}_{\omega =0}\right)}^2.\end{array}$$

(51)

In what follows, we establish the nth derivative of the LCCF related to its $nth$ moment. In this regard, we obtain the important theorem.

Theorem 5.

Let X be a real random variable. Then there exists an nth continuous derivative for the LCCF ${\phi }_X^B\left\{f\right\}\left(\omega \right)$, given by

$$\begin{array}{c}\hfill {\displaystyle \frac{d^n{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d^n\omega }}={\mathbb{E}}_f\left[{\left(i\left({\displaystyle \frac{ad}{b}}-c-{\displaystyle \frac{1}{b}}\right)X+i{\displaystyle \frac{d}{d\omega }}\right)}^n{e}^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right].\end{array}$$

(52)

Proof. 

By invoking Equation (13), we get

$$\begin{array}{c}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)={\mathbb{E}}_f\left[e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right].\end{array}$$

(53)

This equation leads to

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}& ={\mathbb{E}}_f\left[{\displaystyle \frac{d}{d\omega }}\left(e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right)\right]\hfill \\ \hfill & ={\mathbb{E}}_f\left[\left({\displaystyle \frac{iX}{b}}-{\displaystyle \frac{id}{b}}\omega \right)e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]\hfill \\ \hfill & ={\mathbb{E}}_f\left[\left({\displaystyle \frac{i(ad-bc)}{b}}X-{\displaystyle \frac{id}{b}}\omega \right)e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]\hfill \\ \hfill & ={\mathbb{E}}_f\left[\left({\displaystyle \frac{ida}{b}}X-icX-{\displaystyle \frac{id}{b}}\omega \right)e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]\hfill \\ \hfill & ={\mathbb{E}}_f\left[\left(i\left({\displaystyle \frac{ad}{b}}-c-{\displaystyle \frac{1}{b}}\right)X+{\displaystyle \frac{i}{b}}X-i{\displaystyle \frac{d}{b}}\omega \right)e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right]\hfill \\ \hfill & ={\mathbb{E}}_f\left[i\left(\left({\displaystyle \frac{ad}{b}}-c-{\displaystyle \frac{1}{b}}\right)X+{\displaystyle \frac{d}{d\omega }}\right)e^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right].\hfill \end{array}$$

(54)

By induction, it follows that

$$\begin{array}{c}\hfill {\displaystyle \frac{d^n{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d^n\omega }}={\mathbb{E}}_f\left[{\left(i\left({\displaystyle \frac{ad}{b}}-c-{\displaystyle \frac{1}{b}}\right)X+i{\displaystyle \frac{d}{d\omega }}\right)}^n{e}^{-\frac{i}{2}\left(\frac{a}{b}{X}^2-\frac{2}{b}X\omega +\frac{d}{b}{\omega }^2\right)}\right].\end{array}$$

The proof is complete. □

Remark 3.

By selecting $B=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$ in Theorem 5, we obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{d^n{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d^n\omega }}{|}_{\omega =0}={\mathbb{E}}_f\left[i^n{X}^n\right]=i^n{\mathbb{E}}_f\left[X^n\right].\end{array}$$

(55)

Equation (55) explicitly describes the basic relationship between the $nth$ derivative of a classical characteristic function, evaluated at 0, and the $nth$ moment of the random variable X.

5. Illustrative Examples

In this last section, we verify the above results by providing some examples of the LCCF for well-known probability density functions.

Example 1.

Consider the standard exponential distribution whose probability density function is given by

$$f\left(x\right)=\left\{\begin{array}{c}{e}^{-x},\mathrm{for}x\ge 0\hfill \\ 0,\mathrm{elsewhere}.\hfill \end{array}\right.$$

(56)

The LCCF of the above function is derived as follows:

In fact, we have

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& ={\int }_0^{\infty }{e}^{-\frac{i}{2}\left(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2\right)}{e}^{-x}dx\hfill \\ \hfill & ={\int }_0^{\infty }{e}^{-\frac{ia}{2b}{x}^2+(\frac{i}{b}\omega -1)x+i\frac{d}{2b}{\omega }^2}dx\hfill \\ \hfill & =e^{-i\frac{d}{b}{\omega }^2}{\int }_0^{\infty }{e}^{-\frac{ia}{2b}\left(x^2-\left(\frac{2\omega -i2b}{a}\right)x\right)}dx,a\ne 0.\hfill \end{array}$$

(57)

We write (57) as

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& =e^{-i\frac{d}{b}{\omega }^2}{\int }_0^{\infty }{e}^{-\frac{ia}{2b}\left({(x-\left(\frac{\omega -ib}{a}\right))}^2-{\left(\frac{\omega -ib}{a}\right)}^2\right)}dx\hfill \\ \hfill & =e^{-i\frac{d}{2b}{\omega }^2-\frac{i{(\omega -ib)}^2}{8ab}}{\int }_0^{\infty }{e}^{-{\left(\sqrt{\frac{ia}{2b}}\left(x-\frac{\omega -ib}{a}\right)\right)}^2}dx.\hfill \end{array}$$

(58)

Changing the variables $u=\sqrt{\frac{ai}{2b}}\left(x-\frac{\omega -ib}{a}\right)$, we immediately obtain

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& =e^{-i\frac{d}{2b}{\omega }^2-\frac{i{(\omega -ib)}^2}{8ab}}\sqrt{{\displaystyle \frac{2b}{ai}}}{\int }_{-\sqrt{\frac{ai}{2b}}\left(\frac{\omega -ib}{a}\right)}^{\infty }{e}^{-u^2}du\hfill \\ \hfill & =e^{-i\frac{d}{2b}{\omega }^2-\frac{i{(\omega -ib)}^2}{8ab}}\sqrt{{\displaystyle \frac{2b}{ai}}}\left({\int }_{-\sqrt{\frac{ai}{2b}}\left(\frac{\omega -ib}{a}\right)}^0{e}^{-u^2}du+{\int }_0^{\infty }{e}^{-u^2}du\right)\hfill \\ \hfill & =e^{-i\frac{d}{2b}{\omega }^2-\frac{i{(\omega -ib)}^2}{8ab}}\sqrt{{\displaystyle \frac{2b}{ai}}}\left({\int }_0^{\infty }{e}^{-u^2}du-{\int }_0^{-\sqrt{\frac{ai}{2b}}\left(\frac{\omega -ib}{a}\right)}{e}^{-u^2}du\right)\hfill \\ \hfill & =e^{-i\frac{d}{2b}{\omega }^2-\frac{i{(\omega -ib)}^2}{8ab}}\sqrt{{\displaystyle \frac{2b}{ai}}}\left({\displaystyle \frac{\sqrt{\pi }}{2}}-{\displaystyle \frac{\sqrt{\pi }}{2}}erf\left(-\sqrt{{\displaystyle \frac{ai}{2b}}}\left({\displaystyle \frac{\omega -ib}{a}}\right)\right)\right)\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{\pi b}{2ai}}}{e}^{-i\frac{d}{2b}{\omega }^2-\frac{i{(\omega -ib)}^2}{8ab}}\left(1+erf\left(\sqrt{{\displaystyle \frac{ai}{2b}}}\left({\displaystyle \frac{\omega -ib}{a}}\right)\right)\right)a\ne 0.\hfill \end{array}$$

(59)

A graph of the LCCF of Relation (59) for different values, compared to the classical characteristic function in (56), is displayed in Figure 1.

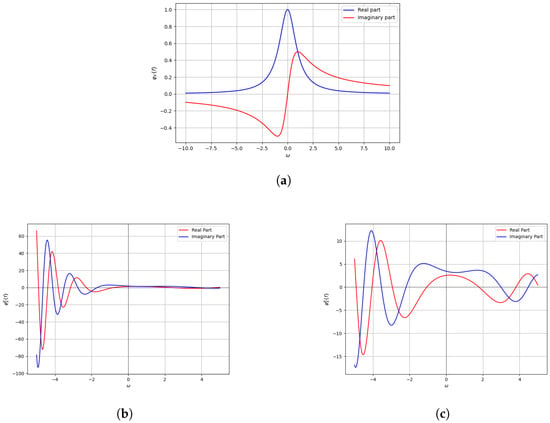
Figure 1. Comparison of characteristic function and LCCF. (a) characteristic function ${\phi }_X\left\{f\right\}$ of (56); LCCF ${\phi }_X^B\left\{f\right\}$ of Example 1 with (b) $a=1$, $b=1$, $d=0.1$; (c) $a=2,b=2,d=1,\omega =-5\dots 5$. This shows that the LCCF is more flexible and superior to the classical characteristic function.

Example 2.

Consider the uniform distribution given by

$$f\left(x\right)=\left\{\begin{array}{c}\frac{1}{2},\mathrm{for}-1<x<1\hfill \\ 0,\mathrm{elsewhere}.\hfill \end{array}\right.$$

(60)

Its LCCF is as follows:

A simple computation shows

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& ={\displaystyle \frac{1}{2}}{\int }_{-1}^1{e}^{-\frac{i}{2}(\frac{a}{b}{x}^2-\frac{2}{b}x\omega +\frac{d}{b}{\omega }^2)}dx\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\int }_{-1}^1{e}^{-\frac{ia}{2b}\left({(x-\frac{\omega }{a})}^2+(\frac{d}{a}{\omega }^2-\frac{{\omega }^2}{a^2})\right)}dx,a\ne 0.\hfill \end{array}$$

(61)

This equation may be further simplified to

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& =\frac{e^{-\frac{ia}{2b}(\frac{d}{a}{\omega }^2-\frac{{\omega }^2}{a^2})}}{2}{\int }_{-1}^1{e}^{-\frac{ia}{2b}{(x-\frac{\omega }{a})}^2}dx\hfill \\ \hfill & =\frac{e^{-\frac{ia}{2b}(\frac{d}{a}{\omega }^2-\frac{{\omega }^2}{a^2})}}{2}{\int }_{-1}^1{e}^{-{\left(\sqrt{i\frac{a}{2b}}(x-\frac{\omega }{a})\right)}^2}dx\hfill \\ \hfill & =e^{-\frac{ia}{2b}(\frac{d}{a}{\omega }^2-\frac{{\omega }^2}{a^2})}{\int }_0^1{e}^{-{\left(\sqrt{i\frac{a}{2b}}(x-\frac{\omega }{a})\right)}^2}dx.\hfill \end{array}$$

(62)

Performing the change of variables, $u=\sqrt{i{\displaystyle \frac{a}{2b}}}\left(x-{\displaystyle \frac{\omega }{a}}\right)$ in Equation (62) yields

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& =\sqrt{{\displaystyle \frac{2b}{ia}}}{e}^{-\frac{ia}{2b}\left(\frac{d}{a}{\omega }^2-\frac{{\omega }^2}{a^2}\right)}\left({\int }_{\sqrt{i\frac{a}{2b}}\left(-\frac{\omega }{a}\right)}^{\sqrt{i\frac{a}{2b}}\left(1-\frac{\omega }{a}\right)}{e}^{-u^2}du\right)\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{8b}{i\pi a}}}{e}^{-\frac{ia}{2b}\left(\frac{d}{a}{\omega }^2-\frac{{\omega }^2}{a^2}\right)}\left(erf\left(\sqrt{i{\displaystyle \frac{a}{2b}}}\left(1-{\displaystyle \frac{\omega }{a}}\right)\right)+erf\left({\displaystyle \frac{\omega }{a}}\sqrt{i{\displaystyle \frac{a}{2b}}}\right)\right).\hfill \end{array}$$

(63)

Figure 2 illustrates a comparison of the LCCF (63) with the characteristic function of (60).

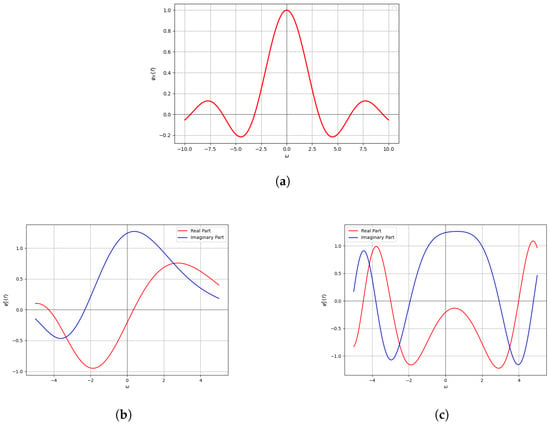
Figure 2. (a) Characteristic function ${\phi }_X\left\{f\right\}$ of (60). LCCF ${\phi }_X^B\left\{f\right\}$ of Example 2 with (b) $a=1$, $b=1$, $d=0.1$; (c) $a=2,b=2,d=1,\omega =-5\dots 5$. This shows that the LCCF is more flexible and superior to the classical characteristic function.

Example 3.

Consider a Gaussian random variable with mean m and variance ${\sigma }^2$ of the form

$$\begin{array}{c}\hfill f\left(x\right)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-\frac{{(x-m)}^2}{2{\sigma }^2}}.\end{array}$$

(64)

By virtue of Equation (13), we have

$$\begin{array}{c}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)={\int }_{\mathbb{R}}{\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-\frac{{(x-m)}^2}{2{\sigma }^2}}{e}^{-i(\frac{a}{2b}{x}^2-\frac{x\omega }{b}+\frac{d}{2b}{\omega }^2)}dx.\end{array}$$

(65)

Substituting $y=x-m$ into the above expression, we get

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& ={\int }_{\mathbb{R}}{\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-\frac{y^2}{2{\sigma }^2}}{e}^{-i(\frac{a}{2b}{(y+m)}^2-\frac{(y+m)\omega }{b}+\frac{d}{2b}{\omega }^2)}dy\hfill \\ \hfill & ={\int }_{\mathbb{R}}{\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-\frac{y^2}{2{\sigma }^2}}{e}^{-i(\frac{a}{2b}(y^2+2ym+m^2)-\frac{(y\omega +m\omega )}{b}+\frac{d}{2b}{\omega }^2)}dy\hfill \\ \hfill & ={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-i\frac{a}{2b}{m}^2-i\frac{d}{2b}{\omega }^2+i\frac{m\omega }{b}}{\int }_{\mathbb{R}}{e}^{-(\frac{1}{2{\sigma }^2}+\frac{ia}{2b})y^2-i(\frac{am}{b}-\frac{\omega }{b})y}dy.\hfill \end{array}$$

(66)

Using the fact that

$$\begin{array}{c}\hfill {\int }_{\mathbb{R}}{e}^{-A{x}^2\pm 2Bx+C}dx=\sqrt{{\displaystyle \frac{\pi }{A}}}{e}^{\frac{B^2}{A}+C},\end{array}$$

(67)

where $A,B,C\in \mathbb{C}$ with $A\ne 0$ and $\Re \left(A\right)\ge 0$. Thus, Equation (65) above leads to

$$\begin{array}{c}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{\left(-i\frac{a}{2b}{m}^2-i\frac{d}{2b}{\omega }^2+i\frac{m\omega }{b}-\frac{{\left(\frac{am-\omega }{b}\right)}^2}{4\left(\frac{1}{2{\sigma }^2}+\frac{ia}{2b}\right)}\right)}\sqrt{\frac{\pi }{\frac{1}{2{\sigma }^2}+\frac{ia}{2b}}}.\end{array}$$

This equation is simplified into

$$\begin{array}{cc}\hfill {\phi }_X^B\left\{f\right\}\left(\omega \right)& =\sqrt{{\displaystyle \frac{2b}{2b+i2a{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-i\frac{d}{2b}{\omega }^2+i\frac{m\omega }{b}-\frac{{\left(\frac{am-\omega }{b}\right)}^2}{4\left(\frac{1}{2{\sigma }^2}+\frac{ia}{2b}\right)}\right)}\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-i\frac{d}{2b}{\omega }^2+i\frac{m\omega }{b}-\frac{(a^2{m}^2-2\omega am+{\omega }^2)}{4b^2\left(\frac{1}{2{\sigma }^2}+i\frac{a}{2b}\right)}\right)}.\hfill \end{array}$$

(68)

It can easily be seen that when $B=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$ in Expression (68), we get

$$\begin{array}{c}\hfill {\phi }_X\left\{f\right\}\left(\omega \right)=e^{im\omega -\frac{{\omega }^2{\sigma }^2}{2}},\end{array}$$

(69)

which is quite similar to the classical characteristic function of the Gaussian function [24]. Figure 3 illustrates the difference and comparison of the LCCF (68) and the characteristic function (69). These figures demonstrate that the LCCF is more flexible than the classical characteristic function.

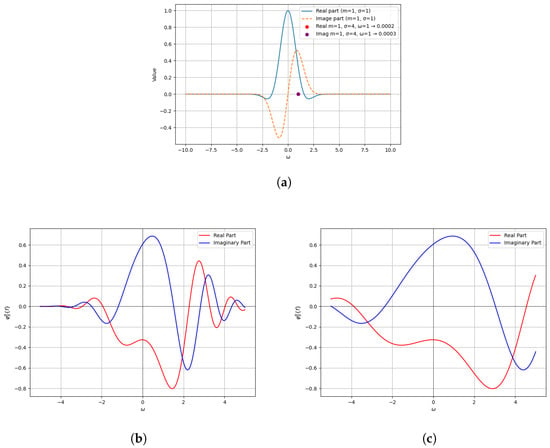
Figure 3. (a) Characteristic function ${\phi }_X\left\{f\right\}$ of Example 3. The LCCF ${\phi }_X^B\left\{f\right\}$ of Example 3 with (b) $a=1$, $b=1,d=2,m=1,\sigma =1$; (c) $a=2,b=2,d=1,m=1,\sigma =1,\omega =-5\dots 5$. This shows that the LCCF is more flexible and superior to the classical characteristic function.

Furthermore, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-i\frac{d}{2b}{\omega }^2+i\frac{m\omega }{b}-\frac{(a^2{m}^2-2\omega am+{\omega }^2)}{4b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}\right)}\left(-{\displaystyle \frac{id\omega }{b}}+i{\displaystyle \frac{m}{b}}-{\displaystyle \frac{(\omega -am)}{2b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}}\right).\hfill \end{array}$$

(70)

According to (43), we obtain

$$\begin{array}{cc}\hfill {\mathbb{E}}_f\left[X{e}^{-\frac{ia}{2b}{X}^2}\right]& =-ib{\displaystyle \frac{d{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d\omega }}{|}_{\omega =0}\hfill \\ \hfill & =-i\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-\frac{{\sigma }^2{a}^2{m}^2}{b^2+2i{\sigma }^2}\right)}\left(im+{\displaystyle \frac{4{\sigma }^{2}am}{2b+4i{\sigma }^2}}\right),\hfill \end{array}$$

(71)

which is the first moment related to the LCCF of Example 3.

Furthermore, simple computations lead to

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-i\frac{d}{2b}{\omega }^2+i\frac{m\omega }{b}-\frac{(a^2{m}^2-2\omega am+{\omega }^2)}{4b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}\right)}{\left(-{\displaystyle \frac{id\omega }{b}}+i{\displaystyle \frac{m}{b}}-{\displaystyle \frac{(\omega -am)}{2b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}}\right)}^2\hfill \\ \hfill & +\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-i\frac{d}{2b}{\omega }^2+i\frac{m\omega }{b}-\frac{(a^2{m}^2-2\omega am+{\omega }^2)}{4b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}\right)}\left(-{\displaystyle \frac{id}{b}}-{\displaystyle \frac{1}{2b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}}\right)\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-i\frac{d}{2b}{\omega }^2+i\frac{m\omega }{b}-\frac{(a^2{m}^2-2\omega am+{\omega }^2)}{4b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}\right)}({\left(-{\displaystyle \frac{id\omega }{b}}+i{\displaystyle \frac{m}{b}}-{\displaystyle \frac{(\omega -am)}{2b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}}\right)}^2\hfill \\ \hfill & +\left(-{\displaystyle \frac{id}{b}}-{\displaystyle \frac{1}{2b^2\left(\frac{1}{4{\sigma }^2}+i\frac{a}{2b}\right)}}\right)).\hfill \end{array}$$

Now, observe that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d^2{\varphi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}\hfill \\ \hfill & =\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-\frac{2a^2{\sigma }^2{m}^2}{2b^2+i4b{\sigma }^{2}a}\right)}\left({\left(i{\displaystyle \frac{m}{b}}+{\displaystyle \frac{4{\sigma }^{2}am}{2b^2+i4b{\sigma }^{2}a}}\right)}^2-\left({\displaystyle \frac{id}{b}}+{\displaystyle \frac{2{\sigma }^2}{2b^2+i4b{\sigma }^{2}a}}\right)\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{b}}\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-\frac{2a^2{\sigma }^2{m}^2}{2b^2+i4b{\sigma }^{2}a}\right)}\left({\left(im+{\displaystyle \frac{4{\sigma }^{2}am}{2b+i4{\sigma }^{2}a}}\right)}^2-\left(id+{\displaystyle \frac{{\sigma }^2}{b+i2{\sigma }^{2}a}}\right)\right).\hfill \end{array}$$

(72)

By virtue of Equation (39), we have

$$\begin{array}{cc}\hfill & {\mathbb{E}}_f\left[X^2{e}^{-i\frac{a}{2b}{X}^2}\right]\hfill \\ \hfill & =idb{\int }_{\mathbb{R}}{f}_X\left(x\right)e^{\frac{ia}{2b}{x}^2}dx-b^2{\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}\hfill \\ \hfill & ={\int }_{\mathbb{R}}{\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-\frac{{(x-m)}^2}{2{\sigma }^2}}{e}^{-i\frac{a}{2b}{x}^2}dx-b^2{\displaystyle \frac{d^2{\phi }_X^B\left\{f\right\}\left(\omega \right)}{d{\omega }^2}}{|}_{\omega =0}\hfill \\ \hfill & =idb\sqrt{{\displaystyle \frac{b}{i{\sigma }^{2}a+b}}}{e}^{\frac{b{m}^2}{{\sigma }^2(2{\sigma }^{2}a+2b)}-\frac{m^2}{2{\sigma }^2}}\hfill \\ \hfill & -b\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-\frac{2a^2{\sigma }^2{m}^2}{2b^2+i4b{\sigma }^{2}a}\right)}\left({\left(im+{\displaystyle \frac{4{\sigma }^{2}am}{2b+i4{\sigma }^{2}a}}\right)}^2-\left(id+{\displaystyle \frac{{\sigma }^2}{b+i2{\sigma }^{2}a}}\right)\right),\hfill \end{array}$$

(73)

which is the second moment related to the LCCF of Example 3. According to Equation (48), we have

$$\begin{array}{cc}\hfill {\sigma }_f^2& ={\mathbb{E}}_f\left[X^2{e}^{-i\frac{a}{2b}{X}^2}\right]-{\mathbb{E}}_f^2\left[X^2{e}^{-i\frac{a}{2b}{X}^2}\right]\hfill \\ \hfill & =idb\sqrt{{\displaystyle \frac{b}{i{\sigma }^{2}a+b}}}{e}^{\frac{b{m}^2}{{\sigma }^2(2{\sigma }^{2}a+2b)}-\frac{m^2}{2{\sigma }^2}}\hfill \\ \hfill & -b\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-\frac{2a^2{\sigma }^2{m}^2}{2b^2+i4b{\sigma }^{2}a}\right)}\left({\left(im+{\displaystyle \frac{4{\sigma }^{2}am}{2b+i4{\sigma }^{2}a}}\right)}^2-\left(id+{\displaystyle \frac{{\sigma }^2}{b+i2{\sigma }^{2}a}}\right)\right)\hfill \\ \hfill & -{\left(-i\sqrt{{\displaystyle \frac{b}{b+ia{\sigma }^2}}}{e}^{\left(-i\frac{a}{2b}{m}^2-\frac{{\sigma }^2{a}^2{m}^2}{b^2+2i{\sigma }^2}\right)}\left(im+{\displaystyle \frac{4{\sigma }^{2}am}{2b+4i{\sigma }^2}}\right)\right)}^2.\hfill \end{array}$$

(74)

In particular, when we put $B=\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$ in Expression (74), we immediately obtain

$$\begin{array}{c}\hfill {\sigma }_f^2=-{\left(im\right)}^2+{\sigma }^2+{\left(im\right)}^2={\sigma }^2.\end{array}$$

(75)

Table 1 summarizes the results derived in Example 3.

Table 1. Comparison of moments and variances in the LCCF domain with those in the classical case in Example 3.

	Moments and Variances in LCCF Domain	Moments and Variances in the Classical Case [24]
First moment	$-i\sqrt{\frac{b}{b+ia{\sigma }^2}}{e}^{\left(-i\frac{a}{2b}{m}^2-\frac{{\sigma }^2{a}^2{m}^2}{b^2+2i{\sigma }^2}\right)}\left(im+\frac{4{\sigma }^{2}am}{2b+4i{\sigma }^2}\right)$	$-i\left(im\right)=m$
Second moment	$idb\sqrt{\frac{b}{i{\sigma }^{2}a+b}}{e}^{\frac{b{m}^2}{{\sigma }^2(2{\sigma }^{2}a+2b)}-\frac{m^2}{2{\sigma }^2}}-b\sqrt{\frac{b}{b+ia{\sigma }^2}}{e}^{\left(-i\frac{a}{2b}{m}^2-\frac{2a^2{\sigma }^2{m}^2}{2b^2+i4b{\sigma }^{2}a}\right)}\left[{\left(im+\frac{4{\sigma }^{2}am}{2b+i4{\sigma }^{2}a}\right)}^2-\left(id+\frac{{\sigma }^2}{b+i2{\sigma }^{2}a}\right)\right]$	${\sigma }^2+m^2$
Variance	$\begin{array}{cc}& idb\sqrt{\frac{b}{i{\sigma }^{2}a+b}}{e}^{\frac{b{m}^2}{{\sigma }^2(2{\sigma }^{2}a+2b)}-\frac{m^2}{2{\sigma }^2}}-b\sqrt{\frac{b}{b+ia{\sigma }^2}}\hfill \\ & e^{\left(-i\frac{a}{2b}{m}^2-\frac{2a^2{\sigma }^2{m}^2}{2b^2+i4b{\sigma }^{2}a}\right)}\times [{\left(im+\frac{4{\sigma }^{2}am}{2b+i4{\sigma }^{2}a}\right)}^2\hfill \\ & -\left(id+\frac{{\sigma }^2}{b+i2{\sigma }^{2}a}\right)]-[-i\sqrt{\frac{b}{b+ia{\sigma }^2}}\hfill \\ & e^{\left(-i\frac{a}{2b}{m}^2-\frac{{\sigma }^2{a}^2{m}^2}{b^2+2i{\sigma }^2}\right)}\hfill \\ & \times \left(im+\frac{4{\sigma }^{2}am}{2b+4i{\sigma }^2}\right){]}^2\hfill \end{array}$	${\sigma }^2$

6. Conclusions

In this work, we constructed the LCCF as a combination of the LCT kernel and the probability density function used in the classical characteristic function. The investigation of some original results related to the proposed LCCF was performed in detail. It was found that some crucial properties of the classical characteristic function are substantially modified in the LCCF setting. As an application, we presented some examples to verify the obtained results. Future work will extend the one-dimensional LCCF to the n-dimensional case. This approach is based on replacing the kernel of the characteristic function with an n-dimensional LCT kernel. Of course, the results of the $one$-dimensional LCCF will change significantly in the newly constructed n-dimensional LCCF.