Study on Microscopic Seepage Simulation of Tight Sandstone Reservoir Based on Digital Core Technology

Abstract

Understanding the flow characteristics of tight sandstone reservoirs is crucial for improving resource recovery efficiency. During fluid flow in porous media, surfactant components in the fluid can adsorb onto solid surfaces, forming a boundary layer. This boundary layer has a pronounced impact on fluid movement within tight sandstone formations. In this study, digital core analysis is employed to investigate how the boundary layer influences non-Darcy flow behavior. A computational model is first developed to quantify the thickness and viscosity of the boundary layer, followed by the construction of a mathematical flow model based on the Navier–Stokes equations that incorporates boundary layer effects. Using CT scan data from actual core samples, a pore network model is then built to represent the reservoir’s complex pore structure. The impact of boundary layer development on microscale flow is subsequently analyzed under varying pore conditions. The results indicate that both boundary layer thickness and viscosity significantly influence fluid transport in microscopic pores. When the relative boundary layer thickness is 0.5, and the relative viscosity reaches 10, the actual outlet flow rate drops to only 12.89% of the value obtained without considering boundary layer effects. Furthermore, in tight reservoirs with smaller pore throat sizes, the boundary layer introduces considerable flow resistance. When boundary layer effects are incorporated into the pore network model, permeability initially increases with pressure gradient and then stabilizes.

1. Introduction

Low-permeability tight oil and gas resources constitute a significant portion of global hydrocarbon reserves. With continued exploration and development, their importance is steadily increasing, positioning tight reservoirs as a key focus of future research [1,2]. In these formations—particularly tight sandstones—the pore channels are extremely narrow, often on the micron, submicron, or even nanometer scale. Such restricted pore sizes lead to fluid migration behaviors that differ fundamentally from those in medium- and high-permeability reservoirs [3,4]. Numerous studies have shown that, at the micron scale, fluid flow deviates from classical Darcy behavior and instead follows low-velocity non-Darcy flow regimes [5]. Among the mechanisms responsible for this deviation, the boundary layer effect has received growing research attention [6]. This effect arises from interactions between fluid components—such as organic matter, ions, and surfactant molecules—and the pore walls, leading to the formation of a thin boundary layer adhered to the solid surface. This layer possesses physical properties (e.g., viscosity) that differ from those of the free-flowing fluid in the pore center [5,7,8]. Figure 1 illustrates a schematic of the boundary layer at the pore wall. Due to the boundary layer effect, some fluid adheres to the pore walls, creating immobile zones, as shown by the dark blue regions. The light blue areas represent mobile zones, where fluid can move freely. As a result, a non-flowing film forms along the pore boundaries, reducing the effective flow space within the pores [9,10,11]. In tight sandstone and similar low-permeability reservoirs, the narrow pore throats mean that a significant portion of the oil becomes trapped within the boundary layer [12,13,14]. Since this portion of oil does not contribute to flow, it substantially affects both fluid transport and recovery efficiency. Therefore, studying the impact of boundary layer effects on fluid flow in tight sandstone reservoirs is essential.

Both domestic and international researchers have extensively investigated the boundary layer effect under low-velocity flow conditions using experimental and numerical approaches. Studies have shown that in porous media saturated with oil, the thickness of the boundary layer is influenced by factors such as oil viscosity, asphaltene content, pressure gradient, and capillary radius [15,16]. Cui et al. [17] incorporated the time-dependent variation of boundary layer thickness into their numerical simulations, and their results demonstrated that, compared with scenarios without boundary layer effects, displacement velocity and cumulative oil production were reduced, whereas water breakthrough occurred earlier. Yao et al. [18] further examined the combined effects of stress sensitivity and boundary layer development on flow behavior. Their findings indicated that as the pressure gradient increases, the influence of the boundary layer becomes more pronounced, while the impact of stress sensitivity gradually diminishes. Chen et al. [19] were the first to consider viscosity heterogeneity induced by the boundary layer and proposed a low-velocity non-Darcy flow model, showing that uneven viscosity distribution within pore throats significantly contributes to nonlinear flow behavior. Xu et al. [20] used microcapillary experiments to evaluate the boundary layer’s impact on fluid flow and found that the smaller the capillary radius, the more pronounced the boundary layer effect, with thickness decreasing exponentially as the pressure gradient decreases. Wang and Sheng [21] analyzed flow mechanisms while accounting for boundary layer effects and concluded that low-speed non-Darcy flow consists of both nonlinear and linear components. Liu et al. [22] employed centrifugal methods to measure the adsorbed water film on glass microspheres, determining a thickness of approximately 0.2 μm. Xiao et al. [23] also used centrifugal experiments to investigate how boundary layer thickness varies under different treatment conditions and flow channel sizes and proposed a formula that effectively describes its dependence on displacement pressure.

Moreover, advancements in digital core technology have enabled three-dimensional visualization and quantitative analysis of microscale structures, laying the technical foundation for in-depth studies of boundary layer mechanisms in tight reservoirs. For example, Wang et al. [24] constructed a pore network model representing complex structures using CT scan and thin-section data from real reservoir cores. They then analyzed the impact of boundary layer effects on effective connectivity, displacement processes, and oil distribution at the pore scale.

In summary, existing studies have primarily focused on the macroscopic manifestations of non-Darcy flow, while the influence of boundary layer effects at the microscale remains insufficiently understood. In particular, how boundary layers alter velocity distribution, permeability, and threshold pressure gradients under realistic pore-scale conditions has not been fully clarified. To address this gap, the present study develops a mathematical flow model that explicitly captures boundary layer behavior. Furthermore, a three-dimensional pore network model is constructed using digital core technology to investigate how boundary layers affect microscale fluid flow within realistic pore geometries.

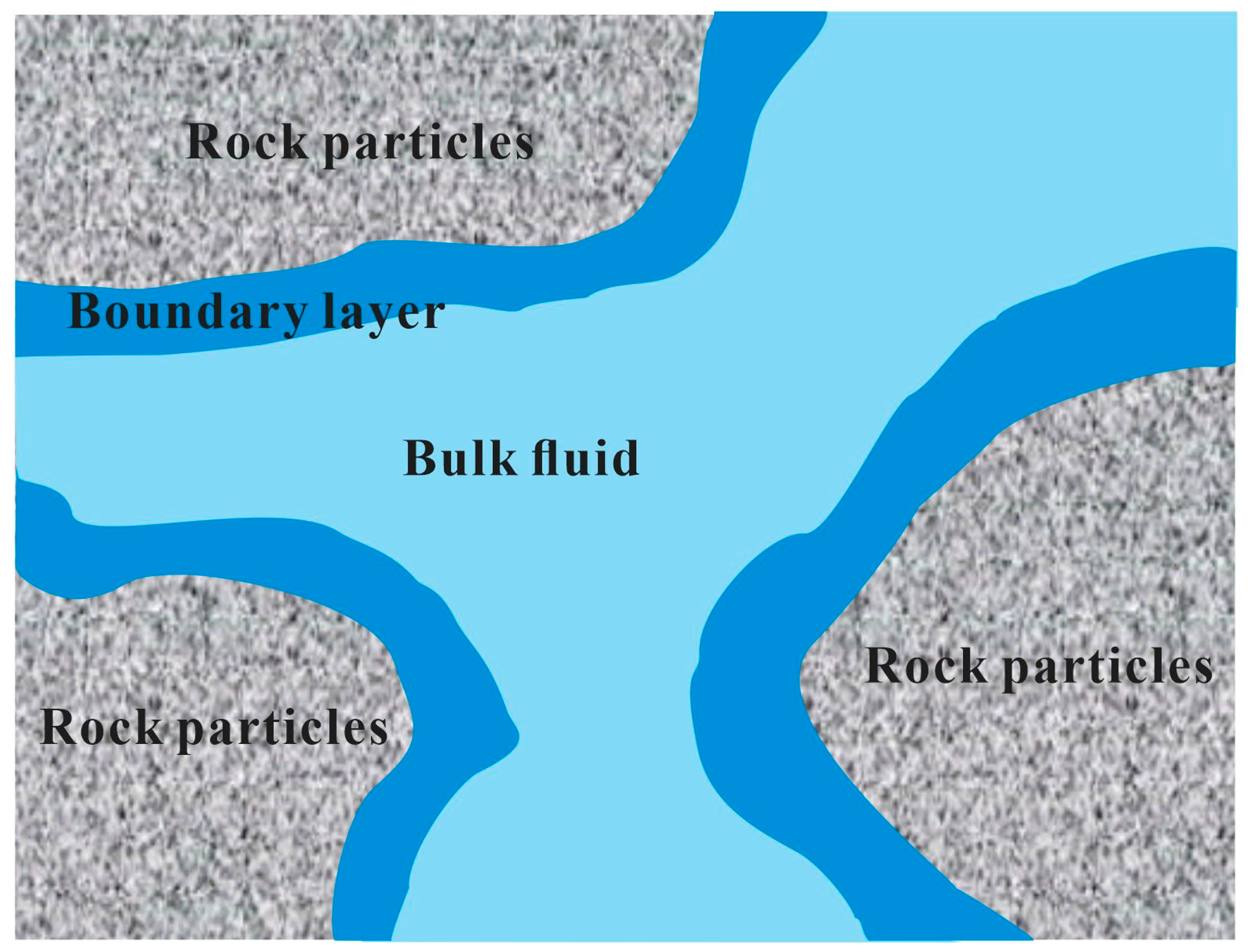
2. Calculation of Boundary Layer Thickness and Viscosity

In the conventional pore network simulation, it is assumed that the micropore throat flow conforms to Hagen–Poiseuille’s law [25]. The Hagen–Poiseuille formula is as follows:

$$Q=\frac{\pi r_E^4\Delta p}{8\mu L}$$

(1)

Therefore, the effective flow radius can be expressed as

$$r_E=\sqrt[4]{\frac{8\mu LQ}{\pi \Delta p}}$$

(2)

The boundary layer thickness is defined as the difference between the actual capillary radius $r_0$ and the effective radius:

$$h=r_0-r_E$$

(3)

Thus, the dimensionless boundary layer thickness can be expressed as

$$h^{*}={\displaystyle \frac{h}{r_0}}$$

(4)

Based on extensive microcapillary experiments, Tian et al. [6] proposed an empirical expression for the dimensionless boundary layer thickness:

$$h^{*}=a\cdot e^{br}(\nabla p{)}^c\cdot \mu$$

(5)

where a, b, and c are parameters related to boundary layer effects; r is pore radius; $\nabla p$ is pressure gradient; $\mu$ is the viscosity of fluid.

The empirical constants a, b, and c used in Equation (5) originate from microcapillary and centrifuge experiments reported by Tian et al. [6], in which boundary layer thickness was directly measured under different pore radii, fluid viscosities, and pressure gradients. These datasets form the basis for calibrating the empirical expression adopted in this study.

The fluid viscosity within the pore throat space can be described by the following equation:

$$\mu =\frac{{\int }_0^{r_0}f\left(\mu \right)2\pi \left(r_0-r\right)dr}{\pi r_0^2}$$

(6)

where $r_0$ is the pore radius.

However, in practical applications, this equation is difficult to handle quantitatively. As a result, an average viscosity approximation is often used, which accounts for the viscosities of both the boundary layer ( ${\mu }_1$) and the free-flowing fluid ( ${\mu }_2$), the boundary layer thickness ( $h$), and the volume ratio ( $A_r$) of boundary fluid to total pore throat fluid. The calculation formula is as follows:

$$\mu =A_r{\mu }_1+(1-A_r){\mu }_2$$

(7)

$$Ar=2{\displaystyle \frac{h}{r_0}}-{\left({\displaystyle \frac{h}{r_0}}\right)}^2$$

(8)

where ${\mu }_1$ is the viscosity of the boundary layer fluid; ${\mu }_2$ is the viscosity of the free-flowing fluid; $h$ is the boundary layer thickness; and $A_r$ is the ratio of the boundary layer fluid volume to the total fluid volume in the pore throat.

The viscosity-averaging approach in Equation (7) represents a simplified treatment of the spatially varying viscosity distribution across the boundary and core regions. This approximation neglects radial viscosity gradients and may underpredict local shear effects when the boundary layer becomes comparable to the pore radius. Nonetheless, it provides a practical and widely used representation of boundary layer-induced viscosity heterogeneity, allowing the model to be efficiently integrated with three-dimensional digital core simulations.

The dimensionless viscosity of the boundary layer can then be expressed as follows:

$${\mu }_r={\displaystyle \frac{{\mu }_1}{{\mu }_2}}$$

(9)

3. Mathematical Model

Substituting the average viscosity into Darcy’s law yields a model for calculating the flow rate through a cross-section affected by boundary layer effects:

$$Q_{cb}=\frac{KA\Delta p}{\mu L}=\frac{KA\Delta p}{\left(A_r{\mu }_1+\left(1-A_r\right){\mu }_2\right)L}=\frac{KA\Delta p}{\left(A_r{\mu }_1-A_r+1\right){\mu }_{2}L}$$

(10)

By comparing these results with the flow rate under ideal conditions—namely, without boundary layer interference—the influence of the boundary layer on effective flow can be quantitatively assessed:

$${\displaystyle \frac{Q_{cb}}{Q_0}}={\displaystyle \frac{1}{A_r{\mu }_r-A_r+1}}$$

(11)

Additionally, the flow velocity can be determined from the modified formulation [24]:

$$v_{eff}={\displaystyle \frac{Q}{A_{eff}}}={\displaystyle \frac{(r-h{)}^4}{8\mu r^2}}\nabla P$$

(12)

where $v_{eff}$ is the effective flow velocity and $A_{eff}$ is the effective flow space.

At the microscale, fluid flow within tight reservoir cores is governed by the Navier–Stokes (N-S) equations, which describe the conservation of mass and momentum [26]. For incompressible fluids, the continuity equation is given by [27]

$$\nabla ·\mathit{u}=0$$

(13)

And the momentum equation is [28]

$$\rho \frac{\partial \mathit{u}}{\partial t}+\rho \left(\mathit{u}·\nabla \right)\mathit{u}=-\nabla P+\mu {\nabla }^2\mathit{u}+\rho \mathit{f}$$

(14)

where u is the velocity, m/s; $\rho$ is the fluid density, kg/m³; $P$ is the pressure, MPa; f is the body force per unit volume.

By incorporating the modified viscosity from the boundary layer model into the momentum equation, a comprehensive flow model is established that fully accounts for the boundary layer’s influence on fluid behavior within tight porous media:

$$\rho \frac{\partial \mathit{u}}{\partial t}+\rho \left(\mathit{u}·\nabla \right)\mathit{u}=-\nabla P+\left(A_r{\mu }_1+\left(1-A_r\right){\mu }_2\right){\nabla }^2\mathit{u}+\rho \mathit{f}$$

(15)

Therefore, the flow model is solved with the boundary layer effect on fluid viscosity fully incorporated. It should be noted that Equation (12) provides a conceptual expression for the effective velocity based on the reduction in flow area due to boundary layer development. In the numerical simulations, however, the pore-scale velocity field is obtained directly from solving the N-S equation (Equation (15)) with the boundary layer-corrected viscosity. Moreover, only the pressure-driven force arising from the inlet–outlet pressure gradient is included in the N–S formulation.

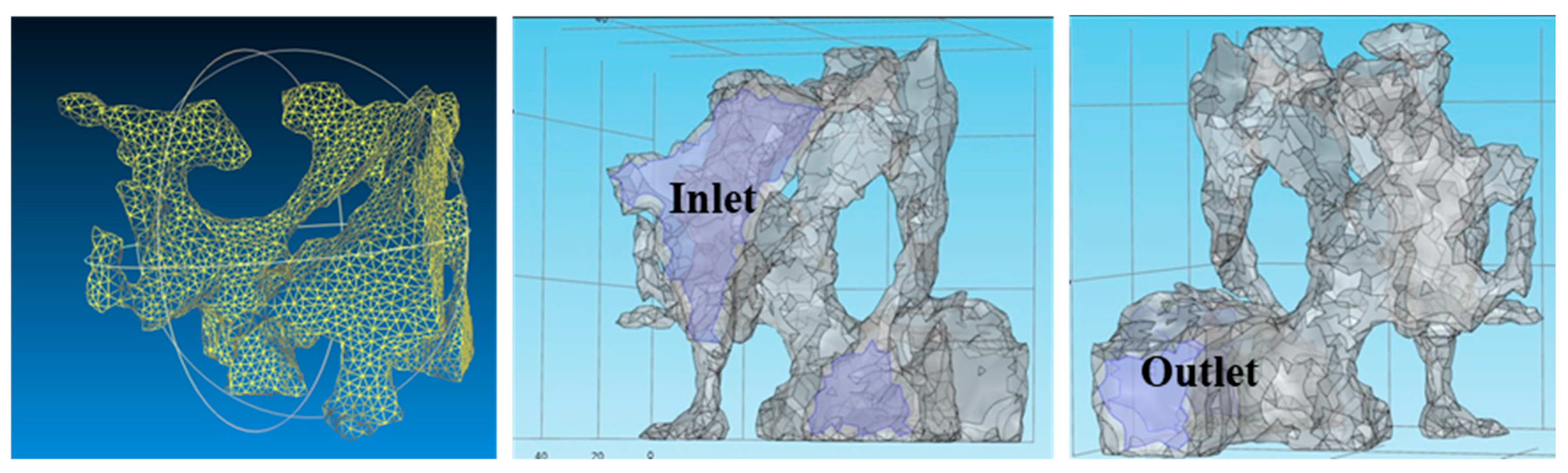
4. Construction of Pore Network Model

This study selected three core samples with different permeabilities: Berea sandstone provided by Imperial College London, 116-C sandstone from the Shengli Oilfield, and a standard artificial sandstone. The parameters of these core samples are presented in

Table 1. Parameters of core samples.

Parameters	Berea Sandstone	116-C	Standard Artificial Sandstone
Porosity, %	19.6	17.0	57.2
Permeability in the X direction, mD	1360	1.05	/
Permeability in the Y direction, mD	1304	1.30	/
Permeability in the Z direction, mD	1193	0.51	/
Average permeability, mD	1286	0.91	156,135

.

CT scanning was performed on the core samples to obtain three-dimensional grayscale datasets. The grayscale images of the three samples are shown in Figure 2. Image processing steps—including grayscale correction, brightness adjustment, sharpening, and binary segmentation—were then applied to construct corresponding 3D digital core models. The X-ray 3D microscopy scans were performed using a nanoVoxel-4000 instrument (Tianjin Sanying Precision Instrument Co., Ltd., Tianjin, China) with a spatial resolution of 1 μm per voxel, enabling visualization of pore-throat structures at the micron scale. For digital core reconstruction, representative sub-volumes with dimensions of 50 μm × 50 μm × 50 μm were extracted from each rock sample. After applying boundary and initial conditions to the model, numerical simulation can be performed. The segmented geometry of the Berea sandstone and the associated boundary conditions are illustrated in Figure 3. The gray region represents the pore space extracted from CT segmentation.

In this study, water was used as the working fluid, with an initial pressure differential of 1 MPa, an inlet velocity of 1 × 10⁻⁴ m/s, a dynamic viscosity of 1 mPa·s, and a density of 1 × 10³ kg/m³. The model’s left boundary was set as the inlet and the right as the outlet. The simulation evaluated the impact of various relative boundary layer thicknesses and viscosities on flow behavior, focusing on flow rate, velocity field, and pressure field. The specific parameter settings for boundary layer thickness and viscosity are provided in

Table 2. Relative thickness and viscosity of the boundary layer.

μr	hr
	0	0.1	0.2	0.3	0.4	0.5
	μ (mPa·s)
1	1.00	1.00	1.00	1.00	1.00	1.00
2	1.00	1.19	1.36	1.51	1.64	1.75
4	1.00	1.57	2.08	2.53	2.92	3.25
6	1.00	1.95	2.80	3.55	4.20	4.75
8	1.00	2.33	3.52	4.57	5.48	6.25
10	1.00	2.71	4.24	5.59	6.76	7.75

. The viscosity values presented in Table 2 were computed using the average viscosity formulation in Equation (7). It should be noted that the pore network simulations conducted in this study do not employ the traditional modified Hagen–Poiseuille equations commonly used in simplified pore network models. Instead, fluid flow within each pore and throat is directly solved using the Navier–Stokes equations, with the effective viscosity corrected by the boundary layer model incorporated into the numerical solver.

5. Result Analysis

Based on Equations (10) and (11), the theoretical relationship between flow rate at a given cross-section and the relative viscosity of the boundary layer was derived under the influence of boundary layer effects. This theoretical result was then compared with numerical simulation data. As shown in Figure 4a, the numerical and theoretical results are in strong agreement, validating the accuracy of the developed mathematical model. Figure 4b illustrates the convergence evolution of the numerical solver when boundary layer effects are included. The stable convergence behavior confirms the numerical consistency and robustness of the model within the CT-derived pore geometry.

Figure 5 illustrates the influence of boundary layer viscosity and thickness on fluid flow. The results show that both parameters significantly impact flow behavior within microscopic pore structures. When the relative boundary layer thickness is 0.5, and the relative viscosity is 10, the actual flow rate at the outlet is only 12.89% of the rate observed without considering boundary layer effects. This demonstrates that boundary layer effects substantially reduce fluid mobility in porous media. Consequently, reducing the impact of boundary layer effects to improve fluid flow within pore spaces is essential for enhancing oil recovery efficiency. It should be noted that the value of 12.89% corresponds to the high-viscosity and large-thickness boundary layer case. Sensitivity across the full parameter range in Figure 5 indicates that although the magnitude varies with boundary layer properties, the reduction in outlet flow rate is consistently significant. Uncertainty in this estimate arises from CT-based pore-throat measurements, empirical boundary layer thickness prediction, and numerical discretization. While these factors may slightly shift the absolute value, they do not alter the overall conclusion that boundary layer development strongly suppresses fluid mobility in tight pore structures.

To examine the influence of boundary layer effects on fluid flow in cores with different permeabilities, simulations were performed using three pore network models. The results indicate that as permeability decreases, accompanied by smaller pore sizes and more complex pore structures, the overall fluid velocity declines. In ultra-low-permeability sandstones, high-speed fluid flow is rarely observed.

Moreover, in the artificial sandstone, fluid flow is more continuous, enabling the formation of multiple layers of isovelocity surfaces with clear and uniform distribution patterns. The relatively homogeneous pore structure and smooth pore walls promote stable flow channels, allowing velocity gradients to develop gradually from the pore centers toward the boundaries. In contrast, the Berea sandstone and the ultra-low-permeability sandstone display highly irregular pore geometries with narrow, tortuous flow paths. This structural complexity leads to a rapid attenuation of flow velocity with increasing distance from the inlet, hindering the formation of coherent isovelocity layers. The disrupted and discontinuous velocity contours reflect stronger viscous drag and localized energy losses within constricted throats. Collectively, these observations indicate that boundary layer resistance becomes increasingly dominant in low-porosity, low-permeability formations, where the effective flow area is significantly reduced, and the no-slip condition exerts a stronger influence on overall transport behavior.

In the Berea and ultra-low-permeability sandstones, the pressure field exhibits a distinct discontinuity, typically located at the narrowest throats where the pore cross-sectional area changes abruptly. Across these constricted regions, the local pressure drops sharply, creating pronounced pressure gradients and localized zones of energy dissipation. By contrast, in the artificial sandstone, the pressure field remains relatively smooth and continuous, reflecting uniform pore connectivity and lower hydraulic resistance. This difference arises from the thickened boundary layer that develops within the narrow throats of the natural sandstones, where increased velocity gradients near the wall lead to enhanced viscous effects and higher frictional losses. Consequently, pressure energy is consumed more rapidly, resulting in steep pressure declines and reduced flow efficiency. These results further confirm that, in tight and ultra-tight formations characterized by small pore throats, boundary layer resistance exerts a first-order control on the spatial distribution of pressure and flow energy. To further elucidate the physical mechanisms underlying the observed pressure discontinuities, the local Reynolds numbers were examined. The calculated local Reynolds number within the narrowest pore throats ranges from 10⁻³ to 10⁻², confirming that flow is strongly dominated by viscous forces in these regions. As a result, even small increases in near-wall viscosity caused by boundary layer development significantly enhance the viscous dissipation rate. The highest dissipation values occur precisely at the locations where steep pressure drops are observed, indicating that the energy consumed by resisting near-wall shear is responsible for the discontinuous pressure distribution.

Figure 6 illustrates the impact of boundary layer viscosity and thickness on fluid flow in core samples with varying permeabilities. The results clearly show that as either boundary layer thickness or viscosity increases, the effective flow velocity and permeability decrease across all three core types. The extent of this reduction, however, varies markedly with permeability. In the high-permeability artificial sandstone, the impact is relatively modest because the wide pore channels allow sufficient space for fluid movement even when the boundary layer expands. In contrast, the ultra-low-permeability 116-C core is highly sensitive to these changes. Its already constrained pore network becomes severely obstructed as the boundary layer thickens, sharply reducing effective flow capacity and increasing the likelihood of near-wall stagnation zones. This phenomenon intensifies reservoir damage, amplifies non-Darcy flow effects, and ultimately degrades overall flow efficiency. Therefore, understanding and quantifying the interplay between boundary layer properties and pore structure are critical for accurately evaluating flow resistance and optimizing fluid injection strategies in tight reservoirs.

Additionally, this study examines the impact of boundary layer effects on permeability and threshold pressure gradients under different driving pressure conditions. A three-dimensional pore network model representing a low-permeability medium was constructed by segmenting the CT-derived digital core and extracting pore bodies and throats through a connectivity-based identification of the three-dimensional pore structure, with relevant parameters summarized in

Table 3. Pore-scale network model parameters.

Parameters	Values
Number of pores	20 × 20 × 20
Number of pores and throats	16,448
Average coordination number	4
Maximum pore throat radius, µm	2
Minimum pore throat radius, µm	0.2
Pore throat ratio	1.0–5.0
Absolute permeability, mD	6.27
Porosity, %	15.07

. The pore throat radii in the model range from 0.2 µm to 2 µm, which aligns with typical distributions found in low-permeability reservoirs. Without considering boundary layer effects, the absolute permeability of the model is 6.27 mD. The model is initially fully saturated with crude oil.

By incorporating boundary layer effects into the pore-scale network model, the relationship between permeability and pressure gradient during single-phase crude oil flow was simulated, as shown in Figure 7. The results indicate that permeability is no longer constant but varies with the displacement pressure gradient. At low-pressure gradients, increased boundary layer thickness reduces permeability; as the gradient increases, the boundary layer thins and permeability rises. Once the gradient surpasses a critical value, the boundary layer effect diminishes and permeability approaches stability. These findings align well with previous studies. For instance, Tian et al. [29] demonstrated through numerical simulations that increased fluid viscosity amplifies boundary layer resistance in porous media, reducing absolute permeability. Similarly, Xu et al. [30] confirmed through microcapillary and glass bead centrifuge experiments the detrimental effect of boundary layers on flow. Consequently, accounting for boundary layer effects, which significantly lower permeability, implies notable reductions in oil production. In low-permeability reservoirs, where boundary layer effects are pronounced, integrating such effects into flow modeling and development forecasts is critical for accurately reflecting real production behavior.

To explore the impact of boundary layer effects on fluid flow across media with varying permeabilities, simulations were conducted on four pore-scale network models, with parameters listed in

Table 4. Pore network model parameters at different permeability levels.

Parameters	Values
	Model 1	Model 2	Model 3	Model 4
Model relative size (number of pores in each direction)	20 × 20 × 20	20 × 20 × 20	20 × 20 × 20	20 × 20 × 20
Absolute size of the model (mm × mm× mm)	0.18 × 0.18 × 0.18	0.26 × 0.26 × 0.26	0.34 × 0.34 × 0.34	0.42 × 0.42 × 0.42
Pore radius, μm	2	4	6	8
Pore throat radius, μm	0.5	1	1.5	2
Pore throat ratio	4	4	4	4
Absolute permeability, mD	0.286185	3.22876	12.409	32.313
Porosity, %	8.0	21.95	32.32	40.142

.

Figure 8 illustrates the relationship between pressure gradient and flow velocity for each model. The results reveal that once boundary layer effects are incorporated, the flow behavior deviates markedly from linear Darcy characteristics, exhibiting pronounced nonlinearity—particularly at low-pressure gradients. In this regime, the presence of a thickened boundary layer significantly suppresses near-wall velocity, causing flow velocity to increase nonlinearly with the pressure gradient. As the gradient continues to rise, the enhanced shear stress progressively thins the boundary layer, allowing the flow to transition toward a linear regime that conforms to Darcy’s law. Once the pressure gradient becomes sufficiently large, the influence of the boundary layer diminishes, and the flow stabilizes, becoming directly proportional to the applied pressure gradient. By fitting the linear segment of the flow curve, the threshold pressure gradient was obtained from its intersection with the X-axis, yielding values of 0.09999 MPa/m, 0.058824 MPa/m, 0.031746 MPa/m, and 0.021672 MPa/m for the four models, respectively. These results demonstrate that the threshold pressure gradient decreases systematically with increasing porosity and permeability, reflecting reduced flow resistance and weaker boundary layer control. Conversely, as pore throat size decreases, boundary layer effects intensify, amplifying flow nonlinearity during the initial displacement stages. Such pronounced nonlinearity can complicate early-stage fluid injection and pressure propagation in low-permeability formations [15]. Therefore, future research should aim to regulate boundary layer thickness or modify near-wall flow characteristics to lower the displacement pressure gradient and enhance overall injection efficiency in tight reservoirs.

6. Conclusions

(1)

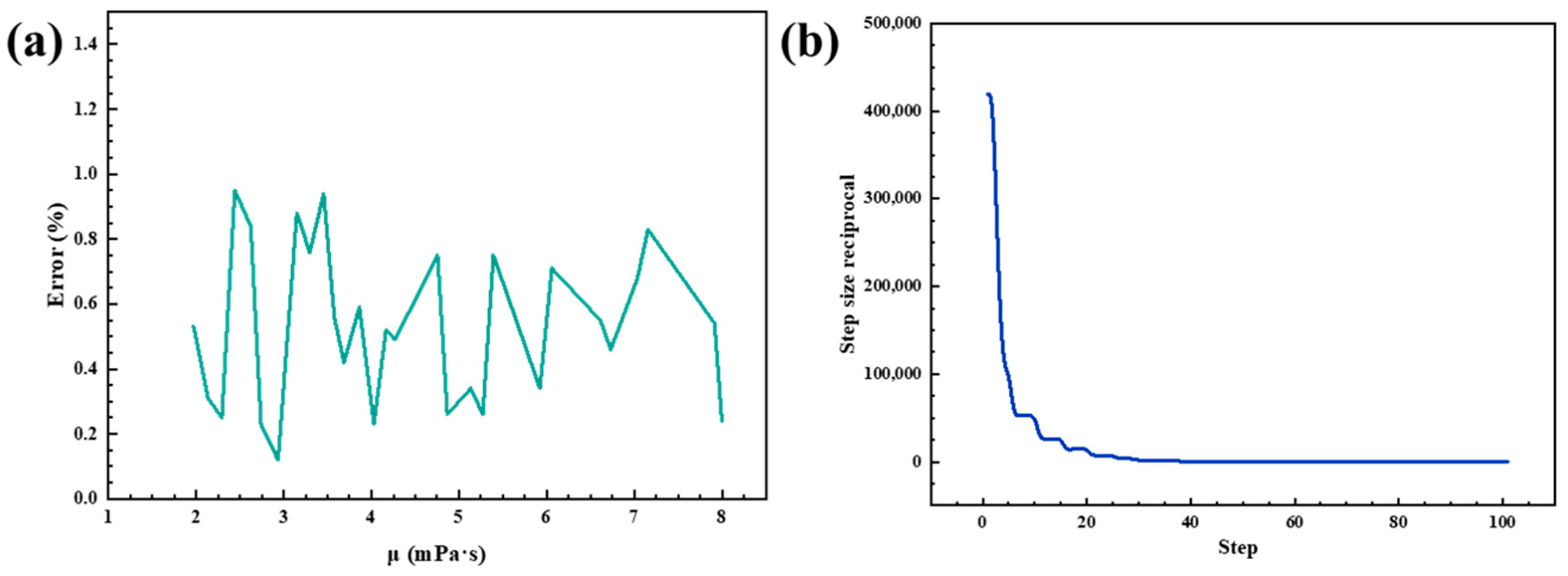
By comparing the numerical simulation results with the theoretical calculations, the accuracy of the proposed flow model incorporating boundary layer effects was effectively validated.

(2)

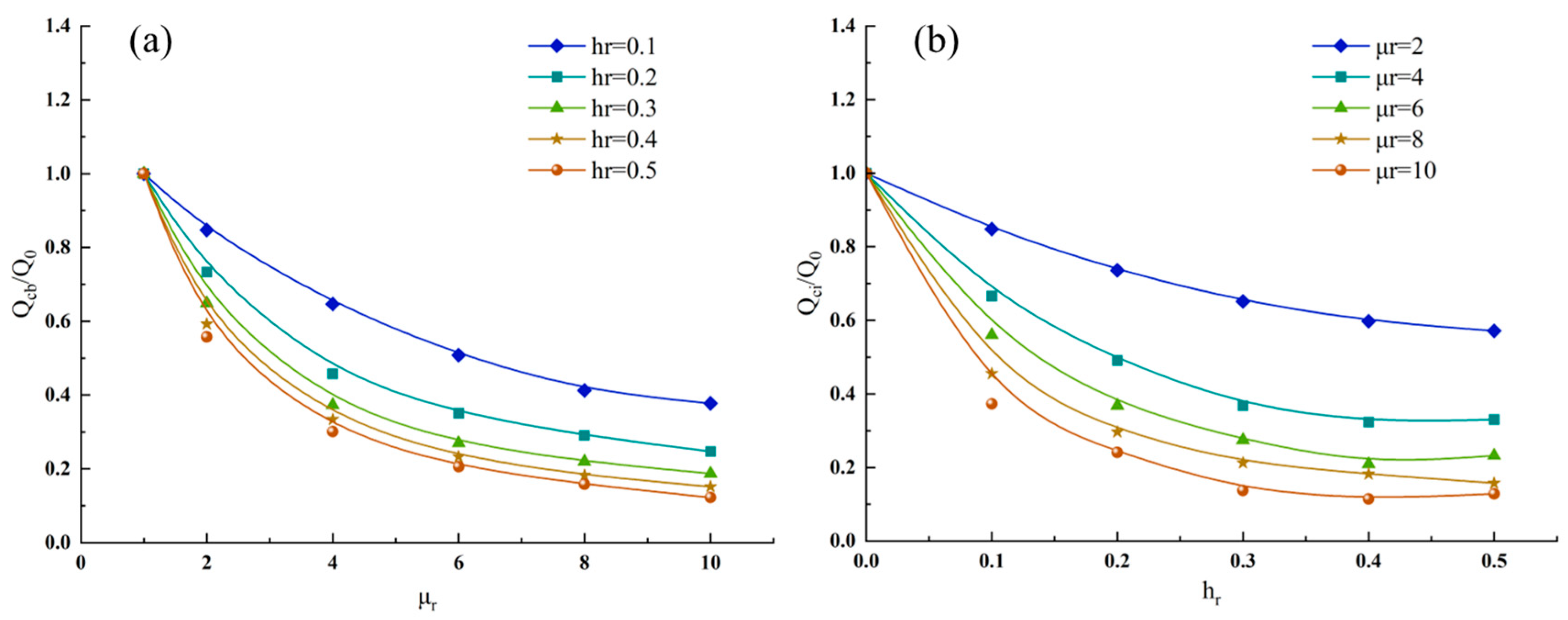
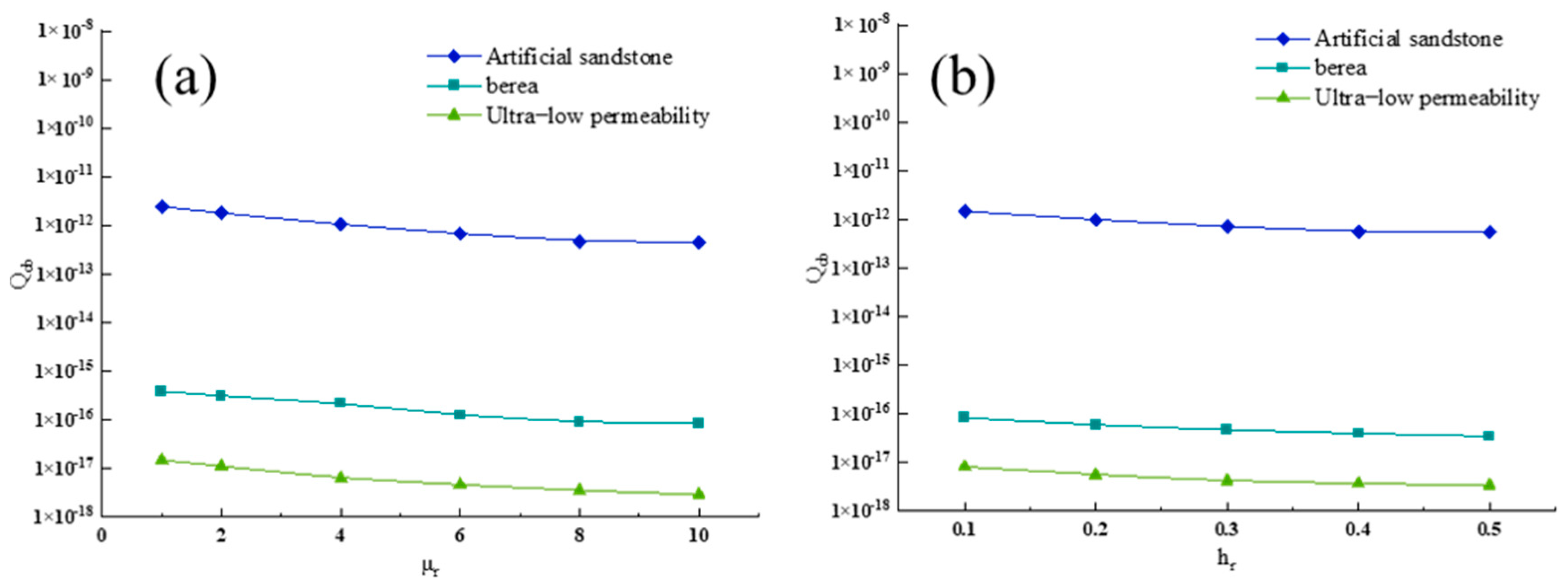
The thickness and viscosity of the boundary layer significantly influence fluid flow in microscale pores. When the relative boundary layer thickness is 0.5, and the relative viscosity is 10, the actual flow rate at the outlet under boundary layer conditions is only 12.89% of that without considering boundary effects. Furthermore, the impact of boundary layers becomes more pronounced in tight reservoirs with smaller pore-throat dimensions.

(3)

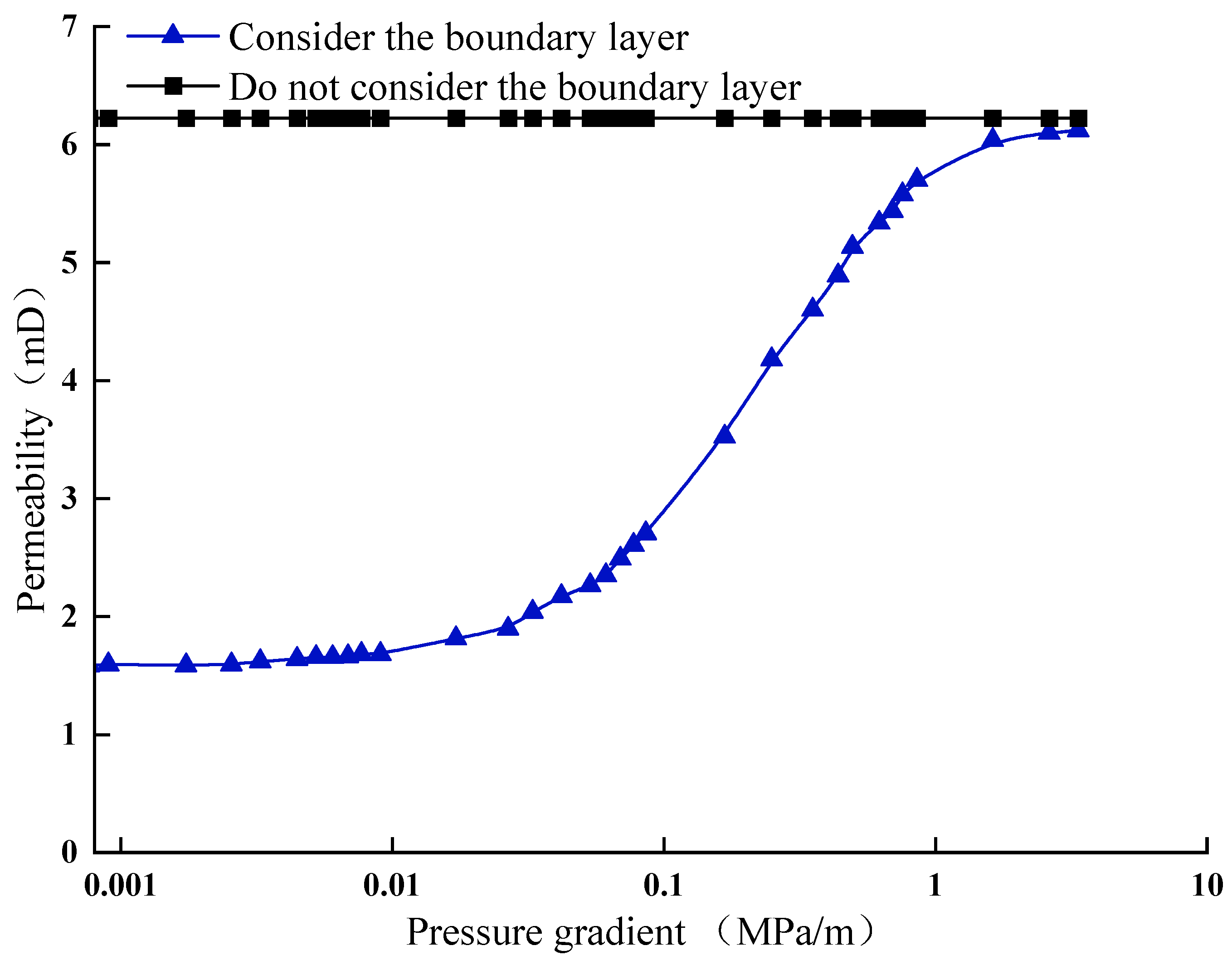
When boundary layer effects are incorporated into the pore-scale network model, the permeability initially increases with increasing pressure gradient and then stabilizes. Under low-pressure gradients, boundary layer effects result in reduced permeability, which can negatively impact reservoir development performance.

(4)

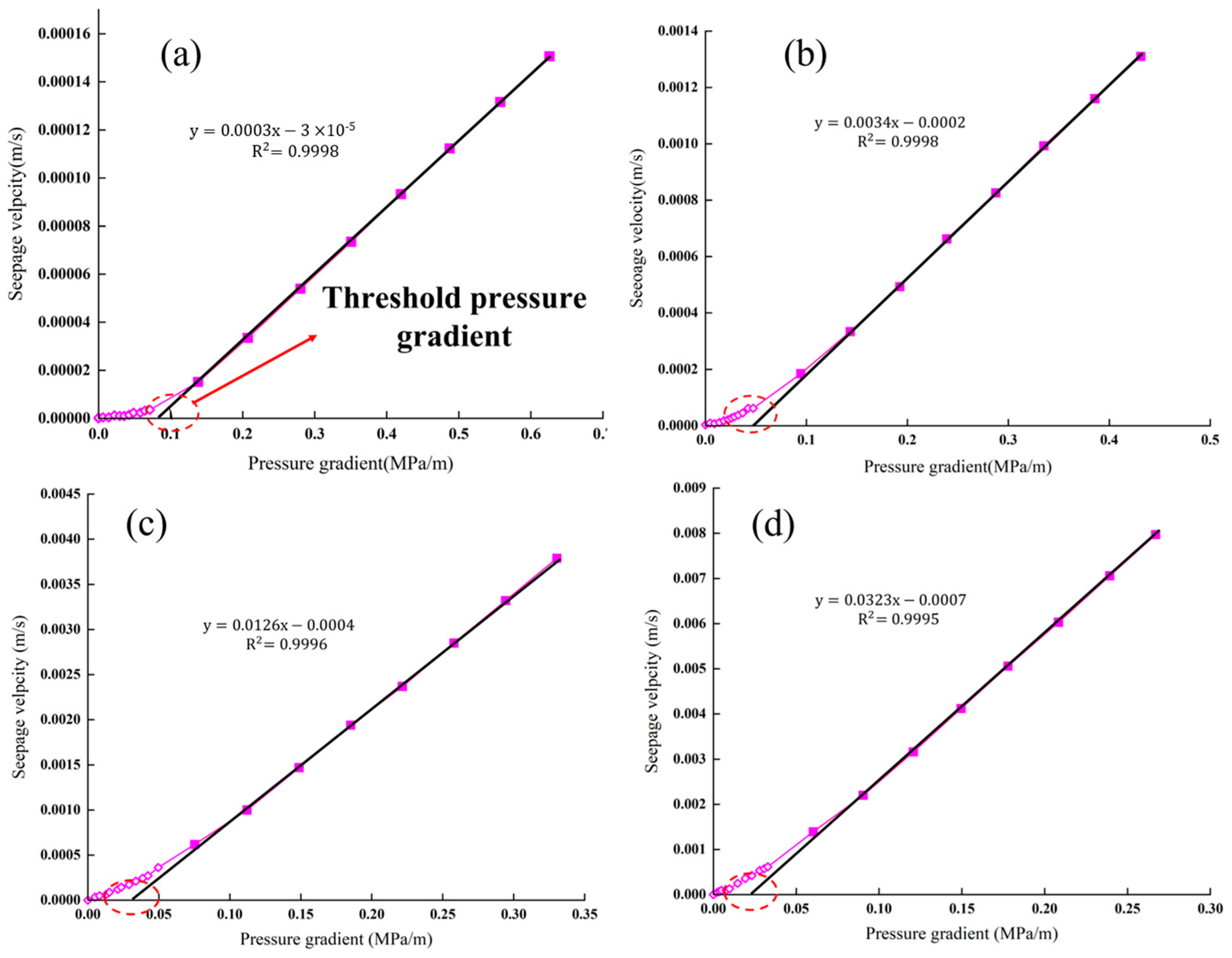
The flow curve exhibits nonlinear behavior in the pore-scale network model when boundary layer effects are included. Under low-gradient conditions, flow velocity increases nonlinearly with pressure gradient, transitioning to linear Darcy flow only after the gradient exceeds a certain threshold. Moreover, the pore-scale network model allows the threshold pressure gradient in low-permeability media to be identified. Higher permeability corresponds to a lower threshold pressure gradient, whereas smaller pore sizes lead to more pronounced nonlinear flow behavior during the early stages of displacement.

(5)

It should be noted that the present study adopts fixed values of relative boundary layer thickness and viscosity, representing a static approximation of boundary layer behavior. In actual reservoir conditions, boundary layer properties may evolve dynamically with temperature, pressure gradient (shear rate), and fluid–rock interactions. Moreover, material-specific characteristics such as wettability and contact angle, which can further influence adsorption behavior and near-wall flow, were not explicitly incorporated in the current model. Future research will focus on coupling the boundary layer formulation with temperature-dependent viscosity, shear-induced evolution, and wettability effects to more accurately capture the dynamic and material-sensitive nature of boundary layer development in tight reservoirs.