Planar Non-Uniformity of Regular and Partially Regular Microreliefs and Method for Its Evaluation

Abstract

Based on the analysis of grooves of regular and partially regular microreliefs formed on flat surfaces, the relationship between the geometric parameters of the grooves of their microreliefs, which ensures their regularity, was revealed. The functionality of the existing parameter for assessing the oil capacity of the surface of the relative area of the grooves of the microrelief was analyzed. It was proved that the parameter—the relative area of the grooves of the microrelief—is insensitive to their distribution on the plane. A new graph-analytical method for determining the planar heterogeneity of the distribution of the area of the grooves of the microreliefs was developed. A numerical parameter—the coefficient of planar heterogeneity, which determines the uniformity of the distribution of the area of the grooves on the plane, was also substantiated. The effectiveness of the new approach was demonstrated and proven. Graphs of longitudinal and transverse planar heterogeneity of the main forms of the grooves of the microreliefs were constructed, which will eliminate the need to obtain complex analytical dependencies to determine the area of these grooves. By analyzing the graphs of planar heterogeneity, numerical values of the heterogeneity coefficient were determined—a parameter that characterizes the homogeneity of microrelief grooves in the axial and interaxial directions. It is proposed to search for optimal placement schemes of adjacent microrelief grooves on the plane based on the analysis of their planar heterogeneity coefficients. This will ensure an increase in the plane heterogeneity coefficient from 0.69 to 0.97 for the triangular shape of the grooves, from 0.87 to 0.83 for the sinusoidal and from 0.46 to 0.69 for the groove shape in the form of a truncated cycloid, with the same relative areas of the microrelief.

1. Introduction

Modern mechanical engineering is focused on technologies that provide for an advanced performance of machine parts. Processing technologies and methods that ensure the improved geometrical, physical and mechanical parameters of load-bearing surfaces are being constantly improved. The technology that creates the periodically repeating self-organised surface structures commonly referred to as regular microreliefs is at the heart of surface engineering. Ensuring a periodic repetition of surface protrusions and depressions is key to a stable performance of the working surfaces of machine parts across their entire plane. When creating periodically repeating protrusions and depressions on the working surfaces of machine parts, care should be taken to provide for the microrelief’s regularity or the periodicity of microrelief’s elements, as this will ensure the surface quality [1,2].

The loss of regularity by microrelief grooves is due to a number of reasons. One of them is technological, that is, microrelief grooves are formed on machines with mechanical feed boxes. The stochastic nature and the accumulated error of such feed boxes, as well as the randomness of their feed, make the groove’s axial step constantly change by the same value. This results in the axial irregularity of the microrelief grooves.

Notwithstanding the above, partially regular and irregular microreliefs have found a broad application in modern machines. Regular microreliefs cannot be created on the end surfaces of rotary bodies. Therefore, partially regular microreliefs are created instead, as they have only one variable geometrical parameter (for example, the axial step), the rest of the geometrical parameters being identical. Owing to this, the microrelief acquires partial regularity [3,4]. As the surface approaches the center of rotation, the distance between the points of the grooves that are in the same phase decreases. Thus, it is impossible to create a completely regular microrelief on such surfaces. These articles do not specify the parameters for evaluating the unevenness of the change in the area of the grooves in the radial direction, so substantiating and recording such an evaluation parameter would allow us to show this unevenness.

Creating a hone on the inner cylindrical surface of a cylinder liner is the most common example of using irregular microreliefs. Such microrelief provides for a better performance of the sleeve surface, while its violation during operation changes the in-service properties of the surface [5,6]. The formed microrelief on the surface of the cylinder liners is not regular, but even a slight change in the angle of inclination of the grooves leads to a significant change in the operational properties of the surface. This confirms the likelihood that the uniformity of the distribution of the groove area will also have a significant impact on the operational properties of the surface. Therefore, the uniformity of the distribution of the groove area requires research to ensure stable operational properties of the surface. The confirmation that the shapes of the grooves of regular microreliefs in industry are becoming more and more diverse is the paper [7].

Optimal shapes of the regular microrelief’s grooves are described in many scientific papers. Thus, the paper presents the research findings dealing with the speed at which droplets roll down the surfaces with different microreliefs. Microrelief surfaces with nine different shapes of grooves were manufactured for this research. Surfaces with microreliefs containing longitudinal grooves were found to retain droplets longer than flat surfaces and those with other microrelief types. To evaluate various forms of grooves of complex shapes, it is necessary to develop a simple methodology that could evaluate using numerical parameters the uniformity of the distribution of the groove area and ensure stable operational properties of the surface properties. More complex groove shapes were investigated in [8]. In the paper, we describe various microrelief types created using a rotary tool. The authors developed a mathematical model that describes the tool’s motion and the microrelief profiles created depending on its service conditions. End milling was shown to be useful in creating partially regular microreliefs with different groove shapes and different mutual arrangements of the grooves. Thus, some grooves are arranged in parallel and some are offset by part of the pitch. A 2-degree-of-freedom (2-DOF) vibration platform was also developed to provide vibration along and across the feed during the micromilling process.

The importance of obtaining a parameter that will link the geometric parameters of the surface microrelief with its operational properties can be assessed by analyzing the article [9]. In this article, the authors try to find the optimal shape of the surface profile that will provide the minimum friction coefficient. For the results of the experiment to be reliable, the test specimens were designed in such a way that the relative area of the microrelief was the same. As we can see, scientists use the parameter relative area of the microrelief (Area ratio) as an important criterion that determines the operational properties of the surface. The results of the article show that although the value of the parameter relative area of the microrelief was the same for different surfaces, the friction coefficients differed significantly. However, the nature of this difference was not described. This proves once again that this parameter cannot continue to be considered as determining the operational properties of the surface, and it is necessary to search for a new, more sensitive parameter.

Surface engineering uses various forms of microrelief grooves, both discrete and continuous, which provide different in-service properties of the flat surface [10,11]. Regularity of microreliefs with discrete elements is ensured more easily, since such microreliefs have fewer geometric parameters. Based on the fact that there are different types of microreliefs, the shapes of their grooves and the connections between them, it would be advisable to investigate the relationships between the geometric parameters of the grooves, the shape of the grooves of microreliefs, with the criteria of regularity.

The relationship between surface performance and roughness parameters can be described by the Abbott-Firestone diagram. The paper in [12,13,14,15,16] describes this relationship. Here, the surface performance is evaluated by the Abbot-Firestone curve rather than the surface roughness. According to the authors, the three main parameters derived from the curve, in particular, R_pk, R_k and R_vk, may characterise the surface’s ability to resist sliding friction. The Abbott-Firestone curve is an example of a graphical–analytic analysis of microreliefs with reference to the operational properties of the surface. This method allows you to assess the properties of the surface both visually and using the numerical parameters of the R_k group. Analysis using the Abbott-Firestone curve is carried out at the microlevel. Analysis at the level of geometric dimensions of the groove has not been carried out before, since there was no corresponding method. This curve describes quite well the relationship between the surface profile at the microlevel and the wear ability. The algorithm for constructing graphs of the planar heterogeneity of microrelief grooves is similar to the algorithm for constructing the Abbott-Firestone curve and is based on the use of a set of secant segments, which, after alignment, form a plane of the curve or graph.

In the paper [17] considered surfaces with regular microreliefs and noted that they have different profile shapes. The shape and dimensions of the grooves of the microreliefs were analyzed to develop a general algorithm for their three-dimensional topographic representation based on their two-dimensional images. It was indicated that the developed algorithm works without errors when the evaluated microrelief has a high degree of regularity. The developed algorithm can be used to quickly obtain three-dimensional models of the topography of surfaces with regular microreliefs to train different types of neural networks.

In his monograph, Yu. G. Schneider [18] noted that for surfaces that perform relative movement in different directions, the optimal value of the relative area of the microrelief, which provides the most favorable friction conditions, is 28–57%. Such a large range of optimal values of this parameter indicates that the relative area of the microrelief does not provide an unambiguous assessment of the operational properties of surfaces with regular microrelief. The operational properties of surfaces with regular microreliefs and technological methods for their formation are also considered in detail in [19,20]. A significant number of experimental results summarized in these monographs confirmed the need to introduce a new, more informative parameter.

Thus, the authors of the article conducted an evaluation of surfaces with regular microreliefs, which takes into account the geometric parameters of the grooves of the microrelief. The importance of the regularity of the microrelief parameters was indicated. However, the analysis of the reasons for the loss of regularity and the phenomenon of uneven distribution of the area of these grooves on the plane was not considered. As a conclusion, it can be stated that many publications provide facts that confirm the need to develop a new approach to evaluating surfaces with regular microreliefs.

2. Regularity Parameters of a Regular Microrelief

The main goal of this article is to present a first-ever developed method for evaluating surfaces with regular and partially regular microreliefs, which takes into account the uneven distribution of the groove area over the surface plane of the samples. A numerical parameter calculated based on this method is also proposed—the coefficient of uneven distribution of the groove area.

Depending on the tools and methods used, as well as the sequence of processing operations, each mechanically treated surface has its own unique microstructure. In fact, the metal surface is a sequence of random-height protrusions and depressions, the values of which vary in a certain range. Mechanical treatment aims at a gradual levelling of the surface profile, that is, reducing the protrusions and depressions of the profile. In addition to improving the physical and mechanical properties of the surface, regular microreliefs formed on the working surfaces of machine parts also make their microstructure regular. Regular and partially regular microreliefs are designed to regularise the microrelief of machine parts’ working surfaces. In other words, they reduce the proportion of random protrusions and depressions and increase the proportion of protrusions and depressions that have an ordered microstructure. This ensures the stability of the geometrical, physical and mechanical properties of machine parts’ working surfaces.

The main geometrical parameters of microrelief grooves are the amplitude A_g, axial step T_g, interaxial distance S_o and groove width b_g. The axial line’s shape of a continuous regular micro-roughness is also important. The axial line may have different shapes. For regular microreliefs, a sinusoidal shape or a periodically repeating triangular shape of the axial line is most common.

Different microrelief types have different numbers of regularity criteria. The regularity of microrelief grooves appears a bigger problem than it might seem.

Axial (pitch) regularity is the repeatability of the microrelief elements’ shapes (grooves, holes, etc.) in the axial direction with a pitch T_g.

Interaxial regularity is the repeatability of the microrelief elements’ shapes (grooves, holes, etc.) in the interaxial direction with a periodicity S_o.

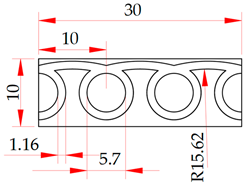
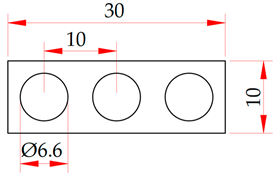
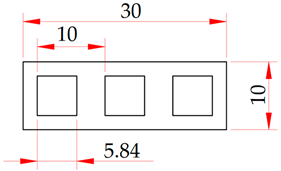
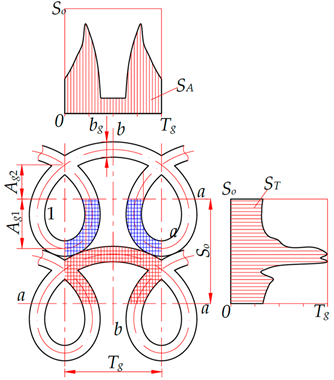
The regularity of discrete elements shown in Figure 1b takes into account the elements’ shape, that is, holes with a diameter D; however, it does not take into account the amplitude, a parameter characteristic of elements with solid grooves.

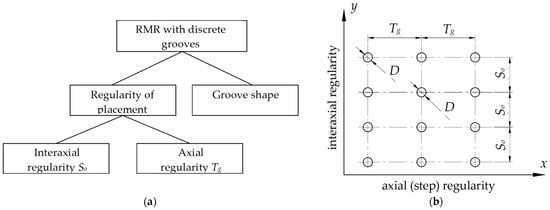
Figure 1. Regularity parameters of a regular microrelief with discrete elements: (a) a scheme for ensuring regularity; (b) graphical display of parameters.

Thus, to provide for a complete regularity of regular microreliefs with discrete elements, we need to ensure the regularity of the microrelief elements’ shape and the regularity of their planar arrangement. In other words, the interaxial and axial (pitch) distances should be the same (Figure 1a).

As seen from Figure 1b, the regularity of this microrelief type requires the periodicity of repetition of only three parameters: the axial step T_g, the interaxial distance S_o and the microrelief element’s shape. The microrelief element’s shape is ensured by the stability of the conditions under which it is formed. When microrelief is formed mechanically, the element’s shape is ensured by the stability of the deformation force.

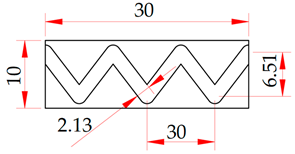
To provide for the regularity of microreliefs with continuous rectilinear grooves (Figure 1), we need to ensure both the regular arrangement of the microrelief grooves on the plane and the identical shape of the microrelief grooves.

Figure 2 shows the relationship between the geometrical parameters that ensure the regularity of microreliefs with continuous grooves. In the axial direction, regularity is provided by the groove’s shape, which includes such parameters as the axial step T_g, the amplitude A_g and the groove’s width b_g. In the interaxial direction, the regularity of the microrelief with solid grooves is ensured by the uniformity of interaxial step S_o.

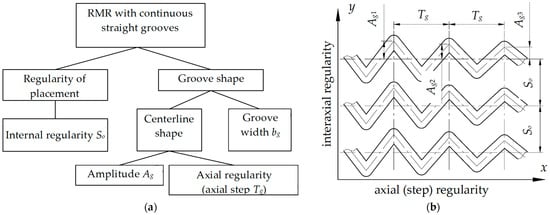
Figure 2. Regularity parameters of a regular microrelief with continuous elements: (a) a scheme for ensuring regularity; (b) graphical display of parameters.

Partially regular microreliefs are characterised by the grooves that have one or several variable geometrical parameters, with the other geometrical parameters being identical. The identical geometrical parameter retains regularity. However, the unstable values, that is, the ones that vary, must have a repetition frequency which is usually equal to the microrelief groove’s pitch. Thus, partially regular microrelief’s grooves formed on the end surfaces of rotary bodies (Figure 3b) have the same amplitude A_g1 = A_g2. However, as the distance to the rotation center of the rotary body’s end surface increases, the axial step of the grooves increases T_g2 > T_g1. At the same time, if we represent the axial step in the polar coordinate system using angle φ, this parameter will be stable for the grooves located at any distance from the rotation center of the rotary body’s end surface.

Figure 3. Regularity parameters of a partially regular microrelief with continuous elements: (a) a scheme for ensuring regularity; (b) graphical display of parameters.

Figure 3 shows the regularity parameters of a partially regular microrelief with continuous circular grooves (elements) formed on a flat surface of a rotary body. Interaxial distance S_o between microrelief grooves is the same, which ensures microrelief’s regularity in the interaxial direction. The axial step T_g for the grooves, the centerlines of which are located at different distances from the center of rotation, will be different, that is, T_g1 ≠ T_g2 (Figure 3b). The concept of the groove’s angular pitch φ_g is introduced, which is the same for all the grooves, the centerline of which is located at different distances from the center of rotation.

Thus, the microrelief’s regularity preserves the law that describes changes in the argument of the continuous regular micro-roughness’ axial line, in which the step and amplitude of the microrelief’s groove remain constant, as well as the arrangement of the upper and lower equidistance relative to this line on the plane where the regular microrelief is formed. This parameter is ensured by a stable groove’s width.

The stages of microrelief grooves’ regularity can be depicted graphically using the diagram shown in Figure 4. An irregular microrelief results from the mechanical processing of surfaces and is characterised by the variability of parameters that account for the groove’s geometrical shape (amplitude A_g, step T_g, groove width b_g) and the parameters that account for the arrangement of microrelief grooves on the plane (interaxial step S_o).

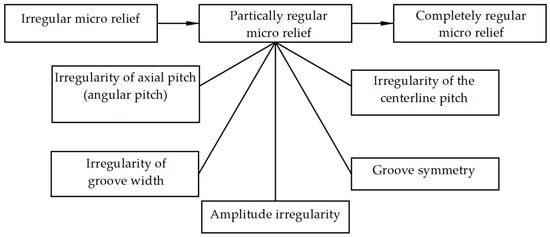
Figure 4. Stages of microrelief’s regularity and irregularity criteria.

A complete regularity of microrelief grooves can be ensured if all of the above parameters are stable. The resulting microrelief will have grooves that touch (microrelief types IV and V according to [21]).

The largest group is represented by partially regular microreliefs. The presence of at least one feature shown in Figure 4, or their combination, allows classifying the microrelief as partially regular. A microrelief cannot be considered partially regular if its grooves are not similar in shape.

Microreliefs created by the rotational method can also be partially regular. They form an axial line of continuous regular micro-roughness in the form of a cycloid. The corresponding elements of the microrelief groove (protrusions, depressions, arcs, etc.) must repeat with an axial step T_g. Owing to this, the regularity of microrelief groove’s parameters will be ensured (Figure 5b). So, the microreliefs shown in Figure 5 have completely repetitive elements with a period T_g. However, the microrelief shown in Figure 5a is symmetrical with respect to the a-a and b-b axes, and the microrelief shown in Figure 5b is symmetrical only with respect to the b-b axis. Grooves of this shape will never add a complete regularity to a microrelief.

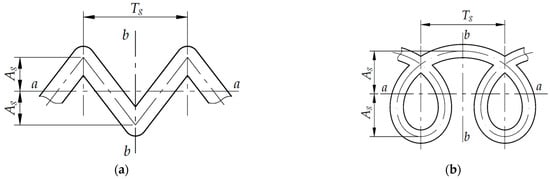
Figure 5. Symmetry of microrelief grooves: (a) triangular profile (b) circular profile.

The numerical value of the groove’s area used to estimate the relative microrelief’s area allows evaluating the ratio of the microrelief’s area to the surface’s area on which it is formed. However, this parameter does not evaluate the arrangement of grooves on the plane, which is almost always non-uniform. That is why it is advisable to introduce a microrelief evaluation parameter that will depict the uniformity of the microrelief grooves’ arrangement, namely, the distribution of their area on the plane. This can be done using a graph that shows the groove area’s distribution in different planar directions.

To evaluate the uniformity of the grooves’ arrangement on a plane, we introduce an indicator of the planar non-uniformity of the microrelief grooves’ shapes. The following method is proposed for plotting planar non-uniformity graphs.

3. Planar Non-Uniformity of Microrelief Grooves’ Shapes

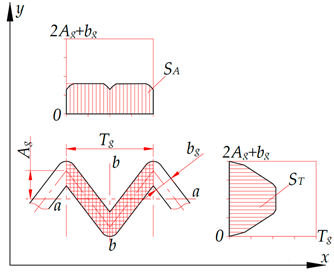
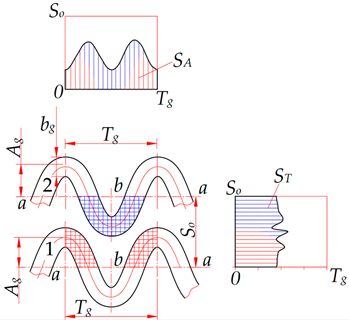
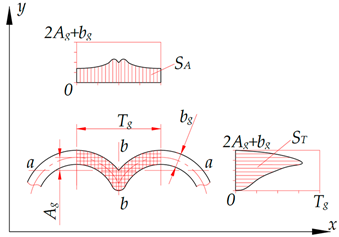
Planar non-uniformity of microrelief grooves’ shapes is a parameter that characterises the uniformity of the groove’s area’s distribution on a plane limited by axial step T_g in the axial (longitudinal) direction and by the value 2A_g + b_g in the interaxial (transverse) direction (Figure 6). The planar non-uniformity is determined by the graph showing the groove’s area’s distribution within the axial step T_g in the longitudinal direction and within value 2A_g + b_g in the transverse direction. Surface areas under the curve on the planar non-uniformity graphs are identical in the axial S_A and interaxial S_T directions. This parameter makes it possible to evaluate the microrelief’s relative area, which is one of the main parameters characterising the performance of surfaces with regular and partially regular microreliefs.

$$F_n={\displaystyle \frac{S_A}{T_g\times 2A_g+b_g}}\times 100\%$$

(1)

where F_n—relative surface area with regular microrelief, %;

S_A—surface area under the curve of plane inhomogeneity of the groove in the axial direction, mm²;

T_g—axial pitch of the groove, mm;

A_g—groove amplitude, mm.

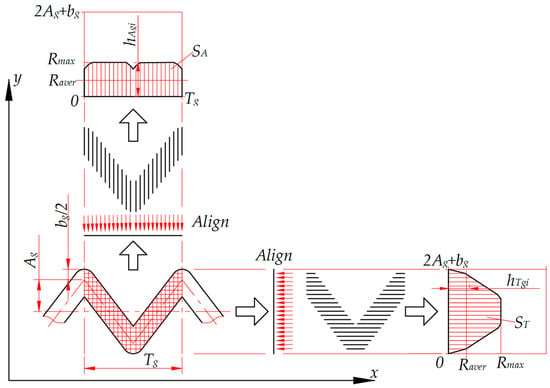
Figure 6. Scheme for plotting the axial and interaxial planar non-uniformity of the microrelief grooves’ shapes.

A graphical-analytical method for determining the relative area of surfaces with regular microreliefs is proposed. The method determines the surface area occupied by a groove element as a set of segments parallel to one of the groove’s axes. These segments intersect the axe’s body and are aligned along the axis to which they are perpendicular (Figure 6). This method also determines the area of complex-shaped microrelief grooves and their intersections. It eliminates the need in deriving complex analytical dependencies and is quite simple to apply, especially using modern programs for processing graphic information.

The surface area formed this way can easily be determined using the graphics software, for instance, AutoCAD 2020. Thus, when determining the relative area of the microrelief, this method eliminates the need in deriving complex analytical relationships to determine the area of the grooves arranged on the surface plane.

To confirm the effectiveness of the proposed method, it is proposed to compare the results of evaluating microreliefs with different shapes of elements/grooves formed on a plane of the same size according to the parameters “relative area of microrelief” and “coefficient of planar heterogeneity” and summarized in Table 1. The physical meaning of the coefficient of planar heterogeneity kg is that it shows the ratio between the average value of the groove cross-section and its maximum value on the graph of planar heterogeneity (Figure 6). Its value will increase if the lengths of the groove sections are the same; for example, if the groove has the shape of a rectangle, and vice versa, it will decrease if the lengths of the groove sections differ significantly.

Table 1. Results of evaluation of microreliefs with different shapes of elements/grooves according to the parameters “relative area of microrelief” and “coefficient of planar heterogeneity”.

Visual Representation of Microrelief with Elements/Grooves and Their Dimensions	Evaluation by the Parameter “Relative Area of Microrelief” Fn (Existing)	Evaluation of the Parameter “Coefficient of Planar Heterogeneity” kg in the Horizontal Direction (Proposed)
	34.1%	0.49
	34.1%	0.51
	34.1%	0.68
	34.1%	0.96
	34.1%	1.0

As can be seen from Table 1, the relative area of the microrelief F_n determined by Formula (1) for all samples is the same and is 34.1%. The coefficient of planar heterogeneity k_g, which is determined for the same samples in the horizontal direction, has a value from 0.49 to 1.0. The maximum value of the coefficient of planar heterogeneity in a groove, in which its area is distributed absolutely evenly along the surface (the shape of the groove is a rectangle), is calculated.

Thus, the proposed numerical parameter of the estimate provides sensitivity to the uniformity of the distribution of the groove area in the selected direction, which cannot be provided by the coefficient of the relative area of the microrelief.

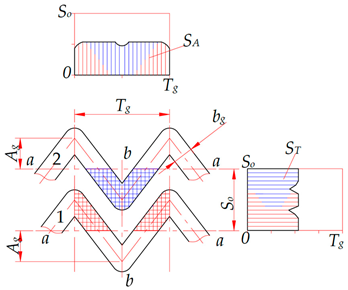
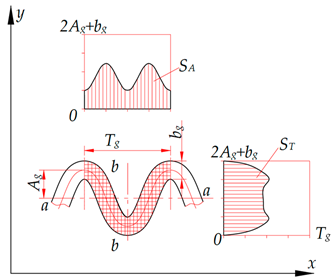
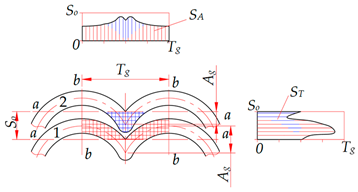
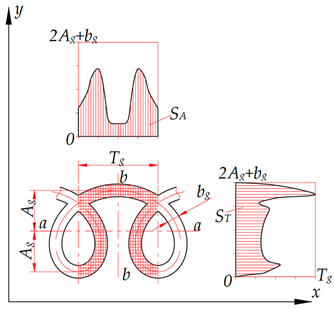
The axial direction is located along the groove’s axis. It coincides with the x axis of the coordinate system. The interaxial direction coincides with the y axis. The symmetry of the microrelief grooves’ planar non-uniformity graph for the triangular and sinusoidal grooves (Table 2) indicates their regularity in the axial direction relative to the b-b axis and in the interaxial direction relative to the a-a axis. In addition, the analysis of the planar non-uniformity graphs for triangular grooves suggests that the distribution of the S_A groove’s area along the x axis is more uniform than that of the S_T groove’s area along the y axis. In this case, the numerical value of the areas occupied by separately studied grooves is always the same, that is, S_A = S_T. However, when plotting the planar non-uniformity graphs for several adjacent grooves, their areas will overlap and will not be the same, that is, S_A ≠ S_T.

Table 2. Graphs of longitudinal and transverse planar non-uniformity of groove shapes of microreliefs formed on flat surfaces.

Groove Shape	Groove Image and Planar Non-Uniformity Graph	Microrelief Grooves Layout Based on the Analysis of Planar Non-Uniformity Graphs
Triangular
Sinusoidal
Truncated cycloid
Elongated cycloid

In the axial direction, the planar non-uniformity of adjacent grooves is determined at a distance equal to the grooves’ axial step T_g. In the interaxial direction, it is determined at a distance equal to the interaxial distance S_o. In case of individual grooves, it is defined at a distance of 2A_g + b_g. This is because the grooves’ shape is repeated periodically. If the interaxial distance between the grooves is less than or equal to 2A_g + b_g, the adjacent grooves will affect the value of the determined area by increasing it.

When analysing the planar non-uniformity graphs for the grooves in the form of the truncated and elongated cycloid (Table 2), we observe a clearly pronounced planar non-uniformity in the axial and interaxial directions in the form of peak protrusions. These protrusions indicate that the groove’s surface area is significantly larger at certain locations along one of the axes. A non-uniform distribution of the groove’s area over the surface accounts for the different geometrical, physical and mechanical parameters of the surface and, accordingly, affects its performance [18,21,22,23].

The non-uniformity of the groove’s surface area distribution should be determined by the uniformity coefficient k_g, a numerical parameter defined as the ratio of the maximum groove’s height R_max to its average height R_aver.

$$k_g={\displaystyle \frac{2·R_{aver}}{R_{max}}}$$

(2)

The value of this coefficient is determined either in the axial or interaxial direction. Under a completely uniform distribution of the groove’s area, the coefficient will be equal to 1. The level of approximation to this value reflects the degree of uniformity of the groove’s area distribution in the selected direction.

$$R_{aver}={\displaystyle \frac{{\displaystyle \sum _{i=1}^n\frac{h_{gi}}{2}}}{n}}$$

(3)

where h_Agi (h_Tgi) is the height of the i-th segment on the corresponding planar non-uniformity graph, mm (Figure 6).

Height values h_Agi are defined within the axial step T_g for the axial planar non-uniformity graphs, while height values h_Tgi are defined within the interaxial step S_o for the interaxial planar non-uniformity graphs.

The analysis of the planar non-uniformity graphs of the microrelief grooves’ shape allowed us to arrange the adjacent microrelief grooves in such a way (Table 2) that the distribution of their areas became more uniform. This is confirmed by the axial and interaxial coefficients of planar non-uniformity k_g.

Table 3 and Table 4 indicate that the planar non-uniformity coefficient can be increased in the axial and interaxial directions by optimising the arrangement of microrelief grooves. Owing to this, the groove’s area will be more uniformly distributed along the plane on which the microrelief is formed. The tables also indicate that the rotational microrelief grooves, which have an asymmetric shape relative to the longitudinal axis, are hard to arrange in a better way.

Table 3. Planar non-uniformity coefficients k_g of microrelief grooves.

Measurement Parameters	Triangular	Sinusoidal	Truncated Cycloid	Elongated Cycloid
Rmax, [mm]	0.814	1.231	0.643	1.984
Raver, [mm]	0.395	0.427	0.237	0.586
Axial, kgA	0.97	0.69	0.74	0.6
Rmax, [mm]	1.250	1.192	1.796	2.334
Raver, [mm]	0.431	0.468	0.418	0.470
Interaxle, kgT	0.69	0.78	0.46	0.4

Table 4. Planar non-uniformity coefficient kg after adjusting the position of microrelief grooves based on the analysis of the planar non-uniformity graphs.

Measurement Parameters	Triangular	Sinusoidal	Truncated Cycloid	Elongated Cycloid
Rmax, [mm]	0.814	1.255	0.641	1.724
Raver, [mm]	0.396	0.425	0.239	0.508
Axial, kgA	0.97	0.68	0.75	0.59
Rmax, [mm]	1.249	1.338	2.089	2.298
Raver, [mm]	0.606	0.556	0.716	0.511
Interaxle, kgT	0.97	0.83	0.69	0.44

Using the results of the proposed method will allow creating surfaces with regular microreliefs, the surface area of the grooves of which will be evenly distributed in the required directions. The uniformity of the distribution of the area of the grooves will ensure the same operational properties of the surface [21]. The friction coefficient will decrease due to the uniformity of the distribution of contact stresses in the friction pair. This, in turn, will increase the resistance of the surface to seizing of the second kind.

The proposed method and the coefficient calculated on its basis can be used for comparative analysis of surfaces with regular microreliefs, Table 5.

Table 5. Comparative characteristics of the application of the coefficient of planar uniformity, k_g and the relative area of microrelief, F_n.

The Described Physical and Mechanical Phenomenon	Parameter
	Coefficient of Planar Uniformity, kg	Relative Area of Microrelief, Fn [18]
1. The total ratio of the projection area of the microrelief grooves to the area of the application surface	+	+
2. Reduction of the surface’s ability to create conditions for the onset of the second-order setting process	+	+
3. Even distribution of lubricant over the surface	+	−
4. Even distribution of contact interaction locations	+	−

Thus, it can be stated that the method of assessing the planar uniformity of grooves of regular and partially regular microreliefs proposed by the authors in this article and the numerical parameter calculated on its basis allow the following advantages to be provided (Table 5).

-

reduction in the surface ability to the onset of conditions for the onset of the second-order setting process, since the reduction in contact interaction locations [18];

-

uniform distribution of lubricant over the surface, since the grooves of the microrelief accumulate it when in contact with the lubricant [19,20];

-

uniform distribution of contact interaction locations of two surfaces of the friction pair, since the surfaces contact evenly spaced locations formed by the grooves of the microrelief [4,14].

4. Conclusions

The main shapes and geometric features of grooves of regular and partially regular microreliefs formed on flat surfaces have been analyzed. Schemes of the relationship between the geometric parameters of grooves of microreliefs, which ensure their regularity, have been constructed, and the criteria for their regularity have been established.

It has been established that the existing parameter for assessing the influence of the groove area—the relative area of the microrelief—is insensitive to the distribution of this area on the plane. A new graph-analytical method for determining the planar heterogeneity of the distribution of the area of grooves of microreliefs has been proposed for the first time. A numerical parameter—the coefficient of planar heterogeneity, which determines the uniformity of the distribution of the area of grooves on the plane, has also been proposed. Graphs of the longitudinal and transverse planar heterogeneity of the main forms of grooves of microreliefs have been constructed, which will eliminate the need to obtain complex analytical dependencies to determine the area of these grooves.

Analysis of the plane heterogeneity graphs allows us to determine the numerical values of the heterogeneity coefficient—a parameter that characterizes the homogeneity of the microrelief grooves in the axial and interaxial directions. It is recommended to search for the optimal layout of adjacent microrelief grooves on the plane based on the analysis of their plane heterogeneity coefficients, which allows us to increase the plane heterogeneity coefficient from 0.69 to 0.97 for the triangular shape of the grooves, from 0.87 to 0.83 for the sinusoidal shape, and from 0.46 to 0.69 for the shape of the groove in the form of a truncated cycloid.