Abstract
In high-density urban areas where ecological protection constraints are increasingly stringent, transportation infrastructure layout must balance service efficiency and environmental preservation. From an ecological-prioritization perspective, this study proposes a three-stage multi-objective optimization strategy for siting underground smart parking facilities using the NSGA-III algorithm, with Haidian District, Beijing, as a case study. First, spatial identification and screening are conducted using GIS, integrating urban fringe-space extraction with POI, AOI, population, and transportation network data to determine candidate locations. Second, a multi-objective model is constructed to minimize green space occupation, walking distance, and construction cost while maximizing service coverage, and is solved with NSGA-III. Third, under the ecological-prioritization strategy, the solution with the lowest land occupation is selected, and marginal benefit analysis is applied to identify the optimal trade-off between ecological and economic objectives, forming a flexible decision-making framework. The findings show that several feasible schemes can achieve zero green-space occupation while maintaining high service coverage, and marginal benefit analysis identifies a cost-effective solution serving about 20,000 residents with an investment of 7 billion CNY. These results confirm that ecological protection and urban service efficiency can be reconciled through quantitative optimization, offering practical guidance for sustainable infrastructure planning. The proposed methodology integrates spatial analysis, multi-objective optimization, and post-Pareto analysis into a unified framework, addressing diverse infrastructure planning problems with conflicting objectives and ecological constraints. It offers both theoretical significance and practical applicability, supporting sustainable urban development under multiple scenarios.
1. Introduction
As the role of ecological protection red lines and rigid control of green spaces continues to grow in urban planning, traditional transportation infrastructure layout models centered on supply–demand balance are encountering new constraints. In high-density developed areas, particularly in older residential neighborhoods and regions concentrated with public service corridors, the spatial configuration of parking facilities must not only meet the requirements for service radius, capacity, and convenience but also avoid encroaching upon or fragmenting existing green spaces and ecological corridors [,]. These issues fundamentally involve a multi-objective, multi-constraint, cross-domain system optimization process: data requires spatial identification and visualization, models demand high-dimensional multi-objective optimization, and decision-making requires interpretable and executable quantitative analysis. Therefore, a single technology or method cannot support the complete process from “spatial identification—optimization computation—decision-making selection,” necessitating a three-stage system-based multi-objective optimization strategy to coordinate all stages.
According to predictions by the International Transport Forum (ITF, 2021) [] and the World Bank (2020) [], the number of motor vehicles worldwide will continue to rise rapidly in the coming decades, particularly in developing countries and during the later stages of urbanization [,,]. The growth of motor vehicle ownership in megacities and the scarcity of land in core urban areas will continue to create a long-term conflict, resulting in dual pressures of “uneven demand distribution + increasing ecological constraints” []. According to the latest statistics from China’s Ministry of Public Security, the national motor vehicle ownership has reached 460 million, with approximately 359 million cars, reflecting the immense pressure on large Chinese cities to coordinate urban transportation and spatial resources []. To alleviate the “parking difficulties” issue, many countries and cities are promoting new facility solutions that combine intelligent management with spatial intensification []. Among them, smart underground parking lots, due to their advantages in land efficiency, intelligent operation, and minimal surface disruption, have become an important direction for urban transportation infrastructure development [,,]. However, in core urban areas with extremely scarce land, how to scientifically select locations for such facilities and achieve collaborative optimization among multiple objectives, including construction cost, transportation convenience, service coverage, and ecological protection, remains a complex global issue [,]. In recent years, China has implemented a series of exemplary projects in the field of smart underground parking. For example, in Shanghai, China Railway Fifteenth Bureau built the world’s largest diameter EUP vertical excavation (shield tunneling) underground smart parking lot, using urban fringe spaces for modular design, significantly improving land use efficiency while reducing damage to surface green spaces and providing substantial parking spaces for old communities, embodying the “green + smart” spatial utilization concept. As a representative of China’s megacities, Beijing’s high-density urban areas face even more complex parking supply and demand contradictions []. To address this issue, Beijing has successively introduced the “Beijing Motor Vehicle Parking Regulations” and the “Beijing ‘14th Five-Year Plan’ for Traffic Development and Construction Planning [], clearly proposing to promote underground space development, strengthen the construction of intelligent parking facilities, improve the intensive use of land resources, and support the development of smart parking projects under the public–private partnership (PPP) model []. Driven by both policy background and practical needs, conducting green-oriented site selection research for smart underground parking facilities in high-density urban areas has significant practical implications and potential for wider application []. However, achieving quantifiable collaborative optimization and decision-making systems between construction cost, service efficiency, and other objectives from an ecological-prioritization perspective remains a key methodological challenge.
The main contributions of this paper are reflected in three aspects:
- •
- Systematic Methodology: A widely applicable system-based three-stage strategy is proposed, integrating spatial analysis, multi-objective optimization, and post-Pareto analysis into a unified system, forming a complete methodology chain from data processing to decision-making.
- •
- Quantitative Decision Support: Under the ecological-prioritization framework, marginal benefit analysis is used to determine the input-output critical point, making the multi-objective optimization process more precise while enhancing the scientific and practical feasibility of decision-making.
- •
- Transferability: The system-based methodology is applicable to a variety of complex scenarios, including surface or underground facility layout, emergency and medical resource allocation, and green infrastructure configuration, making it adaptable to complex ecological and governance constraints.
2. Literature Review
Based on the definition of the above systemic issues and research needs, this paper further consolidates and organizes relevant research progress to clarify the theoretical basis and innovative entry points of the system-based framework. In the fields of urban transportation planning and land use, facility location has always been an important research topic. Faced with the reality of limited high-density urban space resources, diversified demands, and complex goal conflicts [,,,], recent studies on transportation facilities and site selection have moved beyond merely pursuing accessibility and cost optimization. Instead, there is a greater emphasis on integrating low-carbon solutions, ecological protection, and green infrastructure (GI) [,]. In the field of sustainable transportation system construction, embedding GI forms such as vegetative barriers, greenways, bicycle lanes, and ecological stormwater facilities into transportation network design has been shown to reduce emissions, improve public health, and enhance urban environmental quality []. However, incorporating ecological optimization goals directly into transportation facilities, particularly parking lot location optimization models, remains limited in existing research. This gap constitutes the entry point for this study and aligns with the need to achieve better comprehensiveness and multi-objective coordination based on existing technological methods.
To address the diversified objectives and complex constraints, facility location research has evolved from static accessibility and suitability analysis using GIS [,,,,], to incorporating Multi-Criteria Decision Analysis (MCDA) methods (such as AHP, TOPSIS) to integrate expert preferences and multi-dimensional weights [,,,,], and further to applying Multi-Objective Decision-Making (MODM) to handle high-dimensional objectives and generate Pareto optimal solution sets. MODM constructs mathematical models that simultaneously consider multiple objective functions, generating Pareto optimal solutions [,,,,,], thus revealing the trade-offs between conflicting objectives. Table 1 systematically compares three classical algorithms (NSGA-II, SPEA2, MOEA/D) with two frontier algorithms (NSGA-III, MaOEA) [,,,,,,,,,,,,,,,,,,,,], highlighting their differences in convergence, uniformity of distribution, and scalability. Among these, NSGA-III, with its reference point-driven environmental selection and normalization strategy, demonstrates superior solution set uniformity and coverage in the 4–15-dimensional objective space, and has been widely applied in high-dimensional optimization scenarios such as energy consumption scheduling, manufacturing optimization, and urban design [,]. Given that urban underground spaces involve multi-objective conflicts with controllable dimensions, this paper employs NSGA-III to construct an optimization model for researching high-density urban underground parking facility location problems.

Table 1.
Comparison of Five Algorithms.
However, most MODM approaches currently only focus on obtaining the Pareto solution set, without delving into the quantitative differences between the solutions within the set. To address this gap, marginal benefit theory has been introduced in recent years as an important supplement. By quantifying the marginal response of other objectives to unit changes in key objectives, it is possible to identify sensitive intervals and potential optimal compromise points within the solution set []. In the context of green infrastructure and stormwater management planning, Seyedashraf et al. (2021) also used multi-objective optimization to analyze the diminishing marginal benefits of capital investment and ecological services, providing theoretical support for investment decision-making []. Similarly, Tang et al. (2021) introduced cost–benefit analysis in the optimization of the Shenzhen LID system, enabling a quantifiable trade-off between investment and service outcomes []. Dong et al. [] proposed a spatial-explicit multi-objective optimization tool for green infrastructure planning, while Carrese et al. [] designed a government parking space leasing optimization model, and Zhao et al. [] achieved real-time parking space matching through a linear distribution method in parking planning. These studies provide multi-dimensional references for optimizing parking facilities in high-density urban areas.
Overall, existing research has reached a basic consensus on the technical approach: the integration of GIS and MCDA is suitable for low-dimensional scenarios with clear objective relationships [,], while MODM, particularly NSGA-III-based evolutionary algorithms, is more applicable to high-dimensional conflicting objectives, capable of generating diverse optimal solution sets while considering ecological protection, eco-nomic feasibility, and service efficiency []. However, existing studies mainly focus on individual aspects, such as improvements in spatial identification, model optimization, or post-result analysis, and lack an end-to-end methodological framework that integrates data acquisition, spatial analysis, optimization computation, and subsequent decision evaluation into a unified system. Particularly in the field of intelligent transportation and parking facility site selection, how to incorporate ecological-priority indicators into high-dimensional multi-objective optimization, systematically characterize the trade-offs between ecological, economic, and service objectives, and ensure result visualization and interpretability, remains a key bottleneck to overcome [,,].
Based on this, the paper proposes a System-Based Three-Stage Multi-Objective Optimization strategy from an ecological-prioritization perspective, forming a complete system methodology from data to decision-making. In the first stage, spatial identification and screening based on GIS are conducted, integrating urban fringe-space extraction with multi-source data (POI, AOI, population grids, transportation networks) to generate a candidate site set that meets ecological and construction constraints. In the second stage, a multi-objective optimization model is developed that incorporates eco-logical benefits, service efficiency, and economic feasibility, and is solved using NSGA-III to obtain a uniformly distributed Pareto optimal solution set. In the third stage, the solution set is filtered under the ecological-prioritization strategy, and marginal benefit analysis is introduced to quantitatively identify the optimal trade-off be-tween ecological and economic objectives, thereby producing executable decision-making solutions. This framework not only provides a systematic and actionable theoretical basis and practical approach for the layout of underground smart parking facilities in high-density urban areas but also demonstrates transferability, offering a reference for urban infrastructure planning that involves multi-objective conflicts and ecological constraints.
3. Materials and Methods
This study adopts a three-stage system approach (Figure 1) to address the site selection of underground smart parking facilities in high-density urban areas. The framework combines spatial analysis, multi-objective optimization, and marginal benefit analysis to provide comprehensive decision support.
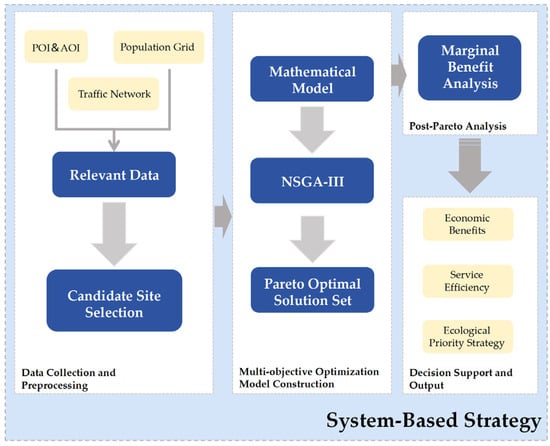
Figure 1.
Research Framework Diagram.
- •
- Stage 1 applies Geographic Information Systems (GIS) to identify potential construction areas and conduct preliminary screening of urban fringe spaces, population distribution, and transportation networks.
- •
- Stage 2 employs the NSGA-III algorithm to perform multi-dimensional optimization across ecological, economic, and social objectives. This step ensures that site selection achieves a balanced outcome in terms of service efficiency, cost-effectiveness, and ecological protection.
- •
- Stage 3 integrates post-Pareto analysis with marginal benefit theory to refine the solution set. By quantifying the trade-offs between investment costs and service coverage under ecological constraints, the most cost-effective and practically valuable schemes are identified.
Overall, this staged approach not only strengthens scientific decision-making for underground parking facilities but also demonstrates transferability to other complex infrastructure planning problems where multiple objectives and ecological requirements must be reconciled.
3.1. Study Area
This study selects Haidian District of Beijing as a typical high-density urban area for the research (see Figure 2), conducting optimization analysis for the location of underground smart parking facilities. The “Beijing Land and Space Ecological Restoration Special Plan (2021–2035)” [] explicitly states the priority to advance ecological space restoration and spatial optimization in the central urban area, with a focus on the rational configuration of parking facilities and urban transportation infrastructure. Additionally, according to data from the “2023 China Parking Industry Development White Paper” [], there is a significant imbalance in the distribution of parking resources in Beijing in both time and space, particularly around medical institutions and old residential communities. Statistics show that in the old residential communities of Haidian District, the off-street parking ratio even reaches as high as 26% []. This issue is particularly prominent in high-density residential areas, highlighting the urgency and practical significance of conducting optimization research for the location of smart underground parking facilities.
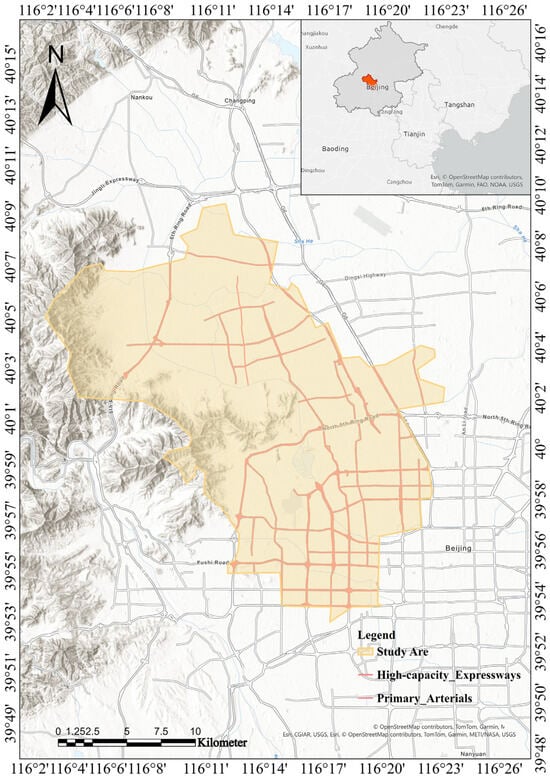
Figure 2.
Overview Map of the Study Area.
To ensure the robustness and policy relevance of the optimization framework, the variables and data sources were selected based on their representativeness and alignment with urban planning requirements. Population distribution and transportation networks were included as they directly reflect spatial demand for parking facilities and accessibility constraints. Green space coverage was incorporated to capture ecological protection priorities, consistent with national and municipal ecological red-line policies. Construction cost data were used to represent economic feasibility, reflecting financial constraints in infrastructure planning. All datasets were required to be derived from authoritative or open-access sources, possess sufficient spatial resolution (e.g., population grids at 100 m × 100 m), and reflect the most recent available year to ensure accuracy and comparability. These criteria guarantee that the selected objectives and data not only address practical siting challenges but also conform to broader sustainability and governance frameworks.
The data sources and processing used in this study are shown in Table 2.

Table 2.
Overview of Data Categories, Origins, and Processing Procedures.
Table 2.
Overview of Data Categories, Origins, and Processing Procedures.
| Type | Data Source | Processing Process |
|---|---|---|
| POI Data | OpenStreetMap [] | Filter and deduplicate data and apply spatial projection |
| AOI Data | ||
| Transportation Road Data | ||
| Population Data | China’s Seventh National Population Census Data [] | Convert into a 100 m × 100 m raster format in ArcMap 10.8.2. |
| The Smart Parking Facility Data | China Railway 15th Bureau Group Corporation Limited (Shanghai, China) | The data were organized and classified as detailed in Table 3. |

Table 3.
Data of the smart parking facility.
Table 3.
Data of the smart parking facility.
| Module | A | B | C | D |
|---|---|---|---|---|
| Capacity | 50 | 100 | 176 | 220 |
| Construction Cos | 20 million CNY | 30 million CNY | 50 million CNY | 65 million CNY |
3.2. GIS-Based Spatial Analysis
When conducting research on parking garage location selection, the first step is to study the current spatial characteristics of Haidian District, Beijing. ArcGIS is used to visually analyze the population distribution and transportation network in the study area (Figure 3 and Figure 4). In addition, key areas such as old residential neighborhoods, office areas, commercial districts, hospitals, schools, and transportation hubs are specifically analyzed, and kernel density analysis is performed using ArcGIS. The aim is to analyze the distribution of these key spaces and the potential parking pressures they may generate. These analyses of the current situation in the study area provide crucial basis for the subsequent parking facility location selection. Then, urban fringe spaces, including urban squares, spaces under overpasses, parks, and vacant land, are selected as potential parking facility sites.
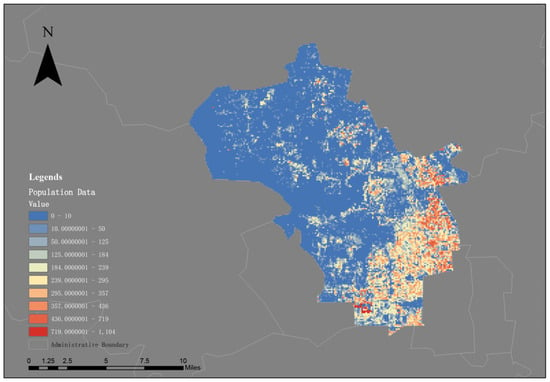
Figure 3.
Population Distribution Map.
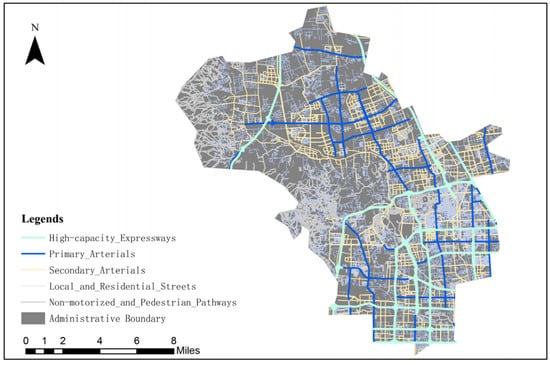
Figure 4.
Transportation Network Map.
3.2.1. Kernel Density Analysis
In ArcGIS, kernel density analysis is a tool used for spatial analysis. Kernel density estimation is a spatial interpolation technique commonly used to reveal the aggregation trends of spatial events or features within a study area. In this study, the ArcGIS platform is used to smooth point data by constructing influence zones centered on each input point, and calculating their density contribution to surrounding areas, thus generating a continuous density distribution map. The core idea of this method is to set a kernel function around each sampling point, with its influence diminishing as the distance from the center increases. The continuous density estimation is obtained by overlaying the effects across the entire space. In the mathematical expression of the kernel density function, the density value of a given raster cell is typically represented as the sum of all sample points’ weighted contributions to that cell. If the coordinates of a point are denoted as (x, y), its density value can be estimated using the following Formula (1):
Here, n represents the number of points involved in the estimation, h is the bandwidth of the kernel function, which controls the degree of spatial smoothing of the estimation surface;
is the Euclidean distance between the i-th sample point and the estimation location (x, y); K is the kernel function, which serves to weight the distance, with points closer to the estimation location contributing more to the density estimation.
3.2.2. Preliminary Screening of Candidate Sites
To save space, this study concentrates the site selection boundaries for parking facilities on urban fringe spaces. Urban fringe spaces refer to fragmented plots that have been marginalized due to factors such as terrain, land use patterns, or planning gaps, such as urban park green spaces, areas beneath overpasses, squares, and other idle areas. Considering the dual objectives of improving land use efficiency and minimizing disruption to residents, this study focuses the site selection range on such spaces. Based on this, and in line with national and local regulations on parking facility layout, spatial extraction and preliminary screening are performed using ArcGIS to identify candidate plots that meet the constraint conditions (Figure 5), forming the foundation for subsequent optimization analysis.
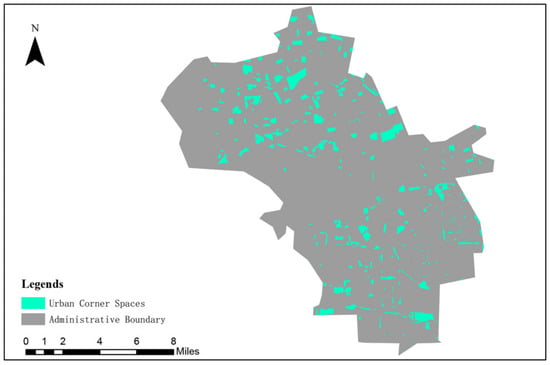
Figure 5.
Selection of Urban Fringe Spaces.
3.3. Multi-Objective Optimization and Post-Pareto Analysis
In the multi-objective optimization phase, this study uses the third-generation Non-dominated Sorting Genetic Algorithm (NSGA-III) as the solving tool. NSGA-III is specifically designed to address multi-objective optimization problems with higher-dimensional objectives (usually ≥3 objectives). The algorithm introduces a set of reference points, guiding the solution set to areas of uniform distribution in the multi-objective space, thus overcoming the issues of insufficient convergence or uneven distribution commonly found in traditional multi-objective algorithms in high-dimensional objective spaces []. The core steps of the NSGA-III algorithm include non-dominated sorting, crowding distance estimation, and population updating guided by reference points. The algorithm flowchart is shown in Figure 6. The design of reference points involves pre-setting a series of points in the objective space, significantly improving multi-objective search efficiency and the quality of solution distribution.
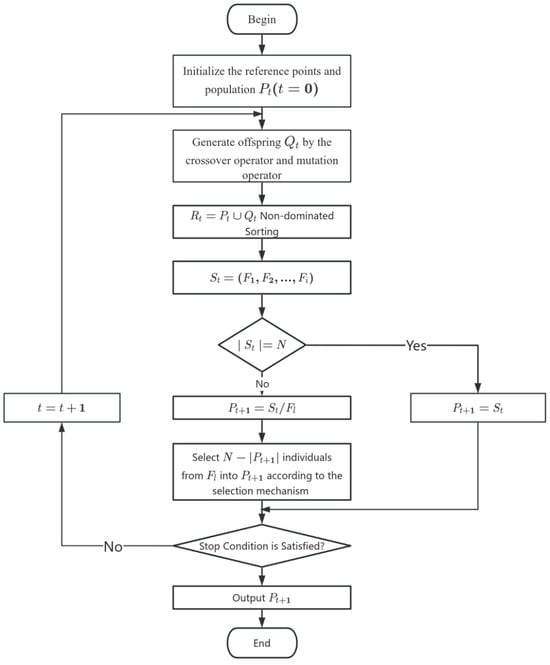
Figure 6.
NSGA-III Algorithm Flowchart.
In terms of computational complexity, NSGA-III has the same order of complexity as NSGA-II, namely
, but the introduction of reference points may result in additional overhead when the number of objectives is large. This makes the algorithm more demanding in high-dimensional scenarios, although in this study with four objectives the computational cost remains manageable. The algorithm’s core steps are shown in the following pseudocode, which illustrates the general process of non-dominated sorting, crowding distance estimation, and updating the population guided by reference points (Algorithm 1).
| Algorithm 1: NSGA-III Pseudocode. |
| Input: // Number of Decision Variables // Lower and Upper Bound of Variables // Maximum Number of Iterations // Population Size // Crossover Percentage // Mutation Percentage // Mutation Rate // Mutation Step Size // Number of divisions for generating reference points Output: ParetoFront 1: Initialize Parameters ← MOP2(x) // Define the cost function ← Number of Objective Functions ← ( , ) // Generate reference points Initialize Population P with nPop individuals For each individual i in P: Randomly initialize Position(i) within bounds [VarMin, VarMax] Evaluate Cost(i) = (Position(i)) 2: Perform Non-Dominated Sorting and Reference Point Assignment ← ( ) 3: for = 1 to do 4: Crossover Operation Create empty offspring population popc of size For k = 1 to /2 do Randomly select Parent1 and Parent2 from P [Child1, Child2] ← Crossover(Parent1, Parent2) // Perform crossover Evaluate Cost(Child1), Cost(Child2) Add Child1, Child2 to popc 5: Mutation Operation Create empty population popm of size For k = 1 to do Randomly select Parent p from P Mutate p to generate new individual with mutation operator Evaluate Cost(new individual) Add mutated individual to popm 6: Merge Population - Combine P (original population), popc (offspring), and popm (mutated) into a single population pop - Perform Non-Dominated Sorting and Reference Point Assignment for pop 7: Select New Population based on Reference Point Assignment Assign individuals to reference points based on their distance to Zr Sort population based on the minimum distance to reference points and crowding distance Select the best nPop individuals to form the new population P 8: Store Front 1 F1← F{1} // First Pareto front (best solutions) 9: Show Iteration Information Display: "Iteration iter: Number of F1 Members = number_of_F1" Plot F1 Costs for visualization 10: end for 11: Return ← // Return the final Pareto front |
The multi-objective optimization model established in this study covers four optimization objectives: maximizing the population coverage, minimizing walking distance, minimizing construction costs, and minimizing green space occupation. Using the NSGA-III algorithm, a set of Pareto non-dominated solutions with good distribution characteristics is obtained, where each solution represents a different parking facility location option. To further identify the most practically valuable solutions, a green-ecology-oriented selection strategy is employed in the post-Pareto analysis phase. This involves first extracting several solutions with the lowest green space occupation from the complete non-dominated solution set as initial candidate options. Then, marginal benefit theory is introduced to quantitatively assess the trade-off between construction investment costs and coverage efficiency. Marginal benefit theory, originating from economics, is based on the core idea of comparing the ratio of additional costs to the corresponding increase in benefits, identifying the critical point with the highest input-output efficiency [], and thus determining the optimal resource utilization solution. The formula for marginal benefit is as follows []:
In this study, marginal benefit analysis is applied by comparing the incremental benefits and incremental costs across candidate solutions, thereby accurately identifying the optimal trade-off between economic feasibility and ecological protection. Ultimately, using marginal benefit maximization as the selection criterion, the most suitable solution is chosen from the ecology-oriented candidate set, achieving the coordinated maximization of economic efficiency, ecological conservation, and social service coverage. This two-stage combined analytical method provides a scientifically rigorous and practically feasible decision support framework for the optimized layout of parking facilities in high-density urban areas.
4. Results
4.1. GIS-Based Spatial Analysis
The results of the kernel density analysis conducted on the ArcGIS platform are shown in Figure 7, reflecting the spatial clustering characteristics of different functional areas within Haidian District, Beijing, and highlighting evident spatial distribution disparities. Figure 7a shows that residential areas are primarily concentrated in the southeast, with densities significantly higher than in other regions, indicating a high degree of population aggregation and strong potential parking demand in this zone. In Figure 7b, office areas exhibit the highest kernel density in the eastern part of the district, identifying it as a core business function area where frequent commuting generates substantial daytime parking pressure. Figure 7c, illustrating the density distribution of commercial centers, indicates a concentration in the southeast, largely overlapping with the residential areas. This suggests a clustering of commercial service facilities, where pronounced fluctuations in pedestrian and vehicular traffic are likely during evenings and weekends. Figure 7d shows that hospitals are also densely clustered in the southeast, forming a multifunctional agglomeration belt with residential and commercial areas, thereby imposing heightened requirements for short-term, high-frequency parking demand. Figure 7e reveals that schools are densely distributed in the eastern region, which may reflect educational resource allocation policies, and underscores the need to address traffic pressures during peak school commuting hours. Figure 7f demonstrates that bus stops are also most concentrated in the southeast, not only highlighting the strong accessibility of public transportation in this area but also reinforcing the identification of this zone as a typical hotspot of overlapping population and functional densities.
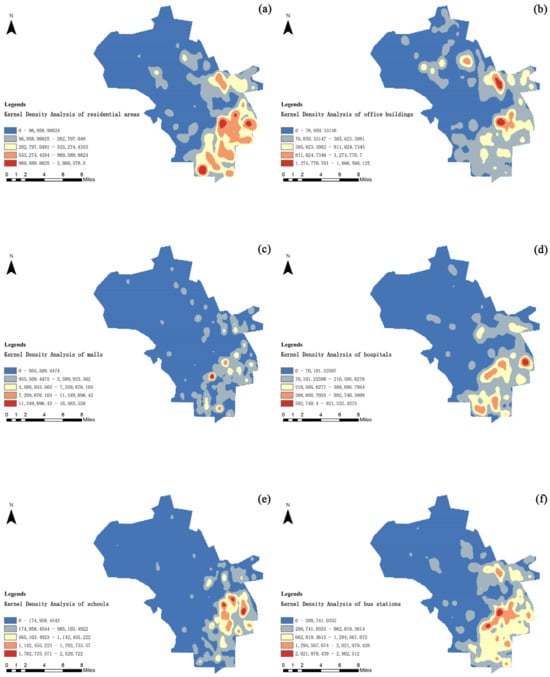
Figure 7.
Kernel Density Analysis Map of Key Areas.
Overall, both the southeastern and eastern areas display pronounced spatial clustering across residential, office, commercial, medical, educational, and transportation functions. This composite pattern of multifunctional density suggests that these regions should be prioritized in future parking resource allocation and given appropriate weighting in site optimization to enhance service efficiency and resource utilization effectiveness.
4.2. Formulation of the Multi-Objective Optimization Model
Guided by the development concept of ecological prioritization, this study constructs a multi-objective parking facility location optimization model for high-density urban areas. Under multiple practical constraints, the model comprehensively considers the economic feasibility and service effectiveness of parking facility construction, with the aim of achieving efficient allocation and sustainable utilization of limited spatial resources. The optimization model incorporates four independent yet synergistic objective functions: maximizing service population coverage, minimizing walking distance, minimizing construction cost, and minimizing green-space occupation. By balancing these objectives, the model seeks to maximize overall benefits across different types of parking demand points.
To ensure both the practical feasibility and spatial rationality of the optimization results, the model introduces a series of real-world constraints. These include restrictions on service radius, minimum parking capacity standards, and construction feasibility requirements for individual parcels. The inclusion of such constraints not only guarantees the feasibility of the solution set from technical and managerial perspectives but also reflects the critical boundary conditions in urban planning and management. Consequently, the model provides a robust decision-making foundation for the subsequent solution process based on evolutionary algorithms.
4.2.1. Parameter Definition
To construct a green-oriented, service-efficient, and economically feasible multi-objective location model for underground smart parking facilities, the variables and parameters are defined as follows. The decision variable
indicates whether candidate site i is selected as a parking facility location. Specifically,
denotes that site i is selected for construction, while
denotes that it is not selected. The variable
represents whether parking facility i provides service to residential point j. Here,
indicates that parking facility i serves residential point j, whereas
indicates that it does not. Additional parameters and their definitions are presented in the following Table 4.

Table 4.
Definitions of Parameters.
4.2.2. Objective Functions and Constraints
To systematically optimize the location of underground smart parking facilities in high-density urban areas, this study develops an optimization model that integrates multiple objectives, aiming to achieve a coordinated balance among service effectiveness, construction costs, and ecological protection. The model is designed with a focus on practical siting requirements, establishing optimization goals across four core dimensions: coverage capacity, accessibility, investment intensity, and green-space impact. At the same time, to ensure both the feasibility and real-world applicability of the solutions, key constraints are incorporated, including service distance, capacity allocation, and land use decisions. The following sections provide a detailed explanation of each objective function and constraint, along with the definitions of related symbols and parameters.
This model includes the following four optimization objectives:
- Minimize total walking distance
- Let denote the shortest walking distance from candidate parking facility i to demand point j, and let be a binary variable indicating whether parking facility i serves demand point j. This objective function aims to minimize the total walking distance between all constructed parking facilities and their corresponding service demand points, which can be expressed as:
- Minimize total construction cost
Let
denote the construction cost of building a parking facility at candidate location i, and let
be a binary variable indicating whether the location is selected for construction. This objective function aims to minimize the total construction investment, expressed as:
- 4.
- Minimize green space occupation
Urban green spaces are vital resources for maintaining ecological balance and ensuring a healthy environment for residents. To reconcile parking facility construction with ecological protection, this model incorporates an objective function that guides site selection to avoid existing green areas as much as possible, thereby reducing disturbances to surface ecosystems. Let
represent the green-space area covered by candidate location i, and let
be the decision variable indicating whether this location is selected. The objective function is expressed as:
- 5.
- Maximize total population coverage
Let
denote the population at demand point j. If this point is served by at least one parking facility, it is considered covered. This objective function aims to maximize the total population served, and is expressed as:
In addition, to ensure the feasibility and practical applicability of the model solutions, the following constraints are established (Table 5).

Table 5.
Expressions and Definitions of Constraints.
To better illustrate the interactions among the four optimization objectives and the associated constraints, a comparative summary table is presented below. Table 6 highlights the potential trade-offs between objectives and the role of ecological and spatial constraints in shaping feasible solutions.

Table 6.
Relationships between optimization objectives and constraints in the site selection model.
4.3. Pareto Optimal Solution Set
After completing the multi-objective optimization with the NSGA-III algorithm, this study obtained multiple sets of Pareto non-dominated solutions representing different trade-off strategy and visualized them using the MATLAB R2024a platform. The simulation experiment was set with an initial population size of 300, a maximum of 1000 iterations, and both crossover and mutation rates fixed at 0.5. The resulting Pareto front solutions are illustrated in Figure 8. Figure 8 presents the Pareto-optimal solution set across the four objectives. Although the figure contains detailed information, the key pattern is the evident trade-off between construction cost and population coverage. In particular, solutions with zero green-space occupation form a distinct subset, confirming the feasibility of achieving ecological protection without sacrificing service efficiency.
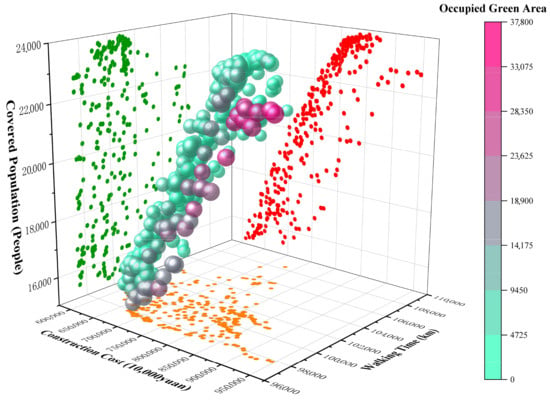
Figure 8.
Distribution of the Pareto Optimal Solution Set.
Overall, the solutions are evenly distributed across the objective space without noticeable gaps. Specifically, green-space occupation ranges from 0 to 37,800 m2, construction costs vary from 6.07 to 9.46 billion CNY, total walking distance falls between 97,426 m and 108,356 m, and population coverage spans from 15,233 to 23,835 people. These results demonstrate that the reference-point guidance strategy enabled NSGA-III to effectively maintain both the diversity and integrity of the Pareto front solutions, thereby providing a rich set of high-quality alternatives for subsequent decision-making.
Further analysis revealed different levels of coupling among the objectives. First, construction cost and population coverage exhibit a strong positive correlation, indicating a clear linear “investment–return” relationship. Second, green-space occupation and construction cost show a moderate positive correlation, suggesting that occupying green spaces often entails higher ecological compensation and additional construction expenditures. Meanwhile, green-space occupation is negatively correlated with total walking distance, showing that occupying green areas generally shortens the distance between facilities and residential communities, thereby reducing residents’ walking distances; conversely, strictly adhering to a “low green-space occupation” principle may result in longer walking distances. Finally, the weak correlation between total walking distance and population coverage indicates that these two objectives are not rigidly conflicting and that optimizing pedestrian paths can help mitigate potential tensions.
Aligned with the “green ecological” orientation, 18% of the Pareto front solutions—54 in total—achieved zero green-space occupation. Among these, the lowest-cost solution required 6.1 billion CNY, further confirming the practical feasibility of simultaneously ensuring economic efficiency and service coverage under strict ecological constraints.
Overall, the Pareto front solution set provides a clear interpretation of the mechanisms and interrelationships among the optimization objectives. On the one hand, the strong positive correlation between cost and population coverage forms the core of decision optimization; on the other hand, the coupling between green-space occupation and walking distance, while mutually constraining, still leaves room for collaborative optimization. In addition, the positive correlation between green-space occupation and cost further underscores the necessity of incorporating ecological costs into comprehensive decision-making.
Summary of Optimization Process
The multi-objective optimization phase successfully generated a diverse set of Pareto-optimal solutions that balanced the trade-offs between ecological protection, service efficiency, and economic feasibility. In the subsequent post-Pareto analysis phase, these solutions were refined by applying ecological-priority constraints and marginal benefit theory to further identify the most practically valuable alternatives for decision-making. This two-step process ensures that the final solutions are both ecologically sustainable and economically viable, thus offering robust decision support for urban planning.
4.4. Post-Pareto Analysis
Within the 300 Pareto non-dominated solutions obtained during the NSGA-III optimization phase, although the solutions already demonstrate favorable distribution characteristics and balanced objectives, further refinement is required to implement the “green ecological” orientation and enhance decision precision. Therefore, a two-step post-Pareto analysis was conducted in this study for fine-grained screening and evaluation.
Figure 9 illustrates the post-Pareto analysis based on marginal benefit theory. While multiple dimensions are displayed, the most important insight is the identification of the input–output inflection point, which highlights the scheme requiring about 7 billion CNY to serve roughly 20,000 residents. This finding provides decision-makers with a clear reference for selecting cost-effective solutions under ecological constraints. First, following the principle of ecological protection, the 54 solutions with the lowest green-space occupation were selected from the complete set of non-dominated solutions as the initial candidate subset for subsequent analysis (Figure 9). This green-oriented subset clearly reflects location optimization strategies under strict ecological protection policies, not only avoiding damage to urban ecological spaces but also aligning with the goals of sustainable urban development in both policy and practice. Specifically, the construction costs of these 54 solutions range from 6.1 to 8.2 billion CNY, while the population coverage spans from 15,465 to 23,675 people. These findings indicate that even under conditions of minimal ecological disturbance, service capacity can still reach relatively high levels compared with the overall solution set. This result not only confirms the economic and social benefits of site selection under strict ecological constraints but also provides policymakers with a clear framework of decision alternatives.
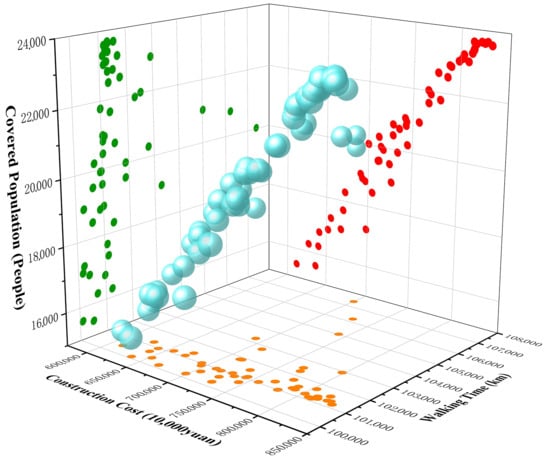
Figure 9.
Pareto Optimal Solution Set Filtered from an Ecological Optimization Perspective.
In addition, this study introduces marginal benefit theory to quantitatively analyze the filtered subset, focusing on the relationship between two critical objectives—construction cost and population coverage—in order to further identify the most decision-valuable solutions within the green-ecology-oriented set. The final results are visualized using ArcGIS to support decision-making in site optimization. Marginal benefit theory, originating from economics, aims to identify the optimal critical point between resource input and output by analyzing the ratio of incremental investment costs to the corresponding incremental benefits. Specifically, in this study, construction cost is treated as the input, while the corresponding population coverage is considered the output, and the marginal benefit values are calculated between adjacent candidate solutions.
Based on Equation (2), the marginal benefits of the 54 green-ecology-prioritized solutions were calculated, yielding a series of quantitative marginal benefit values. The analysis revealed that several solutions demonstrated notably higher marginal benefits than others (Figure 10), indicating superior efficiency in terms of resource input and output. Through further ranking and comparison, this study ultimately identified the solution with the highest marginal benefit. This solution requires a construction cost of 7 billion CNY and provides a service population coverage of 20,029 people, with a marginal benefit value as high as 1.86. In other words, for each additional unit of construction cost, the corresponding increase in population coverage significantly exceeds that of other solutions, highlighting its superior cost efficiency and service capability.
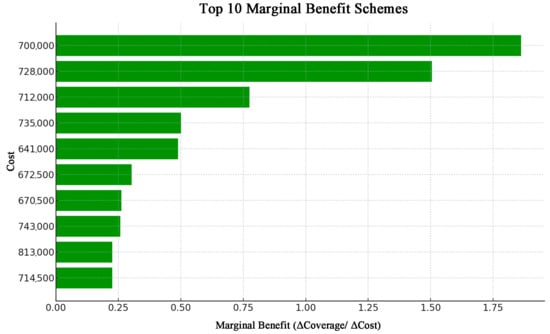
Figure 10.
Top Ten Schemes by Marginal Benefit.
In this study, ArcGIS was further employed to generate the final optimized siting map (Figure 11) corresponding to the scheme with a construction cost of 7 billion CNY and a service population coverage of 20,029 residents. The map clearly illustrates the final locations of the selected parking facilities and their spatial relationships with surrounding residential areas. As shown, the siting of the facilities is rationally distributed, adjacent to high-density residential zones, which effectively reduces residents’ walking distances and travel times, thereby enhancing both accessibility and service efficiency, while simultaneously complying with ecological protection requirements.
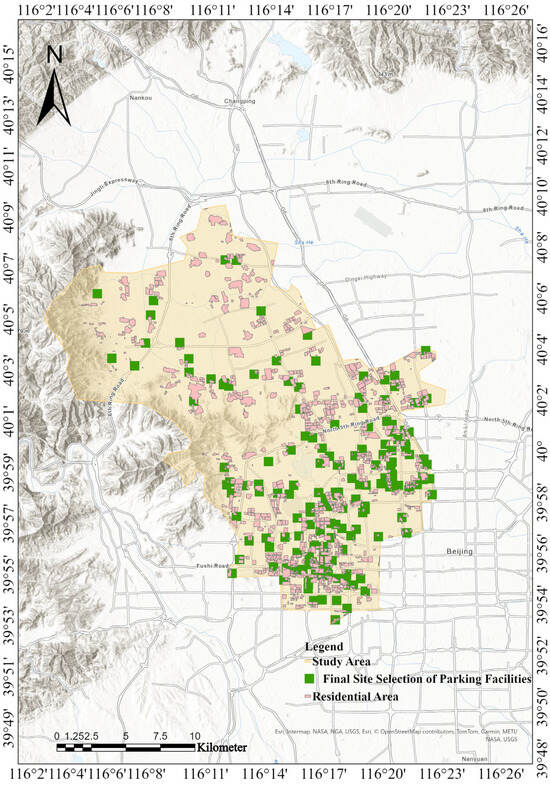
Figure 11.
Final Visualization of the Optimized Site-Selection Scheme.
In summary, through the dual refinement of ecological-priority screening and marginal benefit analysis, this study identified the siting scheme that most effectively achieves the coordinated optimization of economic, social, and environmental benefits under ecological constraints. This analytical approach not only provides rigorous decision support for the siting of underground smart parking facilities, but also offers a systematic methodological reference for addressing similar urban infrastructure planning challenges.
5. Discussion
This study advances a system-based three-stage optimization framework that integrates GIS-based spatial analysis, NSGA-III, and marginal benefit analysis. By combining evolutionary optimization with post-Pareto evaluation, the framework not only generates diverse and balanced solutions but also provides interpretable guidance for decision-making. This integration enhances both the methodological rigor and the practical applicability of multi-objective site selection under ecological constraints.
Beyond methodological contributions, the findings of this study also provide important insights for policy and practice. The identification of feasible solutions with zero green-space occupation demonstrates that ecological protection can be embedded into parking facility planning without undermining service efficiency, aligning with Beijing’s ecological red-line policies. For municipal authorities, this highlights the value of adopting multi-objective optimization frameworks to balance ecological preservation, cost control, and service provision. From a managerial perspective, the introduction of marginal benefit analysis offers a transparent tool for investment prioritization, enabling decision-makers to identify projects with the highest input–output efficiency under ecological constraints. Moreover, the proposed framework is transferable to other megacities with severe land scarcity and is replicable, as its three-stage process—from spatial data screening to optimization and post-Pareto analysis—can be readily applied or adapted to other types of urban infrastructure. Theoretically, this research advances beyond prior studies by quantitatively examining the trade-offs between ecological and economic objectives and by refining the optimization process to prioritize solutions with minimal green-space occupation, thereby establishing a more ecologically oriented and fine-grained strategy.
The robustness of the proposed framework can be supported from three perspectives. First, NSGA-III was adopted because it has been widely recognized in the literature as more effective than traditional algorithms such as NSGA-II and MOEA/D in handling high-dimensional objectives. Second, the trade-off patterns identified in this study—such as the feasibility of zero green-space occupation solutions combined with acceptable costs—are highly consistent with existing planning practices and policy directions in Beijing and other megacities. Third, similar findings have been reported in Shanghai, where the construction of underground smart parking facilities demonstrated that optimizing land use while minimizing ecological disturbance is practically achievable. Taken together, these points indicate that the model provides stable and reliable results across alternative conditions, reinforcing its applicability to complex urban infrastructure planning.
While the proposed framework demonstrates both methodological rigor and practical applicability, several limitations should be acknowledged. First, the analysis is based on publicly available datasets with fixed spatial and temporal resolutions, which may not fully capture the heterogeneity of user behavior or temporal variations in parking demand. Second, although NSGA-III proved effective in balancing multiple objectives, it is computationally more complex than some alternative algorithms and remains sensitive to the choice of reference points, which may affect scalability for larger datasets. Future research could therefore incorporate more detailed travel-behavior data and explore hybrid or adaptive algorithms to enhance computational efficiency and robustness, thereby extending the applicability of the framework to broader urban infrastructure contexts.
This study proposes a system-based strategy for the site selection of underground smart parking facilities, effectively addressing the challenges of siting such infrastructure in high-density urban areas. Under an ecological-priority perspective, the framework integrates multi-objective optimization and marginal benefit analysis to achieve a comprehensive balance among economic, ecological, and social benefits.
6. Conclusions
This study proposes a system-based strategy for the site selection of underground smart parking facilities, effectively addressing the challenges of siting such infrastructure in high-density urban areas. Under an ecological-priority perspective, the framework integrates multi-objective optimization and marginal benefit analysis to achieve a comprehensive balance among economic, ecological, and social benefits. The specific conclusions are as follows:
- System-Based Methodological Framework: The proposed three-stage optimization framework, integrating GIS-based spatial analysis, NSGA-III, and marginal benefit analysis, provides a scientific and operational decision-support tool for siting parking facilities in complex urban contexts. Beyond theoretical significance, it also offers a practical reference for planners and policymakers, enabling transparent and evidence-based decisions in similar infrastructure projects.
- Ecological-Priority Multi-Objective Optimization Strategy: By employing the NSGA-III algorithm, this study achieves comprehensive optimization across ecological, economic, and social objectives, ensuring that site selection schemes maximize service coverage while minimizing construction costs, walking distances, and green-space occupation. Compared with traditional methods, this strategy provides stronger support for balancing conflicting objectives under ecological constraints, thereby offering practical guidance for policy formulation and resource allocation.
- Decision Support through Marginal Benefit Analysis: Incorporating marginal benefit theory enables the identification of critical input–output inflection points and the most cost-effective schemes. This provides decision-makers with a transparent tool to prioritize investment options under ecological constraints, enhancing both the feasibility and managerial value of the proposed solutions.
Overall, the study establishes a replicable three-stage model—comprising data-driven spatial screening, multi-objective optimization, and marginal benefit-based decision refinement—that can be adapted to other types of urban infrastructure planning problems beyond parking facilities. The findings therefore not only strengthen the scientific basis of sustainable site selection under ecological constraints but also highlight the framework’s practical applicability, transferability, and adaptability, ensuring relevance for future urban governance and infrastructure development.
Author Contributions
Conceptualization, X.L., Y.G. and H.W.; methodology, X.L., Y.G. and H.W.; software, X.L. and Y.G.; validation, X.L., Y.G. and H.W.; formal analysis, X.L. and Y.G.; investigation, X.L. and Y.G.; resources, X.L., Y.G., H.W. and D.S.; data curation, H.W. and Y.W.; writing—original draft preparation, X.L., Y.G. and H.W.; writing—review and editing, H.W. and Y.W.; visualization, Y.G. and H.W.; supervision, X.L., Y.G., Z.L., and D.S.; project administration, H.W., Y.W. and Z.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this study are obtained from publicly available sources. All base maps used for GIS analyses are derived from open-access public domain resources. For each dataset cited in the article, the corresponding access link and the date of retrieval are provided in the text.
Acknowledgments
The authors would like to thank all colleagues and institutions who provided valuable suggestions and support during the research and manuscript preparation. In particular, the authors sincerely acknowledge the China Railway 15th Bureau Group Co., Ltd. for providing data support for this study.
Conflicts of Interest
Author Dandan Sun was employed by the company China Railway 15 Bureau Group Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Croeser, T.; Garrard, G.E.; Visintin, C.; Kirk, H.; Ossola, A.; Furlong, C.; Clements, R.; Butt, A.; Taylor, E.; Bekessy, S.A. Finding Space for Nature in Cities: The Considerable Potential of Redundant Car Parking. npj Urban Sustain. 2022, 2, 27. [Google Scholar] [CrossRef]
- Wu, G.; Yang, D.; Niu, X.; Mi, Z. The Impact of Park Green Space Areas on Urban Vitality: A Case Study of 35 Large and Medium-Sized Cities in China. Land 2024, 13, 1560. [Google Scholar] [CrossRef]
- International Transport Forum. Global Transport Outlook 2021. Available online: https://www.oecd.org/ (accessed on 11 June 2025).
- The World Bank. World Development Report 2020: Data, Digitalization, and Development. Available online: https://www.worldbank.org/ (accessed on 11 June 2025).
- Chester, M.; Fraser, A.; Matute, J.; Flower, C.; Pendyala, R. Parking Infrastructure: A Constraint on or Opportunity for Urban Redevelopment? A Study of Los Angeles County Parking Supply and Growth. J. Am. Plann. Assoc. 2015, 81, 268–286. [Google Scholar] [CrossRef]
- Davis, A.Y.; Pijanowski, B.C.; Robinson, K.; Engel, B. The Environmental and Economic Costs of Sprawling Parking Lots in the United States. Land Use Policy 2010, 27, 255–261. [Google Scholar] [CrossRef]
- Aydınoğlu, A.Ç.; Iqbal, A.S.; Şişman, S. Parking Suitability and Site Selection Analysis Using GIS-Based Multi-Criteria Decision Analysis Techniques: AHP, TOPSIS, and VIKOR—A Case Study of Pendik District (Istanbul). Iconarp Int. J. Archit. Plan. 2025, 13, 22–50. [Google Scholar] [CrossRef]
- Jonuzi, E.; Alkan, T.; Durduran, S.S.; Selvi, H.Z. Using GIS-Supported MCDA Method for Appropriate Site Selection of Parking Lots: The Case Study of the City of Tetovo, North Macedonia. Int. J. Eng. Geosci. 2024, 9, 86–98. [Google Scholar] [CrossRef]
- Kabashkin, I.; Kulmurzina, A.; Zhandarbekova, A.; Sansyzbayeva, Z.; Sultanov, T. A Multi-Objective Approach for Optimizing Aisle Widths in Underground Parking. Infrastructures 2025, 10, 100. [Google Scholar] [CrossRef]
- Sisman, S.; Ergul, I.; Aydinoglu, A.C. Designing GIS-Based Site Selection Model for Urban Investment Planning in Smart Cities with the Case of Electric Vehicle Charging Stations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLVI-4/W5-2021, 515–522. [Google Scholar] [CrossRef]
- Shen, T.; Hua, K.; Liu, J. Optimized Public Parking Location Modelling for Green Intelligent Transportation System Using Genetic Algorithms. IEEE Access 2019, 7, 176870–176883. [Google Scholar] [CrossRef]
- Li, X.; Guo, Y.; Liu, Z.; Sun, D.; Liu, Y.; Wang, W. A Study on Multi-Objective Optimization for the Location Selection of Smart Underground Parking Facilities in High-Density Urban Areas of Megacities: A Case Study of Jing’an District, Shanghai. PLoS ONE 2025, 20, e0326455. [Google Scholar] [CrossRef]
- Eskandari, M.; Nookabadi, A.S. Off-Street Parking Facility Location on Urban Transportation Network Considering Multiple Objectives: A Case Study of Isfahan (Iran). Transport 2018, 33, 1067–1078. [Google Scholar] [CrossRef]
- Song, M.; Chen, D. An Improved Knowledge-Informed NSGA-II for Multi-Objective Land Allocation (MOLA). Geo-Spat. Inf. Sci. 2018, 21, 273–287. [Google Scholar] [CrossRef]
- Pătrăușanu, A.; Florea, A.; Neghină, M.; Dicoiu, A.; Chiș, R. A Systematic Review of Multi-Objective Evolutionary Algorithms Optimization Frameworks. Processes 2024, 12, 869. [Google Scholar] [CrossRef]
- Demir, S.; Basaraner, M.; Taskin Gumus, A. Selection of Suitable Parking Lot Sites in Megacities: A Case Study for Four Districts of Istanbul. Land Use Policy 2021, 111, 105731. [Google Scholar] [CrossRef]
- Beijing Municipal Government. Beijing ‘14th Five-Year Plan’ for Traffic Development and Construction Planning. Available online: https://www.beijing.gov.cn/ (accessed on 19 June 2025).
- Xia, B.; Wu, J.; Fang, Y.; Shen, H.; Shen, J. Sustainable Renewal Methods of Urban Public Parking Spaces under the Scenario of Shared Autonomous Vehicles (SAV): A Review and a Proposal. Sustainability 2021, 13, 3629. [Google Scholar] [CrossRef]
- Roijers, D.M.; Vamplew, P.; Whiteson, S.; Dazeley, R. A Survey of Multi-Objective Sequential Decision-Making. J. Artif. Intell. Res. 2013, 48, 67–113. [Google Scholar] [CrossRef]
- Yi, J.-H.; Xing, L.-N.; Wang, G.-G.; Dong, J.; Vasilakos, A.V.; Alavi, A.H.; Wang, L. Behavior of Crossover Operators in NSGA-III for Large-Scale Optimization Problems. Inf. Sci. 2020, 509, 470–487. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Q.; Wong, K.-C.; Coello Coello, C.A.; Li, J.; Ming, Z.; Zhang, J. A Self-Guided Reference Vector Strategy for Many-Objective Optimization. IEEE Trans. Cybern. 2022, 52, 1164–1178. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Sooktip, T.; Wattanapongsakorn, N. Identifying Preferred Solutions for Multi-Objective Optimization: Application to Capacitated Vehicle Routing Problem. Cluster Comput. 2015, 18, 1435–1448. [Google Scholar] [CrossRef]
- Wajeetongratana, S. The Role of Ecological Management and Green Infrastructure in Improving Air Quality. E3S Web Conf. 2023, 452, 05001. [Google Scholar] [CrossRef]
- Jia, Y.-P.; Lu, K.-F.; Zheng, T.; Li, X.-B.; Liu, X.; Peng, Z.-R.; He, H.-D. Effects of Roadside Green Infrastructure on Particle Exposure: A Focus on Cyclists and Pedestrians on Pathways between Urban Roads and Vegetative Barriers. Atmos. Pollut. Res. 2021, 12, 1–12. [Google Scholar] [CrossRef]
- Hapriyanto, A.R.; Azmi, H. Implementation of Green Infrastructure in Sustainable Transportation in Supporting Urban Mobility: A Literature Review. Eng. Proc. 2025, 84, 25. [Google Scholar] [CrossRef]
- Wang, X. GIS Application to Build a New Parking in East Lansing City. Geo-Spat. Inf. Sci. 2008, 11, 308–310. [Google Scholar] [CrossRef]
- Rahimi, S.; Hafezalkotob, A.; Monavari, S.M.; Hafezalkotob, A.; Rahimi, R. Sustainable Landfill Site Selection for Municipal Solid Waste Based on a Hybrid Decision-Making Approach: Fuzzy Group BWM-MULTIMOORA-GIS. J. Clean. Prod. 2020, 248, 119186. [Google Scholar] [CrossRef]
- Aliniai, K.; Yarahmadi, A.; Zarin, J.Z.; Yarahmadi, H.; Lak, S.B. Parking Lot Site Selection: An Opening Gate Towards Sustainable GIS-Based Urban Traffic Management. J. Indian Soc. Remote Sens. 2015, 43, 801–813. [Google Scholar] [CrossRef]
- Oh, K.; Jeong, S. Assessing the Spatial Distribution of Urban Parks Using GIS. Landsc. Urban Plan. 2007, 82, 25–32. [Google Scholar] [CrossRef]
- Geneletti, D. A GIS-Based Decision Support System to Identify Nature Conservation Priorities in an Alpine Valley. Land Use Policy 2004, 21, 149–160. [Google Scholar] [CrossRef]
- Boroushaki, S.; Malczewski, J. Implementing an Extension of the Analytical Hierarchy Process Using Ordered Weighted Averaging Operators with Fuzzy Quantifiers in ArcGIS. Comput. Geosci. 2008, 34, 399–410. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of Art Surveys of Overviews on MCMD/MADM Methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Darani, S.K.; Eslami, A.A.; Jabbari, M.; Asefi, H. Parking Lot Site Selection Using a Fuzzy AHP-TOPSIS Framework in Tuyserkan, Iran. J. Urban Plan. Dev. 2018, 144, 04018022. [Google Scholar] [CrossRef]
- Ayyildiz, E.; Erdogan, M. A Fermatean Fuzzy SWARA-TOPSIS Methodology Based on SCOR Model for Autonomous Vehicle Parking Lot Selection. Appl. Soft Comput. 2024, 166, 112198. [Google Scholar] [CrossRef]
- Prasertsri, N.; Sangpradid, S. Parking Site Selection for Light Rail Stations in Muaeng District, Khon Kaen, Thailand. Symmetry 2020, 12, 1055. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Nowdeh, S.A.; Gandoman, F.H.; Moghaddam, M.J.H. A Multi-Objective Optimization Problem for Optimal Site Selection of Wind Turbines for Reduce Losses and Improve Voltage Profile of Distribution Grids. Energies 2019, 12, 2621. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, W.; Wang, H.; Hou, J.; Wang, H.; Wang, M. An Improved Chaotic Quantum Multi-Objective Harris Hawks Optimization Algorithm for Emergency Centers Site Selection Decision Problem. CMC-Comput. Mat. Contin. 2025, 82, 2177–2198. [Google Scholar] [CrossRef]
- Sicuaio, T.; Zhao, P.; Pilesjo, P.; Shindyapin, A.; Mansourian, A. A Multi-Objective Optimization Approach for Solar Farm Site Selection: Case Study in Maputo, Mozambique. Sustainability 2024, 16, 7333. [Google Scholar] [CrossRef]
- Hocine, A.; Zhuang, Z.-Y.; Kouaissah, N.; Li, D.-C. Weighted-Additive Fuzzy Multi-Choice Goal Programming (WA-FMCGP) for Supporting Renewable Energy Site Selection Decisions. Eur. J. Oper. Res. 2020, 285, 642–654. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, J. Applying Rough Random MODM Model to Resource-Constrained Project Scheduling Problem: A Case Study of Pubugou Hydropower Project in China. KSCE J. Civ. Eng. 2014, 18, 1279–1291. [Google Scholar] [CrossRef]
- Abd El-Wahed, W.F.; Abo-Sinna, M.A. A Hybrid Fuzzy-Goal Programming Approach to Multiple Objective Decision Making Problems. Fuzzy Sets Syst. 2001, 119, 71–85. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A Comprehensive Survey on NSGA-II for Multi-Objective Optimization and Applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, J.; Yan, Q.; Lai, L.; Xu, L. Research on Cell Manufacturing Facility Layout Problem Based on Improved NSGA-II. CMC-Comput. Mat. Contin. 2020, 62, 355–364. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, F.; Wu, A. Research on Multi-Objective Process Parameter Optimization Method in Hard Turning Based on an Improved NSGA-II Algorithm. Processes 2024, 12, 950. [Google Scholar] [CrossRef]
- Dutta, S.; M, S.S.R.; Mallipeddi, R.; Das, K.N.; Lee, D.-G. A Mating Selection Based on Modified Strengthened Dominance Relation for NSGA-III. Mathematics 2021, 9, 2837. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, B. Improving NSGA-II by a Local Search Strategy with Gaussian Mutation. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 1628–1633. [Google Scholar]
- OuYang, J.; Yang, F.; Yang, S.W.; Nie, Z.P. The Improved NSGA-II Approach. J. Electromagn. Waves Appl. 2008, 22, 163–172. [Google Scholar] [CrossRef]
- Celik, H.; Karaboga, N. Blind Source Separation with Strength Pareto Evolutionary Algorithm 2 (SPEA2) Using Discrete Wavelet Transform. Electronics 2023, 12, 4383. [Google Scholar] [CrossRef]
- He, F.; Shen, K.; Guan, L.; Jiang, M. Research on Energy-Saving Scheduling of a Forging Stock Charging Furnace Based on an Improved SPEA2 Algorithm. Sustainability 2017, 9, 2154. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, J.; Yuan, J. Application of SPEA2-MMBB for Distributed Fault Diagnosis in Nuclear Power System. Processes 2024, 12, 2620. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, R.; Zuo, J.; Jing, X. Enhancing MOEA/D with Uniform Population Initialization, Weight Vector Design and Adjustment Using Uniform Design. J. Syst. Eng. Electron. 2015, 26, 1010–1022. [Google Scholar] [CrossRef]
- Liu, Y.; Jiao, Y.-C.; Zhang, Y.-M.; Tan, Y.-Y. Synthesis of Phase-Only Reconfigurable Linear Arrays Using Multiobjective Invasive Weed Optimization Based on Decomposition. Int. J. Antennas Propag. 2014, 2014, 630529. [Google Scholar] [CrossRef]
- Lin, Q.; Tang, C.; Ma, Y.; Du, Z.; Li, J.; Chen, J.; Ming, Z. A Novel Adaptive Control Strategy for Decomposition-Based Multiobjective Algorithm. Comput. Oper. Res. 2017, 78, 94–107. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.-G.; Li, K.; Yeh, W.-C.; Jian, M.; Dong, J. Enhancing MOEA/D with Information Feedback Models for Large-Scale Many-Objective Optimization. Inf. Sci. 2020, 522, 1–16. [Google Scholar] [CrossRef]
- Luan, C.; Liu, R.; Zhang, Q.; Sun, J.; Liu, J. Multi-Objective Land Use Optimization Based on Integrated NSGA–II–PLUS Model: Comprehensive Consideration of Economic Development and Ecosystem Services Value Enhancement. J. Clean. Prod. 2024, 434, 140306. [Google Scholar] [CrossRef]
- Zhang, F. Constructing a Multi-Objective Optimization Model for Engineering Projects Based on NSGA-II Algorithm under the Background of Green Construction. Decis. Mak. Appl. Manag. Eng. 2024, 7, 37–53. [Google Scholar] [CrossRef]
- Yi, J.-H.; Deb, S.; Dong, J.; Alavi, A.H.; Wang, G.-G. An Improved NSGA-III Algorithm with Adaptive Mutation Operator for Big Data Optimization Problems. Futur. Gener. Comput. Syst. 2018, 88, 571–585. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, J.; Hu, Z.; Sun, H. An Adaptive Decomposition Evolutionary Algorithm Based on Environmental Information for Many-Objective Optimization. ISA Trans. 2021, 111, 108–120. [Google Scholar] [CrossRef]
- Hongbo, W.; Fan, Y.; Kena, T.; Xuyan, T. A Many-Objective Evolutionary Algorithm with Spatial Division and Angle Culling Strategy. Chin. J. Electron. 2021, 30, 437–443. [Google Scholar] [CrossRef]
- Liang, Z.; Luo, T.; Hu, K.; Ma, X.; Zhu, Z. An Indicator-Based Many-Objective Evolutionary Algorithm With Boundary Protection. IEEE T. Cybern. 2021, 51, 4553–4566. [Google Scholar] [CrossRef]
- Wei, L.; Li, E. A Many-Objective Evolutionary Algorithm Based on Bi-direction Fusion Niche Dominance. Concurr. Comput. Pract. Exp. 2021, 33, e8196. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, Y.; Li, C.; Jiang, B.; Li, Y. Designing an Urban Air Mobility Corridor Network: A Multi-Objective Optimization Approach Using U-NSGA-III. Aerospace 2025, 12, 229. [Google Scholar] [CrossRef]
- Taboada, H.A.; Coit, D.W. Data Clustering of Solutions for Multiple Objective System Reliability Optimization Problems. Qual. Technol. Quant. Manag. 2007, 4, 191–210. [Google Scholar] [CrossRef]
- Seyedashraf, O.; Bottacin-Busolin, A.; Harou, J.J. Many-Objective Optimization of Sustainable Drainage Systems in Urban Areas with Different Surface Slopes. Water Resour. Manag. 2021, 35, 2449–2464. [Google Scholar] [CrossRef]
- Tang, S.; Jiang, J.; Shamseldin, A.Y.; Shi, H.; Wang, X.; Shang, F.; Wang, S.; Zheng, Y. Comprehensive Optimization Framework for Low Impact Development Facility Layout Design with Cost–Benefit Analysis: A Case Study in Shenzhen City, China. ACS ES&T Water 2022, 2, 63–74. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, S.; Pei, X.; Wang, Y. Spatially Explicit Multi-Objective Optimization Tool for Green Infrastructure Planning Based on InVEST and NSGA-II towards Multifunctionality. Land Use Policy 2025, 150, 107465. [Google Scholar] [CrossRef]
- Carrese, S.; D’Andreagiovanni, F.; Giacchetti, T.; Nardin, A.; Zamberlan, L. An Optimization Model and Genetic-Based Matheuristic for Parking Slot Rent Optimization to Carsharing. Res. Transp. Econ. 2021, 85, 100962. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, K.; Ha, F. An Algorithm of Parking Planning for Smart Parking System. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 27–30 June 2014; pp. 4965–4969. [Google Scholar]
- Lin, Y.-K.; Yeh, C.-T. Multi-Objective Optimization for Stochastic Computer Networks Using NSGA-II and TOPSIS. Eur. J. Oper. Res. 2012, 218, 735–746. [Google Scholar] [CrossRef]
- Goyal, K.K.; Jain, P.K.; Jain, M. Optimal Configuration Selection for Reconfigurable Manufacturing System Using NSGA II and TOPSIS. Int. J. Prod. Res. 2012, 50, 4175–4191. [Google Scholar] [CrossRef]
- Dong, J.; Guo, R.; Lin, M.; Guo, F.; Zheng, X. Multi-Objective Optimization of Green Roof Spatial Layout in High-Density Urban Areas—A Case Study of Xiamen Island, China. Sustain. Cities Soc. 2024, 115, 105827. [Google Scholar] [CrossRef]
- Hou, Q.; Xu, H.; Xie, M.; Luo, P.; Cheng, Y. A Cellular Automata Coupled Multi-Objective Optimization Framework for Blue-Green Infrastructure Spatial Allocation. Water Res. X 2025, 28, 100387. [Google Scholar] [CrossRef]
- Zandniapour, K.; Soroush, A.; Khezerlu Agdam, E.; Sanaieian, H. Integrating GIS, 3D-Isovist, and an NSGA-II Multi-Objective Optimization Algorithm for Automation of Design Process in Urban Parks and Public Open Spaces. Int. J. Geoheritage Parks 2025, 13, 1–16. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Zhang, Z.; Li, Y.; Zhang, H.; Zhang, Y. Intersection Signal Timing Optimization: A Multi-Objective Evolutionary Algorithm. Sustainability 2022, 14, 1506. [Google Scholar] [CrossRef]
- Beijing Municipal Planning and Natural Resources Commission. Beijing Land and Space Ecological Restoration Special Plan (2021–2035). Available online: https://ghzrzyw.beijing.gov.cn/ (accessed on 19 June 2025).
- 2023 China Parking Industry Development White Paper. Available online: https://www.199it.com/ (accessed on 25 February 2024).
- OpenStreetMap. Available online: https://www.openstreetmap.org/ (accessed on 19 June 2025).
- National Bureau of Statistics of China . Available online: https://www.stats.gov.cn/ (accessed on 19 June 2025).
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Mankiw, N.G. Principles of Economics, 9th ed.; Cengage Learning: Boston, MA, USA, 2021; pp. 154–196. [Google Scholar]
- Loecker, J.D.; Goldberg, P.K.; Khandelwal, A.K.; Pavcnik, N. Econometrica. Econometrica 2016, 84, 445–510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).