Automated Detection of Site-to-Site Variations: A Sample-Efficient Framework for Distributed Measurement Networks

Abstract

Distributed measurement networks, from semiconductor testing arrays to environmental sensor grids, medical diagnostic systems, and agricultural monitoring stations, face a fundamental challenge: undetected site-to-site variations that silently corrupt data integrity. These variations create systematic biases between supposedly identical measurement units, which undermine scientific reproducibility and yield. The current site-to-site variation detection methods require extensive sampling or make rigid distributional assumptions, making them impractical for many applications. We introduce a novel framework that transforms measurement data into density-based feature vectors using Kernel Density Estimation, followed by anomaly detection with Isolation Forest. To automate the final classification, we then apply a novel probabilistic thresholding method using Gaussian Mixture Models, which removes the need for user-defined anomaly proportions. This approach identifies problematic measurement sites without predefined anomaly proportions or distributional constraints. Unlike traditional methods, our method works efficiently with limited samples and adapts to diverse measurement contexts. We demonstrate its effectiveness using semiconductor multisite testing as a case study, where our approach consistently outperforms state-of-the-art methods in detection accuracy and sample efficiency when validated against industrial testing environments.

1. Introduction

Modern data-driven science and industry are increasingly built upon a foundational architecture: the distributed measurement network. This paradigm, in which ensembles of nominally identical instruments or “sites” operate in parallel, represents a general class of sampling system designed to achieve massive gains in throughput and efficiency. We see this architecture everywhere: in semiconductor fabs, where hundreds of test sites probe circuits simultaneously [1]; in continental sensor grids that monitor air quality [2]; in fleets of clinical analyzers that process thousands of patient samples a day [3]; and in agricultural networks that assess vast tracts of farmland [4]. While this parallelism has unlocked unprecedented levels of throughput and efficiency, it has also exposed a persistent, often-invisible, threat: a systemic inconsistency between measurement sites that silently corrupts data, invalidates results, and erodes the very foundation of scientific reproducibility. This phenomenon, known as site-to-site variation (SSV), poses a universal challenge with high-stakes consequences across a multitude of critical domains.

The impact of undetected SSV is both widespread and severe. In environmental monitoring, networks of low-cost air quality sensors are essential for public policy, but, as their components age and drift at different rates, the data they produce can become seriously misleading. Field studies confirm that even co-located sensors can diverge significantly, generating phantom pollution hotspots and obscuring true environmental trends, potentially leading to misinformed policy and public health alerts [5]. In clinical medicine, the same blood sample sent to different labs or run on different analyzers can yield conflicting results due to subtle variations in reagent batches or machine calibration [3,6]. Such inter-analyzer variability can mean the difference between a correct diagnosis and a missed one, directly impacting patient care.

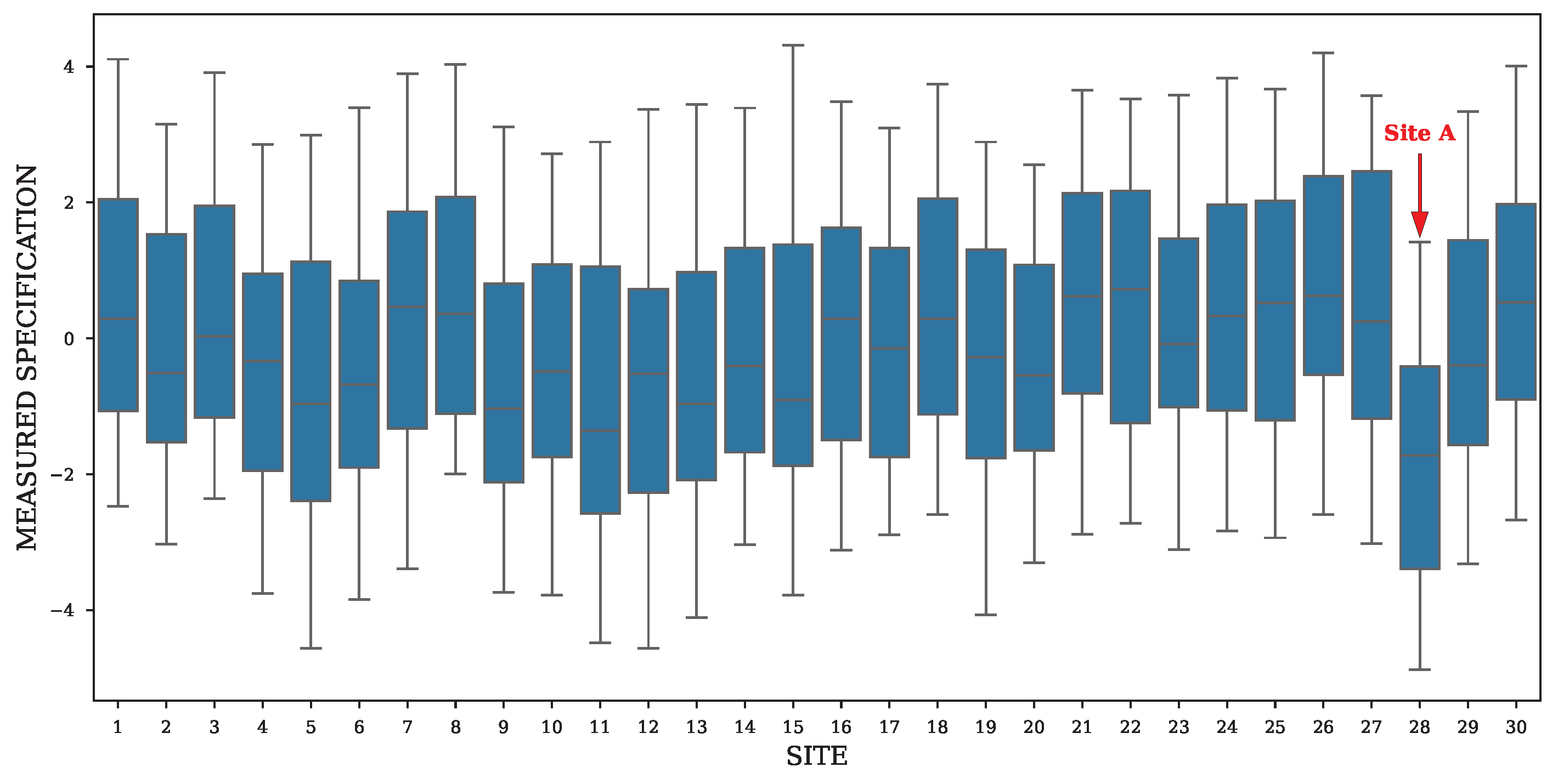
This challenge is just as acute in high-volume manufacturing. In the semiconductor industry, massive multisite testers probe hundreds of circuits in parallel to reduce costs. However, differences in the hardware of each test site, from trace lengths to thermal gradients, can cause one site to systematically fail good devices while another passes faulty ones [7,8]. Figure 1 illustrates a typical instance of site-to-site variation found in industrial test data for a measured device under test (DUT) specification. The boxplots represent the measurement distributions from an ensemble of parallel test sites. While most sites exhibit comparable distributions, Site A displays a markedly different profile. Its median is significantly lower than its peers, indicating a location shift. Such a distinct deviation suggests a systematic error originating from the hardware of Site A rather than reflecting the true performance of the DUTs. It is crucial to distinguish these site-induced errors from the expected intrinsic variations inherent in any manufacturing process, such as die-to-die fluctuations and random measurement noise. The central challenge addressed by this paper, therefore, is not the elimination of all variation but the specific detection of these systematic non-random errors introduced by the test sites themselves, which can mask the true performance of the device under test.

Figure 1. DUT-measured specification across multiple test sites, showing Site A as an issue site.

Despite its critical importance, the detection of SSV remains a significant challenge. The current methods are often a compromise. Visual inspection of boxplots is not scalable and fails to detect subtle anomalies. Traditional statistical tests like ANOVA carry rigid assumptions about data normality that are frequently violated in practice [8,9]. More advanced techniques that compare site distributions often rely on the fragile process of creating a “golden” reference from the data itself or require manual parameter tuning that is impractical for an automated production environment. There exists, therefore, a critical gap for an approach that is automated, sample-efficient, and agnostic to the underlying data distribution.

This paper introduces such a framework. We transform the SSV problem into a high-dimensional pattern recognition task, creating a distributional “fingerprint” for each site and using an anomaly detection algorithm to automatically identify deviant sites. Our approach requires no prior assumptions about the data’s shape and uses a probabilistic method to set detection thresholds automatically. We demonstrate through an application to proprietary industrial data that this framework provides a robust and scalable solution to the pervasive challenge of ensuring data integrity in distributed measurement networks.

1.1. Prior Work on SSV Detection Methods

The most commonly used approach for detecting site-to-site variation is visual inspection of boxplots for each measured specification. Operators manually scan these plots for sites whose medians or quartiles appear shifted or distorted relative to the ensemble, as illustrated in Figure 1. Although this qualitative analysis can be effective under specific conditions, its primary drawbacks are that it lacks a systematic process and requires manual analysis. Consequently, the technique does not scale well, becoming increasingly labor-intensive and susceptible to human error as the number of sites and parameters grow.

To automate flagging, a rule-based system is discussed in [1], where four significant criteria are used for flagging sites: comparison of location using the mean or median; comparison of dispersion using the standard deviation of each site and IQR; comparison of skewness; and comparison of outliers. Test sites that were flagged across multiple criteria are assigned more weight than sites that were only flagged once. Although this removes the need for manual inspection, it typically generates an overwhelming number of flags, all of which require downstream review; moreover, reliance on single-point statistics like mean and median ignores the full distributional shape and is easily confounded by intrinsic variation.

Well-established inferential tests, such as Analysis of Variance (ANOVA), were considered in detecting site-to-site variations, but they carry strong assumptions that often fail in practice [8]. ANOVA, for instance, requires that each site’s measurements are normally distributed with equal variances across the sites [9]. These conditions are not always met in real multisite test data, where distributions can be skewed, heavy-tailed, or heteroscedastic. Non-parametric alternatives like the Kruskal–Wallis test [10] or homogeneity of variance checks such as Levene’s test relax one or both of these assumptions, yet they too suffer from practical drawbacks. In particular, these tests can produce conflicting outcomes when sample sizes or distribution shapes differ between sites [11]. Consequently, inferential methods offer at best a coarse yes/no verdict on whether any site differs but no nuanced anomaly score or site-by-site severity ranking, making them ill-suited for fine-grained SSV detection in high-volume multisite testing [8].

The cross-correlation method introduced in [7] addresses some of the issues presented by the methods above by comparing individual site distributions with a constructed reference distribution. A fundamental limitation arises from error propagation inherent in computing the reference distribution (“site 0”). Since this reference is estimated from selected “good” sites, any misclassification or measurement inaccuracies in these sites directly propagate through the entire analysis, potentially compromising the validity and sensitivity of the detection process. Such propagated errors could lead either to false positives, wrongly flagging healthy sites, or false negatives, overlooking genuine problematic sites and thus impacting the reliability of the proposed methodology.

Principal Component Analysis (PCA) provides another avenue: sites whose measurement vectors exhibit large reconstruction errors in the leading principal subspace are flagged as anomalous [12]. Yet, PCA is inherently linear and may miss non-linear distortions or distributional shifts that do not align with principal axes.

1.2. Contributions and Paper Organization

This paper introduces a novel, sample-efficient, and distribution-agnostic framework for automated site-to-site variation detection in distributed measurement networks. Our main contributions are as follows:

• We propose a KDE–Isolation Forest pipeline to isolate anomalous sites without presupposing parametric forms, enabling unsupervised learning.
• We derive concentration bounds for empirical anomaly scores and establish conditions under which density features reliably approximate true site distributions, providing theoretical sample-efficiency guarantees.
• We introduce a novel probabilistic thresholding method using Gaussian Mixture Models (GMMs) to automatically derive a decision boundary from the anomaly scores.
• We apply our approach to multisite device under test (DUT) measurements from a Texas Instruments analog/mixed-signal test cell, where our framework outperforms state-of-the-art methods like cross-correlation and Quantile–Quantile (QQ) fitting.
• We provide empirical validation of the algorithm’s core mechanics on our data, demonstrated through path length analysis, thus offering transparency beyond a “black-box” application.
• We outline guidelines for adapting the framework to environmental sensor arrays, clinical laboratory networks, agricultural soil testing, and cybersecurity monitoring, showing its broad applicability.

The remainder of this paper is organized as follows. Section 2 details our proposed framework. We first formalize the KDE-based feature extraction process and the Isolation Forest anomaly scoring engine. We then present a comprehensive review of the existing thresholding techniques and introduce our GMM-based thresholding method. This section also includes the theoretical guarantees for the framework and positions it as a holistic alternative to prior rule-based systems. Section 3 is dedicated to semiconductor multisite testing and experimental validation. We demonstrate its effectiveness on industrial data and include an empirical validation of the Isolation Forest’s core principles alongside a hyperparameter sensitivity analysis. Section 4 discusses the broader implications of our findings. Section 5 talks about how the approach can be generalized and adapted to other domains. Finally, Section 6 outlines promising directions for future research, and Section 7 concludes the paper.

2. Methods

The challenge of identifying site-to-site variation (SSV) is fundamentally a problem of detecting subtle deviations in data distributions, a task for which modern machine learning (ML) offers a powerful toolkit. The increasing complexity and scale of data in industrial and scientific applications have spurred the adoption of ML for tasks that were previously intractable with traditional statistical rules [13]. Successes in diverse domains such as predictive maintenance in advanced manufacturing [14], fraud detection in finance [15], network intrusion detection in cybersecurity [16], and power systems [17] demonstrate the unique capability of ML algorithms to learn complex high-dimensional patterns from data without rigid parametric assumptions.

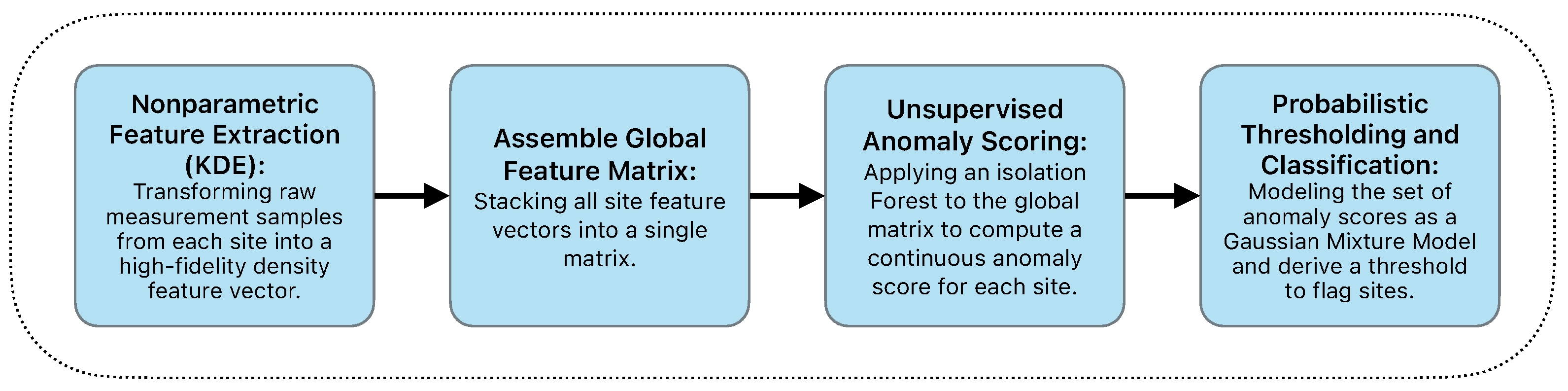
Inspired by these advances, we adopt a machine learning framework specifically designed to address the nuances of SSV. Our approach moves beyond single-point statistics to capture the complete distributional fingerprint of each measurement site. We then leverage an unsupervised ensemble method to automatically identify anomalous sites without requiring manual labeling or fault signatures. Our proposed KDE–Isolation Forest framework comprises four major steps, as summarized in Figure 2.

Figure 2. An overview of our automated site-to-site variation (SSV) detection framework.

2.1. Density Feature Extraction

Kernel Density Estimation (KDE) is a widely used non-parametric technique for approximating the probability density function of a random variable directly from observed samples without assuming any particular parametric form. While simpler non-parametric methods like histograms can also represent data distributions, they are sensitive to the choice of bin width and starting position, which can obscure important features. Kernel Density Estimation was selected because it provides a continuous smooth estimate of the probability density function that is less dependent on arbitrary parameter choices [18].

Kernel Density Estimation (KDE) is a non-parametric method used to estimate the underlying probability distribution from a sample of data. It builds a continuous curve by placing a kernel (commonly Gaussian) over each data point and then summing all of these functions. The resulting estimate is principally shaped by the kernel’s bandwidth h. This bandwidth parameter controls the width of each kernel, which in turn governs the smoothness of the final distribution [18]. KDE captures subtle features such as multimodality, skewness, and heavy tails that single-point statistics (mean and variance) cannot, and it yields a functional representation of the site’s measurements that is suitable for downstream anomaly detection [7].

Formally, for each test site $x=1,\dots ,M$, let its $n_x$ raw measurements be $D_x={\left\{y_{x,i}\right\}}_{i=1}^{n_x}$. The site’s estimated density ${\widehat{f}}_x\left(y\right)$ is calculated as

$${\widehat{f}}_x\left(y\right)={\displaystyle \frac{1}{n_{x}h}}\sum _{i=1}^{n_x}K\left({\displaystyle \frac{y-y_{x,i}}{h}}\right),$$

(1)

where K is the KDE kernel and the bandwidth $h>0$.

We discretize the density function by evaluating it on a shared uniform grid of B points, ${\left\{y_b\right\}}_{b=1}^B$, which spans the measurement range of interest, to make it suitable for our algorithm. This procedure yields a standardized B-dimensional density feature vector, ${\varphi }_x$. For each site, ${\varphi }_x={\left[{\widehat{f}}_x\left(y_1\right),{\widehat{f}}_x\left(y_2\right),\dots ,{\widehat{f}}_x\left(y_B\right)\right]}^{\mathsf{T}}$.

This vector serves as a high-fidelity representation of the site’s entire measurement distribution, preserving its shape and characteristics for the subsequent anomaly detection stage. Figure 3 shows how KDE captures distribution shapes for three randomly selected sites from the industrial data.

Figure 3. Illustration of the KDE feature extraction process.

We stack all site features into an $M\times B$ matrix:

$$\mathbf{\Phi }=\left[\begin{array}{c}{\mathit{\varphi }}_1^{\mathsf{T}}\\ {\mathit{\varphi }}_2^{\mathsf{T}}\\ ⋮\\ {\mathit{\varphi }}_M^{\mathsf{T}}\end{array}\right].$$

(2)

This matrix serves as the input to our anomaly detector.

2.2. Isolation Forest Anomaly Detection

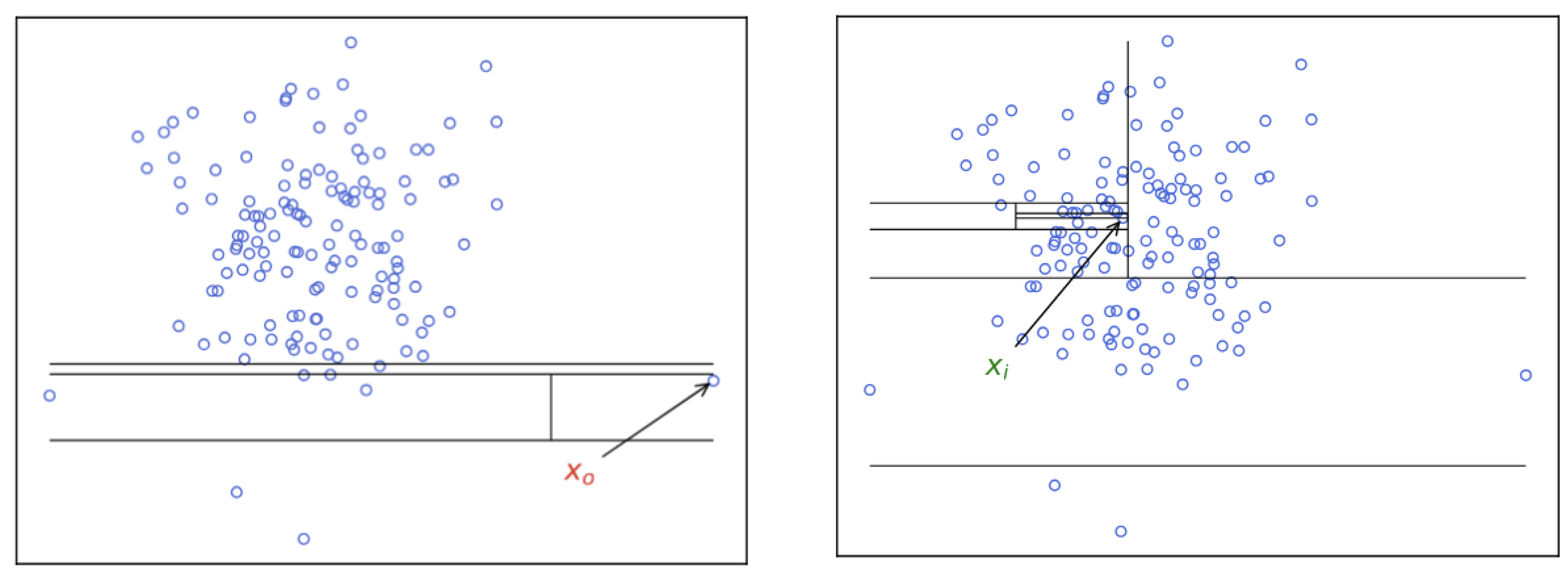
The Isolation Forest (iForest) algorithm is an ensemble-based anomaly detection approach that draws its conceptual foundation from Random Forest methodology [19]. It has been successfully applied to diverse domains, including industrial monitoring [20] and network security [21]. The efficiency of the Isolation Forest algorithm stems from a core principle regarding anomalies: they are both infrequent and significantly different from normal data points. So, when a dataset is recursively partitioned, such anomalies require fewer steps to be isolated from other observations [19]. This process, visualized in Figure 4, demonstrates that an anomalous point ($x_o$), being distant from the dense cluster, is isolated with only four partitions. In contrast, a normal point ($x_i$), deeply embedded within the data, requires ten partitions for full isolation [19,22].

Figure 4. Visual illustration of the core principles of the Isolation Forest algorithm. (Left) An anomalous point ($x_o$), being distant from the main data cloud, is easily isolated in only 4 partitions. (Right) In contrast, a normal inlier ($x_i$), which is deeply embedded within a dense region, requires significantly more partitions (10 in this case) for full isolation. The path length required for this isolation forms the basis for the final anomaly score.

The Isolation Forest algorithm was selected over other common anomaly detection methods due to several key advantages established in the literature. It is both computationally efficient, with linear time complexity, and has a low memory requirement, making it highly scalable for large datasets [19]. This contrasts sharply with distance or density-based alternatives like Local Outlier Factor (LOF), which are known to struggle with the “curse of dimensionality”, where distance metrics become less meaningful in high-dimensional spaces [23]. Furthermore, its ensemble structure lends itself to natural parallel implementation, further enhancing its scalability [19]. This efficiency, combined with its strong performance and low sensitivity to hyperparameters, make it a more robust and practical choice than methods like One-Class Support Vector Machines (SVMs), which require careful tuning of kernel functions and regularization parameters to perform well [24].

2.3. The iForest Algorithm

The Isolation Forest (iForest) algorithm identifies anomalies through a principle of isolation rather than by measuring density or distance. The core concept is that anomalous data points are few and different, making them more susceptible to separation from the majority of the data. The algorithm leverages an ensemble of randomized binary trees, called isolation trees (iTs), to partition the feature space. Anomalies are expected to be isolated in shorter paths within these trees, closer to the root node, as they typically require fewer partitions to be distinguished from normal instances.

For a given dataset, an ensemble of t isolation trees is constructed. Each tree is built on a random subsample of the data, $X^{\prime }$, of size $\psi$. The tree grows by recursively partitioning the subsample. At each node, a feature is randomly selected, and a random split value is chosen between the feature’s minimum and maximum values within the current data subset. This partitioning continues until instances are isolated in individual leaf nodes or a predefined tree depth is met. The use of subsampling without replacement allows the algorithm to achieve linear time complexity and a low memory footprint, making it effective for large high-dimensional datasets.

The degree of anomaly for an observation x is quantified by an anomaly score, $s(x,\psi )$, which is derived from its average path length across all trees in the forest. The path length, $h\left(x\right)$, is the number of edges traversed from the root to a terminal node for instance x. The score is normalized and defined as

$$s(x,\psi )=2^{-\frac{E\left(h\right(x\left)\right)}{c\left(\psi \right)}}$$

(3)

Here, $E\left(h\right(x\left)\right)$ is the average path length of x over the ensemble of trees. The term $c\left(\psi \right)$ is a normalization factor representing the average path length of an unsuccessful search in a Binary Search Tree, given by $c\left(\psi \right)=2H(\psi -1)-\frac{2(\psi -1)}{\psi }$, where $H(·)$ is the harmonic number. Anomaly scores approaching 1 signify clear anomalies as their average path length $E\left(h\right(x\left)\right)$ is very small. Scores much smaller than 0.5 indicate that instances are normal. If the scores for all instances cluster around 0.5, it suggests the dataset does not contain distinct anomalies [20].

This scoring mechanism provides a principled probabilistic assessment of anomaly likelihood that naturally adapts to the underlying data distribution without requiring explicit distributional assumptions. It is important to distinguish the theoretical score defined in Equation (3) from the output of common software libraries. In our implementation, we use the popular Scikit-learn library [25]. Its decision_function method returns an unnormalized score, where negative values indicate anomalies and positive values indicate normal instances; a lower score signifies a higher degree of anomalousness. This difference in score representation has no impact on our proposed thresholding methodology described in the following section. The GMM is tasked with identifying two clusters in the score space regardless of their absolute range. Our procedure correctly identifies the anomalous cluster by selecting the component with the lower mean value, which is fully compatible with Scikit-learn’s scoring convention.

2.4. A Probabilistic Approach to Adaptive Thresholding

The output of the Isolation Forest algorithm is a continuous anomaly score, $s_x$, for each site. While this score provides a relative ranking of anomalousness, a definitive classification of a site as either “normal” or “anomalous” requires the establishment of a decision threshold, $\tau$. The method by which this threshold is determined is a critical, and often overlooked, aspect when using the Isolation Forest. A poorly chosen threshold can either lead to an excess of false alarms or, conversely, allow faulty sites to go undetected.

The most straightforward approach to thresholding is to simply rank all sites by their anomaly score and have a human expert manually select a cutoff. While intuitive, this is subjective, not scalable, and impractical for an automated system. A more systematic approach, common in many implementations, relies on a user-provided hyperparameter known as the contamination ratio. This parameter represents the expected proportion of anomalies in the dataset. The threshold $\tau$ is then set to the score value at the $(1-\mathrm{contamination}\mathrm{ratio})$ quantile of all scores. However, this method suffers from a significant drawback: it requires a priori knowledge of the anomaly rate, which is precisely the information that is unknown in a real-world unsupervised setting. In [21], it was emphasized that providing this information may require a manually labeled dataset, which is a time-consuming and expensive process, especially in big data scenarios. To eliminate the need for such a contamination ratio, recent research has moved towards adaptive methods that use clustering to automatically find a threshold. The core idea is to let the structure of the anomaly scores themselves reveal the boundary between normal and anomalous behavior.

One such method, as shown in [21], combines Isolation Forest with K-Means clustering. In this framework, the one-dimensional set of anomaly scores is partitioned into two clusters ($K=2$) using K-Means. The cluster with fewer instances is then labeled as “anomalous”. This elegantly solves the problem of needing a contamination ratio and avoids the need for other complex parameters, which can degrade performance or cause memory issues on large datasets. The decision boundary is implicitly the one learned by the K-Means algorithm. A more intricate adaptive strategy was proposed in [20], which also uses K-Means as a foundation. This method first clusters the anomaly scores, then calculates a threshold based on the distance between the centroids of the two clusters with the lowest average scores. Critically, their method includes a verification step to ensure that the calculated threshold lies between the bounds of the two clusters. If this verification fails, a fallback mechanism sets the threshold at the boundary of the clusters. This approach is designed to be more flexible and robust by not relying on a single thresholding rule. While these adaptive methods are a major step forward, they both inherit the intrinsic limitations of their K-Means foundation. K-Means is a distance-based algorithm that creates “hard” assignments and performs best on well-separated spherical clusters. If the score distributions for normal and anomalous sites have significant overlap or complex non-spherical shapes, a distance-based partition may not capture the optimal decision boundary.

To address this limitation and create a fully autonomous system, we propose a probabilistic approach that replaces simple quantile-based thresholding with a more statistically robust framework. Our method models the complete set of anomaly scores, $\{s_1,s_2,\dots ,s_M\}$, as a mixture of two Gaussian distributions, ${\mathcal{G}}_{\mathrm{normal}}$ and ${\mathcal{G}}_{\mathrm{anomalous}}$, using a Gaussian Mixture Model (GMM). This provides a flexible “soft” assignment that can gracefully model the often-overlapping score distributions of normal and anomalous populations. The procedure is as follows:

• Fit a Gaussian Mixture Model: A GMM with two components is fitted to the one-dimensional set of all site anomaly scores. The Expectation–Maximization (EM) algorithm determines the optimal parameters for each of the two Gaussian components [26]: the mean (${\mu }_k$), the variance (${\sigma }_k^2$), and the mixture weight (${\pi }_k$), which represents the proportion of data points belonging to component $k\in \{1,2\}$.
• Identify Component Distributions: The two components represent the underlying distributions of normal and anomalous scores. Based on the scoring convention of the Isolation Forest implementation (where lower scores indicate a higher degree of anomaly), the component with the lower mean is designated as the distribution for anomalous scores ($\mathcal{N}({\mu }_{\mathrm{anomalous}},{\sigma }_{\mathrm{anomalous}}^2)$), while the component with the higher mean represents the distribution for normal scores ($\mathcal{N}({\mu }_{\mathrm{normal}},{\sigma }_{\mathrm{normal}}^2)$).
• Derive Probabilistic Threshold: The decision threshold, $\tau$, is set at the score value where an instance has an equal posterior probability of belonging to either component. This is the point where the two weighted probability density functions (PDFs) intersect. The threshold $\tau$ is therefore the value of s that satisfies the following equation:

  $${\pi }_{\mathrm{normal}}·\frac{1}{\sqrt{2\pi {\sigma }_{\mathrm{normal}}^2}}{e}^{-\frac{{(s-{\mu }_{\mathrm{normal}})}^2}{2{\sigma }_{{\mathrm{normal}}^2}}}={\pi }_{\mathrm{anomalous}}·\frac{1}{\sqrt{2\pi {\sigma }_{\mathrm{anomalous}}^2}}{e}^{-\frac{{(s-{\mu }_{\mathrm{anomalous}})}^2}{2{\sigma }_{{\mathrm{anomalous}}^2}}}$$

  (4)
  This equation can be solved numerically to find the optimal decision boundary.
• Final Classification: Any site x with an anomaly score $s_x$ that falls on the anomalous side of the threshold (i.e., $s_x<\tau$) is classified as an anomalous site.

Our proposed GMM-based approach is superior to existing methods for several reasons. Unlike the contamination-based method, it is fully unsupervised and data-driven. Compared to the K-Means-based approaches, it is more statistically robust as it can model overlapping and non-spherical score distributions more effectively. It avoids the potentially brittle “smaller cluster” heuristic of the approach in [21] and the introduction of new tuning parameters (like the ‘alpha’ control parameter in [20]). Most importantly, the threshold is derived from a principled statistical criterion, the point of equal posterior probability, making the final classification more defensible and interpretable. To synthesize the methodological components described above, the complete end-to-end process for our method is formalized in Algorithm 1.

2.5. Theoretical Foundation for Isolation Forest Optimization

2.5.1. Concentration Bound for Anomaly Scores

The practical utility of the Isolation Forest hinges on selecting an appropriate number of trees. An insufficient number yields unstable anomaly scores, while an excess creates unnecessary computational drag. It is therefore essential to provide a theoretical basis for choosing a sufficient number of trees to ensure that the anomaly scores converge, leading to a stable and reliable site ranking. We rigorously establish that the empirical anomaly score $\widehat{s}\left(x\right)$ produced by an Isolation Forest is sharply concentrated around its expected value $\mu \left(x\right)$. Assuming each tree’s contribution is independent and bounded in $[a,b]$, Hoeffding’s inequality yields, for any $ϵ>0$,

$$Pr\left(|\widehat{s}\left(x\right)-\mu \left(x\right)|\ge ϵ\right)\le 2exp\left(-\frac{2N{ϵ}^2}{{(b-a)}^2}\right),$$

(5)

where $\widehat{s}\left(x\right)$ is the score from N trees, $\mu \left(x\right)$ is its expectation, and $ϵ$ is the tolerated deviation. Because the right-hand side decays exponentially in N, the top-k anomaly ranking stabilizes rapidly as more trees are added.

Algorithm 1 KDE–iForest with Probabilistic GMM Thresholding.

1: Input: Measurement sets $D=\{D_1,\dots ,D_M\}$, where $D_x={\left\{y_{x,i}\right\}}_{i=1}^{n_x}$ for each site x, KDE bandwidth h, and a shared grid of B points $Y=\{y_1,\dots ,y_B\}$, Number of trees for Isolation Forest, T.   2: Output: A set of flagged anomalous sites, ${\mathcal{S}}_{\mathrm{issue}}$.   3: for $x=1$ to M do   4:       Compute density estimate ${\widehat{f}}_x\left(y\right)$ for site x; ${\displaystyle {\widehat{f}}_x\left(y\right)\leftarrow \frac{1}{n_{x}h}\sum _{i=1}^{n_x}K\left(\frac{y-y_{x,i}}{h}\right)}$   5:       Form the density feature vector ${\mathit{\varphi }}_x$; ${\mathit{\varphi }}_x\leftarrow {\left[{\widehat{f}}_x\left(y_1\right),{\widehat{f}}_x\left(y_2\right),\dots ,{\widehat{f}}_x\left(y_B\right)\right]}^{\mathsf{T}}$   6: end for   7: Stack all site feature vectors into a single $M\times B$ matrix $\mathbf{\Phi }$: $\mathbf{\Phi }\leftarrow \left[\begin{array}{c}{\mathit{\varphi }}_1^{\mathsf{T}}\\ ⋮\\ {\mathit{\varphi }}_M^{\mathsf{T}}\end{array}\right]$   8: Train an iForest model, ${\mathcal{M}}_{\mathrm{iForest}}$, on the feature matrix $\mathbf{\Phi }$ with T trees.   9: Initialize an empty set of scores, $S_{\mathrm{scores}}\leftarrow \varnothing$. 10: for $x=1$ to M do 11:       Compute the average path length $\mathbb{E}\left[h\left({\mathit{\varphi }}_x\right)\right]$ for vector ${\mathit{\varphi }}_x$ using ${\mathcal{M}}_{\mathrm{iForest}}$. 12:       Calculate the normalization factor $c\left(M\right)=2H(M-1)-{\displaystyle \frac{2(M-1)}{M}}$. 13:       Compute the anomaly score $s_x\leftarrow 2^{-\mathbb{E}\left[h\left({\mathit{\varphi }}_x\right)\right]/c\left(M\right)}$. 14:       Add $s_x$ to $S_{\mathrm{scores}}$. 15: end for 16: Fit a two-component GMM to $S_{\mathrm{scores}}$. 17: Let the fitted components be ${\mathcal{G}}_{\mathrm{normal}}=\mathcal{N}({\mu }_{\mathrm{normal}},{\sigma }_{\mathrm{normal}}^2)$ and ${\mathcal{G}}_{\mathrm{anomalous}}=\mathcal{N}({\mu }_{\mathrm{anomalous}},{\sigma }_{\mathrm{anomalous}}^2)$, with mixture weights ${\pi }_{\mathrm{normal}}$ and ${\pi }_{\mathrm{anomalous}}$. 18: Numerically solve for the threshold $\tau$ that satisfies             ${\pi }_{\mathrm{normal}}·\mathcal{N}\left(\tau \right|{\mu }_{\mathrm{normal}},{\sigma }_{\mathrm{normal}}^2)={\pi }_{\mathrm{anomalous}}·\mathcal{N}\left(\tau \right|{\mu }_{\mathrm{anomalous}},{\sigma }_{\mathrm{anomalous}}^2)$. 19: Initialize an empty set for flagged sites, ${\mathcal{S}}_{\mathrm{issue}}\leftarrow \varnothing$. 20: for $x=1$ to M do 21:       if $s_x<\tau$ then 22:             Add site x to ${\mathcal{S}}_{\mathrm{issue}}$. 23:       end if 24: end for 25: return  ${\mathcal{S}}_{\mathrm{issue}}$

2.5.2. Determining an “Optimal” N

Let $\delta$ be the maximum acceptable probability that the deviation exceeds $ϵ$. Rearranging (5) yields

$$N\ge {\displaystyle \frac{{(b-a)}^2}{2{ϵ}^2}}ln\left({\displaystyle \frac{2}{\delta }}\right).$$

Hence, choosing

$$N^{*}=⌈\frac{{(b-a)}^2}{2{ϵ}^2}ln\left(2/\delta \right)⌉$$

guarantees $Pr\left(\right|\widehat{s}\left(x\right)-\mu \left(x\right)|\ge ϵ)\le \delta$, providing a practical tree count for the desired confidence. Derivation steps are provided in Appendix A.

2.6. Parameter and Hyperparameter Settings

To ensure the reproducibility of our results, this section details the parameter choices for the key components of our proposed framework. The parameters were held constant across all experiments unless otherwise noted.

• KDE Parameters: The fidelity of the feature extraction stage hinges on the choice of the Kernel Density Estimation (KDE) bandwidth, h, which governs the balance between bias and variance in the density estimate. A single fixed bandwidth applied to all sites is suboptimal as it fails to account for the intrinsic variability in the scale and complexity of individual site distributions. To address this, we implemented an adaptive data-driven method to determine the optimal bandwidth for each site individually. This approach ensures that each density feature vector is the most statistically faithful representation of its underlying data, enhancing the reliability of the downstream anomaly detection model. Our method employs a k-fold cross-validation strategy to select the optimal bandwidth for each site from a candidate set of values [27]. For a given site’s measurement data, the dataset is partitioned into k subsets or folds. The KDE model is then trained k times; each time, a different fold is held out for validation while the remaining k-1 folds are used for training. The performance of the model on the held-out fold is quantified by its log-likelihood, a standard measure of goodness-of-fit for density models. This process is repeated for each candidate bandwidth value in a predefined search space. The bandwidth that yields the highest average log-likelihood across all k folds is selected as the optimal choice for that site [28]. For this work, we used 5-fold cross-validation (k = 5) and a search space of 20 logarithmically spaced bandwidth values between 0.01 and 1.0. This procedure replaces a manually tuned hyperparameter with a robust, reproducible, and statistically principled selection process, a critical step for developing an autonomous detection framework. The number of grid points (B) was set to 512, which provides a high-resolution representation of these potentially complex density functions.
• Isolation Forest Parameters: For the anomaly scoring engine, we set the number of trees in the forest, T, to 100. As shown in the original Isolation Forest paper, the algorithm’s performance typically converges well before this point, making 100 trees a robust choice for stable performance [19]. The subsample size, $\psi$, was set to 256, which is also a widely used default that provides high detection performance across a range of datasets by mitigating the effects of swamping and masking [19].
• Contamination Ratio (Not Used for Classification): A standard hyperparameter for many anomaly detection algorithms, including some implementations of Isolation Forest, is the contamination ratio—an estimate of the proportion of outliers in the dataset. While many libraries require this parameter to be set during model initialization (for which we use a default value of 0.1), its typical function is to derive a decision threshold directly from the anomaly scores. A primary advantage of our framework is that our thresholding method completely replaces this step. Our approach autonomously computes a statistically derived threshold from the structure of the scores themselves. Consequently, the initial contamination ratio setting is only a formality for the software library and has no influence on the final classification, removing the requirement for users to supply a meaningful number that is rarely known in a true unsupervised setting.
• Gaussian Mixture Model (GMM) Parameters: For our probabilistic thresholding step, the number of components for the GMM was set to $K=2$. This is a natural choice for our problem as we are explicitly modeling the anomaly scores as a mixture of two underlying distributions: one for the “normal” sites and one for the “anomalous” sites.

2.7. A Holistic Alternative to Rule-Based Flagging Systems

A common strategy for automating the detection of site-to-site variation (SSV) is the use of rule-based flagging systems that emulate manual inspection [1]. These systems attempt to identify issue sites by programmatically evaluating a set of disjointed statistical criteria, such as deviations in location, dispersion, skewness, or outlier rates. While an improvement over manual analysis, this piecemeal approach has noted limitations. Its reliance on single-point statistics may not accurately represent the full distribution, rendering it less effective at identifying subtle issues that manifest as complex distortions in the distribution’s overall shape.

Our proposed framework overcomes these limitations by adopting a fundamentally different philosophy: it transforms the problem from a series of independent statistical checks into a single holistic pattern recognition task. Instead of calculating separate metrics, our method first converts the entire measurement distribution from each site into a high-dimensional feature vector using Kernel Density Estimation (KDE). This vector serves as a high-fidelity “fingerprint” that inherently captures a rich set of statistical properties simultaneously. A change in location results in a lateral shift of the entire KDE vector, while a change in dispersion alters its fundamental shape. Higher-order properties like skewness, kurtosis, and even complex features like multimodality, which rule-based systems cannot easily assess, are all intrinsically encoded in the vector’s structure. Crucially, the task of assigning importance to these different types of variation is not handled by heuristic rules but is implicitly managed by the Isolation Forest algorithm. By treating each site’s distributional fingerprint as a point in a high-dimensional space, the algorithm automatically learns which differences are most effective for separating a site from its peers. It implicitly determines whether a shift in mean, a change in variance, or a complex change in shape is the most “isolating” characteristic for any given dataset, thereby eliminating the need for manual interpretation or the weighting of separate flags. This approach enables the detection of complex variations that prior methods may overlook, providing a more robust and comprehensive solution for automated SSV detection.

3. Case Study: Semiconductor Multisite Testing and Experimental Results

To demonstrate the efficacy of our method in a real-world setting, we apply it to semiconductor multisite testing data drawn from a production analog/mixed-signal ATE. As noted in Section 1, massive multisite testing, where tens to hundreds of devices under test (DUTs) are probed in parallel, is critical for high-throughput and cost-effective IC validation, but it also exacerbates site-to-site variation (SSV).

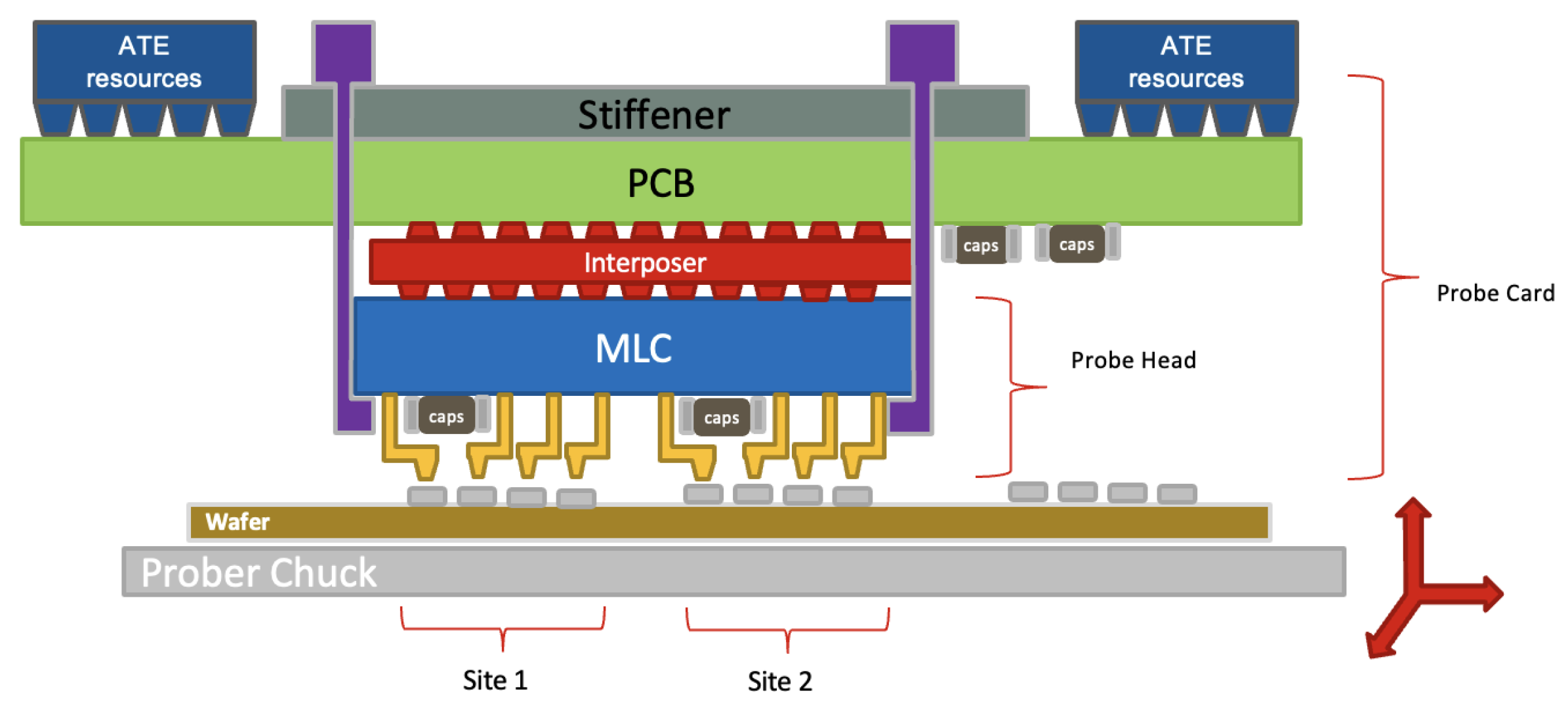
Figure 5 provides a schematic of a typical Automated Test Equipment (ATE) setup configured for multisite testing. During operation, the semiconductor wafer, populated with numerous devices under test (DUTs), is positioned on a prober chuck, which aligns the DUTs for reliable contact with the probe head. Serving as the critical interface, the probe card is responsible for distributing all the necessary signals—including power, timing, and test stimuli—from the ATE to the individual test sites. It also integrates the essential multisite measurement (MSM) hardware. While the diagram illustrates a two-site configuration for clarity, these production test cells are commonly scaled to include dozens or even hundreds of parallel sites to maximize throughput. While this parallelism dramatically reduces per-unit test time and cost, it also induces subtle systematic biases: as the site count grows, variations in trace lengths, contact resistances, thermal gradients, crosstalk, and EMI induce measurement offsets that no longer reflect true device performance.

Figure 5. A section of an Automated Test Equipment (ATE) setup used for multisite testing.

Given that these sources of SSV are inherently complex, high-parallelism ATE hardware, relying solely on improved hardware design or periodic calibration, is often insufficient. An effective strategy must therefore include a robust data-driven monitoring framework that can automatically analyze measurement data as it is collected. To this end, we propose an operational workflow that integrates our detection method directly into the IC test environment. This process operates by analyzing the measurement data from all the test sites in a given batch (e.g., a wafer or lot) simultaneously, identifying any sites whose distributional profiles are anomalous relative to the majority of their peers in that same batch. Figure 6 illustrates how our approach is integrated into an automated process for multisite testing in IC manufacturing. In what follows, we first describe the dataset and test specifications, then present quantitative results comparing our KDE–Isolation Forest detector against state-of-the-art SSV methods (cross-correlation and QQ fitting).

Figure 6. An overview of our proposed model. The input dataset is first pre-processed, and then the relevant features from that dataset are provided as input to the Isolation Forest model. The anomaly scores predicted by Isolation Forest are then provided as input to the GMM model, which partitions the anomaly scores to predict k labels.

3.1. Results on Industry Multi-Site Volume Silicon Measurement Test Data

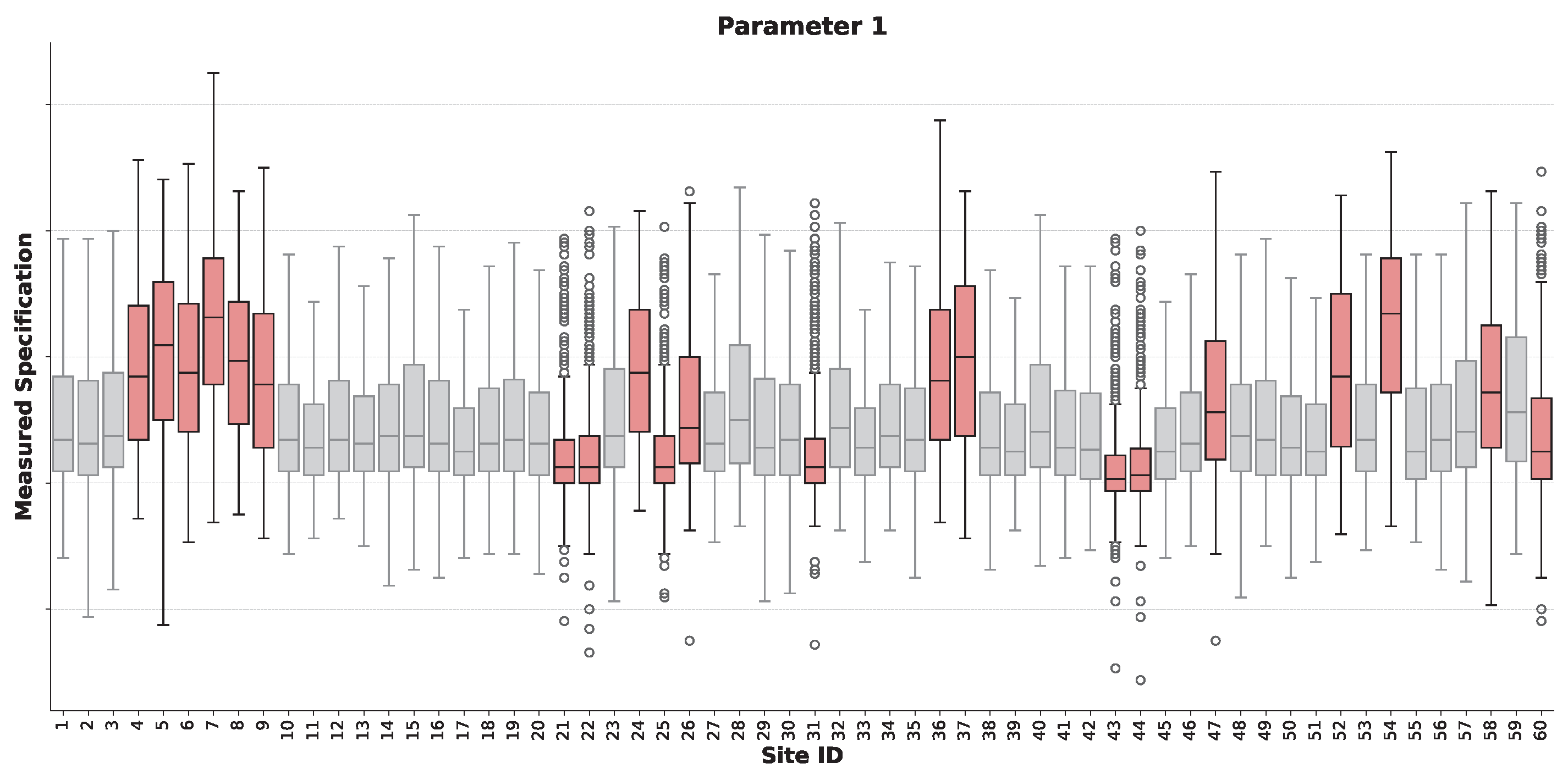
We validate our approach using ATE volume production data sourced from Texas Instruments, focusing on the key performance metrics of a device. Due to proprietary constraints, the exact site count will remain undisclosed. Similarly, actual measurement ranges are withheld to preserve data confidentiality. Only test results from 60 selected sites are presented. The test measurement data are usually visualized via boxplots, and we follow the same approach here to display the results of the algorithm. We take a look at two test parameters from real test data. Since we cannot reveal the parameters’ names for confidentiality reasons, we call the parameters parameter 1 and parameter 2. Parameter 1 is representative of real test data with high variance, while parameter 2 is representative of test data with low variance.

We first present the analysis for parameter 1. Figure 7 presents the boxplot validation for this parameter, with the corresponding anomaly scores shown in Figure 8. The sites flagged as anomalous, highlighted in red in the boxplot, display a variety of failure signatures. As explained in Section 2.7, these flagged sites are characterized by distinct statistical deviations from the nominal population. These deviations can pertain to measures of central tendency, with some anomalous sites—such as sites 4–8 and 35–37—exhibiting a significant upward shift in their median value. In other cases, the deviation relates to measurement dispersion. This can manifest as a markedly larger interquartile range, indicating increased variance, or as a significantly compressed interquartile range, as seen in sites 24, 28, and 43, which suggests an abnormally low measurement variance. A further characteristic of identified sites, like site 22, is the production of a substantially greater quantity of outlier measurements.

Figure 7. Boxplot validation for parameter 1 from industrial data. Sites flagged as anomalous by our framework are highlighted in red. These sites exhibit diverse failure modes, including shifts in median, increased variance (IQR), and higher outlier counts.

Figure 8. Anomaly scores for each site corresponding to the parameter 1 data. The decision boundary derived by the GMM is shown as a dashed line. Sites with scores exceeding this threshold are classified as anomalous.

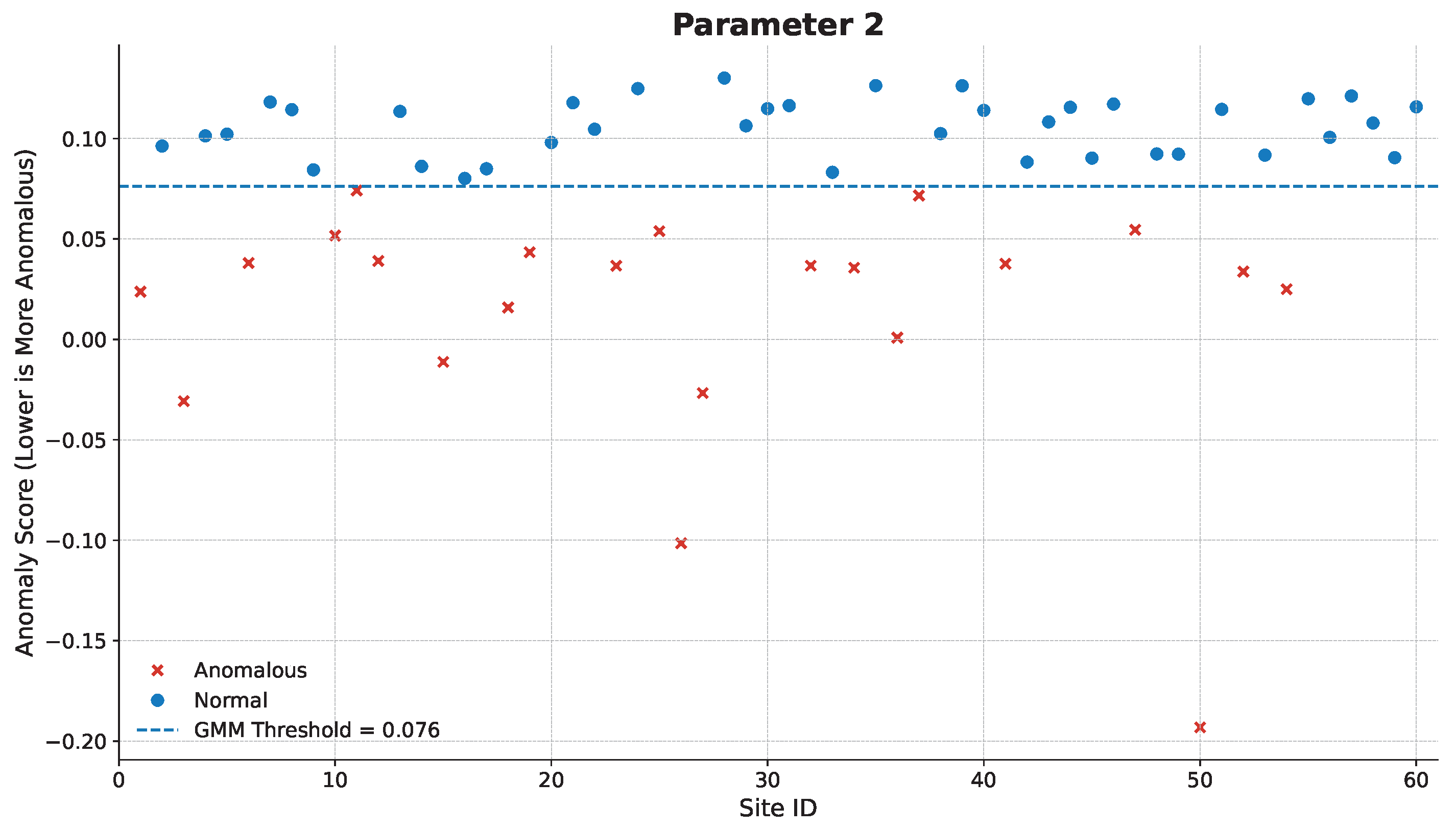
The quantitative basis for this classification is detailed in Figure 8, which plots the anomaly score for each site. The decision boundary, derived automatically by our GMM-based method, is shown as a dashed line. Sites with scores exceeding this threshold are classified as anomalous, aligning with the qualitative deviations observed in the boxplots. This result demonstrates that the method can identify sites with fundamentally different distributional characteristics, distinguishing it from a simple univariate filter.

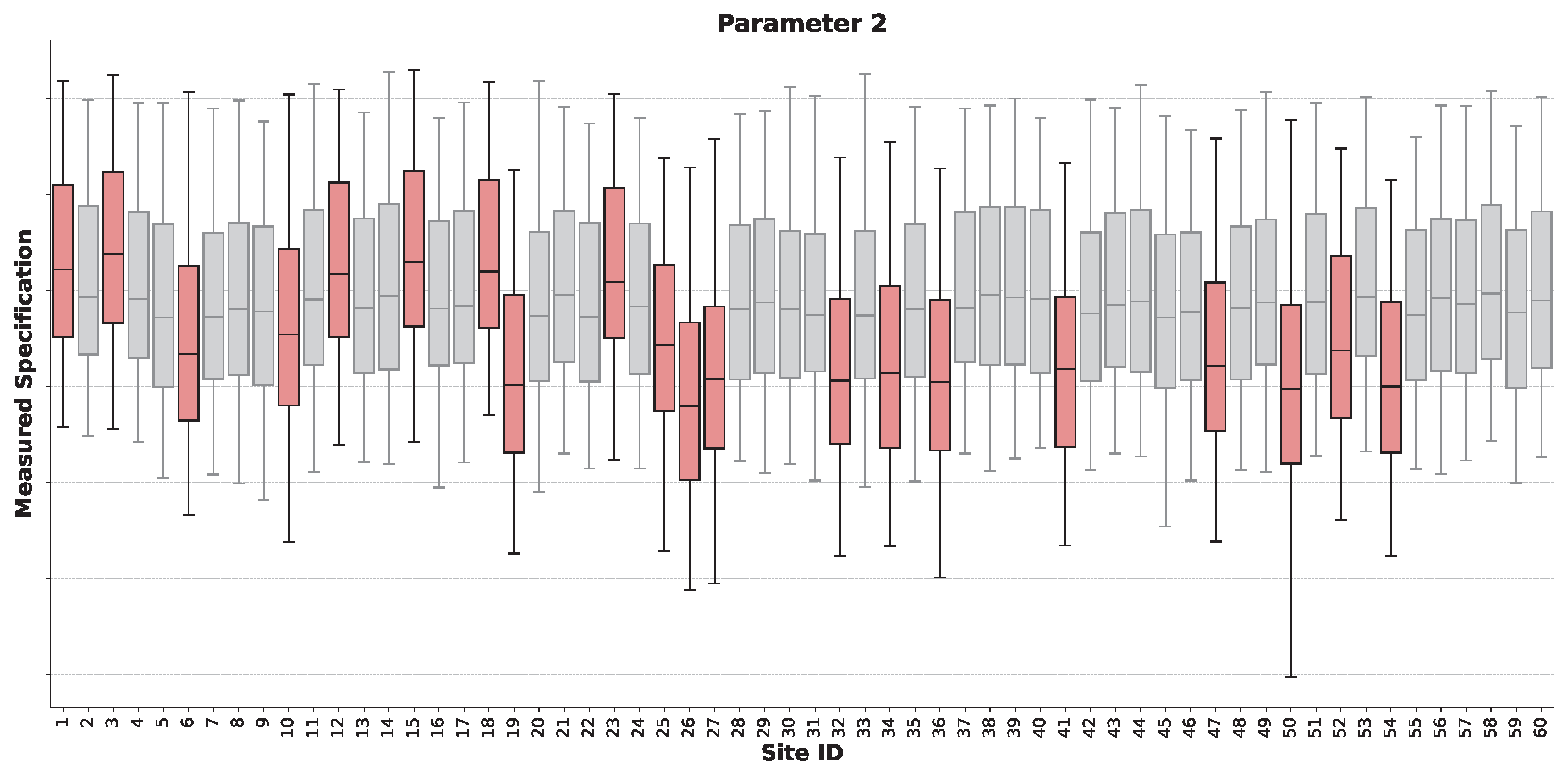
Next, we present the results for parameter 2. The validation boxplot and corresponding anomaly scores are shown in Figure 9 and Figure 10, respectively. In this case, the analysis highlights a different more consistent failure signature. The vast majority of the sites flagged as anomalous by our framework are characterized by a significant downward shift in their median value, indicating a systematic location bias at these sites. While some of these flagged sites also exhibit a concurrent increase in dispersion (a larger IQR), the primary distinguishing feature is the strong deviation in central tendency.

Figure 9. Boxplot validation for parameter 2. The sites flagged by the framework (highlighted in red) consistently show a systematic downward shift in their median value, indicating a location-based anomaly.

Figure 10. Anomaly scores for the parameter 2 data. The GMM-derived threshold correctly separates the systematically shifted sites from the nominal population.

This result, when contrasted with the analysis of parameter 1, powerfully illustrates the adaptability of our method. While the previous case identified sites based primarily on their outlier and variance characteristics, here the framework has correctly identified sites based on a severe location shift. This demonstrates that the same unsupervised pipeline can effectively detect fundamentally different types of site-to-site variation without requiring parameter retuning or algorithm changes, a key advantage over methods tailored to a single statistical deviation.

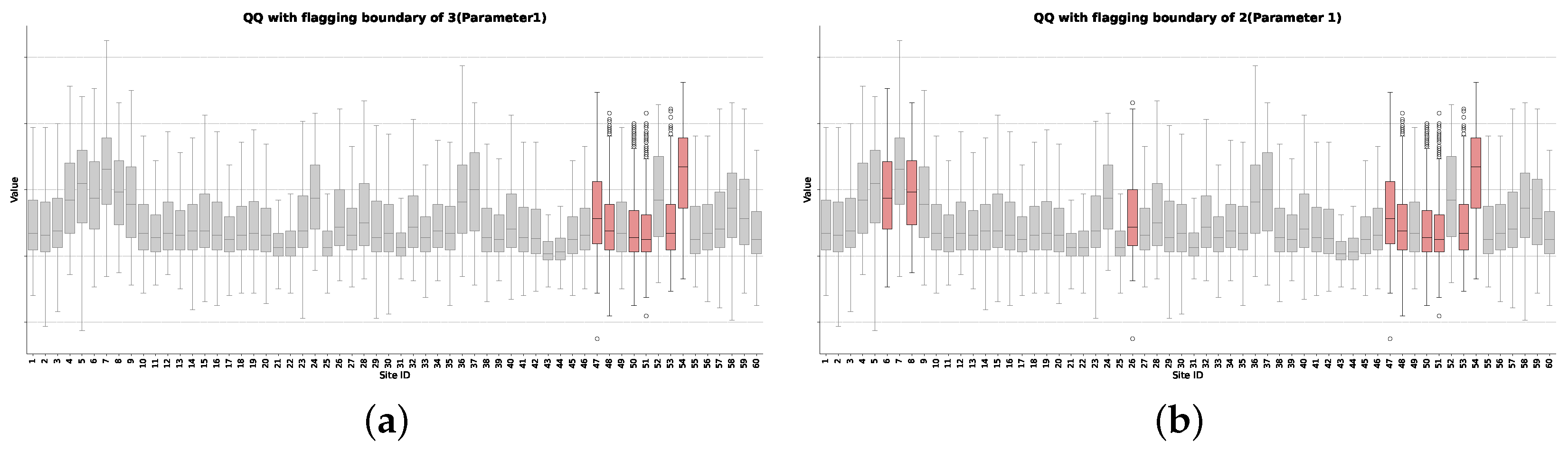
To contrast our framework with prior approaches, we apply the QQ-based detection method to the parameter 1 dataset, with the results shown in Figure 11. The analysis demonstrates a critical weakness of the QQ method: its performance is highly sensitive to the choice of a manually tuned flagging boundary, leading to a trade-off between false negatives and false positives.

Figure 11. Comparison of the QQ-based detection method on parameter 1 data using different flagging boundaries. (a) With a boundary of 3, the method fails to flag some anomalous sites (shown in red). (b) Lowering the boundary to 2 flags some more sites but still leaves some obvious issue sites.

When a flagging boundary of 3 is used (Figure 11a), the method correctly identifies some of the anomalous sites. However, it fails to flag other sites that are obvious problematic sites. In an attempt to correct this, the boundary can be loosened to 2 (Figure 11b). While this successfully flags new issue sites, it still leaves some obvious issue sites undetected. This dilemma highlights the unreliability of the method: there is no single threshold that provides a correct classification. Such sensitivity to a non-intuitive parameter poses a significant operational risk as it could lead engineers to either miss real defects or halt production for non-existent issues. The cross-correlation method [7] suffers from a similar dependency on its user-defined significance level ($\alpha$), and a detailed comparison of these methods is presented in Table 1 in the Discussion section.

Table 1. Comparison of our proposed framework with prior approaches.

Parameters	QQ Method	Cross-Correlation (CC) Method	Our Proposed Method (KDE–iForest–GMM)
Detection Capability	Captures differences in scale and gain, primarily in a linear fashion.	Compares distributional shapes but relies on correct estimation of a reference site.	Captures the entire distributional shape, including location, scale, skewness, kurtosis, and multimodality.
Application Scope	Best suited for distributions that are Gaussian or symmetric.	Can be applied to any measured specification irrespective of distribution.	Fully non-parametric and distribution-agnostic.
Flagging Boundary	No automated boundary presented; relies on visual inspection.	A boundary is derived based on a user-chosen significance level ($\alpha$).	Fully automated and adaptive, eliminating the need for user-defined parameters.

3.2. Hyperparameter Sensitivity Analysis: Invariance to the Contamination Ratio

The robustness of the proposed framework was evaluated by analyzing its sensitivity to the initial ‘contamination’ setting. This analysis, performed on the industrial dataset, validates its primary advantage over standard iForest implementations, which is the elimination of the need for a user-defined anomaly proportion. For these tests, other parameters were held at their default values, as described in Section 2.6.

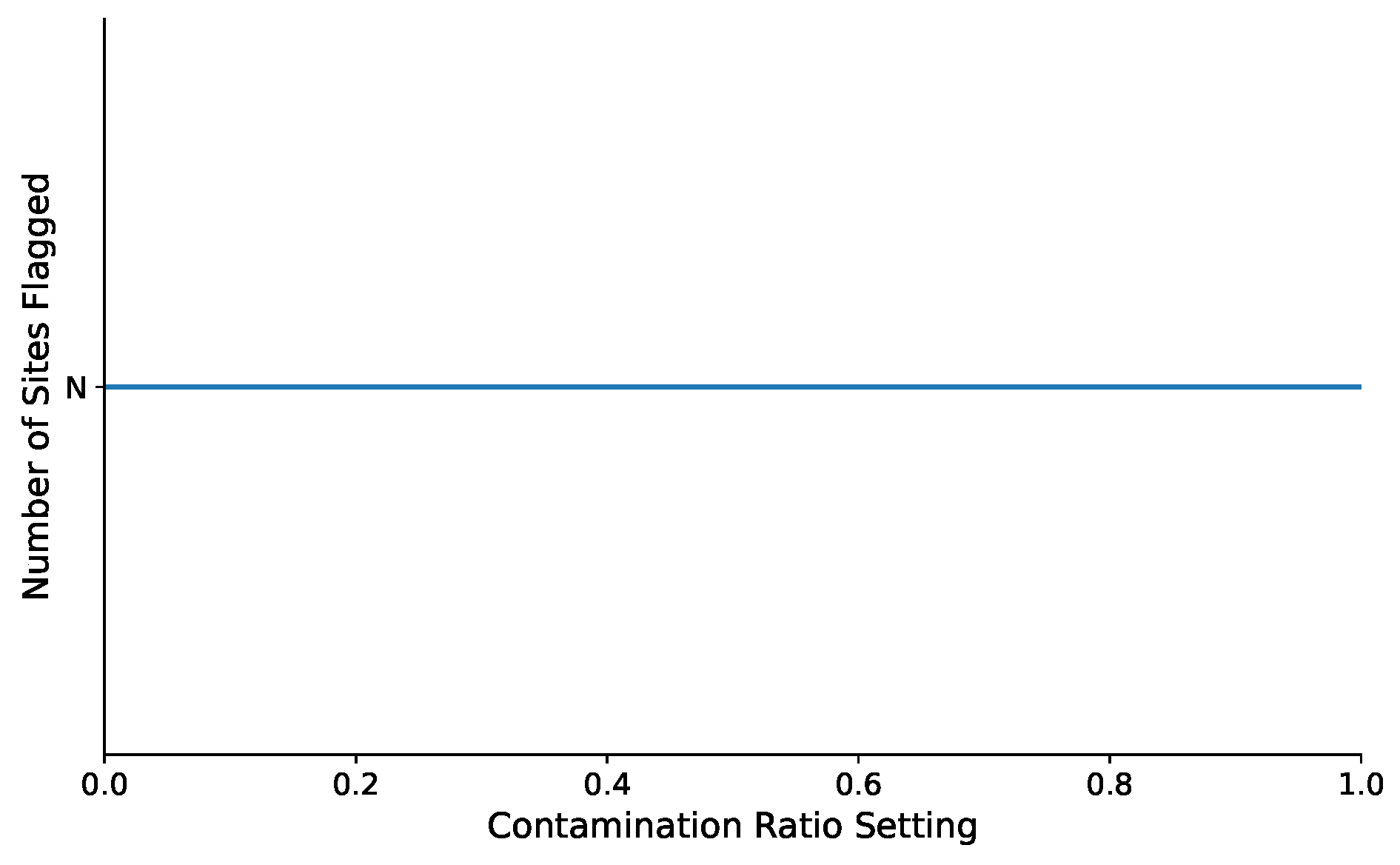
A significant result of this analysis is shown in Figure 12. This experiment contrasts the number of anomalies detected by our proposed method with a standard iForest implementation that uses the ‘contamination’ ratio to set its decision threshold. The number of anomalies, N, detected by our framework remains perfectly stable regardless of the initial ‘contamination’ setting. This is because our GMM-based thresholding step is entirely data-driven, discovering the structure of the scores autonomously and rendering the initial ‘contamination’ parameter irrelevant to the final classification. We manually verify that all the flagged sites were actual issue sites. This experiment provides definitive proof that our method successfully eliminates one of the most problematic and subjective hyperparameters in anomaly detection, reinforcing its suitability for true unsupervised deployment.

Figure 12. Performance comparison as the contamination ratio is varied, demonstrating our framework’s invariance compared to the high sensitivity of a standard iForest implementation.

3.3. Path Length Convergence on Industrial Data

3.3.1. Validating the Core Isolation Principle

A crucial step in deploying any machine learning framework in a high-stakes industrial setting is to move beyond a “black-box” application and provide transparency regarding the algorithm’s decision-making process. To achieve this, we first validate the core theoretical principle of the Isolation Forest algorithm, that anomalies are inherently more susceptible to isolation than normal instances, directly on our industrial dataset. The original authors demonstrated that, because anomalous points are “few and different,” they are consistently isolated in fewer partitioning steps within a random tree structure. Our goal here is to empirically reproduce this finding, thereby building confidence in the fundamental mechanism of our chosen methodology.

To conduct this analysis, we use the final anomaly score for each test site for parameter 1 in the experiment from Section 3.1. From this ranked list, we selected the two most extreme examples: the site with the highest anomaly score (the most anomalous site, denoted $x_o$) and the site with the lowest anomaly score (the most normal site, denoted $x_i$).

3.3.2. Interpretation of Convergence Behavior

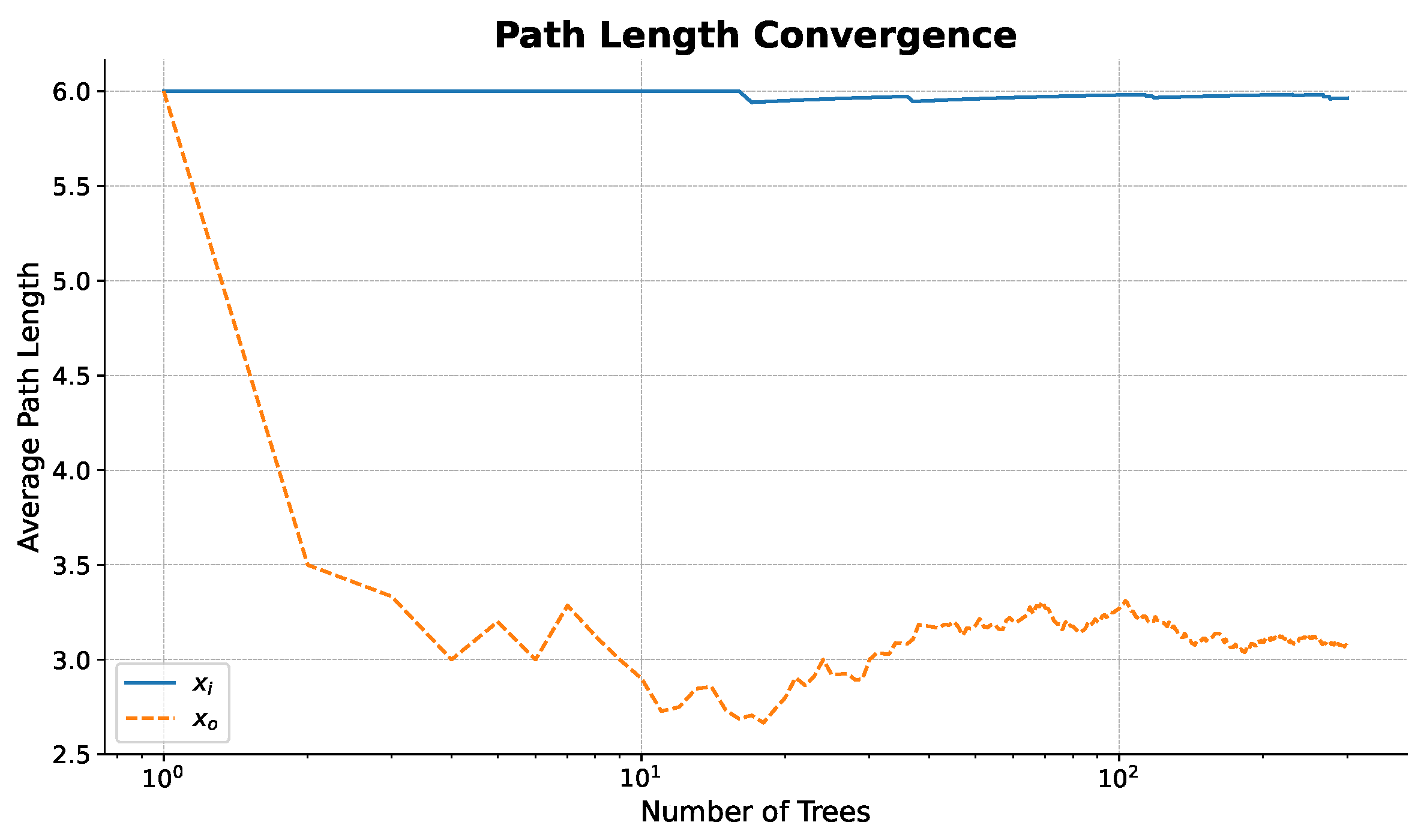
Figure 13 plots the average path length required to isolate each of these two sites as a function of the number of trees in the ensemble. The behavior of each curve is highly informative. The path length for the most normal site, $x_i$, remains consistently high and stable across the ensemble. This indicates that the site is deeply embedded within the dense central cluster of the data distribution, requiring a large number of random partitions to be successfully singled out.

Figure 13. Average path length convergence for the most normal site ($x_i$) and the most anomalous site ($x_o$) from the Texas Instruments dataset. The anomalous site consistently requires a shorter path length to be isolated as the number of trees in the forest increases, validating the core principle of the Isolation Forest algorithm on real-world industrial data.

In stark contrast, the path length for the most anomalous site, $x_o$, is significantly shorter. This empirically confirms that the site’s feature vector resides in a sparse region of the feature space, making it easy to separate from the majority of other sites with very few partitions. As the number of trees in the ensemble increases from one to one thousand, both path lengths converge, demonstrating the stability of this measurement and confirming that the result is not an artifact of a single random tree but a persistent structural property of the data. The wide and consistent gap between the two curves represents a clear separation margin, which is precisely what the Isolation Forest leverages to assign a high anomaly score to site $x_o$ and a low score to site $x_i$.

3.4. Validation of the Assumptions of the Algorithm Through Sensitivity Analysis on Synthetic Datasets with Varying Anomaly Characteristics

To systematically validate the core assumptions of the framework and characterize its performance under controlled conditions, we conducted a comprehensive analysis using synthetic datasets. This validation was designed to test the framework’s ability to detect three distinct and realistic types of anomalies: shifts in location (mean), shifts in scale (variance), and changes in the underlying distribution shape (bimodality). By generating datasets with known ground truth, we could quantitatively assess the algorithm’s accuracy, its sensitivity to key data characteristics, and the validity of its underlying isolation principle.

The synthetic data generation process began with establishing a nominal population of healthy sites, where measurements for each site were drawn from a Gaussian distribution with minor random variations in their mean and standard deviation to simulate a realistic ensemble. Against this baseline, three distinct classes of anomalies were introduced. First, to simulate a systematic offset or bias, a location shift anomaly was modeled by significantly displacing the mean of the generating Gaussian distribution, a behavior consistent with observations in the industrial data. Second, to represent changes in measurement precision or noise, a scale shift anomaly was created by substantially increasing the standard deviation of the distribution, reflecting another common failure mode observed in production testing. Finally, to challenge the framework with complex deviations that would confound methods reliant on simple statistics, a distribution shape anomaly was modeled using a bimodal Gaussian mixture. This anomaly type was chosen specifically to verify that our holistic density-based approach can detect distortions that are not captured by first- or second-order moments alone.

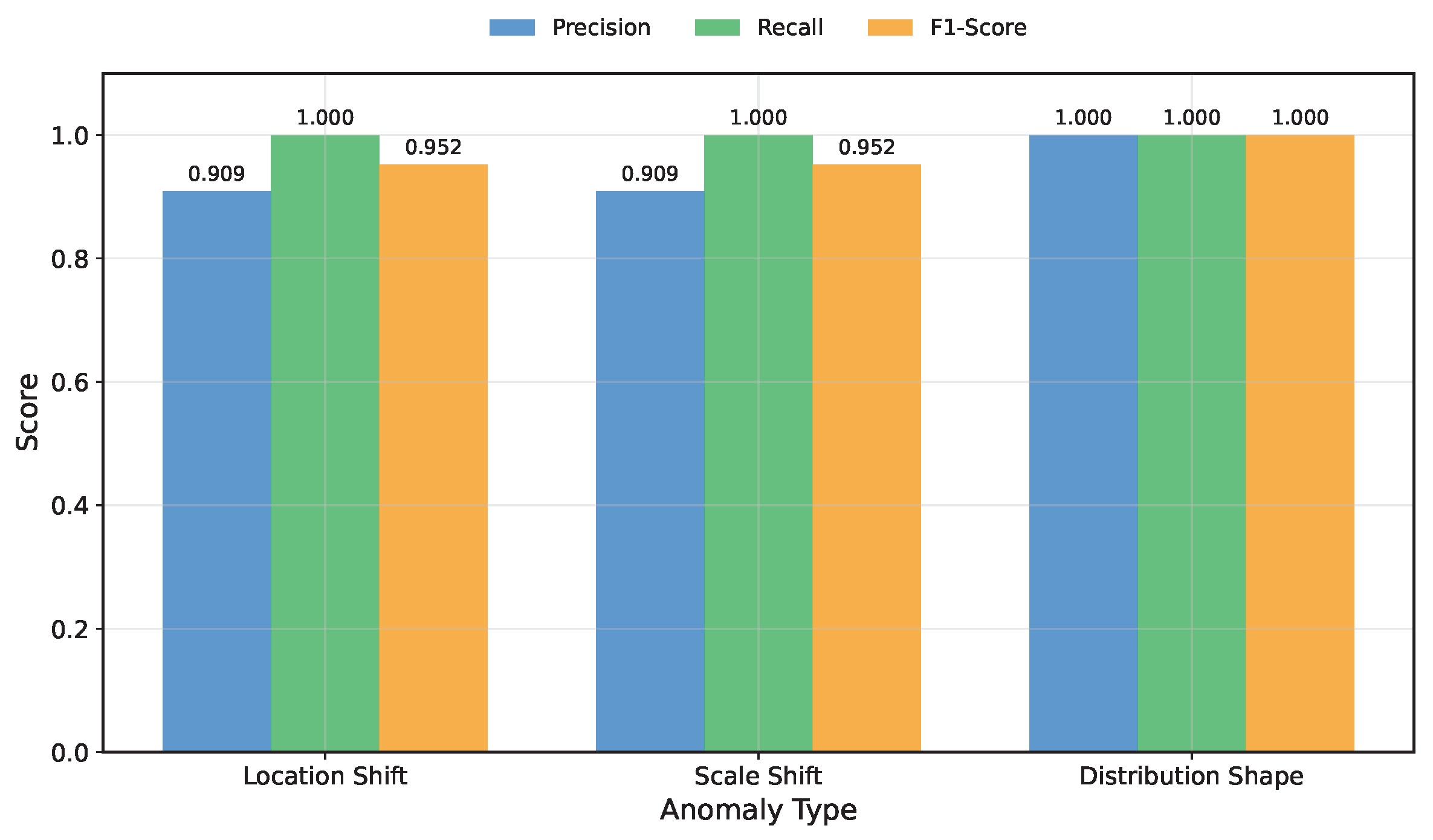
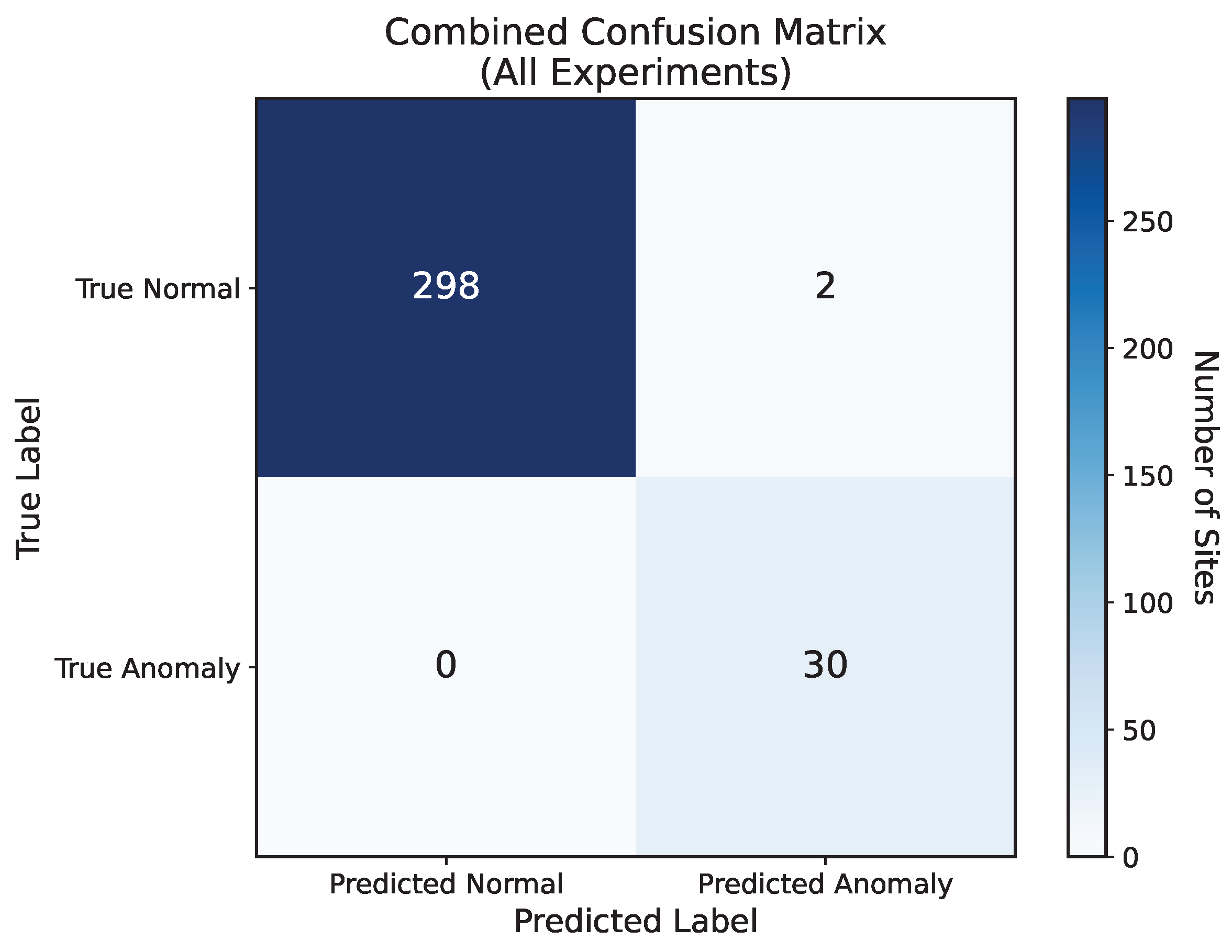
The baseline performance of the framework on these synthetic anomalies was exceptionally strong. Across all three anomaly categories, the method achieved near-perfect detection, with F1-scores of 0.952 for both location and scale shifts and a perfect 1.000 for distribution shape anomalies (Figure 14). A confusion matrix aggregated from all the experiments confirms the high classification accuracy, with the framework correctly identifying 30 of 30 anomalous sites while misclassifying only 2 of 300 normal sites (Figure 15). This demonstrates the method’s fundamental capability to identify a diverse range of distributional deviations.

Figure 14. Quantitative performance metrics for detecting three distinct anomaly types on synthetic data. The framework achieves high precision, recall, and F1-scores across all categories, demonstrating its effectiveness.

Figure 15. Aggregated confusion matrix from all synthetic data experiments. The results show high overall accuracy, with 30 true anomalies correctly identified and only 2 normal sites misclassified.

We further validated the core mechanism of the Isolation Forest on this synthetic data. The results show that, for all three anomaly types, the average path length required to isolate an anomalous site was consistently and significantly shorter than that required for a normal site (Figure 16). This finding empirically confirms that the algorithm’s central assumption, that anomalous points are easier to isolate, holds true for the distributional fingerprints generated by our KDE front-end, providing a transparent validation of the model’s decision-making process.

Figure 16. Average path length convergence for normal and anomalous sites on synthetic data. For all three anomaly types, the anomalous site (red) is consistently isolated with a shorter path length than the normal site (blue), validating the core principle of the Isolation Forest algorithm. The dashed lines indicate the point of convergence.

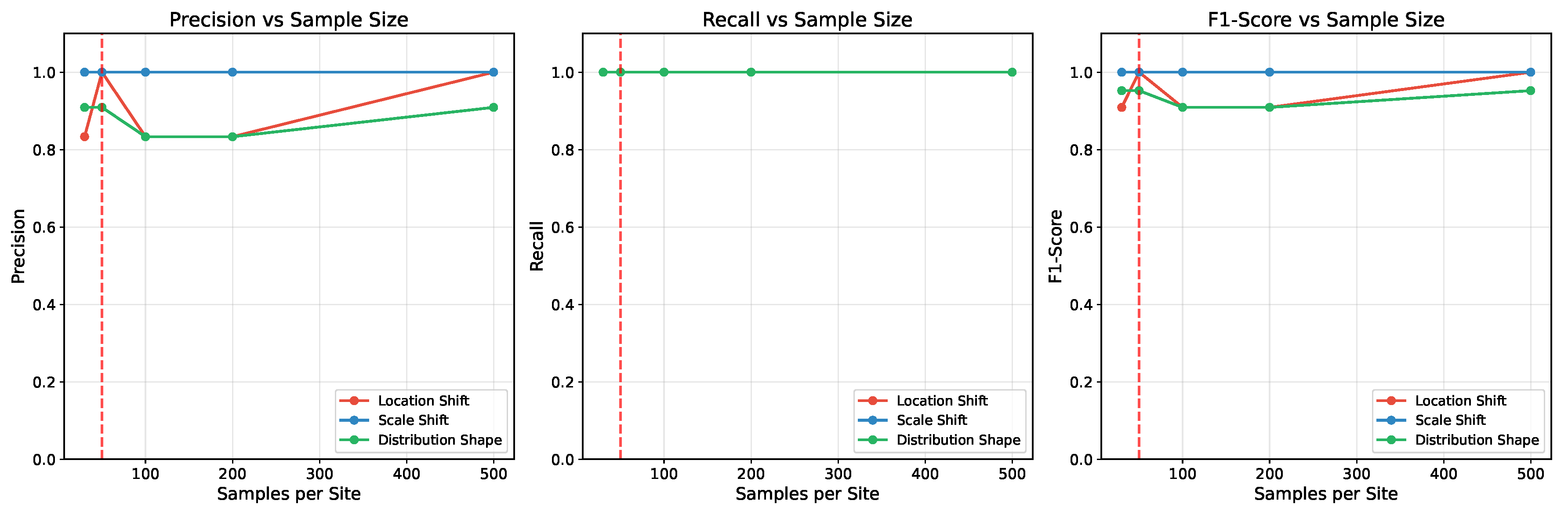
A key aspect of this validation was to understand the framework’s limitations through sensitivity analysis. First, we evaluated its performance as a function of the number of measurement samples available per site (Figure 17). The results highlight the method’s sample efficiency. The performance was robust even with limited data, achieving high F1-scores with as few as 50 samples per site and stabilizing as the sample count increased. This confirms that the KDE feature extraction creates a stable distributional representation from a modest number of samples, a critical requirement for many practical applications.

Figure 17. Framework performance as a function of the number of samples per site. The method demonstrates high sample efficiency, achieving robust F1-scores with as few as 50 samples per site (vertical dashed line). For the middle plot: The blue, red and green lines overlap but only green is shown for simplicity.

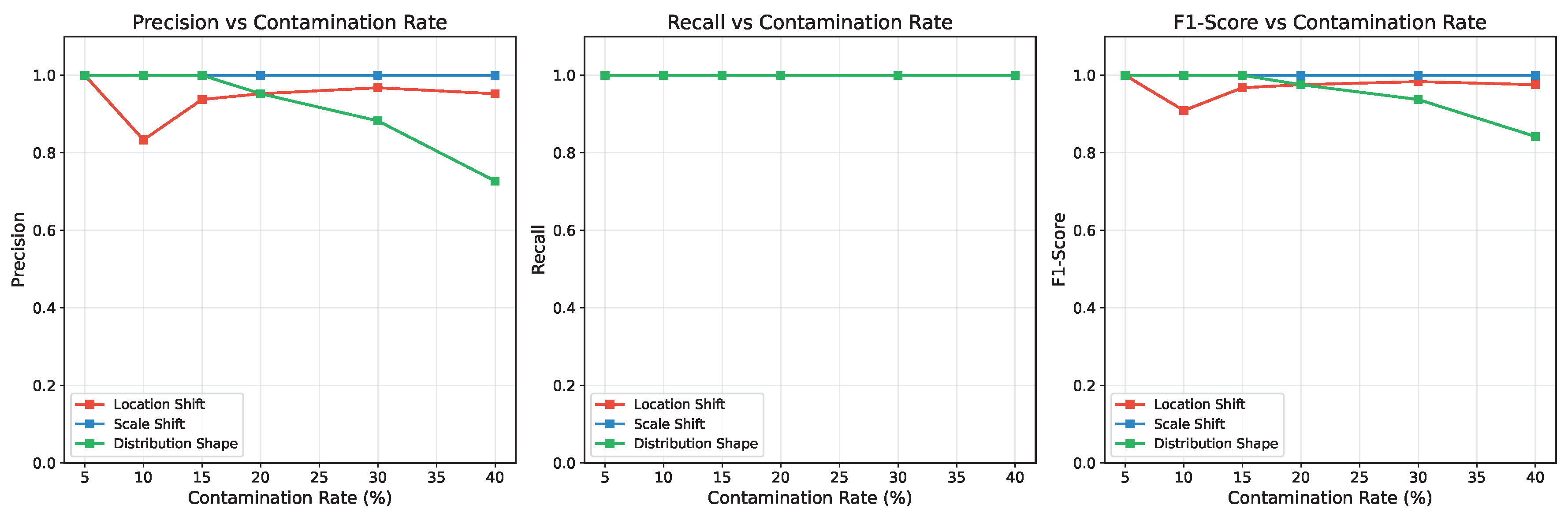
Second, we assessed the framework’s robustness to the contamination rate, which is the proportion of anomalous sites within the dataset (Figure 18). The model maintained excellent performance for scale-shift anomalies even at high contamination levels. For location-shift and distribution-shape anomalies, the framework showed high precision and recall for contamination rates up to approximately 35%, after which its performance began to degrade slightly. Together, these synthetic tests provide a rigorous quantitative confirmation of the framework’s accuracy, robustness, and theoretical underpinnings.

Figure 18. Framework performance as a function of the contamination rate. For the middle plot: The blue, red and green lines overlap but only green is shown for simplicity.

4. Discussion

The experimental results presented in Section 3 demonstrate that the proposed KDE–iForest–GMM framework is a highly effective tool for detecting diverse forms of site-to-site variation in industrial datasets. This discussion interprets the findings within the context of prior approaches and considers their practical implications.

4.1. Interpretation of Key Findings

The framework successfully identified multiple distinct failure signatures in the industrial data. For parameter 1, it flagged sites characterized by increased dispersion and outlier rates, while, for parameter 2, it detected sites with a clear systematic shift in location. This confirms that the holistic distributional approach is not limited to a single type of anomaly but is adaptable enough to capture a wide range of real-world hardware issues. The framework’s robustness was confirmed through hyperparameter sensitivity analysis. The path length convergence analysis further provides empirical evidence that the algorithm’s core isolation principle is effective on complex industrial data.

4.2. Comparison with Prior Methods

The success of our framework can be understood by comparing it to prior methods, as summarized in Table 1. Unlike the Quantile–Quantile (QQ) fitting approach, which is best suited for symmetric distributions [7], our non-parametric method is agnostic to the data’s underlying distribution. This was critical for correctly identifying anomalies in the skewed INL data.

More significantly, our method improves upon both the QQ and cross-correlation (CC) methods by introducing a fully automated and statistically principled thresholding mechanism. The CC method requires a user to choose a significance level ($\alpha$) to set its flagging boundary, a choice that can be subjective and lead to inconsistent results. Our GMM-based approach, in contrast, is entirely data-driven, removing this manual step and enhancing the system’s autonomy and reproducibility.

4.3. Practical Implications

For a production test environment, the implications of this work are significant. An automated and reliable SSV detection system can lead to faster diagnosis of hardware failures (e.g., faulty probe cards or tester channels), reducing equipment downtime. By accurately identifying issue sites, it prevents yield loss that occurs when good devices are incorrectly failed and reduces the risk of test escapes, thereby improving overall product quality and reliability. For this work, we classify the sites as either issue sites or not using the GMM. One practical consideration involves exploring more flexible mixture models beyond two Gaussian distributions. For instance, in [8], there is a discussion on marginal issue sites (those sites that lie between anomalous and normal sites and require monitoring). This can easily be characterized.

4.4. Limitations

While the proposed framework is robust, we acknowledge its limitations. The performance of the KDE feature extraction stage is dependent on having a sufficient number of samples per site (e.g., >30) to form a meaningful density estimate. The framework’s performance on extremely sparse datasets was not evaluated. However, in the application domains we generalize to, collecting tens to hundreds of measurements per site is routine, making this requirement easily met in practice. Additionally, while our method detects anomalous sites, it does not, in its current form, perform root-cause analysis to identify the specific hardware issue responsible for the variation.

4.5. Computational Complexity and Scalability

The practical utility of the proposed framework in an industrial setting depends on its computational efficiency and ability to scale to large datasets. The overall complexity is a composite of its three main stages: KDE-based feature extraction, Isolation Forest anomaly scoring, and GMM-based thresholding. The most computationally intensive stage is the initial feature extraction. For a dataset with M sites, each containing n measurement samples, the Kernel Density Estimation (KDE) is evaluated on a grid of B points. The complexity of this stage is therefore $\mathcal{O}(M·n·B)$.

The second stage involves the Isolation Forest algorithm. The complexity of training an ensemble of T trees on the M feature vectors, using a subsample size of $\psi$, is $\mathcal{O}(T·\psi log\psi )$. Subsequently, scoring each of the M site vectors has a complexity of $\mathcal{O}(M·Tlog\psi )$. Given that $\psi$ and T are fixed hyperparameters that do not grow with the input data size, the complexity of this stage is effectively linear with respect to the number of sites, $\mathcal{O}\left(M\right)$.

Finally, GMM-based thresholding is performed on the M one-dimensional anomaly scores. The Expectation–Maximization algorithm for a GMM with K components running for I iterations has a complexity of $\mathcal{O}(I·M·K)$, which is also linear in the number of sites, $\mathcal{O}\left(M\right)$.

The framework’s scalability is significantly enhanced by its high potential for parallelization. The KDE feature vector for each of the M sites can be computed independently and in parallel. Similarly, the construction of each of the T trees in the Isolation Forest is an independent process that can be distributed across multiple CPU cores. This parallel nature ensures that the framework can be efficiently scaled to handle the large volumes of data characteristic of modern distributed measurement networks, making it a viable solution for high-throughput industrial applications.

5. Generalization to Other Distributed Measurement Networks

While this work has focused on semiconductor testing as a primary case study, the fundamental principles of our framework are not limited to this domain. The method’s strength lies in its abstraction: it operates on collections of measurements grouped by a source (a “site”) and identifies when one source’s distributional “fingerprint” deviates from its peers. This concept of site-to-site variation is a universal challenge in any large-scale distributed sensing or measurement system. Here, we outline how the framework can be directly adapted to other critical domains by citing established challenges and methodologies in each field.

5.1. Environmental Sensor Grids

Large-scale environmental monitoring networks, which deploy hundreds of low-cost sensors for metrics like air quality (PM_2.5) or temperature, are a natural application. These networks are notoriously susceptible to data quality issues that mirror SSV.

• Site: Each individual sensor node in the grid.
• Measurement: The time-series data from a sensor (e.g., hourly PM_2.5 readings over a week).
• SSV Cause: The literature confirms that low-cost sensors suffer from significant calibration drift due to component aging and non-linear confounding influences from ambient temperature and humidity, which cause their readings to diverge from co-located reference instruments over time [5]. Physical obstructions (e.g., spiderwebs) can also cause anomalous readings [29].
• Application: Data-driven quality control is an active area of research for these networks. By analyzing the distribution of readings from each sensor, our framework could automate the detection of faulty nodes, a task currently addressed with methods ranging from statistical process control to machine learning [5,29]. It would automatically flag sensors whose distributional “fingerprint” (e.g., showing a shifted median or collapsed variance) deviates from the network-wide norm, indicating a need for maintenance or recalibration.

5.2. Clinical Laboratory Networks

Hospitals and diagnostic companies operate fleets of identical analyzers across many locations. Ensuring this inter-instrument consistency, often termed “harmonization,” is paramount for patient safety and is a major focus of laboratory medicine.

• Site: Each individual diagnostic machine.
• Measurement: The results from daily quality control (QC) materials, which are samples with known target concentrations.
• SSV Cause: Research confirms that sources of inter-analyzer variability include lot-to-lot differences in reagents and calibrators, minor hardware degradation, and differences in operator procedures or local lab environments.
• Application: Our framework could analyze the distribution of daily QC results from each machine in a network, which is a more advanced form of statistical quality control (SQC) [6]. It would automatically identify specific analyzers that are drifting or exhibiting higher-than-normal variance (imprecision), allowing for proactive maintenance before patient sample results are compromised.

5.3. Agricultural Technology

Precision agriculture relies on networks of in-field sensors to monitor soil conditions (moisture, pH, etc.) to optimize resource use. The reliability of these sensors is a known challenge.

• Site: Each soil moisture probe or nutrient sensor installed in a field.
• Measurement: Daily or hourly readings from the sensor over a growing season.
• SSV Cause: Common faults cited in the literature include electronic failure, poor soil contact upon installation leading to biased readings, and damage from farm equipment. Furthermore, localized irrigation failures can cause a sensor’s readings to deviate significantly from its neighbors [4].
• Application: The framework could ingest data from the entire sensor network and use the spatial and temporal relationships to flag individual probes whose reading distributions are anomalous compared to their peers. This provides a scalable method for sensor fault detection, preventing incorrect irrigation or fertilization decisions based on faulty data [4].

5.4. Network Cybersecurity

In cybersecurity, unsupervised anomaly detection is a primary tool for identifying novel threats. The concept of a stable baseline for network traffic is central to this field.

• Site: Each network sensor, firewall, or tap monitoring a specific corporate subnet or server.
• Measurement: The distribution of a specific traffic metric over a time window (e.g., packet size, flow duration, or ratio of incoming to outgoing connections).
• SSV Cause: A misconfigured firewall on one subnet, a malfunctioning sensor providing corrupted data, or a genuine low-and-slow security breach (e.g., data exfiltration) that subtly changes the traffic profile [15].
• Application: Our method aligns with established network intrusion detection strategies that model the behavior of network traffic. By comparing the daily distributional “fingerprint” of traffic from each site, our method could detect when a specific subnet begins to deviate from its own established norm or from a peer group of similar subnets. This provides an early warning of a potential configuration issue or security threat that might not trigger simpler signature-based alerts [16].

6. Future Work

This work has established a robust framework for detecting site-to-site variations in distributed measurement networks. While accurate detection is the essential first step, it naturally leads to subsequent research questions aimed at moving from passive monitoring to active intervention and deeper understanding. Several key research frontiers remain open.

A primary challenge is the transition from offline calibration [30] to real-time adaptive control. Current methods, including ours, operate on collected batches of data. A significant advancement would be the development of online algorithms that can dynamically model and compensate for systematic site errors during the measurement process itself. Such a system could learn a site-specific error model and apply corrections on the fly, preventing measurement corruption before it occurs and enabling self-calibrating networks that maintain high data integrity with minimal downtime.

Beyond correction lies the challenge of automated root cause analysis. An intelligent monitoring system should not only flag a faulty site but also assist in diagnosing the underlying issue. The next frontier involves moving from simple correlation to causal inference. Future work could employ causal models to determine which specific hardware or environmental factors are the root causes of a site’s anomalous behavior. By integrating hardware telemetry, environmental data, and maintenance logs, such models could learn to distinguish, for instance, between sensor degradation, environmental interference, and operator error, transforming a generic anomaly flag into actionable diagnostic intelligence.

A significant opportunity for future research is the extension of this framework to handle multivariate data. The current univariate approach is effective but may miss complex failures defined by corrupted statistical relationships between multiple parameters. A direct extension using multivariate Kernel Density Estimation (KDE) is challenged by the curse of dimensionality, which renders the method computationally intensive and statistically unreliable in high dimensions. A more robust path forward involves using representation learning to overcome this limitation. An unsupervised deep learning model, such as a variational autoencoder (VAE), could be trained to compress high-dimensional multivariate measurements from each site into a dense low-dimensional latent vector. This vector, inherently capturing the complex inter-parameter correlations, would then serve as a feature set for our existing Isolation Forest and GMM pipeline. Such a hybrid approach would enable a scalable and sensitive framework for detecting complex multidimensional site-to-site variations.

Furthermore, future research should focus on integrating contextual metadata more deeply into the detection framework. Many distributed systems exhibit known non-random patterns, such as geographical gradients in environmental sensor networks or predictable performance variations across different models of clinical analyzers. The challenge is to develop models that can decouple these expected systematic patterns from the unexpected problematic variations introduced by faulty sites. This would allow the framework to maintain high sensitivity to true anomalies while reducing false alarms triggered by known benign variations in the system.

Finally, the principles established here can be extended to create more sophisticated hierarchical models for anomaly detection, particularly in settings where data privacy is a concern. One direction is to develop site-aware measurement-level outlier detection. In this paradigm, the “health score” of a measurement site, as determined by our framework, would serve as a feature or weighting factor when evaluating individual measurements from that site. This creates a context-aware system that is less likely to be confounded by site-level issues. Moreover, for networks where data cannot be centrally pooled (e.g., across different hospitals or corporations), Federated Learning presents a compelling path forward. A global SSV detection model could be trained across the entire network without ever exposing the raw sensitive data from any individual site, enabling collaborative quality control on an unprecedented scale.

7. Conclusions

In this paper, we addressed the critical and pervasive challenge of site-to-site variation (SSV) in a distributed measurement network, a problem that compromises data integrity and operational efficiency. We demonstrated that traditional methods for detecting SSV are often insufficient as they can rely on restrictive parametric assumptions or are susceptible to errors from subjective parameter tuning, as evidenced by the failure of the QQ-plot methodology on real-world industrial data.

To overcome these limitations, we introduced a framework that is both sample-efficient and distribution-agnostic, combining Kernel Density Estimation (KDE) with an Isolation Forest algorithm. The framework’s autonomy is further enhanced by a thresholding technique that provides a statistically principled method for classifying sites without user intervention. By transforming raw measurement data into high-fidelity density feature vectors, our approach captures the complete distributional fingerprint of each site, enabling the Isolation Forest to reliably identify anomalous sites without prior knowledge of anomaly proportions.

Our extensive validation, performed on proprietary volume production data from Texas Instruments, confirms the effectiveness of our framework. The results show that our method successfully identifies subtle real-world anomalies that conventional techniques, such as the QQ-plot methodology, either miss entirely or flag incorrectly.

The significance of this work extends far beyond semiconductor testing. The proposed framework provides a robust and automated solution that is broadly scalable to any distributed measurement system where maintaining inter-site consistency is paramount. By enabling early and accurate detection of problematic measurement sites, this work paves the way for more reliable data analysis, leading to improved yield and quality control as well as more efficient operation of large-scale sensor networks.