Abstract
The centuries-old idea of a lighter-than-air vacuum balloon has not materialized yet as such structure needs to be both light enough to float in the air and strong enough to withstand atmospheric pressure. We propose a design of a rigid spherical sandwich shell and demonstrate that it can satisfy these stringent conditions with commercially available materials, such as boron carbide ceramic and aluminum alloy honeycomb. A finite element analysis was employed to demonstrate that buckling can be prevented in the proposed structure. Also discussed are other modes of failure and approaches to manufacturing.
1. Introduction
The idea of a lighter-than-air vacuum balloon is centuries old. In 1670, F. Lana di Terzi proposed a design of an airship where buoyancy was to be created by evacuated copper spheres (Ref. [1], see also [2] containing historical information related to the design). Vacuum balloons could aid in important applications, such as transportation, internet delivery, and cellular communications, as they have some advantages compared to lighter-than-air gas balloons: they do not need hydrogen, which is hazardous, or helium, which is increasingly expensive and difficult to contain; they do not need constant heating, like hot-air balloons, and they can have simpler altitude control through pumping air in and out. However, this dream of vacuum balloon has not materialized so far because it is very difficult to design and manufacture a shell that is light enough to float in the air and strong enough to reliably withstand the atmospheric pressure. For example, A.F. Zahm [3] calculated the stress in a thin homogeneous one-layer rigid shell with vacuum inside and zero buoyancy, so that its mass equals that of the displaced air:
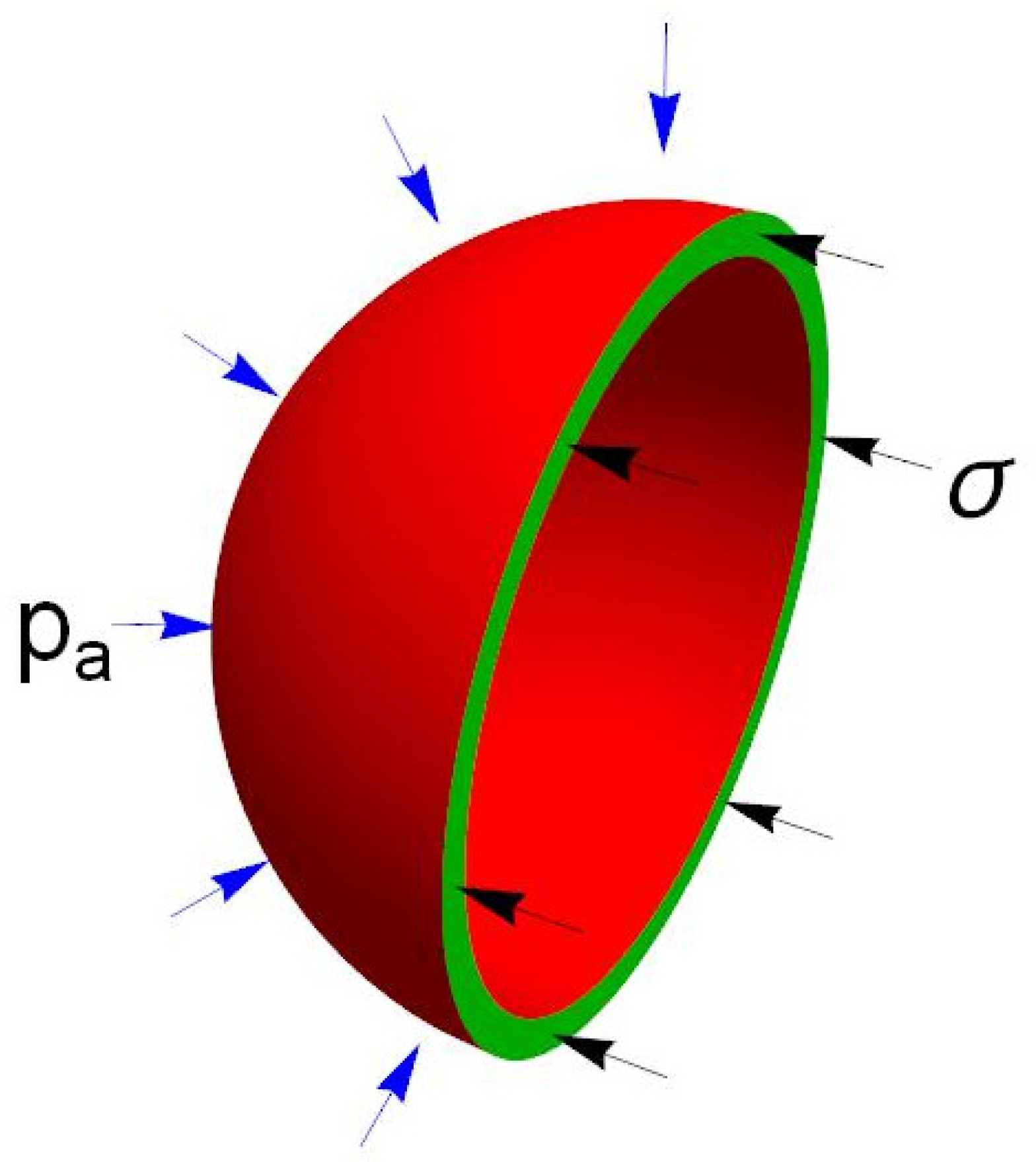
where is the radius of the shell, is the shell thickness, and and are the densities of air and of the shell material, respectively (we use an approximation for a thin shell). Let us then consider the condition of equilibrium for half of the shell (see Figure 1):
where is the compressive stress in the shell and is the atmospheric pressure at 0 °C (we used a condition of equilibrium for a hemisphere of air in the atmosphere to calculate the right-hand side).
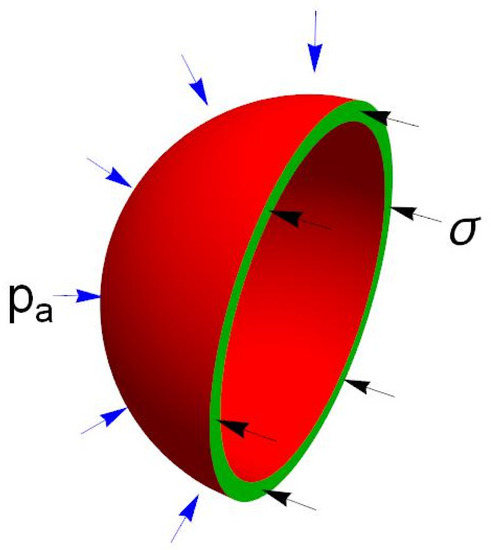
Figure 1.
Stress and atmospheric pressure acting on one half of an evacuated spherical shell (not to scale).
We obtain:
If (the density of aluminum), (the density of air at 0 °C and 1 atm (101 kPa)), and pa = 1.01×105 Pa, then , i.e., the stress is of the same order of magnitude as the compressive strength of contemporary aluminum alloys. It is important to note that this result does not depend on the radius of the shell.
A.F. Zahm notes that, while the results of stress calculation are quite problematic, buckling is an even more dangerous mode of failure for such a structure. Let us perform a simple buckling analysis for this structure [4]. The critical buckling pressure for a thin spherical shell is given by the well-known formula of the linear theory of stability [5]:
where and are the modulus of elasticity and the Poisson’s ratio of the material of the shell, respectively. If and, e.g., , then
Even if we use diamond as the shell material ( and ), we obtain
In other words, even the maximally optimized homogeneous diamond shell of ideally spherical shape would inevitably fail already at . Thus, one-layer shells made of any solid material in existence either cannot float in the air or have no chance of withstanding the atmospheric pressure. (It should be noted that we only considered the spherical shape in our analysis, as this shape provides the best volume-to-surface ratio [6] and is believed to be the optimal one to withstand external pressure with minimum weight [7].)
Problems of this kind are quite common in aircraft design, and typical solutions are multilayer shells with light core or stiffened shells.
In our patent application [4], we defined viable designs of a vacuum balloon based on three-layer shells made of commercially available materials. Numerous patents and articles on vacuum balloons had been published earlier (see, e.g., [8]), but, to the best of our knowledge, none of them properly addressed the crucial issue of buckling. More recently, other work addressing the issue of buckling for vacuum balloons was published (see, e.g., [9,10,11,12,13] and references there). The recent popular articles on vacuum balloons [14,15] also reflect current interest in this topic.
As our design [4] garnered some interest, it is advisable to describe it here, in a journal article format, after significant rework, providing details of the all-important buckling analysis. Detailed comparison with the vastly different designs featured in related work by others [9,10,11,12,13] would perhaps require finite-element analysis of each proposed structure and is beyond the scope of this article. We would just like to note that our design, unlike many others, is spherically symmetric and scalable (multiplying all linear dimensions by the same factor provides an equally viable design; see some caveats related to intracell buckling in Section 2.2.), so it has fewer parameters (as there is no dependence on the polar and azimuthal angles or absolute linear dimensions), which facilitates its analytical optimization. It is also noteworthy that the design does not contain any components under tension. This may be advantageous for using materials such as ceramics, whose compressive properties are typically much better than the tensile properties.
2. Methods and Results
2.1. A Sandwich Vacuum Balloon and Its Buckling Analysis
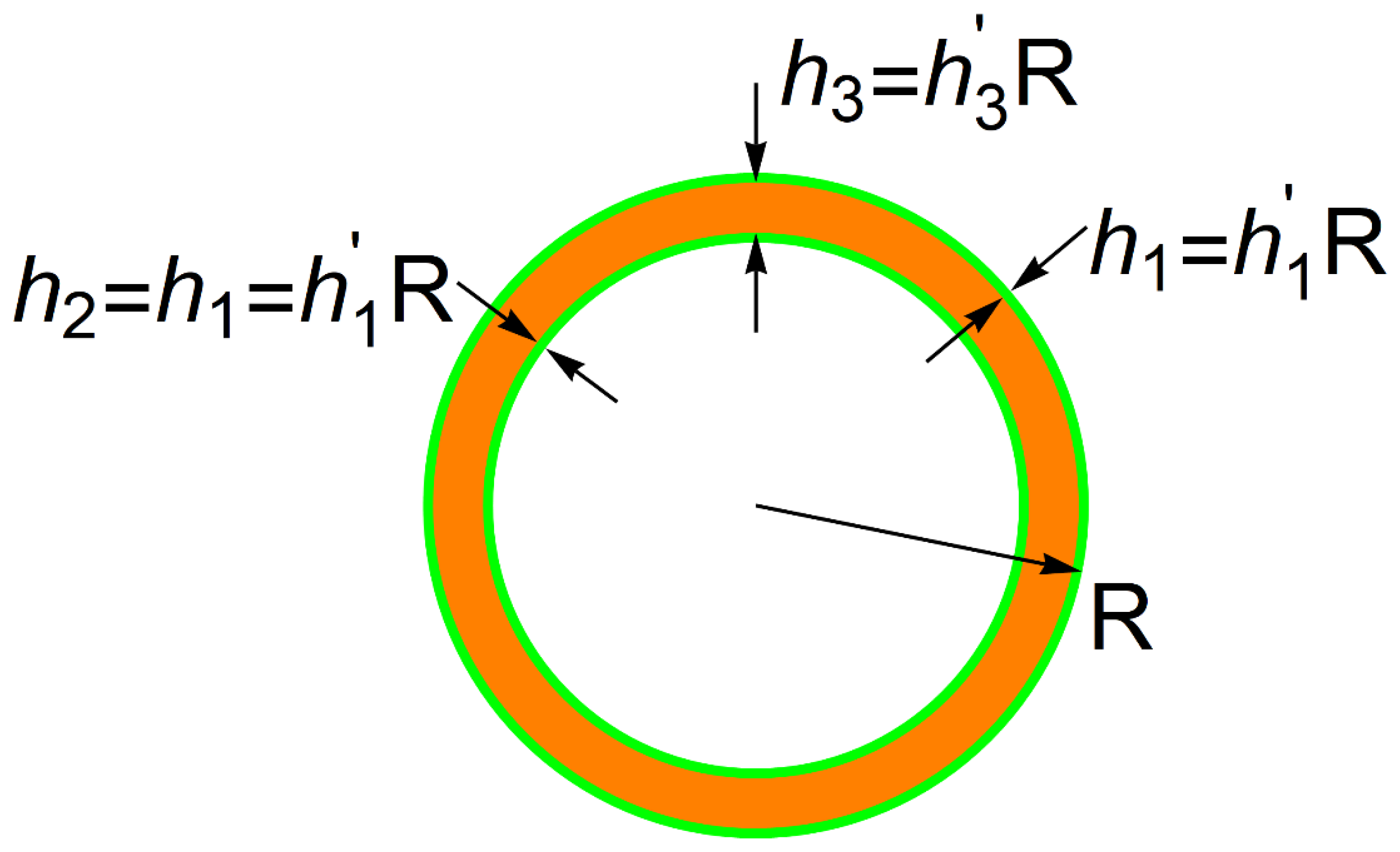
As an example, let us consider a three-layer spherical shell with face skins of equal thickness and a core of aluminum alloy honeycomb of thickness (see Figure 2 and Figure 3 below).
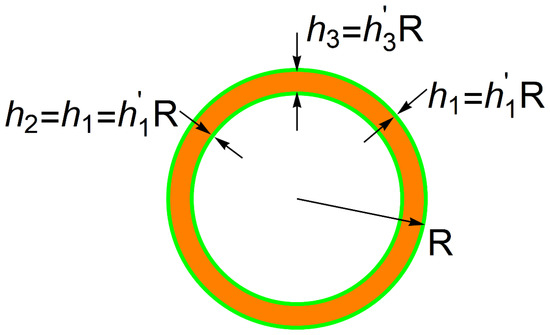
Figure 2.
Dimensions of a spherical sandwich shell (not to scale; note that, e.g., for the optimal design).
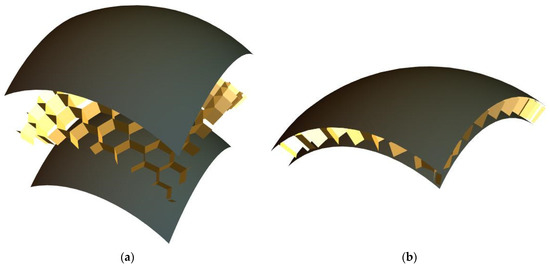
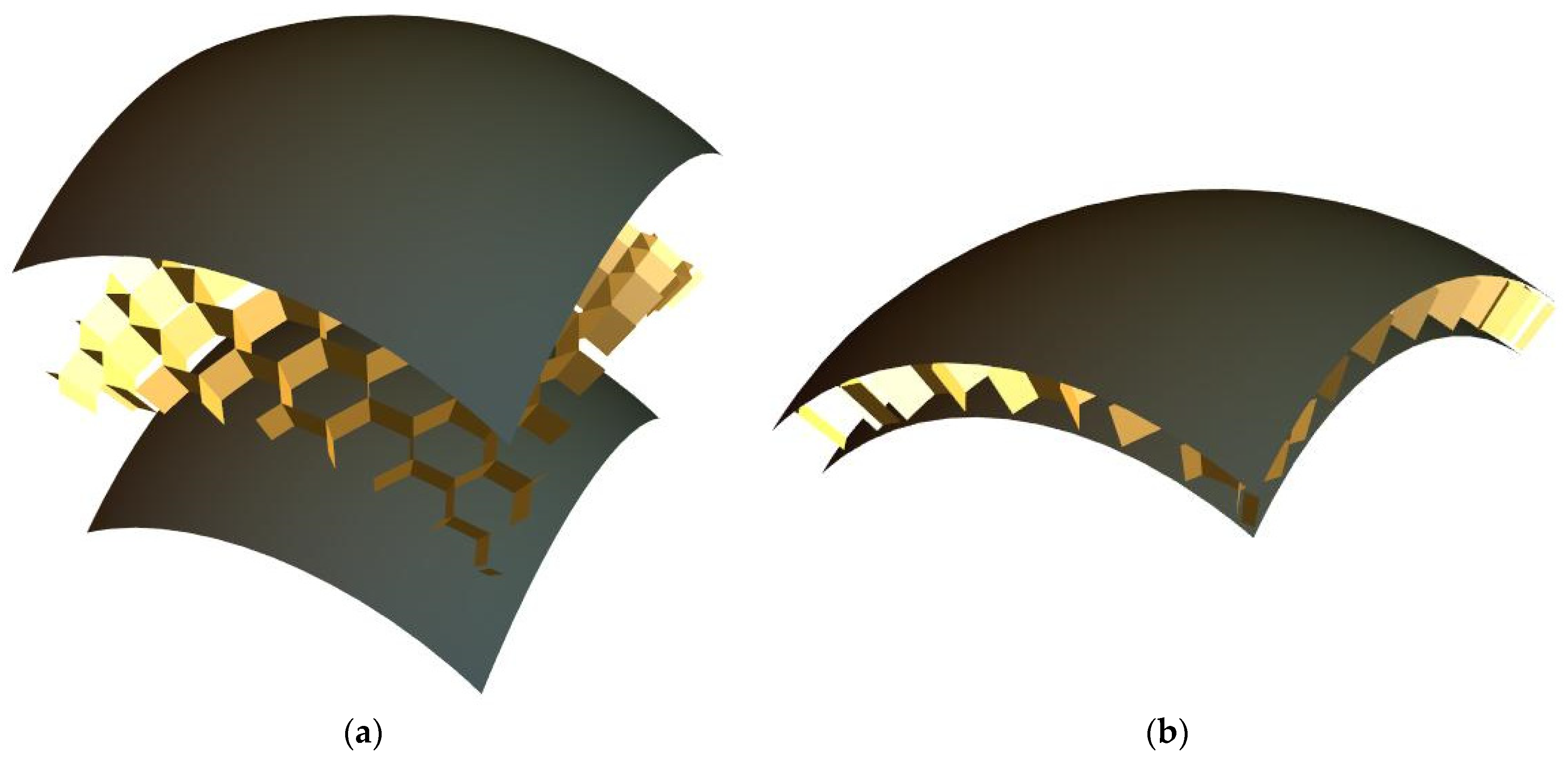
Figure 3.
A fragment of a spherical sandwich shell (a) before and (b) after assembly (not to scale).
In order to prove the design feasibility, we used parameters of commercially available materials in our study. Boron carbide ceramic was chosen as the face skin material (density , elasticity modulus , compressive strength , Poisson’s ratio [16]). PLASCORE PAMG-XR1-3.1-1/8-7-N-5056 honeycomb was chosen as the core material (cell size 1/8 inch (3.2 mm), nominal foil gauge 0.0007 inch (18 μm), nominal density 3.1 pcf (), bare compressive strength 340 psi ()/modulus 97 ksi (), plate shear strength 250 psi () (“L”), 155 psi () (“W”)/modulus 45 ksi () (“L”), 20 ksi () (“W”) [17]).
If is the radius of the shell, we assume that . To assess the design feasibility, we also anticipate that the shell allows a small payload fraction (the ratio of the mass of the payload at zero buoyancy and the mass of the displaced air). Then, the condition of zero buoyancy has the following form:
or
where
The buckling stability condition that we used is described by the following semi-empirical formula for critical pressure obtained for three-layer domes [18]:
In this case, is the modulus of elasticity of the face skin material, and is the maximum pressure at which the three-layer shell is stable. The requirements for core rigidity are discussed below, but let us first find the values of and that maximize . Using Equation (8), let us eliminate from Equation (9):
The value of is maximal for
In that case, the optimal values of and are:
This is a good indication that the design is feasible. However, we need to assess the buckling stability more accurately and consider other modes of failure. We cannot rely on the results of the above analytical approach as it hinges on the semi-empirical formula Equation (9) from [18]. The validity limits of this formula are not clear; in particular, it is not clear how this formula should be modified to take into account manufacturing imperfections when they are different from those in the shells of [18]. The results of the above approach were verified and optimized by a finite element analysis (FEA) using ANSYS (ANSYS Mechanical Enterprise, R19.0), which enabled us to compute the stress and strain in the shell components and to perform the eigenvalue buckling analysis (which is actually a classical Euler buckling analysis). The results of the FEA analysis confirmed that the analytical approach provides reasonable estimates and a good starting point for optimization in our case. However, we base the conclusions of this article on the results of the FEA analysis, not on the results of the analytical approach.
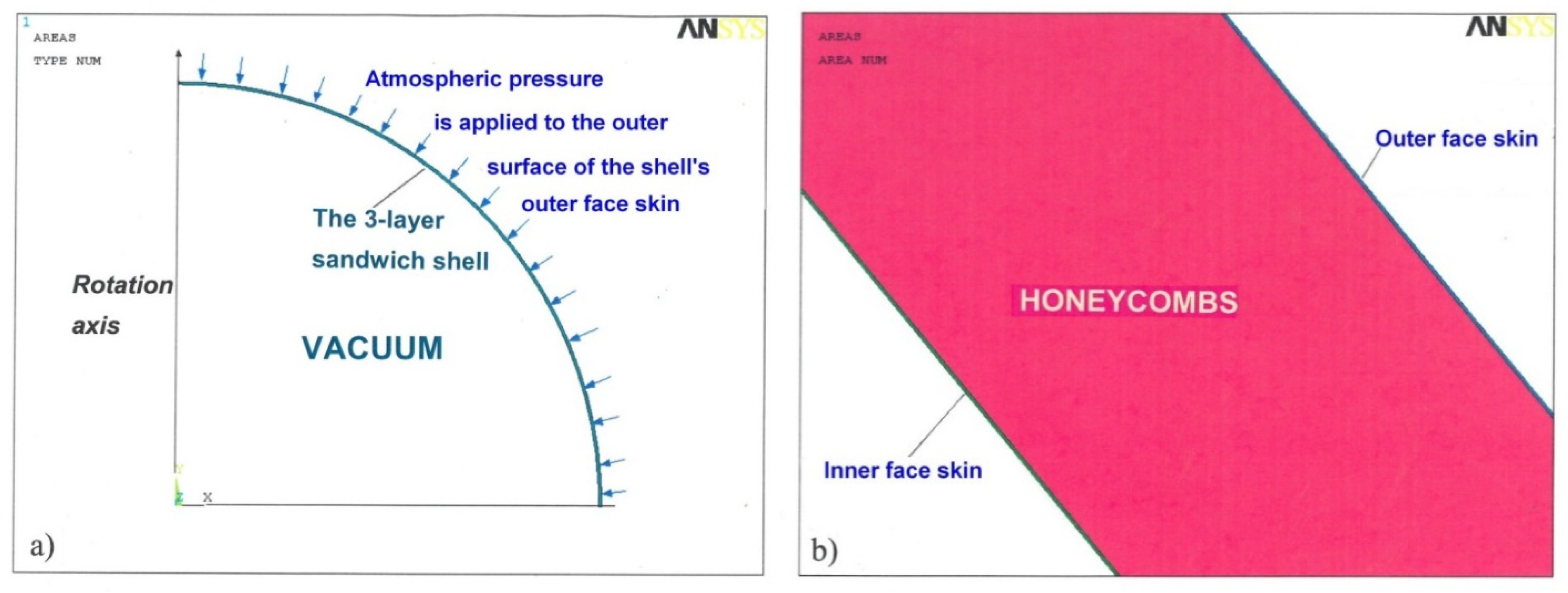
For the FEA analysis, a 2D axisymmetric model in the spherical system of coordinates, with due regard for corresponding boundary conditions at the edges, was found to be sufficient and adequate (Figure 4). In this model, PLANE82 2D high-order 8-node elements, which are well suited for curved boundaries, were used for the finite element mesh in axisymmetric mode. The mesh was heavily refined and the elements’ aspect ratios were appropriately adjusted. The mesh is shown in Figure 5.
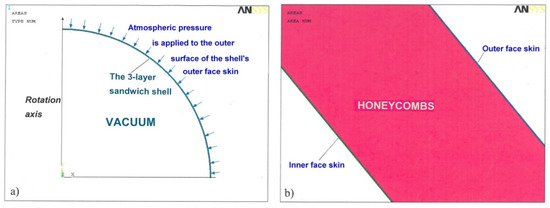
Figure 4.
The ANSYS FEA: (a) a 2D axisymmetric model and (b) an enlarged fragment of the 3-layer sandwich shell’s solid model.

Figure 5.
A fragment of the mesh used for the FEA (portions of the upper face skin and honeycomb are shown). The face skin has 6 divisions radially (the upper six “layers” of elements in the Figure). The honeycomb core has 32 divisions radially.
Some results of FEA are shown in Figure 6.
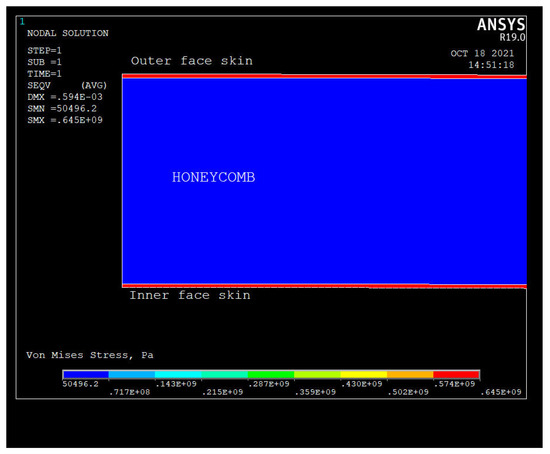
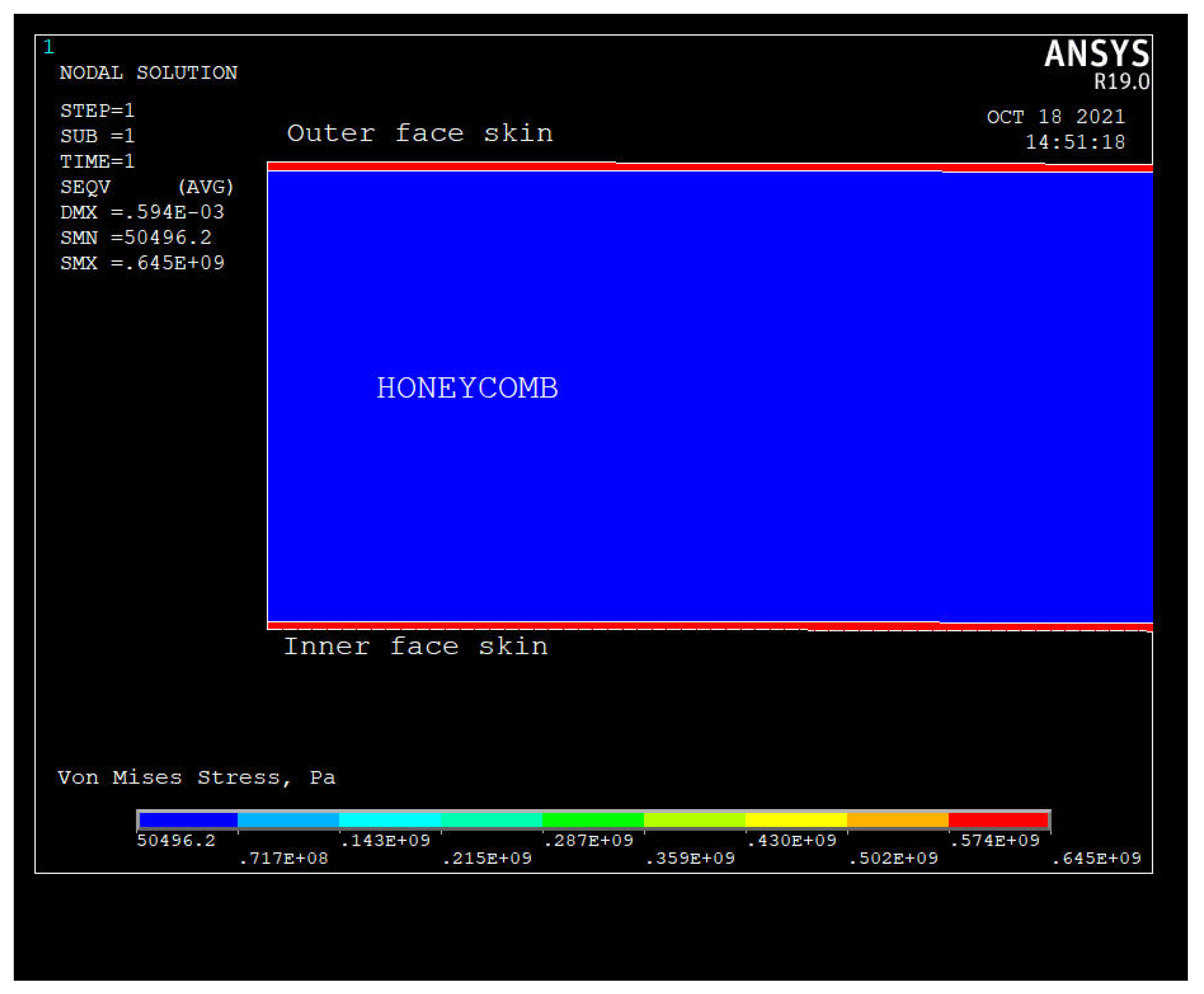
Figure 6.
Von Mises stress in the structure (fragment) from the FEA analysis (buckling safety factor of 2.65 and payload fraction of 0.1). The maximum stress in the face skins does not exceed 645 MPa, and the stress in the honeycomb is comparable to the atmospheric pressure.
In the FEA, the anisotropic material properties of the honeycomb were treated in accordance with recommendations of a honeycomb manufacturer (Ref. [19], p. 20). For the sake of simplicity, we assume that the honeycomb is a transversally isotropic material, so the lesser of the two values of shear modulus from [17] was used (which makes the results more conservative). Thus, we used the following values: the out-of-plane component of the modulus −670 MPa; the in-plane components of the modulus −67 Pa; the out-of-plane components of the shear modulus 140 MPa; the in-plane component of the shear modulus 14 Pa; the Poisson’s ratio 10−5 (very small values of the Poisson’s ratio and the in-plane components of the modulus and the shear modulus were used to avoid singularities, in accordance with [19], p. 20).
Thus, the ANSYS eigenvalue buckling analysis input includes the loads. The output of the analysis is the eigenvalues (buckling load multipliers), which are the safety factors for buckling modes (for the input loads). The minimum eigenvalue obtained in the eigenvalue buckling analysis determines the critical buckling load. As we load our structure with atmospheric pressure , we have the following relation between the minimum eigenvalue and the critical buckling pressure:
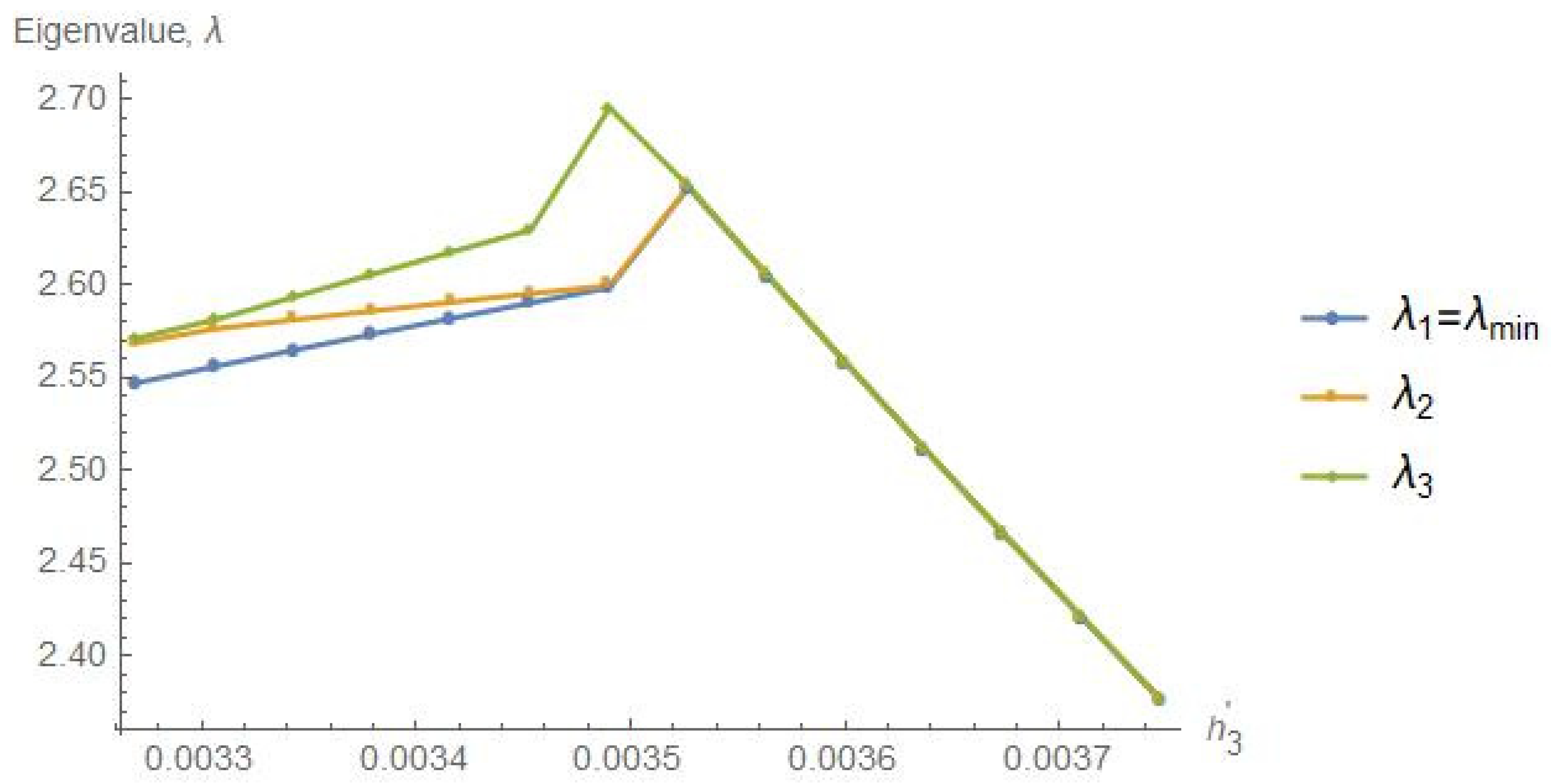
The optimized parameters of the analytical approach were used as initial values for optimization through the FEA. The eigenvalue , regarded as a function of , has a rather sharp maximum of (see Figure 7) for a value of , which is close to the value we arrived at using the simplified method. The corresponding value of approximates . To give an idea of how the eigenvalue varies with the payload fraction , let us note that is approximately 3.21 for an optimized design with zero payload fraction.
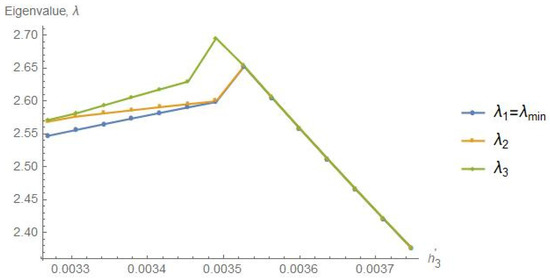
Figure 7.
The 3 least eigenvalues , , and from the ANSYS eigenvalue buckling analysis versus the relative core thickness for payload fraction .
We also performed some preliminary buckling analysis using a 3D model with a coarse mesh and obtained the minimum eigenvalue of 3.0. This result is subject to adjustments after a better mesh is used. We used the optimal linear dimensions obtained for the 2D model with the payload fraction of 0.1.
The safety factor of 2.65 is not very high, as empirical knockdown factors are typically applied to the results of small-deflection analysis for externally pressurized thin-walled spherical shells to take into account initial imperfections and other factors. For example, the knockdown factor of 0.2 is recommended in [20] for hemispherical sandwich domes (there is very good agreement between our FEA results and the results obtained with the use of formulas in [20] with a knockdown factor of 1 for buckling critical pressure/stress). The formulas of [20] are based on the solution from [21,22]. If we perform linear (and, if required, non-linear) buckling analysis with due regard for imperfections of manufacturing, the safety factors will decrease, but the obtained results are high enough to reasonably expect that the safety factors will still be quite sufficient for state-of-the-art manufacturing accuracy, as thoroughly manufactured thin spherical shells were shown to withstand external pressure of up to 80–90% of the critical one [23,24]. The relevant variation of thickness of the shallow spherical shells in the experiments of [23,24] was about ±1% of the thickness. In our design, if the radius is , the thickness of the sandwich shell is about (see the dimensions in Conclusion), so the comparable manufacturing accuracy would be about . While such accuracy may be difficult to achieve, the knockdown coefficient of 0.2 is conservative. According to the review of experimental results on buckling of spherical shells in [25], the knockdown factors for various technologies often exceed 0.4, which would be sufficient in our case (for payload factor of 0.1). If necessary, incoming testing of sandwich plates can be performed before the assembly of the shell to make sure the knockdown factor for the plates exceeds the required value.
Only homogeneous spherical shells are discussed in [23,24,25], and information on spherical sandwich shells is scarce, but the results and recommendations of [18] suggest similar conclusions.
Taking into account the imperfections in the finite-element analysis is beyond the scope of this work as the imperfections depend on the specific technologies.
Let us summarize the approximations used to estimate the critical buckling pressure for the design. We used air pressure of and density of for the temperature of 0 °C, material properties provided by manufacturers, a conservative simplification for honeycomb shear modulus, a 2D linear buckling FEA, and a payload fraction of 0.1. We did not take into account the very small buoyant force reduction due to the shell compression by atmospheric pressure and the weight of adhesives (see the reasoning at the end of Section 2.3.). We provided some arguments based on a review of available experimental data suggesting that the safety factor of the linear buckling analysis should be enough to neutralize the knockdown factor due to imperfections and nonlinear effects.
2.2. Other Modes of Failure
Now let us verify that other modes of failure are not problematic for the design. We used standard unity checks from [19,26]. Providing detailed descriptions of the failure modes and explanations of the standard formulas here does not seem warranted.
Let us first check that the compressive stress in the face skins does not exceed the compressive strength of the face skin material. Instead of Equation (2) we have:
which is much less than the compressive strength of boron carbide ().
The following formula is used to check the design for shear crimping [19,26]:
where is the allowable force per unit length of a sandwich plate in some direction and is the honeycomb shear modulus. The actual force per unit length is much less:
The design was checked for face skin wrinkling using the following formula [26]:
where is the allowable uniaxial wrinkling stress, is a theoretically derived coefficient for honeycomb cores, is the face skin modulus, and is the honeycomb modulus. We obtain: . However, we have biaxial stress, so we should check that [26]:
where and are stresses in two orthogonal directions () and is the shear stress (), . The left side of Equation (18) equals approximately , so this check also yields a satisfactory result.
The design is scalable with respect to all of the above modes of failure: an equally successful design can be obtained by multiplying all linear dimensions by the same factor. However, this is not true for another mode of failure—so-called intracell buckling (also known as dimpling). We use the following formula [26]:
where is the critical stress for intracell buckling, is the Poisson’s ratio of the face skins, and () is the cell size. We obtain . However, we have biaxial stress, so we must make sure that [26]:
where if the cell size (that means for our values of and ) and otherwise (see [26], p. 243). If , we have:
and condition (20) is satisfied. If , we have , or .
Thus, we obtain the following condition of stability for intracell buckling: .
We did not study possible effects of small leaks in the face skins, but they should not present a greater problem than for other vacuum systems, as only rough vacuum is required for vacuum balloons. If pressure difference in neighboring honeycomb cells is a concern, one may need to use a honeycomb with cell perforations [17].
2.3. Towards a Prototype Vacuum Balloon
Manufacturing of the boron carbide face skins seems to be the most challenging part of the design, as they may be very thin, and their density needs to be close to the theoretical boron carbide density, otherwise the elasticity modulus can be insufficient.
For large prototypes (), the face skin thickness exceeds , and parts of the face skins can be produced using traditional methods, such as uniaxial pressing with subsequent sintering [27,28].
For smaller prototypes, the thickness of the face skins is by order of magnitude. Producing such parts is technologically challenging, and the parts may be too fragile. Detailed treatment of these issues is beyond the scope of this article, but a preliminary discussion is clearly necessary.
The face skins can be produced either by deposition on a sacrificial substrate (this can be time consuming if the process is to yield high elasticity modulus) or by using gel casting, which can provide “fine features down to scale” [29]). Another approach to manufacturing uniform spherical boron carbide shells with a thickness of the order of 100 µ by dropping a slurry coating on a molybdenum substrate and subsequent drainage and curing is described in [30]. While the radius of the shells in [30] is small (), the method was used with different materials to manufacture shells of a radius of up to [31]. Shells of larger radius can probably be manufactured by varying the viscosity of the slurry and/or using rotation.
To circumvent the issue of fragility, one can first bond the face skins to the honeycomb and then remove the face skin supports (the substrates or parts of the molds).
To fabricate the entire vacuum balloon, one will need to join several sandwich panels using some standard approach, such as bonded butt joints using H sections [32]. The weight penalty is not estimated in this article, but it will be smaller for larger sandwich panels.
According to [33], “in terms of volume efficiency, convex stellated shells are comparable to spherical shells with a knockdown factor of 0.65”, so the former can achieve better buckling efficiency than the latter “when the effects of geometric imperfections are considered”. If a similar conclusion is also true for sandwich shells, then sandwich stellated shells can be another option for vacuum balloons. In terms of manufacturing, such shells can be attractive as they can be assembled using flat sandwich panels.
The exterior and the interior of the structure can be connected with a valve at a modest weight penalty for initial evacuation of the structure or for altitude control.
The buoyant force reduction due to the shell compression by atmospheric pressure was calculated to be less than 0.4%.
Point loading of the structure should be avoided. For example, it is relatively easy to provide distributed support with larger contact area for the structure on the ground.
The face skins can be bonded to the honeycomb core using adhesives. To reduce the weight, the adhesive can be applied only to the tops of the honeycomb cell walls using the approach of [34]. We did not discuss other issues related to adhesives here (mass requirements, modes of failure, etc.), but these issues are less significant for shells of larger radius, as the adhesive mass scales as , and the mass of the entire structure scales as . Neither did we discuss potential use of more exotic materials (such as chemical vapor deposition (CVD) diamond for the face skins or architected cellular materials [13] for the core) to significantly increase safety factors and/or the payload fraction.
3. Discussion
We showed that a lighter-than-air rigid vacuum balloon can theoretically be built using commercially available materials. The design in this article is an evacuated spherical sandwich shell of outer radius containing two boron carbide face skins of thickness each that are reliably bonded to an aluminum honeycomb core of thickness . The structure is lighter than air (it allows a payload fraction of 0.1) and can withstand the atmospheric pressure. For example, if , the face skin thickness is , the honeycomb thickness is , the mass of the shell is , and the payload capacity for zero buoyancy is .
A prototype vacuum balloon would also become the first ever lighter-than-air solid (for example, aerogels are actually not lighter than air due to the air inside).
Manufacturing a prototype vacuum balloon will be a major breakthrough. It will require detailed engineering to resolve numerous less essential issues, but the results of this article suggest that we can finally bring to fruition the ancient dream of a vacuum balloon.
It took mathematicians 357 years to prove Fermat’s Last Theorem. Will it take us more to build the first vacuum balloon?
Author Contributions
Conceptualization, A.A. and A.V.G.; Methodology, A.A. and A.V.G.; Software, A.A. and A.V.G.; Validation, A.A. and A.V.G.; Formal Analysis, A.A. and A.V.G.; Investigation, A.A. and A.V.G.; Writing—Original Draft Preparation, A.A. and A.V.G.; Writing—Review & Editing, A.A. and A.V.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement DMR 1644779 and the State of Florida. The authors are grateful to A. N. Palazotto for his interest in this work and valuable remarks. One of the authors (A.A.) is grateful to A. I. Afanasyev, who initiated this work by an inquiry on applications of high-strength materials.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
= compressive modulus of elasticity of the material of a thin homogeneous shell. = compressive modulus of elasticity of the face skin material of a sandwich shell. = honeycomb shear modulus. = thickness of a thin homogeneous shell. = thickness of the outer face skin of a sandwich shell, . = relative thickness of the outer face skin of a sandwich shell, . = optimum relative thickness (analytical estimate) of the outer face skin of a sandwich shell. = thickness of the inner face skin of a sandwich shell, . = thickness of the honeycomb core of a sandwich shell. = relative thickness of the honeycomb core of a sandwich shell, . = optimum relative thickness (analytical estimate) of the honeycomb core of a sandwich shell. = a factor in a formula for face skin wrinkling analysis, . = a factor in a formula for face skin wrinkling analysis, . = an exponent in a formula for intracell buckling analysis. = actual force per unit length of a sandwich plate. = allowable force per unit length of a sandwich plate (for shear crimping analysis). = atmospheric pressure, . = critical buckling pressure. q = payload fraction of a vacuum balloon. R = outer radius of a shell. S = honeycomb core cell size. = minimum eigenvalue obtained in the finite element eigenvalue buckling analysis. = Poisson’s ratio of a thin homogeneous shell. = Poisson’s ratio of the face skins of a sandwich shell. = density of the honeycomb core of a sandwich shell. = relative density of the honeycomb core of a sandwich shell, . = atmospheric air density, 1.29 kg·m−3. = density of the face skins of a sandwich shell. = relative density of the face skins of a sandwich shell, . = density of a thin homogeneous shell. = compressive stress in a thin homogeneous shell. = critical uniaxial stress for intracell buckling. = compressive stress in the face skins of a sandwich shell. = allowable uniaxial wrinkling stress (for face skin wrinkling analysis). = stresses in the face skins in two orthogonal directions, . = shear stress in the face skins, .
References
- Lana, F. Prodromo. Ouero Saggio di Alcune Inuentioni Nuoue Premesso All’arte Maestra, Rizzardi, Brescia, 1670, Chapter 6. Available online: https://books.google.ru/books?id=o7AGGIKz0_wC&pg=PP9&hl=ru&source=gbs_selected_pages&cad=2#v=onepage&q&f=false (accessed on 8 July 2018). (In Italian).
- Shikhovtsev, E. Available online: http://mir.k156.ru/aeroplan/de_bausset_aeroplane-03-1.html#a03-1-16 (accessed on 5 February 2019). (In Russian and In English).
- Zahm, A.F. Aërial Navigation: A Popular Treatise on the Growth of Air Craft and on Aeronautical Meteorology; D. Appleton and Company: New York, NY, USA; London, UK, 1911; p. 443. Available online: https://books.google.com/books?id=hRdDAAAAIAAJ&pg=PA443&lpg=PA443&dq=%22zahm%22+vacuum+balloon&source=bl&ots=HO8PwEw0M5&sig=AQGKWimBz3oa9Y32TwTnEgAu-UQ&hl=en&sa=X&ved=2ahUKEwiFroi-s4LfAhUq9YMKHWFHBtwQ6AEwAXoECAkQAQ#v=onepage&q=%22zahm%22%20vacuum%20balloon&f=false (accessed on 2 December 2018).
- Akhmeteli, A.M.; Gavrilin, A.V. Layered Shell Vacuum Balloons. U.S. Patent 11/517,915, 8 September 2006. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M.; Prager, W. Theory of Elastic Stability, Second Edition. J. Appl. Mech. 1962, 29, 220–221. [Google Scholar] [CrossRef]
- Osserman, R. The Isoperimetric Inequality. Bull. Am. Math. Soc. 1978, 84, 1182. [Google Scholar] [CrossRef] [Green Version]
- Alcocer, A.; Forès, P.; Giuffré, G.P.; Parareda, C.; Roca, A.; Roca, J. Pressure Hull Design and Construction of the Manned Submersible Ictineu 3. Instrum. Viewpoint 2009, 8, m3. [Google Scholar]
- Armstrong, L.M.; Peoria, I.L. Aircraft of the Lighter-Than-Air Type. U.S. Patent 1,390,745, 13 September 1921. [Google Scholar]
- Barton, S.A. Florida State University Research Foundation (Tallahassee, FL, US), U.S. Patent 7,708,161 for “Light-Weight Vacuum Chamber and Applications Thereof”. U.S. Patent 7,708,161, 4 May 2010. [Google Scholar]
- Snyder, J.W.; Palazotto, A. Finite Element Design and Modal Analysis of a Hexakis Icosahedron Frame for Use in a Vacuum Lighter-Than-Air Vehicle. J. Eng. Mech. 2018, 144, 04018042. [Google Scholar] [CrossRef]
- Adorno-Rodriguez, R.; Palazotto, A. Nonlinear Structural Analysis of an Icosahedron under an Internal Vacuum. J. Aircr. 2015, 52, 878–883. [Google Scholar] [CrossRef]
- Rapport, N.; Middleton, W.I. U.S. Patent Application for “Lighter-Than-Air Fractal Tensegrity Structures”. U.S. Patent 14/807118, 23 July 2015. [Google Scholar]
- Jenett, B.; Gregg, C.; Cheung, K. Discrete Lattice Material Vacuum Airship. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 815. [Google Scholar] [CrossRef] [Green Version]
- Ball, P. Flying on empty. New Sci. 2019, 244, 68–69. [Google Scholar] [CrossRef]
- Surcouf, O. Dirigeables: Le Miracle du Vide, Science&Vie, No. 1233. June 2020, pp. 90–93. Available online: https://www.science-et-vie.com/technos-et-futur/dirigeables-le-miracle-du-vide-56281 (accessed on 29 July 2020). (In French).
- Available online: http://www.skylinecomponents.com/B4C.html (accessed on 25 December 2018).
- Available online: https://www.plascore.com/honeycomb/honeycomb-cores/aluminum/pamg-xr1-5056-aluminum-honeycomb-core/ (accessed on 25 December 2018).
- Brix, G. Durchschlagen von GFP-Sandwichkuppeln bei gleichförmigem Außendruck, IfL-Mitt. Mitteilung aus dem Institut für Leichtbau und Ökonomische Verwendung von Werkstoffen Dresden 1968, 7, 408–413. (In German) [Google Scholar]
- Available online: https://www.hexcel.com/user_area/content_media/raw/Honeycomb_Sandwich_Design_Technology.pdf (accessed on 25 December 2018).
- Sullins, R.T.; Smith, G.W.; Spier, E.E. Manual for Structural Stability Analysis of Sandwich Plates and Shells, NASA CR-1457. 1969. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a310684.pdf (accessed on 1 August 2020).
- Yao, J.C. Buckling of Sandwich Sphere under Normal Pressure. J. Aerosp. Sci. 1962, 29, 264–268. [Google Scholar] [CrossRef]
- Plantema, F.J. Sandwich Construction: The Bending and Buckling of Sandwich Beams, Plates and Shells; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1966. [Google Scholar]
- Krenzke, M.A.; Kiernan, T.J. Elastic Stability of Near-Perfect Shallow Spherical Shells. AIAA J. 1963, 1, 2855–2857. [Google Scholar] [CrossRef]
- Krenzke, M.A.; Kiernan, T.J. Erratum: Elastic Stability of Near-Perfect Shallow Spherical Shells. AIAA J. 1964, 2, 0784b. [Google Scholar] [CrossRef]
- Błażejewski, P.; Marcinowski, J.; Rotter, M. 04.21: Buckling of externally pressurised spherical shells: Experimental results compared with recent design recommendations. Ce/Papers 2017, 1, 1010–1018. [Google Scholar] [CrossRef]
- Collier, C. Consistent Structural Integrity and Efficient Certification with Analysis, Volume 3, AFRL-VA-WP-TR-2005-3035. 2005. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a444085.pdf (accessed on 27 December 2018).
- Kaiser, A. Hydraulic Pressing of Advanced Ceramics, cfi/Berichte der DKG. 2007, 84, No. 6, pp. 27–32. Available online: http://www.alpha-ceramics.de/system/00/01/52/15245/633855139353281250_1.pdf (accessed on 10 August 2020).
- Kaiser, A.; Lutz, R. Uniaxial Hydraulic Pressing as Shaping Technology for Advanced Ceramic Products of Larger Size, Interceram. 2011. No. 03–04. pp. 230–234. Available online: http://www.laeis.eu/System/00/01/95/19513/634559894557055155_1.pdf (accessed on 10 August 2020).
- Lu, R.; Chandrasekaran, S.; Du Frane, W.L.; Landingham, R.L.; Worsley, M.A.; Kuntz, J.D. Complex shaped boron carbides from negative additive manufacturing. Mater. Des. 2018, 148, 8–16. [Google Scholar] [CrossRef]
- Chen, R.; Qi, J.; Su, L.; Shi, Q.; Guo, X.; Wu, D.; Lu, T.; Liao, Z. Rapid preparation and uniformity control of B4C ceramic double-curvature shells: Aim to advance its applications as ICF capsules. J. Alloy. Compd. 2018, 762, 67–72. [Google Scholar] [CrossRef]
- Lee, A.; Brun, P.-T.; Marthelot, J.; Balestra, G.; Gallaire, F.; Reis, P.M. Fabrication of slender elastic shells by the coating of curved surfaces. Nat. Commun. 2016, 7, 11155. [Google Scholar] [CrossRef] [PubMed]
- Sandwich Panel Fabrication Technology, Hexcel LTU 018. 2001. Available online: https://studylib.net/doc/18103284/sandwich-panel-fabrication-technology (accessed on 21 July 2019).
- Ning, X.; Pellegrino, S. Searching for imperfection insensitive externally pressurized near-spherical thin shells. J. Mech. Phys. Solids 2018, 120, 49–67. [Google Scholar] [CrossRef] [Green Version]
- Rion, J.; Leterrier, Y.; Månson, J.A.E. Prediction of the adhesive fillet size for skin to honeycomb core bonding in ultra-light sandwich structures. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1547–1555. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).