Abstract
Hierarchical Reinforcement Learning (HRL) for UAV Coverage Path Planning (CPP) is hindered by the “subgoal space explosion”, causing inefficient exploration. To address this, we propose a two-stage framework, Hierarchical Reinforcement Learning Guided by Landmarks (HRGL), which synergistically combines HRL with a multi-scale observation space. The framework provides a low-resolution global map for the high-level policy’s strategic planning and a high-resolution local map for the low-level policy’s execution. To bridge the information gap between these hierarchical views, the first stage, ACHMP, introduces a learned Adjacency Network. This network acts as an efficient proxy for local feasibility by mapping coordinates to an embedding space where distances reflect true reachability, allowing the high-level policy to select feasible subgoals without processing complex local data. The second stage, HRGL, further introduces a landmark-guided global guidance mechanism to overcome local myopia. Extensive experiments on a variety of simulated grid-world maps demonstrate that HRGL significantly outperforms baseline methods in terms of both convergence speed and final coverage rate.
1. Introduction
Autonomous Unmanned Aerial Vehicles (UAVs) are being increasingly utilized in a variety of applications, such as smart agriculture, photogrammetry, disaster management, and infrastructure assessment [1,2,3,4]. The challenge of planning efficient paths for data collection is not limited to aerial systems; it is also a critical issue in other domains, such as for Unmanned Marine Vehicles (UMVs) operating in complex underwater environments with severe communication constraints [5]. Furthermore, for many real-world applications, the problem extends beyond a single agent to involve Multi-Agent Systems (MASs), where challenges like achieving rapid consensus under communication constraints become paramount [6]. Regardless of the domain or the number of agents, effective path planning is fundamental, with Coverage Path Planning (CPP) being a key strategy. The aim of CPP is to find a path to cover as many target areas as possible within a limited time or distance while navigating around obstacles or no-fly zones [7,8,9,10].
While traditional geometric or heuristic methods are effective in simple environments, they often struggle with the complexity and dynamism of real-world scenarios. For instance, recent work on UMV path planning has successfully combined established optimization techniques like ant colony optimization and homotopy methods to solve complex, multi-stage data collection tasks [5]. Such model-based approaches can generate optimal paths under well-defined constraints but often lack the flexibility to adapt to unforeseen environmental changes or learn from experience. Consequently, learning-based approaches, particularly Reinforcement Learning (RL), have emerged as a promising alternative due to their inherent adaptability and ability to operate in model-free settings [11,12,13,14,15,16]. Despite challenges like low sample efficiency and poor convergence, RL is a promising paradigm for path planning. However, as the environment grows larger, general RL algorithms encounter significant challenges, such as state space explosion and inefficient exploration, which motivates the use of more structured approaches like Hierarchical Reinforcement Learning (HRL).
HRL improves efficiency by breaking down complex tasks into more manageable sub-tasks using high-level and low-level policies [17,18,19]. In the context of CPP, this often involves a high-level policy selecting a target region (a subgoal) and a low-level policy navigating to it. A key enabler for this decomposition is a multi-scale observation space, allowing the high-level policy to plan strategically using a global view while the low-level policy executes precisely with a local view. However, a critical challenge in HRL is the generation of effective subgoals. Many HRL frameworks for navigation suffer from the “subgoal space explosion” problem, where the high-level policy must select from a vast space of potential subgoals, leading to inefficient exploration. While it is feasible to use external rewards to supervise subgoal generation [20,21], this does not inherently solve the efficiency issue, especially when data is sparse, as documented in studies on data-efficient HRL [22].
To address the challenge of large action spaces in HRL, two primary strategies have emerged from prior work on action space reduction [23,24,25,26]: enforcing local adjacency constraints and employing global landmark guidance. For instance, Zhang et al. [27] first introduced an adjacency network to confine subgoals to a locally reachable region. Subsequently, Kim et al. [28] developed a landmark-guided framework that leverages global planning to provide long-range exploration direction. While these works provide powerful mechanisms for efficient exploration, they are fundamentally designed for goal-reaching tasks with a predefined, static final goal.
The domain of Coverage Path Planning (CPP), however, presents a distinct set of challenges, most notably the absence of a fixed endpoint and the need to reason about dynamic, area-based objectives. A direct application of prior methods is therefore insufficient. Our primary contribution lies in synthesizing and adapting these concepts for the unique demands of CPP. We propose a framework that not only integrates local feasibility checks with global landmark guidance but, crucially, introduces a dynamic goal generation module to handle the evolving nature of coverage tasks. This allows our agent to reason strategically in an environment where the “goal” is constantly changing.
Our main contributions are summarized as follows:
- We propose an adjacency-constrained framework (ACHMP) with a learned Adjacency Network to enforce local reachability of subgoals. This bridges the gap between the high-level global map and the low-level local map, effectively pruning the high-level action space to prevent invalid exploration.
- We leverage a multi-scale observation space that is inherently suited for HRL, enabling efficient information flow for both strategic global planning and precise local execution.
- We develop a complete landmark-guided framework (HRGL) that integrates our local feasibility mechanism with a dual-strategy global guidance system (coverage-based and target-based sampling), balancing broad exploration with task-oriented efficiency.
- We conduct extensive experiments validating our two-stage approach, demonstrating that our full HRGL framework achieves superior performance in both convergence speed and final coverage rate compared to baseline methods.
The structure of this paper is as follows: Section 2 introduces the fundamental concepts of Hierarchical Reinforcement Learning (HRL), and formally defines the Coverage Path Planning (CPP) problem as a Partially Observable Markov Decision Process (POMDP), detailing the environment representation and the multi-scale observation space. Section 3 elaborates on the Adjacency-Constrained Hierarchical Map Planner (ACHMP) framework, including the learned proxy for local feasibility. Section 4 details the HRGL framework, explaining the dynamic goal generation and strategic landmark sampling. Section 5 outlines the experimental settings and conducts an analysis and ablation study of the results. Finally, Section 6 concludes the paper and provides insights into potential future research directions.
2. Preliminaries and Problem Formulation
In this section, we first introduce the fundamental concepts of Hierarchical Reinforcement Learning (HRL). We then formally define the Coverage Path Planning (CPP) problem as a Partially Observable Markov Decision Process (POMDP), detailing the environment representation and the multi-scale observation space designed to enable effective hierarchical decision-making.
2.1. Hierarchical Reinforcement Learning (HRL)
Standard “flat” RL struggles with long-horizon tasks due to challenges in credit assignment and exploration. HRL addresses this by introducing temporal abstraction, structuring the policy into at least two levels; its structure is shown in Figure 1: a high-level policy (or meta-controller) and a low-level policy (or controller) .
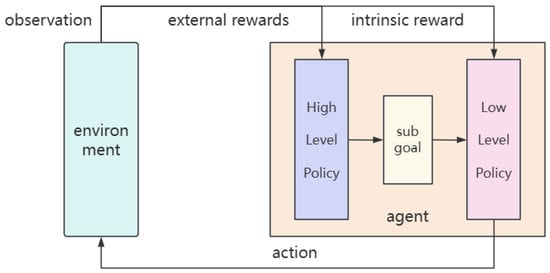
Figure 1.
Hierarchical reinforcement learning framework.
- The High-Level Policy () operates on a slower timescale. At the beginning of a time window, it observes the current state and selects a subgoal . Its objective is to learn a sequence of subgoals that maximizes the cumulative extrinsic reward received from the environment, which reflects overall task progress.
- The Low-Level Policy () operates at every time step. Given the current state and the active subgoal from the meta-controller, it selects a primitive action . The low-level policy is trained to reach the given subgoal efficiently. To facilitate this, it is typically guided by a dense, internally-generated intrinsic reward. A common form of intrinsic reward is the negative distance to the subgoal, such as , where maps a state to its corresponding representation in the goal space.
This hierarchical decomposition allows the agent to reason about problems at different levels of abstraction. The meta-controller focuses on “what to do” (strategic planning), while the controller focuses on “how to do it” (motor control), making the learning process more structured and efficient.
2.2. CPP Problem Formulation
We model the UAV-based CPP task as a Partially Observable Markov Decision Process (POMDP), defined by the tuple . The agent’s true state is not fully available at each time step. Instead, it receives an incomplete observation through the observation function .
2.2.1. Environment Discretization and State-Action Space
To make the problem computationally tractable, we discretize the continuous physical environment into an two-dimensional grid map. Its schematic diagram is shown in Figure 2; each cell in the grid can be assigned one or more of the following attributes:
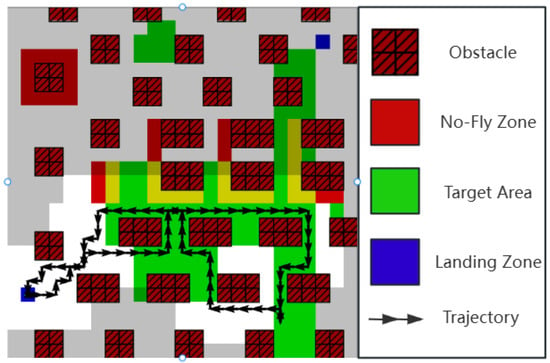
Figure 2.
Task environment description.
- Target Area: A region that needs to be covered by the UAV’s sensor.
- Obstacle: An impassable region that also blocks the sensor’s line of sight.
- No-Fly Zone (NFZ): A region the UAV cannot enter.
- Landing Zone: A designated area for starting and safely concluding the mission.
Based on this discretized environment, we can formally define the agent’s state space and action space .
- State Space (): The true state of the UAV at time t, denoted as , is a tuple, , where:
- -
- is a global map describing the static properties of the environment (obstacles, NFZs, etc.).
- -
- is a dynamic boolean matrix representing the target areas that remain uncovered at time t.
- -
- are the UAV’s coordinates on the grid map.
- -
- is the UAV’s remaining energy or flight time.
- Action Space (): The action space is discrete, comprising the fundamental movement commands the UAV can execute:Each action consumes a certain amount of energy .
This complete state is the theoretical ground truth. In practice, however, the agent does not have perfect information about the entire coverage map and must rely on its sensors. This motivates the design of our observation space.
2.2.2. Multi-Scale Observation Space
To balance the need for detailed local information for navigation and a broad global context for long-term planning, we design a multi-scale observation space . This is achieved by generating two distinct representations from the full world map at each time step: a high-resolution local map and a low-resolution global map. The generation process is detailed below.
- Local Map Generation ()
The local map provides a high-resolution, egocentric view of the agent’s immediate surroundings, essential for the low-level policy’s reactive control and obstacle avoidance. It is generated through the following steps:
- Agent-Centric Cropping: Given the full world map and the UAV’s current coordinates , we perform a crop to extract a fixed-size window centered on . This size l is a hyperparameter that defines the agent’s perceptual range.
- Padding: When the agent is near the boundaries of the world map, the window may extend beyond the defined area. To handle this, we use padding. For obstacle and No-Fly Zone layers, the out-of-bounds area is padded with a value of ‘1’ (impassable), discouraging the agent from leaving the map. For target layers, it is padded with ‘0’ (no target).
The resulting local map, , provides the low-level policy with the precise information needed for fine-grained maneuvering.
- Global Map Generation ()
The global map offers a low-resolution, compressed overview of the entire environment, which is critical for the high-level policy’s strategic, long-term decision-making. It is generated via downsampling:
- Grid-based Pooling: The full world map is divided into non-overlapping blocks of size , where g is the downsampling factor (a hyperparameter).
- Average Pooling: For each block, we compute the average value of all cells within it. This operation creates a new, smaller map of size approximately .
This use of average pooling is deliberate. For an obstacle map, the value in each cell of the resulting global map, , represents the “obstructedness” or density of obstacles in that larger region. For a target map, it represents the density of remaining targets. This compressed summary allows the high-level policy to identify promising, large-scale regions to explore without being overwhelmed by fine details.
Formally, the complete observation at time t is a tuple that aggregates these multi-scale views and the agent’s status:
where the components correspond to the local obstacle, local target, global obstacle, and global target maps, and represents the current battery level. This structured observation is fundamental to our hierarchical approach, providing each policy level with the information it needs to perform its role effectively.
3. Stage One: Grounding Global Strategy with Local Feasibility
Our first stage of optimization directly addresses a fundamental disconnect in applying HRL to CPP: the high-level policy, , and the low-level policy, , operate on different perceptual scales. As established, uses the low-resolution global map () for strategic planning, while relies on the high-resolution local map () for execution. A standard HRL framework lacks a mechanism to ensure that the strategic subgoals from are actually feasible for to achieve in its local context, often leading to wasted exploration.
A naive solution to bridge this gap might be to provide the high-level policy with the same high-resolution local map that the low-level policy sees. However, this would defeat a primary purpose of the hierarchical decomposition. It would drastically increase the dimensionality of the high-level policy’s input, leading to a massive increase in model parameters and computational load, reintroducing the very complexity we sought to avoid.
The core idea of this stage is therefore to ground the high-level policy’s global strategy in local reality without overburdening it with high-dimensional sensory data. We need a lightweight mechanism that can summarize local reachability. This motivates our design of the Adjacency-Constrained Hierarchical Map Planner (ACHMP).
3.1. A Learned Proxy for Local Feasibility
To equip the high-level policy with an understanding of local feasibility without overburdening it with high-dimensional data, we design a mechanism to learn a lightweight, differentiable proxy for reachability. The core of this mechanism is the Adjacency Network, , whose function is illustrated in Figure 3. This approach is inspired by prior work that has demonstrated the effectiveness of using learned networks to approximate state distance [27].
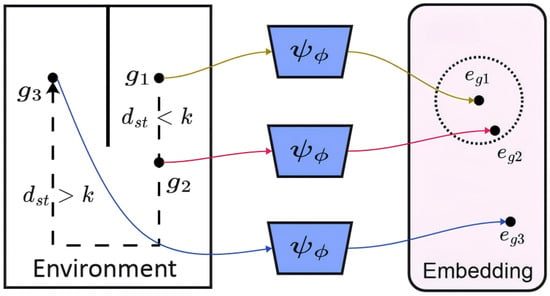
Figure 3.
Function of the adjacency network.
As shown on the left panel of Figure 3, the agent in the “Environment” space must assess the feasibility of reaching various potential subgoals. Simple Euclidean distance is a poor metric here; for instance, subgoal might be far in coordinate terms, while and are close. However, due to obstacles (the solid wall), the true transition distance () tells a different story. Subgoals and are considered “adjacent” to the agent’s current region because they are reachable within a small number of steps (). In contrast, reaching requires a long, complex path, making it “non-adjacent” ().
Our Adjacency Network, , learns to capture this complex relationship. Its function, as depicted in the figure, is to map these goal-space coordinates into a low-dimensional embedding space—the “Adjacency Space”—where geometric distance directly reflects reachability. The network processes each subgoal () and outputs a corresponding embedding vector ().
The network is trained via contrastive learning on online agent trajectories collected during interaction with the environment. States that are close in transition distance (like and relative to the start) form positive pairs. The learning objective pulls their embeddings () close together in the Adjacency Space. Conversely, states that are far in transition distance (like ) form negative pairs, and the objective pushes their embeddings () far apart from the others.
The result is a powerful and efficient proxy for local feasibility. Theoretically, this contrastive learning objective aligns with the principles of metric learning, which aims to learn a distance function that respects the underlying topological structure of the state space. While a formal proof of convergence is beyond the scope of this paper, this learned metric is empirically shown to be a highly effective proxy for the true path cost, as validated by our experiments. By simply calculating the Euclidean distance between embeddings in this new space, the high-level policy can get a reliable estimate of the true transition cost without needing to process the high-resolution local map. This learned metric is the key component we integrate into our ACHMP framework in the following section.
By using this network, we avoid feeding high-dimensional local maps to the high-level policy. Instead, we provide it with a highly compressed, yet deeply informative, signal about local reachability.
3.2. The ACHMP Framework: Integrating the Feasibility Proxy
Our primary contribution in this stage is the Adjacency-Constrained Hierarchical Map Planner (ACHMP), a novel framework designed to enforce local feasibility within the HRL loop. ACHMP integrates the Adjacency Network to create a synergistic coupling between the high-level and low-level policies.
This integration is realized through a soft penalty term, the Adjacency Loss (), which is incorporated into the high-level policy’s objective. This loss function penalizes the choice of a subgoal that is predicted to be unreachable from the current state :
where maps the state to its goal-space representation and is a learned margin.
The total loss for the high-level policy, , is a weighted sum that balances the primary task objective with our proposed feasibility constraint:
where is the main reinforcement learning loss (e.g., from TD-error) and is a balancing coefficient.
This design is highly efficient. The high-level policy can continue to operate on low-dimensional global maps, keeping its parameter count low. The additional computational load comes only from the small Adjacency Network and the simple loss calculation. ACHMP thus effectively guides local exploration and accelerates learning by preventing futile attempts, all while preserving the architectural efficiency of the hierarchical approach. Nonetheless, this focus on local constraints introduces an inherent “myopia”, which we address in the next stage.
4. Stage Two: Global Guidance via Landmark-Driven Exploration
The ACHMP framework, introduced in the previous stage, successfully grounds the high-level policy in local reality. While this accelerates learning, its reliance on local adjacency constraints introduces an inherent “myopia”. The UAV becomes proficient at efficient local exploration but lacks a long-term, global strategy. In complex environments with large obstacles or distant, disjoint target regions, this can lead to the UAV getting trapped in a suboptimal area or failing to discover crucial parts of the map.
To overcome this limitation, our second stage introduces a global guidance mechanism on top of the local feasibility constraints. The core idea is to provide the high-level policy with strategic, long-range “hints” about where to go next. We achieve this by identifying and utilizing a sparse set of informative states, which we call landmarks. The concept of using landmarks to structure the state space for efficient, long-range planning has been effectively demonstrated in universal goal-reaching tasks [29]. Building on this idea, our work introduces a novel approach tailored specifically for CPP, utilizing two parallel sampling strategies—coverage-based and target-based—to generate task-relevant landmarks. This leads to our complete framework: Hierarchical Reinforcement Learning Guided by Landmarks (HRGL).
4.1. Strategic Landmark Sampling
Landmarks are states that are particularly valuable for guiding exploration. Instead of treating all states equally, we sample a small, diverse set of landmarks that serve two strategic purposes: ensuring comprehensive exploration and prioritizing task-relevant areas. To this end, we propose two parallel sampling strategies.
- Coverage-Based Landmark Sampling
To ensure the UAV explores the entire reachable state space, we need landmarks that represent the “frontiers” of exploration. We use Farthest Point Sampling (FPS) on the state space visited by the UAV so far. This iterative method selects a set of states that are maximally distant from each other in the learned adjacency space, effectively creating a “skeleton” of the explored environment. These landmarks encourage the high-level policy to push into novel, under-explored regions.
- Target-Based Landmark Sampling
While coverage-based sampling ensures the UAV explores broadly, it is task-agnostic. To accelerate the completion of the CPP objective, we need a mechanism that provides proactive guidance towards high-value, uncovered target areas. Our target-based landmark sampling strategy is designed precisely for this purpose. The core idea is to prioritize states not just by their location within a target area, but by their “novelty”. A novel state within a target region represents a part of the task that is both important and underexplored, making it a high-priority candidate for exploration.
To quantify this novelty, we employ Random Network Distillation (RND) [30]. RND uses two neural networks: a fixed “target network” and a trainable “predictor network”. The prediction error between them serves as a novelty score. The implementation involves a dynamically maintained priority queue:
- Maintaining a Priority Queue: We maintain a fixed-size priority queue, , which exclusively stores states located within currently uncovered target zones. The priority of each state is its RND novelty score.
- Dynamic Updates: Whenever the UAV visits a new target state, we compute its novelty. If the queue is not full, or if the new state’s score is higher than the lowest in the queue, it is added. This ensures always contains the most “promising” recently encountered target states.
- Sampling Landmarks: The target-based landmarks, , are then sampled from the top entries of this priority queue.
This strategy actively guides the UAV towards the specific parts of the target area where its knowledge is most limited, allowing it to “fill in the gaps” efficiently.
4.2. The HRGL Framework: Integrating Global Guidance with a Dynamic Goal
The HRGL framework integrates these landmarks into the high-level policy’s decision-making. A critical challenge in CPP, however, distinguishes it from standard goal-conditioned tasks: there is no single, predefined “final goal”. Our framework addresses this by dynamically generating a temporary final goal at each planning step, representing the most pressing coverage need.
Dynamic Goal Generation. To provide a concrete target for our high-level planner, we introduce a Dynamic Goal Generation module. Instead of identifying a single target, this module generates a list of potential goal candidates from all uncovered areas, allowing for more flexible and strategic long-term planning. The process is as follows:
- Identify Uncovered Regions: The module takes the low-resolution global target map, , as input and binarizes it.
- Find All Connected Components: It then applies a Connected-Component Labeling (CCL) algorithm (e.g., BFS) to group all adjacent uncovered cells into a set of distinct, disjoint regions.
- Generate a List of Candidate Goals: The geometric centroid is calculated for each identified component. This procedure results in a list of candidate goals (), where each candidate represents the “center of mass” of a significant, yet-to-be-covered region.
- Select the Dynamic Final Goal: From this list of candidates , a single dynamic final goal, , is selected for the current planning episode. The selection of the final goal heuristic involves a critical trade-off. Choosing the centroid of the largest uncovered component (the strategy adopted in this work) prioritizes tackling the most significant coverage gap, which can lead to higher global efficiency over the long term. An alternative heuristic, such as choosing the component closest to the agent’s current position, would minimize short-term travel cost. However, this greedy approach risks trapping the agent in local exploration, potentially causing it to neglect more important but distant target areas. Our choice therefore reflects a bias towards a more globally-aware, strategic planning approach.
This procedural approach provides a stable and task-relevant target, directing the UAV towards the “center of mass” of the biggest or most strategically important outstanding problem.
- Graph-Based Path to the Dynamic Goal
With this dynamic goal defined, we perform high-level planning. We construct a graph where nodes are the UAV’s current state, all landmarks, and . Edges are weighted by the distance from our Adjacency Network. A shortest path algorithm is run to find the optimal path from the current state to the dynamic goal.
- Landmark-Guided Subgoal Generation
The high-level policy’s objective is to make progress towards the first landmark, , on this optimal path. To translate this directional guidance into a subgoal, we adopt a “pseudo-landmark” approach [28]. We define a pseudo-landmark, , as a point a short step from the current state in the direction of . The policy is encouraged to generate a subgoal close to this point via a Landmark Loss:
The final objective for the HRGL high-level policy combines all three components:
where is a new coefficient. The HRGL framework thus creates a powerful synergy: global guidance from landmarks provides a long-term vision, while local adjacency constraints ensure immediate actions are feasible and efficient.
5. Experiments
In this section, we present a comprehensive empirical evaluation designed to progressively validate our two-stage methodology. We first analyze the effectiveness of the local constraints in our Stage One framework, ACHMP. We then demonstrate how our complete Stage Two framework, HRGL, leverages global guidance to achieve superior performance, followed by ablation studies to dissect the contributions of its core components.
5.1. Experimental Setup
Our evaluation strategy is designed to progressively validate our two-stage methodology. We conducted experiments in two groups of different grid world environments as shown in the Figure 4 for this purpose. The ‘Urban Area’ and ‘Industrial Area’ serve as the primary environments for the initial validation of our Stage One (ACHMP) framework. Subsequently, the more complex ‘Mahan Area’ and ‘Metropolis Area’ are used for a test of our complete Stage Two (HRGL) model, comparing it against both the baseline and the Stage One results.
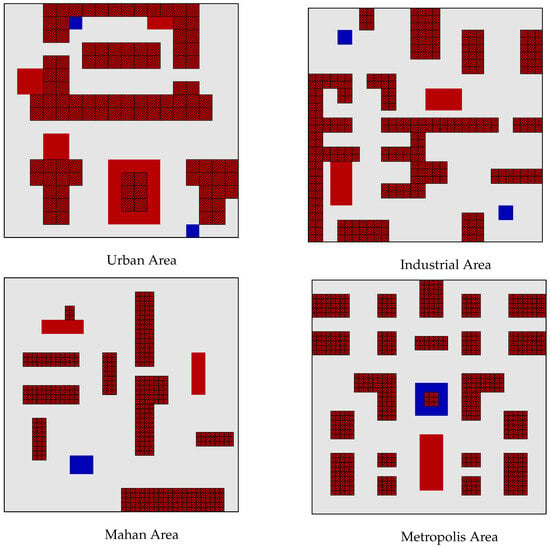
Figure 4.
Two groups of environmental maps.
To conduct this comparison, we evaluate three algorithms: a standard HRL baseline, our Stage One ACHMP framework, and our complete HRGL model. For a fair and reproducible comparison, all algorithms are built upon a common foundation. Both the high-level and low-level policies within our hierarchical structure are implemented as Double Deep Q-Network (DDQN) agents, with Q-networks constructed as multi-layer perceptrons (MLPs). Key hyperparameters were tuned and kept consistent across all applicable algorithms. The high-level policy operates at a frequency of low-level steps.
All experiments were conducted on a workstation equipped with an NVIDIA RTX 3090 Ti GPU. The primary evaluation metric is the Coverage Rate (CR), and we report the average performance over multiple random seeds to ensure statistical significance. We also use qualitative trajectory visualizations to analyze the UAV’s behavior.
5.2. Performance Evaluation and Analysis
- Stage One: Validating the Effectiveness of Local Constraints
A qualitative analysis of the UAV’s flight paths, presented in Figure 5, offers initial insights. In the ‘Urban’ and ‘Industrial’ environments, the trajectories generated by ACHMP are visibly economical, exhibiting a reduction in unnecessary hovering and sharp turns. This suggests that the resulting path planning is of a high quality, enabling safe and efficient coverage.
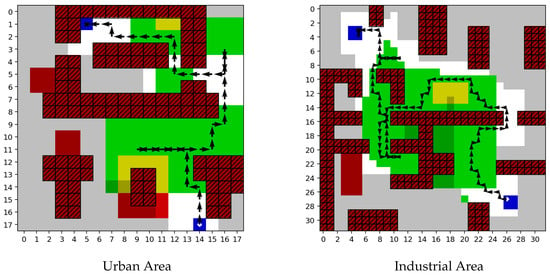
Figure 5.
Algorithm results presentation.
The performance gap between the ACHMP and the baseline HRL algorithms is illustrated in Figure 6. In both environments, ACHMP significantly outperforms the HRL baseline in terms of both final coverage rate and convergence speed. This confirms that enforcing local feasibility via the adjacency constraint is a highly effective mechanism for improving HRL performance and efficiency.
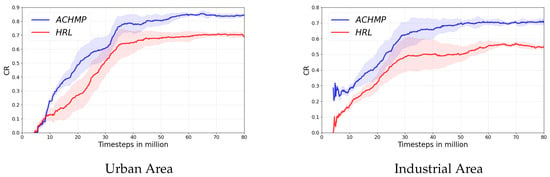
Figure 6.
Algorithm performance presentation.
- Stage Two: Demonstrating the Superiority of Global Guidance
In the more challenging ‘Mahan’ and ‘Metropolis’ environments, the strategic differences become even more apparent. Figure 7 visualizes the exploration differences in the ’Mahan Area’, where the path of the HRL baseline is prone to local wandering. In contrast, HRGL’s path demonstrates clear, long-range strategic movements towards distant, uncovered areas. The UAV appears to possess a stronger global awareness, overcoming the limitations of a purely local field of view.
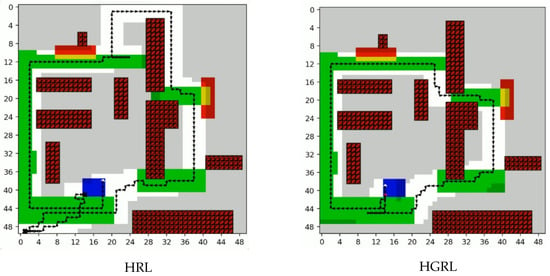
Figure 7.
Exploration differences among different algorithms.
As shown in Figure 8, the quantitative results confirm this qualitative assessment. HRGL achieves a dramatically superior final coverage rate and learns substantially faster than the baseline methods. Its robust performance across these complex maps highlights the necessity of its landmark-based global guidance mechanism for solving large-scale CPP tasks and demonstrates its strong generalization capabilities.
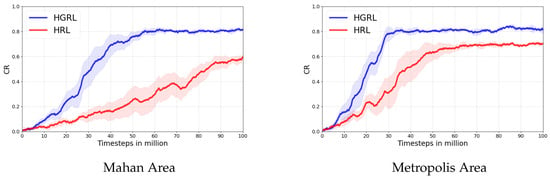
Figure 8.
Performance differences of algorithms on different maps.
5.3. Final Performance Evaluation
To comprehensively evaluate the performance and generalization capabilities of the algorithms, we conducted final tests in two distinct environments: the standard ‘Urban Area’ (18 × 18) and the larger, more challenging ‘Mahan Area’ (50 × 50). The quantitative results of the final trained policies are summarized in Table 1 and Table 2, while the learning process itself is visualized in Figure 9.

Table 1.
Performance evaluation on the Urban Area (18 × 18) map. Metrics are averaged over multiple evaluation runs after 1 million training steps. The best result in each category is highlighted in bold.

Table 2.
Performance evaluation on the more challenging Mahan Area (50 × 50) map. Note that a 55% coverage milestone is used here to assess the fundamental exploration capability in this complex environment.
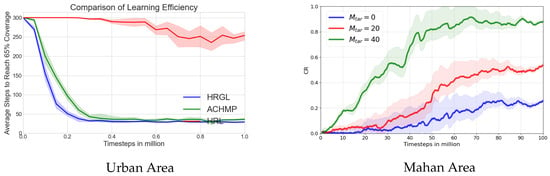
Figure 9.
Performance curve(s) over training.
Performance in the Urban Area: As shown in Table 1, on the relatively simpler Urban Area map, all methods demonstrate a reasonable ability to perform the task. We used a 65% coverage milestone to assess efficiency. Our HRGL method achieves the highest final coverage rate (87.5%) and is the most efficient, requiring only 29 steps to reach the 65% milestone. The learning curves in Figure 9a visually corroborate this finding. The curve for HRGL (blue) shows a significantly steeper descent than its counterparts, indicating a much faster learning speed. It quickly converges to a superior and more stable performance level, as evidenced by its narrow confidence interval.
Performance in the Challenging Mahan Area: The performance gap between the algorithms becomes significantly amplified in the more complex Mahan Area, as detailed in Table 2. Here, we adopted a more fundamental 55% coverage milestone to assess core exploration capabilities. The final coverage rate of the HRL baseline drops sharply to 58.2%, and its arrival rate at the 55% milestone is only 65.0%, highlighting its unreliability in complex scenarios. In contrast, both ACHMP and HRGL maintain 100% reliability.
Most critically, the efficiency metrics reveal a stark difference. HRGL requires only 99 steps to reach the milestone, making it nearly twice as fast as ACHMP (191 steps) and far superior to the HRL baseline (261 steps). This quantitative superiority is vividly illustrated by the learning curves in Figure 9b. The HRL baseline’s curve remains flat at the maximum step count for the vast majority of the training, only beginning to learn very late in the process. This demonstrates a critical failure in exploration. Conversely, the HRGL curve showcases rapid and consistent learning from the early stages, converging to a highly efficient policy.
Overall Analysis: The combined results from both the tables and learning curves provide a consistent and compelling narrative. The quantitative data in the tables offers precise final performance metrics, while the learning curves provide a dynamic view of the learning process, highlighting differences in sample efficiency and stability. Together, they demonstrate that our HRGL framework is superior across all key dimensions: final task effectiveness, learning speed, execution efficiency, and robust generalization to environments of varying complexity.
5.4. Ablation Studies
To understand the internal mechanics of our frameworks, we conducted targeted ablation studies.
- Impact of the Adjacency Constraint Strength
We first analyzed the sensitivity of our framework to the adjacency loss coefficient, . As illustrated in Figure 10, the results show a strong correlation between the value of and overall performance. A well-chosen, non-zero leads to faster training and a higher final coverage rate, confirming that the adjacency constraint is not just a passive component but an influential guidance signal whose strength is critical to the model’s success.
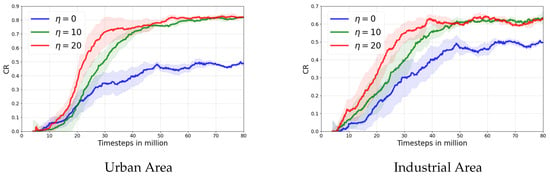
Figure 10.
Impact of adjacency loss coefficient.
- Impact of Landmark Sampling Strategies
Next, we dissected the HRGL framework by evaluating the roles of our two landmark sampling strategies. Figure 11 presents the results of this study, comparing the full model against variants with each sampling strategy individually removed. The findings indicate that both are essential and complementary.
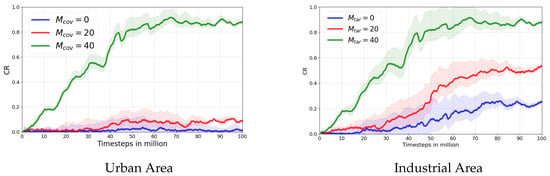
Figure 11.
The impact of landmark quantity on algorithm performance.
- Coverage-based landmarks were found to be critical for establishing broad spatial awareness. The algorithm’s performance degraded noticeably when they were removed, underscoring their importance for building a “skeleton” of the explorable space.
- Target-based landmarks were shown to significantly boost performance by focusing the UAV’s exploration on task-relevant regions. They are responsible for efficiently “filling in the gaps” to complete the coverage task.
The superior performance of the full model validates our dual-strategy approach, which effectively balances broad exploration with goal-directed refinement.
6. Conclusions
In this paper, we addressed the critical challenge of inefficient subgoal generation in Hierarchical Reinforcement Learning (HRL) for Coverage Path Planning (CPP). We proposed a two-stage framework, Hierarchical Reinforcement Learning Guided by Landmarks (HRGL), which systematically improves exploration by grounding high-level strategy in local reality. The framework leverages a multi-scale observation space and introduces two key innovations: (1) the Adjacency-Constrained Hierarchical Map Planner (ACHMP), which uses a learned Adjacency Network to enforce local feasibility, and (2) a landmark-guided global exploration mechanism, which uses dual-strategy sampling to provide long-term strategic direction. Extensive experiments confirmed that our HRGL framework significantly outperforms baseline methods in both convergence speed and final coverage rate.
This work opens several avenues for future research. Key directions include (1) enhancing the core mechanisms with more adaptive landmark management and richer adjacency models; (2) extending the framework to multi-agent systems for collaborative coverage, which would require integration with robust control protocols to manage coordination and communication constraints; (3) incorporating multi-objective optimization to balance coverage with real-world constraints like energy consumption and path smoothness; and (4) validating the framework in high-fidelity continuous environments (e.g., Gazebo) and conducting comprehensive benchmarks against other state-of-the-art HRL methods such as HIRO and HAC. Further theoretical analysis of the framework’s convergence properties would also be a valuable contribution. By pursuing these directions, this research provides a solid foundation for developing more intelligent and efficient autonomous systems for complex real-world planning tasks.
Author Contributions
Conceptualization, Z.L. and K.D.; methodology, Z.L.; software, Z.L.; validation, K.D., Z.L. and Y.Z.; formal analysis, Y.Z.; investigation, Y.Z.; supervision, Y.Z.; funding acquisition, K.D. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 6250021280).
Data Availability Statement
The data used in this study are not available due to technical limitations.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Soroush, N.; Vitchyr, P.; Steven, L.; Sergey, L. Planning with goal-conditioned policies. Adv. Neural Inf. Process. Syst. 2019, 32, 2076–2084. [Google Scholar]
- Eysenbach, B.; Salakhutdinov, R.R.; Levine, S. Search on the replay buffer: Bridging planning and reinforcement learning. Adv. Neural Inf. Process. Syst. 2019, 32, 363–386. [Google Scholar]
- Sipra, S.; Mohan, K.P.; Ranjan, S.B. An efficient path planning algorithm for 2D ground area coverage using multi-UAV. Wirel. Pers. Commun. 2023, 132, 361–407. [Google Scholar] [CrossRef]
- Wu, X.-J.; Xu, L.; Zhen, R.; Wu, X.-L. Global and local moth-flame optimization algorithm for UAV formation path planning under multi-constraints. Int. J. Control Autom. Syst. 2023, 21, 1032–1047. [Google Scholar]
- Yang, Z.; Fu, J.; Sun, Y.; Li, Y. A Pseudo-Trajectory Homotopy Method for UMVs Information Collection IoT System With an Underwater Communication Constraint. IEEE Internet Things J. 2025, 1, 1–16. [Google Scholar] [CrossRef]
- Li, M.; Zhang, K.; Liu, Y.; Song, F.; Li, T. Prescribed-Time Consensus of Nonlinear Multi-Agent Systems by Dynamic Event-Triggered and Self-Triggered Protocol. IEEE Trans. Autom. Sci. Eng. 2025, 22, 16768–16779. [Google Scholar] [CrossRef]
- Mourtzis, D.; Angelopoulos, J.; Panopoulos, N. Unmanned Aerial Vehicle (UAV) path planning and control assisted by Augmented Reality (AR): The case of indoor drones. Int. J. Prod. Res. 2024, 62, 3361–3382. [Google Scholar] [CrossRef]
- Rocha Lidia, G.S.; Kim Pedro, H.C.; Vivaldini, T.; Kelen, C. Performance analysis of path planning techniques for autonomous robots: A deep path planning analysis in 2D environments. Int. J. Intell. Robot. Appl. 2023, 7, 778–794. [Google Scholar] [CrossRef]
- Zhao, S.; Leng, Y.; Zhao, M.; Wang, K.; Zeng, J. Erratum: A Novel Dynamic Lane-Changing Trajectory Planning for Autonomous Vehicles Based on Improved APF and RRT Algorithm. Int. J. Automot. Technol. 2024, 26, 593. [Google Scholar] [CrossRef]
- Ni, J.; Gu, Y.; Gu, Y.; Zhao, Y.; Shi, P. UAV coverage path planning with limited battery energy based on improved deep double Q-network. Int. J. Control Autom. Syst. 2024, 22, 2591–2601. [Google Scholar] [CrossRef]
- Matsuo, Y.; Lecun, Y.; Maneesh, S.; Precup, D.; Silver, D.; Sugiyama, M.; Uchibe, E. Deep learning, reinforcement learning, and world models. Neural Netw. 2022, 152, 267–275. [Google Scholar] [PubMed]
- Benjamin, J.; Jouaneh, M. Building an Educational Automated Mechatronics-Based Sorting System. Automation 2024, 5, 297–309. [Google Scholar] [CrossRef]
- Huthaifa, A.; Taqwa, A.; Mohammed, E.; Nour, K. Leveraging Multimodal Large Language Models (MLLMs) for Enhanced Object Detection and Scene Understanding in Thermal Images for Autonomous Driving Systems. Automation 2024, 5, 508–526. [Google Scholar] [CrossRef]
- Ricky, L.M.-F.; Hassen, Y.S. Mobile robot navigation using deep reinforcement learning. Processes 2022, 10, 2748. [Google Scholar] [CrossRef]
- Fernandez-Figueroa, E.G.; Rogers, S.R.; Neupane, D. Drones and Deep Learning for Detecting Fish Carcasses During Fish Kills. Drones 2025, 9, 482. [Google Scholar] [CrossRef]
- Kim, K.; Park, J.; Kim, J. Optimized Area Partitioning for Cooperative Underwater Search Using Multiple Autonomous Underwater Vehicles. Int. J. Control Autom. Syst. 2025, 23, 392–404. [Google Scholar]
- Li, S.; Wang, R.; Tang, M.; Zhang, C. Hierarchical reinforcement learning with 508 advantage-based auxiliary rewards. Adv. Neural Inf. Process. Syst. 2019, 50, 1209–1228. [Google Scholar]
- Nuksit, N.; Siriwattana, K.; Chantranuwathana, S.; Phanomchoeng, G. The Development of Teleoperated Driving to Cooperate with the Autonomous Driving Experience. Automation 2025, 6, 26–36. [Google Scholar] [CrossRef]
- Shubham, P.; Budhitama, S.; Ah-hwee, T.; Chai, Q. Hierarchical reinforcement learning: A comprehensive survey. ACM Comput. Surv. (CSUR) 2021, 54, 109. [Google Scholar]
- Li, Y.; Lv, R.; Wang, J. A Control Strategy for Autonomous Approaching and Coordinated Landing of UAV and USV. Drones 2025, 9, 340–367. [Google Scholar] [CrossRef]
- Li, L.; He, F.; Fan, R.; Fan, B.; Yan, X. 3D reconstruction based on hierarchical reinforcement learning with transferability. Integr. Comput.-Aided Eng. 2023, 30, 327–339. [Google Scholar] [CrossRef]
- Nachum, O.; Gu, S.; Lee, H. Levine Sergey, Data-efficient hierarchical reinforcement learning. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 3307–3317. [Google Scholar]
- Nat, D.; Christos, K.; Nick, P.; Murray, S. Feature control as intrinsic motivation for hierarchical reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3409–3418. [Google Scholar]
- Dibya, G.; Abhishek, G.; Sergey, L. Learning actionable representations with goal-conditioned policies. arXiv 2018, arXiv:1811.07819, 2018. [Google Scholar]
- Lee, H.-Y.; Zhou, P.; Zhang, B.; Qiu, L.; Fan, B.; Duan, A.; Tang, J.; Lam, T.L.; Navarro-Alarcon, D. A Distributed Dynamic Framework to Allocate Collaborative Tasks Based on Capability Matching in Heterogeneous Multirobot Systems. IEEE Trans. Cogn. Dev. Syst. 2023, 16, 251–265. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, Y.; Zhao, D.; Liu, B.; Lai, Z.; Chen, J. CNN-G: Convolutional neural network combined with graph for image segmentation with theoretical analysis. IEEE Trans. Cogn. Dev. Syst. 2020, 13, 631–644. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, S.; Tan, T.; Hu, X.; Chen, F. Generating adjacency-constrained subgoals in hierarchical reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 21579–21590. [Google Scholar]
- Kim, J.; Seo, Y.; Shin, J. Landmark-guided subgoal generation in hierarchical reinforcement learning. Adv. Neural Inf. Process. Syst. 2021, 34, 28336–28349. [Google Scholar]
- Huang, Z.; Liu, F.; Su, H. Mapping state space using landmarks for universal goal reaching. Adv. Neural Inf. Process. Syst. 2019, 32, 1942–1952. [Google Scholar]
- Yuri, B.; Harrison, E.; Amos, S.; Oleg, K. Exploration by random network distillation. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).